Functional Properties of Threefold and Fourfold Channels in Ferritin Deduced from Electrostatic Calculations (original) (raw)
Abstract
The iron storage protein ferritin contains threefold and fourfold symmetric channels that are thought to provide pathways for the transfer of Fe2+ ions in and out of the protein. Using the known crystal structure of the ferritin protein, we perform electrostatic potential energy calculations to elucidate the functional properties of these channels. The threefold channel is shown to be responsible for the transit of Fe2+ ions. Monovalent ions can also diffuse through the threefold channel but presence of divalent ions in the pore retards this process leading to a selectivity mechanism similar to the one observed in calcium channels. The fourfold channel is found to be impermeant to all cations with the possible exception of protons. Because proton transfer is essential to maintain the electroneutrality of the protein during iron deposition, we suggest that the function of the fourfold channel is to form a “proton wire” that facilitates their transfer in and out of ferritin.
INTRODUCTION
Iron is found in many enzymes and plays a significant role in some biological processes, for example, oxygen transport in hemoglobin and oxidation of hemoproteins. Because iron is toxic, its concentration in the body needs to be controlled tightly. In animals, plants, and prokaryotes, this control is maintained by ferritins—proteins that store iron reversibly in a hydrated iron oxide form (Harrison and Arosio, 1996). The crystal structure of ferritin has been determined in a number of species, e.g., human (Lawson et al., 1991), frog (Trikha et al., 1994), horse (Michaux et al., 1996), and Escherichia coli (Stillman et al., 2001). Although the primary sequences of ferritin show significant differences among species, their three-dimensional conformations are found to be strikingly similar in all cases studied. All ferritin molecules are made of 24 identical peptide subunits that fold into a spherical shell with a water filled cavity inside. This cavity is connected to outside through channels with threefold and fourfold symmetry that are thought to provide permeation pathways for iron ions and protons, essential for proper functioning of ferritin as an iron depository.
The threefold channels are hydrophilic, being lined with six negatively charged residues (Asp-131 and Glu-134) near the center of the channel. The crystal structure of ferritin shows that three Cd2+ ions can occupy this region indicating the presence of a strong binding site for divalent ions in the center of the pore (Hempstead et al., 1997). The Asp-131 and Glu-134 residues are highly conserved in all mammalian ferritins, and their mutation were shown to slow down the rates of iron uptake (Treffry et al., 1993; Levi et al., 1996). Thus there is direct experimental evidence that the threefold channels are involved in uptake of iron ions. Kinetic studies of permeation using small nitroxide spin probes also confirm the role of these channels as providing a charge-selective pathway for entry into the cavity (Yang et al., 2000). In contrast, the fourfold channels are lined with hydrophobic residues, and their role in the iron deposition process is less clear. Nevertheless, mutation of the amino acid residues lining the fourfold channels destabilizes the assembly of 24 subunits and thereby interferes with the function of ferritin forming a stable iron depository (Levi et al., 1988). Thus the fourfold channels also appear to play an important role in the iron uptake process.
Despite the availability of the crystal structure for over a decade, there have been very few model studies of the functional properties of ferritins. In one recent study, Douglas and Ripoll (1998) calculated the electrostatic potential in ferritin using the Poisson-Boltzmann equation. The potential gradients near the threefold channel entrances are found to be directed toward the cavity and those near the fourfold channels are directed in the opposite direction. This was interpreted as evidence that the threefold channels provide a pathway for entry of cations, and the fourfold channels are used in expelling cations from the cavity. Even though entry to the channels is part of the permeation process and this study provides some useful insights in this regard, to understand the complete permeation mechanism, one needs to consider multi-ion potential energy profiles in the channel. Such studies have been recently carried out for potassium (Chung et al., 1999, 2002) and calcium (Corry et al., 2001) channels, and revealed the importance of Coulomb repulsion among multiple ions in enabling ion transport across deep binding pockets. Of particular relevance for ferritin is the blocking of the calcium channel to Na+ permeation in the presence of a Ca2+ ion in the pore. Like calcium, iron concentration in the bulk solution is much smaller than that of sodium, and some selectivity mechanism that prevents free entry of Na+ ions into the cavity may be important for an efficient functioning of ferritin as an iron depository.
Classical electrostatics has been shown to play a vital role in understanding the interactions and thereby the functional properties of proteins (Davis and McCammon, 1990; Sharp and Honig, 1990; Warshel and Åqvist, 1991; Nakamura, 1996). Similar methods have been used to study the permeation properties of membrane channels (Partenskii and Jordan, 1992; Eisenberg, 1999; Roux et al., 2000; Kuyucak et al., 2001; Tieleman et al., 2001). Here we attempt to explain the functional roles of the two types of channels in ferritin through such calculations. Specifically, we construct multi-ion potential energy profiles for monovalent and divalent cations as well as their mixtures and infer the permeation characteristics of the threefold and fourfold channels from these profiles. Recently, metal ion storage capacity of ferritin molecules has been exploited to construct nano-dot arrays suitable for fabrication of quantum electronic devices (Takeda et al., 1995; Yamashita, 2001). Thus understanding and control of the ion transport properties of ferritin may have far reaching applications in electronics industry as well as in biology.
METHODS
Ferritin structure
Atomic coordinates of horse L-chain ferritin is taken from the Protein Data Bank (accession code: 1AEW). The 1AEW data set lacks the oxygen coordinate at C-terminal residue, which is generated assuming a symmetrical structure for the backbone. The structure of D131A-E134A mutant is constructed from that of the wild type by making the appropriate substitutions.
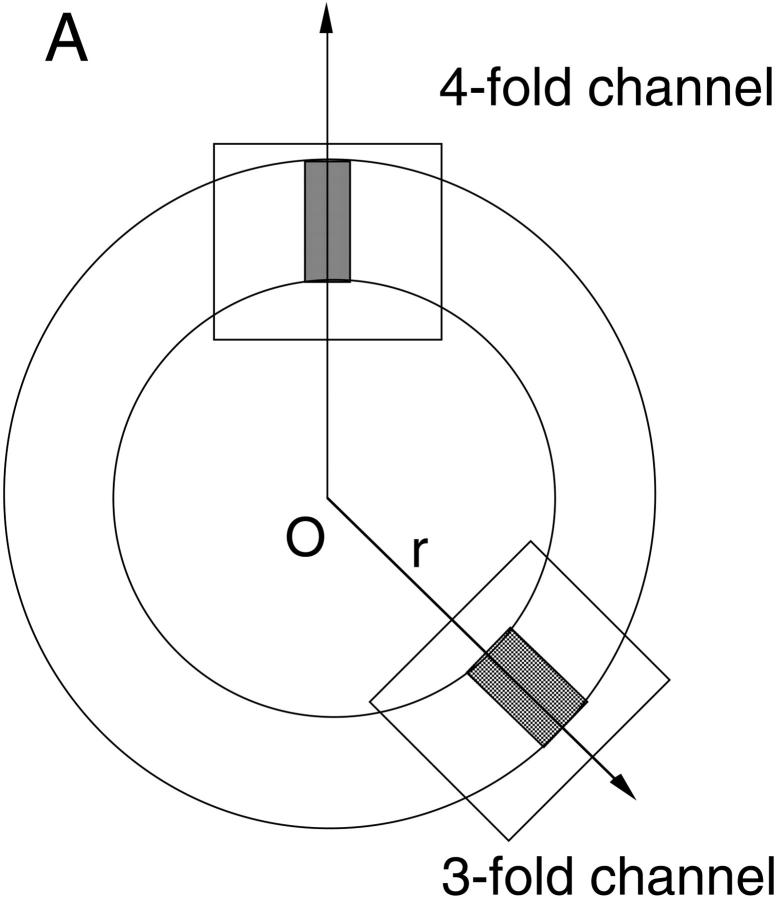
A schematic cross section of the ferritin molecule is shown in Fig. 1 A. The radius of the cavity is ∼40 Å, and the external radius of the ferritin molecule is roughly 60 Å. As indicated by the shaded areas in the figure, the cavity is connected to outside through two types of channels having threefold and fourfold symmetries. The former are located at the corners of a cube so there are eight of them, whereas six of the fourfold channels are located at the faces of this cube. More detailed structures of the threefold and fourfold channels along their central axis are shown in Fig. 1, B and C. Here the solvent accessible boundary is determined by tracing a water molecule of radius 1.4 Å over the protein walls. This boundary is employed in the solution of the Poisson equation. The threefold channel is lined with hydrophilic residues such as His-118, Asp-131, Glu-134, His-136, and Asp-139 (Fig. 1 B). Six carboxyl groups from Asp-131 and Glu-134 help to form three divalent cation binding sites near the center of the pore, whose positions as seen in the x-ray structure are indicated by circles containing 2+. Two more binding sites have been observed further down the channel at considerable distances from the central axis. One is near the Asp-139 residues. The other is formed by Asp-42 and Glu-49 residues and lies just outside the channel (in the cavity) . The fourfold channel, on the other hand, is hydrophobic being surrounded by 16 residues of Leu-165, 169, 173, and Gln-162, as shown in Fig. 1 C. No ion binding sites have been seen in the fourfold channels.
FIGURE 1.
(A) A schematic cross section of horse L-chain ferritin molecule. The threefold and fourfold channels are indicated by the shaded areas, whose detailed structures are shown in B and C, respectively. The locations of the glutamate and aspartate residues are indicated by black circles, histidine by gray circles, and leucine and glutamine by white circles. Circles with a 2+ in the solvent region indicate the binding sites for divalent cations as observed in the x-ray structure. The shaded areas show the solvent accessible pore region. The Poisson equation is solved for ions within these regions, and the Poisson-Boltzmann equation with an ionic strength of 0.1 M is solved outside.
Each subunit of ferritin molecule contains 26 acidic (11 Asp and 15 Glu) and 24 basic (11 Arg, 8 Lys, and 5 His) residues. In addition, there are polar Tyr and Cys residues in the subunits. But because these are neutral at normal pH, they are not considered in the electrostatic calculations. When all the ionizable residues are fully charged, each subunit carries a net charge of −2_e_. This charge state is shown to be inconsistent with the observed binding sites and the mutation data. Therefore, a more careful consideration of the ionization state of the histidine residues is required in model studies of ferritin.
Electrostatic calculations
Ferritin is a fairly large molecule and the transport rate of ions appears to be slower compared to those in ion channels. Thus a straightforward molecular dynamics simulation of the protein-solvent system is not likely to yield much information on the functional properties of ferritin. Therefore we use continuum electrostatics for this purpose. Specifically, we calculate the electrostatic free energy required to transport ions across the two types of channels in ferritin.
The pore regions of the threefold and fourfold channels are quite narrow having a radius of a few Å. Solution of the Poisson equation for a test ion in narrow pores shows that the ion faces a substantial potential energy barrier arising from the induced image charges on the boundary (i.e., dielectric self-energy) (Levitt, 1978; Jordan, 1982; Åqvist and Warshel, 1989). This energy barrier is sufficient to prevent the entry of either cations or anions into the pore. The negative charges on the walls of the threefold channel provide strong enough attraction for cations to cancel the self-energy barrier whereas the opposite happens for the anions and the energy barrier they face is reinforced. Under these conditions, anions cannot enter the pore and there is no possibility for a test cation in the pore to be shielded by counterions. However, when the Poisson-Boltzmann (PB) is used in this situation, it still predicts shielding of the test ion because the smeared out counterion density does not feel the full effect of the repulsive image forces. This intuitive picture has been confirmed quantitatively in a recent comparison of the PB theory with the Brownian dynamics simulations (Moy et al., 2000). To avoid this spurious shielding effect in the PB equation, we solve directly the Poisson equation in the pore region using discrete charges for cations. These regions extend from r = 42–58 Å in the threefold channel, and r = 40–60 Å in the fourfold channel, as indicated by the shaded areas in Fig. 1, B and C. Outside these regions, the linear PB equation is solved with _κ_−1 = 10 Å, which is the appropriate value for a 100 mM electrolyte solution. Because the potential quickly vanishes outside the pore region, the use of the linear PB equation there is justified.
In the initial calculations, all the ionizable acidic and basic residues in the molecular structure of ferritin are assumed to be fully charged. As this charge state fails to reproduce the data, the histidine residues are taken as neutral in the subsequent calculations. The dielectric constant of the protein is set to _ɛ_p = 5, which appears to be a more appropriate value for proteins than the typical hydrocarbon value of 2 (Nakamura, 1996; Schutz and Warshel, 2001). The effect of using different _ɛ_p values on the results of the hydrophobic fourfold channel is discussed further below. The bulk value of _ɛ_w = 80 is employed for the dielectric constant of water throughout, including the pore region. This appears to be a reasonable choice for the threefold channel, which is formed by wide vestibules and has only a short neck region (Fig. 1 B). But it is harder to justify the use of _ɛ_w = 80 for the fourfold channel because it remains narrow for the whole length of the channel (Fig. 1 C). This issue will also be discussed further in the Results section.
Modeling of the binding sites that are far from the central axis of the channel creates problems in electrostatic calculations. Such a situation occurs in the threefold channel when the His-136 residues are taken as neutral, which is necessary to reproduce the observed binding sites near the Asp-139 residues (Fig. 1 B). When electrostatic calculations with divalent ions are performed, the energy minimum corresponding to the Asp-139 binding site occurs at the pore axis, not at the observed binding site far off the axis. We avoid this unrealistic situation by placing three charges with magnitude 2_e_/3 near the Asp-139 residues which mimic the effect of one divalent cation bound at one of the three sites as observed in the x-ray structure. These fixed charges are retained in all the calculations involving the threefold channels where the histidine residues are taken as neutral. Similarly a divalent cation is placed at each binding site associated with the Asp-42 and Glu-49 residues. These charges simply help to maintain electroneutrality in the cavity, which would have a net charge −48_e_ otherwise. They are sufficiently far from the channel and do not have much influence on the calculated potential energy profiles.
The Poisson and linear PB equations are solved using a finite difference method as detailed elsewhere (Nakamura and Nishida, 1987; Takahashi et al., 1993). In initial test runs, the grid size is varied from 2, 1, 0.5, to 0.25 Å. Sufficient convergence in potential profiles is obtained for the grid size of 0.5 Å, which is adopted in the rest of the calculations. We use kT at room temperature (T = 298 K) for an energy unit, which is related to the SI units by 1 kT = 4.11 × 10−21 J. The calculations were carried out on the supercomputers NEC SX5, SGI2800, and SGI ORIGIN server in the Okazaki National Research Institute.
RESULTS AND DISCUSSION
In the following, we solve the Poisson and PB equations for a given configuration of fixed charges in the protein and a number of ions in the channel, and calculate the potential energy of a test ion as it is moved along the channel axis in steps of 0.5 Å. For a single ion, this procedure simply yields the potential energy profile of the ion. In the case of two ions—one is resident in the channel and the other (test ion) is brought into the channel in small (0.5 Å) steps—the potential energy of the resident ion is minimized at each new position of the test ion before calculating its potential energy. Thus the calculated electrostatic free energy corresponds to the work required to push the test ion into the channel. To obtain a complete profile, the test ion is brought into the channel both from outside the ferritin molecule and from within the cavity. When there are more than two ions in the channel, the ones in the middle are also moved in a similar fashion to obtain their potential energy profiles. We note that the electrostatic potential inside the cavity is slightly negative with respect to the outside due to the negative net charge on the molecule.
Threefold channel
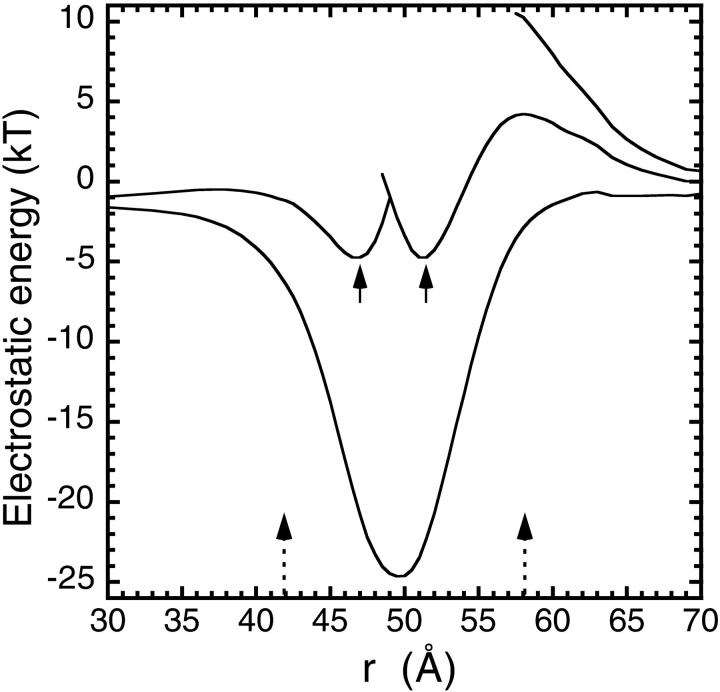
We first study the potential energy profiles of divalent cations in a threefold channel when all the ionizable residues are fully charged. As shown in Fig. 2, a single Fe2+ ion sees a potential well of depth −25 kT, which would trap the ion in the channel permanently. While this Fe2+ ion is resident, a second Fe2+ ion attempting to enter the channel now encounters a 4-kT barrier, which would hamper its entry. But once it succeeds, two Fe2+ ions can coexist in the pore in a semistable equilibrium as indicated by the arrows in Fig. 2. When a third Fe2+ ion is pushed into the channel in this configuration, it meets an 11-kT energy barrier that would forbid its entry. Thus in this charge state, there are only two binding sites in the central pore region. This in itself is not enough to argue against the histidine residues being charged because the three binding sites observed in the crystal structure may be due to two Fe2+ ions shuttling among these three sites. Electrostatics being a coarse-grained theory cannot distinguish such molecular-detail structures in the energy profile. Nevertheless, the present calculations fail to reproduce the binding sites near the Asp-139 residues, which furnishes the strongest argument for the neutrality of the histidine residues. A more subtle argument involves the transport of Fe2+ ions across the channel: although it is still possible with two ions, the rates would be much suppressed because of the barriers faced by the ions in entering and then exiting the pore.
FIGURE 2.
Electrostatic potential energy profiles for Fe2+ ions in a threefold channel in wild type L chain ferritin. All the ionizable residues are assumed to be fully charged. The profile is along the axis that starts from the center of ferritin (r = 0) and goes through the center of the threefold channel. The entrance and exit locations in the pore are indicated by the two arrows at the bottom. The lines in the figure show, in increasing order, the profile encountered by an Fe2+ ion entering the channel when there are 0, 1, and 2 Fe2+ ions already resident in the channel. In the two-ion profile, the positions of two divalent cations in a stable energy minimum are indicated by arrows.
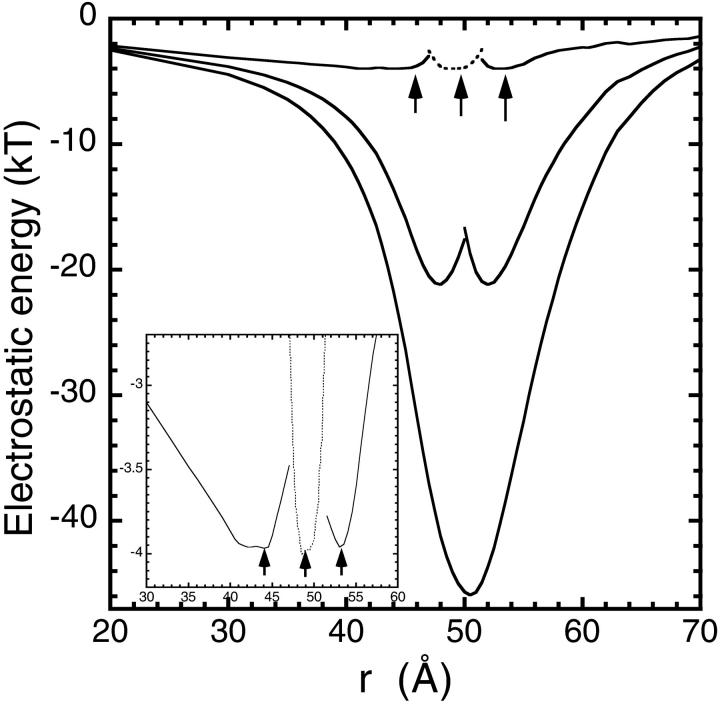
The positively charged histidine residues (and especially His-118) are responsible for the residual barrier at the channel entry, so we need to consider their charge state more carefully. While histidine is 50% charged at normal pH, loading of the channel with divalent ions is expected to lead to deprotonation of His residues, reducing their probability of being charged considerably. In Fig. 3, we show the same energy profiles as in Fig. 2 but with the histidine residues taken as neutral. Here a charge of 2_e_ is distributed among the three Asp-139 binding sites, so the main problem with the charged-histidine calculation is resolved from the outset. The other differences between the two cases are also quite significant: 1), the depth of the potential well for a single Fe2+ ion is now almost doubled (−48 kT); 2), the barrier for the entry of a second Fe2+ ion into the pore has disappeared; and 3), a third ion can also enter the pore easily and three Fe2+ ions can occupy the channel in equilibrium. The positions of these minima, as indicated by arrows in the figure, are in reasonable agreement with the observed binding sites. More importantly though, the free energy barriers encountered by the ions are around 1 kT—on the order of the thermal fluctuations—so that they can move in and out of the pore with almost no impediment. This suggests that the usual conducting state of the threefold channels involves three Fe2+ ions. When the leftmost ion moves into the cavity (or the rightmost ion into bulk for an outward current), the channel reverts into a waiting state with two Fe2+ ions.
FIGURE 3.
Same as Fig. 2 but with the histidine residues taken as neutral. The inset shows the three-ion profile in greater detail. The dotted lines show the profile of the ion in the middle. The positions of three divalent cations in a stable energy minimum are indicated by arrows.
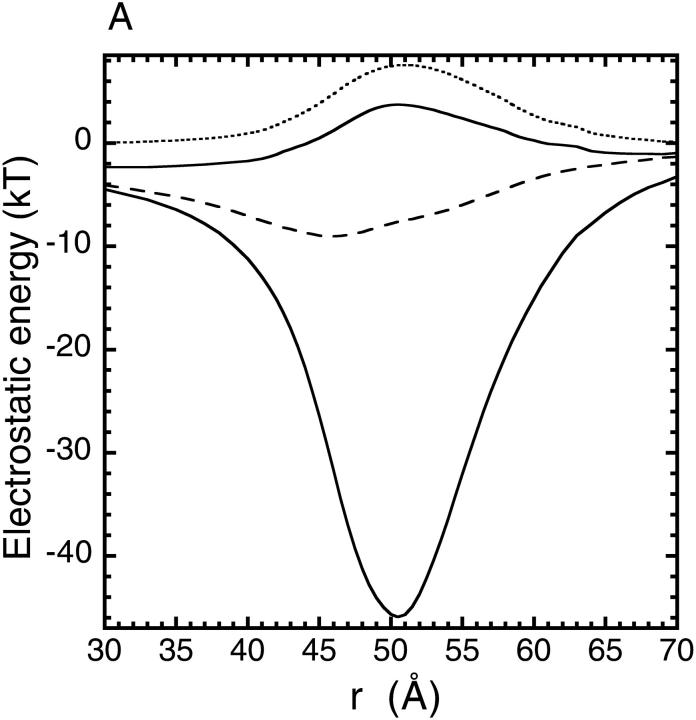
The Asp-131 and Glu-134 residues are highly conserved in all mammalian ferritins, and their mutation to neutral Ala residues were shown to slow down (but not completely stop) the rates of iron uptake (Treffry et al., 1993; Levi et al., 1996). When the calculations are performed using this mutant structure with neutral His residues, the deep well found for a single Fe2+ ion in the wild type channel is replaced with a 4-kT barrier (upper solid line in Fig. 4 A). Decomposition of this potential energy profile into protein-ion (dashed line) and dielectric self energy (dotted line) components shows that the former is severely reduced and is unable to cancel the repulsive image potential. Nevertheless, the residual barrier is not insurmountable, and iron transport can still take place, albeit at a much slower rate compared to the wild type. Repeating the same calculation with all the histidine residues fully charged, we find that the barrier faced by a Fe2+ ion reaches 26 kT (Fig. 4 B), which should completely stop the iron transport in ferritin. This contradicts with the observed iron uptake in the mutant ferritin, and hence provides yet another justification for using neutral histidines in the electrostatic calculations. Therefore, the histidine residues are taken as neutral in the rest of this work.
FIGURE 4.
Potential energy profiles for a single Fe2+ ion in the mutant ferritin (D131A and E134A) along the axis of the threefold channel, when the histidine residues are taken neutral (A) and when they are all fully charged (B). In each case the upper solid line shows the total potential energy obtained from the mutant structure and the lower solid line shows the wild type profile obtained previously. The dashed and dotted lines indicate, respectively, the ion-protein interaction and the dielectric self energy components of the total potential energy in the mutant case.
In Fig. 5, we show the potential energy profiles for monovalent cations in the threefold channel. For a single Na+ ion, the well depth is about half the size for a Fe2+ ion. Loading the channel with multiple ions and calculating the respective potential energy profiles as before, we find that the channel can hold up to five Na+ ions in a stable equilibrium. Just as in the case of three Fe2+ ions (Fig. 3), the residual barriers in the presence of five Na+ ions in the channel are on the order of 1 kT. Hence the monovalent ions can also diffuse across the threefold channel without much impediment. This raises the question of whether there is a selectivity mechanism similar to the calcium channels that would suppress the conduction of Na+ ions in the presence of Fe2+ ions. Calcium channels operate with 2 Ca2+ ions (or 3 Na+ ions) in the pore, and the presence of a single Ca2+ ion in the selectivity filter is sufficient to stop conduction of Na+ ions (Corry et al., 2001).
FIGURE 5.
Potential energy profiles for Na+ ions along the central axis of the threefold channel. All the histidine residues are assumed to be neutral. The five curves, from bottom to top, correspond to 1, 2, 3, 4, and 5 ions in the channel. The profiles of the middle ions are indicated with dotted lines.
To test this hypothesis we have constructed multi-ion potential energy profiles in the threefold channel with mixed Na+ and Fe2+ ions. Because the possibilities for mixed ion configurations are too many, we consider only those that are most relevant for checking the selectivity of the channel. We first assume that the channel is loaded with Fe2+ ions and study entrance of Na+ ions to the pore from outside. When there are two Fe2+ ions resident in the channel, there are no barriers for a Na+ ion, which is attracted to the pore to form a stable equilibrium. In the case of three Fe2+ ions resident in the pore, the potential profile of a Na+ ion entering the channel from outside is again almost flat. As the Na+ ion moves into the channel, the leftmost Fe2+ ion moves out to the cavity simultaneously. This process again leads to a stable equilibrium for two Fe2+ ions and one Na+ ion in the pore. The crucial question at this stage is whether a second Na+ ion can enter the channel from outside. Electrostatic energy calculations with two Fe2+ and two Na+ ions indicate that there is no stable equilibrium for this charge configuration. As the second Na+ ion is pushed into the pore, it faces a rising barrier and it is unable to push the divalent ion out to the cavity. In contrast, if a Fe2+ ion is pushed into pore, instead of the Na+ ion, it has little problem in displacing the leftmost divalent ion to the cavity, leading to a charge configuration with a Na+ ion sandwiched between two Fe2+ ions. Similar observations apply to this and all other mixed charge configurations. That is, a divalent ion can easily enter the channel from outside pushing the leftmost ion to the cavity whereas a monovalent ion has trouble in duplicating this feat.
These results suggest that there is a selectivity mechanism operating in the threefold channel that enhances conduction of divalent ions over the monovalent ones. But, unlike the calcium channel, this is not an absolute mechanism—monovalent ions can also diffuse into the cavity when they are packed in between the divalent ions. Of course, presence of Na+ ions in the cavity does not interfere with the iron deposition process, so an absolute selectivity is not essential for functioning of ferritin. Nevertheless, considering the orders of magnitude difference in bulk concentrations of sodium and iron ions, even a partial selectivity mechanism would greatly improve efficiency of the iron deposition process in ferritin.
Fourfold channel
The hydrophobic fourfold channels are even narrower than the threefold channels and have no charged residues on the channel lining that would help to reduce the dielectric self energy barrier. As a result, the calculated single ion energy profiles exhibit substantial barriers for both Na+ (7 kT) and Fe2+ (30 kT) ions (solid lines in Fig. 6). The barrier for divalent ions is nearly four times larger than the monovalent ions, which gives an indication of the dominance of the repulsive self energy contribution (self energy is proportional to the charge squared). The dielectric constant of the protein is assumed to be _ɛ_p = 5 in this calculation, same as in the threefold channels. Because the fourfold channels are lined mostly with nonpolar residues, the effective dielectric constant of the protein is likely to be less than _ɛ_p = 5 in this region. The effect of using a lower dielectric constant is shown with the dashed lines in Fig. 6, which are obtained using _ɛ_p = 2. The barrier heights are seen to be substantially higher for the lower _ɛ_p value: ∼11 kT for Na+ and 47 kT for Fe2+. We note that the dependence of the potential energy on _ɛ_p is roughly like 1/_ɛ_p. Hence using a higher dielectric constant (e.g. _ɛ_p = 8) as advocated in some models (Schutz and Warshel, 2001), would lower the barriers slightly from the solid lines in Fig. 6. One could also take up issue with the use of _ɛ_w = 80 for channel waters in such a narrow pore. As shown in a recent study of the electrostatic energy profiles of ions in the gramicidin A channel (Edwards et al., 2002), using lower _ɛ_w values in narrow pores leads to substantially higher energy barriers. Thus such a possibility also strengthens the arguments about the impermeability of the fourfold channel to ions.
FIGURE 6.
Electrostatic potential energy profiles for a monovalent or a divalent cation along the central axis of the fourfold channel. The solid lines are obtained using _ɛ_p = 5 for the dielectric constant of the protein and the dashed lines are obtained using _ɛ_p = 2. The entrance and exit locations in the pore are indicated by the two arrows at the top. The histidine residues in other parts of the protein are assumed to be neutral.
These results clearly demonstrate that the fourfold channels cannot be involved in the transport Fe2+ ions. Their capability to conduct monovalent ions such as Na+ is also severely hampered by the presence of a large energy barrier (a 7-kT barrier would suppress the conductance by about a factor of thousand). This raises the question of the functional role of the fourfold channels in iron deposition because mutation of the residues lining the channel is known to interfere with this process (Levi et al., 1988). A possible functional role for the fourfold channels is that they provide pathways for expulsion of excess protons that are created when Fe2+ ions are converted to ferrihydrite in the cavity. A separate pathway for protons is desirable because of the selectivity of the threefold channels against the monovalent cations as noted above. Both in terms of geometric structure and composition, the fourfold channels display a striking similarity to the gramicidin A channel, which conducts protons at much higher rates compared to those of cations (Hille, 2001). This is explained by the fact that water molecules in gramicidin A are in single file and form a hydrogen-bonded chain, over which protons can hop without actually displacing the water column in the pore (Pomes and Roux, 1998). It is plausible that the water molecules in the fourfold channel form a similar “proton wire” that can translocate protons much more efficiently than cations. This is inherently a quantum mechanical process, and its modeling along the lines of gramicidin A poses a challenging problem for future studies of ferritin.
CONCLUSIONS
We have used the crystal structure of the ferritin molecule in electrostatic calculations to study the functional roles of the two types of channels in the iron deposition process. The electrostatic potential energy profiles, calculated for multiple ions in the threefold and fourfold channels, have revealed important insights about their functional roles. It is found that the hydrophilic threefold channels are responsible for the transfer of iron ions into the ferritin cavity. A consistent description of all the experimental observations is obtained when the histidine residues in the protein are taken as neutral. In this charge state, the threefold channel has a very deep binding pocket that can attract up to three Fe2+ ions or five Na+ ions. When the channel is fully loaded with one type of ion, the residual barriers they face are quiet small (∼1 kT), which enables transfer of ions into the ferritin cavity without any impediments. In the case of mixed ions in the pore, entry and transit of monovalent ions are hindered relative to divalent ions, which provides a selectivity mechanism for efficient functioning of the iron deposition process. The hydrophobic fourfold channels, in contrast, present large energy barriers for both monovalent and divalent ions, practically insurmountable for the latter. Since they are known to play an important functional role in ferritin, we conjecture that the water molecules in the fourfold channel form a “proton wire” much like that in the gramicidin A channel, which facilitates the transfer of protons in and out of ferritin.
The threefold channels in ferritin has many analogies to membrane channels, in particular to calcium channels that can selectively conduct Ca2+ ions at very fast rates. The deep binding site in both channels is essential in attracting the relatively scarce divalent ions from the bulk solution. Once the channel is loaded with divalent ions, the multi-ion profile becomes flat ensuring a smooth conductance path while the double charge on divalent ions provides a natural mechanism to select against the singly charged Na+ ions. It appears that nature has exploited similar mechanisms for selective conductance of dilute divalent ions in widely different protein structures.
Acknowledgments
This work was supported by grants from the Japanese Ministry of Education, Culture, Sports, Science and Technology.
References
- Åqvist, J., and A. Warshel. 1989. Energetics of ion permeation through membrane channels. Solvation of Na+ by gramicidin A. Biophys. J. 56:171–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung, S. H., T. W. Allen, M. Hoyles, and S. Kuyucak. 1999. Permeation of ions across the potassium channel: Brownian dynamics studies. Biophys. J. 77:2517–2533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung, S. H., T. W. Allen, and S. Kuyucak. 2002. Modeling diverse range of potassium channels with Brownian dynamics. Biophys. J. 83:263–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corry, B., T. W. Allen, S. Kuyucak, and S. H. Chung. 2001. Mechanisms of permeation and selectivity in calcium channels. Biophys. J. 80:195–214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis, M. E., and J. A. McCammon. 1990. Electrostatics in biomolecular structure and dynamics. Chem. Rev. 90:509–521. [Google Scholar]
- Douglas, T., and D. R. Ripoll. 1998. Calculated electrostatic gradients in recombinant human H-chain ferritin. Protein Sci. 7:1083–1091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards, S., B. Corry, S. Kuyucak, and S. H. Chung. 2002. Continuum electrostatics fails to describe ion permeation in the gramicidin channel. Biophys. J. 83:1348–1360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eisenberg, R. S. 1999. From structure to function in open ionic channels. J. Membr. Biol. 171:1–24. [DOI] [PubMed] [Google Scholar]
- Harrison, P. M., and P. Arosio. 1996. Ferritins: molecular properties, iron storage function and cellular regulation. Biochim. Biophys. Acta. 1275:161–203. [DOI] [PubMed] [Google Scholar]
- Hempstead, P. D., S. J. Yewdall, A. R. Fernie, D. M. Lawson, P. J. Artymiuk, D. W. Rice, G. C. Ford, and P. M. Harrison. 1997. Comparison of the three-dimensional structures of recombinant human H and horse L ferritins at high resolution. J. Mol. Biol. 268:424–448. [DOI] [PubMed] [Google Scholar]
- Hille, B. 2001. Ionic Channels of Excitable Membranes. 3rd ed. Sinauer Associates Inc., Sunderland, MA.
- Jordan, P. C. 1982. Electrostatic modeling of ion pores. Energy barriers and electric field profiles. Biophys. J. 39:157–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuyucak, S., O. S. Andersen, and S. H. Chung. 2001. Models of permeation in ion channels. Reports on Progress in Physics. 64:1427–1472. [Google Scholar]
- Lawson, D. M., P. J. Artymiuk, S. J. Yewdall, J. M. A. Smith, J. C. Livingstone, A. Treffry, S. Levy, P. Arosio, G. Cesareni, C. D. Thomas, W. V. Shaw, and P. M. Harrison. 1991. Solving the structure of human H ferritin by genetically engineering intermolecular crystal contacts. Nature. 349:541–544. [DOI] [PubMed] [Google Scholar]
- Levi, S., P. Santambrogio, B. Corsi, A. Cozzi, and P. Arosio. 1996. Evidence that residues exposed on the three-fold channels have active roles in the mechanism of ferritin iron incorporation. Biochem. J. 317:467–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levi, S., A. Luzzago, G. Cesareni, A. Cozzi, F. Francheschinelli, A. Albertini, and P. Arosio. 1988. Mechanism of ferritin iron uptake: Activity of the H-chain and deletion mapping of the ferroxidase site. J. Biol. Chem. 263:18086–18092. [PubMed] [Google Scholar]
- Levitt, D. G. 1978. Electrostatic calculations for an ion channel. I. Energy and potential profiles and interactions between ions. Biophys. J. 22:209–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michaux, M. A., A. Dautant, B. Gallois, T. Granier, B. L. d'Estaintot, and G. Precigoux. 1996. Structural investigation of the complexation properties between horse spleen apoferritin and metalloporphyrins. Proteins. 24:314–321. [DOI] [PubMed] [Google Scholar]
- Moy, G., B. Corry, S. Kuyucak, and S. H. Chung. 2000. Tests of continuum theories as models of ion channels: I. Poisson-Boltzmann theory versus Brownian dynamics. Biophys. J. 78:2349–2363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakamura, H. 1996. Roles of electrostatic interactions in proteins. Q. Rev. Biophys. 29:1–90. [DOI] [PubMed] [Google Scholar]
- Nakamura, H., and S. Nishida. 1987. Numerical calculations of electrostatic potentials of protein-solvent systems by the self consistent boundary method. J. Phys. Soc. Jpn. 56:1609–1622. [Google Scholar]
- Partenskii, M. B., and P. C. Jordan. 1992. Theoretical perspectives on ion-channel electrostatics: continuum and microscopic approaches. Q. Rev. Biophys. 25:477–510. [DOI] [PubMed] [Google Scholar]
- Pomes, R., and B. Roux. 1998. Free energy profiles for H+ conduction along hydrogen-bonded chains of water molecules. Biophys. J. 75:33–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roux, B., S. Bernèche, and W. Im. 2000. Ion channels, permeation, and electrostatics: insight into the function of KcsA. Biochemistry. 39:13295–13306. [DOI] [PubMed] [Google Scholar]
- Schutz, C. N., and A. Warshel. 2001. What are the dielectric “constants” of proteins and how to validate electrostatic models? Proteins. 44:400–417. [DOI] [PubMed] [Google Scholar]
- Sharp, K. A., and B. Honig. 1990. Electrostatic interactions in macromolecules: theory and applications. Annu. Rev. Biophys. Biophys. Chem. 19:301–332. [DOI] [PubMed] [Google Scholar]
- Stillman, T. J., P. D. Hempstead, P. J. Artymiuk, S. C. Andrews, A. J. Hudson, A. Treffry, J. R. Guest, and P. M. Harrison. 2001. The high-resolution x-ray crystallographic structure of the ferritin (EcFtnA) of escherichia coli; comparison with human H ferritin (HuHF) and the structures of Fe3+ and Zn2+ derivatives. J. Mol. Biol. 307:587–603. [DOI] [PubMed] [Google Scholar]
- Takahashi, T., S. Endo, and K. Nagayama. 1993. Stabilization of protein crystals by electrostatic interactions as revealed by a numerical approach. J. Mol. Biol. 234:421–432. [DOI] [PubMed] [Google Scholar]
- Takeda, S., H. Yoshimura, S. Endo, T. Takahashi, and K. Nagayama. 1995. Control of crystal forms of apoferritin by site-directed mutagenesis. Proteins. 23:548–556. [DOI] [PubMed] [Google Scholar]
- Tieleman, D. P., P. C. Biggin, G. R. Smith, and M. S. P. Sansom. 2001. Simulation approaches to ion channel structure-function relationships. Q. Rev. Biophys. 34:473–561. [DOI] [PubMed] [Google Scholar]
- Treffry, A., E. R. Bauminger, D. Hechel, N. W. Hodson, I. Nowik, S. J. Yewdall, and P. M. Harrison. 1993. Defining the roles of the three-fold channels in iron uptake, iron oxidation and iron-core formation in ferritin: a study aided by site-directed mutagenesis. Biochem. J. 296:721–728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trikha, J., G. S. Waldo, F. A. Lewandowski, Y. Ha, E. C. Theil, P. C. Weber, and N. M. Allewel. 1994. Crystallization and structural analysis of bullfrog red cell L-subunit ferritins. Proteins. 18:107–118. [DOI] [PubMed] [Google Scholar]
- Warshel, A., and J. Åqvist. 1991. Electrostatic energy and macromolecular function. Annu. Rev. Biophys. Biophys. Chem. 20:267–298. [DOI] [PubMed] [Google Scholar]
- Yamashita, I. 2001. Fabrication of a two-dimensional array of nano-particles using ferritin molecule. Thin Solid Films. 393:12–18. [Google Scholar]
- Yang, X., P. Arosio, and N. D. Chasteen. 2000. Molecular diffusion into ferritin: pathways, temperature dependence, incubation time, and concentration effects. Biophys. J. 78:2049–2059. [DOI] [PMC free article] [PubMed] [Google Scholar]