Absolute rate theories of epigenetic stability (original) (raw)

Abstract

Spontaneous switching events in most characterized genetic switches are rare, resulting in extremely stable epigenetic properties. We show how simple arguments lead to theories of the rate of such events much like the absolute rate theory of chemical reactions corrected by a transmission factor. Both the probability of the rare cellular states that allow epigenetic escape and the transmission factor depend on the rates of DNA binding and unbinding events and on the rates of protein synthesis and degradation. Different mechanisms of escape from the stable attractors occur in the nonadiabatic, weakly adiabatic, and strictly adiabatic regimes, characterized by the relative values of those input rates.

Keywords: rate theory, stochastic gene expression, gene switches

Information may be passed from one cellular generation to another not just in the form of the DNA sequence but also in the long-lived expression patterns of genes. The epigenetic state of the cell, i.e., which genes are expressed at a given time, is determined in part by binding and unbinding of transcription factor proteins to the DNA. The genes with their partner proteins form complex dynamical systems known as genetic networks, which can have many steady states, i.e., an attractor landscape (1, 2). The attractors are more stable than the individual molecular protein–DNA adducts, because the proteomic atmosphere of gene products renews the DNA's binding state, ultimately creating autocatalytically its own proteomic atmosphere (1, 3, 4). The attractors of such a genetic network may be associated with distinct cell types (2, 5). Experimental evidence for this view has recently been presented (6, 7). The growing experimental interest in this problem (6) as well as a number of theoretical puzzles involving the stability of the attractors (8, 9) call for a flexible and intuitive theory of the lifetime of such genetic network attractors. Some progress has already been made toward the goal (8, 10–12, 31), but existing formalisms are cumbersome, certainly when compared with the theory of activated events in molecular systems based ultimately on transition-state ideas (13, 14). Our goal here is to present a simple treatment of the noise-induced transitions between two attractors on a landscape that is parallel to the treatment of simple molecular rate processes, which starts with Wigner's absolute rate theory (15). In chemical kinetics, the ratio of escape is proportional to the probability of rare configurations equally likely to become reactant or product. These rare configurations represent a stochastic separatrix of the motion.

Whereas thermal atomic motions cause the escape from energy minima in molecular physics, the noise in genetic networks comes from the probabilistic nature of the chemical reactions, because only a small number of proteins and individual copies of the target DNA are involved. Unlike molecules, genetic systems being far from equilibrium cannot strictly be described by thermodynamic free-energy functions. The stochastic separatrix for molecular activated events is a dividing surface passing through saddle regions of the free energy. We argue that, even in the absence of a free-energy function, the notion of a stochastic separatrix between basins of attraction remains a good approximation (10, 12, 31) and allows a treatment of stochastic switching along the lines of a transition-state theory with dynamic corrections involving the rates of elementary processes (13, 16).

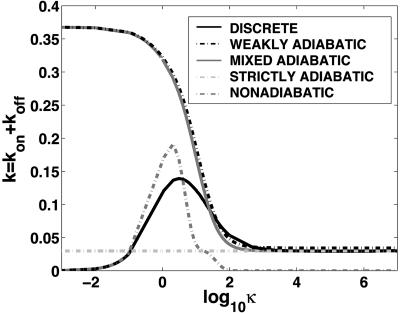
The dynamics of gene networks involves two very different processes whose rates must be compared, protein synthesis and DNA binding. The complexity and energy-consuming nature of protein synthesis in prokaryotic cells generally causes changes in protein number to take longer than the diffusion-controlled binding times of transcription factors, even at their low concentrations. For this reason, it has been argued that one can describe the binding of the transcription factors to each DNA-binding site as an instantaneously equilibrated process, when considering protein production. For steady states this approximation appears to be reasonably accurate. It has also been noted (17–20), however, that the DNA state fluctuations may influence the protein-number state fluctuations. Here we show that the impact of DNA state fluctuations on the escape process is considerable in a rather wide parameter regime for which the steady states are not much influenced by the DNA state fluctuations (Fig. 1). For biologically relevant parameters, the DNA occupancy fluctuations may significantly increase the spontaneous switching rate from a given attractor. In what we call the nonadiabatic limit, where DNA state fluctuations dominate the protein number fluctuations, individual binding and unbinding events of the transcription factors are directly responsible for the transition. For much of the adiabatic regime, although the influence of DNA fluctuations on the steady-state protein levels is negligible, these fluctuations still modify the lifetime of a state; we will call these transitions “weakly adiabatic.” DNA occupancy fluctuations can only be neglected at very high values of the rate ratios, in what we call the strongly adiabatic limit.

Fig. 1.

Fig. 1.

The sum of the escape rates k = _k_on + _k_off as a function of the adiabiaticity parameter κ = (_hg_2↑)/(2_k_3) for a self-activating switch with _g_↑ = 100, _g_↓ = 8, k = 1, 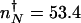Inline graphic. Comparison of the exact discrete n numerical calculation based on the mean free passage time (black solid line), with approximate methods: in the nonadiabatic limit (small κ) (gray dashed line; Eqs. 1 and 3), in the weakly adiabatic regime (black dashed line; Eqs. 5 and 8), and mixed crossover regime (gray solid line). The adiabatic results tend asymptotically to the strictly adiabatic limit (large κ-flat escape rate) (light gray dashed line; Eqs. 6 and 9). In the strictly adiabatic limit the binding of transcription factors to the DNA-binding site is equilibrated. In the nonadiabatic and weakly adiabatic limits the escape rates show a dependence on the adiabaticity parameter; the process is influenced by the DNA-binding state fluctuations.

As Sasai and Wolynes (1) have pointed out, the stochastic theory of a simple genetic switch can be considered analogous to the physicists' Kondo problem or the chemists' electron-transfer process, where DNA occupancy plays the role of a spin or electronic state variable (13). In a simple and intuitive way, here we exploit these analogies to compute the lifetime of a genetic switch, using the idea of a landscape with a stochastic separatrix (10), much like in the earlier proposed threshold model (12). Our treatment is quite analogous to that used for characterizing adiabatic vs. nonadiabatic regimes of quantum rates (13, 14). The approach we present is easily generalizable to a many-gene system. In the general case the present approximation yields the lifetime of a given state of the switch, which is governed purely by a few local properties of the landscape and does not require computing complicated trajectories. Global properties, sensed by the most probable escape paths, generally enter rates for far-from-equilibrium systems (21). The present approach, therefore, must be admitted to be approximate. The simplicity hopefully will make up for some inaccuracy.

Several treatments of the mean first passage time between epigenetic states have already appeared. Most of these studies assume the DNA state equilibrates on a much faster time scale than the protein number (22, 23). We refer to this as the adiabatic limit. In this limit the protein number states may then be treated as a continuous variable giving an expression for the mean first passage time à la the Smoluchowski theory of diffusive rates as sketched by Bialek (11). A more rigorous approach finds the rate by constructing the most probable escape path (8) or by calculating the distribution of paths (10, 24). These methods are powerful, but they are hard to visualize, especially for more complex switching systems. Although the usually invoked adiabatic limit seems to be appropriate for simple switches in prokaryotes, it is not an obviously correct approximation for switches that have more complex operators, in which multiple protein elements must combinatorically assemble at a given site, slowing the binding (25). Nonadiabatic effects also should play a significant role in eukaryotic systems where chromosome restructuring, which may be quite slow, dominates the epigenetic transition. Artificially engineered switches (26) may be constructed with parameters spanning the entire phase diagram.

The Simplest Switch

For illustration we will present our ideas using the simplest example of a system in which we can consider the escape from one minimum to another: a bistable self-activating switch (20). We emphasize the approach is more generally applicable. The self-activating switch consists of a single gene, which may be found in one of two states: on or off. In the off state proteins are produced at a basal level, but in the on state proteins are produced at an enhanced level, leading to a number, n, of proteins in the cell at any moment. The proteins act as activators by binding to the same operator site as the gene governing their production. We assume they bind as dimers with a rate h(n) = hn(_n_–1)/2. The unbinding of the transcription factors is described by a rate f. We neglect time delays due to mRNA synthesis, etc. (which admittedly may play a key role), so that protein population dynamics is governed by a birth–death process. Protein degradation occurs with a rate k, production with the activated rate _g_↑ in the on state and the basal rate _g_↓ in the off state. The system is characterized by a two-state joint probability distribution 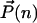Inline graphic, describing the probability of having n proteins in the system and the DNA binding site being in the bound (on-↑) or unbound (off-↓) state. A recent combined experimental and theoretical study (26) has brought attention to the bistability of a switch in previously unexplored limits, when the degree of operon repression is small. Our discussion will turn also to the nonadiabatic limit. Here the equilibration of the DNA and changes in the protein number occur on comparable time scales.

To compute escape rates from the steady-state attractors, one must determine the stochastic separatrix (10). In the adiabatic limit, the position 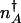Inline graphic of the minimum of the total probability distribution P(n) = _P_↑(n) + P_↓(n) is given by the condition of zero mean protein flow 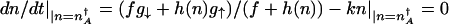Inline graphic. 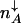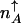For a bistable switch, this equation is satisfied by three values of n; one solution gives the separatrix, and the other two give the positions of the high and low protein number stable steady-state attractors, Inline graphic and Inline graphic. In the non-adiabatic limit the stochastic separatrix refers both to the DNA and protein number state. Therefore, the values of the critical separatrix numbers 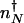Inline graphic in the nonadiabatic, and 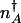Inline graphic in the adiabatic limits are different. The direction of flow changes when the DNA state changes. Therefore, the position of 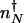Inline graphic corresponds to that number of proteins needed for the system to have comparable probability to be in the on or off state. 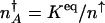For simplicity, we can approximate in the large n limit h(n) = h/2_n(_n_–1) ≈ _hn_2/2 and determine the position of the nonadiabatic separatrix by means of mass action, using the chemical equilibrium constant Inline graphic, where K_eq = 2_f/(_hV_2), where V is the cell volume. The steady-state attractors in the nonadiabatic limit are determined by the birth–death processes in the particular DNA states: _n_↓ = _g_↓/k in the off state and _n_↑ = _g_↑/ in the on state. 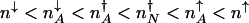To function as a switch _n_↓ must be less than Inline graphic, and _n_↑ must be greater than Inline graphic. We can rewrite the adiabatic separatrix positions in terms of the volumescaled equilibrium constant _K_eq 2↓ _V_2, which scales with Inline graphic,as Inline graphic and Inline graphic.

Nonadiabatic Rate Theory

Here we compute the rate of escape of the system from the low protein number attractor to the high protein number attractor (_k_on) and vice versa (_k_off). Because in the nonadiabatic limit the low protein number attractor corresponds to the off DNA occupancy state and the high protein number state corresponds to the on DNA occupancy state, the transition from the low protein number to the high protein number state requires the binding of an activator. Without the possibility of binding and unbinding, the dynamics in each attractor would be described by stochastic destruction and production of proteins alone, resulting in fluctuations of the mean protein number around each steady state. Consider a system maintained in the off DNA binding state and that now has _n_↓ proteins. The initial probability of being in the off DNA state, with precisely _n_↓ proteins present is _p_off(_n_↓) = _P_↓(_n_↓)/(_P_↑(_n_↓) + _P_↓(_n_↓)). _n_↓ may be generally assumed to be close to the mean number of proteins in the off state (_n_↓ = _g_↓/k). If a binding event now occurs at time t = 0, the gene spontaneously flips into the on state, and proteins are now produced at an enhanced rate. The protein number increases toward the mean number in the high protein state (_n_↑ = _g_↑/k). If the activator does not unbind before the number of proteins becomes characteristic of the on state attractor a successful switching event will have taken place, and the protein number will now fluctuate around the on steady-state value. However, because we are in the nonadiabatic limit, the time scales to reach the steady state for both the DNA-binding state and protein synthesis and degradation are assumed comparable, so an activator may in fact unbind before reaching the separatrix at nN. If an activator does unbind during that time, the gene returns to an off state, albeit with a slightly higher number of proteins than initially. Another binding event will repeat the above scenario, until the protein number safely crosses the separatrix at 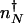Inline graphic, and the steady state corresponding to an activated gene is reached (Fig. 2_A_). The average time needed to cross the barrier from an initial point _n_↓, which is also the time allowed for a unbinding event to occur, is the mean time to reach 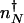Inline graphic for the enhanced production rate. The initial rate of binding an activator h(_n_↓) = h/2_n_↓(_n_↓–1) must be modified to account for the possibility of unbinding again before the system crosses the separatrix. Summing of these attempted crossings results in an expression for the rate of escape from the off state minimum (_n_↓) to the on state (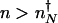Inline graphic) in the nonadiabatic regime given by

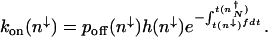graphic file with name M18.gif [1]

The exponential term gives the successful fraction of attempts to reach the protein number-based separatrix, launched from the steady n ↓ state. The total time to reach the separatrix is given by 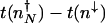Inline graphic, as determined by the average flows in the initial DNA state, and the mean time for an unbinding event to occur is _f_–1. Explicitly, the escape rate from the off state becomes 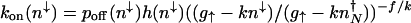Inline graphic. The power-law term describes the motion on the surface with enhanced production after binding of the activator. In the nonadiabatic limit, the probability distributions for the on and off states are unimodal. Therefore, it is unlikely for the gene to be in the on state if the number of proteins is small; thus, _p_off(_n_↓) ≈ 1. If the protein number is large and the unbinding rate is comparable with the death rate, this expression yields

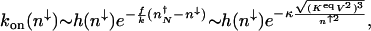graphic file with name M21.gif [2]

where κ = _hg_2↑/(2_k_3). In the extreme nonadiabatic limit κ → 0, the first attempt may be successful; hence, the result simplifies to _k_on(_n_↓) ∼ h(_n_↓).

Fig. 2.

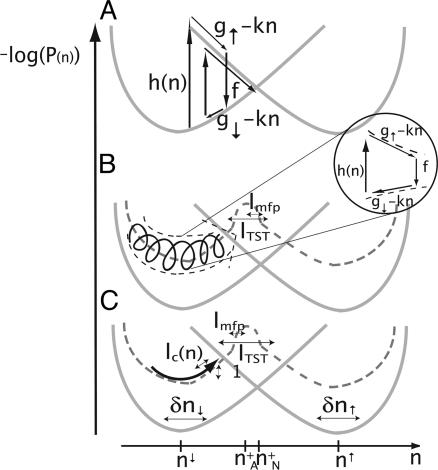
Fig. 2.

A schematic diagram of the difference in the character of the transitions from the state with a small mean number of proteins to the state with a large mean steady-state number of proteins in the nonadiabatic (A) where the escape rate is given by Eqs. 1 and 3, adiabatic (B) where the escape rate is given by Eqs. 5 and 8, and extremely adiabatic (C) regimes. The dark gray dashed line marks the effective potential for protein number change. The horizontal arrows signify binding and unbinding events.

A similar calculation can be carried out starting from the other steady state. The escape rate from the on state, with 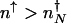Inline graphic proteins, is given by the rate of binding of an activator at time t = 0, providing the system is in the on state _p_on(_n_↑) = _P_↑(_n_↑)/(_P_↑(_n_↑) + _P_↓(_n_↑)), reduced by the probability that an activator rebinds before the protein number decreases to numbers characteristic of in the off state (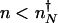Inline graphic). The time available to rebind is calculated by using protein production at a basal level. The _k_off rate is therefore

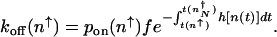graphic file with name M24.gif [3]

For the off rate the mean free path before a rebinding event depends on the mean number of proteins in the system n. The argument of the exponential still describes the number of rebinding events. In the strongly nonadiabatic case, _p_on(_n_↑) ≈ 1, and for very large mean protein numbers the escape rate tends to

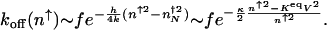graphic file with name M25.gif [4]

Because of the time scale separation in the nonadiabatic limit the system may be approximated as a two-state system. The ratio of the escape rates, therefore, yields the ratio of the probabilities to be in the individual steady states. The equilibrium constant for the “dressed” genetic states in the nonadiabatic limit _K_GS = _k_off/_k_on therefore becomes 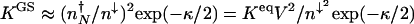Inline graphic. When κ = 0 the proteomic atmosphere has no effect on the relative stability of the DNA occupancy, which follows the ordinary mass action law.

The formulae described above provide quite intuitive representations of specific escape mechanisms. These results also may be formally obtained by means of the path integral solution of the master equation by using the method described by Wang, Onuchic, and Wolynes (27) for kinetic protein folding. This result also coincides with the heuristic approach of Ninio (28).

Adiabatic Rate Theories: Weak and Strong Regimes

In the nonadiabatic limit the switch reaches the separatrix within the time for a few binding events, as schematically portrayed in Fig. 2 A. In what we call the weakly adiabatic regime, the escape process proceeds differently. The DNA occupancy responds quickly to the changing proteomic atmosphere reaching a local steady state before the protein number changes by a large amount. The average occupancy then determines the average local rate of protein synthesis and degradation. A few binding and unbinding events are required in the nonadiabatic limit, but in the adiabatic limit those events are much too common to allow the direct mechanism. One is tempted to equate the local diffusion rate to that coming from synthesis and degradation. But this temptation can only be rigorously indulged at an extraordinary high binding rate. Instead a random, but cyclic, process of binding, growth, and unbinding churns the protein number like a turbulent surf. The cyclic motions of eddies in an ocean wave, if interrupted, contribute to a diffusive transport of flotsam to the shore. In the same way, in most of the weak adiabatic regime, protein numbers fluctuate from the mean flow through this “churning mechanism.” The protein number changes slightly with each cycle of binding/growth/unbinding and eventually reaches the separatrix point because of the resulting diffusive motion. One can show the system acts as if it were diffusing along an effective potential, whose gradient gives the mean flow expected from the average occupancy V(n) = g_eff(n)–_kn (Fig. 2_B_). The diffusion rate in this outwardly adiabatic regime however depends on the nonadiabatic events. Only at very high adiabaticity is diffusion ascribable to birth–death alone.

It is helpful to understand the “eddy-induced” diffusion in an intuitive way. The effective production rate _g_eff(n) = (_fg_↓ + h(n)g_↑)/(f + h(n)) is the production rate averaged over the binding and unbinding states, if they were in equilibrium. The diffusion expected solely from the birth–death processes would just be D_BD(n) = g_eff(n) + kn. This fluctuation mechanism is augmented by diffusion in the orthogonal two-state “bindingspace,” that is, the eddy motion. The difference in the mean distance in protein number that would be traveled in the two DNA states during a typical eddy cycle will be Δ_n = (g_↑–_g_↓)/(f + h(n)). It is the typical difference in protein number expected after a full cycle of an eddy has been traversed. It is given by the difference in velocity in protein number space in a given binding state, Δ_v = |g_↑–_g_↓| times the mean time before the binding state changes Δ_t = (f + h(n))–1, such that Δ_n =Δ_v_Δ_t. The mean free time, or the eddy mixing time, is given by the sum of the characteristic times for binding and unbinding, both of which must occur to return to the original binding state, τ = _f_–1 + (h(n))–1. The rate that describes the eddy cycling thus becomes τ–1 = fh(n)/(f + h(n)). The diffusion coefficient D = Δ_n_2/τ is the square of the mean change in protein number divided by the characteristic time spent within a given eddy. The latter depends on both binding and unbinding events. One thus finds _D_binding(n) = fh(n)(_g_↑–_g_↓)2/(f + h(n))3.

The mean number of proteins of a given type produced in the active state is of the order of _g_↑/k ∼ 102. The degradation rate of proteins gives lifetimes of the order of a bacterial generation k ∼ 10–3_s_–1. Dissociation rates from the DNA vary from f ∼ 1 to 10–3_s_–1, and typical equilibrium constants may be taken to be _K_eq_V_2 ∼ 102 to 104, which results in association constants h/2 = f/(_K_eq_V_2) ∼ 10–2 to 10–7_s_–1 (based on λ phage data as assembled in ref. 29 and references therein). We therefore see that typical adiabaticity parameters scan a wide range: κ = _hg_2↑ /(2_k_3) ∼ 100 to 105. The diffusion coefficient from churning, which depends on the DNA occupancy dynamics, typically influences the escape rate over four orders of magnitude of the adiabaticity parameter κ ∈ (100 to 104), nearly covering the biologically relevant regime. For escape processes the DNA-binding dynamics cannot be neglected until the adiabaticity parameter becomes extremely large, ultimately yielding the strongly adiabatic regime. As shown in Fig. 2, the eddies due to the influence of the DNA-binding state become smaller with faster binding until the motion becomes dominated by simple birth–death diffusion along the effective potential, giving the steady-state probabilities, averaged over the DNA-binding states (Fig. 2_C_).

In the adiabatic limit, the escape rate is governed largely by the fraction of systems at the separatrix 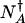Inline graphic compared with the fraction residing near the original attractor 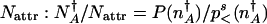Inline graphic, where 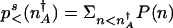Inline graphic, and P(n) is the steady-state probability density for a state with n proteins. Clearly 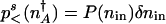Inline graphic, where δ_n_in is the width of the attractor. It is important to understand the spatial variation of P(n), described by the “potentials” in Fig. 2. The spatial variation depends on the balance of the local mean flow against the flow due to diffusion. We can understand this balance by considering the motion pictured in Fig. 2_B_. The mean local velocity by which the protein number changes is v̄ = g_eff–_kn. In addition to this drift the protein number changes by diffusive motion from places of low to high probability, with a velocity of _v_diffusion = Di(n)/(2_l_c), where _l_c is a characteristic “length scale” over which the steady-state probability changes by roughly one _e_-fold. Di(n) refers to the diffusion coefficient, which governs the motion in a particular regime. It is equal to _D_binding(n) in the weakly adiabatic regime, _D_BD(n) in the strictly adiabatic regime and is roughly _D_BD(n) + _D_binding(n) in the small crossover region in between. To traverse this scale the local velocity has to be at least as large as the velocity of the diffusive motion v̄ ≥ _v_diffusion. The equality v̄ = _v_diffusion sets a characteristic length scale of the problem l_c = Di(n)/|2_v̄(n)|, over which locally the probability in a steady state should change by a factor of e. This relation is valid both in the adiabatic and nonadiabatic regimes. The quantity _l_c is analogous to the “scale height” in the equilibrium barometric problem. How many of these characteristic steps of length _l_c are needed for the system to reach 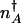Inline graphic from its steady-state value? Bearing in mind that the length of each step depends on n, we must concatenate these steps to give the probability to be at the separatrix relative to being near the initial state. The probability exponentially depends on the number of scale heights of varying length _l_c needed to reach the improbable separatrix starting from the most probable situation at the basin center,

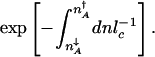
graphic file with name M32.gif

To find the rate, we finally need the width δ_n_in. The size of the attractor δ_n_in is analogous to l_c at the bottom of the basin, but quadratic-order effects must be included. To compare the velocities of the motion near the basin center due to drift and diffusion, the drift velocity must be computed as the “drift frequency” in the initial state ω(n_in) = (∂_v(n)/∂_n)|n = _fhn_in(_g_↑–_g_↓)/(f + h(n_in))2–_k times the distance from the stationary point. Comparing drift and diffusion velocities in the same region ω(_n_in)δ_n_in = Di(_n_in)/δ_n_in, gives the size of the attractor 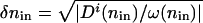Inline graphic. The exponential term counts the paths from all possible positions within the attractor. We therefore must divide the by the width of the attractor.

To determine the epigenetic escape rate we also need the transmission factor. In the adiabatic limit, reaching the separatrix does not yet guarantee a successful escape. Once the protein number reaches the vicinity of the stochastic separatrix the system may directly cross the separatrix or recross it many times before committing to the new attractor. The number of escapes per unit time is thus proportional to the velocity with which the system moves over the separatrix, divided by the number of attempts before it successfully commits to the new attractor k = δ_v_/NP(_n_in → n ∼ peak). The velocity around the peak is determined by a mean free path for number fluctuations l_mfp and a mean free time τ relevant to that region, δ_v = _l_mfp/τ. Only in the crossover region is it necessary to take all processes into account on equal footing when evaluating the mean free path _l_mfp and the associated mean free time τ. In the weakly and strongly adiabatic limits the results simplify. In the weakly adiabatic region, the mean free path is dominated by the DNA churning cycles and is given by the typical eddy size _l_mfp ≈ (_g_↑–_g_↓)/(f + h(n)) and τ = _f_–1 + (h(n))–1. In the strictly adiabatic limit, the motion is determined by the birth and death of proteins. Effectively, the protein number changes by _l_mfp equal to one protein in the mean free time τ = (_g_eff(n) + k)–1. Once the mean free path has been determined, the number of crossings is then the number of steps of the size of the mean free path needed to cross the transition state region _l_TST. Like the basin size, the size of the transition state region is 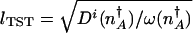Inline graphic. The escape rate from the left attractor, n_↓_A, is

graphic file with name M35.gif

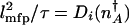where Inline graphic and i indicates BD, binding and mixed in the appropriate regimes. The rate of the escape from the low protein number state in the weakly adiabatic regime becomes

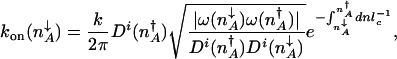graphic file with name M37.gif [5]

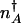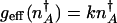where Inline graphic is the number of proteins corresponding to the minimum of the total steady-state probability distribution. In the adiabatic regime the separatrix is given as the fixed point of the average flow: Inline graphic.

In the strictly adiabatic limit, the eddy motion may be neglected. So 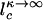Inline graphic is determined solely by the equilibrated diffusion in protein number space 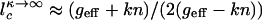Inline graphic. All of the components in Eq. 5 can be obtained by using quadrature, in this case, yielding a complex expansion. A more simplified result, explicit in terms of chemical rate constants, follows if we linearize 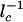Inline graphic in the region, which contributes most to the result of the integral. In this situation Eq. 5 becomes

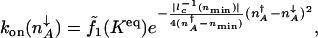graphic file with name M43.gif [6]

where _n_min is the number of proteins for which 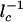Inline graphic has the largest value. The largest value of _l_–1 c corresponds to the smallest characteristic length scale in the region of integration. The value of 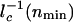Inline graphic scales as 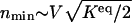Inline graphic. The preexponential factor has the form _f_1(_K_eq) = kV/(2π)(_K_eq/(_a_0_n_↑6)(_n_↑4–(_K_eq_V_2)2–2_K_eq_V_2(_n_↑)2))1/2, where _a_0 = _g_↓/_g_↑. The escape rate decreases with the equilibrium constant and system size. By using the dependence of the minimum of the integrand as a function of the equilibrium constant _K_eq _V_2, one finds the escape rate scales as e–α1_n_↑–2(Keq V2_–3_a_0_n)3/2, where α1 is a numerical factor of the order of 1/2. The rate of escaping from the off-state attractor exponentially decreases with increasing of the equilibrium constant.

How the escape rate depends on the molecular parameters can be seen by assuming, for simplicity, a highly cooperative variation of the equilibrium DNA occupancy with protein concentration. In this case the effective production rate can be approximated by the production rate in the off-state attractor, _g_eff(n) ≈ _g_↓. Now, the protein dynamics will be determined by the rates characteristic of the attractors, until the system reaches the separatrix. This approximation is like the threshold picture of Metzler and Wolynes (12). In this approximation one finds

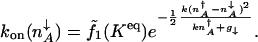graphic file with name M47.gif [7]

When the cell is sufficiently small the separatrix merges with both attractors. In such a regime, this simple formula correctly predicts the functional dependence of the escape rate on the equilibrium constant and the protein production rates. When the separatrix begins to merge the attractor, the exponential term approaches unity. Thus, stability is compromised. When the attractors merge with the separatrix the preexponential factor becomes important for quantitative analysis (8, 23).

In the κ-dependent weakly adiabatic region, the probability distributions look qualitatively similar to those in the strictly adiabatic limit: the extrema do not change as κ increases. In the escape-rate calculation, however, one compares the ratios of the probabilities near the minimum and the saddle regions. This ratio is significantly different in the weak and strong adiabatic regimes and strongly affects the spontaneous switching rates, as seen in Fig. 1. In the weak adiabatic regime one finds the escape rates depend exponentially on the adiabaticity parameter κ. The escape rate therefore is approximately dominated by 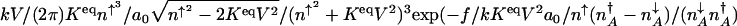Inline graphic. In the weakly adiabatic regime, the effective growth rate can be well approximated as that with a fixed DNA occupancy, as in the Metzler–Wolynes threshold model (12).

The transition can be treated from the high protein number state to the low protein number state much as above in the adiabatic limit. The rate of escape from high to low protein number depends on the relative probability that the system is to the right of the separatrix, characterized by a mean protein number _n_↑ compared with the steady-state probability of being at the separatrix 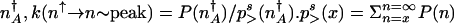Inline graphic. The escape rate turns out to be

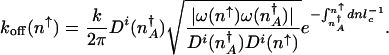graphic file with name M50.gif [8]

We can approximate 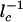Inline graphic in the strictly adiabatic limit as for the _k_on calculation. Then the strictly adiabatic escape rate becomes

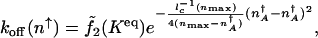graphic file with name M52.gif [9]

where _n_max is the number of proteins at the maximum of 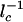Inline graphic, which scales as 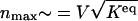Inline graphic. The preexponential factor has the form 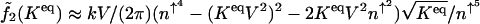Inline graphic. More explicitly, the escape rate from the on state scales as

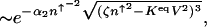
graphic file with name M56.gif

where α2 ≈ 2 and ζ ≈ 1/4 + _a_0/2 are constant numerical factors. The escape rate from the on-state attractor exponentially increases with the increase of the equilibrium constant. A simple result also is obtained by replacing the effective production rate by the value of the effective production rate in the on-state attractor _g_eff(n) ≈ _g_eff(n_↑_A)

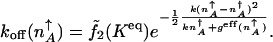graphic file with name M57.gif [10]

The equilibrium constant for the dressed genetic switch state in the strongly adiabatic limit is

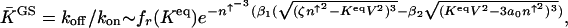
graphic file with name M58.gif

which sharply depends on the proteomic atmosphere. 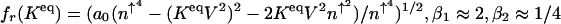Inline graphic are numerical factors.

In the weakly adiabatic regime the exponential term in the off escape rate becomes 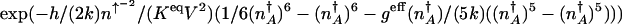Inline graphic. So in the weakly adiabatic limit the equilibrium coefficient for the dressed genetic switch states K GS = _k_off/_k_on scales as 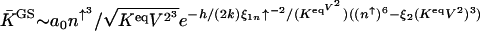Inline graphic, where the coefficients are determined by the positions of the on- and off-state attractors and are of the order of ξ1 ≈ 0.01 and ξ2 ≈ 100.

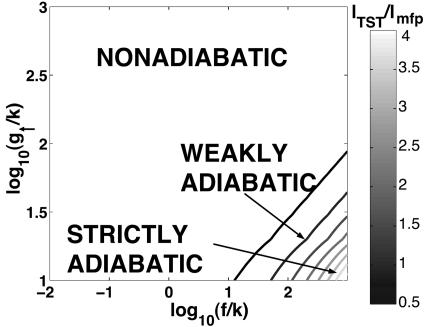
Whether the switch is nonadiabatic or adiabatic can be determined by comparing the mean free path to the size of the transition region. If _l_TST/_l_mfp > 1 many crossings are required and the transition is adiabatic. If _l_TST/_l_mfp < 1 the system commits to the new attractor once it reaches the separatrix, hence the transition is nonadiabatic. In the strictly adiabatic regime the diffusion of the system is governed by protein diffusion induced by the birth–death process, as opposed to the weakly adiabatic regime, where diffusion due to churns dominates. A phase diagram showing the different escape mechanisms in parameter space for fixed _K_eq_V_2 is shown in Fig. 3.

Fig. 3.

Fig. 3.

A phase diagram as a function of the activated production rate _g_↑ and the unbinding rate f for constant _K_eq_V_2, showing the areas of parameter space where a given escape mechanism dominates based on the ratio of the size of the transition-state region _l_TST to the mean free path _l_mfp. If the number of crossings of the separatrix is large, _l_TST/_l_mfp > 1, the transition is adiabatic. If the system commits to a new attractor after one crossing, _l_TST/_l_mfp < 1, the transition is nonadiabatic.

Comparison with Numerically Exact Results

Although the mechanism of spontaneous switching or epigenetic escape is different in the various regimes, we understand the rates in all regimes using the notion of a stochastic separatrix. We can compare these approximations with numerical calculations due to Kepler and Elston (22, 30) and our own full numerical results.

In the nonadiabatic limit (small κ = _hg_2↑/(2_k_3)) the escape process is determined by the rate of DNA state fluctuations. In this regime the rates are given by Eqs. 1 and 3 (gray dashed line) (Fig. 1). These rates agree with the discrete numerical calculation of the mean free passage time from each basin. Our numerical calculations confirm that only in the extremely adiabatic limit (large κ–flat escape rate) can the DNA fluctuations safely be neglected. Only for this extreme limit does the lifetime become determined by protein synthesis/degradation fluctuations alone (light gray dashed line). Estimates of the input parameter would suggest that the weakly adiabatic regime is common for biological switches. In the weakly adiabatic regime the escape rate does not just depend on occupancy averaged growth rates but still depends on the adiabaticity parameter, as shown in Fig. 1. Neglecting the influence of DNA fluctuations in this limit, as many treatments have done, would give the extreme adiabatic asymptotic value of the escape rate also pictured on the graph. Both the strictly and weakly adiabatic regimes can be obtained from the more general calculation by using the full diffusion coefficient. The full treatment is only required in a small crossover regime (gray solid line).

Summary

Spontaneous transitions between attractors of genetic systems are caused by coupled stochastic fluctuations in the DNA state and protein number. Even in parameter regimes where the DNA state locally would appear to reach a steady state much more rapidly than the protein number state, the fluctuations due to binding and unbinding of transcription factors greatly influence the protein number fluctuations and hence modify the rate of spontaneous transitions between epigenetic states. We call such a regime the weakly adiabatic by contrast to the strongly adiabatic limit, where the DNA-binding state may be taken to be in equilibrium. The mechanism of spontaneous switching between stable attractors in the weakly adiabatic regime is graphically explained by a churning process, which causes protein numbers to fluctuate from the mean flow. How the escape rates _k_on and _k_off depend on molecular parameters in the nonadiabatic, weakly, and strongly adiabatic should allow one to understand the evolutionary constraints necessary to achieve stable yet responsive switches, a topic we hope to revisit. By considering both the DNA and protein degrees of freedom, the rate theories we have presented provide an intuitive description of spontaneous switching events, in terms of the molecular parameters that determine the functioning of a genetic switch.

Acknowledgments

We thank Patrick H. Diamond and Jin Wang for insightful comments on the manuscript. This work was supported by the Center for Theoretical Biological Physics through National Science Foundation Grants PHY0216576 and PHY0225630.

Author contributions: A.M.W., J.N.O., and P.G.W. designed research, performed research, contributed new reagents/analytic tools, analyzed data, and wrote the paper.

Conflict of interest statement: No conflicts declared.

References