Visualization of Synaptic Vesicle Movement in Intact Synaptic Boutons Using Fluorescence Fluctuation Spectroscopy (original) (raw)
Abstract
Not much is known about the mobility of synaptic vesicles inside small synapses of the central nervous system, reflecting a lack of methods for visualizing these dynamics. We adapted confocal spot detection with fluctuation analysis to monitor the mobility of fluorescently labeled synaptic vesicles inside individual boutons of cultured hippocampal neurons. Using Monte Carlo simulations we were able to propose a simple quantitative model that can describe vesicle mobility in small hippocampal boutons under resting conditions and different pharmacological treatments. We find that vesicle mobility in a time window of 20 s can be well described by caged diffusion (D ∼ 5×10−5 _μ_m2/s, cage sizes of ∼50 nm). Mobility can be upregulated by phosphatase blockage and increased further by actin disruption in a dose-dependent manner. Inhibition of the myosin light chain kinase slows down vesicle mobility 10-fold, whereas other kinases like protein kinase C (PKC), A (PKA), and calmodulin kinase II (caMKII) do not affect mobility in unstimulated boutons.
INTRODUCTION
Maintenance of synaptic transmission requires retrieval of exocytosed vesicles as well as transport of newly formed vesicles into the correct pools; the underlying mechanisms, however, are poorly understood, yet of seminal interest (1,2). A puzzling question has been whether synaptic vesicles within the synapse are exclusively transported in an active manner or also passively by diffusion and, even more important, what molecular machinery is controlling vesicle dynamics. Studies addressing these questions are scarce because of a lack of suitable techniques.
Most information about vesicle dynamics comes from ultrastructural analysis (3–5). Real time imaging of synaptic boutons labeled with the styryl dye FM 1-43 yielded a plethora of information about the exoendocytic cycling of vesicles but allowed only indirect conclusions about vesicle mobility. This way it was shown in hippocampal synapses that inhibitors of myosin light chain kinase (MLCK) reduce vesicle recycling (6), consistent with an involvement of molecular motors. Evidence for molecular motors targeting synaptic vesicles, however, is very poor (see Doussau and Augustine (7) and Rizzoli and Betz (8) for reviews). On the other hand, a growing body of physiological evidence supports the notion that synaptic vesicles are sorted differentially and nonrandomly into different pools, although the spatial organization of pools is a matter of debate (5,9–13).
In past years evanescent wave microscopy was used to study the dynamics of vesicles in endocrine cells (14) and in goldfish bipolar cell terminals (15). However, since hippocampal synapses cannot be easily separated from the postsynaptic compartment, this powerful tool could not be used so far in small boutons.
Fluorescence recovery after photobleaching (FRAP) allowed visualization of vesicle dynamics in small boutons (16,17). Hippocampal boutons, however, had to be stained by strong stimuli, since FRAP experiments require large numbers of moving particles and give no meaningful results in the limit of the stochastic behavior of a few particles.
Here we present the application of confocal spot detection combined with fluorescence fluctuation analysis (FFS) (18). This method is easy to set up, is noninvasive, has a time resolution of milliseconds, and allows investigating the behavior of very few vesicles.
First we confirmed the reliability of our technique using pharmacological treatments expected to affect vesicle mobility and this way demonstrate its potential for probing the mechanisms of vesicle mobility down to the molecular level. We then determined to which extent certain kinases and phosphatases regulate overall vesicle mobility. Our results are in favor of a model where synaptic vesicle movement is controlled and restricted. As shown by Monte Carlo simulations, our results can be quantitatively well described by caged diffusion with typical cage sizes of 50–100 nm and a diffusion constant of ∼5 × 10−5 _μ_m2/s.
METHODS
Hippocampal cell culture
Hippocampal neurons from regions CA1–CA3 of 1–3-day-old Wistar rats were cultured according to previous protocols (19). After 14–20 days in vitro, cultures were used for experiments.
Experimental conditions and FM dye loading
Coverslips were mounted in a perfusion chamber on a movable stage of an inverted microscope equipped for FCS measurements (Zeiss Confocor 1, Oberkochem, Germany). Cells were perfused at room temperature in a modified Tyrode's solution consisting of 150 mM NaCl, 5 mM KCl, 2 mM CaCl2, 1 mM MgCl2, 10 mM Hepes (pH 7.4), 30 mM glucose. For electric field stimulation 10 _μ_M 6-cyano-7-nitroquinoxaline-2,3-dione and 50 _μ_M D,L-2-amino-5-phosphonovaleric acid were added to prevent recurrent activity.
Synaptic boutons were labeled by electric field stimulation (1-ms current pulses of 40 mA and alternating polarity delivered by platinum electrodes spaced at ∼10 mm) in saline containing 15 _μ_M FM 1–43.
If not stated otherwise, one of the three following staining protocols was used.
Staining protocol for FFS experiments
A total of 120 APs at 10 Hz were evoked in the presence of 15 _μ_m FM 1–43 (FM was washed out after 60 s). Two to three synapses on one neuronal process (clearly visible on images taken with a charge-coupled device (CCD) camera) were measured per coverslip. Initially functionality was checked by destaining with 2 × 600 APs (CCD images of the respective areas were taken immediately before and after the stimulation). Since failures were not observed when selecting fluorescent spots lying in a row on top of a neuronal process, in later experiments 0.5 μM tetrodotoxin was applied to prevent rundown, and the destaining step was omitted.
Maximal staining protocol for laser scanning microscopy
A total of 600 APs at 20 Hz were evoked during 60 s bath application of 15 _μ_m FM 1–43. Destaining with 3 × 600 APs.
Minimal staining protocol for laser scanning microscopy
The culture was stimulated with 5 APs at 5 Hz during a 10 s bath application of 15 _μ_m FM 1–43. Destaining with 3 × 600 APs.
Confocal spot detection and fluorescence fluctuation spectroscopy
The laser beam of an argon ion laser (488 nm) passes a lens system for beam expansion coupled to an Axiovert 135 (ConfoCor, Zeiss) and is focused with a 63 × /1.2 W objective. The emitted photons passing the pinhole are collected by an avalanche photo diode (APD) (SPCM-AQ-231, EG&G Optoelectronics, Vaudreuil, Canada). A 530–600 or 520–600 nm emission filter was used (Zeiss, and AHF, Tübingen, Germany). Single photon counts are processed online by a hardware correlator (ALV-5000, ALV, Langen, Germany) as well as by a counting card (CIO-CTR05, Measurement Computing, Middleboro, MA) in a separate PC. To avoid photobleaching and phototoxic effects, synaptic boutons were illuminated for only 10 ms per 100 ms time interval, and data were acquired at 10 Hz sampling rate if not stated otherwise in the text. The excitation power was chosen to be ∼50 nW (measured in front of the objective back pupil). Fast shuttering of the laser light was accomplished by an acousto-optic modulator (AA-MTS.110, AA Opto-Electronique, St. Remy les Chevreuse, France).
Before each measurement our detection volume was calibrated using the fluorophore Rhodamine 6G by standard fluorescence correlation spectroscopical measurements (20). A focal plane above the cell layer was chosen. Fluorescent beads used in some experiments were 40 nm in size (FluoSpheres 505/515, Molecular Probes, Eugene, OR).
Offline autocorrelation and powerspectral analysis was performed with self-written macros in PV-WAVE (Visual Numerics, San Ramon, CA) or IgorPro (Wavemetrics, Lake Oswego, OR).
Please note that for comparison of power spectra and variances, it is important to work with boutons of similar brightness. We discarded very dim boutons (mean < 6 kilocounts per second, kcps) and pooled boutons with similar fluorescence intensities, such that the standard deviation of the average fluorescence is <40%. This way we avoid large offsets in the power spectra simply reflecting different numbers of stained vesicles, which would make comparison under different conditions more difficult.
Fluorescence microscopy
To select a region and maneuver a single bouton into the confocal spot, images were taken by a cooled slow-scan CCD camera (PCO SensiCam, Kelheim, Germany) and a modified filter set (DCLP 505). Epifluorescence illumination was achieved by repetitive Xe-arc lamp illumination at 475 nm (Monochromator Polychrom II, T.I.L.L. Photonics, Gräfelfing, Germany). Exact positioning in the x, y plane was achieved by stepwise movement of the motorized stage (Märzheuser, Wetzlar, Germany) until a maximum signal was obtained with the APD. For positioning in the z direction, confocal z scans were taken and the objective was moved to the position that gave a maximum signal.
Laser-scanning microscopy
Images were taken on a Leica SP2 confocal scanning microscope with a 63 × /1.2 W objective (Leica Microsystems, Mannheim, Germany) using an argon ion laser (488 nm) for excitation and APDs in photon counting mode (only operated in the linear range, <2 MHz) as detector. The pixel dwell time was kept constant, and the same emission filters (530–600 nm or 520–600 nm) were used as for the confocal spot experiments. The detected fluorescence signal is given in counts.
For selecting boutons we followed a protocol similar to that of Ryan et al. (32) and Murthy and Stevens (31). A fluorescent spot was visible after minimal staining of the bouton which lost its fluorescence after 3 × 600 APs. The intensity was measured by centering a circular region of 13 pixels (1 pixel = 58 nm) on the fluorescence spot and subtracting an image taken after complete destaining with 3 × 600 APs. To avoid a bias caused by out-of-focus spots, we performed z scans and selected always the plane of best focus. Boutons whose Δ_F_ signals (intensity difference before and after destaining) were <25 counts, corresponding to 1.5 times the standard deviation of the residual background distribution (r), were considered to be below threshold and not included in the analysis (for further details, see Fig. 3). The existence of a functional synapse was confirmed by a subsequent round of strong staining (2 × 600 APs), which resulted in a bright fluorescent spot. The fluorescence from this spot could be released with another destaining stimulus of 3 × 600 APs. These criteria select for functional synapses that were stained during the minimal staining protocol with at least one vesicle.
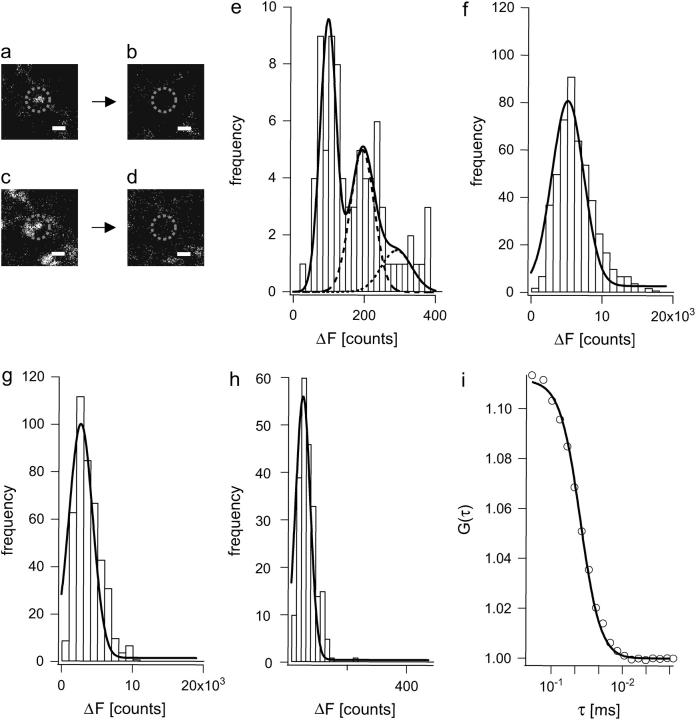
FIGURE 3.
Determination of single vesicle fluorescence contribution in FFS measurements. (a and b) Fluorescent puncta with similar appearance as 40-nm fluorescent beads are visible after very week stimulation with 5 APs at 5 Hz during a 10 s application of 15 _μ_M FM 1−43. Scale bars are 1 _μ_m (a). FM dye fluorescence is lost after applying 3 × 600 APs (b). At the beginning of every experiment, a z stack of the region of interest was obtained. The fluorescence (in counts) of a punctum was determined as the intensity difference between images in the plane of best focus before and after a destaining stimulus of 3 × 600 APs in a circular region of 13 pixels (1 pixel = 58 nm). The existence of a functional synapse was confirmed by a subsequent round of strong stimulation (600 APs at 20 Hz during 60 s application of 15 _μ_m FM 1–43), which resulted in a bright fluorescent spot (c). The fluorescence from this spot could be released with 3 × 600 APs (d). Note that these images were acquired at ∼12 times lower laser intensity than in a and b. Scale bars are 1 μ_m. (e) Histogram of fluorescence intensities of puncta (determined as difference between a and b) for 5 APs shows a quantal distribution, which could be fit with a sum of three Gaussians (black line) according to the model of Murthy and Stevens (31) (the individual Gaussians for peak 2 and 3 are also shown in dashed lines): 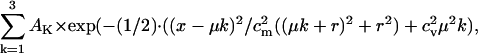 with peak spacing μ, amplitude of each peak A, and residual background fluorescence r. The coefficient of variation for measurements c_m = 0.08 was estimated from repeated measurements of fluorescent puncta; the coefficient of variation of vesicle surface area c_v has been estimated by Murthy and Stevens to be 0.2 (31). The residual fluorescence after the destaining stimulus was found to be r = 40 counts on average. The fit yields a single vesicle fluorescence intensity of μ = 96.8 ± 3.2 counts. (f) Fluorescence intensity (Δ_F) histogram of fully loaded boutons (loaded with 3 × 600 APs at 20 Hz during 180 s of dye application and destained with 3 × 600 APs) yields an average intensity of 5137 ± 122 counts. Thus a fully stained bouton contains ∼52 stained vesicles, which is in good agreement with findings in the literature (30–32). Note that some boutons failed to take up dye during the 5 AP stimulus (see (a) and (c)). (g) Fluorescence intensity (Δ_F) histogram of boutons stained with 120 APs (at 10 Hz, 1 min dye application) as in the FFS experiments. The average bouton intensity was found to be 2353 ± 206 counts corresponding to ∼24 labeled vesicles. (h) Fluorescence intensity histogram of 40-nm fluorescent beads settled on a cell layer (plotted is Δ_F determined by subtracting the background). Images were taken as in a. A single Gaussian fit yields an average intensity of 48.6 ± 1.2 counts. A single vesicle (see a and d) is thus ∼2-fold brighter than a bead. (i) Autocorrelation of beads diffusing freely over a cell layer (measuring conditions as in confocal spot detection experiments). A fit with a three-dimensional diffusion model gives a diffusion time of _τ_D = 1.65 ms and N = 8.96 beads, corresponding to 4.44 ± 0.06 kcps per bead (cpb).
with peak spacing μ, amplitude of each peak A, and residual background fluorescence r. The coefficient of variation for measurements c_m = 0.08 was estimated from repeated measurements of fluorescent puncta; the coefficient of variation of vesicle surface area c_v has been estimated by Murthy and Stevens to be 0.2 (31). The residual fluorescence after the destaining stimulus was found to be r = 40 counts on average. The fit yields a single vesicle fluorescence intensity of μ = 96.8 ± 3.2 counts. (f) Fluorescence intensity (Δ_F) histogram of fully loaded boutons (loaded with 3 × 600 APs at 20 Hz during 180 s of dye application and destained with 3 × 600 APs) yields an average intensity of 5137 ± 122 counts. Thus a fully stained bouton contains ∼52 stained vesicles, which is in good agreement with findings in the literature (30–32). Note that some boutons failed to take up dye during the 5 AP stimulus (see (a) and (c)). (g) Fluorescence intensity (Δ_F) histogram of boutons stained with 120 APs (at 10 Hz, 1 min dye application) as in the FFS experiments. The average bouton intensity was found to be 2353 ± 206 counts corresponding to ∼24 labeled vesicles. (h) Fluorescence intensity histogram of 40-nm fluorescent beads settled on a cell layer (plotted is Δ_F determined by subtracting the background). Images were taken as in a. A single Gaussian fit yields an average intensity of 48.6 ± 1.2 counts. A single vesicle (see a and d) is thus ∼2-fold brighter than a bead. (i) Autocorrelation of beads diffusing freely over a cell layer (measuring conditions as in confocal spot detection experiments). A fit with a three-dimensional diffusion model gives a diffusion time of _τ_D = 1.65 ms and N = 8.96 beads, corresponding to 4.44 ± 0.06 kcps per bead (cpb).
Monte Carlo simulation of confined vesicle movement
The confocal detection volume along the optical axis extends significantly beyond the synaptic bouton, such that movements in the z direction do not significantly contribute to fluctuations (21). It was thus sufficient to simulate movement of vesicles within the x, y plane (Fig. 1).
FIGURE 1.
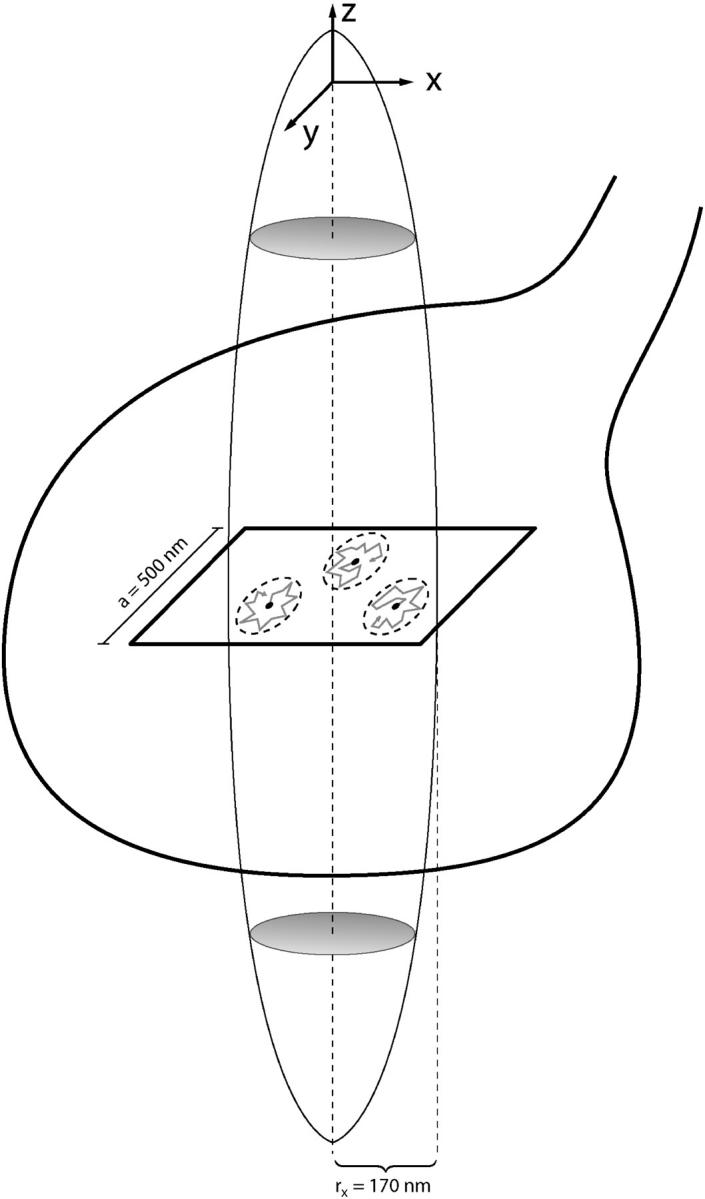
Schematic of model for simulating confined synaptic vesicle movement. A sketch of the confocal detection volume (_r_xy = 170 nm, structural parameter ∼6) is overlaid on the outline of a typical synapse with Ø ∼ 1 _μ_m. Since the detection volume is extending in the z direction by approximately a factor of 1.8, only movements in the x, y plane will significantly contribute to fluctuations. Vesicles were simulated as nonextended fluorescent objects and placed at random positions in a square of 500 nm edge length. Since the detection volume has an _e_−2 radius of 170 nm, vesicles outside this square do not contribute significantly to overall fluorescence. Vesicles were allowed to undergo a random walk (shaded lines) within a confined region (for illustration purposes, three confined regions are shown as dashed ellipses). The space constant of the grid was 1 nm.
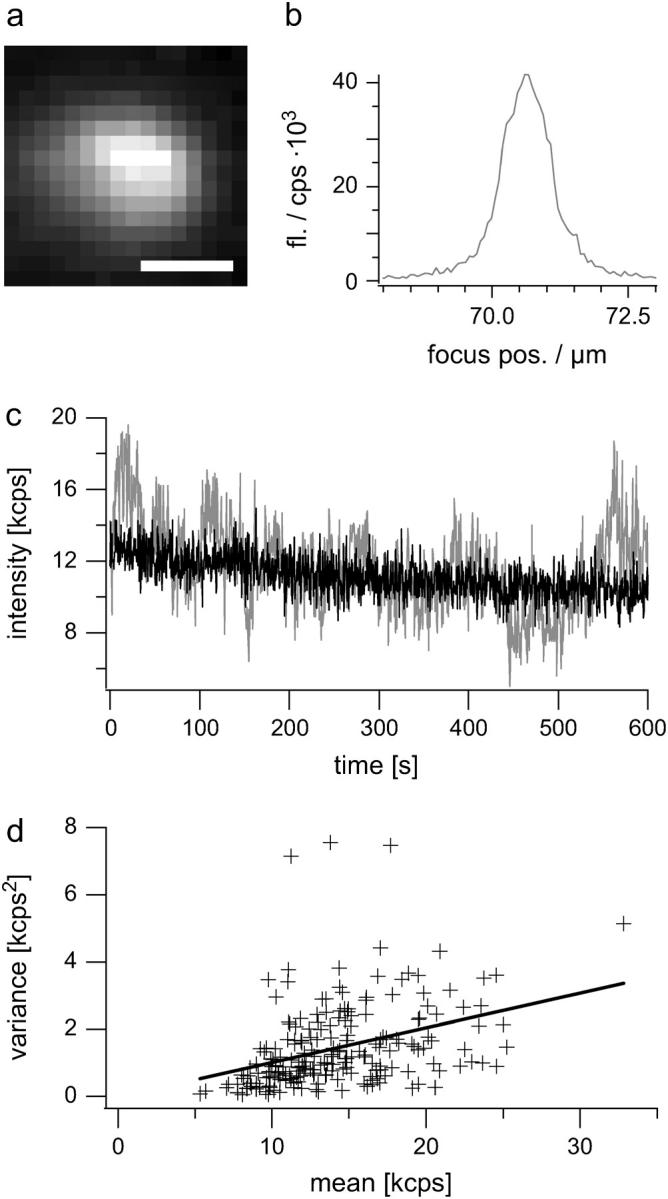
For this, vesicles were placed at random positions within a square of 500 nm edge length. Since the detection volume has an _e_−2 radius of 170 nm, vesicles outside this square do not contribute significantly to overall fluorescence. Vesicles were allowed to undergo a random walk in a confined region (circular cage) according to 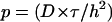 , with p being the probability to jump to the next grid point, D being the diffusion coefficient, τ the time step (0.01 ms), and h the grid space constant (1 nm). The object is reflected if it hits the borders of the predefined cage. The detection volume was assumed to be centered on the synapse. Vesicles were simulated as dimensionless fluorescent point sources. Simulated cage sizes (radii) thus give the width of free space around a vesicle, and the vesicle radius would have to be added to a given cage size to reflect its real radius.
, with p being the probability to jump to the next grid point, D being the diffusion coefficient, τ the time step (0.01 ms), and h the grid space constant (1 nm). The object is reflected if it hits the borders of the predefined cage. The detection volume was assumed to be centered on the synapse. Vesicles were simulated as dimensionless fluorescent point sources. Simulated cage sizes (radii) thus give the width of free space around a vesicle, and the vesicle radius would have to be added to a given cage size to reflect its real radius.
Since a synaptic vesicle is small compared to the detection volume, it can be assumed nonextended without significant error. Its average fluorescence in the center of the beam waist under our measurement conditions was 1.57×2×sqrt(8) kcps = 8.88 kcps (cf. Results). With the experimentally determined Gaussian illumination profile in the x, y plane (_e_−2 radius of 170 nm), the simulated trajectory for each vesicle was transformed into a fluorescence time series. The two-dimensional grid covers ∼1/3 of the whole bouton. Thus, with on average 24 stained vesicles in boutons stimulated with 120 APs (see Fig. 3), intensities of 8–10 simulated trajectories had to be integrated to give similar mean fluorescences as experimentally measured. To such a simulated time series, photon shot noise was added by drawing random numbers from a Poisson probability distribution with an expectation value given by the actual fluorescence. Random walk simulations were performed for a time period of 120 s and the integrated fluorescence sampled at 10 Hz identical to the experimental conditions. All further analysis of the fluorescence fluctuation traces is identical to the analysis performed on measured data. Each simulation is repeated 5–10 times and results are averaged. Error bars reflect standard error of the mean.
RESULTS
Confocal spot detection in resting hippocampal boutons
Most synaptic boutons in the mammalian central nervous system are too small to be investigated directly with electrophysiological tools on the single synapse level. In the past, however, optical methods like confocal spot detection techniques in combination with fluctuation analysis have been used successfully to measure fast calcium dynamics in a cultured neuromuscular junction preparation or cerebellar synapses (22,23). In principle, the same methodology should unmask some of the basic properties of the synaptic vesicle cluster; if it was possible to detect a confocal spot within the synaptic bouton (Fig. 1 and Fig. 2, a and b), any movement of fluorescently stained synaptic vesicles in this detection volume should result in upward and downward deflections of fluorescence (Fig. 2 c). From ensemble fluctuations of such recordings it should then be possible to derive information about the number of vesicles in the volume as well as their dynamics, i.e., their mobility and movement, either by autocorrelation (ACF) analysis or directly by variance analysis (24,25). We attempted to do so and calibrated our spot detection system (see Methods) yielding an apparent detection volume of _V_det ∼ 0.06 fl (1/_e_2 radius in the x, y plane, _r_0 = 0.17 _μ_m, and along the optical axes _z_0 = 1.03 _μ_m, see Fig. 1). For comparison the volume of a typical bouton with a diameter of 1 _μ_m (13) is ∼0.5 fl; ∼50% of the confocal detection volume extends below and above the bouton along the optical axis, such that the detected bouton volume is <1/9 of the total bouton volume.
FIGURE 2.
Confocal spot detection of stained synaptic vesicles in resting boutons reveals macroscopic fluctuations reflecting vesicle movement. (a) Fluorescence image of an exemplar hippocampal bouton 20 days in vitro. stained with 15 _μ_M FM 1–43 by electric field stimulation (120 APs, 10 Hz). Scale bar is 1 _μ_m. After dye washout (10 min), a fluorescence image was taken and a single identified bouton was placed in the center of the laser beam. (b) A z scan through the bouton was performed for positioning in the focal plane. (c) Exemplar spot confocal fluorescence time course of a resting bouton (shaded) measured for 10 min (sampling rate 2 Hz, with 6 ms illumination of the sample per interval). Large up- and downward steps in fluorescence can be seen signifying synaptic vesicle movement in and out of the detection volume. For comparison, the time series of a bouton in a preparation fixed with 4% paraformaldehyde (black). Note the slight decrease in the fluorescent signal that either arises from slight “stage drift” or slight concerted movement of fluorescent vesicles on a very slow timescale (bleaching was minimal under these measurement conditions). (d) Plotted is the variance of 229 individual recordings from control cells versus their mean. Data were fit with a line yielding an intercept of −0.02 ± 0.27 and a slope of b = 0.103 ± 0.018, i.e., a variance-over-mean ratio of ∼0.1 for control cells.
We next stained individual synaptic boutons with the styryl dye FM 1–43 (26) by applying 120 action potentials (APs) at 10 Hz. A single identified bouton was then moved into the focal plane with its fluorescence maximum (Fig. 2, b and c, cf. Methods). As can be seen in Fig. 2 c large macroscopic fluctuations of fluorescence intensity around a mean value of ∼13 kcps can be observed in an unstimulated bouton. After gently fixing boutons with 4% paraformaldehyde, these macroscopic changes in fluorescence vanished completely (Fig. 2 c, black trace), showing that the origin of fluctuations is biological. Fluctuations could arise from whole bouton movements as well as from movement of vesicles in the detection volume. In fact we did also observe in very rare cases such bouton movements, which occurred on a slower timescale (>20 s) and eventually led to a loss of the signal. These slow movements (>20 s) resemble the well-studied spine dynamics (27). Such whole bouton or spine movements are, however, mainly prominent at 37°C and especially in young cultures (28) and strictly dependent on actin, i.e., they are easily blocked by cytochalasin D (CD).
Thus, we conducted several experiments using different drugs that destabilize actin filaments and tubulins but did not detect any effect with our method (see Fig. 5 and supplementary figures). Also we limited our analysis to fluctuations occurring on timescales faster than 20 s, thereby minimizing the contribution of slow dendritic, axonal, or spine rearrangements.
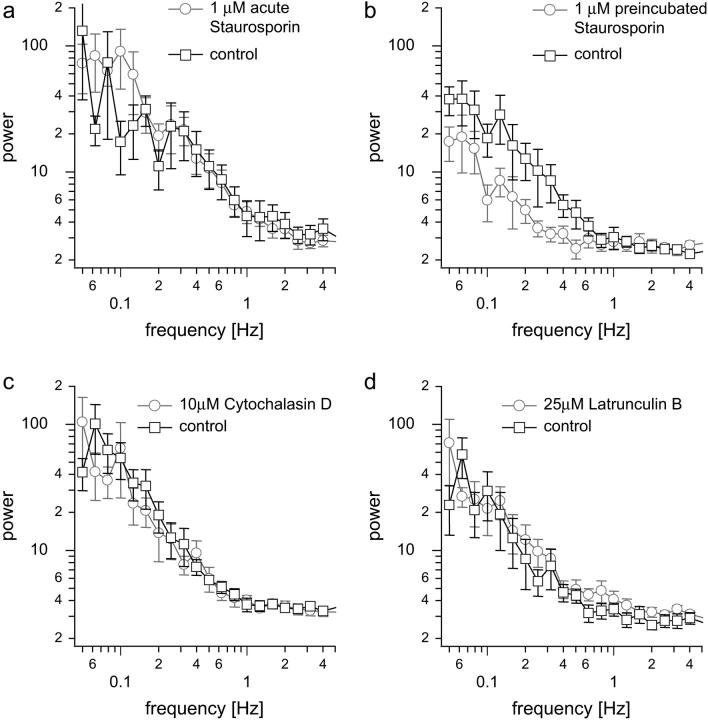
FIGURE 5.
Acute staurosporine treatment and disruption of actin or tubulin alone does not affect vesicle mobility. (a) Averaged power spectra for control conditions and for acute application of 1 _μ_M staurosporine. (b) Averaged power spectra for control conditions and after 1 h preincubation (at 37°C) 1 _μ_M staurosporine (lower trace). (c) Averaged PSD for control conditions and application of 10 _μ_M CD. (d) Averaged PSD for control conditions and application of 25 _μ_M LB.
Variance depends on the number of stained vesicles in the detection volume
The time-averaged mean fluorescence scales with the average number of fluorescent objects in the detection volume, whereas the variance reflects the mobility of the objects. If fluctuations were indeed solely caused by movement of individual stained vesicles within the focal plane rather than by concerted movement of the whole synaptic vesicle cluster, the variance of the fluorescence traces should depend on the number of stained vesicles, i.e., on the mean fluorescence in the detection volume. For the case of concerted movement, the variance should not depend on the mean fluorescence (after removing photon shot noise, see Methods). Indeed the variance increases with the mean bouton fluorescence (Fig. 2 d) although there is some scatter, probably reflecting bouton-to-bouton variability of vesicle mobilities. A tighter correlation is expected if it was possible to measure the very same bouton after FM loading with stimuli of different lengths. Experimentally this is not feasible.
For the case of one species of freely and independently moving particles, the slope in Fig. 2 d should correspond to the single particle fluorescence contribution. The average number of particles in the detection volume then would be given by 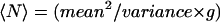 , where the geometry factor g is sqrt(8) for a three-dimensional Gaussian and 2 for a two-dimensional Gaussian illumination profile (29). If we calculate the number of vesicles this way for our experiments, we end up with ∼50–100 vesicles. This number is higher than the estimated size of the recycling pool (4,30–32), especially when considering that we sample <10% of the whole bouton. This indicates that the model of freely diffusing particles typically used in autocorrelation analysis does not approximate the movement of vesicles tightly packed and clustered in a synaptic bouton. Thus, the single vesicle fluorescence contribution has to be determined independently.
, where the geometry factor g is sqrt(8) for a three-dimensional Gaussian and 2 for a two-dimensional Gaussian illumination profile (29). If we calculate the number of vesicles this way for our experiments, we end up with ∼50–100 vesicles. This number is higher than the estimated size of the recycling pool (4,30–32), especially when considering that we sample <10% of the whole bouton. This indicates that the model of freely diffusing particles typically used in autocorrelation analysis does not approximate the movement of vesicles tightly packed and clustered in a synaptic bouton. Thus, the single vesicle fluorescence contribution has to be determined independently.
Determination of the fluorescence intensity contribution of a single vesicle
The basic idea is to express the average brightness of a single vesicle in equivalent fluorescent bead units and to determine the average fluorescence contribution per bead in confocal spot detection experiments by standard ACF analysis, which can be easily performed for beads in solution. We first stimulated hippocampal boutons in the presence of 15 _μ_M FM 1–43 with only 5 APs (minimal staining protocol) and imaged boutons using laser scanning microscopy. We then measured the intensity of individual fluorescence puncta within a circular region (Ø = 0.75 μ_m) before and after destaining (3 × 600 APs) and plotted the intensity differences Δ_F given in counts in a histogram (Fig. 3 e). A multimodal distribution with equally spaced peaks was obtained as described previously (30–32), indicating that in most cases, where FM 1–43 was taken up, only one, two, or three vesicles were stained. These fluorescent puncta (Fig. 3 a), which can be destained by APs (Fig. 3 b), show a fluorescence distribution like the measured point spread function (PSF) of 40-nm fluorescent beads (∼340 nm at full width half-maximum of the PSF) and are absent if no APs are triggered during dye application. The histogram is well fit with a multimodal distribution, yielding a single vesicle fluorescence of 96.8 counts (see figure legend and Methods for details). The presence of an active synapse was verified at the end of each experiment by successful dye uptake and release under strong stimulation (maximal staining protocol 600 APs at 20 Hz, destaining with 3 × 600 APs, Fig. 3, c and d). A fluorescence histogram of maximally stained boutons is shown in Fig. 3 f. Since fluorescent styryl dye uptake was shown to be quantal (although release might occur in subquanta), the intensity of the whole synapse scales with the number of vesicles turned over during stimulation (30,32,33). A single peak around 5137 counts is observed for boutons that were fully loaded (2 × 600 APs at 20 Hz, 120 s FM dye application, and destaining with 3 × 600 APs), indicating that for this load ∼52 vesicles are turned over and stained on average, which is in good agreement with the literature (30,32,33). Next we stimulated synaptic boutons with 120 APs, i.e., the same stimulus as in the confocal spot detection experiments (destaining with 2 × 600 APs). The histogram in Fig. 3 g shows that under these conditions 24 vesicles are stained on average.
We next determined the intensity of 40-nm fluorescent beads (which were allowed to settle on a neuronal cell layer) under the same imaging conditions to be 45.6 counts (Fig. 3 h), i.e., approximately half the counts of a single vesicle. Since both FM 1–43 and fluorescent bead measurements were performed with the same excitation wavelength and emission filter characteristics as in the confocal spot detection experiments, this ratio is the same for both setups. The single bead fluorescence for confocal spot detection was 1.57×sqrt(8) kcps, as determined from the amplitude of the ACF and the mean fluorescence (see Fig. 3 i) or directly by variance analysis, which returns equal results (24).
Note that the factor sqrt(8) relates the average fluorescence measured to the true fluorescence of a bead placed in the center of the illumination profile (25,29). With a vesicle/bead fluorescence ratio of ∼2, a single vesicle in the center of the beam waist contributes on average 1.57×2×sqrt(8) kcps = 8.88 kcps.
Quantitative description of vesicle mobility in small synaptic boutons
With average count rates of 10–20 kcps (see Table 1), we estimate that on average ∼3 stained vesicles are present in the detection volume, compared to ∼25 stained vesicles in the whole bouton (Fig. 3 f). This agrees well with the fact that we sample only ∼1/9 of the total bouton volume.
TABLE 1.
Variance analysis for different experimental conditions
| Number of measurements n | Mean 〈F(t)〉 [kcps] | Variance 〈_δ_F(t)2〉 [kcps2] | _t_-test variance-over-mean _p_-value | |
|---|---|---|---|---|
| See Fig. 4 | ||||
| 15 _μ_M ML7 | 14 | 9.98 ± 1.09 | 0.54 ± 0.09 | 0.0627 |
| Control | 13 | 10.70 ± 0.78 | 1.38 ± 0.30 | |
| See Fig. 5 | ||||
| 1 _μ_M acute staurosporine | 13 | 11.89 ± 1.34 | 1.50 ± 0.37 | 0.4419 |
| Control | 6 | 13.99 ± 1.86 | 1.46 ± 0.41 | |
| See Fig. 5 | ||||
| 1 _μ_M preincubated staurosporine | 11 | 12.59 ± 1.22 | 0.48 ± 0.12 | 0.0337 |
| Control | 12 | 9.71 ± 0.76 | 1.15 ± 0.32 | |
| See Fig. 5 | ||||
| 10 _μ_M CD | 9 | 14.30 ± 0.88 | 1.15 ± 0.27 | 0.2120 |
| Control | 12 | 15.19 ± 1.17 | 1.87 ± 0.58 | |
| See Fig. 5 | ||||
| 25 _μ_M LB | 13 | 12.63 ± 0.57 | 0.99 ± 0.34 | 0.4259 |
| Control | 10 | 12.35 ± 1.23 | 0.76 ± 0.25 | |
| See Fig. 6 | ||||
| 5 _μ_M OA | 10 | 14.87 ± 1.60 | 5.11 ± 0.73 | 0.0007*** |
| Control | 14 | 13.51 ± 0.82 | 2.42 ± 0.52 | |
| See Fig. 6 | ||||
| 5 _μ_M OA | 9 | 12.31 ± 0.84 | 2.81 ± 0.46 | 0.0020** |
| 5 _μ_M OA + 1 _μ_M LB | 11 | 12.90 ± 0.82 | 2.38 ± 0.37 | 0.0055** |
| 5 _μ_M OA +10 _μ_M LB | 6 | 14.29 ± 1.83 | 3.59 ± 0.75 | 0.0061** |
| 5 _μ_M OA +25 _μ_M LB | 6 | 14.66 ± 2.30 | 5.00 ± 1.43 | 0.0134* |
| Control | 11 | 13.43 ± 1.17 | 1.40 ± 0.27 |
In contrast a number of 50 and more was calculated from the inverse of the ACF amplitude or by variance analysis (see above). This discrepancy could arise from an immobile fraction of vesicles contributing only to the mean fluorescence but not the variance (24,25). The mobile fraction can be calculated from 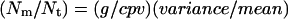 (cpv = counts per vesicle in the center of the beam = 2×1.57×sqrt (8) as measured; g = 2 for a two-dimensional Gaussian; _N_m = number of mobile particles, and _N_t = total number of particles). For control conditions this would yield a mobile fraction of only ∼2–4%, a number difficult to interpret considering that only ∼3 vesicles are on average present in the detection volume. This suggests that all vesicles display a high degree of immobility, or put differently, all vesicles are highly confined in their movements.
(cpv = counts per vesicle in the center of the beam = 2×1.57×sqrt (8) as measured; g = 2 for a two-dimensional Gaussian; _N_m = number of mobile particles, and _N_t = total number of particles). For control conditions this would yield a mobile fraction of only ∼2–4%, a number difficult to interpret considering that only ∼3 vesicles are on average present in the detection volume. This suggests that all vesicles display a high degree of immobility, or put differently, all vesicles are highly confined in their movements.
Thus, for a quantitative characterization it seems reasonable to assume that vesicles are anchored at certain positions and can only move in a restricted space. With this picture of a vesicle cluster in mind we performed Monte Carlo simulations (see Methods for details), where vesicles were placed randomly within a synapse with the detection volume centered at the bouton midpoint. Vesicles were only allowed to freely move within a confined cage (radius = 12.5–200 nm). For simplicity this movement was modeled as a random walk with diffusion coefficients ranging from D = 5 × 10−3 to 5 × 10−6 _μ_m2/s, i.e., with values as found in other preparations (14,15,34,35).
The model has only two free parameters that can be estimated from the two observables, the shape of the power spectral density (PSD) and the variance. As stated above the average fluorescence is a direct measure of the number of particles and was chosen in the simulations to match the experimental mean fluorescence (∼3 vesicles in the detection volume). In general, increasing the diffusion constant or decreasing cage size leads to high frequency components in the PSD function.
An excellent agreement between model and experiment was obtained for cage sizes between 50–100 nm and a diffusion coefficient of D = 5 × 10−5 _μ_m2/s for control conditions (see Fig. 4, a, c, and f).
FIGURE 4.
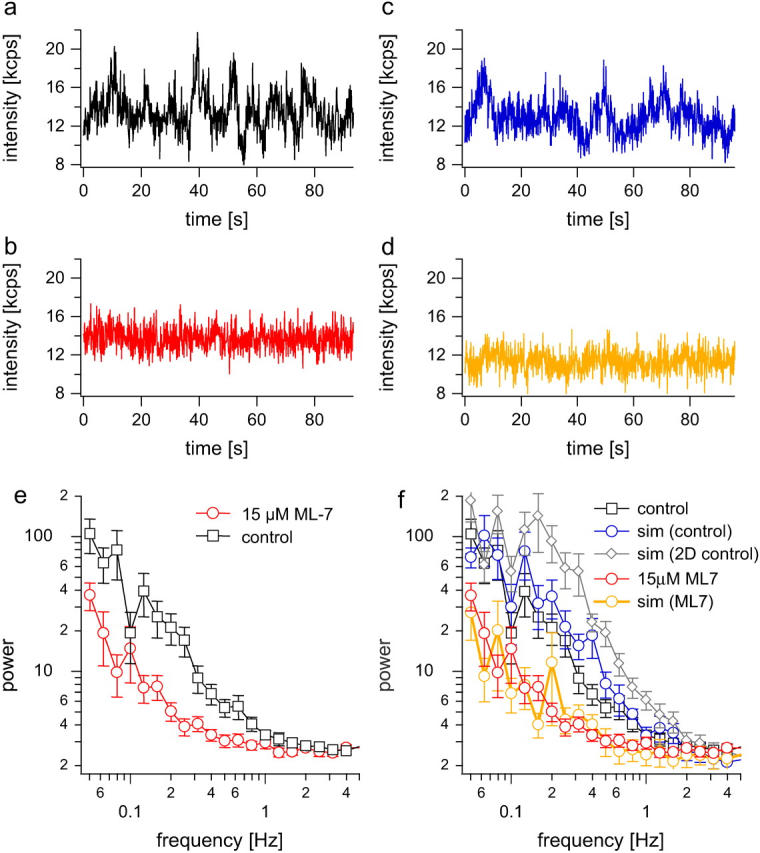
Movement of synaptic vesicles is controlled by MLCK. (a) and (b) Exemplar time series of boutons stained with FM 1–43 (15 _μ_m) by 120 APs (at 10 Hz) before (a) and after application of 15 _μ_M ML7 (the data were already high-pass filtered at 0.05 Hz). (c) Simulated fluorescence time series for control vesicles. (d) Simulated fluorescence time series for ML-7. (e) Respective averaged power spectra for control and in the presence of 15 _μ_M ML-7. For power spectral analysis of fluorescence traces, the average value was subtracted and the data were high-pass filtered at 0.05 Hz to remove slow trends in the data that could arise from stage drift or slow movements of boutons. (f) Shown are the same PSDs as in the left panel, but overlaid are results from simulations with diffusion coefficient D = 5 × 10−5 _μ_m2/s and a cage size of 50 nm (blue circles). Mean fluorescence for this simulation is 11.2 kcps and the variance 0.96 kcps2 (as expected for control cells, see Fig. 1). Simulation for the same cage size but with diffusion coefficient doubled to D = 1 × 10−4 _μ_m2/s is shown in gray (rhombs). The PSD is shifted upwards, and the variance increases to 2.02 kcps2. The mean fluorescence is 11.3 kcps for this simulation. Red circles show the PSD of experiments after ML-7 treatment (cf. left panel). A simulation with D = 5 × 10−6 _μ_m2/s (10-fold lower than control) and a cage size of 50 nm (orange circles) mimics experimental ML-7 data quite well. The mean fluorescence for this simulation was 11.5 kcps and the variance 0.17 kcps2.
To further test this model, we attempted to modulate the vesicle mobility by different pharmacological means expected to significantly change mobility. We analyzed for each condition the PSD in the frequency range of 0.05–5 Hz (the given borders by filtering and our sampling frequency) and the variance-over-mean ratio as an index of mobility. In principle the autocorrelation function (ACF) of the time series of fluctuations (36,37) should yield the same information as the PSD, as both form a transform pair. In praxis, however, a proper interpretation of the ACF by fitting requires a priori knowledge about the underlying process, and ACF analysis of filtered data is even more difficult. Exemplar ACFs of unfiltered fluctuation time series for control and fixed boutons are shown in the supplementary material (Fig. S1).
Movement of synaptic vesicles is active and controlled by MLCK
The MLCK blocker ML-7 has been shown to decrease the fraction of releasable vesicles in hippocampal boutons, pointing to a role of MLCK in vesicle recruitment, since endocytosis seemed to be normal after drug application (6). To test whether this decrease in the fraction of releasable vesicles can be directly related to a mobility change of vesicles, we applied confocal spot detection and compared the PSD of vesicle mobility under control conditions with the one after ML-7 treatment (Fig. 4).
As can be seen in the fluorescence time course in. Fig. 4, a and b, fluctuations are clearly reduced after ML-7 treatment. Accordingly the PSD shows a clear reduction of fluctuations in the range of 0.05–1 Hz (Fig. 4 e). Judging from the variance analysis in Table 1 we can see a small decrease in the variance-over-mean ratio (p = 0.067, _t_-test). Thus using combined confocal spot detection and variance analysis, we could verify a reduction of vesicle mobility by ML-7 at the level of a few vesicles, verifying directly that vesicle movement is controlled by molecular motors as suggested previously (6).
For ML-7 we observed a reduction of the power in the frequency band between 0.05 and 1 Hz as well as a decrease in the variance. Monte Carlo simulations show (Fig. 4, c, d, and f) that this can be explained by a 10-fold reduction in the diffusion coefficient, whereas the cage size remains unchanged.
It is known that ML-7 and ML-9 can also target PKC and PKA at higher concentrations (38). Thus, we tested whether more specific activation of PKC with 200 nM phorbol 12 myristate 13 acetate or of PKA with 10 _μ_M forskolin also alter vesicle mobility. No significant change was found (see Supplementary Material Figs. S2, S3, and S4, and Table S1). Similarly inhibition of both kinases by either 1 _μ_M bisindolylmaleimide (against PKC) or 100 _μ_M Rp-8-Br-cAMPS (for blocking PKA) did not affect vesicle mobility under resting conditions (see supplementary material, Figs. S5 and S6, and Table S1).
Staurosporine can also reduce vesicle mobility, probably by acting on MLCK
In the past, the PKC blocker staurosporine has been shown to decrease vesicle mobility (16). However experiments focusing on destaining efficiency of FM 1–43 after staurosporine treatment (19,39,40) were also in line with a shift in the mode of exoendocytosis from a full collapse to a transient fusion pore opening (“kiss-and-run”), such that FM 1–43 is only partially released during exocytosis. In all cases staurosporine had to be preincubated for 1 h at a concentration of 1 _μ_M, conditions under which it also blocks MLCK (41). We challenged hippocampal boutons with 1 _μ_M staurosporine and tested its effect on vesicle mobility immediately (Fig. 5 a) and 1 h after application (Fig. 5 b). Only in the latter case we found a clear decrease of vesicle mobility. This result together with the data for more specific PKC and PKA blockers and activators in resting boutons suggest that the well-described staurosporine effect is not mediated by PKC. At this high concentration a number of kinases will be blocked including MLCK. Since the measured reduction in vesicle mobility is indistinguishable from the ML-7 action, it is highly likely that most of the staurosporine effect on vesicle mobility and reserve pool mobilization is due to reduced active transport by blocking MLCK.
Involvement of cytoskeletal elements
To test the involvement of cytoskeletal elements like actin filaments and tubulins in synaptic vesicle movement, we applied either cytochalasin D (CD, 10 _μ_M, Fig. 5 c) and latrunculin B (LB, 1 _μ_M or 25 _μ_M, supplementary Fig. S7, Fig. 5 d) to shift the equilibrium from F-actin to G-actin or colchicine (supplementary Fig. S8) to destabilize microtubules. Interestingly, none of these maneuvers affected vesicle mobility. If, however, vesicle recruitment depended on active transport by myosins, actin depolymerization should influence vesicle transport and thus mobility. This unexpected finding, however, corroborates the notion that the observed fluctuations are not caused by synapse movement. The latter is blocked completely by cytochalasin and latrunculin, which have been shown to block spine movement completely (27). One explanation might be that vesicles within the synaptic vesicle cluster are held together by other proteins like the phosphoprotein synapsin (see below, (42)) and are also linked to actin. Thus an important role of actin in vesicle mobility might be masked by synapsin tethers and disruption of actin alone is not enough to increase vesicle mobility. To test this model we aimed at releasing vesicles from synapsins.
Block of phosphatases drastically increases vesicle mobility
It has been shown that the broadband phosphatase blocker okadaic acid (OA) disperses the presynaptic vesicle cluster in frog neuromuscular junction (43). Similarly OA leads to a spreading of fluorescence in hippocampal terminals labeled with a fluorescently tagged antibody against the lumenal domain of the vesicle protein synaptotagmin (44). Interestingly, OA also blocks the myosin light chain phosphatase (45).
Application of OA to hippocampal boutons increases fluctuations in the range of 0.1–5 Hz (Fig. 6, a–c). Furthermore we observe a significant increase in the variance-over-mean ratio (Table 1).
FIGURE 6.
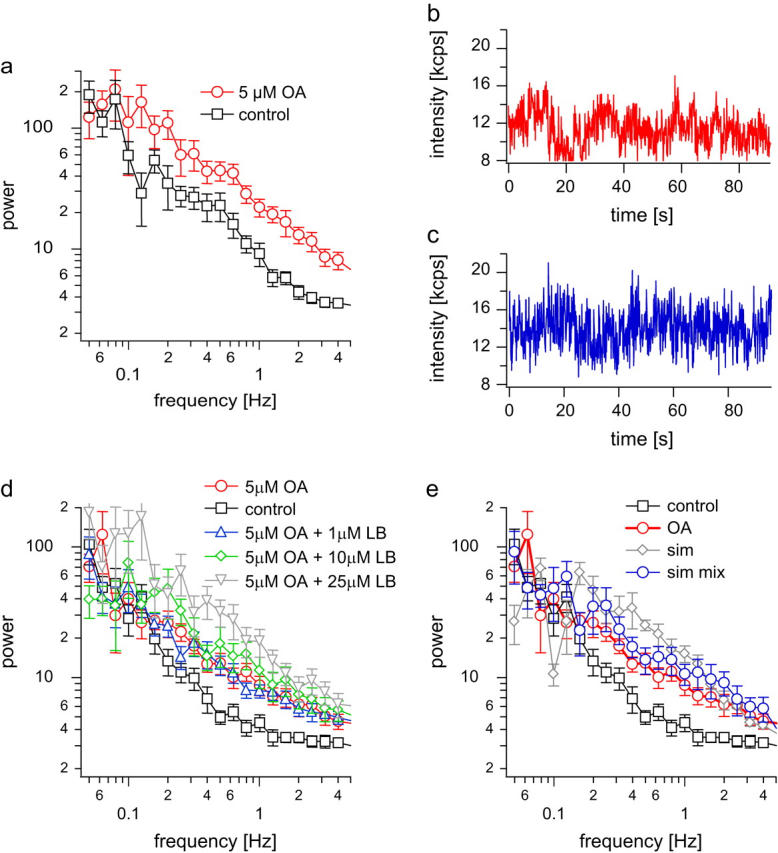
OA treatment increases observed fluctuations. (a) Respective ensemble-averaged power spectra after application of 5 _μ_M OA reveal a large increase in vesicle mobility compared to control conditions. (b) Exemplar time series of individual resting boutons after application of 5 _μ_M OA to the bathing medium. OA was applied for at least 25 min. (c) Exemplar simulated fluorescence time series for OA vesicles with two populations with different diffusion coefficients (cf. panel e, PSD with blue circles). (d) In the presence of 5 _μ_M OA, increasing concentrations of LB (preincubated for 1 h) substantially increase vesicle mobility in a dose-dependent manner: control; 5 _μ_M OA; 5 _μ_M OA + 1 _μ_M LB; 5 _μ_M OA + 10 _μ_M LB, 5 _μ_M OA + 25 _μ_M LB. (e) PSD of experiments after OA treatment in red. Superimposed (gray rhombs) is a simulation with D = 5 × 10−4 _μ_m2/s and a cage size of 30 nm with mean = 12.7 kcps and variance = 1.80 kcps2. Shown in blue circles is a simulation where 75% of the vesicles were modeled using control parameters (D = 5 × 10−5 _μ_m2/s, cage size = 50 nm), but 25% had a 100-fold higher diffusion coefficient (5 × 10−3 _μ_m2/s) and a cage size of 50 nm. The mean intensity for this simulation is 12.0 kcps, and the variance is 2.17 kcps2. Experimental PSD (black squares) is shown for comparison.
In fact it has been shown that OA also destabilizes actin (46). This shift in modes should be pronounced if OA is applied along with LB. Powerspectral analysis of such experiments is shown in Fig. 6 d. The mobility can be further increased with increasing concentrations of LB in a dose-dependent manner (see Fig. 6 d and Table 1).
Although the application of LB alone does not influence mobility, LB shows a drastic effect in combination with OA. It seems that vesicles have to be freed from some sort of tether by OA before a role of actin in mobility becomes apparent. This “tether”, likely to be synapsin, could even link vesicles among each other. The OA effect was somewhat more difficult to model and can be described assuming D = 5 × 10−4 _μ_m2/s and a cage diameter of 30 nm. An even better simulation is obtained if 75% of vesicles have a D = 5 × 10−5 _μ_m2/s like control and 25% a 100-fold higher D value (Fig. 6 e). Such large changes in single vesicle mobility are expected for OA from previous FRAP experiments, which indicated that vesicles after OA treatment can even diffuse across the whole bouton within minutes (17), implying that they can leave or move together with the cage. Such slower processes, however, had to be discarded in our model and experimental analysis since they occur on timescales where whole bouton movements might contribute to fluctuations (>20 s).
For a given diffusion coefficient such as for control conditions, the variance increases only weakly with cage size. This is due to the necessary high-pass filtering of the data (see supplementary Fig. S10) resulting in an uncertainty in cage size estimation by a factor of ∼2. Increasing the diffusion coefficient for control conditions twofold results already in a detectable change in the PSD and the variance (cf. Fig. 4 f).
Our model simulations provide a good framework to describe mobility in synaptic vesicle clusters in quantitative terms, and they show that even subtle changes in mobility of very few vesicles within the otherwise rather static vesicle cluster can be picked up by confocal spot detection.
DISCUSSION
We showed that confocal spot detection is a sensitive technique to monitor vesicle mobility and movement in small central nervous synapses in real time. By using an independent approach for determining the number of particles in the detection volume we could show that standard FCS analysis with models of freely and independently diffusing particles cannot be applied to describe movements of large organelles like synaptic vesicles in living cells as somewhat expected considering the tight clustering of vesicles in a hippocampal bouton. Instead, PSD and variance-over-mean analysis not requiring a priori knowledge for qualitative interpretation proved to be superior for characterizing vesicle mobility.
Fluorescence fluctuation spectroscopy (FFS) bolstered by Monte Carlo simulations allowed us to propose a realistic model of confined diffusion for vesicle mobility in the synaptic vesicle cluster and quantifying vesicle mobility under different conditions, which was so far not possible for small hippocampal synapses. Changes in vesicle mobility can be easily explained by a change of the local diffusion coefficient and/or the size of the confined region (cage). Even subtle changes of the diffusion constant are easily observed in spot confocal measurements by examining only two characteristics, the power spectral density and the variance-over-mean ratio.
Alternatively our data could be described by assuming a significant immobile fraction of vesicles. We then obtained a mobile fraction of only ∼2–4% for control cells, which could be increased to ∼8% by application of OA (Fig. 6 and Table 1). This seems at odds with FRAP experiments in neuromuscular junction, which showed a large increase in vesicle mobility after OA treatment (43). Furthermore, since only ∼3 vesicles are present in the detection volume, we expected to see fluorescence bursts if a mobile vesicle happens to pass the detection volume. At last, a fast recovery of fluorescence originating from mobile vesicles was also not visualized in FRAP experiments in hippocampal boutons (16). However, this could reflect a shortcoming of the FRAP method as the small mobile fraction of 4% might have been lost during the bleaching pulse. More likely, however, the concept of freely diffusing particles on an immobile background does not hold for a tightly packed synaptic vesicle cluster.
The results obtained for ML-7 show that vesicle mobility is active. This was already suggested by previous studies where vesicle dynamics, however, could not be observed directly. The mobility of vesicles within the cage at resting conditions can be formally described by diffusion, which does not exclude the possibility that vesicles are anchored at certain positions with a certain force or are actively transported in a stochastic fashion. Our results from the experiments using OA and latrunculin are in favor of a model where vesicles are linked to each other by synapsins. Since readying recycling vesicles for fusion requires removing the synapsin cross-links, another element is needed for confining or guiding their movement to prevent dispersal and loss from the cluster or even bouton. Our experiments support a role for actin as cage (47) but also argue for a function as guiding track. This function, however, is only unmasked in a concentration-dependent manner after removal of synapsins by CaMKII-dependent phosphorylation or block of phophatases by OA.
All data are well in line with our model of confined diffusion. Very slow processes, which are likely to be of less physiological relevance for fast synaptic transmission, are not included in our model because they could not be separated from whole-bouton movement or remodeling in our experiments. Certainly, our model does not describe all features of vesicle mobility under resting conditions or the shown drug applications. But we find it very intriguing that this simple model can explain quite well the measured data showing that vesicle mobility on a timescale of 20 s is dominated by restricted stochastic movements.
Other powerful imaging methods like total internal reflection fluorescence microscopy are unfortunately not yet applicable to the study of these small central nervous system synapses. It is interesting to note that in preparations where it could be applied, rather immobile secretory granules or vesicles at the membrane displayed confined diffusion with diffusion constants and cage sizes very similar to those reported here. Steyer and coworkers found for granule motion in endocrine cells diffusion constants as low as D = 2 × 10−4 _μ_m2/s and cage sizes ∼70 nm (48). The FRAP method has been used for studying vesicle mobility in small synapses, but it has not been possible so far to derive a quantitative model for vesicle mobility. Most of our knowledge on vesicle mobility in small hippocampal synapses so far was inferred either from exoendocytosis measurements or from studies of other model systems.
Besides this, FFS offers several other advantages: a sensitivity down to very few and/or even single vesicle level and a time resolution down to milliseconds. However, besides its great potential for investigating synaptic structure and function, confocal spot detection has some shortcomings. We were only able to assign average cage sizes and diffusion coefficients and could not differentiate, e.g., between vesicles docked at the active zone or positioned in the middle or periphery of the vesicle cluster as any spectroscopic technique in general lacks spatial information. If, however, vesicles belonging to specific pools could be stained selectively, spot confocal detection would also allow studying the mobility of vesicles in individual pools and thus open up an avenue to elucidate the mechanisms of postendocytic vesicle trafficking in small central nervous synaptic boutons. This study, however, was only carried out in resting boutons. An extension to boutons during stimulation will require an extension of the theory to the nonstationary case.
The method can certainly be easily adjusted for studying dynamics in larger synapses like calyx of held or frog neuromuscular junction preparations. It only requires a standard fluorescence correlation spectroscopy setup and can thus be easily adapted by all researchers interested in vesicle dynamics. This method might be especially suited for screening for altered vesicle mobility in null-mutant mice where side effects on exoendocytosis might have masked a major role in mobility, thus leading to opposing results in electrophysiological recordings for different experimental conditions.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
[supplemental]
Acknowledgments
We thank Erwin Neher for encouragement and fruitful discussions throughout this work, Michael Pilot for expert technical assistance, and Olexiy Kochubey for help with programming and modeling.
This work was supported by grants from the Deutsche Forschungsgemeinschaft (SFB 406 and GRK 723 to J.K.) and a fellowship from the Boehringer Ingelheim Fonds (E.A.L.).
Randolf Jordan and Edward A. Lemke contributed equally to this work.
References
- 1.Betz, W. J., and J. K. Angleson. 1998. The synaptic vesicle cycle. Annu. Rev. Physiol. 60:347–363. [DOI] [PubMed] [Google Scholar]
- 2.Matthews, G. 2004. Cycling the synapse; scenic versus direct routes for vesicles. Neuron. 44:223–226. [DOI] [PubMed] [Google Scholar]
- 3.Henkel, A. W., J. Lubke, and W. J. Betz. 1996. FM1-43 dye ultrastructural localization in and release from frog motor nerve terminals. Proc. Natl. Acad. Sci. USA. 93:1918–1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Harata, N., T. A. Ryan, S. J. Smith, J. Buchanan, and R. W. Tsien. 2001. Visualizing recycling synaptic vesicles in hippocampal neurons by FM 1-43 photoconversion. Proc. Natl. Acad. Sci. USA. 98:12748–12753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Rizzoli, S. O., and W. J. Betz. 2004. The structural organization of the readily releasable pool of synaptic vesicles. Science. 303:2037–2039. [DOI] [PubMed] [Google Scholar]
- 6.Ryan, T. A. 1999. Inhibitors of myosin light chain kinase block synaptic vesicle pool mobilization during action potential firing. J. Neurosci. 19:1317–1323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Doussau, F., and G. J. Augustine. 2000. The actin cytoskeleton and neurotransmitter release: an overview. Biochimie. 82:353–363. [DOI] [PubMed] [Google Scholar]
- 8.Rizzoli, S. O., and W. J. Betz. 2005. Synaptic vesicle pools. Nat. Rev. Neurosci. 6:57–69. [DOI] [PubMed] [Google Scholar]
- 9.Pyle, J. L., E. T. Kavalali, E. S. Piedras-Renteria, and R. W. Tsien. 2000. Rapid reuse of readily releasable pool vesicles at hippocampal synapses. Neuron. 28:221–231. [DOI] [PubMed] [Google Scholar]
- 10.Richards, D. A., C. Guatimosim, and W. J. Betz. 2000. Two endocytic recycling routes selectively fill two vesicle pools in frog motor nerve terminals. Neuron. 27:551–559. [DOI] [PubMed] [Google Scholar]
- 11.Richards, D. A., C. Guatimosim, S. O. Rizzoli, and W. J. Betz. 2003. Synaptic vesicle pools at the frog neuromuscular junction. Neuron. 39:529–541. [DOI] [PubMed] [Google Scholar]
- 12.Schikorski, T., and C. F. Stevens. 2001. Morphological correlates of functionally defined synaptic vesicle populations. Nat. Neurosci. 4:391–395. [DOI] [PubMed] [Google Scholar]
- 13.Schikorski, T., and C. F. Stevens. 1997. Quantitative ultrastructural analysis of hippocampal excitatory synapses. J. Neurosci. 17:5858–5867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Steyer, J. A., H. Horstmann, and W. Almers. 1997. Transport, docking and exocytosis of single secretory granules in live chromaffin cells. Nature. 388:474–478. [DOI] [PubMed] [Google Scholar]
- 15.Zenisek, D., J. A. Steyer, and W. Almers. 2000. Transport, capture and exocytosis of single synaptic vesicles at active zones. Nature. 406:849–854. [DOI] [PubMed] [Google Scholar]
- 16.Kraszewski, K., L. Daniell, O. Mundigl, and P. De Camilli. 1996. Mobility of synaptic vesicles in nerve endings monitored by recovery from photobleaching of synaptic vesicle-associated fluorescence. J. Neurosci. 16:5905–5913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Henkel, A. W., L. L. Simpson, R. M. Ridge, and W. J. Betz. 1996. Synaptic vesicle movements monitored by fluorescence recovery after photobleaching in nerve terminals stained with FM1-43. J. Neurosci. 16:3960–3967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Magde, D., E. Elson, and W. W. Webb. 1972. Thermodynamic fluctuations in a reacting system-measurement by fluorescence correlation spectroscopy. Phys. Rev. Lett. 29:705–708. [Google Scholar]
- 19.Klingauf, J., E. T. Kavalali, and R. W. Tsien. 1998. Kinetics and regulation of fast endocytosis at hippocampal synapses. Nature. 394:581–585. [DOI] [PubMed] [Google Scholar]
- 20.Widengren, J., U. Mets, and R. Rigler. 1995. Fluorescence correlation spectroscopy of triplet sates in solution: a theoretical and experimental study. J. Phys. Chem. 99:13368–13379. [Google Scholar]
- 21.Gennerich, A., and D. Schild. 2000. Fluorescence correlation spectroscopy in small cytosolic compartments depends critically on the diffusion model used. Biophys. J. 79:3294–3306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.DiGregorio, D. A., A. Peskoff, and J. L. Vergara. 1999. Measurement of action potential-induced presynaptic calcium domains at a cultured neuromuscular junction. J. Neurosci. 19:7846–7859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nielsen, T. A., D. A. DiGregorio, and R. A. Silver. 2004. Modulation of glutamate mobility reveals the mechanism underlying slow-rising AMPAR EPSCs and the diffusion coefficient in the synaptic cleft. Neuron. 42:757–771. [DOI] [PubMed] [Google Scholar]
- 24.Qian, H., and E. L. Elson. 1990. On the analysis of high order moments of fluorescence fluctuations. Biophys. J. 57:375–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Qian, H., and E. L. Elson. 1990. Distribution of molecular aggregation by analysis of fluctuation moments. Proc. Natl. Acad. Sci. USA. 87:5479–5483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Betz, W. J., and G. S. Bewick. 1992. Optical analysis of synaptic vesicle recycling at the frog neuromuscular junction. Science. 255:200–203. [DOI] [PubMed] [Google Scholar]
- 27.Fischer, M., S. Kaech, D. Knutti, and A. Matus. 1998. Rapid actin-based plasticity in dendritic spines. Neuron. 20:847–854. [DOI] [PubMed] [Google Scholar]
- 28.Dunaevsky, A., A. Tashiro, A. Majewska, C. Mason, and R. Yuste. 1999. Developmental regulation of spine motility in the mammalian central nervous system. Proc. Natl. Acad. Sci. USA. 96:13438–13443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kask, P., R. Guenther, and P. Axhausen. 1997. Statistical accuracy in fluorescence fluctuation experiments. Eur. Biophys. J. 25:163–169. [Google Scholar]
- 30.Aravanis, A. M., J. L. Pyle, and R. W. Tsien. 2003. Single synaptic vesicles fusing transiently and successively without loss of identity. Nature. 423:643–647. [DOI] [PubMed] [Google Scholar]
- 31.Murthy, V. N., and C. F. Stevens. 1998. Synaptic vesicles retain their identity through the endocytic cycle. Nature. 392:497–501. [DOI] [PubMed] [Google Scholar]
- 32.Ryan, T. A., H. Reuter, and S. J. Smith. 1997. Optical detection of a quantal presynaptic membrane turnover. Nature. 388:478–482. [DOI] [PubMed] [Google Scholar]
- 33.Murthy, V. N., and C. F. Stevens. 1999. Reversal of synaptic vesicle docking at central synapses. Nat. Neurosci. 2:503–507. [DOI] [PubMed] [Google Scholar]
- 34.Holt, M., A. Cooke, A. Neef, and L. Lagnado. 2004. High mobility of vesicles supports continuous exocytosis at a ribbon synapse. Curr. Biol. 14:173–183. [DOI] [PubMed] [Google Scholar]
- 35.Rea, R., J. Li, A. Dharia, E. S. Levitan, P. Sterling, and R. H. Kramer. 2004. Streamlined synaptic vesicle cycle in cone photoreceptor terminals. Neuron. 41:755–766. [DOI] [PubMed] [Google Scholar]
- 36.Magde, D., E. L. Elson, and W. W. Webb. 1974. Fluorescence correlation spectroscopy. II. An experimental realization. Biopolymers. 13:29–61. [DOI] [PubMed] [Google Scholar]
- 37.Thompson, N. L. 1989. Fluorescence correlation spectroscopy. In Topics in Fluorescence Spectroscopy. J. R. Lakowicz, editor. Plenum Press, New York.
- 38.Saitoh, M., T. Ishikawa, S. Matsushima, M. Naka, and H. Hidaka. 1987. Selective inhibition of catalytic activity of smooth muscle myosin light chain kinase. J. Biol. Chem. 262:7796–7801. [PubMed] [Google Scholar]
- 39.Henkel, A. W., and W. J. Betz. 1995. Monitoring of black widow spider venom (BWSV) induced exo- and endocytosis in living frog motor nerve terminals with FM1-43. Neuropharmacology. 34:1397–1406. [DOI] [PubMed] [Google Scholar]
- 40.Becherer, U., C. Guatimosim, and W. Betz. 2001. Effects of staurosporine on exocytosis and endocytosis at frog motor nerve terminals. J. Neurosci. 21:782–787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Asano, M., K. Matsunaga, M. Miura, K. M. Ito, M. Seto, K. Sakurada, H. Nagumo, Y. Sasaki, and K. Ito. 1995. Selectivity of action of staurosporine on Ca2+ movements and contractions in vascular smooth muscles. Eur. J. Pharmacol. 294:693–701. [DOI] [PubMed] [Google Scholar]
- 42.Greengard, P., F. Valtorta, A. J. Czernik, and F. Benfenati. 1993. Synaptic vesicle phosphoproteins and regulation of synaptic function. Science. 259:780–785. [DOI] [PubMed] [Google Scholar]
- 43.Betz, W. J., and A. Henkel. 1994. Okadaic acid disrupts clusters of synaptic vesicles in frog motor nerve terminals. J. Cell Biol. 124:843–854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kraszewski, K., O. Mundigl, L. Daniell, C. Verderio, M. Matteoli, and P. De Camilli. 1995. Synaptic vesicle dynamics in living cultured hippocampal neurons visualized with CY3-conjugated antibodies directed against the lumenal domain of synaptotagmin. J. Neurosci. 15:4328–4342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gong, M. C., P. Cohen, T. Kitazawa, M. Ikebe, M. Masuo, A. P. Somlyo, and A. V. Somlyo. 1992. Myosin light chain phosphatase activities and the effects of phosphatase inhibitors in tonic and phasic smooth muscle. J. Biol. Chem. 267:14662–14668. [PubMed] [Google Scholar]
- 46.Chen, F., and P. D. Wagner. 1998. Pertussis toxin modification of PC12 cells lowers cytoskeletal F-actin and enhances norepinephrine secretion: involvement of protein kinase C and protein phosphatases. Arch. Physiol. Biochem. 105:317–328. [PubMed] [Google Scholar]
- 47.Sankaranarayanan, S., P. P. Atluri, and T. A. Ryan. 2003. Actin has a molecular scaffolding, not propulsive, role in presynaptic function. Nat. Neurosci. 6:127–135. [DOI] [PubMed] [Google Scholar]
- 48.Steyer, J. A., and W. Almers. 1999. Tracking single secretory granules in live chromaffin cells by evanescent-field fluorescence microscopy. Biophys. J. 76:2262–2271. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
[supplemental]