Is the Mechanical Activity of Epithelial Cells Controlled by Deformations or Forces? (original) (raw)

Abstract

The traction forces developed by cells depend strongly on the substrate rigidity. In this letter, we characterize quantitatively this effect on MDCK epithelial cells by using a microfabricated force sensor consisting in a high-density array of soft pillars whose stiffness can be tailored by changing their height and radius to obtain a rigidity range from 2 nN/_μ_m up to 130 nN/_μ_m. We find that the forces exerted by the cells are proportional to the spring constant of the pillars meaning that, on average, the cells deform the pillars by the same amount whatever their rigidity. The relevant parameter may thus be a deformation rather than a force. These dynamic observations are correlated with the reinforcement of focal adhesions that increases with the substrate rigidity.

Cell adhesion and migration are governed not only by chemical signalization processes but also by mechanical interactions. It has long been assumed that the measurement of the traction forces between the cells and their surrounding environment was a good way to quantify these interactions. Indeed, pioneer experiments using optical tweezers have measured forces in the range of the nanonewton but have also shown that they depend on an effective rigidity of the extra cellular matrix (1). Further studies using deformable substrates have mapped the traction forces (2–6) and have confirmed that cell mechanics strongly depend on the rigidity of the substrate (7–9).

In this study, we have used a dense and regular array of independent silicone elastomer microposts (10) to map the cell traction forces at a subcellular level and to quantify the effects of the stiffness of the substrate. Local traction forces on each of these vertical micropillars were determined by measuring their deflections on video-captured images using a homemade multiple particle tracking software (10). The accuracy on the displacement of the top of the pillars was ∼40 nm. For small deformations, the deflection of a post is directly proportional to the lateral force applied on its top via a spring constant. We obtain the following relationship between the force F and the deflection of the post 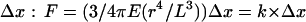Inline graphic (Eq. 1), where r is the radius of the pillar, L its height, and E the Young's modulus of the elastomer (∼2 MPa) (11); k is the spring constant of the pillars. Surfaces of different spring constants were obtained by changing the geometrical parameters of the pillars (length and radius), according to Eq. 1. We varied the dimensions of the posts from 1 to 2 _μ_m in diameter and from 1.6 to 6 _μ_m in height leading to a wide range of spring constants, from 2 to 130 nN/_μ_m.

To culture MDCK cells, these microfabricated force sensor arrays were immersed in a fibronectin solution. Capillarity ensures that this solution does not penetrate between the pillars and thus that fibronectin only adsorbs at their top preventing cells to enter between the posts (Fig. 1). The experiments were performed on islands of subconfluent MDCK cells containing 10–20 cells. For each experiment, images were captured over time periods of several hours. The forces detected for all the pillars were collected into histograms (Fig. 2, inset). Despite the large width of the distribution of the force magnitude due to the variability of the mechanical activity within an island of cells (10), the mean value 〈_F_〉 of the forces in these histograms was strongly correlated to the surface stiffness as can be observed on Fig. 2 where we have plotted 〈_F_〉 versus k (blue plot). These data are well fitted by a linear function (Fig. 2, blue line to be compared with the dashed line of slope = 1). By considering the histograms tails, the same dependence was found for the highest forces, _F_max, detected within cellular assemblies (red line). These maximal traction forces, about one order of magnitude larger than the mean value, are caused by the contribution of the lamellipodium activity at the periphery of the cell monolayer (10). These experiments were conducted on microfabricated force sensor arrays of different surface densities demonstrating that between 10 and 40%, the cells are insensitive to this parameter (Fig. 2). By increasing the stiffness even more, one expects to reach a plateau but the force resolution on very rigid posts did not allow us to study this regime.

FIGURE 1.

FIGURE 1

(A) Distribution of fluorescently labeled fibronectin (red). (B) Scanning electron micrograph of edge detail of a MDCK monolayer showing cell-to-substrate interactions. Scale bars correspond to 5 _μ_m.

FIGURE 2.

FIGURE 2

Log-log plot of the force as a function of substrate rigidity. 〈_F_〉 (blue) and _F_max (red) within an island of cells are represented for different surface densities (ratio of the post surface over the total surface) 10% (○), 22% (□), and 40% (▵). Open and solid symbols, respectively, correspond to pillars of 1 and 2 _μ_m in diameter. The slope of the dashed line is 1. (Inset) Typical histogram of force distribution (spring constant 64 nN/_μ_m).

Qualitatively, these results are consistent with previous studies made on continuous flexible substrates that show that softer surfaces induce an enhancement of fluctuations at the cell boundaries, and a decrease in force magnitudes (7,8). Here, we quantitatively demonstrate that the forces exerted by cells are proportional to the substrate rigidity meaning that the mean displacement of the pillars remains constant over the two decades of our microposts flexibility. This deformation is found to be ∼130 ± 20 nm if we consider the average force.

The organization of stress fibers and focal adhesions is modulated by the stiffness of the substrate (8,9). To test further the correlation between traction forces and focal contacts, we have studied the distribution of vinculin expression as a marker for focal adhesion formation. Cells were labeled and imaged by immunofluorescence microscopy to localize vinculin expression. On flexible substrates (∼2 nN/_μ_m; Fig. 3, A and B), adhesion sites appeared as blurred spots irregularly distributed. In contrast, cells lying on more rigid ones (∼70 nN/_μ_m, Fig. 3, C and D) formed stable and well-defined elongated focal adhesions. Taken together, these results demonstrate that the reinforcement of focal adhesions appeared only on stiff substrates, where large forces were observed.

FIGURE 3.

FIGURE 3

(A and C) Confocal images of immunofluorescence staining of the focal adhesion protein vinculin for different substrate rigidities (pillar spring constants, respectively, 2 and 71 nN/_μ_m). (B and D) Details corresponding to the indicated regions in panels A and C, respectively. Scale bars correspond to 10 _μ_m.

To compare our experiments based on discrete substrates with the case of continuous gels, it is useful to introduce an effective Young's modulus, _E_eq, for the micropillar arrays corresponding to an equivalent continuous elastic substrate. For such substrates, the force-displacement relation is given by Landau and Lifschitz (11): 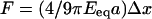Inline graphic (Eq. 2), where a is a characteristic length; a corresponds to the radius of the pillars in our case or to the mean size of a focal adhesion for continuous substrates. In any case, it is of the order of the micrometer. By varying the spring constants of the posts from 2 to 130 nN/_μ_m, we obtained corresponding _E_eq values ranging from 1 to 100 kPa. Numerous large focal adhesions were only observed on stiff substrates (Fig. 3, C and D, _E_eq ∼ 100 kPa). For _E_eq < 10 kPa, focal contacts are more diffuse. These ranges of the Young's modulus values are in agreement with previous studies on flexible continuous gels (8,9).

In conclusion, we found that epithelial cell traction forces are proportional to the substrate rigidity implying that the deformation remains constant. This deformation is strongly correlated to the formation of focal adhesions. Although the intracellular signaling processes remain to be clarified, these results question the commonly accepted mechanism of an active feedback based on a probing of the surface stiffness by the cells. These experiments suggest an alternative possible model where a characteristic intracellular length controls the amount of deformation.

Acknowledgments

We thank Robert H. Austin, Julien Browaeys, Philippe Chavrier, Jacques Prost, Olivia du Roure, Alain Richert, and Manuel Théry. This work was performed in part at the Cornell Nano-Scale Science & Technology Facility.

This work was supported by grants from the Ministère de la Recherche, the CNRS, the Institut Curie, the Association pour la Recherche contre le Cancer, and the Fondation de France.

References