In vivo dynamics of T cell activation, proliferation, and death in HIV-1 infection: Why are CD4+ but not CD8+ T cells depleted? (original) (raw)
Abstract
Deuterated glucose labeling was used to measure the in vivo turnover of T lymphocytes. A realistic T cell kinetic model, with populations of resting and activated T cells, was fitted to d-glucose labeling data from healthy and HIV-1-infected individuals before and after antiretroviral treatment. Our analysis highlights why HIV-1 infection, which increases the fraction of both CD4+ and CD8+ T lymphocytes that are proliferating (Ki67+), leads to CD4 but not CD8 depletion. We find that HIV-1 infection tends to increase the rates of death and proliferation of activated CD4+ T cells, and to increase the rate at which resting CD4 T cells become activated, but does not increase the fraction of activated CD4+ T cells, consistent with their preferential loss in HIV-1-infected individuals. In contrast, HIV-1 infection does not lead to an increase in proliferation or death rates of activated CD8+ T cells, but did increase the fraction of activated CD8+ T cells, consistent with these cells remaining in an activated state longer and undergoing more rounds of proliferation than CD4+ T cells. Our results also explain why telomeres shorten in CD8+ cells, but not in CD4+ cells of HIV-1-infected patients, compared with age-matched controls.
Infection with HIV-1 leads to impairment of immune functions, due in large part to a decrease in the number of CD4+ T cells. Several explanations for the reduction in CD4+ T cell counts have been proposed: impaired production of T cells by the thymus, decreased proliferative capacity of CD4+ T cells, and increased death due to HIV-1 cytopathicity or apoptosis as a consequence of increased immune activation. Interestingly, the mechanisms responsible for the decline in CD4+ T cells do not act equally on CD8+ T cells, which increase until the late stages of HIV-1 infection.
Several methods have been used to assess the dynamics of T cells in healthy and infected individuals, sometimes giving different, even contradictory, results. These methods include the decrease in telomere length as a surrogate marker of T cell proliferation (1, 2); measurements of proliferation with Ki67, a natural marker expressed by cells in late G1 and successive stages of the cell cycle (3, 4); and direct labeling of dividing cells with 5-bromodeoxyuridine (BrdUrd) and deuterated glucose (d-glucose). Human and macaque studies with BrdUrd have shown that both CD4 and CD8 T cell subsets have a 3- to 4-fold increase in turnover during HIV/simian immunodeficiency virus **(**SIV) infection (5–8). In addition, Lempicki et al. (5) showed that a marked reduction in the turnover rates of CD4+ and CD8+ T cells occurred after initiation of highly active antiretroviral therapy. Using d-glucose labeling, Hellerstein et al. (9) also reported enhanced turnover in both CD4+ and CD8+ lymphocyte populations of untreated HIV-1-infected individuals.
In most of these studies, similar dynamics were found for CD4+ and CD8+ T cells. In particular, both subsets showed similar increases in proliferation rates in HIV-1-infected vs. uninfected individuals, the only exception being that CD8+ T cell telomeres were shortened in HIV-1-infected individuals but those of CD4+ T cells were not. The results of all these studies, which are compatible with similar enhanced turnover of both CD4+ and CD8+ T cells, do not explain why CD4+ T cells are depleted in HIV-1 infection, while CD8+ T cells are not.
We recently reported on a study with d-glucose where an uninfected-control group was compared with an HIV-1-infected group followed longitudinally, before and after the initiation of highly active antiretroviral therapy (HAART; ref. 10). Here, we analyze the data from that study by using a mathematical model that takes into consideration that only a fraction of the T cell population is proliferating at any given moment (6, 11). This observation is implemented in the model by including populations of resting and activated cells. Labeling occurs mainly in the activated cell population, through proliferation, but the activated cell population also has an input from the resting population, through an activation term. We have analyzed this model mathematically (11), and here use it to fit the available data. The results obtained give insight into the differences between CD4+ and CD8+ T cell dynamics in the context of HIV-1 infection.
Materials and Methods
In Vivo Labeling of CD4+ and CD8+ T Cells.
As described (10), uninfected (n = 4) and HIV-1-infected (n = 7), therapy-naive volunteers received a 7-day infusion of d-glucose, during which time blood was drawn every 1 or 2 days to assess labeling of T cells. These individuals were then followed for up to 6 wk, with blood samples collected every week. Some of the infected patients (n = 5) started antiretroviral therapy, and shortly after (1–2.5 months) returned for a second period of d-glucose infusion to study the impact of short-term treatment on T cell dynamics. Of these five, three returned for a third period of d-glucose infusion after 8–12.5 months on treatment, allowing us to study the effect of long-term therapy. All subjects gave informed consent, and the study was approved by the Institutional Review Board of The Rockefeller University Hospital. Cells were sorted into CD4+ and CD8+ T cell fractions, and enrichment of dA in their DNA was measured by mass spectrometry. The data are given as percentage of DNA labeled. Because glucose is rapidly metabolized (12), d-glucose is to a good approximation only available for incorporation into cellular DNA during d-glucose infusion.
Model of T Cell Labeling in Vivo.
We developed a mathematical model to analyze this experiment and to estimate the proliferation and death rates from the experimental measurements of the fraction of labeled DNA as a function of time (11). This model is a generalization of the one presented in Mohri et al. (10), in which we explicitly model the source of proliferating cells as activation from a resting compartment. Thus, we account for all labeling of DNA within the model populations.
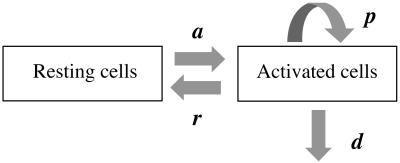
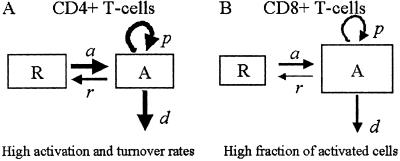
The model (Fig. 1) has two populations, resting cells, R, and activated cells, A. Here, resting and activated refer to the cell's state during the time of the experiment. Thus, it is possible that resting cells proliferate at a small rate π, but we assume that this is negligible during the period of the experiments. Resting cells die at a rate dR. Preliminary data fitting showed that the value of dR was very small in all cases (of the order of 10−3 day−1, i.e., half-lives longer than 6 mo), and that the fits were qualitatively the same and estimates of other parameters approximately the same with dR = 0 (data not shown). That is, on the timescale of this experiment, the death rate of the resting population does not contribute to the dynamics. Thus, to reduce the number of estimated parameters and make the fits more robust, we set dR = 0 in the analysis reported below (for the full model see ref. 11). Finally, resting cells can be activated at rate a. Activated cells proliferate at rate p, die at rate d, and revert to the resting state at rate r per cell. The model has no external sources, from other dynamically active compartments, as in previous models (6, 7, 10, 13). We assume that thymic input, presumably into the resting population, is not important for this short-term experiment, because thymic production is small in adults (14), and may even be smaller in HIV-1+ individuals (15). In addition, we assume that T cells in lymph nodes, where most T cell proliferation occurs, and in peripheral blood are in equilibrium, as described (6, 10). However, we allow for a delay between the initiation of d-glucose infusion and the appearance of labeled cells in the periphery. This delay is also a parameter of the model (11). The equations describing the behavior of the two populations, R and A, are then (11):
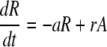
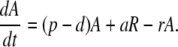
[1]
Fig 1.
Scheme of the model with two cell populations, resting and activated, used to fit d-glucose experimental data.
d-glucose is nontoxic and does not interfere with cellular dynamics (12). Because these studies are short-term, we assume the T cell populations are at steady state. That is, we assume the numbers of T cells in the resting, R, and activated, A, populations do not change during the course of the experiment. From Eqs. 1, this steady state condition implies that activated cells die and proliferate at the same rate, i.e., p = d. We note that this condition is valid only when dR = 0. In addition, at steady state, the fraction of activated cells, fA = A/(R + A), is constant, and from the steady state condition, aR = rA, we have fA = a/(a + r). Hence, we can calculate the fraction of activated cells, if a and r are estimated from the data. The fraction of resting cells is fR = 1 − fA. From these fractions, we define the average T cell death and proliferation rates as _d_ave = dRfR + dfA = dfA and _p_ave = πfR + pfA = pfA, respectively, because we assume dR = 0 and π = 0.
During d-glucose infusion, newly formed DNA strands will incorporate deoxyribonucleotides labeled with deuterium. Thus, at any time after the start of the infusion, in the activated cell pool there will be labeled DNA (LA), and unlabeled DNA (UA). Because we allow reversion of activated cells to the resting state, there will also be labeled DNA in resting cells (LR), as well as unlabeled DNA (UR). From Eqs. 1, we deduce that the amount of unlabeled and labeled DNA in the resting and activated populations during the d-glucose infusion obey the following equations:
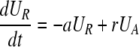
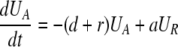
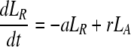
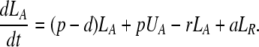
[2]
Notice that proliferation increases the amount of labeled DNA in activated cells (LA), but does not reduce the amount of unlabeled DNA, because of the semiconservative nature of DNA replication, in which the template strand remains unchanged and thus only the newly synthesized strand is labeled.
After d-glucose infusion is stopped, labeled glucose is quickly depleted (12, 16), and cells that divide no longer incorporate deuterium into their DNA. The changes in the amounts of unlabeled and labeled DNA in the resting and activated populations are described by the equations:
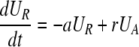
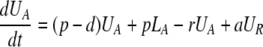
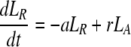
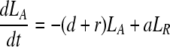
[3]
where now DNA synthesis in dividing cells increases only unlabeled DNA, UA.
We used Eqs. 2 and 3 to fit data obtained during the labeling and delabeling periods of the experiment (10), respectively. The model has four parameters: p, d, r, and a. However, the proliferation rate is obtained from the steady state condition, p = d, and, in our fitting, we use fA instead of r, because r = a(1 − fA)/fA. Thus, only three parameters are estimated from the data: fA, d, and a.
Statistical Analysis and Data Fitting.
The data were fitted by using nonlinear least squares regression. The results were analyzed by using the Wilcoxon-rank sum test and Wilcoxon-signed rank test for paired data, unless otherwise indicated. Significance was defined at the 0.05 level.
Results
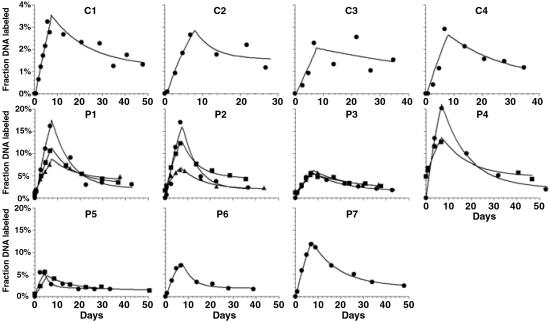
We used the model to fit experimental data on the fraction of labeled DNA extracted from purified CD4+ and CD8+ T cell populations. In Fig. 2, the fits of the model to the CD4+ T cell data are shown for the four uninfected and the seven HIV-1-infected individuals. In every case, the model provides a good fit to the experimental data. This data fitting allowed us to estimate the parameters of T cell dynamics for the four groups of patients (see Materials and Methods): uninfected, infected untreated, short course of HAART, and long course of HAART (Table 1).
Fig 2.
Best fit of the model to the CD4+ DNA labeling data of each subject studied, both uninfected (C1–C4) and infected (P1–P7). The data are indicated by the following symbols: •, first infusion study; ▪, second infusion study; and ▴, third infusion study. The lines are the best-fit model solutions.
Table 1.
Parameter estimates for healthy controls (C1–C4) and HIV-1-infected patients (P1–P7), obtained by fitting the model in Fig. 1 to the d-glucose data in ref. 10
| Subject | CD4+ T cells | CD8+ T cells | ||||||
|---|---|---|---|---|---|---|---|---|
| d | fA | a | r | d | fA | a | r | |
| Control | ||||||||
| C1 | 0.043 | 0.127 | 0.003 | 0.019 | 0.078 | 0.053 | 0.001 | 0.015 |
| C2 | 0.132 | 0.043 | 0.003 | 0.078 | 0.019 | 0.120 | 0.000 | 0.000 |
| C3 | 0.013 | 0.219 | 0.000 | 0.000 | 0.010 | 0.212 | 0.000 | 0.000 |
| C4 | 0.039 | 0.105 | 0.001 | 0.009 | 0.042 | 0.054 | 0.003 | 0.047 |
| Mean | 0.057 | 0.124 | 0.002 | 0.026 | 0.037 | 0.110 | 0.001 | 0.015 |
| SE | 0.026 | 0.037 | 0.001 | 0.018 | 0.015 | 0.037 | 0.001 | 0.011 |
| Untreated | ||||||||
| P1-I | 0.109 | 0.312 | 0.005 | 0.011 | 0.075 | 0.490 | 0.010 | 0.010 |
| P2-I | 0.142 | 0.249 | 0.004 | 0.012 | 0.096 | 0.189 | 0.002 | 0.009 |
| P3-I | 0.056 | 0.178 | 0.003 | 0.016 | 0.046 | 0.229 | 0.004 | 0.013 |
| P4-I | 0.081 | 0.488 | 0.009 | 0.009 | 0.033 | 0.721 | 0.000 | 0.000 |
| P5-I | 0.303 | 0.066 | 0.006 | 0.090 | 0.053 | 0.528 | 0.000 | 0.000 |
| P6-I | 0.190 | 0.100 | 0.004 | 0.033 | 0.045 | 0.538 | 0.005 | 0.005 |
| P7-I | 0.073 | 0.307 | 0.006 | 0.014 | 0.027 | 0.612 | 0.000 | 0.000 |
| Mean | 0.136 | 0.243 | 0.005 | 0.026 | 0.054 | 0.472 | 0.003 | 0.005 |
| SE | 0.033 | 0.055 | 0.001 | 0.011 | 0.009 | 0.074 | 0.001 | 0.002 |
| Short-term treatment | ||||||||
| P1-II | 0.089 | 0.220 | 0.007 | 0.024 | 0.083 | 0.302 | 0.038 | 0.087 |
| P2-II | 0.127 | 0.184 | 0.008 | 0.034 | 0.104 | 0.087 | 0.006 | 0.060 |
| P3-II | 0.037 | 0.204 | 0.002 | 0.008 | 0.025 | 0.199 | 0.026 | 0.104 |
| P4-II | 0.083 | 0.198 | 0.000 | 0.000 | 0.038 | 0.355 | 0.000 | 0.000 |
| P5-II | 0.074 | 0.131 | 0.003 | 0.018 | 0.031 | 0.316 | 0.013 | 0.028 |
| Mean | 0.082 | 0.188 | 0.004 | 0.017 | 0.056 | 0.252 | 0.016 | 0.056 |
| SE | 0.014 | 0.015 | 0.001 | 0.006 | 0.016 | 0.049 | 0.007 | 0.019 |
| Long-term treatment | ||||||||
| P1-III | 0.069 | 0.168 | 0.005 | 0.026 | 0.046 | 0.231 | 0.007 | 0.025 |
| P2-III | 0.099 | 0.100 | 0.000 | 0.002 | NA | NA | NA | NA |
| P3-III | 0.057 | 0.135 | 0.002 | 0.011 | 0.051 | 0.109 | 0.003 | 0.021 |
| Mean | 0.075 | 0.134 | 0.002 | 0.013 | 0.049 | 0.170 | 0.005 | 0.023 |
| SE | 0.013 | 0.020 | 0.002 | 0.009 | 0.003 | 0.061 | 0.002 | 0.002 |
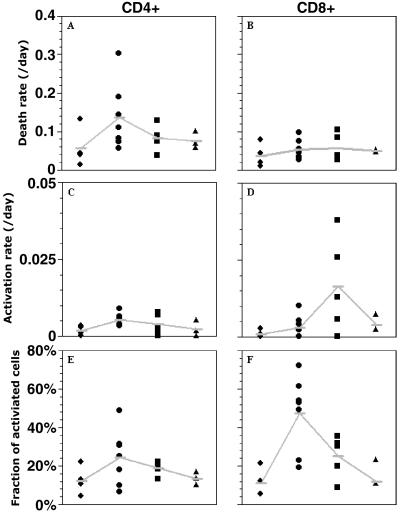
Fig. 3A shows the estimated death rate of activated CD4+ T cells (d), in each uninfected and infected subject studied. There is a trend for higher death rates in infected individuals than in healthy controls (medians 0.11 day−1 vs. 0.04 day−1, respectively, P = 0.07). Effective treatment with viral suppression below the detection limit (10) reduces the death rates of activated CD4+ T cells in infected individuals (medians 0.08 day−1 for short-term HAART, and 0.07 day−1 for long-term HAART), without quite reaching normal values. For CD8+ T cells, the median death rate in the uninfected group is 0.03 day−1, whereas in the untreated, short-term treated and long-term treated groups the median death rates are 0.05 day−1, 0.04 day−1, and 0.05 day−1, respectively (Fig. 3B). There is no statistical difference among these death rates, indicating that activated CD8+ T cells die at the same rate in uninfected and infected individuals. In the activated cell population, the proliferation rate is identical to the death rate, because we assumed steady state.
Fig 3.
Parameter estimates from the fitting of d-glucose data to the model in Fig. 1. (A and B) Death rate of activated cells. (C and D) Transition rate from the resting to the activated population. (E and F) Fraction of activated cells. The four columns in each graph represent the four groups studied: ♦, uninfected; •, infected; ▪, short-term HAART; and ▴, long-term HAART.
Fig. 3 C and D shows the estimated activation rate, a, for CD4+ and CD8+ T cells, respectively. For CD4+ T cells, the activation rate is significantly increased in HIV-1-infected individuals in comparison with healthy controls (median a = 0.005 day−1 vs. a = 0.002 day−1, P = 0.006), indicating that CD4+ T cells are entering the activated compartment faster in infected individuals. However, for CD8+ T cells, the difference in the activation rate between healthy and infected individuals is not significant (P > 0.5). Treatment leads to a reduction in the activation rate of CD4+ T cells. From Fig. 3D, it seems that there might be an unexplained increase in the activation rate of CD8+ T cells in patients treated for a short period, but the difference does not reach significance (P = 0.11).
Fig. 3 E and F indicates that, in the CD4+ and CD8+ T cell populations, respectively, there is a trend toward an increased fraction of activated cells in infected as compared with uninfected individuals. However, only for the CD8+ population is the difference statistically significant, P = 0.01 (P = 0.23 for CD4+ T cells). One reason for this result might be that activated CD4+ T cells in infected individuals die too fast to lead to a significant increase. Treatment reduces the fraction of activated cells. This effect is more pronounced in the CD8+ compartment, because untreated individuals have a much higher fraction of activated cells.
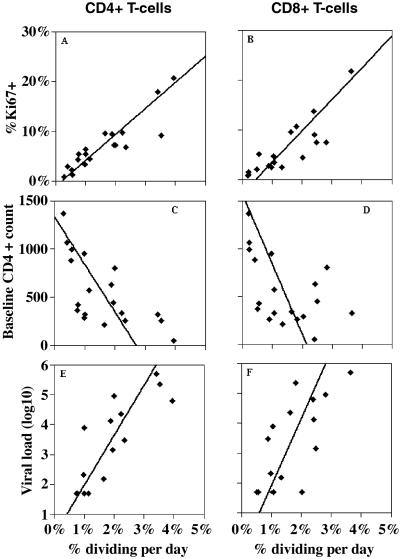
We calculated the fraction of cells dividing per day by multiplying the percentage of activated cells (fA) by the proliferation rate per cell per day (p). We compared our estimates of this fraction with independent measurements, taken at baseline, of the percentage of Ki67+ cells in these individuals. Ki67 is a cell cycle antigen that is expressed in late G1, S, G2, and M phases of the cell cycle (17). The fraction of cells dividing per day is correlated with %Ki67+ cells (P < 10−6, _r_2 = 0.8 for CD4+ T cells, Fig. 4_A_, and _P_ < 10−5, _r_2 = 0.7 for CD8+ T cells, Fig. 4_B_). Also, as was demonstrated for the percentage of cells proliferating measured by %Ki67+ (3), our estimates of the percentage of cells dividing per day are inversely correlated with baseline CD4+ T cells (_P_ = 0.002 and _P_ = 0.036 for dividing CD4+, Fig. 4_C_, and CD8+ T cells, Fig. 4_D_). Finally, the fractions of CD4+ and CD8+ T cells dividing per day are also correlated with the logarithm of baseline viral load (_P_ = 0.0001, _P_ = 0.003, for CD4+ and CD8+ T cells, Figs. 4 _E_ and _F_, respectively). Interestingly, the slope of this correlation is not statistically different for CD4+ and CD8+ T cells (_P_ > 0.4), perhaps indicating a common mechanism of T cell activation for those two lymphocyte populations.
Fig 4.
Correlations between fraction of cells dividing per day and baseline parameters.
Discussion
It has been argued that the dynamics of T cells in HIV-1 infection are driven by a general state of immune activation (4, 7, 8, 18, 27). However, this general state of immune activation must impact CD4+ and CD8+ T cells distinctly, because the dynamics of these two lymphocyte populations are different in HIV-1 infection. During the asymptomatic phase of HIV-1 infection, the CD8+ T cell count is elevated in relation to that of uninfected individuals, whereas the CD4+ T cell count decreases slowly but continuously (19). It is possible that HIV-1 infection plays a role in the depletion of CD4+ T cells, either by direct or indirect effects. Here, we looked at the effects of immune activation and cell death, by using a new model to analyze d-glucose labeling of dividing T cells. Our separation of the T cell population into resting and activated subpopulations means that comparisons between healthy and infected individuals are not hindered by different levels of immune activation.
Fig. 5 represents our findings in schematic form. We have shown that the death and proliferation rates of activated CD8+ T cells, and the activation rate into this pool are not statistically different between HIV-1-infected and uninfected individuals. However, the two groups differ in the state of immune activation, with infected individuals having a much higher fraction of activated CD8+ T cells (larger compartment A in Fig. 5B). Because the fraction of activated cells is fA = a/(a + r), this suggests that, in infected individuals, CD8+ T cells once activated remain activated for longer before returning to rest, i.e., r is lower (thin arrow, r, in Fig. 5B, Table 1). In the CD4+ T cell population, however, we find an increase in the death and proliferation rates of activated cells in infected individuals (bold arrows, p and d, in Fig. 5A) in relation to healthy controls. This discrepancy between CD4+ and CD8+ T cells is compatible with our knowledge that HIV-1 preferentially infects activated CD4+ T cells (20, 21). This higher death rate seen in HIV-1 infection could also be responsible for our observation that the fraction of activated CD4+ T cells in infected patients is not statistically different from the fraction of activated cells in healthy individuals. The enhanced death rate of activated CD4+ T cells in infected individuals prevents a significant build-up in this cell population, even though the rate of transition from the resting to the activated compartment is clearly higher in infected individuals (bold arrow, a, in Fig. 5A). Indeed, we can show that, outside the steady state, the fraction of activated cells decreases with increasing death rate. This result is consistent with our observation that, in infected individuals, the fraction of activated CD8+ T cells is significantly larger than the fraction of activated CD4+ T cells (P = 0.047), but that is not the case in uninfected controls. Finally, because it has been shown that the fraction of Ki67+ CD4+ T cells inversely correlates with CD4+ T cell count (3), another possible reason contributing to our observation of no significant difference in the fraction of activated CD4+ T cells between controls and infected individuals may be that we have two infected individuals with high CD4+ T cell counts (>500).
Fig 5.
Representation of the main findings regarding the differential dynamics of CD4+ (A) and CD8+ (B) T cells. Bold arrows mean that the parameter is increased in relation to normal individuals, and the larger size of the activated population box in CD8+ represents the increase in this population in relation to healthy individuals.
A recent study of the dynamics of T lymphocytes in HIV-1 infection by pulse labeling with BrdUrd found a two-phase decay in the percentage of labeled cells, during the delabeling period of the experiment (6). This decay was analyzed with an empirical two-compartment model of slowly and rapidly proliferating T cells. Their results for CD8+ T cells are in general agreement with our results: increased fraction of activated cells but no difference in death rate between untreated and treated HIV-1-infection. However, our results for the CD4+ T cell populations are in contrast to those in ref. 6. They find that HAART leads to a decrease in the fraction of rapidly proliferating CD4+ cells, with no change in the death rate of this population; whereas we find that HAART decreases the death rate of CD4+ cells, but does not lead to a significant change in the fraction of activated CD4 cells. Two possible reasons for this difference are that in ref. 6 fitting was only done to the decreasing portion of the labeling curve, and an empirical, rather than kinetic, model was used. Because the CD4+ and CD8+ labeling profiles were similar, comparable conclusions were reached about both populations. We also find analogous labeling profiles in CD4+ and CD8+ T cells (10), although we emphasize that there are differences. For example, the loss of label is consistently faster in the CD4+ fraction, indicating that death is faster in CD4+ than CD8+ T cells. Further, in our two-compartment model, Eqs. 2 and 3, the initial up slope of the fraction of labeled DNA (=dfA) depends both on the death rate, d, and the fraction of activated cells, fA, whereas the down slope depends on d. Thus, similar increased up slopes in CD4+ and CD8+ T cells in HIV infection may be due to increased death rate or to increased fraction of activated cells. We can distinguish between these two possibilities by fitting data to the full kinetic labeling curve, and separately estimating d and fA. Doing so indicates that, in CD4+ T cells, the (per cell) death rate is increased whereas, in the CD8+ pool, it is the fraction of labeled activated cells that is increased.
Our results are compatible with and indeed shed light on the reports that telomere lengths are not reduced in CD4+ T cells of HIV-1-infected individuals, but the telomeres of CD8+ T cells are shortened (1, 2). The authors of those studies argued that the decrease in the length of the CD8+ T cell telomeres is compatible with an increase in the division rate of this population, and they proposed two hypotheses to explain the normal telomere length in the CD4+ population: (i) the division rate in the CD4+ T cell compartment of HIV-1-infected individuals is similar to that of uninfected people, or is not increased more than a few fold; or (ii) there is an increased transition rate from naive to memory CD4+ T cells, which increases the average telomere length of memory cells and masks any telomere shortening secondary to increased CD4+ T memory cell proliferation (2). They deemed this second hypothesis less appropriate, because it was argued that similar increases in the transition of naive CD8+ T cells into the memory population should also be expected, and this result would not be compatible with the observed shortening of the telomeres in the CD8+ T cells. Here, we show that indeed there is an increased transition rate from a resting to an activated pool in the CD4+ T cells population, and that this T cell population has higher division rates than in healthy individuals, without a similar increase in the transition rate of CD8+ T cells. Thus, our results support the second hypothesis, assuming our resting and activated populations are mostly composed of naive and memory CD4+ T cells, respectively. In our framework, the telomeres in the CD8+ T cell compartment are shortened on average, because there is a larger proportion of activated CD8+ cells in HIV-1-infected individuals. This explanation is also compatible with the normal division rates that we found in the activated CD8+ T cell compartment; these cells just take longer to return to a resting state and hence divide more times.
Previous studies (22–24) have demonstrated that, in the context of HIV-1 infection, activation markers such as HLA-DR and CD38 can be expressed at levels comparable to the fraction of activated cells estimated here. In our infected individuals, this fraction ranges between 18–49% and 19–72% for CD4+ and CD8+ T cells, respectively (Table 1). We define activated cells as those cells that have the potential to proliferate within the time span of the experiment, and do not claim that they correspond to any defined population expressing specific activation markers. This interpretation is supported by the fact that, numerically, the fraction of activated cells is indistinguishable from the asymptote for the fraction of labeled DNA, that is, the maximum achievable labeling that would result from d-glucose infusion for a long period. When we calculate the percentage of cells dividing per day, i.e., the percentage of activated cells times the proliferation rate of activated cells, we find that only a small percentage of cells are dividing per day: medians 0.5% day−1 and 2.2% day−1 for CD4+ T cells in uninfected and infected individuals, respectively, P = 0.006; and 0.2% day−1 and 2.4% day−1 for CD8+ T cells in uninfected and infected individuals, respectively, P = 0.006. This fraction of cells proliferating per day is strongly correlated with %Ki67+ cells. The slopes of these relationships are 0.19 day and 0.16 day for CD4+ and CD8+ cells, indicating that fewer cells are dividing on any given day than are Ki67+, as has been demonstrated (25).
It is interesting to compare the results obtained here with previous estimates of death and proliferation rates of T cells in HIV-1-infected and healthy individuals. The death rates we report here for activated cells are essentially identical on a patient-by-patient basis to the ones calculated previously with a one-compartment model (10). Moreover, the death rates estimated here are in general agreement with previous studies on SIV infection (7, 8) and HIV-1 infection (5, 9, 26). On the other hand, the proliferation rates estimated here for the activated cells are much higher than the proliferation rates estimated with the one-compartment model (10). However, if we define the average T cell proliferation rate as the weighted average of the proliferation rates in the resting and activated compartments, _p_ave = πfR + pfA (R. J. de Boer, H.M., D.D.H., and A.S.P., unpublished work), then _p_ave = pfA, because we have assumed π = 0. When we use this formula to calculate the average proliferation rate, we recover on a patient-by-patient basis proliferation rates almost identical to the ones presented in ref. 10. Thus, this work makes obvious why we previously found a large disparity between death and proliferation rates. In our previous analysis, by using a model that did not distinguish between resting and activated cells, the estimated death rates were those of the activated population of T cells alone, whereas the proliferation rates corresponded to an average over both the resting and activated populations. With hindsight, this finding is clear from the biology of the system, because proliferation of any cell leads to an increase of labeled DNA, but only death of labeled cells, i.e., those that have divided, leads to a decrease in labeled DNA.
In this paper, we have distinguished the impact of HIV-1 infection on CD4 and CD8 T cells. Whereas the percentages of CD4 and CD8 cells that label with d-glucose or that are Ki67+ are both elevated in HIV-1 infection, this result occurs for different reasons. We found that, for CD8+ T cells, more cells are proliferating due to infection, but with no change in per cell parameters. In contrast, for activated CD4+ T cells, the per cell death rate is elevated in HIV-1-infected individuals, even though the fraction of proliferating cells is not significantly elevated. However, if one calculates the fraction of cells that divide per day (i.e., activated cells times per cell proliferation rate) we find that it is similar for CD4+ (2.2% day−1) and CD8+ (2.4% day−1) T cells in HIV-1-infected individuals, explaining the similar labeling. Thus, whereas short-term labeling experiments cannot tell us why CD4 cells are depleted on a time scale of years, they do show that HIV-1 infection causes fundamental changes in the lifecycle of CD4+ but not CD8+ T cells.
Acknowledgments
We thank our clinical and laboratory collaborators for help in generating the data in the original experiment and R. de Boer and M. Davenport for helpful discussions. This work was partially performed under the auspices of the U.S. Department of Energy and was supported by National Institutes of Health Grants RR06555 and AI28433 (to A.S.P.) and AI40387 (to D.D.H.), and the General Clinical Research Center at The Rockefeller University Hospital.
Abbreviations
- HAART, highly active antiretroviral therapy
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Wolthers K. C., Wisman, G. B. A., Otto, S. A., Husman, A. M. R., Schaft, N., de Wolf, F., Goudsmit, J., Coutinho, R. A., van der Zee, A. G. J., Meyaard, L. & Miedema, F. (1996) Science 274 1543-1547. [DOI] [PubMed] [Google Scholar]
- 2.Wolthers K. C., Noest, A. J., Otto, S. A., Miedema, F. & de Boer, R. J. (1999) AIDS Res. Hum. Retroviruses 15 1053-1062. [DOI] [PubMed] [Google Scholar]
- 3.Sachsenberg N., Perelson, A. S., Yerly, S., Schockmel, G. A., Leduc, D., Hirschel, B. & Perrin, L. (1998) J. Exp. Med. 187 1295-1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Hazenberg M. D., Stuart, J. C., Otto, S. A., Borleffs, J. C. C., Boucher, C. A. B., de Boer, R. J., Miedema, F. & Hamann, D. (2000) Blood 95 249-255. [PubMed] [Google Scholar]
- 5.Lempicki R. A., Kovacs, J. A., Baseler, M. W., Adelsberger, J. W., Dewar, R. L., Natarajan, V., Bosche, M. C., Metcalf, J. A., Stevens, R. A., Lambert, L. A., et al. (2000) Proc. Natl. Acad. Sci. USA 97 13778-13783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kovacs J. A., Lempicki, R. A., Sidorov, I. A., Adelsberger, J. W., Herpin, B., Metcalf, J. A., Sereti, I., Polis, M. A., Davey, R. T., Tavel, J., et al. (2001) J. Exp. Med. 194 1731-1741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mohri H., Bonhoeffer, S., Monard, S., Perelson, A. S. & Ho, D. D. (1998) Science 279 1223-1227. [DOI] [PubMed] [Google Scholar]
- 8.Rosenzweig M., DeMaria, M. A., Harper, D. M., Friedrich, S., Jain, R. K. & Jonhnson, R. P. (1998) Proc. Natl. Acad. Sci. USA 95 6388-6393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hellerstein M., Hanley, M. B., Cesar, D., Siler, S., Papageorgopoulos, C., Wieder, E., Schmidt, D., Hoh, R., Neese, R., Macallan, D., Deeks, S. & McCune, J. M. (1999) Nat. Med. 5 83-89. [DOI] [PubMed] [Google Scholar]
- 10.Mohri H., Perelson, A. S., Tung, K., Ribeiro, R. M., Ramratnam, B., Markowitz, M., Kost, R., Hurley, A., Weinberger, L., Cesar, D., Hellerstein, M. & Ho, D. D. (2001) J. Exp. Med. 194 1277-1287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ribeiro R. M., Mohri, H., Ho, D. D. & Perelson, A. S. (2002) Bull. Math. Biol. 64 385-405. [DOI] [PubMed] [Google Scholar]
- 12.Macallan D. C., Fullerton, C. A., Neese, R. A., Haddock, K., Park, S. S. & Hellerstein, M. K. (1998) Proc. Natl. Acad. Sci. USA 95 708-713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bonhoeffer S., Mohri, H., Ho, D. D. & Perelson, A. S. (2000) J. Immunol. 164 5049-5054. [DOI] [PubMed] [Google Scholar]
- 14.Mackall C. L., Fleisher, T. A., Brown, M. R., Andrich, M. P., Chen, C. C., Feuerstein, I. M., Horowitz, M. E., Magrath, I. T., Shad, A. T., Steinberg, S. M., et al. (1995) N. Engl. J. Med. 332 143-149. [DOI] [PubMed] [Google Scholar]
- 15.Douek D. C., Betts, M. R., Hill, B. J., Little, S. J., Lempicki, R., Metcalf, J. A., Casazza, J., Yoder, C., Adelsberger, J. W., Stevens, R. A., et al. (2001) J. Immunol. 167 6663-6668. [DOI] [PubMed] [Google Scholar]
- 16.Hellerstein M. (1999) Immunol. Today 20 438-441. [DOI] [PubMed] [Google Scholar]
- 17.Gerdes J., Lemke, H., Baisch, H., Wacker, H. H., Schwab, U. & Stein, H. (1984) J. Immunol. 133 1710-1715. [PubMed] [Google Scholar]
- 18.Leng Q., Borkow, G., Weisman, Z., Stein, M., Kalinkovich, A. & Bentwich, Z. (2001) J. Acquired Immune Defic. Syndr. 27 389-397. [DOI] [PubMed] [Google Scholar]
- 19.Pantaleo G. & Fauci, A. S. (1996) Annu. Rev. Microbiol. 50 825-854. [DOI] [PubMed] [Google Scholar]
- 20.Bukrinsky M. I., Stanwick, T. L., Dempsey, M. P. & Stevenson, M. (1991) Science 254 423-427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Saha K., Zhang, J., Gupta, A., Dave, R., Yimen, M. & Zerhouni, B. (2001) Nat. Med. 7 65-72. [DOI] [PubMed] [Google Scholar]
- 22.Ho H. N., Hultin, L. E., Mitsuyasu, R. T., Matud, J. L., Hausner, M. A., Bockstoce, D., Chou, C. C., O'Rourke, S., Taylor, J. M. & Giorgi, J. V. (1993) J. Immunol. 150 3078-3079. [PubMed] [Google Scholar]
- 23.Kestens L., Vanham, G., Gigase, P., Young, G., Hannet, I., Vanlangendonck, F., Hulstaert, F. & Bach, B. A. (1992) AIDS 6 793-797. [DOI] [PubMed] [Google Scholar]
- 24.Orendi J. M., Bloem, A. C., Borleffs, J. C. C., Wijnholds, F. J., deVos, N. M., Nottet, H. S. L., Visser, M. R., Snippe, H., Verhoef, J. & Boucher, C. A. B. (1998) J. Infect. Dis. 178 1279-1287. [DOI] [PubMed] [Google Scholar]
- 25.Combadere B., Blanc, C., Li, T., Carcelain, G., Delaugerre, C., Calvez, V., Tubiana, R., Debre, P., Katlama, C. & Autran, B. (2000) Eur. J. Immunol. 30 3598-3603. [DOI] [PubMed] [Google Scholar]
- 26.McCune J. M., Hanley, M. B., Cesar, D., Halvorsen, R., Hoh, R., Schmidt, D., Wieder, E., Deeks, S., Siler, S., Neese, R. & Hellerstein, M. (2000) J. Clin. Invest. 105 R1-R18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sousa A. E., Carneiro, J., Meier-Schellersheim, M., Grossman, Z. & Victorino, R. M. (2002) J. Immunol. 169 3400-3406. [DOI] [PubMed] [Google Scholar]