Rapid Subfunctionalization Accompanied by Prolonged and Substantial Neofunctionalization in Duplicate Gene Evolution (original) (raw)
Abstract
Gene duplication is the primary source of new genes. Duplicate genes that are stably preserved in genomes usually have divergent functions. The general rules governing the functional divergence, however, are not well understood and are controversial. The neofunctionalization (NF) hypothesis asserts that after duplication one daughter gene retains the ancestral function while the other acquires new functions. In contrast, the subfunctionalization (SF) hypothesis argues that duplicate genes experience degenerate mutations that reduce their joint levels and patterns of activity to that of the single ancestral gene. We here show that neither NF nor SF alone adequately explains the genome-wide patterns of yeast protein interaction and human gene expression for duplicate genes. Instead, our analysis reveals rapid SF, accompanied by prolonged and substantial NF in a large proportion of duplicate genes, suggesting a new model termed subneofunctionalization (SNF). Our results demonstrate that enormous numbers of new functions have originated via gene duplication.
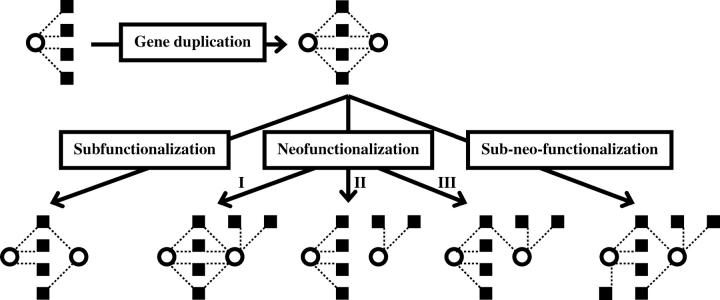
GENE duplication is believed to be the primary source of new genes (Ohno 1970) and “evolution by gene duplication” has emerged as a general principle of biological evolution, evident from the prevalence of duplicate genes in all sequenced genomes of Bacteria, Archaea, and Eukaryota (reviewed in Zhang 2003). Population genetic theories predict that an entirely redundant duplicate copy cannot be maintained in the genome for a long time, as deleterious mutations will accumulate and render the gene nonfunctional. The only exception may be the concerted evolution among certain duplicate genes for which a larger amount of gene product is beneficial (Zhang 2003). In other words, functional divergence between duplicates is usually required for their long-term retention in the genome. The evolutionary process of this divergence, however, is not well understood. The neofunctionalization (NF) hypothesis proposes that after duplication one daughter gene retains the ancestral function while the other can gain novel functions (Ohno 1970). In Ohno's view, the duplicate gene that eventually acquires new function experiences a period of complete functional relaxation, behaving like a pseudogene (Ohno 1973). This, however, does not have to be the case during NF. We therefore consider a broader NF hypothesis in which the gene acquiring new function may retain all (NF-I), none (NF-II), or some (NF-III) of the ancestral functions (Figure 1). Ohno's (1973) NF model is represented by our NF-II. In recent years, an alternative to the NF hypothesis termed the subfunctionalization (SF) hypothesis has been developed. The SF hypothesis argues that ancestral functions of the progenitor gene are partitioned between the duplicates so that the joint levels and patterns of activity of the duplicates are equivalent to that of the progenitor gene (Hughes 1994; Force et al. 1999; Stoltzfus 1999). It should be noted that there are several versions of the SF hypothesis depending on the meaning of “gene function.” For example, Hughes (1994) meant protein function when he formulated the SF hypothesis, whereas Force et al. (1999) emphasized the pattern of gene expression when they proposed SF. Lynch and Force (2000) further formulated their SF hypothesis mathematically in a so-called “duplication-degeneration-complementation (DDC)” model. Because gene function includes both gene expression and protein function, we do not attempt to differentiate the different forms of SF in this work.
Figure 1.—
Evolutionary models of functional divergence between duplicate genes. The three neofunctionalization (NF) models differ in the number of ancestral functions retained by the gene that acquires novel functions. The newly proposed subneofunctionalization (SNF) model is a combination of NF and subfunctionalization (SF). Duplicate genes are depicted by open circles and different gene functions are shown by solid squares. Dotted lines link genes with their functions. In this article, we analyze functions of duplicate genes by their protein interaction partners and expression sites.
Several authors have attempted to test the NF and SF hypotheses at the genomic level by comparing the nucleotide substitution rates of duplicate genes (Van de Peer et al. 2001; Kondrashov et al. 2002; Kellis et al. 2004). Their results were equivocal because the two hypotheses do not make contrasting predictions on substitution rates. For example, asymmetric evolutionary rates between duplicates have been used to support NF (Kellis et al. 2004). But this observation can also be explained by asymmetric SF because the two daughter genes could have inherited different numbers of ancestral functions and thus could be under different levels of functional constraint. The presence of functional constraint (indicated by the ratio of the nonsynonymous to synonymous substitution rates) in both daughter genes immediately after duplication led some to reject the NF hypothesis (Kondrashov et al. 2002), although a certain degree of functional constraint is compatible with a broader NF model (e.g., NF-I and NF-III in Figure 1). Because the NF and SF hypotheses are explicitly about gene function, the most direct test would be to use functional genomic data. In this article, we use genome-wide protein-protein interaction data from yeast and gene (spatial) expression data from human to test the NF and SF models. We show that neither NF nor SF alone adequately explains functional divergence of duplicate genes. Instead, our analysis reveals rapid SF, accompanied by prolonged and substantial NF in a large proportion of duplicate genes, suggesting a new model termed subneofunctionalization (SNF).
MATERIALS AND METHODS
Yeast data and analyses:
A total of 6402 open reading frames (ORFs) in Saccharomyces cerevisiae were downloaded from the Comprehensive Yeast Genome Database at the Munich Information Center for Protein Sequences (MIPS; http://mips.gsf.de/). Among these, 4362 are encoded in the nuclear genome and have gene names in MIPS, the Saccharomyces Genome Database (http://www.yeastgenome.org/), or NCBI (http://www.ncbi.nlm.nih.gov/). These genes formed our database of _c_onfirmed _n_uclear _g_enes (CNG). All (6402 ORFs)-against-all BLASTP searches were carried out with E = 10−20 as the cutoff, and the reciprocal best hits that both appear in CNG were regarded as duplicates. After removing transposable elements, 625 duplicate gene pairs were found. To identify singleton genes, all-against-all BLASTP searches were conducted with E = 0.1 as the cutoff. A total of 1022 members of CNG were found to have no nonself hits and were regarded as singletons for further analysis.
Yeast protein-protein interaction data were obtained from MIPS and from the high-confidence subset of interaction data compiled by von Mering et al. (2002). Only physical interactions were considered. After excluding self-interactions and interactions involving mitochondrion proteins, a nonredundant protein interaction data set containing 9316 pairwise interactions among 4292 ORFs was obtained, including 331 pairs of the above identified duplicate genes and 745 singleton genes.
The DNA sequences of duplicate genes were aligned following the protein sequence alignment by CLUSTALW (Thompson et al. 1994). Numbers of synonymous substitutions per synonymous site (_d_S) between duplicates were estimated by the likelihood method using PAML (Yang 1997). Because codon usage bias may reduce the rate of synonymous substitution, we computed the effective number of codons (ENC; Wright 1990) for all the duplicate genes using codonW (http://bioweb.pasteur.fr/seqanal/interfaces/codonw.html). Following Gu et al. (2002) and Papp et al. (2003), we reanalyzed the data after removing those genes with ENC <35 (48 pairs), but the results did not change. Duplicate genes were grouped according to the _d_S values between duplicates. _d_S = 1 was used as a cutoff because _d_S estimates <1 are relatively reliable. We further divided genes of _d_S < 1 into two groups of approximately equal size using the cutoff of _d_S = 0.25. Because most gene pairs had _d_S > 1 (299 out of 331), we separated these duplicate genes into two groups using _d_S = 20 as the cutoff; use of other cutoffs did not change our results as the two groups were similar in general.
It is generally agreed that an ancestral function of a progenitor gene will be retained in at least one of the daughter genes after duplication and that shared functions between duplicates are ancestral functions. It follows that SF reduces the number of shared functions between duplicates (s), whereas NF does not affect s. In the absence of NF, SF can be measured by ISF = (1 − s/t)[1 − δ/(t − s)] = 1 − (s + δ)/t, where t is the total number of functions of the duplicates and δ is the difference in the number of functions between the duplicates. In the above formula, 1 − s/t measures the proportion of ancestral functions that are no longer shared by the duplicates and 1 − δ/(t − s) measures the extent of SF for these functions. Given t and s, expected values of _I_SF under random SF (i.e., an ancestral function is equally likely to be retained by either of the two genes) can be calculated using probability theories.
To estimate the number of yeast genes produced by duplication, all-against-all BLASTP searches were carried out with E = 10−5 as the cutoff. A minimum of 2250 duplications were necessary to explain the gene families suggested by the BLASTP search results.
Human data and analyses:
The human gene expression data were generated by Su et al. (2002) using the U95A arrays of Affymetrix (http://www.affymetrix.com) and were downloaded from http://expression.gnf.org. Annotation files of U95A arrays were downloaded from Affymetrix. Following Su et al. (2002), we used an average difference (AD) value of 200 as the cutoff for determining whether a gene is expressed in a given tissue. Use of AD = 400 did not change our results. The human protein data containing 28,681 sequences were downloaded from NCBI. All-against-all BLASTP (E = 0.1) was carried out to identify 3283 singletons, including 515 that were found in the gene expression data. A total of 1230 pairs of duplicate genes that appeared in the expression data were identified by Makova and Li (2003) and the _d_S values were estimated by these authors using PAML.
RESULTS
Analysis of yeast protein-protein interaction data:
To test the NF and SF models at the genomic level, it is necessary to use a measure of gene function that is applicable to and available in a large number of genes. Protein-protein interaction is an important function of many protein-coding genes and it has been investigated in the yeast S. cerevisiae by various high-throughput methods in the past few years (summarized in Von Mering et al. 2002). Wagner (2001)(2002, 2003) pioneered the analysis of yeast protein-protein interactions in the context of duplicate gene evolution. But he focused on the functional divergence of duplicate genes without properly differentiating NF from SF. In our analysis, we specifically test the NF and SF models. To reduce errors, particularly false-positive errors, we analyzed the high-confidence interaction data compiled in von Mering et al. (2002) and those annotated in the MIPS database. From the yeast genome, we identified nonredundant pairs of duplicate genes and genes that do not have recognizable duplicate copies in the genome (singleton genes). A total of 331 duplicate gene pairs and 745 singleton genes appeared in our protein interaction data set and these genes were subjected to further analysis.
For a given pair of duplicates, let _a_1 and _a_2 be the numbers of interaction partners for each of them, and let s be the number of shared partners between them (Table 1). Thus, t = _a_1 + _a_2 − s is the total number of partners for the pair. Immediately after gene duplication, the two daughter genes have the same interaction partners. Under the SF model, each daughter gene gradually loses partners, but t remains constant over time (Figure 1). Furthermore, t should equal the number of partners that the progenitor gene had before duplication. We found that the mean t for duplicate genes is 8.57 ± 0.64, which is significantly greater than A = 4.69 ± 0.30, the number of interaction partners that an average singleton gene has (P < 0.0001, _t_-test). The statistical significance was further confirmed by the nonparametric Mann-Whitney _U_-test (P < 0.0001). This observation is inconsistent with the pure SF model and indicates the occurrence of NF.
TABLE 1.
Notations used in this article
| Symbols | Meaning for the yeast protein-protein interaction dataa |
|---|---|
| _a_1 | No. of protein interaction partners for duplicate gene 1 |
| _a_2 | No. of protein interaction partners for duplicate gene 2 |
| s | No. of shared partners between gene 1 and gene 2 |
| t (= _a_1 + _a_2 − s) | Total no. of nonredundant partners for gene 1 and gene 2 |
| A | Average no. of partners per singleton gene |
| S | Average no. of shared partners per randomly picked singleton pair |
| T | Average total no. of nonredundant partners per randomly picked singleton pair |
| δ (= |_a_1 − _a_2 | ) |
| min (_a_1, _a_2) | The smaller of _a_1 and _a_2 |
| max (_a_1, _a_2) | The bigger of _a_1 and _a_2 |
| _d_S | No. of synonymous substitutions per synonymous site between a pair of duplicates |
| _I_SF [= 1 − (s + δ)/_t_] | Subfunctionalization index |
| SF | Subfunctionalization |
| NF | Neofunctionalization |
| SNF | Subneofunctionalization |
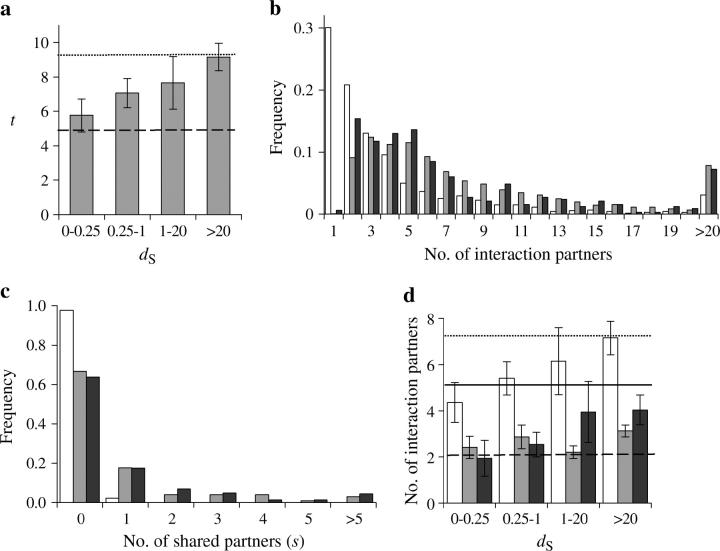
To estimate the speed with which NF occurs, we computed the number of synonymous substitutions per synonymous site (_d_S) between duplicate genes. Because synonymous changes are largely neutral and occur at an approximately constant rate, _d_S is widely used as a proxy for time (Lynch and Conery 2000; Wagner 2001; Gu et al. 2002; Papp et al. 2003). However, because estimates of _d_S > 1 are associated with large stochastic errors and t varies substantially among duplicate pairs, we grouped the 331 gene pairs into four bins according to _d_S (see materials and methods). We found that t and _d_S are positively correlated (Spearman's rank correlation coefficient r = 0.14, n = 331, P = 0.01). Furthermore, the mean t per bin increases with _d_S (linear correlation r = 0.987 between mean t and _d_S category, P < 0.01; Figure 2a). When _d_S < 0.25, mean _t_ is 5.76 ± 0.96, ∼23% greater than _A_. For duplicates with _d_S between 0.25 and 1, mean _t_ is 7.07 ± 0.85, ∼51% higher than _A_, suggesting gain of numerous new protein partners by this time. An earlier study established that _d_S = 1 corresponds approximately to a gene age of 100 million years (MY) in yeasts (Wolfe and Shields 1997). Thus, our results suggest that many new protein interactions have emerged 25–100 MY after duplication and that NF continues to occur even long after duplication (_i.e._, when _d_S > 1). To compare duplicates with singleton genes, we randomly drew 4000 pairs of singletons with replacement from our sample of 745 singletons and estimated that the mean t for singleton pairs was T = 9.29 ± 0.17. Interestingly, for duplicates with _d_S > 20, the mean t is 9.16 ± 0.80, virtually identical to T (P > 0.5, _t_-test), indicating that eventually the total number of partners for a duplicate pair is almost the same as that for two singletons.
Figure 2.—
Number of protein interaction partners of yeast duplicate and singleton genes. (a) Mean number of partners (t) for duplicate pairs with different _d_S. The error bar shows one standard error of the mean. The dashed line shows the average number of partners per singleton (A) and the dotted line shows the average number per random pair of singletons (T). There are 17, 15, 70, and 229 duplicate pairs in the four bins, respectively. (b) Frequency distributions of the number of interaction partners for singletons (open bars), singleton pairs (shaded bars), and duplicates (solid bars). (c) Frequency distributions of the number of shared partners between singleton pairs (open bars), duplicates with _d_S < 20 (shaded bars), and duplicates with _d_S > 20 (solid bars). (d) Difference in the number of partners between duplicates. The mean max(_a_1, _a_2), min(_a_1, _a_2), and δ = |_a_1 − _a_2| for duplicates are shown in open, shaded, and solid bars, respectively, with their corresponding mean values from random singleton pairs shown by the dotted, dashed, and solid lines, respectively. For any given pair of duplicates, _a_1 and _a_2 are the numbers of partners that they each have.
The observed high mean t in duplicates and the rejection of the pure SF model for the genome as a whole could be due to a small number of outliers with huge NF. To examine this possibility, we compared the distributions of the number of partners for singleton genes, randomly paired singleton gene pairs, and duplicate gene pairs (Figure 2b). The latter two distributions are much more similar to each other than each of them is to the first distribution. The duplicate gene data fit the singleton-pair distribution (χ2 = 39.97, d.f. = 17 after combining bins with expectations <5, P = 0.0013) significantly better than the singleton distribution (χ2 = 275.11, d.f. = 14 after combining bins with expectations <5, P = 1.8 × 10−50). Furthermore, the median for the duplicate gene distribution (5) is much closer to the singleton-pair distribution (6) than to the singleton distribution (2; Figure 2b). These results show that the larger number of partners for duplicates than for singletons is not due to the presence of a few outliers, but reflects a general trend for most duplicate genes.
Can NF alone explain the observed protein interaction pattern? As mentioned earlier, we consider three NF models in which the duplicate gene that acquires new function could retain all, none, or some of the ancestral functions, respectively (Figure 1). If all ancestral functions are retained by this gene (NF-I), s should be a constant equal to the number of partners of the progenitor gene before duplication. That is, mean s for duplicates is expected to equal A. In fact, mean s = 1.02 ± 0.14, ∼22% of and significantly smaller than A (P < 10−14, _t_-test), which strongly rejects the NF-I model. On the other hand, mean _s_ is significantly >0 (P < 10−11, _t_-test), suggesting that duplicate genes share partners. From the 4000 randomly chosen pairs of singletons, we estimated that the mean _s_ for singleton pairs is _S_ = 0.028 ± 0.003, significantly smaller than the mean _s_ for duplicates (_P_ < 10−10, _t_-test). We also compared the distribution of _s_ for duplicates and for random pairs of singletons. Significant differences were observed regardless of whether duplicates with _d_S < 20 or _d_S > 20 were considered (P < 10−65, χ2-test; Figure 2c). The finding that duplicates share more protein partners than random pairs of singletons do even long after duplication strongly rejects the NF-II model, which predicts _s_ = 0. The distributions of _s_ (Figure 2c) also indicate that the rejection of NF-I and NF-II is not due to a small number of outliers, because 35% of duplicates _vs._ 2.4% of singleton pairs share partners. It is important to note that the mean _s_ for the duplicates with _d_S < 0.25 already reduces to 1.0, virtually identical to the mean _s_ (1.1) for duplicates with _d_S > 20. This indicates that the reduction of s by loss of partners has already been completed when _d_S reaches 0.25, in agreement with previous observations from fewer data (Wagner 2001). There is no detectable difference in the proportion of shared partners between duplicate genes with more partners and those with fewer partners.
Let us denote _a_1 the number of partners for the gene retaining all the ancestral functions in the three NF models and _a_2 the corresponding number for the gene acquiring new functions. We observed an increase in the mean t after _d_S > 0.25 (Figure 2a), indicating the occurrence of NF after the completion of the loss of partners in the second gene. Under the NF-III model, this will render the absolute difference between _a_1 and _a_2 (δ = |_a_1 − _a_2|) smaller for a period of time, because the deduction of _a_2 by loss of partners has made it smaller than _a_1, and the subsequent increase of _a_2 by NF will reduce the difference between them. However, contradictory to the prediction of NF-III, mean δ increases steadily with _d_S (Figure 2d). The linear correlation between mean δ and the _d_S category is r = 0.954 (P < 0.05) and the Spearman's rank correlation between δ and _d_S is _r_ = 0.15 (_n_ = 331, _P_ = 0.005). Furthermore, NF-III predicts that min(_a_1, _a_2), the smaller of _a_1 and _a_2, should increase with _d_S under this condition because _a_1 is constant and _a_2 increases by NF. But this was not observed (Figure 2d), as neither the linear correlation between mean min(_a_1, _a_2) and the _d_S category (_r_ = 0.450, _P_ > 0.2) nor the Spearman's rank correlation between δ and _d_S (r = 0.085, n = 331, P > 0.10) is significant. NF-III also predicts that max(_a_1, _a_2), the bigger of _a_1 and _a_2, should stay constant for a period of time after the first bin, because _a_2 < _a_1 due to loss of partners and _a_1 does not change by NF. But max(_a_1, _a_2) was found to increase with _d_S steadily (Figure 2d). The linear correlation between mean max(_a_1, _a_2) and the _d_S category is r = 0.998 (P < 0.01) and the Spearman's rank correlation between max(_a_1, _a_2) and _d_S is r = 0.14 (n = 331, P = 0.01). Thus, NF-III is not supported by the observations.
The rejection of all three NF models is due to the presence of SF. When there is no NF, the level of SF can be measured by _I_SF = 1 − (s + δ)/t (see materials and methods). _I_SF varies from 0 for no SF to 1 when s = 0 and _a_1 = _a_2. We estimated that _I_SF = 0.51 ± 0.08 for duplicates with _d_S < 0.25, after ignoring the small amount of NF in these relatively young duplicates. Since SF is completed when _d_S reaches 0.25, it may be inferred that the average _I_SF for all duplicates is ∼0.5. This level of SF is substantial, as random partition of ancestral partners between a duplicate pair with t = 5 and s = 1 results in an expected _I_SF of 0.5.
The demonstration of both NF and SF from the genomic data could be due to the presence of some genes following NF and some other genes following SF. We think that this explanation is unlikely to be correct because it cannot explain the observation that the genome-wide average number of protein interaction partners per duplicate pair is equivalent to that for two singletons. Furthermore, it cannot explain the virtually maximum level of SF (as reflected by _I_SF) observed for the genome-wide data. Rather, our observations suggest that the majority of duplicate genes undergo both SF and NF. Thus, we propose a new model termed SNF to account for the evolutionary changes in interaction partners after gene duplication. This model easily explains the increase of mean t over time by NF and the decrease of mean s to a level that is between 0 and A by incomplete SF. This incompletion may have arisen from shared structural constraints between duplicates. Under general models of SNF in which SF and NF occur more or less randomly between the two duplicates, max(_a_1, _a_2) and δ should both be raised by NF after the end of the SF process, as observed in this study. Similar to NF-III, the SNF model predicts an increase of min(_a_1, _a_2) by continuous NF after the completion of SF. However, given the same amount of rise in t, the increase in min(_a_1, _a_2) is expected to be slower under SNF than under NF-III. This is because in SNF only 50% of NF is expected to occur in the gene with the smaller number of partners and to raise min(_a_1, _a_2). By contrast, under NF-III, one daughter gene does not change at all while the other loses many partners and then gains new partners, leading to a situation where almost all NF will raise min(_a_1, _a_2). Given this comparison, the negligible increase in min(_a_1, _a_2) is not incompatible with the SNF model, though a further test with more data is needed. Our results suggest that SF occurs rapidly after duplication, as the mean s reduces from the expected value of 4.69 immediately after duplication to a final value of ∼1 before _d_S reaches 0.25. At that time, the mean t has increased by only 23%, and it continues to rise even when _d_S > 20, to a final value that is ∼1.96 times that before duplication.
Analysis of human gene expression data:
Although the protein-protein interaction data provide key information on gene function, temporal and spatial patterns of gene expression offer other important aspects of gene function. Furthermore, one version of the SF hypothesis was specifically proposed to explain the change in gene expression after duplication (Force et al. 1999). Therefore, it is necessary to evaluate the SF and NF models by examining genome-wide gene expression patterns in a multicellular organism. We analyzed a large data set that included the expression levels of 7565 human genes in 25 independent and nonredundant tissues (Su et al. 2002). Using conventional criteria, we transformed the quantitative expression levels to discrete expression patterns (expressed or unexpressed). The expression patterns of 515 singletons and 1230 pairs of duplicate genes were analyzed.
All the notations defined above can be used for the expression data if we replace the number of interaction partners by the number of expression sites. We found that the number of expression sites per duplicate pair (mean t = 13.04 ± 0.26) is significantly greater than that per singleton gene (A = 8.85 ± 0.43; P < 10−17, _t_-test; _P_ < 0.0001, Mann-Whitney _U_-test). This rejects the pure SF model that predicts equal mean _t_ and _A_. To examine how _t_ increases over time since duplication, we again used _d_S between duplicates as a proxy for time [_d_S = 1 in mammals corresponds to ∼250 MY after duplication (Kumar and Subramanian 2002)]. To reduce random fluctuations, we grouped the duplicates into seven bins by their _d_S values (Figure 3a). Each of the first six bins contains 100 pairs of duplicates whereas the seventh bin includes the remaining 630 duplicates. We lumped the final 630 gene pairs into one bin because their _d_S values are so large (>3.06) that their estimates have substantial variances. We found that t and _d_S are positively correlated (Spearman's rank correlation coefficient r = 0.07, n = 1230, P = 0.01). Furthermore, the mean t per bin increases with _d_S (linear correlation r = 0.647 between mean t and _d_S category, P < 0.03; Figure 2a). In the first bin (0 < _d_S < 0.68, with a median of 0.18), mean _t_ is 10.28 ± 0.93, 16% greater than _A_. The second bin (0.71 < _d_S < 1.64, with a median of 1.35) has a mean _t_ of 10.97 ± 0.89, 24% greater than _A_. By this time, acquisition of new expression sites is substantial. To compare duplicates with singletons, we randomly drew 3500 pairs of singletons with replacement from our sample of 515 singletons and estimated that the mean _t_ for singleton pairs is _T_ = 14.47 ± 0.16. This number is substantially <2_A_ = 17.70 because two randomly picked singletons share on average _S_ = 3.17 ± 0.10 expression sites. We noted that in the third bin (1.94 < _d_S < 2.23, with a median of 1.80), mean _t_ (13.09 ± 0.88) already approaches _T_ (_P_ > 0.05, _t_-test), indicating that by this time the total number of expression sites for a duplicate pair is indistinguishable from that for two singletons.
Figure 3.—
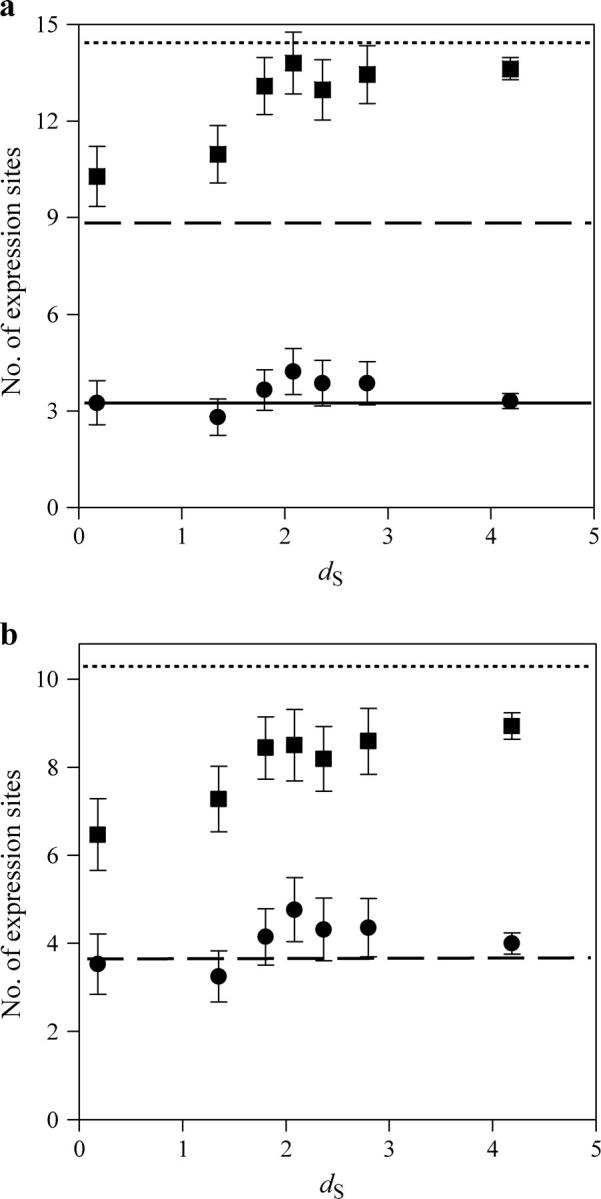
Number of expression sites of human duplicate and singleton genes. (a) Mean number of expression sites (t, squares) and mean number of shared expression sites (s, circles) for duplicate pairs with different _d_S. The 1230 duplicate gene pairs are ranked by their _d_S. Each square (or circle) represents the median _d_S and mean t (or mean s) for 100 gene pairs, with the exception of the last square (or circle), which is derived from 630 gene pairs. The error bar shows one standard error of the mean. The dashed line shows the average number of expression sites per singleton (A) and the dotted line shows the average number per random pair of singletons (T). The solid line shows the average number of shared expression sites per random pair of singletons. (b) Difference in the number of expression sites between duplicates. The mean δ = |_a_1 − _a_2| and min(_a_1, _a_2) for duplicates are shown in squares and circles, respectively, with their corresponding mean values from singleton pairs shown by the dotted and dashed lines, respectively. For any given pair of duplicates, _a_1 and _a_2 are the numbers of expression sites that they each have.
We next examined the three NF models. NF-I predicts that the number of shared expression sites between a duplicate pair (s) is a constant that equals the number of expression sites of the progenitor gene before duplication (Figure 1). We found that mean s = 3.45 ± 0.18, ∼39% of and significantly lower than A (P < 10−25, _t_-test), which strongly rejects the NF-I model. Figure 3a shows that mean _s_ declines quickly from the expected value of 8.85 right after duplication to ∼3.25 ± 0.68 for the first bin (_d_S < 0.68). This value is no longer distinguishable from the mean _s_ (_P_ > 0.1, _t_-test) of any other bin or from S (P > 0.1, _t_-test). This indicates that the loss of expression sites has been completed before _d_S reaches 0.68. Under NF-II and NF-III, the continuous growth of t is entirely due to NF in the gene that first loses expression sites. Thus, these two models predict that min(_a_1, _a_2) should continuously rise after the first bin, to the expected value Min, which is the mean minimum for randomly picked pairs of singletons and is estimated to be 3.64 ± 0.11. But, in fact, the mean min(_a_1, _a_2) for the first bin is already 3.53 ± 0.69, not significantly different from Min (P > 0.1, _t_-test; Figure 3b). Furthermore, the two models predict that after the first bin δ = |_a_1 − _a_2| will decrease for a period of time and then increase as NF continues, but this was again not observed. Instead, δ increases continuously with _d_S (linear correlation r = 0.887 between δ and _d_S category, P < 0.01; Spearman's rank correlation r = 0.09 between δ and _d_S, n = 1230, P = 0.001; Figure 3b). Taken together, none of the three NF models adequately describe the evolutionary patterns of human gene expression. Rather, they are compatible with the SNF model with contributions of both NF and SF, for the same reasons aforementioned for the protein interaction data.
DISCUSSION
In this work we used functional genomic data to study the evolutionary mechanisms underlying the divergence of duplicate genes. Because functional divergence may occur by either SF or NF, it is important to separate them explicitly. Our results show that the pure SF or NF model is inadequate to explain the genomic patterns of protein interaction or gene expression for duplicate genes. Rather, a large proportion of duplicate genes undergo rapid SF, accompanied by prolonged and substantial NF. The large-scale protein interaction and gene expression data likely contain some false-positive and false-negative errors. If the data are entirely random without any biological reality, we expect to see similar behaviors between duplicates and random pairs of singletons. This, however, is not the case. For example, s is significantly higher in duplicate genes than in singleton pairs for the yeast protein interaction data (Figure 2c) and δ is significantly lower in duplicate genes than in singleton pairs for the human gene expression data (Figure 3b). Most importantly, experimental errors, whether negative or positive, cannot generate the positive correlation between t and _d_S for either data set. In this work, several properties were compared between duplicate genes of different ages. This comparison would be biased if duplicate genes of different ages represent different types of genes (in terms of gene function). Lynch and Conery (2000) showed that duplicate genes destined to die usually die in a few million years after duplication. Thus, except for a small number of genes in the first bin of Figure 2a (or Figure 3a), duplicates analyzed here are stably retained in genomes and they should be comparable. We also compared singleton genes with duplicate genes in this work. A recent study in yeasts suggested that genes of low evolutionary rates are more likely to duplicate than those with high rates (Davis and Petrov 2004). This could be a statistical artifact because rapidly evolving duplicate genes are more likely to be misclassified as singletons due to the low power of BLAST in finding highly divergent paralogs. Furthermore, the evolutionary rate has at most a weak negative correlation with the number of interaction partners (Fraser et al. 2002; Jordan et al. 2003; Hahn et al. 2004) and the difference observed by Davis and Petrov (2004) seems much too small to explain the twofold difference between mean t (for ancient duplicates) and A. No bias in the comparison of expression sites between duplicate genes and singleton genes is expected because house-keeping genes (with high numbers of expression sites) and tissue-specific genes are known to have similar rates of duplication (Zhang and Li 2004). Nonetheless, it remains possible that our results have been biased quantitatively, if singleton genes and duplicate genes indeed have somewhat different properties (X. He and J. Zhang, unpublished data). But the bias, even if it exists, is unlikely to be large enough to alter our conclusions qualitatively. In the analysis, we also assumed that duplicate genes cannot independently acquire the same new functions after duplication. Although this assumption may not be true for every duplicate pair, it is likely correct for the majority of them. In fact, the negligible number of shared protein partners between random pairs of singletons (S = 0.028 ± 0.003) supports our assumption. For the gene expression data, however, our assumption may be less robust due to the limited number of tissues and NF might have been underestimated.
Our analyses show that both SF and NF play prominent roles during functional divergence of duplicate genes and that most duplicate genes follow the new SNF model. Our results do not exclude the possibility that a minority of duplicate genes evolve by pure SF or pure NF. We found that SF occurs rapidly after gene duplication, whereas NF is a lengthy process that continues even long after duplication. Thus, the short-term retention of duplicate genes in the genome is primarily due to SF, consistent with a much higher rate of degenerate mutations than beneficial mutations (Walsh 1995; Lynch and Force 2000). Preservation of the duplicate genes in the genome and partial functional relaxation caused by loss of ancestral functions subsequently provide the opportunity for advantageous mutations, which can lead to new functions. The SNF model is supported by the genome-wide evolutionary pattern of regulatory sequences of duplicate genes in yeasts (Papp et al. 2003). The model is also consistent with accelerated sequence evolution immediately after gene duplication (Ohta 1994; Lynch and Conery 2000; Van de Peer et al. 2001; Kondrashov et al. 2002). Although this acceleration may be explained by either reduction of purifying selection or action of positive selection (Zhang et al. 1998), our observation of rapid SF suggests the former as the primary cause. This general pattern does not preclude the possibility of positive selection occurring immediately after duplication, as has been observed in a few cases (Zhang et al. 1998; Johnson et al. 2001; Zhang et al. 2002; Moore and Purugganan 2003), but it suggests that positive selection may play a long-lasting role in the divergence of duplicates.
The finding that the total number of interaction partners and total number of expression sites for duplicates approximate those of randomly picked singleton pairs demonstrates enormous NF in duplicate genes. This, together with the similar NF patterns observed in a vertebrate (small population size) and a fungus (large population size), suggests that passive evolution (Lynch and Conery 2003) cannot fully explain the origin of genome complexity. Gene duplication is responsible for the origins of at least one-third of yeast genes (see materials and methods), without which the yeast protein interaction network would be reduced substantially. If we assume that the rate of gene duplication is 1% per gene per million years (Lynch and Conery 2000) and ∼10% of duplicate genes are stably retained in the genome (Kellis et al. 2004), the total number of functions of a genome can double in 700 MY simply by individual gene duplication. Extrapolated to mammals, ∼10,000 new protein-protein interactions would have evolved in humans since they diverged from mice via gene duplication alone. Thus, gene duplication plays an essential role in the evolution of new functions.
Acknowledgments
We thank D. J. Futuyma, D. Ó Foighil, Y.-L. Qiu, A. P. Rooney, members of the Zhang lab, and two anonymous reviewers for valuable comments on earlier versions of this article. This work was supported by a start-up fund of the University of Michigan and by a research grant (GM67030) from National Institutes of Health to J.Z.
References
- Davis, J. C., and D. A. Petrov, 2004. Preferential duplication of conserved proteins in eukaryotic genomes. PLoS Biol. 2**:** 318–326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Force, A., M. Lynch, F. B. Pickett, A. Amores, Y. L. Yan et al., 1999. Preservation of duplicate genes by complementary, degenerative mutations. Genetics 151**:** 1531–1545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser, H. B., A. E. Hirsh, L. M. Steinmetz, C. Scharfe and M. W. Feldman, 2002. Evolutionary rate in the protein interaction network. Science 296**:** 750–752. [DOI] [PubMed] [Google Scholar]
- Gu, Z., D. Nicolae, H. H.-S. Lu and W. H. Li, 2002. Rapid divergence in expression between duplicate genes inferred from microarray data. Trends Genet. 18**:** 609–613. [DOI] [PubMed] [Google Scholar]
- Hahn, M. W., G. C. Conant and A. Wagner, 2004. Molecular evolution in large genetic networks: Does connectivity equal constraint? J. Mol. Evol. 58**:** 203–211. [DOI] [PubMed] [Google Scholar]
- Hughes, A. L., 1994. The evolution of functionally novel proteins after gene duplication. Proc. R. Soc. Lond. Ser. B Biol. Sci. 256**:** 119–124. [DOI] [PubMed] [Google Scholar]
- Johnson, M. E., L. Viggiano, J. A. Bailey, M. Abdul-Rauf, G. Goodwin et al., 2001. Positive selection of a gene family during the emergence of humans and African apes. Nature 413**:** 514–519. [DOI] [PubMed] [Google Scholar]
- Jordan, I. K., Y. I. Wolf and E. V. Koonin, 2003. No simple dependence between protein evolution rate and the number of protein-protein interactions: only the most prolific interactors tend to evolve slowly. BMC Evol. Biol. 3**:** 1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kellis, M., B. W. Birren and E. S. Lander, 2004. Proof and evolutionary analysis of ancient genome duplication in the yeast Saccharomyces cerevisiae. Nature 428**:** 617–624. [DOI] [PubMed] [Google Scholar]
- Kondrashov, F. A., I. B. Rogozin, Y. I. Wolf and E. V. Koonin, 2002 Selection in the evolution of gene duplications. Genome Biol. 3: RESEARCH0008.1–0008.9. [DOI] [PMC free article] [PubMed]
- Kumar, S., and S. Subramanian, 2002. Mutation rates in mammalian genomes. Proc. Natl. Acad. Sci. USA 99**:** 803–808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch, M., and J. S. Conery, 2000. The evolutionary fate and consequences of duplicate genes. Science 290**:** 1151–1155. [DOI] [PubMed] [Google Scholar]
- Lynch, M., and J. S. Conery, 2003. The origins of genome complexity. Science 302**:** 1401–1404. [DOI] [PubMed] [Google Scholar]
- Lynch, M., and A. Force, 2000. The probability of duplicate gene preservation by subfunctionalization. Genetics 154**:** 459–473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makova, K. D., and W. H. Li, 2003. Divergence in the spatial pattern of gene expression between human duplicate genes. Genome Res. 13**:** 1638–1645. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore, R. C., and M. D. Purugganan, 2003. The early stages of duplicate gene evolution. Proc. Natl. Acad. Sci. USA 100**:** 15682–15687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohno, S., 1970 Evolution by Gene Duplication. Springer-Verlag, New York.
- Ohno, S., 1973. Ancient linkage groups and frozen accidents. Nature 244**:** 259–262. [DOI] [PubMed] [Google Scholar]
- Ohta, T., 1994. Further examples of evolution by gene duplication revealed through DNA sequence comparisons. Genetics 138**:** 1331–1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papp, B., C. Pal and L. D. Hurst, 2003. Evolution of cis-regulatory elements in duplicated genes of yeast. Trends Genet. 19**:** 417–422. [DOI] [PubMed] [Google Scholar]
- Stoltzfus, A., 1999. On the possibility of constructive neutral evolution. J. Mol. Evol. 49**:** 169–181. [DOI] [PubMed] [Google Scholar]
- Su, A. I., M. P. Cooke, K. A. Ching, Y. Hakak, J. R. Walker et al., 2002. Large-scale analysis of the human and mouse transcriptomes. Proc. Natl. Acad. Sci. USA 99**:** 4465–4470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson, J. D., D. G. Higgins and T. J. Gibson, 1994. CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, positions-specific gap penalties and weight matrix choice. Nucleic Acids Res. 22**:** 4673–4680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van de Peer, Y., J. S. Taylor, I. Braasch and A. Meyer, 2001. The ghost of selection past: rates of evolution and functional divergence of anciently duplicated genes. J. Mol. Evol. 53**:** 436–446. [DOI] [PubMed] [Google Scholar]
- von Mering, C., R. Krause, B. Snel, M. Cornell, S. G. Oliver et al., 2002. Comparative assessment of large-scale data sets of protein-protein interactions. Nature 417**:** 399–403. [DOI] [PubMed] [Google Scholar]
- Wagner, A., 2001. The yeast protein interaction network evolves rapidly and contains few redundant duplicate genes. Mol. Biol. Evol. 18**:** 1283–1292. [DOI] [PubMed] [Google Scholar]
- Wagner, A., 2002. Asymmetric functional divergence of duplicate genes in yeast. Mol. Biol. Evol. 19**:** 1760–1768. [DOI] [PubMed] [Google Scholar]
- Wagner, A., 2003. How the global structure of protein interaction networks evolves. Proc. R. Soc. Lond. Ser. B Biol. Sci. 270**:** 457–466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walsh, J. B., 1995. How often do duplicated genes evolve new functions? Genetics 139**:** 421–428. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe, K. H., and D. C. Shields, 1997. Molecular evidence for an ancient duplication of the entire yeast genome. Nature 387**:** 708–713. [DOI] [PubMed] [Google Scholar]
- Wright, F., 1990. The “effective number of codons” used in a gene. Gene 87**:** 23–29. [DOI] [PubMed] [Google Scholar]
- Yang, Z., 1997. PAML: a program package for phylogenetic analysis by maximum likelihood. Comput. Appl. Biosci. 13**:** 555–556. [DOI] [PubMed] [Google Scholar]
- Zhang, J., 2003. Evolution by gene duplication—an update. Trends Ecol. Evol. 18**:** 292–298. [Google Scholar]
- Zhang, J., H. F. Rosenberg and M. Nei, 1998. Positive Darwinian selection after gene duplication in primate ribonuclease genes. Proc. Natl. Acad. Sci. USA 95**:** 3708–3713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, J., Y.-P. Zhang and H. F. Rosenberg, 2002. Adaptive evolution of a duplicated pancreatic ribonuclease gene in a leaf-eating monkey. Nat. Genet. 30**:** 411–415. [DOI] [PubMed] [Google Scholar]
- Zhang, L., and W. H. Li, 2004. Mammalian housekeeping genes evolve more slowly than tissue-specific genes. Mol. Biol. Evol. 21**:** 236–239. [DOI] [PubMed] [Google Scholar]