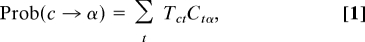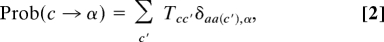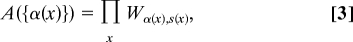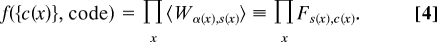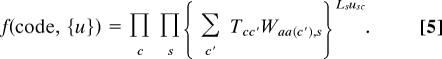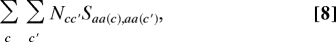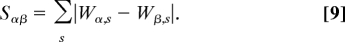Collective evolution and the genetic code (original) (raw)
Abstract
A dynamical theory for the evolution of the genetic code is presented, which accounts for its universality and optimality. The central concept is that a variety of collective, but non-Darwinian, mechanisms likely to be present in early communal life generically lead to refinement and selection of innovation-sharing protocols, such as the genetic code. Our proposal is illustrated by using a simplified computer model and placed within the context of a sequence of transitions that early life may have made, before the emergence of vertical descent.
Keywords: horizontal, gene transfer
The genetic code could well be optimized to a greater extent than anything else in biology and yet is generally regarded as the biological element least capable of evolving.
There would seem to be four reasons for this paradoxical situation, all of which reflect the reductionist molecular perspective that so shaped biological thought throughout the 20th century. First, the basic explanation of gene expression appears to lie in its evolution, and not primarily in the specific structural or stereochemical considerations that are sufficient to account for gene replication. Second, the problem’s motto, “genetic code,” is a misnomer that makes the codon table the defining issue of gene expression. A satisfactory level of understanding of the gene should provide a unifying account of replication and expression as two sides of the same coin. The genetic code is merely the linkage between these two facets. Thus, and thirdly, the assumption that the code and the decoding mechanism are separate problems, individually solvable, is a reductionist fallacy that serves to deny the fundamental biological nature of the problem. Finally, the evolutionary dynamic that gave rise to translation is undoubtedly non-Darwinian, to most an unthinkable notion that we now need to entertain seriously. These four considerations structure the approach we take in this article.
To this point in time, biologists have seen the universality of the code as either a manifestation of the Doctrine of Common Descent or simply as a “frozen accident.” Viewing universality as following from common descent renders unthinkable the notion explored here that a universal code may be a necessary precondition for common ancestry, indeed even for life as we know it. We will argue in this article [a maturation of the earlier concept of the progenote (1)] that the very fact of the code’s evolvability, together with the details of its internal structure, provides strong clues to the nature of early life, and in particular its essential communal character (2).
Beyond the code’s universality we have very few clues to guide us in trying to understand its evolution and that of the underlying decoding mechanism. The principal ones again are properties of the code itself; specifically, the obvious structure of the codon table. The table possesses (at least) two types of order: synonym order and relatedness order. The first is the relatedness of codons assigned to the same amino acid; the second is the relatedness of codons assigned to related amino acids. Relatedness among the amino acids is context-dependent and in the context of the codon table could a priori reflect almost anything about the amino acids: their various properties, either individually or in combination; the several macromolecular contexts in which they are found, such as protein structure, the translation mechanism, and the evolution of translation; or the pretranslational context of the so-called RNA world. Although we do not know what defines amino acid “similarity” in the case of the code, we do know one particular amino acid measure that seems to express it quite remarkably in the coding context. That measure is amino acid polar requirement (3–5). Although the relatedness order of the code is marginally evident from simple inspection of the codon table (3, 4, 6–8), it is pronounced when the amino acids are represented by their respective polar requirements (4).
A major advance was provided by computer simulation studies (9–14) of the relatedness ordering of the amino acids over the codon table, which showed that the code is indeed relationally ordered and moreover is optimized to near the maximum extent possible. Compared with randomly generated codes, the canonical code is “one in a million” when the relatedness measure is the polar requirement. No other amino acid measure is known to possess this characteristic (14) (in our opinion, the significance of this observation has not been adequately recognized or pursued). These precisely defined relatedness constraints in the codon table were unexpected and still cry out for explanation.
As far as interpretation goes, the optimal aspect of the genetic code is surely a reflection of the last aspect of the coding problem that needs to be brought into consideration: namely, the precision or biological specificity with which translation functions. Precision, along with every aspect of the genetic code, needs to be understood as part of an evolutionary process. We would contend that at early stages in cellular evolution, ambiguous translation was tolerated (there being no alternative) and was an important and essential part of the evolutionary dynamic (see below). What we imply by ambiguity here is inherent in the concept of group codon assignments, where a group of related codons is assigned as a whole to a corresponding group of related amino acids (3). From this flows the concept of a “statistical protein,” wherein a given gene can be translated not into a unique protein but instead into a family of related protein sequences. Note that we do not say that these are an approximation to a perfect translation of the gene, thereby implying that these sequences are in some sense erroneous. Early life did not require a refined level of tolerance, and so there was no need for a perfect translation. Ambiguity is therefore not the same thing as “error.”
The phylogenetic expression of ambiguity is reticulate evolution. In reticulate evolution, there is no unique notion of genealogical descent: genetic content can be distributed collectively. Accordingly, as we now turn the emphasis away from the documentation of the static features of the genetic code and toward their evolutionary origins, we must necessarily invoke an evolutionary dynamic distinct from that identified originally by Darwin. This dynamic can be seen as a kind of biological game in which both the players and the rules of play are unfamiliar, at least in the non-microbial world. The players are cell-like entities still in early stages of their evolutions. The evolutionary dynamic (the “rules”) involves communal descent. The key element in this dynamic is innovation-sharing, an evolutionary protocol whereby descent with variation from one “generation” to the next is not genealogically traceable but is a descent of a cellular community as a whole. Even if an organismal ancestry were to some extent traceable, it would have no significance, because it is the community as a unit, not the individual organismal lineages therein, that varies in descent.
The purpose of this article is to show that evolvability, universality, and optimality can all be understood naturally and comprehensively, but not within a framework of strictly vertical evolution. Specifically, we will herein model the evolution of translation, the codon table, the constraints therein, the universality of the code, and the decoding mechanism, not as a sum of parts but as a whole. The central conjecture in our model is that innovation-sharing, which involves horizontal transfer of genes and perhaps other complex elements among the evolving entities [a dynamic far more rampant and pervasive than our current perception of horizontal gene transfer (HGT)], is required to bring the evolving translation apparatus, its code, and by implication the cell itself to their current condition.
Our point of view alleviates the need for any assumption of a unique common ancestor. We argue that the universality of the code is a generic consequence of early communal evolution mediated by HGT, and that HGT enhances optimality. Our arguments are backed up by computer simulation studies, which are necessary to probe the complex interactions between the variety of collective mechanisms that we shall present. We show that there are virtuous cycles of cooperativity: (i) the more similar the genetic codes, the greater the intensity of HGT, and the stronger the tendency for codes to become more similar; and (ii) HGT helps the codes to optimize, and optimization enforces universality and compatibility between translational machineries. These cooperative dynamics arise because of the dual role played by the genetic code: it is not only a protocol for encoding amino acid sequences in the genome but also an innovation-sharing protocol. Here, we identify two synergistically interacting mechanisms for the emergence of a universal innovation-sharing protocol: dynamic competition between protocols favoring the popular ones and effective attraction of codes due to exchange of protein coding regions.
If Darwin had been a microbiologist, he surely would not have pictured a “struggle” for existence as “red in tooth and claw.” Our view of competition in a communal world as a dynamical process is very different from the widely understood notion of Darwinian evolution. “Survival of the fittest” literally implies that there can only be one winner from the forces of selection, whereas in a communal world, the entire distributed community benefits and its structure becomes modified by the forces of a selection that is an inherently biocomplex phenomenon involving the dynamics between the community elements and the interaction with the environment. The most general sense in which we mean competition in this article is the complex dynamical rearrangement of the community structure.
Our framework fits naturally the recently proposed picture that early evolution was dominated by HGT, as evidenced by detailed phylogenetic (15), biochemical (16), and structural (17) analyses of the aminoacyl-tRNA synthetases. The broader implication of this scenario is that innovation-sharing led to the emergence of modern cell designs (18) from a communal state, not a unique, shared ancestor. Such a communal state existed before the point of emergence of vertical evolution, which has been termed the Darwinian transition (18). The defining property of the communal state was that it was capable of tolerating and using ambiguity, as reflected in the pervasive role of HGT. A Darwinian transition corresponds to a state of affairs when sufficient complexity has arisen that the state is incapable of tolerating ambiguity, and so there is a distinct change in the nature of the evolutionary dynamics (to vertical descent). We envision that such Darwinian transitions occurred in each of the three major lineages. The present work does not address the Darwinian transition itself but explains how the communal state could have arisen in the first place: in our scenario, it is the inevitable by-product of the establishment of an innovation-sharing protocol (the genetic code), leading to the explosive growth of complexity. Thus, we may speculate that the emergence of life should best be viewed in three phases, distinguished by the nature of their evolutionary dynamics. In the first phase, treated in the present article, life was very robust to ambiguity, but there was no fully unified innovation-sharing protocol. The ambiguity in this stage led inexorably to a dynamic from which a universal and optimized innovation-sharing protocol emerged, through a cooperative mechanism. In the second phase, the community rapidly developed complexity through the frictionless exchange of novelty enabled by the genetic code, a dynamic we recognize to be patently Lamarckian (19). With the increasing level of complexity there arose necessarily a lower tolerance of ambiguity, leading finally to a transition to a state wherein communal dynamics had to be suppressed and refinement superseded innovation. This Darwinian transition led to the third phase, which was dominated by vertical descent and characterized by the slow and tempered accumulation of complexity.
Universality and HGT
Previous arguments about universality rely on the existence of a universal common ancestor with a frozen code. A detailed deconstruction of such arguments is presented in Supporting Text (which is published as supporting information on the PNAS web site) and further supported by the computer simulations presented in Model of Code Attraction Due to HGT, but the unambiguous conclusion is that vertical descent on its own is insufficient to explain the universality of the genetic code. Here, we present an alternative: the universality of the genetic code is a generic consequence of the communal evolution of early life. HGT of protein coding regions and HGT of translational components ensures the emergence of clusters of similar codes and compatible translational machineries. Different clusters compete for niches, and because of the benefits of the communal evolution, the only stable solution of the cluster dynamics is universality. Within clusters, concerted optimization of codes is possible. These mechanisms are consistent with two macroevolutionary scenarios. (i) The code stayed nearly universal at all times. (ii) The codes diverged at first but then gradually became universal.
Competition Between Innovation Pools.
One of the advantages of communal evolution is that universally good traits and refinements can spread through HGT to organisms occupying different niches, preserving their diversity. In a world increasingly dominated by protein, most innovations would involve them, and correspondingly HGT will be most effective between organisms having the same genetic code. In this way, the organisms sort into communities sharing related genetic codes. A single code community can span cells adapted to different niches and with different organization.
The larger the community and diversity of organisms sharing sufficiently related genetic codes, the larger the pool of protein innovations accessible to everyone. This leads to faster evolution among the larger communities than the smaller ones and therefore a greater potential to invade niches occupied by organisms with different incompatible genetic codes. With this dynamics larger communities will tend to become even larger at the expense of smaller ones. The only stable solution is a universal genetic code. Thus, it is not better genetic codes that give an advantage but more common ones.
The elementary step in this process is the overtaking of an occupied niche by the descendants of an organism with a different genetic code. If two groups of organisms compete with each other, the one that has access to more innovations (the one belonging to the larger community of common/compatible genetic codes) will on average out-compete the other. In contrast to the case with only vertical evolution, there is an active feedback loop, driven by innovation-sharing through HGT, which not only singles out the genetic code from all other properties of a cell but also provides a mechanism that drives competition between codes.
This mechanism (referred to below as “competition between innovation pools,” or CIP) assumes that the protocols are fixed. But how did the protocols themselves emerge and evolve? How can a protocol be upgraded without destroying it?
Code Attraction and Optimization Due to HGT of Protein Coding Regions.
A population of organisms occupying a niche is subject to spontaneous code mutations and is bombarded by foreign genetic material from organisms occupying different niches. Horizontally transferred genes can be useful for the recipient even if the donor has a (somewhat) different code. For example, the codon usage (e.g., synonym codon usage frequency) of a transferred gene is adapted to the donor code and is therefore different from that of the recipient. Correspondingly, there will be indirect pressure for the recipient code to readjust itself to make a better use of the new gene.
We expect that the code response would involve several characteristic time scales. On the long scale, the direction of change is to reduce ambiguity, but on the short scale, the code must be able to tolerate a greater level of ambiguity while ingesting new genes. The means available to the cell to detune the level of precision of translation may be considered to be of two essential origins: those internal to the cell, and those which are communal, reflecting the influence of the environment and neighboring cells. Mechanisms internal to the cell include change in tRNA expression levels and detuning of the ribosomal machinery itself, as is known to occur through variations in Mg ion concentration, antibiotics, and structural mutations. Communal mechanisms are likely to involve the import of tRNA from other organisms. The increase on the short time scale in translational ambiguity is compensated for on the same time scale by the beneficial effects of the new gene. Eventually, the codon and amino acid usage of the newly transferred segment will equilibrate with the rest of the genome and the indirect pressure of the donor code on the recipient code will disappear, while leaving behind its accumulated effects.
In somewhat more detail, these arguments indicate that, after a HGT event, the genetic code of the donor influences the genetic code of the acceptor. Given an alien gene, the host–alien gene system undergoes a cyclical dynamical process leading to full utilization of the new gene. In one part of the cycle, the host detunes its own code for purposes of recognizing the alien code; an example of such a detuning process has been documented in streptomycin-dependent mutants (20, 21) and ribosomal ambiguity mutants (22, 23) in bacteria. In the other part of the cycle, the alien gene codons are mutated to conform to the host code. This process results in the detection with greater precision of the alien signal. A snapshot of this process would reveal a genome as a mosaic of horizontally transferred fragments from other genomes with different characteristic patterns of codon usage. However, these are only the tip of the iceberg: beyond codon usage are the subtle but important changes in aminoacyl tRNA synthetase precision and the ambiguity level of the translational mechanism itself.
The interaction between the genetic codes is attractive. Typically, the closer the translation of a foreign coding region is to that in the donor, the higher is the probability that it is functional. Therefore, the selective pressure will be to change codons of the recipient code in the direction of the donor code, even if only in a probabilistic fashion. The dynamical outcome of this attraction must be uniformization. This expectation is confirmed by the computer simulations presented below.
HGT requires that the genetic codes of the host and the recipient are sufficiently similar, but how similar is sufficient depends on the nature of the proteins and the overall accuracy of decoding. There are strong reasons to believe that the more primitive the code of the donor, the greater the genetic code distance over which HGT is possible. This is because the tolerance of the proteins to errors in their primary structure is coadapted to the error rates of the translational machinery. A cell with a non-optimal code cannot afford very capricious and therefore highly fine-tuned proteins because of the cost of discarding defective proteins. A protein that is robust to translational errors a fortiori is also more tolerant to translation with a different code. Conversely, the less optimized the recipient code, the more error-tolerant its proteins, and therefore the less harmful the effect on the established genes of a code change in the direction of the donor code. This has the important consequence that in the initial stages of the genetic code evolution, when the diversification tendency of codes was strongest, HGT was possible and must have been extensive despite the presence of many different codes.
HGT of Translational Components.
To this point, our discussion has managed to avoid the specifics of how the genetic code is implemented in hardware, as it were. However, we cannot ignore the possibility that the translational components themselves benefited from HGT, and we now turn to this briefly.
The genetic code is a representation of a family of modules, which are universal across all organisms and are specified by the mechanisms of translation, such as tRNAs and charging enzymes (aminoacyl-tRNA synthetases in a modern-day setting). The task of improving translation and the code is also universal, i.e., largely insensitive to the niches organisms are occupying. So, is it possible that HGT of translational components played an important role in the evolution of the codes? Is there any significance in the functional separation between the translational machinery (the ribosome) and the code specificators (tRNAs and charging enzymes)? Imagine for simplicity a situation in which organisms occupying diverse niches have the same malleable genetic code and ensembles of tRNAs. The discovery of a tRNA modification that changes the code and increases its optimality (and therefore the efficiency of translation) in one organism will also be beneficial for organisms in the other niches, because of the universal benefit of optimality. Therefore, a spread of the discovery is beneficial to all recipients and can be assumed to occur through various HGT mechanisms including via active elements such as viruses and plasmids.
Therefore, if the spread through HGT is rapid compared with innovations, a core of organisms having the same genetic code can maintain its integrity while evolving toward optimality. Notice that this mechanism does not rely on common ancestry and preserves the diversity of the organisms. Moreover, this mechanism is distinct from any survival of any “fittest” species. In the absence of an attractive force that restrains deviant codes, this core of organisms would become depleted, if there was any circumstance that prevented a code update from invading specific populations. If the depletion is slow enough, the deviants will be at a communal disadvantage and disappear as described in Competition Between Innovation Pools. The depletion mechanism will compete against an expansion of the core because of the benefit of a common protocol shared by a large population.
Diversification of the Translation Mechanism.
The special role of the genetic code as an innovation-sharing protocol leads to a possible observational consequence. In a core community of organisms that is in the process of code optimization, the compatibility of code specificators is enforced. Once the optimization of the genetic code is complete, there is no pressure to maintain compatibility. Therefore, the “freezing” of the universal genetic code could trigger the radiation of the underlying translational machineries. So, even if translation emerged earlier than the other basic cellular systems, but the optimization of the code took an extended time, the translational componentry would have diversified less. This is consistent with the observation that the translation mechanism is more conserved evolutionarily than the replication and transcription mechanisms. Although we do not have a complete understanding of the Darwinian transition (18), our argument suggests that code universality and optimality were necessary but not sufficient mechanisms for the transition to vertical evolution.
Interactions Between HGT Mechanisms.
The different collective mechanisms enabled by HGT and outlined above are also capable of synergistically interacting with each other.
We saw above that the evolutionary expansion of the most popular cluster of codes provides the necessary support for the maintenance of an otherwise weakly depleting universal core. The opposite is also true. The CIP mechanism is ineffective if there are no clusters of sufficient size on which it can operate. The establishment of such clusters is greatly facilitated by the HGT of code specificators and protein coding regions. Distribution of modules enforces modularity that in turn enforces the distribution of modules. Similarly, exchange of protein coding regions enforces universality, thus making it easier to exchange genes. Therefore, there are positive feedback loops that provide at least local stability to the protocols and turn them into effective degrees of freedom at a longer time scale. The global stability and universality is then guaranteed by the “winner takes all” nature of the CIP.
HGTs of code specificators and protein coding regions interact not only through the CIP mechanism but directly as well. If an organism obtains a gene from another niche, its place in the ecosystem is such that it has potential contact with the genetic material of the donor. Therefore, the recipient has a better than random chance to obtain the right code specificator from the donor as well, before the special codon usage of a recently acquired trait drifts. The exchange of code specificators provides a channel through which codes can become more similar in response to the attraction of codes due to exchange of protein coding regions.
In summary, it is the interaction between the different mechanisms outlined above that makes the emergence and maintenance of universality robust. At the same time, because of the complexity of the problem, it is useful to study the different components in isolation as well.
HGT and the Observed Statistical Properties of the Genetic Code.
So far, we have argued that HGT and the special role of the genetic code as an innovation-sharing protocol alleviate the conceptual difficulties in understanding the simultaneous universality and evolvability of the genetic code. Does this improved understanding help us explain some of the statistical features of the modern genetic code? And how can we expose the signatures of the above mechanisms that are buried in the functional and structural design of the translational system and its phylogenetic variations?
To address this, one needs to complement the above generic mechanisms with insight about the elementary evolutionary changes of the genetic code. Our goal in the remainder of this article is to attempt to identify robust or generic statistical properties of translation that arise from our proposed evolutionary mechanisms but that are relatively insensitive to fine details. To begin, we model the code attraction mechanism and ask, What is the effect of HGT on the optimality of the genetic code?
We employ genetic code dynamics similar to that first introduced by Sella and Ardell (24–26). The main feature is the coevolution between the genetic code and codon usage at different functional sites. The code determines the codon usage at mutation selection equilibrium. In turn, the codon usage determines the fitness costs or benefits of the accessible code changes, thus guiding the code’s evolution. Code changes that are beneficial given the typical codon usage of a population can invade it. To account for HGT, we couple the evolution of different codes by postulating that a fraction of each genome consists of pieces coming from other genomes.
The virtue of the model of Sella and Ardell is that it is a closed model of the evolution of the genetic code and shows that the evolvability barrier is surmountable in a protein-dominated world. Its shortcoming is that it does not address the fact that translation is a dynamical process, with competition between its various components. This means that the model of Sella and Ardell on its own is not adequate to identify generic statistical signatures of the evolutionary mechanisms of translation, because the statistical properties of the code and the structure of the translational system are precisely the stable resolutions of the design tradeoffs and evolutionary conflicts inherent to translation.
The code attraction mechanism that we use at this point is also insensitive to the implementation of translation and so has the same shortcoming. Thus, combining it with the model of Sella and Ardell, we will still not be able to address all evolutionary aspects of the problem. Nevertheless, such a model, although admittedly too simple for our ultimate goals, can, encouragingly, still explain the universality and optimality of the genetic code. The only key aspect of translation that it is necessary to incorporate, even if by introducing it by hand, is mistranslation.
At a next level in the hierarchy of models, one needs to incorporate the tRNAs as agents of both the collective molecular effort of translation and the communal evolution of the genetic codes. In contrast to the above, in such models mistranslation would become a dynamical variable that emerges from the competition itself. This lower level of description entails a richer suite of observational outcomes and provides a unique and essential role for the organism as a resource manager and conflict regulator for the various dynamical processes within it.
Model of Code Attraction Due to HGT
We first describe the modeling of the genetic code and mistranslation errors, then define the proteome structure and the reproductive success of genomes as a function of their codon sequences. We show how to compute the probability distribution of codons at different functional sites at mutation selection equilibrium. Finally, we present a simulation algorithm that incorporates HGT.
Genetic Code.
The genetic code is a probabilistic map Prob(c → α) between codons and amino acids. The map is probabilistic because the charging of tRNAs with particular amino acids and the decoding of codons through competition of tRNAs are probabilistic molecular events. Quite generally,
where Tct is the probability that a codon c is read by tRNA species t, and Ctα is the probability that it is charged with amino acid α. Assuming one-to-one mapping between tRNA species and codons and equal concentrations of different tRNAs, and ignoring mischarging, we set
where the sum is over the codons and Tcc′ = ν/9 if c and c′ are nearest neighbors, Tcc = 1 − ν and Tcc′ = 0 otherwise, with ν being the mistranslation rate. (9 is the number of neighbors for codons consisting of three letters and an alphabet of size 4.) aa(c) is a map between the codons and amino acids, which will be referred to as the code.
Genome and Proteome Structure.
A genome is a sequence of codons that is translated to an amino acid sequence. Each genome position x belongs to a site type s(x). A site type s is characterized by the fitness score W_α_s of the different amino acids that can be present at that site. The matrix W, together with the frequencies {Ls} of the different site types in the genome, constitutes the structure of the proteome. Assuming that amino acid substitutions at different genome positions have independent effects on fitness, we construct the proteome fitness score
where the product is over all genome positions and α(x) is the amino acid at position x.
Codon Usage.
Since different positions belonging to the same site type are phenotypically indistinguishable in the model, we can describe the genome by the matrix {usc} that specifies the frequency of codon c among sites of type s.
Genome Fitness.
Accommodating the probabilistic nature of translation, we set the fitness of a genome to be the average of the proteome fitness score over many translations, i.e., f = 〈_A_〉. Since translations of different codons are independent,
Putting everything together and switching from codon sequence to codon usage representation, we end up with
Equilibration of Codon Usage.
Given the matrix of mutational effects {Fsc(code)}, defined above, what is the codon usage {usc} in an asexual population of an infinite size and large genomes at a mutation selection equilibrium? Mutational pressure is characterized by the matrix Mcc′ specifying the probability that codon c will mutate into codon c′ in one generation. It is assumed independent of the site type and genome position. Any mutational biases could be incorporated in Mcc′. Here, we focus on equally probable single nucleotide changes. In this case, M is specified by a single parameter μ, which is the probability for a mutation at a given site in one generation. Following Sella and Ardell (24), the codon usage at a site of type s is given by the eigenvector corresponding to the largest eigenvalue of the matrix
The matrix Q reflects the application of selection followed by mutation.
The parameters of the model described above are _N_s, the number of site types; _N_a, the number of amino acids; the _N_a × _N_s matrix W; and a vector {Ls}, specifying the relative frequencies of the different site types, the mutation rate μ, and the mistranslation rate ν.
Model Dynamics.
Now we consider an ensemble of populations with different codes and present the dynamics.
- There are N entities, each with its own genetic code aa(c) and codon usage usc.
- At each step an entity, the acceptor, and K random donor entities are chosen at random. The acceptor codon usage is updated according to the rule
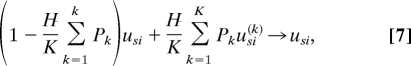
where usi(k) is the codon usage of donor k, and pk is some measure of the compatibility between the donor and acceptor codes expressing the probability of acceptance. Here, we study the case with no barrier to HGT of coding regions, i.e., pk = 1. H is the fraction of the acceptor genome that is a mosaic due to HGT. - We attempt to change the code of the acceptor. We examine in random order the possible elementary changes of the code until we find one that is acceptable or exhaust all of the possibilities. We accept a candidate change if it increases or at least preserves the fitness, calculated by using the mosaic codon usage {usc} and Eq. 5. An elementary code change reassigns a single codon to a different amino acid.
- We equilibrate the acceptor codon usage by finding the eigenvectors corresponding to the largest eigenvalues of the matrices Qs.
- We repeat the cycle.
The CIP mechanism, which clearly facilitates universality (and given enough time generically leads to universality), is factored out from the simulations to concentrate on the code attraction mechanism. Each evolving entity in the ensemble can be thought of as a different “species” (or ecotype). While within each species the evolution proceeds through invasions of code variants with higher fitness, the different species are stable and their number is fixed, thus blocking the CIP mechanism.
Results: Genetic Code Coevolution Toward Optimality and Universality
We evolved ensembles of codes with and without HGT and measured the time evolution of the average distance between codes and the distribution of optimality scores. We compare the optimality scores with the corresponding distribution for randomly generated codes. The ensemble of randomly generated codes is constructed by assigning random amino acids to the codons. Initially, all of the codes are identical, and the initial code is generated by randomly assigning amino acids to the codons.
The average code distance is obtained by considering all pairs of entities with equal weight. The code distance between two entities is the Hamming distance, which counts the numbers of codons that code for different amino acids.
We define the optimality score of a code as the average amino acid similarity distance between neighboring codons.
where Ncc′ is 1 if codons c and c′ differ by a single letter, and zero otherwise. S is an the amino acid similarity matrix defined as follows:
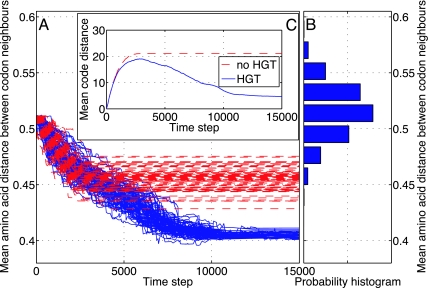
Fig. 1 presents the simulation results for the following parameters: N = 80; Na = Ns = 20; 64 codons; μ = 10−4; ν = 0.01; _W_αβ = φ|_A_α−_A_β| with {_A_α} being uniformly distributed random numbers in the interval (0, 1); and φ = 0.99. The HGT parameters are H = 0.4 and K = 1.
Fig. 1.
Communal evolution toward optimality of 80 codes with (blue) and without (red) HGT of coding regions. There is no barrier to HGT between different codes. The initial conditions are the same for both runs. Parameters: H = 0.4, φ = 0.99, μ = 10−4, ν = 0.01. (A) Time development of the average amino acid distance between neighboring codons, a proxy for code optimality. (B) Probability distribution histogram of code optimality for randomly generated codes. The horizontal axis is the frequency with which a given code optimality occurs; the vertical axis is the same as in A. (C) Time development of the average distance between codes.
Fig. 1A demonstrates that HGT of coding regions not only brings universality but greatly enhances the joint ability of the codes to optimize. Comparison with the distribution of optimality scores for random codes, Fig. 1B, shows that, in the presence of HGT, the achieved optimality is highly significant. Thus, in a qualitative way, we have provided a dynamical mechanism that would give rise to the statistical properties of the genetic code identified in refs. 9 and 10.
Fig. 1C shows that without HGT the codes diversify form each other. However, when HGT is present the tendency to diversify is eventually reversed and the codes get attracted to each other, gradually achieving near universality. It should be stressed that the probability for achieving universality, in the absence of the CIP mechanism, depends on H, and is equal to one above a threshold. Whereas H is a constant in this set of simulations, the discussion in ref. 18 suggests that it is in fact a dynamical variable that is initially large and gradually decreases as better translation allows the evolution of a protein network with more specific interactions.
We interpret these results as supporting two key concepts that underlie the arguments in this article. First and foremost is the role of communal evolution in leading to a universal genetic code. Vertical or Darwinian evolution does not lead to a reduction in the distance between codes. This is seen from the long-time behavior of the red curves in Fig. 1A. Only the incorporation of HGT gives rise to code convergence, as shown by the long-time behavior of the blue curves in Fig. 1A: they get closer together with time. In a sense, a Darwinian (genealogical) evolution would get trapped or, perhaps, frozen into metastable states. Second is the role of communal evolution in leading to an optimal code. Vertical or Darwinian evolution gets frozen into non-optimal states, whereas with HGT, the code becomes optimized to a much greater extent. This is seen by comparing the final values of the Darwinian evolution (red) curves and the communal evolution (blue) curves with the vertical axis of Fig. 1B. Communal evolution results in a genetic code that is much further from the mean of random distributions than the results of Darwinian evolution.
Conclusions
With this work, we have revisited the largely overlooked problem of genetic code universality and the conceptual difficulties associated with it. These difficulties can all be avoided if one takes, as we do, the stance that evolution was essentially communal from the very beginning. We have argued that there are three distinct stages of evolution, which we might classify as (i) weak communal evolution, which gave way via development of an innovation-sharing protocol and the emergence of a universal genetic code to (ii) strong communal evolution, which developed exponential complexity of genes, finally leading via the Darwinian transition to (iii) individual evolution—vertical, and so, Darwinian.
Most of our analysis explored the transition between regimes i and ii, through detailed consideration of the way in which a generalized form of HGT operating on long evolutionary time scales brings universality via dynamic competition between a wide variety of collective innovation-sharing protocols. In particular, we argued how such protocols emerge through the important coevolutionary mechanism of code attraction and presented a specific model that is capable of explaining the simultaneous universality and optimality of the genetic code.
The genetic code is an expression of the translation process, and therefore its state and significance reflect the various stages in the evolutionary development of translation and the organization of the cell. Thus, a fuller account of the evolution of the genetic code requires modeling physical components of the translational apparatus, including the dynamics of tRNAs and the aminoacyl tRNA synthetases. Only with this level of description is it possible to address issues such as the special role played by the polar requirement. This latter point is, we believe, an essential clue to the early evolution of translational components, when the genetic code presumably had a rather different function.
Evolution of the genetic code, translation, and cellular organization itself follows a dynamic whose mode is, if anything, Lamarckian.
Supplementary Material
Supporting Text
Acknowledgments
We thank Patrick O’Donoghue, Gary Olsen, Yoshi Oono, Zan Luthey-Schulten, and Matt Gordon for many insightful discussions. This work was supported in part by National Science Foundation Grant NSF-0526747.
Abbreviations
CIP
competition between innovation pools
HGT
horizontal gene transfer.
Footnotes
Conflict of interest statement: No conflicts declared.
References
- 1.Woese C. R., Fox G. E. J. Mol. Evol. 1977;10:1–6. doi: 10.1007/BF01796132. [DOI] [PubMed] [Google Scholar]
- 2.Woese C. R. Zentralbl. Bakteriol. Hyg. Abt. 1 Orig. C. 1982;3:1–17. reprinted in. [Google Scholar]; Woese C. R. In: Archaebacteria. Kandler O., editor. Stuttgart: Fischer; 1982. pp. 1–17. [Google Scholar]
- 3.Woese C. Proc. Natl. Acad. Sci. USA. 1965;54:1546–1552. doi: 10.1073/pnas.54.6.1546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Woese C., Dugre D., Dugre S., Kondo M., Saxinger W. Cold Spring Harbor Symp. Quant. Biol. 1966;31:723–736. doi: 10.1101/sqb.1966.031.01.093. [DOI] [PubMed] [Google Scholar]
- 5.Woese C. R. The Genetic Code. New York: Harper & Row; 1967. [Google Scholar]
- 6.Sonneborn T. In: Degeneracy of the Genetic Code: Extent, Nature and Genetic Implications. Bryson V., Vogel H. J., editors. New York: Academic; 1965. pp. 277–297. [Google Scholar]
- 7.Alff-Steinberger C. Proc. Natl. Acad. Sci. USA. 1969;64:584–591. doi: 10.1073/pnas.64.2.584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wong J. T.-F. Proc. Natl. Acad. Sci. USA. 1980;77:1083–1086. doi: 10.1073/pnas.77.2.1083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Haig D., Hurst L. J. Mol. Evol. 1991;33:412–417. doi: 10.1007/BF02103132. [DOI] [PubMed] [Google Scholar]
- 10.Freeland S., Hurst L. J. Mol. Evol. 1998;47:238–248. doi: 10.1007/pl00006381. [DOI] [PubMed] [Google Scholar]
- 11.Goldman N. J. Mol. Evol. 1993;37:662–664. doi: 10.1007/BF00182752. [DOI] [PubMed] [Google Scholar]
- 12.Freeland S., Knight R., Landweber L., Hurst L. Mol. Biol. Evol. 2000;17:511–518. doi: 10.1093/oxfordjournals.molbev.a026331. [DOI] [PubMed] [Google Scholar]
- 13.Knight R., Freeland S., Landweber L. Nat. Rev. Genet. 2001;2:49–58. doi: 10.1038/35047500. [DOI] [PubMed] [Google Scholar]
- 14.Knight R. Ph.D. thesis. Princeton: Princeton Univ; 2001. [Google Scholar]
- 15.Woese C. R., Olsen G., Ibba M., Söll D. Microbiol. Mol. Biol. Rev. 2000;64:202–236. doi: 10.1128/mmbr.64.1.202-236.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Sauerwald A., Zhu W., Major T., Roy H., Palioura S., Jahn D., Whitman W., Yates J., Ibba M., Söll D. Science. 2005;307:1969–1972. doi: 10.1126/science.1108329. [DOI] [PubMed] [Google Scholar]
- 17.O’Donoghue P., Sethi A., Woese C. R., Luthey-Schulten Z. A. Proc. Natl. Acad. Sci. USA. 2005;102:19003–19008. doi: 10.1073/pnas.0509617102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Woese C. Proc. Natl. Acad. Sci. USA. 2002;99:8742–8747. doi: 10.1073/pnas.132266999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Burkhardt R. W., Jr . The Spirit of System: Lamarck and Evolutionary Biology. Cambridge, MA: Harvard Univ. Press; 1977. [Google Scholar]
- 20.Davies J., Gilbert W., Gorini L. Proc. Natl. Acad. Sci. USA. 1964;51:883–890. doi: 10.1073/pnas.51.5.883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Garvin R. T., Rosset R., Gorini L. Proc. Natl. Acad. Sci. USA. 1973;70:2762–2766. doi: 10.1073/pnas.70.10.2762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Rosset R., Gorini L. J. Mol. Biol. 1969;39:95–112. doi: 10.1016/0022-2836(69)90336-2. [DOI] [PubMed] [Google Scholar]
- 23.Gorini L. Annu. Rev. Genet. 1970;4:107–134. doi: 10.1146/annurev.ge.04.120170.000543. [DOI] [PubMed] [Google Scholar]
- 24.Sella G., Ardell D. J. Mol. Evol. 2002;54:638–651. doi: 10.1007/s00239-001-0060-7. [DOI] [PubMed] [Google Scholar]
- 25.Ardell D., Sella G. Philos. Trans. R. Soc. London B. 2002;357:1625–1642. doi: 10.1098/rstb.2002.1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ardell D., Sella G. J. Mol. Evol. 2001;53:269–281. doi: 10.1007/s002390010217. [DOI] [PubMed] [Google Scholar]
- 27.Crick F. J. Mol. Biol. 1968;38:367–379. doi: 10.1016/0022-2836(68)90392-6. [DOI] [PubMed] [Google Scholar]
- 28.Wong J. T. Proc. Natl. Acad. Sci. USA. 1976;73:2336–2340. doi: 10.1073/pnas.73.7.2336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Freeland S. Genet. Programming Evolvable Mach. 2002;3:113–127. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Text