Noise-based switches and amplifiers for gene expression (original) (raw)
Abstract
The regulation of cellular function is often controlled at the level of gene transcription. Such genetic regulation usually consists of interacting networks, whereby gene products from a single network can act to control their own expression or the production of protein in another network. Engineered control of cellular function through the design and manipulation of such networks lies within the constraints of current technology. Here we develop a model describing the regulation of gene expression and elucidate the effects of noise on the formulation. We consider a single network derived from bacteriophage λ and construct a two-parameter deterministic model describing the temporal evolution of the concentration of λ repressor protein. Bistability in the steady-state protein concentration arises naturally, and we show how the bistable regime is enhanced with the addition of the first operator site in the promotor region. We then show how additive and multiplicative external noise can be used to regulate expression. In the additive case, we demonstrate the utility of such control through the construction of a protein switch, whereby protein production is turned “on” and “off” by using short noise pulses. In the multiplicative case, we show that small deviations in the transcription rate can lead to large fluctuations in the production of protein, and we describe how these fluctuations can be used to amplify protein production significantly. These results suggest that an external noise source could be used as a switch and/or amplifier for gene expression. Such a development could have important implications for gene therapy.
Regulated gene expression is the process through which cells control fundamental functions such as the production of enzymatic and structural proteins and the time sequence of this production during development (1, 2). Many of these regulatory processes take place at the level of gene transcription (3), and there is evidence that the underlying reactions governing transcription can be affected by external influences from the environment (4).
Because experimental techniques are increasingly capable of providing reliable data pertaining to gene regulation, theoretical models are becoming important in the understanding and manipulation of such processes. The most common theoretical approach is to model the interactions of elements in a regulatory network as biochemical reactions. Given such a set of chemical reactions, the individual jump processes (i.e., the creation or destruction of a given reaction species) and their associated probabilities are considered. In its most general form, this approach often leads to a type of Monte Carlo simulation of the interaction probabilities (5). Although this approach suffers from a lack of analytic tractability, its strength is its completeness—fluctuations in species' concentrations are embedded in the modeling process. These internal fluctuations are important for systems containing modest numbers of elements, or when the volume is small.
Rate equations originate as a first approximation to such a general approach, whereby internal fluctuations are ignored. These deterministic differential equations describe the evolution of the mean value of some property of the set of reactions, typically the concentrations of the various elements involved. The existence of positive or negative feedback in a regulatory network is thought to be common (6), and, within the reaction framework, feedback leads to nonlinear rate equations (7–9).
Noise in the form of random fluctuations arises in these systems in one of two ways. As discussed above, internal noise is inherent in the biochemical reactions. Its magnitude is proportional to the inverse of the system size, and its origin is often thermal. On the other hand, external noise originates in the random variation of one or more of the externally set control parameters, such as the rate constants associated with a given set of reactions. If the noise source is small, its effect can often be incorporated post hoc into the rate equations. In the case of internal noise, this is done in an attempt to recapture the lost information embodied in the rate equation approximation. But in the case of external noise, one often wishes to introduce some new phenomenon where the details of the effect are not precisely known. In either case, the governing rate equations are augmented with additive or multiplicative stochastic terms. These terms, viewed as a random perturbation to the deterministic picture, can induce various effects, most notably the switching between potential attractors (i.e., fixed points, limit cycles, chaotic attractors) (10).
Although impressive progress has been made in genome sequencing and the understanding of certain qualitative features of gene expression, there have been comparatively few advancements in the quantitative understanding of genetic networks. This is because of the inherent complexity of such biological systems. In this work, we adopt an engineering approach in studying a solitary gene network. We envision that a plasmid, or genetic applet (11), containing a small self-contained gene regulatory network, can be designed and studied in isolation. Such an approach has two distinct advantages. First, because the approach is inherently reductionist, it can make gene network problems tractable and thus more amenable to a mathematical formulation. Second, such an approach could form the basis for new techniques in the regulation of in vivo gene networks, whereby a genetic applet is designed to control cellular function.
In this paper, we develop a model describing the dynamics of protein concentration in such a genetic applet and demonstrate how external noise can be used to control the network. Although our results are general for networks designed with positive autoregulation, we ground the discussion by considering an applet derived from the promoter region of bacteriophage λ. Because the range of potentially interesting behavior is wide, we focus primarily on the steady-state mean value of the concentration of the λ repressor protein. This choice is motivated by experiment; detailed dynamical information is still rather difficult to obtain, as are statistical data concerning higher moments. We show how an additive noise term can be introduced to our model and how the subsequent Langevin equation is analyzed by way of transforming to an equation describing the evolution of a probability function. We then obtain the steady-state mean (ssm) repressor concentration by solving this equation in the long-time limit and discuss its relationship to the magnitude of the external perturbation. This formulation leads to a potentially useful application, whereby one utilizes the noise to construct a genetic switch. We then consider noise at the level of transcription, where noise enters the formulation in a multiplicative manner. As in the additive case, we transform to an equation describing a probability distribution and solve for the SSM concentration as a function of noise strength. Finally, we demonstrate how such a noise source can be used to amplify the repressor concentration by several orders of magnitude.
A Model for Repressor Expression
In the context of the lysis–lysogeny pathway in the λ virus, the autoregulation of λ repressor expression is well characterized (12, 13). In this section, we present two models describing the regulation of such a network. We envision that our system is a plasmid consisting of the P R_–_P RM operator region and components necessary for transcription, translation, and degradation.
Although the full promoter region in λ phage contains the three operator sites known as OR1, OR2, and OR3, we first consider a mutant system whereby the operator site OR1 is absent from the region. The basic dynamical properties of this network, along with a categorization of the biochemical reactions, are as follows (12, 13). The gene cI expresses repressor (CI), which in turn dimerizes and binds to the DNA as a transcription factor. In the mutant system, this binding can take place at one of the two binding sites, OR2 or OR3. (Here we ignore nonspecific binding.) Binding at OR2 enhances transcription, which takes place downstream of OR3, whereas binding at OR3 represses transcription, effectively turning off production.
The chemical reactions describing the network are naturally divided into two categories—fast and slow. The fast reactions have rate constants of order seconds and are therefore assumed to be in equilibrium with respect to the slow reactions, which are described by rates of order minutes. If we let X, _X_2, and D denote the repressor, repressor dimer, and DNA promoter site, respectively, then we may write the equilibrium reactions
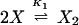
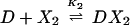
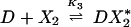
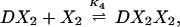 |
1 |
|---|
where the _DX_2 and DX*2 complexes denote binding to the OR2 or OR3 sites, respectively, _DX_2_X_2 denotes binding to both sites, and the K i are forward equilibrium constants. We let _K_3 = σ1_K_2 and _K_4 = σ2_K_2, so that σ1 and σ2 represent binding strengths relative to the dimer–OR2 strength.
The slow reactions are transcription and degradation,
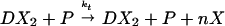
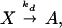 |
2 |
|---|
where P denotes the concentration of RNA polymerase, and n is the number of proteins per mRNA transcript. These reactions are considered irreversible.
If we consider an in vitro system with high copy-number plasmids,§ we may define concentrations as our dynamical variables. Letting x = [_X_], y = [_X_2], d = [_D_], u = [_DX_2], v = [DX*2], and z = [_DX_2_X_2], we can write a rate equation describing the evolution of the concentration of repressor,
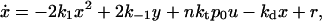 |
3 |
|---|
where we assume that the concentration of RNA polymerase _p_0 remains constant during time. The parameter r is the basal rate of production of CI, i.e., the expression rate of the cI gene in the absence of a transcription factor.
We next eliminate y, u, and d from Eq. 3 as follows. We utilize the fact that the reactions in Eq. 1 are fast compared to expression and degradation and write algebraic expressions
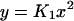
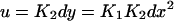
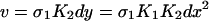
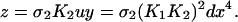 |
4 |
|---|
Further, the total concentration of DNA promoter sites d T is constant, so that
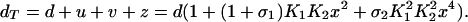 |
5 |
|---|
Under these assumptions, Eq. 3 becomes
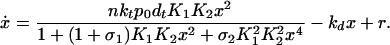 |
6 |
|---|
Without loss of generality, we may eliminate two of the parameters in Eq. 3 by rescaling the repressor concentration x and time. To this end, we define the dimensionless variables x̃ = x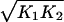 and t̃ = t(r
and t̃ = t(r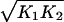 ). On substitution into Eq. 3, we obtain
). On substitution into Eq. 3, we obtain
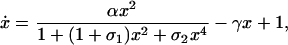 |
7 |
|---|
where the time derivative is with respect to t̃, and we have suppressed the overbar on x. The dimensionless parameter α ≡ nk t p_0_d T/r is effectively a measure of the degree in which the transcription rate is increased above the basal rate by repressor binding, and γ ≡ k d/(r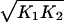 ) is proportional to the relative strengths of the degradation and basal rates.
) is proportional to the relative strengths of the degradation and basal rates.
For the mutant operator region of λ phage, we have σ1 ∼ 1 and σ2 ∼ 5 (12–14), so that the two parameters α and γ in Eq. 7 determine the steady-state concentration of repressor. For this equation, there are two types of behavior. For one set of parameter values, we have monostability, whereby all initial concentrations evolve to the same fixed-point value. For another set, we have three fixed points, and the initial concentration will determine which steady state is selected. Additionally, in the multiple fixed-point regime, stability analysis indicates that the middle fixed point x m is unstable, so that all initial values x < _x_ _m_ will evolve to the lower fixed point, whereas those satisfying _x_ > x m will evolve to the upper. This bistability arises as a consequence of the competition between the production of x along with dimerization and its degradation. For certain parameter values, the initial concentration is irrelevant, but for those that more closely balance production and loss, the final concentration is determined by the initial value.
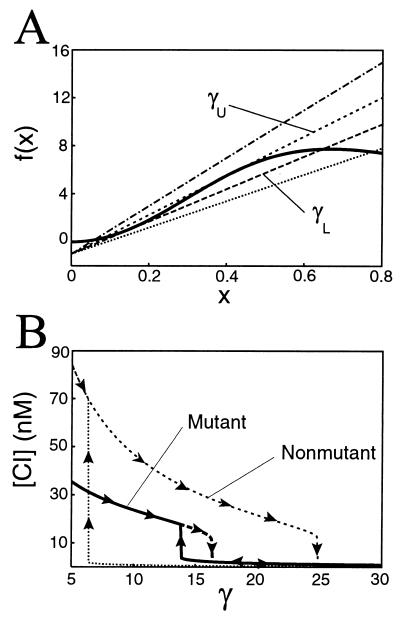
Graphically, we can see how bistability arises in Eq. 7 by setting α _x_2/(1 + 2 _x_2 + 5 x_4) = γ_x − 1. In Fig. 1A, we plot the functions α _x_2/(1 + 2 x_2 + 5 x_4) and γ x − 1 for fixed α and several values of the slope γ. We see that for γ small (whereby degradation is minimal compared with production), there is one possible steady-state value of x (and therefore CI). As we increase γ above some critical value γ_L, we observe that three fixed-point values appear. As we increase γ still further beyond a second critical value γ_U, the concentration “jumps” to a lower value, and the system returns to a state of monostability.
Figure 1.
Bifurcation plots for the variable x and concentration of λ repressor. (A) Graphical depiction of the fixed points of Eq. 7, generated by setting ẋ = 0 and plotting α x_2/(1 + 2_x_2 + 5_x_4) and the line γ_x − 1. As the slope γ is increased, the system traverses a region of multistability and returns to a state of monostability. (B) Hysterisis loops for the mutant and nonmutant systems obtained by setting ẋ = 0 in Eqs. 7 and 8. Beginning with concentrations of 35 nM for the mutant system and 85 nM for the nonmutant system, we steadily increase the degradation parameter γ. In both systems, the concentration of repressor slowly decreases until a bifurcation point. In the mutant (nonmutant) system, the repressor concentration abruptly drops to a lower value at γ ∼ 16 (γ ∼ 24). Then, on reversing course and decreasing γ, the repressor concentration increases slowly until γ encounters a second bifurcation point at γ ∼ 14 (γ ∼ 6), whereby the concentration immediately jumps to a value of 15 nM (mutant) or 70 nM (nonmutant). The subsequent hysterisis loop is approximately 10 times larger in the nonmutant case. Parameter values are α = 50, _K_1 = 0.05 nM−1, and _K_2 = 0.026 nM−1 for the mutant system, and _K_2 = 0.033 nM−1 for the nonmutant system (12, 13).
The preceding ideas lead to a plausible method whereby the system may be experimentally probed for bistability. We envision that α is fixed by the transcription rate and DNA binding site concentration, and that the degradation parameter γ is an adjustable control. Beginning with a low initial value of γ = γ0 = 5, we slowly increase the degradation rate. The effect is illustrated in Fig. 1B. We see that as γ is slowly increased, the concentration of CI slowly decreases as the system tracks the fixed point. Then, at the moment when γ is greater than γ_U_, the concentration abruptly jumps to a lower value, followed by a further slow increase. Now suppose we reverse course and begin to decrease γ. Then the system will track along the lower fixed point until a point when γ is greater than γ_L_. At this point, the system will again jump, this time to a higher fixed-point value. The trademark of hysterisis is that the two jumps, one when increasing γ and the other when decreasing, occur for different values of γ.
As is well known, the full operator region of λ phage contains three sites. We turn briefly to the effect of the additional site OR1 on the above network. In order to incorporate its effect, Eq. 1 must be generalized to account for additional equilibrium reactions. This generalization amounts to the incorporation of dimer binding to OR1 (12, 13) and permutations of multiple binding possibilities at the three operator sites. Then, by using known relationships between the cooperative binding rates, the above steps can be repeated and an equation analogous to Eq. 7 constructed. We obtain
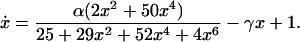 |
8 |
|---|
As can be seen, the addition of OR1 has the effect of changing the first term on the right-hand side of the equation. Although this augmentation does not affect the qualitative features of the above discussion, one important quantitative difference is depicted in Fig. 1B. In this figure, we see that the addition of OR1 has a large effect on the bistability region, increasing the overall size of the region by roughly an order of magnitude. Additionally, the model predicts that, whereas the drop in the concentration of repressor at the first bifurcation point will be approximately the same in both cases, the jump to the higher concentration will be around five times greater in the system containing OR1. Finally, because one effect of a larger bistable region is to make the switching mechanism more robust to noise, these results are of notable significance in the context of the lysogeny-to-lysis switching of λ phage.
Additive Noise
We now focus on parameter values leading to bistability and consider how an additive external noise source affects the production of repressor. Physically, we take the dynamical variable x described above to represent the repressor concentration within a colony of cells and consider the noise to act on many copies of this colony. In the absence of noise, each colony will evolve identically to one of the two fixed points, as discussed above. The presence of a noise source will at times modify this simple behavior, whereby colony-to-colony fluctuations can induce novel behavior.
An additive noise source alters the “background” repressor production. As an example, consider the effect of a randomly varying external field on the biochemical reactions. The field could, in principle, impact the individual reaction rates (15, 16), and, because the rate equations are probabilistic in origin, its influence enters statistically. We posit that such an effect will be small and can be treated as a random perturbation to our existing treatment; we envision that events induced will affect the basal production rate, and that this will translate to a rapidly varying background repressor production. In order to introduce this effect, we generalize the aforementioned model such that random fluctuations enter Eq. 8 linearly,
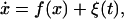 |
9 |
|---|
where f(x) is the right-hand side of Eq. 8, and ξ(t) is a rapidly fluctuating random term with zero mean (〈ξ(t)〉 = 0). In order to encapsulate the rapid random fluctuations, we make the standard requirement that the autocorrelation be “δ-correlated,” i.e., the statistics of ξ(t) are such that 〈ξ(t)ξ(_t_′)〉 = _D_δ(t − _t_′), with D proportional to the strength of the perturbation.
Eq. 9 can be rewritten as
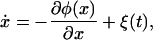 |
10 |
|---|
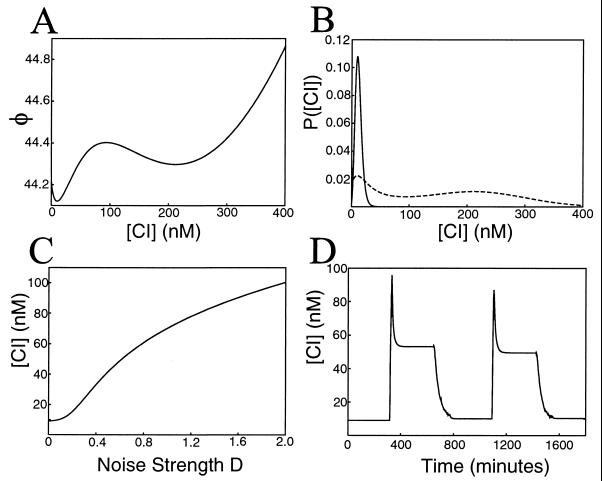
where we introduce the potential φ(x), which is simply the integral of the right-hand side of Eq. 7. φ(x) can be viewed as an “energy landscape,” whereby x is considered the position of a particle moving in the landscape. One such landscape is plotted in Fig. 2A. Note that the stable fixed values of repressor concentration correspond to the minima of the potential φ in Fig. 2A, and the effect of the additive noise term is to cause random kicks to the particle (system state point) lying in one of these minima. On occasion, a sequence of kicks may enable the particle to escape a local minimum and reside in a new valley.
Figure 2.
Results for additive noise with parameter values α = 10 and γ = 5.5. (A) The energy landscape. Stable equilibrium concentration values of Eq. 8 correspond to the valleys at [CI] = 10 and 200 nM, with an unstable value at [CI] = 99 nM. (B) Steady-state probability distributions for noise strengths of D = 0.04 (solid line) and D = 0.4 (dotted line). (C) The steady-state equilibrium protein concentration plotted vs. noise strength. The concentration increases as the noise causes the upper state of A to become increasingly populated. (D) Simulation of Eq. 9 demonstrating the utilization of external noise for protein switching. Initially, the concentration begins at a level of [CI] = 10 nM corresponding to a low noise value of D = 0.01. After 6 hr, a large 30-min noise pulse of strength D = 1.0 is used to drive the concentration to 58 nM. After this pulse, the noise is returned to its original value. At 11 hr, a smaller 90-min noise pulse of strength D = 0.04 is used to return the concentration to near its original value. The simulation technique is that of ref. 23.
To solve Eq. 10, we introduce the probability distribution P(x, t), which is effectively the probability of finding the system in a state with concentration x at time t. Given Eq. 10, a Fokker–Planck equation for P(x, t) can be constructed (17)
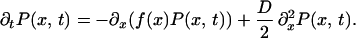 |
11 |
|---|
We focus here on the value of the ssm concentration. To this end, we first solve for the steady-state distribution, obtaining
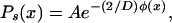 |
12 |
|---|
where A is a normalization constant determined by requiring the integral of P s(x) over all x be unity. In Fig. 2B, we plot P s(x), corresponding to the landscape of Fig. 2A, for two values of the noise strength D. It can be seen that for the smaller noise value, the probability is distributed around the lower concentration of repressor, whereas for the larger noise value, the probability is split and distributed around both concentrations. This is consistent with our conceptual picture of the landscape: low noise will enable only transitions from the upper state to the lower state, because random kicks are not sufficient to climb the steep barrier from the lower state, whereas high noise induces transitions between both of the states. Additionally, the larger noise value leads to a spreading of the distribution, as expected.
Using the steady-state distribution, the ssm value of x ≡ 〈x_〉_ss is given by
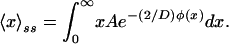 |
13 |
|---|
In Fig. 2C, we plot the ssm concentration as a function of D, obtained by numerically integrating Eq. 13 and transforming from the dimensionless variable x to repressor concentration. It can be seen that the ssm concentration increases with D, corresponding to the increasing likelihood of populating the upper state, as discussed previously with respect to Fig. 2 A and B.
Fig. 2C indicates that the external noise can be used to control the ssm concentration. As a candidate application, consider the following protein switch. Given parameter values leading to the landscape of Fig. 2A, we begin the switch in the “off” position by tuning the noise strength to a very low value. This will cause a high population in the lower state and a correspondingly low value of the concentration. Then at some time later, consider pulsing the system by increasing the noise to some large value for a short period of time, followed by a decrease back to the original low value. The pulse will cause the upper state to become populated, corresponding to a concentration increase and a flipping of the switch to the “on” position. As the pulse quickly subsides, the upper state remains populated because the noise is not of sufficient strength to drive the system across either barrier (on relevant time scales). To return the switch to the off position, the upper-state population needs to be decreased to a low value. This can be achieved by applying a second noise pulse of intermediate strength. This intermediate value is chosen large enough so as to enhance transitions to the lower state but small enough to remain prohibitive to upper-state transitions.
Fig. 2D depicts the time evolution of the switching process for noise pulses of strengths D = 1.0 and D = 0.05. Initially, the concentration begins at a level of [CI] = 10 nM, corresponding to a low noise value of D = 0.01. After 6 hr in this low state, a 30-min noise pulse of strength D = 1.0 is used to drive the concentration to a value of [CI] ∼ 58 nM. After this burst, the noise is returned to its original value. At 11 hr, a second 90-min pulse of strength D = 0.05 is used to return the concentration to its original value.
Multiplicative Noise
We now consider the effect of a noise source that alters the transcription rate. Although transcription is represented by a single biochemical reaction, it is actually a complex sequence of reactions (18), and it is natural to assume that this part of the gene regulatory sequence is likely to be affected by fluctuations of many internal or external parameters. We vary the transcription rate by allowing the parameter α in Eq. 8 to vary stochastically, i.e., we set α → α + ξ(t). In this manner, we obtain an equation describing the evolution of the protein concentration x
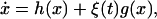 |
14 |
|---|
where h(x) is the right-hand side of Eq. 8, and
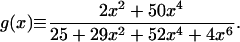 |
15 |
|---|
Thus, in this case, the noise is multiplicative, as opposed to additive, as in the previous case.
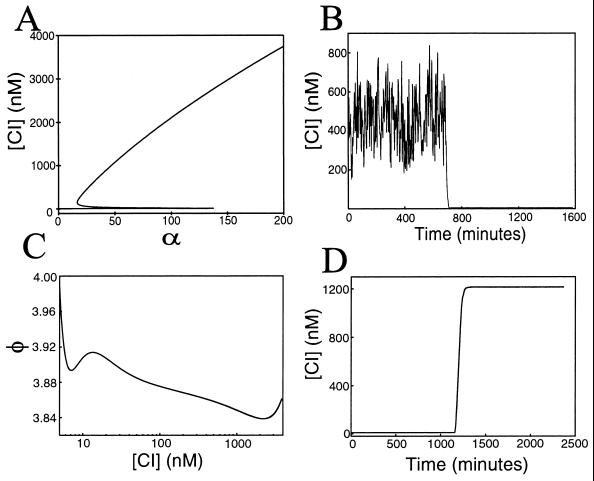
Qualitatively, we can use the bifurcation plot of Fig. 3A to anticipate one effect of allowing the parameter α to fluctuate. Such a bifurcation plot is yet another way of depicting the behavior seen in Fig. 1A; it can be seen that for certain values of α, there is one unique steady-state value of repressor concentration, and that for other values, there are three. To incorporate fluctuations, if we envision α to stochastically vary in the bistable region of Fig. 3A, we notice that the steep top branch implies the corresponding fluctuations in repressor concentration will be quite large. This is contrasted with the flat lower branch, where modest fluctuations in α will induce small variations. In order to verify this observation quantitatively, we simulated Eq. 14, the results of which are presented in Fig. 3B. Beginning with repressor concentration equal to its upper value of approximately 500 nM, we notice that the immediate fluctuations are quite large, even though α varies by only a few percent (Fig. 3A). Then, at around 700 min, the concentration quickly drops to its lower value, indicating that the fluctuations envisioned in Fig. 3A were sufficient to drive the repressor concentration to the dotted line of Fig. 3A and off the upper branch (across the unstable fixed point). The final state is then one of very small variation, as anticipated.
Figure 3.
Results for multiplicative noise. (A) Bifurcation plot for the repressor concentration vs. the model parameter α. The steep upper branch implies that modest fluctuations in α will cause large fluctuations around the upper fixed value of repressor concentration, whereas the flat lower branch implies small fluctuations about the lower value. (B) The evolution of the repressor concentration in a single colony, obtained by simulation of Eq. 14. Relatively small random variations of the parameter α (∼6%) induce large fluctuations in the steady-state concentration until around 700 min and small fluctuations thereafter. (C) Energy landscape for parameter values α = 100 and γ = 8.5. (D) Large-scale amplification of the protein concentration obtained by simulation of Eq. 14. At 20 hr, a 60-min noise pulse of strength D = 1.0 is used to quickly increase the protein concentration by over three orders of magnitude. The parameter values are the same as those in C.
As in the previous section, the steady-state probability distribution is obtained by transforming Eq. 14 to an equivalent Fokker-Planck equation (17),
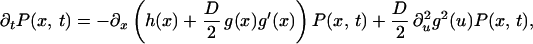 |
16 |
|---|
where the prime denotes the derivative of g(x) with respect to x. We again solve for the steady-state distribution, obtaining
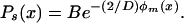 |
17 |
|---|
As before, the steady-state distribution can be used to obtain the ssm concentration.
Although not originating from a deterministic equation like that of Eq. 7, the function φ_m_(u) in Eq. 17 can still be viewed as a potential. We now consider parameter values leading to one such landscape in Fig. 3C. This landscape implies that we will have two steady-state repressor concentrations of approximately 5 and 1,200 nM. This large difference is because of the largeness of the parameter α, implying that repressor “induced” transcription amplifies the basal rate by a large amount. (Because d T enters in the numerator of the definition of α, one could construct such a system experimentally with a high copy-number plasmid.) This feature suggests that multiplicative noise could be used to amplify protein production, as described in the following example. We begin with zero protein concentration and very low noise strength D, leading to a highly populated lower state and low overall concentration. Then, at some later time, we pulse the system by increasing D for some short interval. This will cause the upper state to become quickly populated, because it is easy to escape the shallow valley of the landscape and move into the large basin. In Fig. 3D, we plot the temporal evolution of the mean repressor concentration obtained from the simulation of Eq. 14. We see that the short noise pulse at around 20 hr indeed causes the concentration to increase abruptly by over three orders of magnitude, making this type of amplification an interesting case for experimental exploration.
Discussion
From an engineering perspective, the control of cellular function through the design and manipulation of genetic regulatory networks is an intriguing possibility. In this paper, we have shown how external noise can be used to control the dynamics of a regulatory network, and how such control can be practically utilized in the design of a genetic switch and/or amplifier. Although the main focus of this work was on a network derived from the promotor region of λ phage, our approach is generally applicable to any autoregulatory network where a protein–multimer acts as a transcription factor.
An important element of our control scheme is bistability. This implies that a necessary criterion in the design of a noise-controlled applet be that the network is poised in a bistable region. This could potentially be achieved by methods such as the utilization of a temperature-dependent repressor protein, DNA titration, ssrA tagging, or pH control.
Physically, the noise might be generated by using an external field. Importantly, it has been claimed that electromagnetic fields can exert biological effects (19–22). In addition, recent theoretical (16) and experimental (15) work suggests a possible mechanism whereby an electric field can alter an enzyme-catalyzed reaction. These findings suggest that, although there is global charge neutrality, an external field can interact with local dipoles that arise through transient conformational changes or in membrane transport.
Current gene therapy techniques are limited in that transfected genes are typically either in an “on” or “off” state. However, for the effective treatment of many diseases, the expression of a transfected gene needs to be regulated in some systematic fashion. Thus, the development of externally controllable noise-based switches and amplifiers for gene expression could have significant clinical implications.
Acknowledgments
We respectfully acknowledge insightful discussions with Kurt Wiesenfeld, Farren Issacs, Tim Gardner, and Peter Jung. This work was supported by the Office of Naval Research (Grant N00014-99-1-0554) and the United States Department of Energy.
Abbreviation
ssm
steady-state mean
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
Article published online before print: Proc. Natl. Acad. Sci. USA, 10.1073/pnas.040411297.
§
This assumption is necessary, because the number of relevant molecules per cell is small in vivo. Because there are many cells, we could alternatively use state probabilities as dynamical variables describing an in vivo system.
References
- 1.Dickson R, Abelson J, Barnes W. Science. 1975;187:27–35. doi: 10.1126/science.1088926. [DOI] [PubMed] [Google Scholar]
- 2.Yuh C H, Bolouri H, Davidson E H. Science. 1998;279:1896–1902. doi: 10.1126/science.279.5358.1896. [DOI] [PubMed] [Google Scholar]
- 3.Lewin B. Genes VI. Oxford: Oxford Univ. Press; 1997. [Google Scholar]
- 4.Harada Y, Funatsu T, Murakami K, Nonoyama Y, Ishihama A, Yarnagida T. Biophys J. 1999;76:709–715. doi: 10.1016/S0006-3495(99)77237-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.McAdams H H, Arkin A. Proc Natl Acad Sci USA. 1997;94:814–819. doi: 10.1073/pnas.94.3.814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.McAdams H H, Shapiro L. Science. 1995;269:650–656. doi: 10.1126/science.7624793. [DOI] [PubMed] [Google Scholar]
- 7.Keller A. J Theor Biol. 1995;172:169–185. doi: 10.1006/jtbi.1995.0014. [DOI] [PubMed] [Google Scholar]
- 8.Smolen P, Baxter D A, Byrne J H. Am J Physiol. 1998;43:C531–C542. doi: 10.1152/ajpcell.1998.274.2.C531. [DOI] [PubMed] [Google Scholar]
- 9.Wolf D M, Eeckman F H. J Theor Biol. 1998;195:167–186. doi: 10.1006/jtbi.1998.0790. [DOI] [PubMed] [Google Scholar]
- 10.Horsthemke W, Lefever R. Noise-Induced Transitions. Berlin: Springer; 1984. [Google Scholar]
- 11.Gardner T S, Cantor C R, Collins J J. Nature (London) 2000;403:339–342. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- 12.Ptashne M, Jeffrey A, Johnson A D, Maurer R, Meyer B J, Pabo C O, Roberts T M, Sauer R T. Cell. 1980;19:1–11. doi: 10.1016/0092-8674(80)90383-9. [DOI] [PubMed] [Google Scholar]
- 13.Johnson A D, Poteete A R, Lauer G, Sauer R T, Ackers G K, Ptashne M. Nature (London) 1981;294:217–223. doi: 10.1038/294217a0. [DOI] [PubMed] [Google Scholar]
- 14.Johnson A D, Pabo C O, Sauer R T. Methods Enzymol. 1980;65:839–856. doi: 10.1016/s0076-6879(80)65078-2. [DOI] [PubMed] [Google Scholar]
- 15.Xie T D, Marszalek P, Chen Y. Biophys J. 1994;67:1247–1251. doi: 10.1016/S0006-3495(94)80594-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Astumian R D, Robertson B. J Am Chem Soc. 1993;115:11063–11068. [Google Scholar]
- 17.Van Kampen N G. Stochastic Processes in Physics and Chemistry. Amsterdam: North-Holland; 1992. [Google Scholar]
- 18.von Hippel P H. Science. 1998;281:660–665. doi: 10.1126/science.281.5377.660. [DOI] [PubMed] [Google Scholar]
- 19.Berg H. Bioelectrochem Bioenerg. 1995;38:153–159. [Google Scholar]
- 20.Liu D S, Astumian R D, Tsong T Y. J Biol Chem. 1990;265:7260–7271. [PubMed] [Google Scholar]
- 21.Otter M W, McLeod K J, Rubin C T. Clin Orthop. 1998;355:S90–S104. doi: 10.1097/00003086-199810001-00011. [DOI] [PubMed] [Google Scholar]
- 22.Asbury C L, van den Engh G. Biophys J. 1998;74:1024–1130. doi: 10.1016/s0006-3495(98)74027-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sancho J, Miguel M S, Katz S. Phys Rev A. 1982;26:1589–1593. [Google Scholar]