Origins and evolution of the Europeans' genome: evidence from multiple microsatellite loci (original) (raw)
Abstract
There is general agreement that the current European gene pool is mainly derived from Palaeolithic hunting–gathering and Neolithic farming ancestors, but different studies disagree on the relative weight of these contributions. We estimated admixture rates in European populations from data on 377 autosomal microsatellite loci in 235 individuals, using five different numerical methods. On average, the Near Eastern (and presumably Neolithic) contribution was between 46 and 66%, and admixture estimates showed, with all methods, a strong and significant negative correlation with distance from the Near East. If the assumptions of the model are approximately correct, i.e. if the Basques' and Near Easterners' genomes represent a good approximation to the Palaeolithic and Neolithic settlers of Europe, respectively, these results imply that half or more of the Europeans' genes are descended from Near Eastern ancestors who immigrated in Europe 10 000 years ago. If these assumptions are incorrect, our results show anyway that clinal variation is the rule in the Europeans' genomes and that lower estimates of Near Eastern admixture obtained from the analysis of single markers do not reflect the patterns observed at the genomic level.
Keywords: human, short tandem repeat polymorphisms, genome diversity, demic diffusion, admixture
1. Introduction
The origins and evolution of the European gene pool are controversial. According to archaeological sources, the main demographic phenomena affecting the whole continent were its first Palaeolithic colonization (starting approx. 35 000 years BP: Otte 2000) and the Neolithic transition to agriculture (starting approx. 10 000 years BP: Pinhasi et al. 2000). The peopling of Europe has doubtless been more complex than this, with late Palaeolithic contraction and re-expansions in response to climate changes (between 20 000 and 15 000 years ago: Otte 2000) and extensive phenomena of local gene flow (Sokal et al. 1989). But even assuming a very simplified scenario in which the genome of the present-day Europeans only reflects admixture between the first settlers (Palaeolithic hunter–gatherers) and Neolithic immigrant farmers, there is little consensus on the relative importance of their contributions. The demic diffusion model (DD) suggests that farming spread because farmers did: large numbers of people dispersed from the Near East in Neolithic times, carrying with them, besides their genes, the techniques for farming and animal breeding (Menozzi et al. 1978; Ammerman & Cavalli-Sforza 1984; Pinhasi et al. 2005). Alternatively, the cultural diffusion model (CD) suggests that farming technologies were largely adopted by the hunting and gathering people who already dwelt in Europe, with limited Neolithic immigration (Zvelebil & Zvelebil 1988; Haak et al. 2005).
The DD model was first proposed to explain the broad allele-frequency gradients observed for many protein markers in Europe (Menozzi et al. 1978). Gradients spanning much of the continent can arise if four conditions are met, namely: (i) sufficiently large allele-frequency differences between Palaeolithic hunting–gathering and Neolithic farming communities of the Near East; (ii) increase in the farmers' population size, due to the availability of improved subsistence technologies; (iii) westward dispersal of the farmers into Europe; and (iv) non-immediate admixture after contact, so that initially farmers would keep increasing in numbers while the hunter–gatherers would not. At the genetic level, the CD model predicts a low contribution of immigrating Near Eastern farmers to the European gene pool, but also the DD model is compatible with a low average contribution of Near Eastern genes across Europe, depending on the speed and patterns of farmers' dispersal (Chikhi et al. 2002). On the contrary, a high Near Eastern admixture seems consistent only with the DD model.
Two phylogeographic studies were interpreted as suggesting a Neolithic admixture of around 20 or 25% and therefore as supporting the CD model. These figures correspond, respectively, to the frequencies of mitochondrial haplogroups, which coalesce in Neolithic times (Richards et al. 2002) and of Y-chromosome haplogroups exhibiting a gradient in Europe (Semino et al. 2000). Conversely, when specific methods were used to model and quantify admixture, the Neolithic contribution to the European genome appeared greater than 50% (Chikhi et al. 2002; Dupanloup et al. 2004), in agreement with earlier simulations of European prehistoric demography (Rendine et al. 1986; Barbujani et al. 1995). However, Currat & Excoffier (2005) showed that biased ascertainment of biallelic DNA (or protein) sites may cause overestimation of the clinal patterns and hence of the Neolithic contribution to the European gene pool.
In single-gene studies, it is impossible to compare results across loci and hence to discriminate between locus-specific effects (those due to selection and mutation) and genome-wide effects (those of gene flow and admixture; Goldstein & Chikhi 2002). In addition, the statistical errors of the estimated admixture coefficients are inversely proportional to the number of loci considered (Bertorelle & Excoffier 1998). Therefore, robust estimates of admixture proportions can only be sought by studying a large number of genomic loci. In that case, however, the ascertainment bias may be a problem, that is to say, the possibility that the sample of loci contains an excess of highly polymorphic biallelic DNA sites (Currat & Excoffier 2005). A solution to that problem is to analyse short tandem repeat (STR or microsatellite) data, namely loci for which there is no evidence so far suggesting biased ascertainment (see Nielsen 2004) and which, at any rate, are expected to suffer less, if at all, from ascertainment effects, because of their generally high level of polymorphism (Eller 2001).
2. Material and methods
We analysed variation at 377 autosomal STR loci distributed on all 22 autosomes and published by Rosenberg et al. (2002). These microsatellites were typed in 1064 worldwide-distributed individuals, and for this study we selected 99 individuals from the Near East (48 Druze, 51 Palestinians; the dataset also comprises 49 Bedouins whom we excluded because they are nomadic and could not be placed with confidence on the map) and 161 individuals from eight populations of Europe (24 Basques, 29 French, 14 northern Italians, 28 Sardinians, 8 Tuscans, 16 Orcadians, 25 Russians and 17 Adygei).
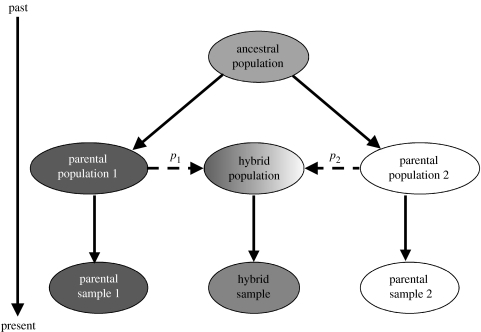
Admixture models regard populations as hybrids formed by the mixing of genes from two or more parental populations (figure 1). To quantify admixture, we here used five different numerical approaches, two of them based on coalescence times. The quantities being estimated in all cases were the respective contributions (or admixture coefficients) _p_1 and _p_2 of the parental populations—Neolithic farmers and Palaeolithic hunter–gatherers—to the presumably hybrid gene pools of the other populations. We quantified admixture using the following methods/approaches.
- A method that estimates _p_1 and _p_2 by a least-square regression (Roberts & Hiorns 1965); we refer to this estimator as _m_R.
- A method of maximum likelihood, first proposed by Long (1991) and further developed by Chakraborty et al. (1992), which expresses the likelihood of the hybrid sample as a function of the parental allele frequencies and the admixture proportion and quantifies the admixture rate as the parameter value which maximizes the likelihood; we refer to this estimator as _m_C.
- A method based on the estimation of average coalescence times between random pairs of genes sampled both within and between populations (Bertorelle & Excoffier 1998). This method can be used considering the molecular distance between alleles or assuming all alleles equally divergent. Because by considering allele frequencies the estimated coefficients are less affected by the stochasticity of the mutation process and because the time-scale of the admixture process we want to investigate is comparable to the short times through which genetic drift acts rather than to the long times through which mutations accumulate (Barbujani 1997), we chose the latter approach and refer to this estimator as _m_Y.
- A genealogical likelihood-based approach, estimating the admixture coefficients by means of a Monte Carlo Chain Markov (MCMC) algorithm (Chikhi et al. 2001); we report the average admixture coefficients updated every five steps of the MCMC and we refer to this estimator as _m_L.
- A recent maximum-likelihood method implemented in the programme Leadmix, which estimates admixture proportions also taking into account genetic drift leading to divergence between admixed and parental populations in the period between the admixture event and the sampling (Wang 2003). We refer to this estimator as _m_W.
Figure 1.
A model for admixture. Solid lines represent genealogical descent, dashed lines represent admixture. The five methods used differ regarding the assumptions and numerical procedures for estimating _p_1 and _p_2.
Standard deviations (s.d.) of the admixture coefficients were estimated by bootstrapping the loci 100 times. To generate bootstrapped datasets that could be used to recalculate three of the admixture coefficients (all but _m_L for which s.d.s were part of the standard output of the programme), we modified the software MsatBootstrap (Landry et al. 2002).
A crucial point in estimating admixture coefficients is the choice of parental populations, namely in this case populations whose genes can approximate the genes of Near Eastern Neolithic farmers and of European Palaeolithic hunter–gatherers. Based on linguistic, archaeological and genetic data and in agreement with all previous literature (Menozzi et al. 1978; Richards et al. 1996; Semino et al. 2000; Torroni et al. 2001; Wilson et al. 2001; Chikhi et al. 2002; Dupanloup et al. 2004), we considered that the current populations from the Near East (Palestinians and Druze) and the Basques represent, respectively, the best approximations for Neolithic farmers and for Palaeolithic hunter–gatherers.
Geographic clines at multiple loci can reflect not only admixture, but also isolation by distance, namely the interaction between genetic drift and spatially restricted gene flow (Wright 1943; Barbujani 1987). To test whether the geographic distribution of allelic variants is compatible with the effects of isolation by distance, we calculated genetic distances between populations, estimated from pairwise _F_st values as _F_st/(1−_F_st) (Rousset 1997). We then estimated by two Mantel tests (Mantel 1967) the correlations between genetic distances and both the spatial distances and their logarithms, by means of the software Passage (Rosenberg 2001). The significance of the correlations thus obtained was empirically assessed through 1 000 000 permutations.
3. Results
Under a simple model in which the European populations result from admixture between Palaeolithic (Basque) and Neolithic (Near Eastern) ancestors, the main genome component, representing on average between 45.8 and 66.0% of the total across Europe, appears to derive from ancestors whose genetic features were similar to those of the Near Easterners (table 1). With the exception of _m_Y, for which differences among bootstrap replications were greater, standard deviations of the coefficients were all less than 6.4%. Some of the 377 loci considered are likely to be linked, so that the standard deviations of the admixture coefficients obtained assuming they are independent could be slightly too conservative. However, with such a high number of loci, we believe that linkage did not dramatically affect the uncertainties of the estimates.
Table 1.
Estimated Near Eastern admixture (_p_2) in different modern European populations (per cent values) and distances (d) from the Near East barycentre and associated standard deviations (s.d.); averages of bootstrapped values across loci are given in parentheses.
| European population | _m_R | _m_C | _m_Y | _m_L | _m_W | d (km) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| _p_2 | s.d. | _p_2 | s.d. | _p_2 | s.d. | _p_2 | s.d. | _p_2 | s.d. | ||
| French | 59.7 (61.1) | 2.3 | 55.2 (59.9) | 2.5 | 44.3 (46.7) | 7.7 | 59.1 | 2.9 | 34.1 | 6.4 | 3216 |
| northern Italians | 66.1 (66.0) | 2.8 | 67.9 (68.2) | 2.8 | 54.2 (51.9) | 9.8 | 64.6 | 3.3 | 50.7 | 6.3 | 2644 |
| Sardinians | 64.0 (65.0) | 2.3 | 66.3 (66.1) | 2.5 | 49.3 (50.6) | 7.9 | 62.5 | 3.7 | 45.8 | 3.3 | 2491 |
| Tuscans | 72.5 (72.7) | 3.2 | 70.5 (70.6) | 3.3 | 62.3 (63.3) | 11.0 | 69.6 | 3.6 | 54.1 | 5.6 | 2432 |
| Orcadians. | 59.6 (58.9) | 3.2 | 60.3 (60.0) | 3.4 | 52.7 (52.9) | 11.7 | 58.9 | 3.6 | 37.3 | 5.8 | 4116 |
| Russians | 64.9 (63.9) | 2.9 | 67.4 (64.5) | 2.9 | 66.4 (66.6) | 9.7 | 60.1 | 3.1 | 43.8 | 5.4 | 3245 |
| Adygei | 75.2 (75.2) | 2.7 | 76.0 (75.6) | 2.9 | 80.5 (82.6) | 9.0 | 71.4 | 3.3 | 68.8 | 4.3 | 1379 |
| Europeans | 66.0 (65.1) | 1.7 | 63.7 (62.9) | 2.3 | 59.5 (57.7) | 6.3 | 64.9 | 2.7 | 45.8 | 3.3 | — |
Because of the large number of loci, the computing time necessary for the likelihood to reach equilibrium with the MCMC method (_m_L) was extremely long, of the order of months on Pentium IV PCs. Therefore, we fixed the estimation procedure to 10 000 iterations, each including 100 steps. To validate the results thus obtained we then ran several additional tests, namely: (i) we estimated the contribution of both parental populations by inverting _p_1 and _p_2, so as to check that their sum was 1 in all runs; (ii) in specific cases we increased the numbers of iterations to 50 000 (and the number of steps to 500 per iteration); and (iii) we reanalysed selected random subsets of 10 and 100 loci. The sum of _p_1 and _p_2 was always 1, despite the programme not having reached equilibrium, and the admixture estimates obtained were in all cases very similar with less than 5% fluctuations, although the standard deviations were predictably larger with fewer loci.
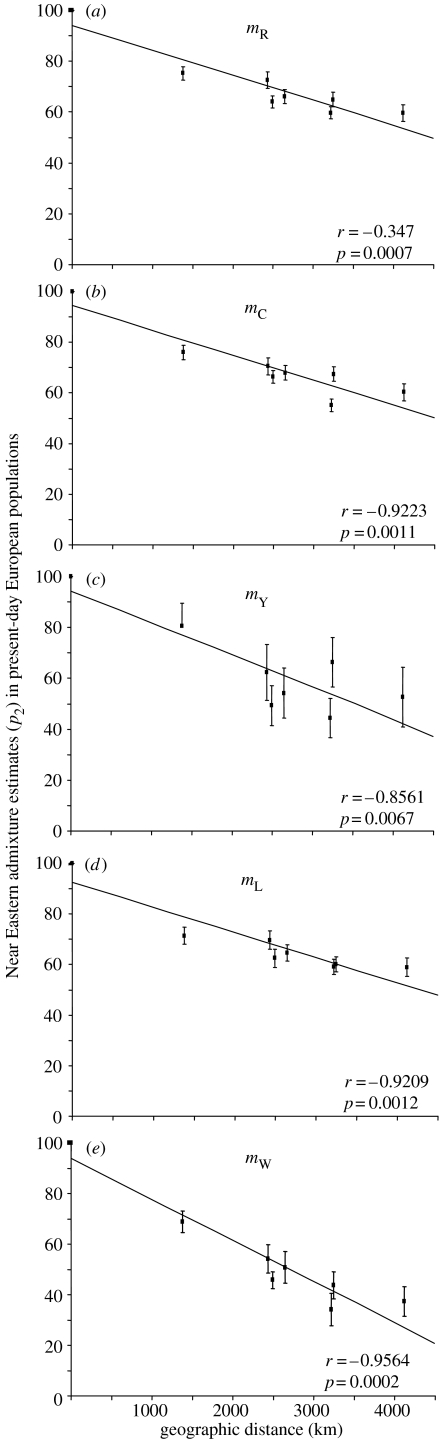
Considering each population individually, Near Eastern admixture appears almost always to be greater than 50%, except with the estimators _m_Y and _m_W in some populations like France or Sardinia (table 1). The lowest values are consistently observed in France (_m_W=34.1%, _m_Y=44.3%, _m_C=55.2%) or in the Orkney Islands (_m_L=58.9%, _m_R=59.6%). The highest value is always found among Adygei (between 68.8 and 80.5%). With all the methods used, there is a negative and significant correlation between Near Eastern admixture and great circle distances from the Near East (figure 2). Conversely, only the _m_Y estimates are negatively correlated with the distances from the Basques, suggesting that the gradient identified in this study is not a generic longitudinal pattern but is likely to represent a specific effect of dispersal from the Near East. Because it is unclear whether agriculture arose independently in the Caucasus (Nasidze et al. 2004) and because the population of the Orkney islands has undergone recent admixture from Scandinavia (Wilson et al. 2001), we removed them from the analysis, but in both cases the correlation with distances from the Near East remains significant (data not given). All these correlations are still significant after Bonferroni correction for multiple tests, with the significance threshold brought to _p_=0.01 (i.e. the original significance threshold of 0.05 divided by 5 because of the five admixture coefficients estimated).
Figure 2.
Linear regressions of the Near Eastern admixture estimates (_p_2) in the present-day European populations (in percentages) against the geographic distance (in kilometres) from the Near East, using the five admixture estimators; standard deviations are represented by vertical bars. (a) _m_R, (b) _m_C, (c) _m_Y, (d) _m_L and (e) _m_W.
The matrix of genetic distance estimated from the data (table 2, where the estimated parameters of isolation by distance are given) shows a significant and negative relationship with both geographic distance (_r_=0.57, _p_=0.0025) and its natural logarithm (_r_=0.56, _p_=0.0024). Both the correlation coefficients and their probabilities are very close. Therefore, the data do not allow one to judge whether the decline of genetic similarity with distance is linear (which would be compatible with an admixture model) or exponential (which is the expected consequence of isolation by distance).
Table 2.
Matrix of _F_st values between sampled populations. (The estimated parameters of isolation by distance, obtained by fitting _F_st/(1−_F_st) to the equation _Y_=a+b ln(d), where d is the great-circle distance, are _a_=−0.0124, _b_=0.0027.)
| Basques | French | northern Italians | Sardinians | Tuscans | Orcadians | Russians | Adygei | Middle Easterners | |
|---|---|---|---|---|---|---|---|---|---|
| Basques | 0 | ||||||||
| French | 0.0048 | 0 | |||||||
| northern Italians | 0.0085 | 0.0046 | 0 | ||||||
| Sardinians | 0.0084 | 0.0053 | 0.0068 | 0 | |||||
| Tuscans | 0.0061 | 0.0011 | 0.0017 | 0.0025 | 0 | ||||
| Orcadians | 0.0114 | 0.0056 | 0.0096 | 0.0125 | 0.0084 | 0 | |||
| Russians | 0.0101 | 0.0044 | 0.0077 | 0.0107 | 0.0048 | 0.0092 | 0 | ||
| Adygei | 0.0115 | 0.0058 | 0.0056 | 0.0102 | 0.0025 | 0.0111 | 0.0069 | 0 | |
| Middle Easterners | 0.0124 | 0.0076 | 0.0076 | 0.0088 | 0.0014 | 0.0138 | 0.0100 | 0.0060 | 0 |
4. Discussion
(a) Admixture estimates
The Near Eastern contribution to the European gene pool, inferred from 377 STR loci, appears close to the values estimated using explicit admixture models and at least twice as large as the values of 20–25% proposed in single-locus phylogeographic analyses. The populations that we analysed do not fully represent European genetic diversity and the overall pattern must be more complex than modelled in this study. However, we demonstrated that there is a large Near Eastern contribution to the Europeans' genome irrespective of the numerical method chosen for estimation. This contribution decreases with the distance from the area of origin of agriculture—the Near East—and neither the admixture rates nor the spatial pattern depend on the effect of possible demographic outliers, such as the Adygei and the Orkney islanders.
In their phylogeographic studies of single loci, Semino et al. (2000) and Richards et al. (2002) identified haplogroups whose ages or clinal distributions suggested an origin in the Neolithic and equated the frequencies of these haplogroups to the Neolithic admixture rate, thus entirely attributing to Palaeolithic ancestors all other haplogroups. However, the ages of particular genealogical lineages observed in a geographical region do not correspond to the arrival of the population in that region (Barbujani & Goldstein 2004). For instance, in a study of the DNA of Neolithic individuals from Central Europe (Haak et al. 2005) most of the miochondrial DNAs (71%) appear to belong to haplogroups considered Palaeolithic by Richards et al. (2000). On the contrary, the distributions of haplogroups reflect the combined effects of both biochemical (mutation within the fertile cells) and demographic (migration and drift) processes. There is no reason to assume that haplogroups older than 10 000 years, or showing no cline, were absent in Near Eastern farming populations. If they were present there, Neolithic immigrants spread in Europe alleles that originated in Palaeolithic times, in exactly the same way as the Europeans spread in the Americas alleles that originated long before 1492.
Chikhi et al. (2002) estimated admixture rates from Y-chromosome data using the genealogical likelihood-based method and Dupanloup et al. (2004) extended the analysis to several genomic regions, both nuclear and mitochondrial. In both cases, the average Near Eastern admixture was higher than 50% and showed a gradient from the Southeast into the Northwest. Thus, all studies where the admixture process was not oversimplified yield consistent results, including the present one. Because our estimate is based on many genome regions, it is unlikely to reflect to any significant extent the action of selection over specific loci (Goldstein & Chikhi 2002).
(b) Effects of possible errors in the parameters
How confident can one be that the high Near Eastern component estimated really represents Neolithic admixture? Any estimate is as good as the assumptions underlying the model. Basques and Near Easterners have been considered good proxies for the Palaeolithic and Neolithic settlers of Europe in all previous studies. However, if the modern populations' genes are very different from those of their prehistoric counterparts, which cannot be tested at present, the estimated admixture rates will be inaccurate or wrong. Factors that can lead to that include: (i) erroneous definition of the parental populations; (ii) extensive gene flow from other sources into the hybrid populations; and (iii) extensive genetic drift since admixture, and will be discussed in the following paragraphs.
- There is no way to evaluate how accurately the genes of a modern population approximate the genes of a population of the past. For a detailed discussion of this issue, see Chikhi et al. (2002). However, in all previous studies on European diversity, the assumption was made that Basques represent the most direct descendants of Palaeolithic Europeans (Menozzi et al. 1978; Sokal et al. 1991; Cavalli-Sforza et al. 1993; Bertranpetit et al. 1995; Semino et al. 2000; Torroni et al. 2001; Wilson et al. 2001). In addition, the only suitable data on ancient DNA, referring to mitochondrial DNA in relatively recent Iberian populations of the sixth and second centuries BC, show close similarities with the sequence of modern individuals (Sampietro et al. 2005). As for the genes of the Neolithic population, the exact place of origin of farming is uncertain (see Salamini et al. 2002), with some studies (Lev-Yadun et al. 2000) tending to suggest that most founder crops first occurred in Anatolia rather than in the Near East. However, if farming originated in Anatolia the Neolithic parental population was spatially closer than we assumed to the hybrid populations. Because the allele frequencies of the markers we considered form geographic clines (figure 1), the estimated Neolithic admixture would be greater had we chosen Neolithic ancestors from Anatolia.
- Most likely, people also came to Europe from North Africa, northern Asia and other regions (Rosser et al. 2000). However, the question here is whether that gene flow has been large enough to substantially affect the results of our analysis. Simulations by Dupanloup et al. (2004) showed that if parental populations that significantly contributed to admixture are neglected, admixture estimates will typically have very large standard deviations, 170% or more of the respective estimates under the simulated scenarios. That value cannot be mechanically transposed to the different set of populations and loci of this study, but the standard deviations for our five estimators were low, most of them between 2 and 5% and never exceeded 12% (table 1). This does not suggest that other immigration phenomena substantially distorted the ratio between Palaeolithic and Neolithic admixture rates estimated in this study.
- Wang's (2003) _m_W estimator accounts for the uncertainty due to population divergence after admixture. In this study, the standard errors of _m_W tend to be large, whereas its values tend to be lower than those obtained using other methods. It is hard to decide whether one should trust more the values ≥60% for the Neolithic contribution across Europe that are consistently suggested by four different methods, or the _m_W value around 46% based on a method modelling drift in greater detail than alternative methods. However, even if we accept the lowest estimates of Neolithic admixture we obtained, these values are still twice as large as proposed by authors supporting the model of CD (Semino et al. 2000; Richards et al. 2002). In addition, in a detailed analysis of Y-chromosome data, Chikhi et al. (2002) concluded that the demographic growth prompted by the development of food production technologies reduced the effect of drift in comparison to drift in hunting–gathering communities of Europe. Because effective population sizes are four times as large for autosomal than for Y-chromosome markers, it is reasonable to expect an even smaller impact of drift on our autosomal data.
(c) Spatial patterning and isolation by distance
The data available are not sufficient to rule out the possibility that the observed clines reflect isolation by distance rather than directional dispersal. On the other hand, clines encompassing the whole continent were not observed in simulations of prehistoric isolation by distance in Europe (Barbujani et al. 1995). In addition, previous autocorrelation studies have shown broad European gradients only from the Southeast to the Northwest (Sokal et al. 1989), while one would expect random orientation of gradients under isolation by distance. Therefore, the continental pattern we observed is more likely explained by directional dispersal (Sokal et al. 1991) and indeed similar clines in northern China (Wen et al. 2004) and India (Cordaux et al. 2004) were attributed to DD accompanying the spread of agriculture.
(d) Effects of possible ascertainment bias and interpretation
When a set of loci is biased by an excess of highly variable biallelic sites, clines can be found in Europe even in the absence of Neolithic admixture (Currat & Excoffier 2005). We cannot say whether the 377 loci considered here are unbiased samples of the European genome diversity, but we found no evidence in the literature of ascertainment biases for STR polymorphisms. The fact that the same patterns are observed in the analysis of this dataset and in those of biallelic DNA polymorphisms (Chikhi et al. 2002; Dupanloup et al. 2004) suggests that clines radiating from the Near East into Europe are not an artefact due to ascertainment biases, but indeed reflect some form of directional dispersal. Currat & Excoffier's simulations showing that poorly polymorphic loci seldom produce clinal patterns do not mean that ascertainment bias is the only explanation or the simplest. Endler (1977) has shown that the mixing of parental populations differing by a few per cent in allele frequencies is likely to result in unstable clines, which are blurred by successive genetic drift. Therefore, absence of clines at loci showing little variation between populations may simply reflect the fact that a cline can persist through time only if the two admixing groups differed enough, as stated in the original proposal of the DD model (Menozzi et al. 1978).
At present, this analysis of a large dataset of DNA polymorphisms demonstrates that the Near Eastern contribution to the European gene pool is large and forms a clear Southwest–Northeast cline, regardless of the method used to analyse the data. If the model under which our study was conducted (as well as all comparable studies: Richards et al. 1996, 2002; Semino et al. 2000; Chikhi et al. 2002; Dupanloup et al. 2004) is correct, these results imply a high rate of Neolithic immigration, in contrast with the CD model. Conversely, if the model is not correct, we cannot say whether those patterns reflect Palaeolithic, Neolithic or later gene flow. However, we can still say that: (i) the patterns are there and clinal variation is the rule at the genomic level, in agreement with previous evidence on protein (Menozzi et al. 1978; Sokal et al. 1991) and DNA diversity (Chikhi et al. 1998; Rosser et al. 2000); (ii) such clines cannot just be a statistical artefact due to a biased selection of genetic markers because they are apparent both using single-nucleotide polymorphisms (SNP) and microsatellite polymorphisms; markers not showing gradients are the exception, no matter how informative they are perceived to be and so any model of European prehistory ought to explain the widespread clinal patterns observed across the continent; and (iii) continentwide clines can only be accounted for by a substantial input of genes from the Near East, roughly twice as large as estimated from single genes by approximate phylogeographic methods.
Acknowledgments
This study was supported by the Fondo Integrativo Speciale per la Ricerca (FISR) of the Italian Ministry of the Universities and by funds of the University of Ferrara. Many thanks to Sandy Rutherford and the IRMACS Centre (Simon Fraser University, Vancouver, Canada) for the generous help in the partial parallelization and the numerous runs of the Leadmix software. Thanks also to Jinliang Wang for the customized version of Leadmix able to handle 377 loci, and to Lounès Chikhi, Giorgio Bertorelle, Daniel Falush and Bill Martin for constructive comments on previous versions of this manuscript.
References
- Ammerman A.J, Cavalli-Sforza L.L. Princeton University Press; Princeton, NJ: 1984. The Neolithic transition and the genetics of populations in Europe. [Google Scholar]
- Barbujani G. Autocorrelation of gene frequencies under isolation by distance. Genetics. 1987;117:777–782. doi: 10.1093/genetics/117.4.777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbujani G. DNA variation and language affinities. Am. J. Hum. Genet. 1997;61:1011–1014. doi: 10.1086/301620. 10.1086/301620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbujani G, Goldstein D.B. Africans and Asians abroad: genetic diversity in Europe. Annu. Rev. Genomics Hum. Genet. 2004;5:119–150. doi: 10.1146/annurev.genom.5.061903.180021. 10.1146/annurev.genom.5.061903.180021 [DOI] [PubMed] [Google Scholar]
- Barbujani G, Sokal R.R, Oden N.L. Indo-European origins: a computer-simulation test of five hypotheses. Am. J. Phys. Anthropol. 1995;96:109–132. doi: 10.1002/ajpa.1330960202. 10.1002/ajpa.1330960202 [DOI] [PubMed] [Google Scholar]
- Bertorelle G, Excoffier L. Inferring admixture proportions from molecular data. Mol. Biol. Evol. 1998;15:1298–1311. doi: 10.1093/oxfordjournals.molbev.a025858. [DOI] [PubMed] [Google Scholar]
- Bertranpetit J, Sala J, Calafell F, Underhill P.A, Moral P, Comas D. Human mitochondrial DNA variation and the origin of Basques. Ann. Hum. Genet. 1995;59:63–81. doi: 10.1111/j.1469-1809.1995.tb01606.x. [DOI] [PubMed] [Google Scholar]
- Cavalli-Sforza L.L, Menozzi P, Piazza A. Demic expansions and human evolution. Science. 1993;259:639–646. doi: 10.1126/science.8430313. [DOI] [PubMed] [Google Scholar]
- Chakraborty R, Kamboh M.I, Nwankwo M, Ferrell R.E. Caucasian genes in American blacks: new data. Am. J. Hum. Genet. 1992;50:145–155. [PMC free article] [PubMed] [Google Scholar]
- Chikhi L, Destro-Bisol G, Bertorelle G, Pascali V, Barbujani G. Clines of nuclear DNA markers suggest a recent Neolithic ancestry of the European gene pool. Proc. Natl Acad. Sci. USA. 1998;95:9053–9058. doi: 10.1073/pnas.95.15.9053. 10.1073/pnas.95.15.9053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chikhi L, Bruford M.W, Beaumont M.A. Estimation of admixture proportions: a likelihood-based approach using Markov Chain Monte Carlo. Genetics. 2001;158:1347–1362. doi: 10.1093/genetics/158.3.1347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chikhi L, Nichols R.A, Barbujani G, Beaumont M.A. Y genetic data support the Neolithic demic diffusion model. Proc. Natl Acad. Sci. USA. 2002;99:10 008–10 013. doi: 10.1073/pnas.162158799. 10.1073/pnas.162158799 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordaux R, Deepa E, Vishwanathan H, Stoneking M. Genetic evidence for the demic diffusion of agriculture to India. Science. 2004;304:1125. doi: 10.1126/science.1095819. 10.1126/science.1095819 [DOI] [PubMed] [Google Scholar]
- Currat M, Excoffier L. The effect of the Neolithic expansion on European molecular diversity. Proc. R. Soc. B. 2005;272:679–688. doi: 10.1098/rspb.2004.2999. 10.1098/rspb.2004.2999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dupanloup I, Bertorelle G, Chikhi L, Barbujani G. Estimating the impact of prehistoric admixture on the genome of Europeans. Mol. Biol. Evol. 2004;21:1361–1372. doi: 10.1093/molbev/msh135. 10.1093/molbev/msh135 [DOI] [PubMed] [Google Scholar]
- Eller E. Effects of ascertainment bias on recovering human demographic history. Hum. Biol. 2001;73:411–427. doi: 10.1353/hub.2001.0034. [DOI] [PubMed] [Google Scholar]
- Endler J.A. Princeton University Press; Princeton, NJ: 1977. Geographic variation, speciation, and clines. [PubMed] [Google Scholar]
- Goldstein D.B, Chikhi L. Human migrations and population structure: what we know and why it matters. Annu. Rev. Genomics Hum. Genet. 2002;3:129–152. doi: 10.1146/annurev.genom.3.022502.103200. 10.1146/annurev.genom.3.022502.103200 [DOI] [PubMed] [Google Scholar]
- Haak W, et al. Ancient DNA from the first European farmers in 7500-year-old Neolithic sites. Science. 2005;310:1016–1018. doi: 10.1126/science.1118725. 10.1126/science.1118725 [DOI] [PubMed] [Google Scholar]
- Landry P.A, Koskinen M.T, Primmer C.R. Deriving evolutionary relationships among populations using microsatellites and (δμ)2: all loci are equal, but some are more equal than others. Genetics. 2002;161:1339–1347. doi: 10.1093/genetics/161.3.1339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lev-Yadun S, Gopher A, Abbo S. The cradle of agriculture. Science. 2000;288:1602–1603. doi: 10.1126/science.288.5471.1602. 10.1126/science.288.5471.1602 [DOI] [PubMed] [Google Scholar]
- Long J.C. The genetic structure of admixed populations. Genetics. 1991;127:417–428. doi: 10.1093/genetics/127.2.417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mantel N.A. The detection of disease clustering and a generalized regression approach. Cancer Res. 1967;27:209–220. [PubMed] [Google Scholar]
- Menozzi P, Piazza A, Cavalli-Sforza L.L. Synthetic maps of human gene frequencies in Europeans. Science. 1978;201:786–792. doi: 10.1126/science.356262. [DOI] [PubMed] [Google Scholar]
- Nasidze I, et al. Mitochondrial DNA and Y-chromosome variation in the Caucasus. Ann. Hum. Genet. 2004;68:205–221. doi: 10.1046/j.1529-8817.2004.00092.x. 10.1046/j.1529-8817.2004.00092.x [DOI] [PubMed] [Google Scholar]
- Nielsen R. Population genetic analyses of ascertained SNP data. Hum. Genomics. 2004;1:218–224. doi: 10.1186/1479-7364-1-3-218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otte M. The history of European populations as seen by archaeology. In: Renfrew C, Boyle K, editors. Archaeogenetics: DNA and the population prehistory of Europe. McDonald Institute for Archaeological Research; Cambridge, UK: 2000. pp. 41–44. [Google Scholar]
- Pinhasi R, Foley R.A, Mirazon-Lahr M. Spatial and temporal patterns in the Mesolithic–Neolithic archaeological record of Europe. In: Renfrew C, Boyle K, editors. Archaeogenetics: DNA and the population prehistory of Europe. McDonald Institute for Archaeological Research; Cambridge, UK: 2000. pp. 45–56. [Google Scholar]
- Pinhasi R, Fort J, Ammerman A.J. Tracing the origin and spread of agriculture in Europe. PLoS Biol. 2005;3:e410. doi: 10.1371/journal.pbio.0030410. 10.1371/journal.pbio.0030410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rendine S, Piazza A, Cavalli-Sforza L.L. Simulation and separation by principal components of multiple demic expansions in Europe. Am. Nat. 1986;128:681–706. 10.1086/284597 [Google Scholar]
- Richards M, et al. Paleolithic and Neolithic lineages in the European mitochondrial gene pool. Am. J. Hum. Genet. 1996;59:185–203. [PMC free article] [PubMed] [Google Scholar]
- Richards M, et al. Tracing European founder lineages in the Near Eastern mtDNA pool. Am. J. Hum. Genet. 2000;67:1251–1276. [PMC free article] [PubMed] [Google Scholar]
- Richards M, Macaulay V, Torroni A, Bandelt H.J. In search of geographical patterns in European mitochondrial DNA. Am. J. Hum. Genet. 2002;71:1168–1174. doi: 10.1086/342930. 10.1086/342930 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts D.F, Hiorns R.W. Methods of analysis of the genetic composition of a hybrid population. Hum. Biol. 1965;37:38–43. [PubMed] [Google Scholar]
- Rosenberg, M. S. 2001 Passage Pattern analysis, spatial statistics and geographic exegesis. Version 1.0. Department of Biology, Arizona State University, Tempe, AZ.
- Rosenberg N.A, Pritchard J.K, Weber J.L, Cann H.M, Kidd K.K, Zhivotovsky L.A, Feldman M.W. Genetic structure of human populations. Science. 2002;298:2381–2385. doi: 10.1126/science.1078311. 10.1126/science.1078311 [DOI] [PubMed] [Google Scholar]
- Rosser Z.H, et al. Y-chromosomal diversity in Europe is clinal and influenced primarily by geography, rather than by language. Am. J. Hum. Genet. 2000;67:1526–1543. doi: 10.1086/316890. 10.1086/316890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousset F. Genetic differentiation and estimation of gene flow from F-statistics under isolation by distance. Genetics. 1997;145:1219–1228. doi: 10.1093/genetics/145.4.1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salamini F, Ozkan H, Brandolini A, Schafer-Pregl R, Martin W. Genetics and geography of wild cereal domestication in the near east. Nat. Rev. Genet. 2002;3:429–441. doi: 10.1038/nrg817. [DOI] [PubMed] [Google Scholar]
- Sampietro M.L, Caramelli D, Lao O, Calafell F, Comas D, Lari M, Agusti B, Bertranpetit J, Lalueza-Fox C. The genetics of the pre-Roman Iberian Peninsula: a mtDNA study of ancient Iberians. Ann. Hum. Genet. 2005;69:535–548. doi: 10.1111/j.1529-8817.2005.00194.x. 10.1111/j.1529-8817.2005.00194.x [DOI] [PubMed] [Google Scholar]
- Semino O, et al. The genetic legacy of Paleolithic Homo sapiens in extant Europeans: a Y chromosome perspective. Science. 2000;290:1155–1159. doi: 10.1126/science.290.5494.1155. 10.1126/science.290.5494.1155 [DOI] [PubMed] [Google Scholar]
- Sokal R.R, Harding R.M, Oden N.L. Spatial patterns of human gene frequencies in Europe. Am. J. Phys. Anthropol. 1989;80:267–294. doi: 10.1002/ajpa.1330800302. 10.1002/ajpa.1330800302 [DOI] [PubMed] [Google Scholar]
- Sokal R.R, Oden N.L, Wilson C. Genetic evidence for the spread of agriculture in Europe by demic diffusion. Nature. 1991;351:143–145. doi: 10.1038/351143a0. 10.1038/351143a0 [DOI] [PubMed] [Google Scholar]
- Torroni A, et al. A signal, from human mtDNA, of postglacial recolonization in Europe. Am. J. Hum. Genet. 2001;69:844–852. doi: 10.1086/323485. 10.1086/323485 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J. Maximum-likelihood estimation of admixture proportions from genetic data. Genetics. 2003;164:747–765. doi: 10.1093/genetics/164.2.747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wen B, et al. Genetic evidence supports demic diffusion of Han culture. Nature. 2004;431:302–305. doi: 10.1038/nature02878. 10.1038/nature02878 [DOI] [PubMed] [Google Scholar]
- Wilson J.F, Weiss D.A, Richards M, Thomas M.G, Bradman N, Goldstein D.B. Genetic evidence for different male and female roles during cultural transitions in the British Isles. Proc. Natl Acad. Sci. USA. 2001;98:5078–5083. doi: 10.1073/pnas.071036898. 10.1073/pnas.071036898 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright S. Isolation by distance. Genetics. 1943;28:114–138. doi: 10.1093/genetics/28.2.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zvelebil M, Zvelebil K. Agricultural transition and Indo-European dispersal. Antiquity. 1988;62:574–583. [Google Scholar]