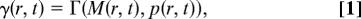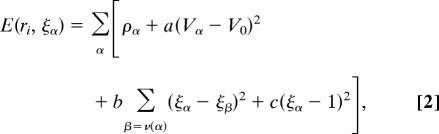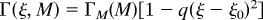On the mechanism of wing size determination in fly development (original) (raw)

Abstract

A fundamental and unresolved problem in animal development is the question of how a growing tissue knows when it has achieved its correct final size. A widely held view suggests that this process is controlled by morphogen gradients, which adapt to tissue size and become flatter as tissue grows, leading eventually to growth arrest. Here, we present evidence that the decapentaplegic (Dpp) morphogen distribution in the developing Drosophila wing imaginal disk does not adapt to disk size. We measure the distribution of a functional Dpp-GFP transgene and the Dpp signal transduced by phospho-Mad and show that the characteristic length scale of the Dpp profile remains approximately constant during growth. This finding suggests an alternative scenario of size determination, where disk size is determined relative to the fixed morphogen distribution by a certain threshold level of morphogen required for growth. We propose that when disk boundary reaches the threshold the arrest of cell proliferation throughout the disk is induced by mechanical stress in the tissue. Mechanical stress is expected to arise from the nonuniformity of morphogen distribution that drives growth. This stress, through a negative feedback on growth, can compensate for the nonuniformity of morphogen, achieving uniform growth with the rate that vanishes when disk boundary reaches the threshold. The mechanism is demonstrated through computer simulations of a tissue growth model that identifies the key assumptions and testable predictions. This analysis provides an alternative hypothesis for the size determination process. Novel experimental approaches will be needed to test this model.

Keywords: growth regulation, imaginal disc, mechanics

Two fundamental processes must occur concurrently in tissues during animal development. First, tissues must grow rapidly to generate the final adult size of the organism. When the final size is achieved, all cells in the tissue must know to stop growing and dividing. Second, tissues need to be specified and patterned with each cell adopting the appropriate fate and gene expression profile for its position. These processes need to be coordinated. The spatial patterning aspect of tissue development has been well studied and characterized, with morphogen gradients thought to be playing a central role (reviewed in refs. 1–5). How tissue growth is controlled and how these two processes are coordinated, however, remain largely unanswered questions.

Drosophila imaginal discs have provided a useful model for the analysis of concurrent tissue patterning and growth control. Wing imaginal discs, for instance, originate as a group of ≈50 cells attached to the inside of the larval epidermis (6, 7). After a 30-h quiescent period, these cells start dividing and follow a sigmoidal growth curve, averaging a cell division every 8.5 h (8). Cell division is unsynchronized and appears to be stochastic, occurring on average uniformly throughout the disk (9). Toward the end of third instar a stripe of cells along the DV boundary arrests its cell cycle forming a zone of nonproliferation (10, 11). Other cells continue to proliferate until the time when all cell division throughout the disk stops almost simultaneously (8). At this point, the disk comprises ≈50,000 cells and is to a large extent patterned and fully grown, with only two net cell-size reduction divisions to follow in the early pupal stage.

The structure of the adult wing is determined by the spatial pattern of gene expression in the imaginal disk. Disk pattern is specified by morphogen gradients, with a decapentaplegic (Dpp) determining pattern along the anterior-posterior (AP) axis and Wingless (Wg) patterning the dorso-ventral axis (reviewed in ref. 12). Both of these morphogens were found to be required for cell survival and proliferation in the disk (13–15). The details of how morphogens control growth are still being elucidated (16). However, the fact that the same two morphogens regulate patterning and growth of the discs is highly suggestive from the point of view of coordinating the two processes.

There are two main mechanisms controlling final size of imaginal discs in the fly. The first is a disk-intrinsic mechanism in which each disk assesses its size and arrests growth when the appropriate size is achieved. The second mechanism is an organismal, hormonal one in which growth is arrested in the entire animal in response to environmental stress conditions such as nutrient withdrawal (mimicked molecularly by manipulation of the insulin signaling pathway as in ref. 17). Our work here focuses on the disk-intrinsic size determination.

A number of models have been proposed to explain tissue growth control. One class of models is based on the idea that cells posses “positional values,” which vary monotonically throughout the tissue and serve as a cell's spatial coordinate (18–21). The molecular identity of this positional value is unknown, but the positional value is assumed to be a permanent attribute of a cell, fixed upon cell's birth to a value interpolating those of neighboring cells. As the tissue grows, new cells intercalate in between the existing ones, gradually decreasing the positional value differential of neighboring cells until it falls below a certain threshold, whereupon growth is assumed to stop (21). However, experiments in which cells of disparate positional values have been experimentally juxtaposed (e.g., clones of cells in which the Dpp signal transduction pathway is active in lateral positions; refs. 22 and 23) produced results incompatible with the idea that intercalation of positional values drives growth of the wing disk.

As an alternative to intercalation of positional values, Day and Lawrence (24) have suggested that size might be controlled by the gradient of morphogen itself. This model assumes that (i) cell division is driven by the slope of morphogen profile, or the morphogen gradient in the mathematical sense of the latter term and (ii) that the slope of the morphogen profile is determined by disk size, so that increasing disk size leads to reduction of the gradient. Cessation of growth would then occur when the slope of the morphogen profile falls below the minimal level required to promote growth. This scenario is appealing because it offers an explicit link between growth and patterning of gene expression. It would predict allometric growth where the pattern of gene expression induced by morphogens would scale up in proportion with the growing size of the disk.

However, both of the assumptions underlying the Day–Lawrence model (24) are equivocal. The assumption that cell proliferation requires a morphogen differential in excess of a certain threshold is called into question by experimental observation that a gradient of Dpp is not necessary for cell proliferation (14, 22, 23). Similarly, the assumption that the morphogen gradient decreases in inverse proportion to disk size and thus can act as a “sensor” of disk size has neither experimental nor theoretical support. Whereas, the Day–Lawrence model presumes that the morphogen distribution interpolates linearly between a fixed value at the source and zero at the boundary, in reality morphogen concentrations decay rapidly with distance from the source, consistent with the notion that morphogens are relatively rapidly lost, degraded, or taken up by the cells (25–28). On the theoretical side, the mathematical models proposed for morphogen gradient formation predict that morphogen profile is determined by the balance between its diffusion and degradation, and thus might be expected to be a property independent of tissue size (29–31). Specifically, the length scale, which describes how quickly the morphogen concentration drops as a function of distance from its source, increases with increased stability of the morphogen molecule and increased diffusion rate.

Here, we analyze the spatial distribution of Dpp in wing imaginal discs of varying age to determine how the Dpp gradient changes as the tissue grows. Interestingly, we find that the Dpp length scale is independent of disk size, in agreement with the theoretical models described above. This observation, however, invalidates a key aspect of the Day–Lawrence model (24) and leads us to seek alternative models for disk size determination. We propose a model in which the final size of the disk is specified by the distance at which the morphogen signal crosses a minimum threshold necessary to promote growth. This distance is set by two parameters: the maximal concentration of morphogen (set by the rate of morphogen secretion at the source) and the decay length scale of the morphogen profile. In contrast to the allometric growth in the Day–Lawrence model, in our model the proportions of the morphogen-induced gene expression pattern continuously change as the disk grows so that growth arrest under normal conditions must correspond to establishing correct proportions for the disk pattern relative to the size of the disk. Thus the mechanism that determines disk size relative to morphogen profile may be thought of as a proportion checkpoint. We refer to this model as the “proportion checkpoint model.” For this mechanism to work there must also be a long-range interaction that propagates information about the size of the disk so that when the boundary reaches the threshold, growth would stop uniformly throughout the disk. This long-range interaction could be provided by mechanical stress and deformation in the growing tissue, and we propose a “mechanical compression” model detailing this mechanism. See supporting information (SI) Text and SI Fig. 7. An appealing feature of the mechanical model is that it does not require introduction of an unknown factor for long-range feedback signaling.

Results

Morphogen Gradients Do Not Adapt to Disk Size.

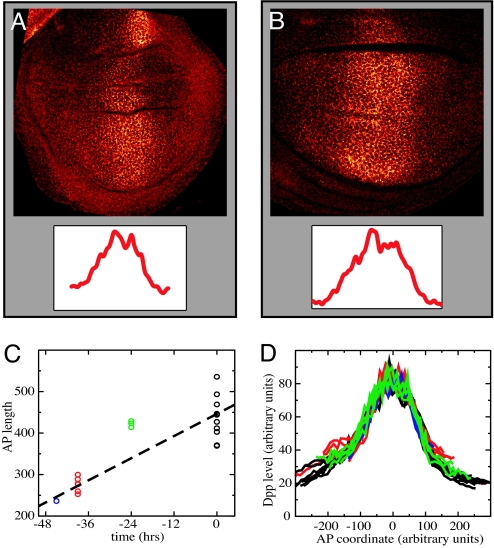
To directly assess the dependence of morphogen distribution on tissue size, we examined Dpp in wing imaginal discs from larvae of different ages. To circumvent the limitations to visualization of endogenous Dpp caused by the quality of available antibodies to Dpp, we used a Dpp–GFP fusion protein, expressed in the endogenous Dpp domain by the dpp-GAL4 driver (26). We have previously shown that this protein can support normal growth and patterning of discs lacking Dpp, indicating that it functions very similarly to the endogenous protein. Furthermore, in these experiments we expressed the Dpp–GFP fusion protein at levels appropriate for rescue. Fig. 1 A and B shows typical optical sections of wing discs expressing Dpp–GFP under control of dpp-GAL4 and stained for extracellular protein with anti-GFP antibody. The observed Dpp–GFP distribution agrees with the Dpp–GFP distributions reported (28). Fluorescence intensity levels are highest in the central region of the disk near where Dpp is produced and form a broad shallow gradient on both sides. We measured Dpp morphogen profiles in >30 discs of varying size and age (45, 39, 24, and 0 h before the wandering stage). For each confocal image the outline of the pouch was determined, and its area and AP and dorsal-ventral dimensions were calculated. Fig. 1C shows the measured disk sizes as a function of time, indicating a factor of ≈2 increase during the period covered.

Fig. 1.

Fig. 1.

Imaging Dpp-GFP in imaginal discs. (A and B) Confocal images (×130) of a wing imaginal discs expressing Dpp-GFP in the endogenous Dpp domain using Dpp-Gal4, stained for extracellular Dpp-GFP. The discs are of different ages: 40 h (A) and 0 h (B) before wandering stage. (Insets) Dpp-GFP profiles along the AP axis. (C) Dependence of wing pouch size on disk age (measured in hours before the wandering stage). (D) Compilation of Dpp–GFP profiles (along the AP axis). Groups of discs of different ages are in different colors (as in C). To eliminate variability of image intensity between different samples, the profiles were normalized by average intensity in the Dpp-producing region (next to the AP boundary). The approximate overlap of the profiles indicates that the shape of the Dpp profiles does not significantly change with time and increasing disk size.

To compare all measured Dpp profiles, we rescaled them vertically by the peak intensity (determined by averaging over the Dpp-producing stripe at the AP boundary) (Fig. 1D). Surprisingly, although the size of the wing pouch almost doubled over the 45-h range of the experiment, the Dpp profiles of all age groups show essentially the same functional dependence on the AP coordinate. This finding indicates that the rate of decay of Dpp concentration moving away from the central production region does not depend on disk size, and that the Dpp gradient does not become shallower as the wing disk grows. In fact, the unscaled raw data shows that larger discs had slightly higher peak intensities of Dpp than smaller discs (see SI Fig. 8), indicating that larger, older discs actually have slightly steeper Dpp profiles than younger, smaller discs.

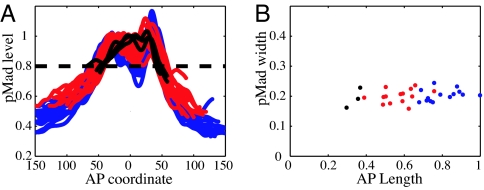
To confirm this conclusion and rule out possible artifacts caused by measuring the spread of Dpp–GFP rather than the endogenous protein, we examined the profile of endogenous Dpp signal transduction by using an antibody specific to the phosphorylated form of the Dpp signal transducer, Mad (26, 32, 33). Mad phosphorylation provides a direct read-out of Dpp signaling intensity. Profiles of pMad distribution along the AP axis obtained from >30 discs of different ages are shown in Fig. 2A. In concordance with measurements of Dpp–GFP, profiles of pMad (Fig. 2A) in discs of different age and size overlap to within resolution of the measurement. To associate a length scale describing the rate of decay of the pMad distributions in Fig. 2A, we plot in Fig. 2B the width of the pMad profiles at a given level relative to (the anterior) maximum. Fig. 2B shows that pMad profile width remains fairly constant as wing pouch size increases with time. Hence, we conclude that the steepness of the Dpp protein profile and resulting Dpp signaling gradient do not decrease with increasing disk size during development. Instead, Dpp distribution is characterized by a fixed length scale, which we believe is defined by its interactions with glypicans and cell surface receptors, which control morphogen lifetime and spreading.

Fig. 2.

Fig. 2.

Lack of disk size dependence for pMad profiles. (A) pMad immunofluorescence profiles along the AP axis for different discs. Profiles were normalized to their anterior maximum intensity and aligned at the AP boundary. (B) The pMad profile width as a function of disk size. Profile width is defined arbitrarily by a dashed line in A. Colors indicate different age groups (blue, at the wandering stage; red, 1 day before wandering; and black, 2 days before wandering).

Compression Model.

Given that the Dpp gradient does not seems to flatten during development, an alternative to the Day–Lawrence model (24) could be that growth stops when cells at the edge of the growing disk fall below the threshold value of the morphogen signal required for growth. Because to arrest disk growth all of the cells must stop dividing, a mechanism must exist that propagates the instruction to stop growing to the cells in the interior of the disk that are still above threshold. We propose that this role can be played by mechanical interactions.

The mechanical integrity of the 2D layer of cells comprising the disk arises from adherens junctions that hold neighboring cells together. Adherens junctions involve cadherins that bind apposing cell surfaces and link to the cortical actin cytoskeleton on the intracellular side (34–36). Recent experiments visualizing cell division in ex vivo late third-instar imaginal discs have demonstrated a remarkable lack of cell rearrangement (37). This fact strongly suggests that imaginal disk tissue behaves more like an elastic “solid,” than a “fluid” where cells would be free to rearrange rapidly. Given that cells do not rearrange to relieve stress, one can argue that a spatial variation in cell proliferation rates would result in a build-up of local stresses. For example, a region of rapidly proliferating cells surrounded by the more slowly growing tissue will be compressed, whereas the surrounding tissue will be stretched. This effect was analyzed by Shraiman (38), who showed that stress dependence of the rate of cell division could provide a negative feedback ensuring uniformity of tissue growth. Hence, we propose a model in which local cell proliferation rates depend not only on morphogen levels but also on local stress, with morphogen promoting growth and compression inhibiting it. Let γ(r, t) denote the local growth rate at position r and time t. The dependence on position and time arises from its dependence on the morphogen level and on stress parameterized by:

graphic file with name zpq01007-5069-m01.jpg

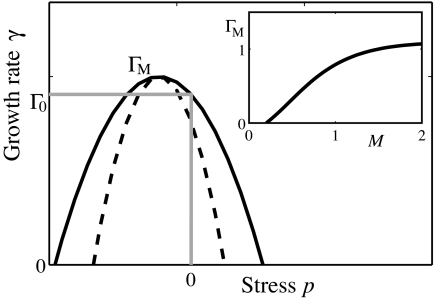
where M represents the morphogen concentration and p represents the local uniaxial compression stress within the cell layer. The details of the functional dependence of Γ(M, p) on its arguments do not strongly affect our model as long as (i) the rate of growth Γ goes down with increasing stress (as shown in Fig. 3) and has a maximum, Γ_M_(M), which monotonically increases with morphogen concentration M, and (ii) growth requires M above certain threshold M_0 so that Γ_M (M) = 0 for M < _M_0. Stress dependence introduces a negative feedback on growth. In the absence of this feedback a nonuniform distribution of morphogen would induce a nonuniform growth, resulting in an accumulation of mechanical stress. In the presence of feedback, the accumulated stress suppresses growth in the high morphogen region, effectively compensating for the excess morphogen. This effect should lead to a more uniform rate of growth across the tissue. We shall see that with the above assumptions the rate of the resulting uniform growth eventually goes to zero once the edge of the disk falls below the threshold morphogen level, _M_0.

Fig. 3.

Fig. 3.

Rate of cell proliferation (in the model) depends on morphogen levels and mechanical strain. Schematic shows functional dependence of the growth rate Γ on the lateral stress p within the cell layer for a fixed morphogen level. The dashed line indicates stronger mechanical feedback. The essential feature is the inhibition of growth by sufficiently high stress. A thinner layer, P < 0, corresponds to cells under tensile stress, whereas P_ > 0 corresponds to compression. We chose the maximum growth rate to occur at P < 0 as suggested by the observation that tension promotes growth in epithelial cell cultures (50, 60). (Inset) Maximal growth rate Γ_M(M) as a function of morphogen level. The essential feature here is the threshold _M_0 and the monotonic increase with M.

To illustrate the proposed mechanism we have implemented a numerical simulation of the disk growth process. In the simulation, the 2D layer of cells is represented as a polygonal tiling, each cell corresponding to a polygon and in addition having certain “height.” The positions, shapes, and heights of the polygonal cells are determined by the condition of mechanical equilibrium that reconciles cell packing with their intrinsic volume. For example, the effect of lateral compression will be a reduction of cell area and increase in its height, the latter deformation providing a “visualization” of the corresponding uniaxial stress. The simulation will determine these stresses and deformations and implement cell growth in accordance with Eq. 1. The mechanical equilibrium corresponds to minimizing the total energy:

graphic file with name zpq01007-5069-m02.jpg

where ρα, _V_α, and ξα denote the perimeter, volume, and the height of cell α, respectively. Cell volume is _V_α = _A_αξα, where _A_α is the cell area, which like the perimeter of a cell, is determined by the position, ri, of its vertices. This mechanical energy is minimized when the actual volume of each cell is close to its intrinsic volume‖ _V_0, while minimizing cell perimeter and the height differences between neighboring cells. The surface tension-like perimeter term represents the cytoskeletal tension (39, 40). (Because only the relative size of different contributions matter, we have set the prefactor of the perimeter term to one.) Parameter a controls deviations of cell volume from _V_0, while b imposes a penalty on the variation of cell height ξα between adjacent cells [labeled by v(α)]. Parameter c controls deviations of cell height from its unstressed value, which without loss of generality can be set to one. Minimization of E with respect to ri and ξα determines cell positions and deformations and corresponding local stresses. In particular, the uniaxial compression of the cell, _p_α, which by our assumption affects cell proliferation, is proportional to ξα − 1 and is therefore directly obtained from the minimization of E. Tissue growth is implemented by dividing cells chosen at random with probability proportional to γα defined by Eq. 1. Because deformation ξα − 1 and stress _p_α are proportional to each other, we replace _p_α in the parameterization of γ by ξα (see Methods), which simplifies the computation and the visualization of the results. Each cell division is followed by minimizing E, so that daughter cells approach the fixed “adult” cell volume in a single relaxation step after division. The implementation of cell growth and division dynamics is described in detail in SI Text.

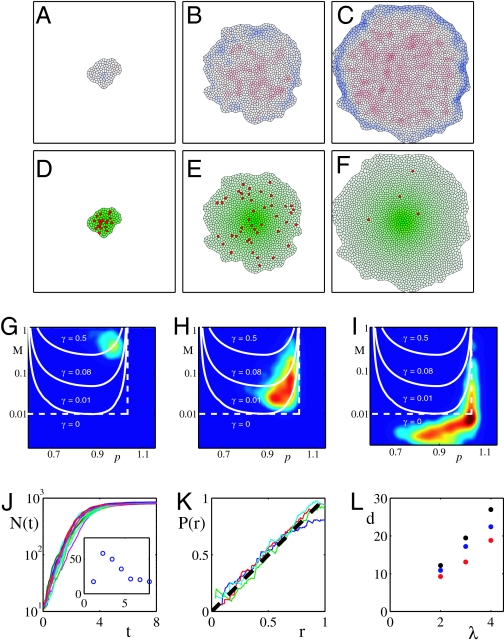
In Fig. 4 A–I we present simulated disk growth driven by a static axial morphogen gradient of the form M(r) = me−r/λ, so chosen for the sake of simplicity. Generalization to a more realistic dual morphogen gradient with two orthogonal axes is straightforward (and could be used to account for the shape of the disk). Fig. 4 A–C shows how compression builds up in the center of the disk as growth progresses and tension builds up at the periphery. Fig. 4 D–F shows that despite the nonuniform distribution of morphogen cell division events are distributed approximately uniformly throughout the disk. Fig. 4 G–I gives the distribution of “operating points” (_M_α, ξα) for individual cells at different times during the simulation and show that they cluster along the constant growth lines in the (M, ξ) plane as expected on the basis of the feedback argument. As the disk grows, its rate of growth slows down (compare Fig. 4 G and H) until in Fig. 4I we see that distribution has shifted essentially to the zero growth region corresponding to the arrest of growth throughout the disk. Fig. 4J shows time courses of disk growth from several simulations. Because cell division is stochastic, each realization produces a different time course. Interestingly, the coefficient of variation (Fig. 4J Inset) for the final size is much smaller than fluctuations at any fixed time during growth. Fig. 4K presents the average rate of cell division as a function of distance from the center and proves that proliferation is indeed uniform throughout the disk. Fig. 4L explores how the final size of the disk depends on the morphogen scale and other relevant parameters such as morphogen level m and the strength of mechanical feedback, q, which parameterizes the sensitivity of the growth rate to stress and deformation (see Fig. 3 and Methods). We observe that the proposed mechanism of size determination acts as a proportion checkpoint in the sense that final size of the disk is proportional to the morphogen length scale λ, with the proportionality constant logarithmically depending on the amplitude m of the morphogen signal. By comparison the dependence on the parameters, such as q, which characterize mechanical feedback, is relatively weak. Thus, the model predicts that increasing morphogen length scale or increasing morphogen level both lead to enlargement of the disk, with the former being the stronger dependence (linear compared with logarithmic).

Fig. 4.

Fig. 4.

Numerical simulation of the mechanical feedback model of disk size determination. (A–C) Snapshots of the simulated growth at different times with A corresponding to the start of the simulation, B the intermediate time, and C close to cessation of growth. Color code indicates layer deformation with red corresponding to lateral compression (ξ − 1 > 0) and blue corresponding to tension (ξ − 1 > 0). (D–F) Shown (green) is the level of morphogen M(r) peaked at its source cell. Cells that are about to divide are marked red (this is intended to emulate BrdU staining of mitotic cells). Note that cell proliferation is approximately uniform throughout the disk as is the case for in vivo observations (61, 62). This uniformization of growth is a result of the mechanical feedback mediated by the build-up of compression (as seen in A–C), which compensates for the excess of morphogen in the central region. Shortly after the disk expands beyond the range where morphogen is above threshold, the build-up of stress arrests growth throughout the disk (F). (G–I) Shown is the distribution of cells in the (M, ξ) parameter plane at three different times corresponding to A–C). Also shown (white) are the lines of constant rate of growth. Note that cells cluster along the lines of constant growth rate, which decreases with time and is close to zero in I, which corresponds to growth arrest. (J) Total number of cells as a function of time for 20 different runs of simulated disk growth (as shown in A–C). Note that rms fluctuations are significant early during growth but are reduced by the time of growth arrest as shown in G Inset. (K) Probability of cell division at distance r from the morphogen source. Linear dependence on r corresponds to uniform growth. Different traces correspond to different times with blue just before growth arrest. The uniformity of growth is a consequence of the mechanical feedback used in the simulation. (L) Disk size as a function of growth parameters. Average final diameter of the disk versus λ, the characteristic length scale of morphogen, for different values of the morphogen level, m, and the strength of mechanical feedback, q. Blue corresponds to the (m, q) values (see Methods) used in the simulation in A–F); black corresponds to “overexpressed” morphogen (2_m_, q), which leads to larger discs; red corresponds to increased feedback (m, 2q), which decreases disk size. Note that disk size scales with the morphogen length scale λ.

Relation Between Dpp and Disk Size.

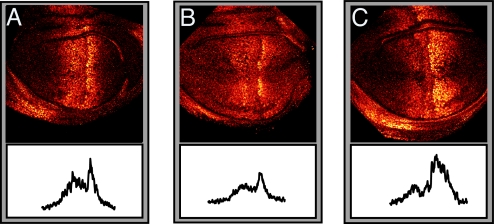
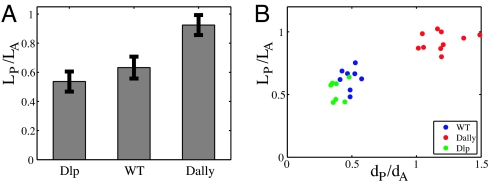
Our model predicts that anything that extends the effective range of Dpp in the wing disk should result in a larger disk. An increase in Dpp range can be achieved biologically either by increasing its production at the source, which will increase the amplitude of the Dpp gradient and leave the decay length unchanged, or increasing Dpp stability, which will effect both the characteristic length scale and the amplitude. It has already been reported that increasing Dpp production causes an increase in disk size (23). We asked whether we could change disk size by modulating Dpp stability and its distribution over the wing disk by modifying the glypican matrix on the surface of disk cells. We used glypicans Dally and Dally-like (Dlp) (28, 41–44), components of the proteoglycan matrix on the disk surface that are known to affect Dpp and Wg morphogen distributions. We overexpressed Dally and Dlp in the posterior compartment of the wing disk with engrailed-GAL4 and monitored Dpp signaling by using pMad antibody. Dally and Dlp appear to have different effects on Dpp distribution. Dally overexpression increases the overall levels of Dpp and significantly broadens the spatial extent of Dpp signaling, increasing the decay length scale (Fig. 5). This finding is consistent with an increased stability of Dpp by Dally [we favor the view that Dally affects Dpp stability by preventing loss (31)]. In contrast, Dlp overexpression has a weaker effect on Dpp signaling, slightly reducing the decay length scale while leaving unchanged peak pMad level in the posterior compartment relative to anterior maximum. We measured the internally controlled ratio of posterior disk size to anterior disk size and found that Dally overexpression causes a relative overgrowth of the posterior compartment, whereas Dlp overexpression yields a mild reduction (Fig. 6 and SI Fig. 9). These results are consistent with our proportion checkpoint model. We expect disk size to behave as λ_f_(m/_M_0), where function f is determined by morphogen profile and _M_0 is the morphogen threshold. Because the glypican manipulations affect both Dpp amplitude m and characteristic length scale λ, the present measurements do not isolate the dependence of the disk size on λ. A manipulation that permitted modulation of λ independently of m would provide a direct quantitative test of the model, but no means exist at present to do so.

Fig. 5.

Fig. 5.

Effect of Dally and Dlp overexpression on pMad profiles. Late third-instar wing discs labeled to visualize pMad·UAS-Dlp overexpressed by enGAL4 (A), WT (B), and UAS-Dally overexpressed by enGAL4 (C). The corresponding pMad intensity profiles (unscaled) are shown at the bottom. Note the enhanced spread and elevated level of pMad in the posterior (to the right) of the wing pouch caused by Dally overexpression and the somewhat reduced spread of pMad in the posterior caused by Dlp overexpression. (Magnification: ×84.)

Fig. 6.

Fig. 6.

Effect of Dally and Dlp overexpression on the disk size and pMad length scales. (A) Overexpression of Dally and Dlp in the posterior compartment with enGAL4 had different effects on the disk size. Whereas Dally overexpression caused an increase in the size of the posterior compartment _L_P relative to the anterior compartment size _L_A, Dlp overexpression yielded a slight reduction of the posterior compartment size. Data are from 10 discs each. (B) Correlation between pMad length scale and disk size. For each disk, the length scale of the pMad extend of the pMad profile in the anterior _d_A and posterior _d_P compartment were measured as described in Fig. 2 (see also SI Fig. 9).

It is also interesting that the data show distinct effects of Dally and Dlp on Dpp distribution. This result is consistent with earlier work showing that Dlp more strongly affects the Wg activity gradient and disk growth along the DV axis (41, 42, 44), whereas Dally more strongly influences Dpp (28, 43). The observed dependence of disk size on Dpp profile is also consistent with the recent report on the effect of Dpp modulations (direct or via modulations of Ubx or tkv) on the size of the Drosophila haltere (45, 46).

Discussion

We have presented evidence that the Dpp morphogen distribution is characterized by a length scale that is independent of disk size during the growth phase but depends on the parameters of morphogen production and spreading. This finding leads us to propose a proportion checkpoint, where final disk size is determined in proportion to morphogen scale and to develop a specific model for a possible mechanism for the checkpoint function.

Some of the most direct evidence for the regulatory role of cytoskeletal mechanics in growth control comes from mammalian cell culture experiments. For example, Folkman and Moscona (47) found that cell growth and proliferation in vitro depends on cell shape. An active role of the cytoskeleton in regulation of cellular function was further explored by Ingber and coworkers (reviewed in refs. 48 and 49). A direct observation of mechanical stress-induced growth in confluent cultures was reported in ref. 50. Thus, cell proliferation can be controlled by mechanical forces.

Does mechanics regulate growth in imaginal discs? Loss of epithelial integrity permits loss of growth control and can lead to metastasis (e.g., refs. 51–55). Yet mutants that exhibit strong overgrowth while retaining epithelial integrity have been described, including the membrane cytoskeleton linkers Expanded and Merlin (56, 57). Recently, Expanded and Merlin have been identified as upstream regulators of the “hippo” growth signaling pathway (58). While speculative, this connection suggests a possible molecular basis for coupling mechanical force transduction to growth control in an epithelium. A second possibility involves Armadillo/β-catenin, which plays a dual role (59): (i) transducing Wg/Wnt signaling and therefore implicated in regulation of cell growth and survival and (ii) as an adaptor for the assembly of E-cadherin and cortical F-actin in adherens junctions, which join neighboring cells into an elastic network. Whether these two functions of Armadillo/β-catenin are coordinated to mediate to mechanical coupling remains to be determined.

Mechanical deformation could be invoked to explain recent experiments of Rogulja and Irvine (16), which found that clones expressing a constitutively active form of Dpp receptor (Tkv) exhibit autonomous suppression of growth and nonautonomous transient stimulation of growth. Both effects could be explained by mechanical feedback with compression inhibiting and tension promoting growth as shown in Fig. 3. More direct tests of the role of mechanics will require the ability to maintain imaginal disk growth ex vivo.

A potential difficulty with mechanics as the sole long-range interaction establishing communication between disk center and disk boundary is the possibility of tissue folding that actually occurs in vivo at the periphery of the wing pouch during the third instar. Folding can be initiated as a buckling instability, which relieves compression within a planar layer by bending. However, buckling occurs when internal stress exceeds a certain threshold, which increases with layer thickness. We expect that folding can relieve the mechanical constraint on the center only while the tissue is sufficiently thin, so that folding would delay, but not abolish, growth arrest. Understanding this process will require an extension of the mechanical model to 3D surfaces. The added benefit of such analysis would be the insight into the generation of the 3D structure from 2D epithelial sheets.

In conclusion, the purpose of this article was to present data indicating that the currently accepted paradigm of limb size determination based on intercalation of positional values or adaptation of morphogen gradient must be reconsidered. As an alternative we propose a model where final disk size is determined relative to the scale of the morphogen via a proportion checkpoint, which is mediated by mechanical interactions within a growing tissue layer.

Methods

Experiment.

To obtain wing discs of various ages and sizes the larvae were staged by collecting eggs laid on apple plates within a 4-h time window and subsequently picking newly hatched first-instar larvae and transferring them to vials with normal food for growth.

Dpp-GFP was detected with an anti-GFP antibody (Torrey Pines Biolabs, Houston, TX) and imaged by using confocal fluorescence microscopy. Staining for extracellular Dpp-GFP was done by a standard technique in which imaginal discs were dissected and incubated with anti-GFP antibody before fixation and permeabilization. For quantitative analysis we used projections of four confocal image sections taken at different depths of the wing discs.

UAS Dally and UAS-Dlp are described in ref. 28. Engrailed-Gal4 is described at www.flybase.net.

Simulation.

Numerical simulation of the growth model described in SI Table 1 was carried out on a Linux computer using a custom C program available on request from L.H. (hufnagel@kitp.ucsb.edu). Growth rate as a function of deformation ξ − 1 and morphogen M was parameterized by:

graphic file with name zpq01007-5069-m03.jpg

with Γ0 = (M − _M_0)θ (M − _M_0).

Supplementary Material

Supporting Information

Acknowledgments

This work was supported in part by National Institutes of Health Grant R01 GM65396 (to B.I.S.).

Abbreviations

AP

anterior-posterior

Dpp

decapentaplegic

Dlp

Dally-like.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS direct submission.

In general, one may expect the growth rate to depend on other components of stress as well, but this expectation will not significantly affect our conclusions.

‖

The model can be readily generalized to include a realistic time dependence of the intrinsic volume corresponding to the gradual growth of cell mass.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information