Point-Like Protrusion as a Prestalk Intermediate in Membrane Fusion Pathway (original) (raw)

Abstract

The widely accepted pathway of membrane fusion begins with the fusion stalk representing the initial intermediate of hemifusion. The lipid structures preceding hemifusion and their possible influence on fusion kinetics were not addressed. Here, we suggest the point-like protrusion as a prestalk fusion intermediate, which has energy lower than that of stalk and, therefore, does not limit the fusion rate. We demonstrate that by calculating the energy of the point-like protrusion, which depends on the lipid monolayer elastic parameters and the strength of the intermembrane hydration repulsion. The point-like protrusion completes the fusion-through-hemifusion model of membrane merger.

INTRODUCTION

Fusion of biological membranes boils down to merger of their bilayer lipid matrices (1,2). Currently, it is largely accepted that merger of protein-free lipid bilayers as well as fusion between viral and cell membranes, intracellular and developmental membrane fusion reactions proceed according to a universal scenario called the fusion-through-hemifusion pathway (3,4). Within this model, fusion begins with formation of a minimal lipidic bridge between the contacting monolayers of the apposing membranes referred to as the fusion stalk. Further expansion of the fusion stalk into a hemifusion diaphragm and its decay into a growing fusion pore completes the fusion process (1).

Recently, an extensive analysis of the energies of the fusion intermediates was performed aimed at revealing the rate-limiting step of the fusion reaction (see for review Chernomordik and Kozlov (1)). It was shown that for lipid compositions typical for an average biological membrane, the stalk energy is only slightly larger than 40_kT_ (where kT is the product of the Boltzmann constant and the absolute temperature), and can be overcome in the biologically relevant timescale (5). In most cases, the fusion stages downstream the stalk formation and, especially, the fusion pore growth are more energy consuming (1).

Despite its current recognition and successful applications, the fusion-through-hemifusion model leaves open important questions about the structures and energies of lipid intermediates preceding the fusion stalk formation and a possibility that these intermediates limit the rate of the whole fusion reaction. Indeed, to form a stalk, the membranes have to establish, at least locally, a dehydrated contact allowing them to perturb the continuity of their surfaces and merge, without exposure of the hydrophobic moieties of lipids to the aqueous surrounding. Such membrane contact requires overcoming the resistance of the powerful short-range repulsion forces referred to as the hydration forces (6). Straightforward estimations based on the representation of the prestalk intermediates as conventional wave-like membrane bulges approaching each other and creating extended dehydrated contacts predict the energies of hundreds of kT. Such intermediates are unfeasible and, hence, a more delicate structure must emerge on the way from two separated flat membranes to the fusion stalk.

Point-like protrusion

Here we suggest an energetically feasible structure of prestalk intermediate, which will be referred to as the point-like protrusion (PLP), and is illustrated in Fig. 1.

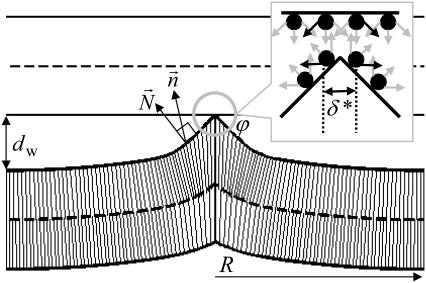
FIGURE 1.

FIGURE 1

A typical computed structure of PLP. The thin dense lines represent the average directions of the lipid hydrocarbon chains. The angle at the PLP tip is ϕ. Beyond the radius R, the two membranes are flat, parallel, and separated by a water distance _d_w. Discreteness of hydration centers is qualitatively illustrated in the enclosure.

A characteristic feature of the PLP is its sharp tip allowing for establishment of a point-like rather than extended dehydrated contact between the membranes. Obviously, this shape minimizes the energy of the hydration repulsion between the membranes. At the same time, a sharp bend of the membrane monolayers, may result in a large elastic energy making the structure unfeasible. Although aware of the latter issue, we were encouraged by the results of our previous modeling of the fusion stalk showing that interplay between the splay of the lipid hydrocarbon chains and their tilt with respect to the monolayer surface results in modest elastic energy costs of similar kinks of the monolayer profiles (7).

Below, we analyze the overall energy of the PLP (Fig. 1) using the elastic tilt-splay model for the membrane deformations (8) and the hydration force model for the intermembrane repulsion (6). The results below have to be considered as semiquantitative.

Model

We consider a point-like protrusion formed on one membrane, while the second membrane remains flat (Fig. 1). The PLP configuration is determined by the tip angle ϕ, the distance _d_w between the flat parts of the two membranes and the requirement that no empty void forms inside the structure. The PLP monolayers undergo deformations of splay of the lipid hydrocarbon chains and tilt of the chains with respect to the monolayer surface (Fig. 1). Because we are using the essentially continuous description of a system consisting of discrete lipid molecules, the meaning of a point-like membrane contact (Fig. 1) is that of a contact with an area smaller than the area per lipid molecule a ≤ 1 nm2.

Elastic energy

The elastic theory of the tilt and splay deformations was presented in Hamm and Kozlov (8) and applied to calculation of the energy of fusion intermediates (7). In brief, the tilt-splay energy per unit area of lipid monolayer is given by

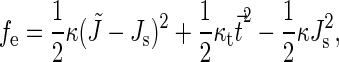graphic file with name M1.gif (1)

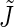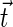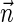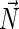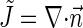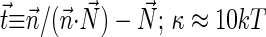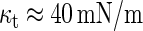where the splay Inline graphic and tilt Inline graphic are related to the unit vector Inline graphic of the average direction of the hydrocarbon chains and the unit vector Inline graphic normal to the monolayer surface by Inline graphic (∇ being the two-dimensional divergence operator at the monolayer surface) and Inline graphic and Inline graphic are the monolayer splay (bending) and tilt elastic moduli, respectively, while _J_s is the monolayer spontaneous curvature (spontaneous splay). The total elastic energy is given by integration of Eq. 1 over the surfaces of the two monolayers constituting the PLP.

Energy of hydration repulsion

To calculate the hydration repulsion energy of PLP formation, we have to account for the discreteness of distribution, on the membrane surface, of the effective centers generating hydration of the lipid-water interface. The characteristic distance between the hydration centers has to be of the order of dimension of a lipid polar head δ* ≈ 1 nm. Hence, the discreteness effects should be irrelevant and can be neglected if extended membrane contacts of tens of nanometers and larger are produced by smooth membrane bulges. At the same time, these effects must become significant for the point-like membrane contacts considered in this work, which are of the order of the discreteness length.

The energy of hydration repulsion per unit area of the monolayer surface is given in Rand and Parsegian (6)

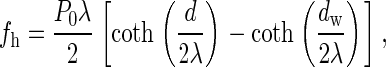graphic file with name M9.gif (2)

where _d_w and d are the initial and current intermembrane distance at each point; _P_0 = 1000 kT/nm3 and λ = 0.2 nm are, respectively, the upper boundary for the measured values of the hydration pressure and the decay length of the hydration interaction (6). The total hydration energy is obtained by integration of Eq. 2 over the PLP surface facing the flat membrane. We assume that the point of contact between PLP and the flat membrane is in the middle between the adjacent hydration centers, which reduces the overall hydration energy. Therefore, the area of diameter δ* around the PLP tip is not included in the integration.

To find the optimal conformation of the PLP, we calculate the sum of its elastic and hydration energies and minimize it, numerically, with respect to the PLP shape and distribution along the PLP surface of the tilt and splay of the hydrocarbon chains of the two PLP monolayers. Full details of the numerical technique we use for the energy calculation are presented in Kozlovsky and Kozlov (7).

RESULTS

We explored whether the sharpness of the tip of the PLP indeed decreases its overall energy, how the PLP energy depends on the initial transmembrane distance _d_w, and to what extent the intrinsic properties of the membrane such as its monolayer spontaneous curvature _J_s and the discreteness of the hydration centers δ* influence the probability of the PLP formation.

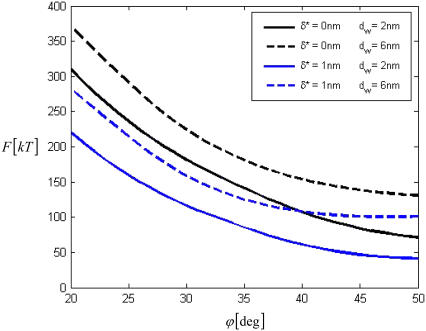
The PLP energy dependence on the tip angle ϕ, which determines the PLP sharpness, is presented in Fig. 2. We found that the change of ϕ from almost zero (smooth bulge) to 45° decreases the energy by nearly an order of magnitude (the angle range between 0° and 20° is not shown). Requirement of small tilt implied by the model (Eq. 1) does not allow us to extend the results beyond ϕ = 45° but, as indicated by Fig. 2, the energy continues to decrease with growing sharpness.

FIGURE 2.

FIGURE 2

The energy of PLP as a function of the tip angle for different intermembrane distances _d_w and different parameter of the hydration charge discreteness δ*. The monolayer spontaneous curvature is taken as _J_s = −0.1 nm−1.

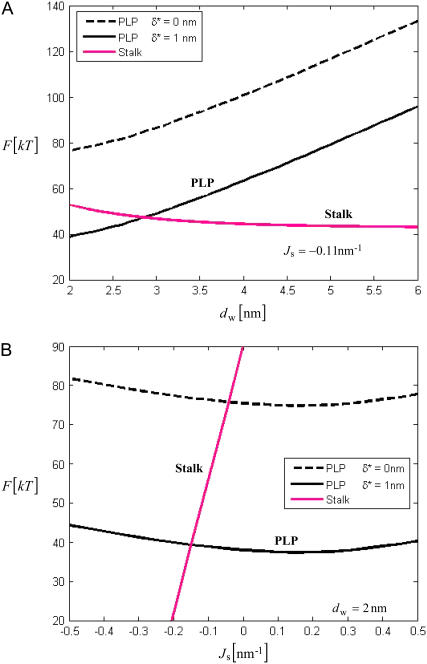
The PLP energy increases considerably with the distance _d_w (Fig. 3 a), is rather sensitive to the discreteness parameter δ*, and depends weakly on the monolayer spontaneous curvature _J_s (Fig. 3 b). The PLP energy depends on _d_w stronger, and on _J_s weaker than the energy of the stalk (red line). The PLP energy is smaller than that of the stalk for the experimentally relevant values of _J_s ∼ −0.1 nm−1 and _d_w ≥ 3 nm provided that the distance between the hydration centers has a feasible value of δ* ≈ 1 nm.

FIGURE 3.

FIGURE 3

PLP energy as a function of the intermembrane distance (a), and the monolayer spontaneous curvature _J_s (b) for different discreteness parameter δ*. The red line shows the stalk energy.

CONCLUSION

We found that, in contrast to the straightforward expectations, the elastic energy of the monolayer deformation in PLP adopts modest values of the order of 10_kT_ (not shown). Further, we obtained that, due to the shape of PLP, along with the discreteness of the hydration centers, also the hydration repulsion energy of PLP formation remains in the range of a few tens of kT.

Altogether we showed that for the relevant lipid compositions of membrane monolayers, the overall energy of PLP is lower than that of the fusion stalk, which may exceed the values presented in Fig. 3 due to contribution of the saddle-splay elasticity (9). Consequently, PLP does not limit the rate of hemifusion and the lipid dependency of hemifusion is determined by the stalk and the hemifusion diaphragm. Moreover, a point-like dehydrated contact between PLP and the target membrane facilitates stalk formation. Summarizing, PLP is a feasible prestalk intermediate completing the model pathway of fusion reaction. Experiments and/or molecular dynamics simulations are needed to confirm formation of PLP at the very initial steps of membrane fusion.

Acknowledgments

The financial support for M.M.K. by the Israel Science Foundation, the Binational United States-Israel Science Foundation, the Marie Curie Network “Flippases” and the Intramural Research Program of the National Institute of Child Health and Human Development, National Institutes of Health, is gratefully acknowledged.

References