GAZE: A Generic Framework for the Integration of Gene-Prediction Data by Dynamic Programming (original) (raw)
Abstract
We describe a method (implemented in a program, GAZE) for assembling arbitrary evidence for individual gene components (features) into predictions of complete gene structures. Our system is generic in that both the features themselves, and the model of gene structure against which potential assemblies are validated and scored, are external to the system and supplied by the user. GAZE uses a dynamic programming algorithm to obtain the highest scoring gene structure according to the model and posterior probabilities that each input feature is part of a gene. A novel pruning strategy ensures that the algorithm has a run-time effectively linear in sequence length. To demonstrate the flexibility of our system in the incorporation of additional evidence into the gene prediction process, we show how it can be used to both represent nonstandard gene structures (in the form of _trans_-spliced genes in Caenorhabditis elegans), and make use of similarity information (in the form of Expressed Sequence Tag alignments), while requiring no change to the underlying software. GAZE is available at http://www.sanger.ac.uk/Software/analysis/GAZE.
Computational methods for the identification of protein-coding genes in genomic DNA have progressed rapidly in recent years. It remains the case however that automated identification of gene structures is not a solved problem (Guigó et al. 2000; Reece et al. 2000a), and therefore still attracts considerable research interest. Most existing gene prediction methods (for reviews, see Burge and Karlin 1998; Stormo 2000) attempt to identify gene structures by scanning the sequence for (1) localized signals displayed by individual gene components (e.g., splice sites and translation start sites), and (2) more extensive content evidence for the regions between the components (e.g., codon-bias in the region between acceptor and donor splice sites flanking a candidate exon). Where specific methods differ is in how the signal and content evidence is integrated into predictions of complete gene structures. In some of the more recent programs, signal and content data are integrated under the probabilistic framework of a Hidden Markov Model (HMM), examples being Genie (Kulp et al. 1996), GENSCAN (Burge and Karlin 1997), HMMGene (Krogh 1997), and Fgenesh (Salamov and Solovyev 2000). A more classical approach is to use the signal and content data to generate a list of scored candidate exons, which are then assembled into complete gene structures; GeneID (Guigó et al. 1992), GRAIL (Xu et al. 1994), and Fgenes (Solovyev et al. 1995) are programs that adopt this strategy. In both approaches, dynamic programming is used to find the gene structure that is optimal with respect to some discrimination measure, and this is often performed over an assumed model of how gene components relate to each other and fit together into complete gene structures.
As we find out more about genes and the elements that they consist of, we might want to extend these gene prediction methods to reflect our greater understanding, with the aim of making them more accurate. For example, promoter identification methods are at present considered too unreliable to be used in many gene prediction programs. Accurate promoter identification however, as well as having many other utilities, can help address the difficult problem of identifying the 5′ ends of genes. There would therefore be much to gain by incorporating a new, more accurate promoter prediction technique into the gene prediction process. Furthermore, programs that make use of similarity information (e.g., alignments of ESTs or homologous proteins to the sequence being searched for genes) have been shown to produce the most accurate results for genes that have supporting evidence of this nature (Guigó et al. 2000). By extending ab initio methods to make use of it, we might hope to improve prediction accuracy where similarity evidence exists, without compromising the ability to discover novel genes where it does not.
The incorporation of new information into many of the existing programs may not be easy due to inherent rigidities in their implementation. At best, knowledge of the underlying implementation of the software is required, and even given this, it is often necessary to produce a custom-built version of the program to make use of the new information; at least four of the programs mentioned above have variants developed specifically to make use of similarity information (Krogh 2000; Reese et al. 2000b; Salamov and Solovyev 2000; Yeh et al. 2001).
Here, we present a methodology (and an associated program, GAZE) for the assembly of features (corresponding to signal sensors) and segments (corresponding to content sensors) into complete gene structures in a way that is tied neither to any specific signal or content sensors nor any assumed model of gene structure; both of these elements are external to the program and supplied by the user. Our goal is to provide a framework for the seamless incorporation of new and/or improved signal/content information into the gene prediction process.
A key novelty of the GAZE system is that it does not work directly with genomic DNA sequence. It instead predicts gene structures from an input file containing the results of arbitrary signal and content sensors with associated scores, typically log probability values. This file is assumed to be in the general feature format (GFF), a format designed primarily for the exchange of gene prediction information (http://www.sanger.ac.uk/Software/GFF). A second “configuration” file (in XML format) directs the assembly of the signal and content data into complete gene structures, by specifying first a mapping from GFF lines to features and segments, and second the model of gene structure over which their assembly will take place. A generic, effective linear-time dynamic programming algorithm is used to obtain both the highest scoring gene structure consistent with the model and posterior probabilities that each feature is part of a gene.
The idea of performing gene prediction over an external model of gene structure has been presented before (Guigó 1998), and is used in the GeneID system. We take this concept further by providing a rich language for the specification and scoring of legal gene structures. GAZE works with signal data in raw form before it has been preprocessed to produce a set of candidate exons with preassigned frames and scores. To demonstrate flexibility that results from this approach, we show how GAZE models can be developed, by extending a basic model first to represent a novel type of gene structure (specifically _trans_-spliced genes in Caenorhabditis elegans), and second to make use of similarity information (specifically Expressed Sequence Tag (EST) alignments).
RESULTS
Definition of Models of Gene Structure
The approach we take is that a gene structure can be defined by an ordered list of specific features. For example, for a sequence 1400 bases long, [BEGIN@1, start@201, donor@305, acceptor@900, stop@1040, start@1101, stop@1220, END@1400] defines a structure with two genes, the protein-coding portions, of which consist of two exons and a single exon, respectively; [BEGIN@1, stop_rev@1051, start_rev@1230, END@1400] defines a single-exon coding portion of a gene on the reverse strand; and [BEGIN@1, END@1400] defines a structure with no genes. We assign a score to each possible gene structure and define the most likely gene structure to be that with the highest score.
The purpose of the user-supplied gene structure model is twofold: first to define which lists of features represent legal gene structures, and second to specify how the score for each gene structure is obtained.
Defining Legal Gene Structures
The model is initially constructed by giving a set of rules for each type of “target” feature, defining which types of “source” feature can precede them in the sequence. In the first gene structure above, a ‘stop’ target feature can be immediately preceded upstream by ‘start’ or ‘acceptor’ source features, and the model would therefore need to contain rules for start → stop and acceptor → stop (as well as others) to allow this gene structure to be built. The rules themselves can be qualified with constraints:
Distance constraints, specifying that there should be no more than a maximum and no fewer than a minimum number of bases between the source and target.
Phase constraints, specifying that the source and target should occur 0, 1, or 2 bases (modulo 3) apart.
Interruption constraints, specifying that a source and target are illegal if the region between them is interrupted by the occurrence of some specified feature at the specified distance (modulo 3) from either the source or target. These are used to invalidate potential coding exons that are interrupted by an in-frame stop codon.
DNA constraints, specifying that a source and target are illegal if the DNA located at the source and/or target has a certain sequence. These are used to invalidate gene structures that would give rise to in-frame stop codons across exon-exon junctions in the spliced mRNA.
Scoring Legal Gene Structures
The overall score of a gene structure is the sum of scores for the individual features (as given in the GFF file) and for the regions between each adjacent pair of features in the structure. The region scores can be tailored precisely for each source and target pair, by specifying in the source → target rule:
A length-penalty function reflecting the fact that it will be more likely for pairs of features of these types to occur at some distances apart than others. These functions are defined elsewhere in the configuration file by listing a set of (distance, penalty) pairs, with linear interpolation being used to derive penalties for points not given.
A segment qualifier for each of the various types of segment that act as supporting evidence for the region between the source and target. Since the region between an acceptor and donor (for example) is expected to be protein coding, both a likely_coding segment (indicative of a region of high coding potential by some statistical measure), and a protein_match segment (corresponding to a hit from a database search) lying in this region can be used to increase the score of the corresponding exon. Segment qualifiers can contain constraints to restrict which segments of a particular type should contribute to the region score, namely: (1) a phase constraint, specifying that the starts of segments of this type should occur at 0, 1, or 2 bases (modulo 3) away from the target. This gives the option to allow only segments of this type that are in-frame with respect to the target; (2) a match constraint, specifying that the start and/or end of the segment must lie at the same position as the source and/or target, giving the option to use only segments that fit the region precisely. This allows GAZE to make use of the output of programs that identify potential exact introns, exons, or other functional regions that are part of genes.
The scores that we use are derived as log-probability ratios from probabilistic models, so adding them to produce a complete gene score corresponds to an assumption of independence. These assumptions form the basis of the probability analysis described below. However, GAZE will accept feature scores obtained in any fashion, in which case the probability distributions can be viewed as Boltzmann distributions derived by treating the scores as “energies”.
Predicting Gene Structures
GAZE is not a complete integrated gene prediction program, and as such requires a set of features, segments, and length penalty functions. For all analyses presented here, the 980506 version of Genefinder (P. Green, unpubl.), a gene prediction program optimized for performance in C. elegans genomic sequences, was the effective source for these data (see Methods). GAZE was originally envisaged as a curation tool for C. elegans annotation. As a result, our work has focused on gene prediction in the worm, although one of the key advantages of the methodology that we present is that it is not organism-specific. As a basis for an evaluation of performance, we used a set of 325 gene structures from the WormBase database (Stein et al. 2001, http://www.wormbase.org), all confirmed by full-length mRNA sequences. These were used to construct an artificial sequence of 2.1Mb (full details in Methods), which we refer to as Wormseq.
For purposes of comparison, we additionally present the performance of Fgenesh; as well as being one of the more well known published gene prediction programs, it also has a version specifically tuned for performance on C. elegans sequences.
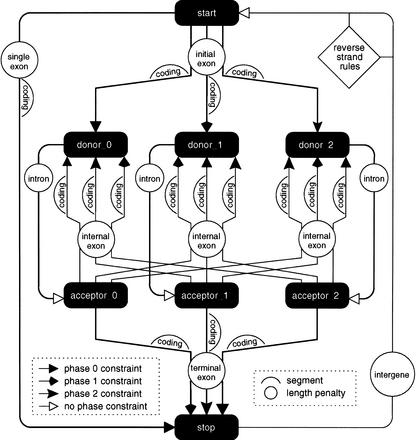
Using the constructs defined in the previous section, it is straightforward to define a model for multiple genes on both strands, as shown in Figure 1, with which GAZE produces the results referred to as GAZE_std in Table 1.
Figure 1.
A pictorial representation of a GAZE-XML model for multiple genes on both strands. The features are represented by filled boxes, and ’source → target' rules by different types of arrows, each corresponding to a phase constraint as explained in the text. The labeled circles give the name of the length penalty function used for each pair of features, which are themselves defined elsewhere in the configuration file (not shown); the labeled humps indicate the segments that contribute to the score for each pair of features, where “coding” humps are the likely_coding segments referred to in the text. The rules for reverse-strand target features are not shown in their entirety, for clarity, but are formed by a simple reverse complementation of the forward-strand rules. Also omitted are the BEGIN and END features (which mark the two ends of the sequence being searched for genes, and act respectively as source and target to every other feature), as well as the distance, interruption, and DNA constraints explained in the text. The XML configuration file contains a directive to create three separate features for each predicted splice site seen in the GFF file. The effect of this, together with phase constraints between pairs of features giving rise to exons, is to carry forward whether each intron interrupts a codon at position 0, 1, or 2 to the rest of the gene structure, allowing us to ensure that the length of the coding part of each predicted gene is divisible by three.
Table 1.
Performance Comparison for Wormseq (325 genes, 2254 exons)
| Precise Identification of Exons and Complete Gene Structures | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Program | Exon-level accuracy | Gene-level accuracy | ||||||||
| Sn | Sp | Av. | ME | WE | Sn | Sp | Av. | MG | WG | |
| GAZE_std | 0.84 | 0.77 | 0.80 | 12 | 303 | 0.35 | 0.35 | 0.35 | 4 | 25 |
| GAZE_tsplice | 0.86 | 0.80 | 0.83 | 12 | 273 | 0.47 | 0.42 | 0.44 | 4 | 34 |
| GAZE_EST | 0.90 | 0.84 | 0.87 | 8 | 222 | 0.59 | 0.53 | 0.56 | 3 | 31 |
| Fgenesh | 0.88 | 0.80 | 0.84 | 5 | 319 | 0.51 | 0.42 | 0.47 | 2 | 57 |
| Breakdown of Exon-Level Accuracy by Exon Type | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Program | Initial | Internal | Terminal | Single | ||||||||
| Sn | Sp | Av. | Sn | Sp | Av. | Sn | Sp | Av. | Sn | Sp | Av. | |
| GAZE_std | 0.57 | 0.56 | 0.57 | 0.90 | 0.80 | 0.85 | 0.78 | 0.78 | 0.78 | 0.94 | 0.71 | 0.83 |
| GAZE_tsplice | 0.72 | 0.67 | 0.70 | 0.89 | 0.83 | 0.86 | 0.81 | 0.74 | 0.78 | 0.94 | 0.59 | 0.77 |
| GAZE_EST | 0.79 | 0.74 | 0.77 | 0.92 | 0.86 | 0.89 | 0.85 | 0.80 | 0.83 | 0.94 | 0.73 | 0.84 |
| Fgenesh | 0.75 | 0.61 | 0.68 | 0.92 | 0.87 | 0.90 | 0.84 | 0.68 | 0.71 | 0.63 | 0.77 | 0.70 |
Modeling _Trans_-Splicing in C. elegans
The more accurate identification of internal exons by GAZE_std compared to initial and terminal exons supports the commonly made observation that the starts and ends of genes are more difficult to accurately identify than the internal exon-intron structure. This problem is confounded in C. elegans by the fact that a significant fraction of genes undergo _trans_-splicing, where a 21–23 basepair sequence transcribed from elsewhere in the genome is spliced onto an acceptor situated upstream of the translation start site in the pre-mRNA (Krause and Hirsh 1987; for review see Blumenthal and Steward 1997). Gene prediction programs that do not take _trans_-splicing into account are likely to be confused into mistaking the initial exon of a _trans_-spliced gene for an internal exon of a longer gene, linking the _trans_-splice acceptor to some upstream donor belonging to a different gene. Examination of the gene predictions made by GAZE_std shows this to be the case.
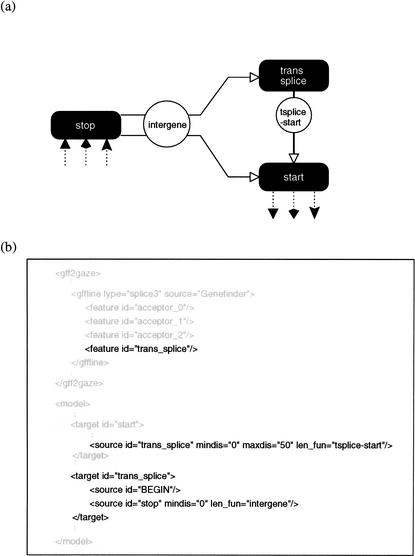
The flexibility of GAZE allows us to incorporate _trans_-splicing by making only minimal modifications to the standard model of gene structure (Fig. 2). Note that no change to the feature input is needed, because GAZE itself makes the candidate _trans_-splice-site features from acceptor splice-site predictions. Table 1 shows that the GAZE_tsplice model does improve the prediction of initial and terminal exons, and that there is a significant improvement in the correct identification of complete genes. GAZE_tsplice is more specific than Fgenesh for initial and terminal exons, although slightly less sensitive, whereas for single-exon genes the reverse is true. The strength of Fgenesh seems to be in the identification of internal exons, for which it is both slightly more sensitive and specific than GAZE_tsplice. Fgenesh has submodels for transcription start and polyadenylation cleavage sites to help better identify the initial and terminal exons of genes. By defining a worm-specific model of gene structure (accounting for _trans_-splicing), we can improve the accuracy of identification of initial and terminal exons (as measured by the average of sensitivity and specificity) to above that of Fgenesh without modeling transcription starts or poly-A cleavage sites.
Figure 2.
(a) Changes necessary to the standard model in Fig. 1 to allow for _Caenorhabditis elegans trans_-splicing, and (b) the fragment of the XML configuration file affected by the changes.
Integrating Similarity Information
We have produced a simple variant of GAZE_tsplice that uses protein database matches in addition to segments of high coding potential as evidence of protein-coding regions, and this produced a marginal increase in performance (results not shown). Here we describe the slightly more complicated use of EST matches. The version of WormBase we used to construct our dataset contained matches to C. elegans ESTs that had been aligned to the genome using EST_GENOME (Mott 1997). This program aligns spliced cDNA to genomic DNA, producing a set of scored EST exons and their genomic position. We used this data as a source for EST_match segments (see Methods). To take advantage of the accuracy in EST_GENOME in identifying exon-intron boundaries, we postprocessed the matches to make EST_intron segments from the regions between exons. Since these segments are expected to match introns precisely, we made use of the match-constraint in the segment qualifier to ensure that they only contribute to the score when this is the case.
As well as being useful for identifying exon-intron boundaries, ESTs can also give information on gene extents. WormBase contains many pairs of ESTs that correspond to 5′ and 3′ reads of the same cDNA. We therefore expect the region between the alignments to the genome of each of the partners of such a pair to contain only a single gene. To achieve this, we made EST_span segments for the regions between the alignments of 5'/3' EST partners. By assigning high negative scores to these segments for intergenic regions, we strongly penalize the prediction of more than one gene in the region defined by an EST_span.
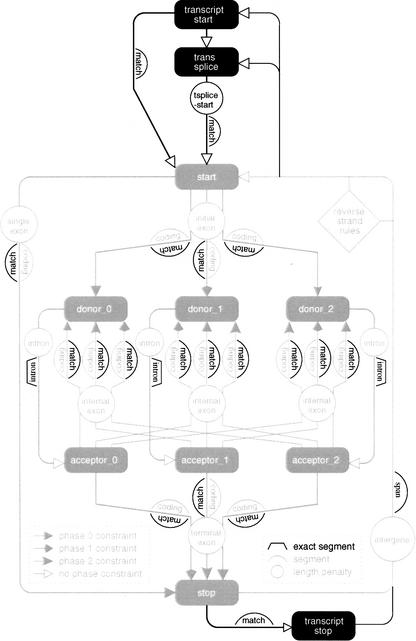
The use of EST information requires a slightly more sophisticated model of gene structure, due to the fact that matches will be expected to run into the noncoding untranslated regions (UTRs) of genes. Figure 3 shows the additions to the model necessary to incorporate UTRs, and make use of the EST-based segments explained above. The results for this model, referred to GAZE_EST in Table 1, display an improvement over all other models to date as well as Fgenesh, most noticeably in whole-gene accuracy. The net gain of 37 additional correct gene-structures identified with the GAZE_EST over GAZE_tsplice consisted of 39 that GAZE_EST identified and GAZE_tsplice did not, and two that GAZE_tsplice identified that GAZE_EST did not. Apart from these, there were also cases where GAZE_tsplice identified more exons of a gene correctly than did GAZE_EST. In these few cases where EST data made the prediction worse, the main contributing factors were misalignment and incorrect assignments of orientation. This demonstrates well both the benefits to be gained from using ESTs in gene prediction and the problems caused by their sometimes questionable reliability.
Figure 3.
A GAZE model to allow for _trans_-spliced genes and untranslated regions. It is a simple extension of the standard model in Fig. 1, which is shown in pale-shade for reference. The transcript_start and transcript_stop features were not predicted a priori for the practical use of this model, but were derived from the starts and ends of EST alignments (see Methods). The “match”, “intron”, and “span” segments shown are the EST_match, EST_intron, and EST_span segments referred to in the text.
Genome-Scale Analysis
The precise identification of complete gene structures can depend on the genomic context of the genes, that is, their relationships to each other with respect to distance and orientation. It might be argued that extracting genes from their genomic context, as was done in the construction of WormSeq, provides an artificial problem for gene prediction programs. To address this, we ran GAZE across the half of the C. elegans genome sequenced and curated at the Sanger Institute, from which the original test-set was taken, amounting to approximately 48 Mb of genomic DNA. Table 2 shows the accuracy of the gene predictions of the same 325 genes, but this time in their true genomic context. The results are comparable to those obtained for WormSeq.
Table 2.
Exon-Level and Gene-Level Sensitivity for the Genes in WormSeq in Their Genomic Context
| Program | Exon-level accuracy | Gene-level accuracy | ||||
|---|---|---|---|---|---|---|
| Predicted | Sn | ME | Predicted | Sn | MG | |
| GAZE_std | 61487 | 0.85 | 8 | 8645 | 0.39 | 3 |
| GAZE_tsplice | 60860 | 0.86 | 8 | 9393 | 0.48 | 3 |
| GAZE_EST | 60559 | 0.90 | 12 | 9075 | 0.57 | 4 |
| Fgenesh | 62668 | 0.88 | 2 | 10707 | 0.50 | 1 |
Posterior Feature Probabilities
We have included a facility in GAZE to calculate the posterior probability (pf) of features, as described in Methods. These correspond directly to the “forward_backward” exon probabilities of GENSCAN in a mathematical sense; more informally, they can be regarded as indicators of how well the features fit into sensible gene structures.
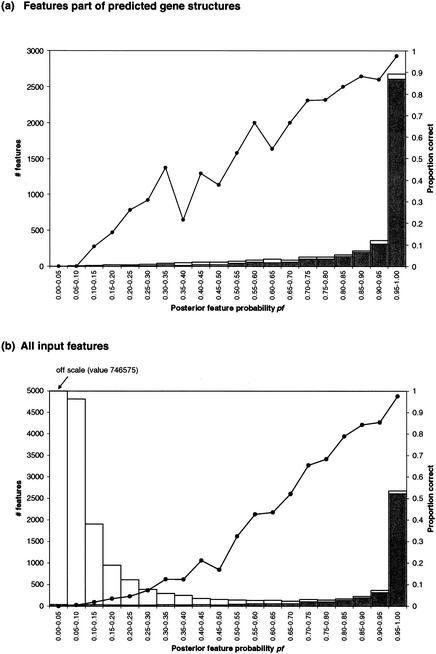
Figure 4a shows the proportion of features predicted by GAZE as part of gene structures that are correct, for different values of pf. In particular, of the 4329 features predicted by the GAZE_EST model as belonging to gene structures in WormSeq, 2045 had a pf >0.99 of which 98% were correct, and 301 had a pf ≥0.5, of which 33% were correct. GAZE can also report probabilities for all input features, in addition to the subset that belongs to predicted gene structures (Fig. 4b). This could provide an aid to manual curation of gene structures, because as well as acting as confidence values that features are correct (and therefore drawing attention to features that are not part of curated genes that perhaps should be), they also reduce the space of gene elements that need to be considered; features with zero pf values do not fit into valid gene structures and can be ignored.
Figure 4.
Posterior feature probabilities and their accuracies. Shown for (a) features part of gene-structures predicted by GAZE and (b) all features given as input to GAZE are the number of features with a posterior probability, pf in each interval (bars), the number of those features that were correct (shaded portions of the bars), and the proportion of those features that were correct (line). These data were calculated for the GAZE_EST model. Plots for other models are similar (data not shown).
Like most existing gene prediction programs, GAZE does not explicitly address the problem of identifying genes giving rise to alternatively spliced transcripts, and this is still very much an open problem. However, the pf values do provide a useful basis for the curation of such genes. Figure 5 shows a gene with two alternatively spliced isoforms, neither of which is identified precisely by either GAZE or Fgenesh. Upon examining the pf values we find first that of the features predicted by GAZE that are not part of either correct gene structure, none of them have strikingly high pf values (0.87, 0.01, and 0.68 for the initial start, donor splice, and acceptor splice predicted by GAZE), and of those predicted features that are part of both correct gene structures, all have pf values above 0.99. The pf values are in this case accurate in the sense that GAZE has reported a higher degree of confidence about the parts of its prediction that turn out to be correct. Where the two isoforms differ, in their choice of acceptor splice site at the 5′ end of the second exon, GAZE is less confident; the pf value for the acceptor that is part of the GAZE prediction is only 0.62. Upon inspection, the “missing probability” can be found in the alternative acceptor, which has a pf value of 0.38. This shows that there is potential to use the pf values to identify the multiple isoforms of alternatively spliced genes, though there is still much to be done to develop this into an automated system.
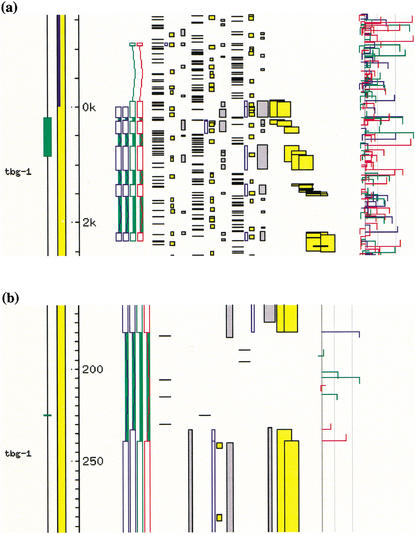
Figure 5.
An AceDB Fmap showing two alternatively spliced isoforms of a gene with WormBase WS52 identifier F54A4.7. The correct gene structures are in blue, with the Fgenesh and GAZE predictions shown in green and red, respectively. Genefinder splice-site predictions are the colored horizontal hooked bars running vertically down the righthand-side of the panel. (a) Both Fgenesh and GAZE fail to correctly identify the initial exon of either isoform. (b) An enlargement of the 5′ ends of the second exons of the two correct gene structures, showing alternative acceptor splice sites. These alternatives are supported by alignments of ESTs to the genome by EST_GENOME (shown in yellow). Although only one of the two alternative acceptors belongs to the predicted gene structure, the posterior feature probabilities reported by GAZE provide evidence for both, as explained in the text.
DISCUSSION
We have designed a highly flexible framework for the integration of gene prediction information on a genome-wide scale. GAZE is intended as a practical tool for the development of gene prediction methods, and as such it is important to say something about its efficiency. The fact that the system allows arbitrary user-defined length penalty functions makes it difficult to design a linear-time dynamic programming algorithm that obtains both the highest-scoring gene structure and the posterior feature probabilities. However, our algorithm runs in effective linear time due to a novel pruning strategy that we use (see Methods). This means that the analysis of the whole C. elegans genome with GAZE_tsplice can be performed in around 5 h on a single DS10 Alpha desktop workstation. The memory consumed by GAZE depends on the model being used, and the number of input features and segments; GAZE_tsplice uses approximately 10 MB per megabase of sequence. We have developed a wrapper for GAZE that allows it to run on arbitrary length sequences, independent of the resource limitations of any particular machine (see Methods). We employed this method in the genome-scale analysis presented earlier.
Two issues that existing gene prediction programs do not in general address are alternative splicing and nested genes. GAZE does not explicitly deal with alternative splicing, although we discuss above how the posterior feature probabilities can be used to begin to address this problem. Nested genes are not uncommon in C. elegans; around 2% of all curated gene structures in WormBase are situated in the introns of other genes (almost always on the opposite strand). The models we have presented cannot predict nested genes, but it is possible to design models that do. In the current formalism however, the definition of such models is cumbersome, due to a large increase in the number of feature types required; separate, complete nested-gene models are needed for each of the six different types of intron in our standard model that can contain them (see Fig. 1). The ability to define submodels that act as sources for a given target would facilitate the definition of complex gene structure models. We intend to implement this idea in a future version of GAZE.
A key strength of our system is that it is easy to include content information from multiple, arbitrary sources, as we have done in the GAZE_EST model with EST_match and likely_coding segments both contributing to the score for potential coding exons. For this to work, the evidence from the various sources must be weighted appropriately. In the analyses presented here, we have addressed this problem in a rather ad hoc manner, by applying a scaling function to the scores of EST matches (for example) to make them of approximately the same order as the likely_coding segments (see Methods). However, it is unlikely that this weighting function is optimal. Far more desirable would be a way to automatically derive optimal weights for the segments used in a given model. Stormo and Haussler (1994) have published an algorithm for optimally parsing a sequence into regions of different functional classes using multiple types of weighted evidence. Included in their presentation is a method to derive the weight for each type of evidence that maximizes (by gradient descent) the probability of the parse corresponding to the correct gene structure. We have implemented a version of their algorithm, modified for our own scoring function and generalized to work over a GAZE model of gene structure (details not shown). We found that the set of weights that maximizes the probability of the correct gene structure does not necessarily give the most accurate gene predictions; although the total probability of all incorrect gene structures is minimized, the probabilities of individual incorrect gene structures may (and often does) increase. It may be that the probability of the correct gene structure is not the best objective function to be optimizing, and we are currently investigating whether other objective functions can give more accurate results.
METHODS
Dataset
We used WormBase WS52 (September 2001) to obtain a set of confirmed genes, in particular the curated gene structures associated with the “NDB_CDS” objects in the half of the C. elegans genome maintained at the Sanger Institute (which we refer to as Sanger_WormBase). These objects are the gene structures implied by the alignment of non-genome-project mRNAs to the genome. From this set, we removed those that were not supported by at least one mRNA annotated as having “complete CDS” in its EMBL entry. We further removed genes that overlapped with other genes. This left us with a set of 325 mRNA-confirmed gene structures (157 forward and 168 reverse strand) not known to have alternative splice variants, or to overlap with genes on the opposite strand. The average number of exons per gene in this dataset was 6.9 (compared to 6.3 for all curated gene structures in WormBase).
To construct the artificial test sequence Wormseq, we extracted the genomic DNA underlying each gene structure, along with half of the intergenic DNA to the nearest other curated gene in each upstream and downstream direction. These sequences were then concatenated to make an artificial sequence of 2,079,582 bases. The proportion of the test sequence that consisted of coding DNA was 0.24 (compared to an estimate based on the curated genes in WormBase of 0.25 for the whole genome). Wormseq is available at http://www.sanger.ac.uk/Software/analysis/GAZE/wormseq.
For the analysis of the prediction of these genes in their genomic context, we used the nine contigs in Sanger_WormBase on which the confirmed genes were situated, amounting to 48,722,743 nucleotides of genomic DNA.
Features, Segments, and Length-Penalty Functions
Splice sites and translation start and stop sites were predicted using weight matrices calculated as log-likelihood ratios of nucleotide i at position j in a frequency table for true sites compared to randomized DNA. The AceDB package (http://www.acedb.org) contains a module adapted from the original Genefinder code to construct such weight matrices and predict features with them using given frequency tables.
We used the frequency tables supplied with Genefinder, with the kind permission of the author (P. Green, pers. comm.). The table for translation starts represents position −9 to +11 (where 0 is the position of the A in the conserved ATG, which is enforced). Both the donor and acceptor splice-site tables represent 6 and 25 nucleotides of the corresponding exon and intron respectively, and the GT-AG rule is enforced. The translation stop table represents 13 bases of the upstream exon and 92 bases of the downstream untranslated region, and the (TAG|TAA|TGA) rule is enforced. AceDB was used to scan Wormseq with the matrices built from these tables using the default Genefinder cutoff values.
For the likely_coding segments, a log likelihood ratio was calculated for each codon in the manner described above, using Genefinder tables. A set of maximal scoring segments in each of the six reading frames was obtained, discarding those that scored less than 1.0.
For EST-related features and segments, the precalculated EST_GENOME alignments in Sanger_WormBase were used. For the genome-scale analysis, these alignments could be used directly. For Wormseq, the positions of the EST matches lying in the regions extracted from the genome to make the sequence were remapped, discarding matches outside these regions, and truncating matches with partial overlap where necessary. “Transcripts” (corresponding to the list of EST match ‘exons’ for a single EST) having an average match identity to the genome of less than 95% were discarded. This left 261 of the 325 gene loci extracted from the genome in the construction of Wormseq with at least one EST match. The EST_match segments were made directly from these remain-ing EST_GENOME matches, and given the score (identity − 95) × length / 100. The EST_intron segments were made from the regions between the EST exons of each transcript and given a score equal to the average identity of the flanking exons divided by 20. The EST_span segments were made for each transcript, and also for each transcript pair corresponding to 5′/3′ reads of the same cDNA. These were given a score of −10000. The starts and ends of the transcripts were also used to make the transcript_start and transcript_stop features, which were given a score of 0.
Separate length penalty functions were used for each of introns, intergenic regions, single exon genes, the initial, internal, and terminal exons of multiexon genes, and the distance between trans-splice sites and the downstream translation start site. These were taken from the Genefinder distribution.
Initial use of the Genefinder features, segments, and length penalty functions led to a slight overprediction of genes. We therefore removed genes structures scoring less than 7.0 (as is done in Genefinder) to obtain the results presented.
The length penalty tables and configuration files used in the analyses presented here are available with the GAZE source-code (written in C) at http://www.sanger.ac.uk/Software/analysis/GAZE.
Scoring and Algorithmic Issues
Given a list of φ1…φ_n_ features defining a legal structure according to a GAZE model, their types t(φ_i_), their positions on the sequence l(φ_i_), and their given scores g(φ_i_), then the score of φ, E(φ), is calculated as
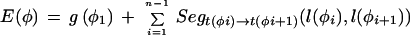
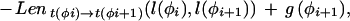
where Lensrc→tgt(x, y) is the length penalty functions specified in the rule for src_→_tgt, or zero if no function is given in the rule; and Segsrc→tgt(x, y) is a sum of separate scores for each segment type that has a segment qualifier in the src_→_tgt rule. The score for segment type is calculated by applying one of two functions to the scores of the relevant subset S of the complete list of segments of that type (i.e., those that meet the phase and match constraints specified in the segment qualifier):
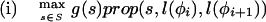
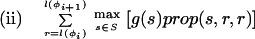
where prop(_s,x,_y) is the proportion of segment s that lies in the sequence region [_x,y_].
Which of these two functions is used is specified as a directive in the segment qualifier. The default is the second, but some segments, by their construction (e.g., the maximal coding segments described above), require the first.
We use dynamic programming to obtain the highest-scoring gene structure. Now taking φ1…φ_n_ to be the complete list of candidate features ordered by sequence position, where BEGIN and END are features φ0 and φ_n_+1, respectively, the maximal-scoring legal gene structure is obtained by the following recursion:
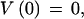
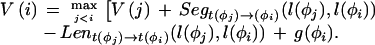
The score of the best structure is V(n+1), and the best structure itself is obtained by a traceback procedure, simplified by storing at each stage the index j that was obtained as the maximum.
Following Stormo and Haussler (1994), we define a probability distribution over the space of all gene structures φ:
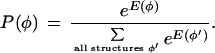
The denominator is found using the following recursion, defined in log-space to keep the computation within the limits of machine precision:
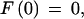
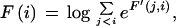
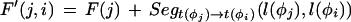
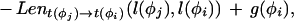
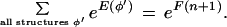
The V and F recursions given above correspond to the Viterbi and Forward recursions used to obtain similar values for HMMs (Rabiner 1989). By calculating a Backward vector B in a similar way, we obtain feature probabilities pf referred to in the text by conditioning, as described by Durbin et al. (1998):
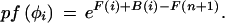
In defining a probability distribution over gene structures in this way, the given feature scores (and hence the overall gene structure scores) are interpreted as log probabilities (or log-likelihood ratios). In the event that the given feature scores are not log-probability based, the above corresponds to a statistical mechanics interpretation (specifically a Boltzmann distribution), where the feature scores are treated as energies.
Time and Space Complexity
The above calculations are quadratic in the number of features and therefore in the length of the sequence (assuming that the number of features grows linearly with sequence length, which is normally the case). The run time of our implementation, however, increases linearly in sequence length. This is achieved by pruning the search space. It often occurs that all of the rules for a target feature contain the same interruption constraint. This means that when scanning back through the sources for a given target tgtk, encountering a feature srci that violates the interruption constraint will invalidate the region between tgtk and all features srcj for j < i, so no other sources need be considered.
For the models that we have presented, this strategy is only useful for targets that mark the end of coding regions, where occurrences of stop codons that are in-frame with the target terminate the search for potential sources. We have therefore implemented a more general pruning strategy that uses the idea of dominance. For a given target feature tgtk and two valid source features of the same type srcj and srci, where j < i, srcj_ is dominated by srci if the contribution made to the forward score by srcj is insignificant (given limits of machine precision) compared to the contribution made by srci. If for tgtk, all sources srcj of a given type t are dominated by a source srci (for j < _i_), then for a future target of the same type _tgtq_ (_q_ > k) we need not search further back than srci for sources of type t. To judge whether src_i dominates src_j_, we calculate the difference between the F_‘ values above after replacing the previously subtracted length penalty component, because the effective length-penalty difference between src_i and src_j_ will be different when calculated with respect to tgtq. This strategy relies on the assumption that the length penalty for srci_→_tgtq will be lower than that for srcj_→_tgtq, that is, that length-penalty increases with distance, at least for distances greater than some minimal l(tgtq) − l(tgtk). This assumption is valid for practical uses of GAZE; its violation would imply a pair of features that, in the limit, become more likely the further they are apart.
Although the space requirements are linear in the length of the sequence, the memory of a standard desktop machine is not likely to be sufficient to handle feature-sets from sequences of genome order in size. For such analyses, we have developed a wrapper for GAZE to allow it to be run on arbitrary size sequences, based on a split-and-merge strategy. GAZE has a feature to allow it to consider a subsequence window of a given arbitrary sized sequence. The wrapper uses this feature when dealing with large sequences by running GAZE on windows wi..wn to produce output files o1..on, where the window size is chosen to be small enough to be handled by the available resources, and n is chosen to be large enough to cover the whole sequence with a specified overlap between wi and wi+1. The overlap allows us to deal with cases where a gene straddles the boundary between two windows. The output gene prediction is formed by printing the predicted features from o1 to on in turn, except in the overlapping regions. For the first predicted feature in oi that lies in a region that is also covered by the start of wi+1, oi+1 is searched for the occurrence of that feature. If it is found, the rest of the features in oi are ignored and printing continues from that point in oi+1. If it is not found, the same is done for the next feature in oi, until an appropriate “crossover” point is identified. For posterior probabilities, which are reported for all potential features, the crossover point is selected to be the midpoint of the overlap region.
This split-and-merge method offers a natural parallelization strategy, because each window wi can be analyzed by GAZE independently of the other windows. Only the final stage of forming the consensus gene structure for all windows relies on their order on the sequence, and therefore cannot be done until all windows have been processed by GAZE.
WEB SITE REFERENCES
http://www.acedb.org; Ace DB database system, including source code and documentation.
http://www.sanger.ac.uk/Software/analysis/GAZE; materials relating to the GAZE project, including source code and documentation.
http://www.sanger.ac.uk/Software/GFF; GFF is an exchange format for feature description.
http://www.wormbase.org; the WormBase database, containing information on the genome and biology of C. elegans.
Acknowledgments
We thank Phil Green for allowing us to use the Genefinder tables and Kerstin Jekosch for checking the curated gene structures in WormBase that were used as a basis for evaluation. K.H. is funded by a Wellcome Trust Prize studentship. T.C. developed a prototype of GAZE while working as a summer student. R.D. is supported by the Wellcome Trust.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
E-MAIL rd@sanger.ac.uk; FAX 44-1223-414-919.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.149502.
REFERENCES
- Blumenthal T, Steward K. RNA processing and gene structure. In: Riddle DL, et al., editors. C. elegans II. Cold Spring Harbor, New York: Cold Spring Harbor Laboratory Press; 1997. pp. 117–145. [PubMed] [Google Scholar]
- Burge C, Karlin S. Prediction of complete gene structures in human genomic DNA. J Mol Biol. 1997;268:78–94. doi: 10.1006/jmbi.1997.0951. [DOI] [PubMed] [Google Scholar]
- Burge C, Karlin S. Finding the genes in genomic DNA. Curr Opin Struct Biol. 1998;8:346–354. doi: 10.1016/s0959-440x(98)80069-9. [DOI] [PubMed] [Google Scholar]
- Durbin R, Eddy S, Krogh A, Mitchison G. Biological sequence analysis: Probabilistic models of proteins and nucleic acids (Chapter 3). Cambridge, UK: Cambridge University Press; 1998. [Google Scholar]
- Guigó R. Assembling genes from predicted exons in linear time with dynamic programming. J Comp Biol. 1998;5:681–702. doi: 10.1089/cmb.1998.5.681. [DOI] [PubMed] [Google Scholar]
- Guigó R, Knudsen SND, Smith T. Prediction of gene structure. J Mol Biol. 1992;226:141–157. doi: 10.1016/0022-2836(92)90130-c. [DOI] [PubMed] [Google Scholar]
- Guigó R, Agarwal P, Abril JF, Burset M, Fickett JW. An assessment of gene prediction accuracy in large DNA sequences. Genome Res. 2000;10:1631–1642. doi: 10.1101/gr.122800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krause M, Hirsh D. A trans-spliced leader sequence on actin mRNA in C. elegans. Cell. 1987;49:753–761. doi: 10.1016/0092-8674(87)90613-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krogh A. Two methods for improving performance of a HMM and their application for gene finding. Proc Intell Syst Mol Biol. 1997;5:179–186. [PubMed] [Google Scholar]
- Krogh A. Using database matches with HMMGene for automated gene detection on Drosophila. Genome Res. 2000;10:523–528. doi: 10.1101/gr.10.4.523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulp D, Haussler D, Reese MG, Eeckman FH. A generalized hidden Markov model for the recognition of human genes in DNA. Proc Intell Syst Mol Biol. 1996;4:134–142. [PubMed] [Google Scholar]
- Mott R. EST GENOME: A program to align spliced DNA sequences to unspliced genomic DNA. Comput Appl Biosci. 1997;13:477–478. doi: 10.1093/bioinformatics/13.4.477. [DOI] [PubMed] [Google Scholar]
- Rabiner LR. A tutorial on hidden Markov models and selected applications in speech recognition. Proc IEEE. 1989;77:257–286. [Google Scholar]
- Reese MG, Hartzell G, Harris NL, Ohler U, Abril JF, Lewis SE. Genome annotation assessment in Drosophila. Genome Res. 2000a;10:483–501. doi: 10.1101/gr.10.4.483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reese MG, Kulp D, Tammana H, Haussler D. Genie: Gene-finding in Drosophila melanogaster. Genome Res. 2000b;10:529–538. doi: 10.1101/gr.10.4.529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salamov AA, Solovyev VV. Ab initio gene finding in Drosophila genomic DNA. Genome Res. 2000;10:516–522. doi: 10.1101/gr.10.4.516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solovyev VV, Salamov AA, Lawrence CB. Identification of human gene structure using linear discriminant functions and dynamic programming. Proc Intell Syst Mol Biol. 1995;3:367–375. [PubMed] [Google Scholar]
- Stormo GD. Gene-finding approaches for eukaryotes. Genome Res. 2000;10:394–397. doi: 10.1101/gr.10.4.394. [DOI] [PubMed] [Google Scholar]
- Stormo GD, Haussler D. Optimally parsing a sequence into different classes based on multiple types of evidence. Proc Intell Syst Mol Biol. 1994;4:369–375. [PubMed] [Google Scholar]
- Xu Y, Mural RJ, Uberbacher EC. Constructing gene models from accurately predicted exons: An application of dynamic programming. Comput Appl Biosci. 1994;10:613–623. doi: 10.1093/bioinformatics/10.6.613. [DOI] [PubMed] [Google Scholar]
- Yeh RF, Burge, Lim LP, Burge CB. Computational inference of homologous gene structures in the human genome. Genome Res. 2001;11:803–816. doi: 10.1101/gr.175701. [DOI] [PMC free article] [PubMed] [Google Scholar]