Joint Estimates of Quantitative Trait Locus Effect and Frequency Using Synthetic Recombinant Populations of Drosophila melanogaster (original) (raw)
Abstract
We develop and implement a strategy to map QTL in two synthetic populations of Drosophila melanogaster each initiated with eight inbred founder strains. These recombinant populations allow simultaneous estimates of QTL location, effect, and frequency. Five _X_-linked QTL influencing bristle number were resolved to intervals of ∼1.3 cM. We confirm previous observations of bristle number QTL distal to 4A at the tip of the chromosome and identify two novel QTL in 7F–8C, an interval that does not include any classic bristle number candidate genes. If QTL at the tip of the X are biallelic they appear to be intermediate in frequency, although there is evidence that these QTL may reside in multiallelic haplotypes. Conversely, the two QTL mapping to the middle of the X chromosome are likely rare: in each case the minor allele is observed in only 1 of the 16 founders. Assuming additivity and biallelism we estimate that identified QTL contribute 1.0 and 8.7%, respectively, to total phenotypic variation in male abdominal and sternopleural bristle number in nature. Models that seek to explain the maintenance of genetic variation make different predictions about the population frequency of QTL alleles. Thus, mapping QTL in eight-way recombinant populations can distinguish between these models.
VARIATION in quantitative, or complex, traits is influenced by numerous genetic loci and by environmental factors. For many complex traits we have estimates of the fraction of phenotypic variation that is due to genetic factors, but we do not have a general understanding of the number, effect, and frequency of the alleles that contribute to phenotypic variation. Are alleles at quantitative trait loci (QTL) generally of large effect, but low in frequency, consistent with models of mutation–selection balance (MSB; reviewed by Johnson and Barton 2005)? Alternatively, is the bulk of standing genetic variation for complex traits due to modest-effect intermediate frequency alleles maintained by some form of balancing selection (reviewed by Barton and Turelli 1989; Barton and Keightley 2002)? In the human genetics community the idea that complex trait variation is due to intermediate frequency polymorphisms has been termed the common disease–common variant (CDCV) hypothesis (Cargill et al. 1999). The distinction between MSB models and balancing selection/CDCV models not only is important for understanding how genetic variation is maintained in populations, but also will affect the power of current population-based approaches to identify risk alleles for human disease (Wang et al. 2005).
The most effective way to clarify the contribution of MSB and CDCV forces in maintaining phenotypic variation is to experimentally identify and characterize the underlying molecular genetic basis of several QTL. With this ultimate goal in mind, two non-mutually exclusive experimental programs are predominant in the literature: QTL mapping and association or linkage disequilibrium (LD) mapping. In its simplest form QTL mapping involves crossing a pair of lines that are differentially fixed for alleles at a genomewide set of marker loci and at QTL contributing to the phenotype. Genotyping and phenotyping a large number of recombinant progeny from this cross identifies genetic intervals that harbor factors contributing to segregating variation in the cross. Since the publication of influential articles by Paterson et al. (1988) and Lander and Botstein (1989), the community has enjoyed considerable success mapping QTL for a wide range of traits in a diverse set of genetic systems. Typically QTL are resolved to broad intervals of ∼10 cM (Mackay 2001), which may represent millions of base pairs. This lack of resolution has hindered identification of the molecular variants involved, particularly in QTL mapping studies of intraspecific variation where QTL can have subtle effects. Physically close genetic factors also pose a problem for QTL mapping, as it may be impossible to accurately estimate the effects and locations of linked QTL, and the number of QTL may be underestimated (Wright and Kong 1997; Cornforth and Long 2003). Additionally, since recombinant individuals for QTL mapping are generally derived from a pair of inbred parental lines, only QTL that segregate between the parents can be identified. As a result there is no way to know the population frequency of mapped QTL.
Association mapping is a population-based genetic mapping strategy. The approach involves genotyping a large number of single nucleotide polymorphisms (SNPs) in a large sample of individuals and at each marker testing for an association between genotype and phenotype. A strong association signal at a SNP suggests either that the SNP itself contributes to trait variation or that the causal site is in strong LD with the SNP marker genotyped. Instead of relying on meiotic recombination in experimental crosses, association mapping utilizes the pattern of historical recombination in a panel of natural chromosomes. Thus, association mapping has the potential for much higher resolution than QTL mapping, and in principal the actual quantitative trait nucleotide (QTN) can be identified and its effect and frequency estimated directly. In practice, association mapping has met with modest success, and the literature is rife with failures to replicate published associations (although see Todd 2006 for a positive view of the future). This reflects a variety of factors, such as cryptic population structure, different patterns of LD or genetic heterogeneity in different populations, or simply insufficient power to detect variants with only subtle effects (Kruglyak 1999; Long and Langley 1999). Association mapping can be effective only when the density of genotyped SNPs is sufficiently high that real associations are not missed (Risch and Merikangas 1996). Since powerful genomewide association studies are tremendously difficult to carry out, even in humans where resources are considerable (Hirschhorn and Daly 2005; Wang et al. 2005), researchers have elected to carry out localized mapping on candidate gene regions (e.g., Genissel et al. 2004; Palsson and Gibson 2004; Macdonald et al. 2005a). Such a strategy will fail if the presumed candidate does not actually contribute to trait variation (e.g., Florez et al. 2006). Finally, an aspect of association mapping that is often overlooked is that if much of the genetic variation underlying complex traits is due to rare variants of large effect (as predicted by MSB models) the association mapping paradigm is not very powerful at all, and is almost guaranteed to fail (Weiss and Terwilliger 2000; Pritchard 2001; Reich and Lander 2001; Pritchard and Cox 2002).
It is quite clear that both QTL and association mapping approaches, while powerful in many respects, suffer from distinct drawbacks that prevent the routine identification and characterization of QTN. To make the dissection of complex traits more routine we require a methodology that has some of the resolution of association mapping, combined with the power of QTL mapping to identify factors on a genomewide scale. To determine if standing variation is generally consistent with MSB or CDCV models a method allowing for direct estimation of the population frequency of mapped factors is highly desirable. An ideal methodology would also provide some mechanism with which to identify the precise molecular variants involved.
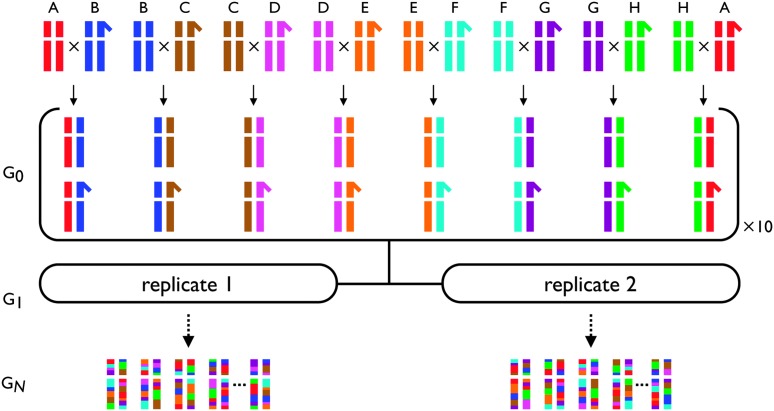
In this study we describe a mapping scheme that allows joint estimates of QTL effects and frequencies from a recombinant panel derived from multiple founder chromosomes. Conceptually, our approach is similar to the mouse “Collaborative Cross” scheme envisioned by the Complex Trait Consortium (Threadgill et al. 2002; Churchill et al. 2004) and has parallels with the “heterogeneous stock” strategy (Talbot et al. 1999; Mott et al. 2000; Demarest et al. 2001) most recently used by Valdar et al. (2006b) to map QTL for 97 traits in mice. We take two independent sets of eight inbred Drosophila melanogaster lines, and from each set initiate a recombinant population. The genetic material for each synthetic population is thus derived from just eight founders, and after multiple generations of maintenance the genome of each recombinant individual is a mosaic of the founder chromosomes (Figure 1). Chromosomal segments transmitted to the recombinant flies by each of the founders are distinguished using markers composed of short runs of nonrecombining SNPs. Multiple rounds of recombination allow these synthetic populations to be used to map QTL with a fairly high level of resolution. Since each synthetic population is derived from eight founders, a key feature of our approach is that we obtain simultaneous estimates of the effect and the population frequency of each mapped QTL. Furthermore, because mapping resolution is generally a function of the number of generations of recombination since population inception, later generations can be used to map more precisely those QTL detected at an earlier generation in a coarse genomewide scan. Here we detail an experiment to map bristle number QTL on the D. melanogaster X chromosome and describe the analytical platform required to deal with experimental mapping data generated using eight-way synthetic populations.
Figure 1.—
Creation of the synthetic recombinant D. melanogaster populations. A recombinant mapping population is initiated from a set of eight inbred lines, A–H, that are intercrossed (virgin females crossed to males) in a one-way round-robin design: line A crossed to line B, line B crossed to line C, …, and line H crossed to line A. From each of the eight crosses, 10 male and 10 virgin female F1 progeny were collected, pooled, and used to initiate the two replicate synthetic recombinant populations. Only the sex chromosomes and one set of autosomes are presented. Full details of the precise crosses performed are provided in the materials and methods.
MATERIALS AND METHODS
D. melanogaster stocks:
All 16 wild-type D. melanogaster lines used to found the synthetic populations (Table 1) have been examined for both PM and IR dysgenesis and were shown to be MI (Kidwell et al. 1983). We also made use of the strain of D. melanogaster used for genome sequencing, the “sequenced strain” (Bloomington Drosophila Stock Center no. 2057, Adams et al. 2000; Celniker et al. 2002), which has the M cytotype. We further verified that all lines are free of P elements using a PCR-based transposon-display assay (details available on request). After founding the synthetic populations we found that lines A7 and B8 (Table 1) were genetically indistinguishable on the basis of the _X_-linked markers we describe here. This likely represents an error that occurred at the stock center.
TABLE 1.
D. melanogaster stocks
| Line no.a | Stock no.b | Stock nameb | Collection details |
|---|---|---|---|
| A1 | bl1 | Canton-S | Canton, Ohio |
| A2 | bl3841 | BOG 1 | Bogata, Colombia, 1962 |
| A3 | bl3844 | BS 1 | Barcelona, Spain, 1954 |
| A4 | bl3852 | KSA 2 | Koriba Dam, South Africa, 1963 |
| A5 | bl3875 | VAG 1 | Athens, Greece, 1965 |
| A6 | bl3886 | Wild 5B | Red Top Mountain, Georgia, 1966 |
| A7 | tu14021-0231.6 | — | Mysore, India, 1958 |
| A8 | tu14021-0231.7 | — | Ken-ting, Taiwan, 1968 |
| B1 | bl3839 | BER 1 | Bermuda, 1954 |
| B2 | bl3846 | CA 1 | Cape Town, South Africa, 1954 |
| B3 | bl3853 | KSA 3 | Koriba Dam, South Africa, 1963 |
| B4 | bl3864 | QI 2 | Israel, 1954 |
| B5 | bl3870 | RVC 3 | Riverside, California, 1963 |
| B6 | tu14021-0231.0 | — | Oahu, Hawaii, 1955 |
| B7 | tu14021-0231.1 | — | Ica, Peru, 1956 |
| B8 | tu14021-0231.4 | — | Kuala Lumpur, Malaysia, 1962 |
Synthetic recombinant populations:
Four synthetic populations were created: population A replicates 1 and 2 (pAr1, pAr2) were initiated from lines A1–A8, and population B replicates 1 and 2 (pBr1, pBr2) were initiated from lines B1–B8 (Table 1 and Figure 1). To initiate the pA populations the following line crosses were carried out: A4 × A3, A3 × A7, A7 × A8, A8 × A5, A5 × A2, A2 × A6, A6 × A1, and A1 × A4 (virgin females × males in each case). In the following generation (generation G0), 10 male and 10 virgin female progeny from each of these eight crosses were combined into a single bottle and allowed to lay eggs. These 160 flies were transferred to a fresh bottle on three successive days to generate four replicate bottles (b1, b2, b3, and b4). In the following generation (generation G1) offspring from bottles b1 and b4 were mixed and distributed into four fresh bottles (pAr1–b1, pAr1–b2, pAr2–b1, pAr2–b2), and offspring from bottles b2 and b3 were mixed and distributed into a further four bottles (pAr1–b3, pAr1–b4, pAr2–b3, pAr2–b4). This procedure produced eight bottles, four for each of the two replicate pA populations. From this point onward the replicate populations pAr1 and pAr2 were maintained independently. At generation G2, and in every subsequent generation, within each replicate, bottles b1 and b4 were mixed and distributed into two fresh bottles numbered b1 and b2, and bottles b2 and b3 were mixed and distributed into two fresh bottles numbered b3 and b4. This strategy effectively maintained each replicate population as a single, large, interbreeding cohort despite being split across four bottles. The census size for each population was maintained at well over 1000 individuals to minimize the effects of random genetic drift. The pair of replicate pB populations was established and maintained in a similar fashion.
Experimental flies:
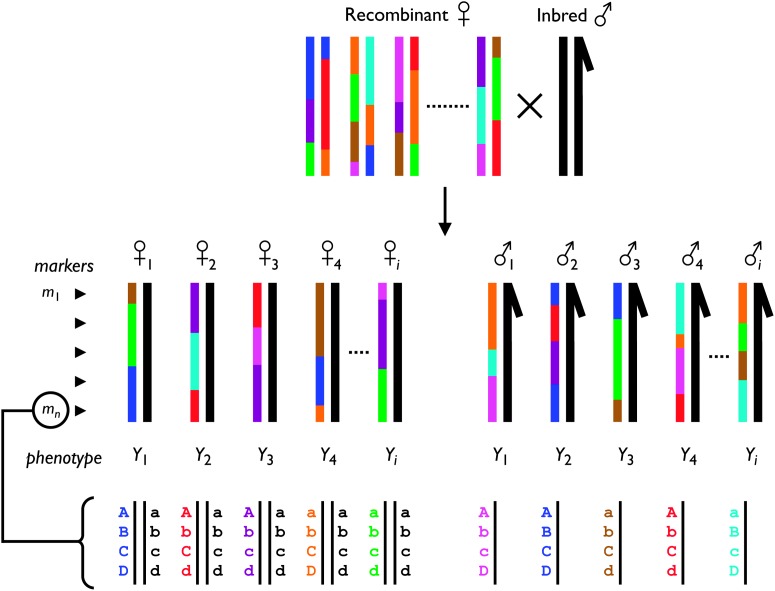
Figure 2 presents the strategy used to create the individuals used for phenotyping and genotyping.
Figure 2.—
Overview of the experimental strategy. Virgin females from the synthetic D. melanogaster mapping population (colored mosaic chromosomes) are crossed to males of the isogenic strain of D. melanogaster used for genome sequencing (uniform black chromosomes). All F1 progeny from this cross are _trans_-heterozygotes of a maternally inherited synthetic recombinant chromosome against a paternally inherited chromosome from the isogenic strain. Male F1 are hemizygous for the recombinant X chromosome. F1 _trans_-heterozygotes are each phenotyped for the trait of interest and genotyped for a set of molecular markers spanning the chromosome(s). As shown, a marker represents a multilocus genotype from a set of nonrecombining SNPs (four in this example). Markers allow the eight lines founding the recombinant population to be distinguished. Only the sex chromosomes are presented in this figure—autosomes would behave similarly to female X chromosomes.
Coarse mapping:
Virgin females were collected from each of the four synthetic populations and aged in groups of 50 in vials for 2–5 days. Twelve aged virgin females from a given population were crossed to 12 males from the sequenced strain in vials. Multiple replicate vials were created, and from each vial 4 male and 4 female offspring were used for phenotyping and genotyping. The experimental flies are thus F1 progeny of a recombinant female and an isogenic male. The coarse-mapping experiment was split into four blocks: in block 1 (generation G16 of the synthetic populations) 24 vials were set up for each of the four populations (pAr1, pAr2, pBr1, and pBr2), and in blocks 2–4 (generations G17–G19) 36 vials were set up for each population. This resulted in a total of 528 male and female experimental flies collected for each population. For each fly two phenotypic measurements were taken: sternopleural bristle number (SBN) is the sum of the number of macro- and microchaetae on the left and right sternopleural plates, and abdominal bristle number (ABN) is the number of microchaetae on the most posterior sternite, corresponding to segment six of females and segment five of males.
A subset of the coarse-mapping experimental flies was tested for the presence of P elements using a transposon-display assay. All flies should be P free. We found that flies derived from population pAr2 showed P elements, implying that pAr2 was contaminated. This population was destroyed, and experimental flies from this population are not considered further.
Fine mapping:
Virgin females were collected from synthetic populations pAr1 and pBr1 and aged as for the coarse-mapping experiment. Multiple vial crosses were set up between 10 aged virgin females and 10 sequenced-strain males, and from each vial 4 male offspring were used for phenotyping and genotyping. The fine-mapping experiment was split into two blocks. In block 1 (generation G55) 144 vials were set up for each of the two populations pAr1 and pBr1, and in block 2 (generation G56) 120 vials were set up for each population. This resulted in a total of 1056 male experimental progeny collected for the pAr1 and pBr1 synthetic populations. Populations pAr1 and pBr1 were shown to be free of P elements at generation G52, just prior to beginning the fine-mapping experiment.
Molecular marker development:
We sought to identify 1-kb sequence fragments harboring several polymorphisms that collectively distinguish the founders (Figure 2), and over the coarse- and fine-mapping experiments developed 24 such markers (Table 2). Fourteen of these were identified via blind resequencing of 1-kb, primarily noncoding regions of the D. melanogaster genome for the founder lines (this study and Macdonald and Long 2005). The remaining 10 markers were taken from resequencing data generated by others (Harr et al. 2002; Orengo and Aguadé 2004; DuMont and Aquadro 2005; Ometto et al. 2005). Intermarker recombination fractions for the experimental panels of flies are estimated from the genotyping data (described below). To place markers to the standard D. melanogaster genetic map we extracted from FlyBase (http://www.FlyBase.org) all those genes with a known physical position (in base pairs), and an estimated genetic position (in centimorgans). For each chromosome we plotted base pairs against centimorgans, and using the ksmooth function in the statistical programming language R (http://www.R-project.org) generated a smoothed curve through the data. For each marker, using the smoothed curve we estimated the genetic position (on the standard map) from the known physical position. These marker positions were subsequently used as anchors to estimate QTL positions on the standard D. melanogaster genetic and physical maps.
TABLE 2.
Details of the PCR amplicons used for genotyping
Genotyping:
Following phenotyping, experimental flies were deposited directly into 96-well plates on ice. We also collected 12 female flies from each of the 16 lines used to found the synthetic populations and multiple females from the sequenced strain. Subsequently, DNA from all flies was extracted in 96-well format (described in Gruber et al. 2007), and diluted DNA was aliquoted into 384-well plates and dried down in preparation for PCR. Together with blanks and various control samples, the coarse-mapping DNA panel consisted of 12 384-well plates, and the fine-mapping DNA panel consisted of 6 384-well plates. The entire coarse-mapping (fine-mapping) DNA panel was PCR amplified for the appropriate 12 (17) 1-kb amplicons in standard 5-μl PCR reactions. These PCR products were pooled in groups of two or three and used as a template for multiplex genotyping of SNPs contained within the fragments. Macdonald et al. (2005b) provides full details of this genotyping methodology.
The genotype data were processed using custom routines implemented in the statistical programming language R (http://www.R-project.org). First, we ensured that none of the SNPs genotyped segregated within the sequenced strain. Next, for each of the experimental flies we found the maternally inherited haplotype from the synthetic recombinant population. No change to the genotyping data from males is required, since all SNPs are X linked and Drosophila males have a hemizygous X. Experimental females have both a paternally inherited sequenced-strain X and a maternally inherited recombinant X. Because the sequenced strain is isogenic, the haplotype of the recombinant chromosome for each experimental female can be obtained by subtraction. For example, if the sequenced strain is abc, and we observe an experimental female genotype of aaBbCc, we know the inherited recombinant maternal chromosome is aBC. Thus, the maternally inherited recombinant haplotype can always be unambiguously defined.
The next step is to transform the haplotype data from the experimental individuals into a three dimensional matrix, G, where Gimk takes a binary value describing whether the observed maternal haplotype for individual i at marker m is consistent with the haplotype of founder k (k = 1, 2, …, 8); i.e., Gimk = 1 if the haplotype is compatible with that of the _k_th founder, and Gimk = 0 otherwise. Using the data from the 12 females genotyped for each founder line, we can list all of the multilocus haplotypes present for each founder and marker. Generally the founder lines are completely inbred, although there is some residual heterozygosity and more than one haplotype can be present within a line at a given marker. Also, founders are not always unique at every marker, and missing data are unavoidable with a project on this scale. Typically we find that markers are not fully informative and fail to distinguish all eight possible founder chromosomes for one or both synthetic populations. Each test individual/marker combination is coded as follows. Consider that the marker haplotypes for the eight founder lines are (1) ABC, (2) AbC, (3) ABc, (4) aBC, (5) AbC, (6) aBc, (7) ABC, and (8) Abc (in this example founders 1 and 7, and 2 and 5, are indistinguishable). If an experimental fly is aBc it must have the chromosome from founder 6 and is coded as 2(6−1) = 32. Alternatively, if the experimental individual is found to be ABC it might equally be derived from founders 1 or 7 and is assigned the value 2(1−1) + 2(7−1) = 65. Finally, a haplotype with missing data, ?B?, is compatible with founders 1, 3, 4, 6, and 7, and is assigned the value 2(1−1) + 2(3−1) + 2(4−1) + 2(6−1) + 2(7−1) = 109. By extension it is obvious that an experimental individual will be assigned a value of 1–255 for each marker, precisely defining the potential ancestry of the chromosomal segment. Using this coding scheme the raw three-dimensional data matrix, G, can be alternatively represented as a two-dimensional matrix, C, with Cij (the code for the _i_th individual at the _j_th position) taking an integer value between 1 and 255. We provide C, along with the corresponding bristle phenotypes, as supplemental material on the Genetics website (http://www.genetics.org/supplemental).
Statistical platform:
Data analysis consists of three steps, and the statistical machinery is implemented as series of functions in the statistical programming language R, expanding on the R/qtl package (http://www.rqtl.org; Broman et al. 2003). First, we consider a 1-cM grid along the chromosome and calculate the probability pijk that individual i carries founder allele k at position j, given the available genotype data, G. This is done using the standard hidden Markov model (HMM) technology of Baum et al. (1970), first applied in a genetics context by Lander and Green (1987) and adapted to allow for genotyping errors by Lincoln and Lander (1992). The observed data, G, are viewed as marker “phenotypes” that are possibly subject to error. The true underlying genotypes are assumed to follow a Markov chain, with each of the eight possible founder alleles being equally likely. For any two positions, the probability of a transition from founder allele _k_1 to founder allele _k_2 is r/7 if _k_1 ≠ _k_2 (recombination in the interval) and 1 − r if k_1 = k_2 (no recombination). Here, r is analogous to the recombination fraction for the interval, but represents recombination events from multiple generations and is estimated from the data. The observed marker genotype at a locus is assumed to be compatible with the true underlying genotype with probability 1 − ε, where ε is the genotyping error rate. A readable tutorial on implementing the HMM is provided by Broman (2006). The information content of the available marker genotype data may be measured by the proportion of missing information, which we take to be Hj = Σ_i Σ_k pijk log pijk/n log 8, where n is the number of individuals.
The second step is to fit a model relating phenotype to genotype. Initially, at the _j_th position we calculate the average phenotype by founder genotype (with the _i_th individual's phenotypic contribution to the mean of the _k_th founder chromosome weighted by the pij's) and sort these eight means from smallest to largest. We then fit a maximum of seven linear models to the data at each position: model 1 tests the difference between founder material with the smallest mean against all others, model 2 tests the difference between the pair of founders with the two smallest means against all others, and so on. For each model, we create a regressor variable for individual i at position j that is the sum of the elements of pij associated with these contrasts. The test is accomplished by regressing phenotypes on this regressor variable, with the additional constraint that the sum (over individuals) of the regressor variable must be >50. The resulting LOD score at position j uses a model of all eight founders having the same mean as a null and accepts the above contrast with the maximal likelihood as the alternate. Implicit in this analysis is the idea that there is a single biallelic QTL at some position on the chromosome that is segregating among the eight founder chromosomes and that some optimal partitioning of the founders can be used to identify that QTL. We note that the LOD scores resulting from our approach are strongly correlated with the _F_-statistic obtained from a multiple regression of phenotype onto the pj's at each position over the X chromosome. In the simulations the correlation between the LOD scores and _F_-statistics is generally >99%, and across all of the experimental panels (both sexes, both traits, both synthetic populations, and both the coarse and fine mapping) the correlation is 97.2%.
The third step of the data analysis is then to estimate the probability that each of the eight founder chromosomes harbors the high, or Q, QTL allele at position j (pQk's) for the model implied by the best partitioning of the founders. This is simply the probability of observing each of the eight founder means given the estimated slope and intercept of that model, conditional on each founder harboring the high QTL. After all three steps are complete we obtain LOD scores and phenotypic effects at J positions in the genome and J corresponding pQ's. Our conservative estimate of the frequency of a QTL located at a local maximum in the LOD profile is the number of elements of pQ ≥ 0.95 divided by the number of elements of pQ ≥ 0.95 or pQ ≤ 0.05 (i.e., we ignore founder lines that do not allow for an accurate estimation of “phase”).
Variation due to QTL:
Estimates of QTL effect and frequency can be derived from eight-way synthetic populations, and we can use these values to estimate the fraction of segregating variation, _V_a, due to identified QTL. We can estimate this both in our (effectively haploid) mapping population as _V_a = _pq_α2, and in a natural, outbred diploid population under additivity as _V_a = 2_pq_α2, where p and q are the allele frequencies and α is the effect of the QTL (Falconer and Mackay 1996, p. 126). In both our mapping population and a natural population, male QTL on the hemizygous X chromosome have _V_a = _pq_α2. We can place a 95% confidence interval on _V_a using Monte Carlo simulation. For α this is accomplished by drawing 10,000 random samples from a normal distribution with mean equal to the observed effect of the QTL and standard deviation equal to the observed standard error on the QTL effect. We estimate the allele frequency, p, differently depending on whether we wish to estimate the variance due to the QTL within our mapping population, or in a natural population. Allele frequency, p, in the mapping population is simply the observed QTL frequency. To estimate allele frequencies of mapped factors in natural populations we draw samples from an allele frequency distribution, whose derivation is conditional on the fact that we observe i copies of a QTL allele among N founder chromosomes. Under neutrality the distribution of allele frequencies is described by Wright–Fisher sampling as
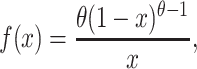
where θ is the per-site heterozygosity under neutrality. The probability of drawing i copies of an allele in a sample of size N is described by a binomial distribution,

where 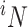 is “N choose i.” By Bayes' theorem,
is “N choose i.” By Bayes' theorem,
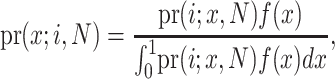
which after some simplification (and recognizing a Beta integral) reduces to
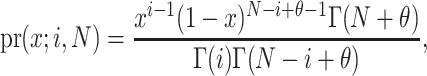
where 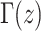 is the gamma integral. Two properties of pr(x;i,N) are noteworthy. First, typically θ ≪ 1, and therefore θ has little effect on the shape of pr(x;i,N), and second, for large N, and i not close to one or N, pr(x;i,N) is approximately a binomial distribution, and the “prior” assumption of neutrality has little weight. In a natural population, for any given QTL, we assume D. melanogaster θ = 0.006 (averaged over 98 loci collated in Presgraves 2005) and use “rejection sampling” (Press et al. 1996) to draw 10,000 random deviates from pr(x;i,N) to represent allele frequencies. For each pair of simulated α /p estimates we calculate _V_a as above. The 95% confidence interval on _V_a is taken as the 25th and 975th elements of the sorted vector of _V_a estimates. These values can be transformed to a percentage of the total bristle number variation explained by the QTL by dividing by the observed phenotypic variance.
is the gamma integral. Two properties of pr(x;i,N) are noteworthy. First, typically θ ≪ 1, and therefore θ has little effect on the shape of pr(x;i,N), and second, for large N, and i not close to one or N, pr(x;i,N) is approximately a binomial distribution, and the “prior” assumption of neutrality has little weight. In a natural population, for any given QTL, we assume D. melanogaster θ = 0.006 (averaged over 98 loci collated in Presgraves 2005) and use “rejection sampling” (Press et al. 1996) to draw 10,000 random deviates from pr(x;i,N) to represent allele frequencies. For each pair of simulated α /p estimates we calculate _V_a as above. The 95% confidence interval on _V_a is taken as the 25th and 975th elements of the sorted vector of _V_a estimates. These values can be transformed to a percentage of the total bristle number variation explained by the QTL by dividing by the observed phenotypic variance.
RESULTS
We develop synthetic recombinant populations, each derived from eight inbred lines of D. melanogaster allowed to recombine at large population size for many generations. We use these populations to map bristle number QTL segregating on the D. melanogaster X chromosome. The mapping strategy we employ relies on the ability to take a recombinant individual, and specify which of the eight founders contributed each segment of the genome. Since we require haplotypic information for the recombinant chromosomes, all experimental individuals are the progeny of crosses between recombinant females and males from the isogenic sequenced strain of D. melanogaster (Figure 2). Thus, haplotypes can be defined unambiguously. The molecular markers we employed were 1-kb PCR fragments within which we genotyped 3–6 SNPs (Table 2). The SNPs were genotyped not only in the experimental individuals, but also in several individuals from each of the 16 founder lines used to initiate the synthetic populations. These procedures allowed us to define, for each experimental recombinant individual, the probability that each marked segment of the chromosome was contributed by each of the eight possible founder lines. Together with the phenotypic scores, this information allows us to map QTL, and obtain joint estimates of QTL effect and frequency.
Simulations:
We carried out simulations to assess our ability to accurately map QTL and jointly estimate their effect and frequency, and used parameters (chromosome size, marker density, marker informativeness) that realistically mimic the experimental data we collected. We sampled 1152 recombinants from an eight-way synthetic population 16 generations after founding to simulate the chromosome scan, and 56 generations after founding to simulate fine mapping. In each case we assume recombination occurs only in females. At the test generation (G16 or G56) recombinant individuals were created by concatenating chromosomal fragments derived from each of the eight founders with equal probability. Fragment lengths were drawn from an exponential distribution with mean 100/(16/2) or 100/(56/2) cM for the coarse and fine mapping, respectively. For the coarse mapping we simulated 12 partially informative markers equally spaced along a 66 cM chromosome and 5% missing data. For the fine-mapping simulation the 12 markers were placed in a more focused 10 cM region. For simplicity we assume the same level of informativeness at each marker, with four segregating haplotypes that group the founder lines as follows: haplotype 1 (three founders), haplotype 2 (two founders), haplotype 3 (two founders), haplotype 4 (single founder). The separation of founders into different haplotypes was random across markers. Finally, we place a biallelic QTL accounting for 5% of the total phenotypic variation at a random position within the mapping region, with the number of founders having the Q allele varied between one and four out of eight. Five-hundred realizations of each simulation were performed.
The probability of observing a peak in the LOD score >4 is ≥99%, with an expected maximum LOD score of ∼9.4 and ∼11.4 for the coarse- and fine-mapping simulations, respectively. For those peaks associated with a LOD score >4, a 2.5-LOD drop from the maximum includes the simulated position of the QTL >99% of the time. On average, a 2.5-LOD drop maps a significant QTL to a 13.2 cM window with a standard deviation of 6.1 cM (coarse mapping) or a 2.3 cM window with a standard deviation of 0.9 cM (fine mapping). When the LOD score is >4, in no case do we incorrectly infer the “phase” of the QTL, and phase is assigned for an average of 7.8/8 founders. The simulated frequency of the QTL does not appear to affect the probability of inferring the allelic state of the QTL, the power to map a QTL, the average maximum LOD score, or the accuracy in localizing QTL. This is perhaps not surprising given that the simulations hold the proportion of variance attributable to the QTL constant at 5% (Long and Langley 1999). With the same simulations, but no QTL, the false positive rate at a LOD of four is 2 and 1.6% for the coarse- and fine-mapping simulations, respectively. With our current recombinant panel, marker density, and marker informativeness we can map QTL to the eight founder chromosomes in each of the synthetic recombinant populations. Additional simulations suggest that reducing sample size, marker density, or marker informativeness is detrimental.
Marker informativeness:
Ideally, every marker (a 1-kb fragment genotyped for several SNPs) would completely distinguish among all eight founders in both the pA and pB synthetic populations. In our experimental data this is typically not the case and markers are not fully informative. In fact, it is frequently not possible to distinguish among the eight founders within either population based on the DNA sequence of the entire 1-kb marker amplicon. For those 11 markers for which we had access to sequence from all founders, the average number of distinguishable haplotypes is 6.5/8. This is likely an overestimate of the number of distinguishable founder haplotypes for any arbitrary 1-kb region of the Drosophila genome, as a number of potential markers were sequenced and discarded due to a lack of polymorphism (data not shown). As with any “haplotype tagging” strategy, the SNP genotyping approach we employ further reduces the number of distinguishable haplotypes, both because we do not genotype all available SNPs, and because a proportion of the developed genotyping assays failed (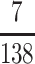 , or 5.1%). Over the 24 independent markers examined in this study, we successfully genotyped 4.5 SNPs per marker on average, and the mean number of unique haplotypes identified per population per marker is 4.5 (pA = 4.4, pB = 4.6). Markers used solely for fine mapping were slightly more informative (5.0 unique haplotypes per marker on average) than those used solely for coarse mapping (4.1 haplotypes). The increase in informativeness for the fine-mapping markers is due to those used to map the region in the middle of the X chromosome (_X-_middle markers average 5.4 haplotypes, while _X-_tip markers average 4.1). Contrary to our intuition the number of distinguishable haplotypes in the founders was not strongly a function of how SNPs were ascertained: Markers developed by sequencing the actual founders, where SNPs were chosen to maximize within-marker haplotype diversity, yielded 4.7 haplotypes per population on average. Markers harvested from published sequencing surveys, where SNPs were simply chosen to have high frequency and little LD with other SNPs in the same fragment, showed similar haplotype diversity in our founders (4.3 haplotypes per population).
, or 5.1%). Over the 24 independent markers examined in this study, we successfully genotyped 4.5 SNPs per marker on average, and the mean number of unique haplotypes identified per population per marker is 4.5 (pA = 4.4, pB = 4.6). Markers used solely for fine mapping were slightly more informative (5.0 unique haplotypes per marker on average) than those used solely for coarse mapping (4.1 haplotypes). The increase in informativeness for the fine-mapping markers is due to those used to map the region in the middle of the X chromosome (_X-_middle markers average 5.4 haplotypes, while _X-_tip markers average 4.1). Contrary to our intuition the number of distinguishable haplotypes in the founders was not strongly a function of how SNPs were ascertained: Markers developed by sequencing the actual founders, where SNPs were chosen to maximize within-marker haplotype diversity, yielded 4.7 haplotypes per population on average. Markers harvested from published sequencing surveys, where SNPs were simply chosen to have high frequency and little LD with other SNPs in the same fragment, showed similar haplotype diversity in our founders (4.3 haplotypes per population).
The inbred founder lines used to derive the synthetic populations are not isogenic, and 28/384 (7.3%) independent marker/founder combinations show heterozygosity. The heterozygosity is not localized to any particular marker as 17/24 markers show at least one heterozygous line. Half of the 16 founders show no evidence for heterozygosity, while 3 of the lines (A1, B3, and B7) are heterozygous at multiple amplicons. This trio of lines collectively contributes to 23/28 (82.1%) of the heterozygous marker/founder combinations, implying they are less well inbred than the remaining 13 lines. It is of interest that all 16 founder lines were maintained in stock centers at small effective population sizes for >40 years (without being contaminated by _P_-element-harboring flies). The observation that these lines are not completely homozygous suggests a relatively high rate of tightly linked deleterious alleles in trans.
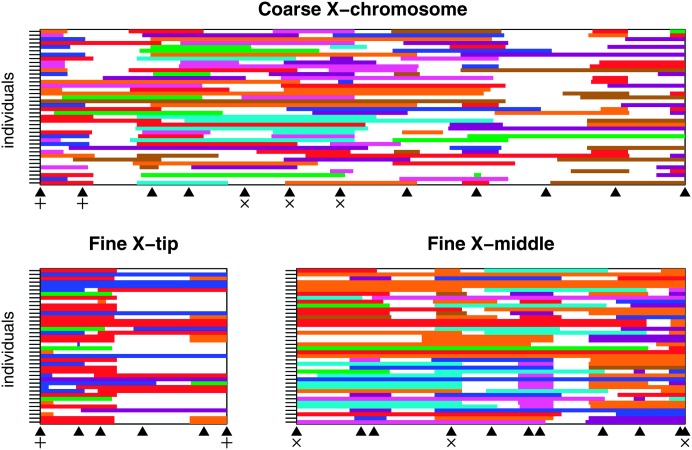
The HMM employs the genotype data to infer (for every individual and every position) the probability that the chromosomal segment is derived from each of the eight founders. Founder assignment becomes more accurate as the information level in the genotype data increases. We can visualize spatial variation in the information level by color coding (by founder of origin) those chromosomal segments inferred to come from a single founder with a probability >75%. Figure 3 depicts this information for 40 typical males from the pBr1 population. Colored blocks represent highly likely founders, and the information content at any position can be loosely assessed by the amount of white space (i.e., where the probability was <0.75 for all eight founders). For the coarse-mapping scan, information is generally high at the markers, with the obvious exception of marker or.84 (third marker from the right), where only two haplotypes are distinguishable among the eight pB founders. Overall, there appears to be greater information in the fine-mapping population. One exception is the region around marker no.01 (fourth from the left) at the tip of X chromosome. This is likely due to its low marker informativeness (just three haplotypes are distinguishable at no.01 in pB), and because it is relatively distant from either of the flanking markers. We note that the relative size of nonrecombinant fragments is consistent with their expectation given the number of generations the populations experienced recombination/drift. Finally, with reduced information and/or a poorly performing HMM we may expect the most likely founder to “flip-flop” frequently along the chromosome, and this does not appear generally the case.
Figure 3.—
Visual representation of genotyping information. Each row of each plot represents a single experimental male, for which the X chromosome is derived from the pBr1 synthetic recombinant population. The top plot shows 40 flies from the coarse-mapping sample for the entire X chromosome, and the bottom two plots show 40 flies from the two small fine-mapped regions of the X chromosome. For each male, every 1 cM (on the expanded genetic map) across the mapped region we examine the probability that the segment of chromosome is derived from each of the eight possible founder lines. If the probability for any one founder is >0.75, the position is colored according to the founder (colors are as in Figures 1 and 2); otherwise the position is white. Marker positions are shown beneath each plot as solid triangles. Markers used for both the coarse mapping and the _X_-tip fine mapping are indicated with plus symbols (+), while markers used for both coarse mapping and the _X_-middle fine mapping are indicated with cross symbols (×).
We can examine marker informativeness more quantitatively using the measure H to estimate the proportion of missing genotypic information (H = 0, complete information; H = 1, no information). Figure 4, E and F, and Figure 5, E and F, present the amount of missing information across the three mapped regions (the entire X chromosome for the coarse-mapping scan, and two smaller regions of the X for the fine-mapping scans). It is easy to see that at the markers themselves the amount of missing information is lower than between the markers. The value of H, averaging over individuals for all sites, from both sexes from both synthetic populations is 0.374 (coarse), 0.346 (_X_-tip fine), and 0.187 (_X_-middle fine). The _X_-middle fine-mapping panel data has greater information content, both because the markers themselves are more informative (see above), and also because this region has the highest marker density relative to the recombination distance. For the _X_-middle fine-mapping region markers are placed every 21.2 cM on average (on the expanded scale), while for the _X_-tip fine region markers are 25.2 cM apart, and for the entire X in the coarse-mapping experiment markers are 39.4 cM apart.
Figure 4.—
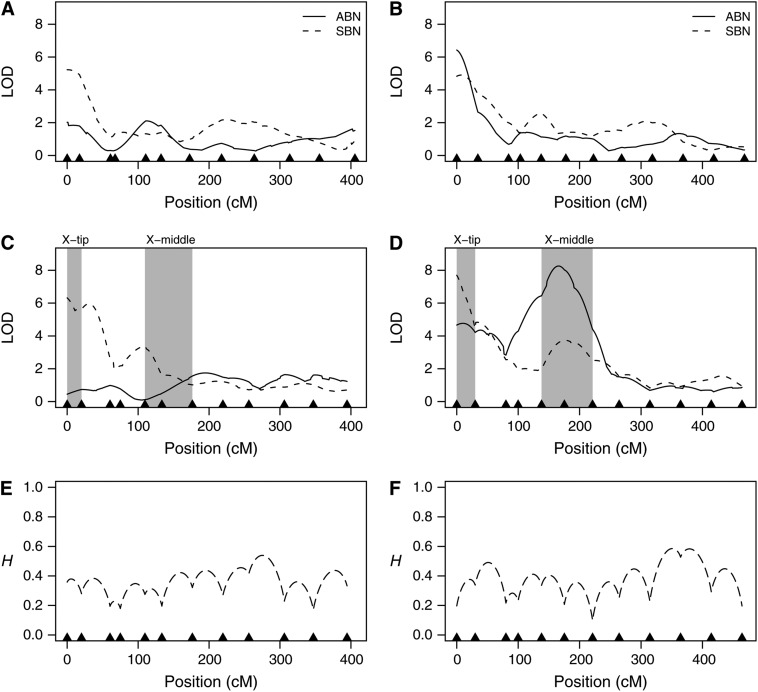
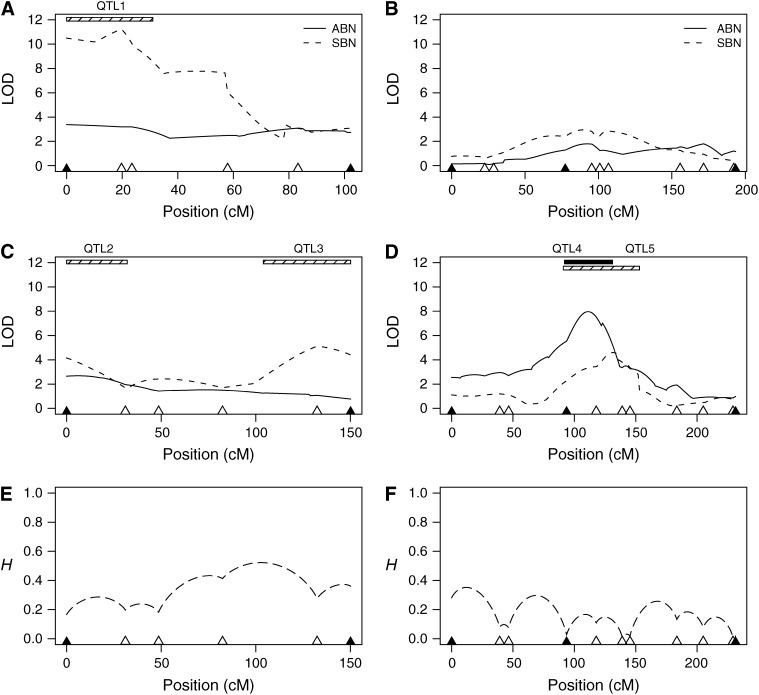
Coarse-mapping bristle number across the X chromosome. pAr1, experimental flies have recombinant chromosomes derived from synthetic population pAr1. pBr1+2, experimental flies with recombinant chromosomes derived from synthetic populations pBr1 or pBr2 were pooled prior to analysis. (A) pAr1 female LOD; (B) pBr1+2 female LOD; (C) pAr1 male LOD; (D) pBr1+2 male LOD; (E) genotype information (pAr1 male); (F) genotype information (pBr1+2 male). (A–D) Likelihood profiles. Each curve shows the likelihood that a given region of the chromosome harbors a QTL for bristle number (solid curves, ABN; dashed curves, SBN). Marker positions are shown as solid triangles along the _x_-axis. LOD scores are plotted against position (in centimorgans) on the expanded genetic map. The expansion is due to the large number of meiotic recombination events the synthetic population was subjected to prior to mapping. Note that the genetic map positions are not identical across the four plots. Vertical shaded bars represent regions used for fine mapping (Figure 5). (E and F) Missing genotypic information. The proportion of missing genotypic information, H, is plotted against the expanded genetic map position. H = 0, no missing information; H = 1, no information; described fully in the materials and methods. For population pAr1 (E) and the pooled pBr1+2 population (F), missing information is provided only for the experimental males. Missing data from females are very similar.
Figure 5.—
Fine-mapping bristle number in two small regions of the X chromosome. pAr1 (pBr1) indicates the synthetic population from which the recombinant chromosomes of the experimental flies are derived. _X_-tip and _X_-middle refer to the regions of the X chromosome showing evidence for a QTL in the coarse-mapping study and represent those regions of the chromosome shaded in Figure 4. (A) _X_-tip, pAr1 male LOD; (B) _X_-middle, pAr1 male LOD; (C) _X_-tip, pBr1 male LOD; (D) _X_-middle, pBr1 male LOD; (E) _X_-tip, genotype information (pBr1); (F) _X_-middle, genotype information (pBr1). (A–D) Likelihood profiles. Each curve shows the likelihood that a given region of the chromosome harbors a QTL for bristle number (solid curves, ABN; dashed curves, SBN). Marker positions are shown as triangles along the _x_-axis (solid triangles, markers used in coarse mapping [Figure 4]; open triangles, markers used only for fine mapping). LOD scores are plotted against position (in centimorgans) on an expanded genetic map. Note that the genetic map positions are not identical across the four plots. Bars at the top of the plots represent 2.5-LOD drop intervals across five fine-mapped QTL (solid bar, QTL for ABN; hatched bar, QTL for SBN). (E and F) Missing genotypic information. The proportion of missing genotypic information, H, is plotted against the expanded genetic map position. H = 0, no missing information; H = 1, no information—described fully in the materials and methods. For the _X_-tip region (E) and the _X_-middle region (F), missing information is provided only for flies derived from population pBr1. Missing data from pAr1 flies are very similar.
Phenotypes of synthetic populations:
We scored two bristle phenotypes per experimental fly—abdominal bristle number (ABN) and sternopleural bristle number (SBN). Within each population (pAr1, pBr1, and pBr2), mapping generation (coarse and fine mapping), sex, and phenotype the bristle count distributions are approximately normal, similar to those measured in large outbred cohorts of flies sampled directly from nature (Genissel et al. 2004; Macdonald and Long 2004; Macdonald et al. 2005a). Table 3 presents phenotype means and standard deviations for all sets of flies examined in this study. We note that panels pBr1 and pBr2 are very similar for both sexes and bristle counts, and that flies from pAr1 have more abdominal and sternopleural bristles than flies from either pB population. On average, pAr1 flies have 0.5–1.1 more bristles than pB flies (Table 3). A difference in body size between the pA and pB panels may contribute to this pattern. The within-population phenotype means, and more importantly variances, do not change over time, and values are consistent between the coarse- and fine-mapping studies. Finally, we note that the within-panel/sex/trait phenotypic variances we observe are lower than variances observed for the same traits in two wild-caught D. melanogaster cohorts (Genissel et al. 2004; Macdonald and Long 2004; Macdonald et al. 2005a). This is presumably because each of the phenotyped flies in this study harbors a common set of isogenic, paternally derived chromosomes, and flies were reared under a controlled laboratory environment.
TABLE 3.
Bristle number variation in synthetic populations
| Bristle no. mean (SD)a | ||||
|---|---|---|---|---|
| Sex | Traitb | Panel | Coarse mappingc | Fine mappingc |
| F | ABN | pAr1 | 20.6 (1.82) | — |
| F | ABN | pBr1 | 19.8 (1.87) | — |
| F | ABN | pBr2 | 20.0 (1.78) | — |
| F | SBN | pAr1 | 19.9 (1.98) | — |
| F | SBN | pBr1 | 19.0 (1.75) | — |
| F | SBN | pBr2 | 19.4 (1.85) | — |
| M | ABN | pAr1 | 18.4 (1.79) | 18.6 (1.78) |
| M | ABN | pBr1 | 17.4 (1.73) | 17.5 (1.74) |
| M | ABN | pBr2 | 17.4 (1.75) | — |
| M | SBN | pAr1 | 19.2 (2.07) | 19.4 (2.06) |
| M | SBN | pBr1 | 18.1 (1.65) | 18.2 (1.65) |
| M | SBN | pBr2 | 18.4 (1.78) | — |
Position and effect of _X_-linked bristle number QTL:
Coarse scan of the X chromosome:
Initially we conducted a coarse scan of the entire X chromosome for QTL for two bristle traits for both sexes. For the coarse mapping we collected ∼500 experimental flies of each sex from the populations pAr1, pBr1, and pBr2 (population pAr2 became contaminated during maintenance and was destroyed). Experimental individuals from the replicate populations pBr1 and pBr2 were pooled, and we refer to this pooled sample as pBr1+2. Comparison of the data from pBr1 and pBr2 alone with that from the pooled sample does not reveal any obvious inconsistencies. Since the sample size of population pAr1 is around half the size used in our simulations, we likely have reduced power to detect QTL in the pAr1 coarse-mapping sample. We only consider QTL to be present when the peak in the likelihood profile is >4-LOD.
The likelihood profiles for the coarse-mapping samples shown in Figure 4 (A–D) reveal the existence of QTL for bristle number at the very tip of the X chromosome in both females and males. We find no evidence for bristle number QTL anywhere else on the X for females, but do identify a male-specific QTL for ABN in the middle of the X chromosome (Figure 4D). Details of all QTL identified in the coarse-mapping study are presented in Table 4. For both populations, pAr1 and pBr1+2, and for both sexes QTL for SBN were detected at the tip of the X chromosome with LOD scores between 4.9 and 7.7. The effects of the pBr1+2 _X_-tip SBN QTL are lower than those detected in pAr1 (0.70 and 0.73 in pBr1+2 vs. 1.36 and 1.42 in pAr1), which may due to the smaller pAr1 sample leading to less robust estimates of the genetic effect. A single _X_-tip ABN QTL was identified in females of the pBr1+2 sample (Figure 4B). Figure 4D does show a peak at the tip of the X for ABN in pBr1+2 males, but the 2.5-LOD drop for this peak overlaps the larger ABN QTL in the middle of the chromosome, thus we do not consider it an independent QTL. All five _X_-tip QTL map somewhere between the distal end of the X chromosome and band 5B6 (Table 4). Our identification of five QTL mapping to the very tip of the X chromosome replicates the well-documented effect of this region on bristle number variation in D. melanogaster (Long et al. 1995; Gurganus et al. 1998, 1999; Nuzhdin et al. 1999; Dilda and Mackay 2002).
TABLE 4.
Coarse-mapped X-linked bristle number QTL
| QTL position (expanded cM)c | 2.5-LOD dropa | ||||||
|---|---|---|---|---|---|---|---|
| Sex | Traitb | Panel | LOD | cM | Cytology | Effect (SE)d | |
| F | ABN | pBr1+2 | 6.4 | 0.0 | <0.4–3.3 | <1F1–3E1 | −0.70 (0.129) |
| F | SBN | pAr1 | 5.2 | 1.0 | <0.4–9.7 | <1F1–4D4 | −1.36 (0.265) |
| F | SBN | pBr1+2 | 4.9 | 7.0 | <0.4–12.6 | <1F1–5A2 | −0.70 (0.143) |
| M | ABN | pBr1+2 | 8.3 | 166.0 | 18.7–27.7 | 6F1–8E1 | −0.91 (0.145) |
| M | SBN | pAr1 | 6.3 | 0.0 | <0.4–13.5 | <1F1–5B6 | −1.42 (0.266) |
| M | SBN | pBr1+2 | 7.7 | 0.0 | <0.4–3.6 | <1F1–3E5 | −0.73 (0.121) |
| M | SBN | pBr1+2 | 3.7e | 177.0 | <0.4–41.1 | <1F1–11D3 | −0.58 (0.143) |
The largest bristle number QTL identified in the coarse-mapping scan is for male ABN in pBr1+2 (Table 4, Figure 4D). This QTL has a LOD peak of 8.3, an effect of 0.91 bristles, and was resolved to a 9 cM window (on the nonexpanded D. melanogaster recombination map) in the middle of the X chromosome between cytological bands 6F1–8E1. The peak is also evident in the separate analyses of populations pBr1 and pBr2 (data not shown). There is no evidence that a corresponding QTL exists in pAr1 males, despite largely equivalent genotypic information across the two panels at the QTL position (Figure 4, compare E and F), suggesting fairly strongly that this QTL segregates only in the pB populations. One caveat is that the sample size for the pAr1 population was low.
The coarse-mapped QTL are resolved to intervals averaging 8.3 cM (∼4 Mb). We elected to fine map two interesting QTL regions (Figure 4, C and D) in males only from the populations pAr1 and pBr1. Figure 5 (A–D) presents the likelihood profiles for the two fine mapped regions (_X_-tip and _X_-middle) for the populations pAr1 and pBr1, and Table 5 gives details of the fine-mapped QTL. Overall, there is remarkable concordance between the coarse- and fine-mapped QTL (compare Figure 4, C–D, with Figure 5, A–D).
TABLE 5.
Fine-mapped X-linked male bristle number QTL
| QTL position (expanded cM)c | 2.5-LOD dropd | |||||||
|---|---|---|---|---|---|---|---|---|
| QTLa | Region | Traitb | Panel | LOD | cM | Cytology | Effect (SE)e | |
| 1 | Tip | SBN | pAr1 | 11.3 | 19.8 | <0.4–1.7 | <1F1–3C3 | −1.06 (0.144) |
| 2 | Tip | SBN | pBr1 | 4.2 | 0.0 | <0.4–1.4 | <1F1–3B3 | −0.51 (0.118) |
| 3 | Tip | SBN | pBr1 | 5.1 | 133.0 | 2.4–4.2 < | 3D2–3F3 < | −0.68 (0.138) |
| 4 | Middle | ABN | pBr1 | 8.0 | 111.0 | 24.0–24.9 | 7F10–8B2 | −0.97 (0.160) |
| 5 | Middle | SBN | pBrl | 4.6 | 131.0 | 24.0–25.7 | 7F8–8C3 | −1.31 (0.292) |
X-tip fine mapping:
The QTL for male SBN coarse mapped to the tip of the X chromosome in population pAr1 replicates in the fine-mapping experiment (QTL1 in Figure 5A), and the interval harboring the QTL was reduced from 13.5 to 1.7 cM (on the nonexpanded Drosophila melanogaster recombination map). The effect of the QTL in the coarse and fine mapping alters slightly from 1.42 bristles to 1.06 bristles, respectively. The latter is likely a more robust estimate of the effect, as the sample size of the fine-mapping panel was higher, and the extra generations of recombination have stretched the genetic map, separating the QTL from any linked factors. The coarse-mapped pBr1+2 male SBN _X_-tip QTL splits into two on fine mapping in population pBr1 (QTL2 and QTL3 in Figure 5C), each having an effect similar to that estimated for the initial coarse-mapped QTL (coarse = 0.73, fine QTL2 = 0.51, and fine QTL3 = 0.68). These two QTL barely achieve the 4-LOD threshold required (QTL2 = 4.2 LOD, QTL3 = 5.1 LOD), but since the QTL intervals do not overlap, it is probable that two unlinked SBN QTL do exist at the tip of the X in population pBr1. It is not clear whether either pBr1 QTL2 or QTL3 correspond to pAr1 QTL1. We note that there is no evidence from the fine mapping for an _X_-tip male ABN QTL in either the pA or pB populations (Figure 5, A and C). This supports our earlier assertion that in the coarse mapping of pBr1+2 the peak at the tip of the chromosome for male ABN is spurious.
The two best bristle number candidate genes in the fine-mapped _X_-tip region are the _achaete_-scute complex, ASC, at cytological position 1A6, and Notch at 3C7-3C9. In Figure 5 (A and C) ASC is located distal to the leftmost marker (or.05), while the fourth marker from the left (no.01) is at Notch. Thus, our data is compatible with the notion that variation at ASC may be responsible for QTL1 and QTL2. It does not seem likely that variation at Notch contributes to QTL3, as the LOD at Notch is 3.4 less than that at QTL3 in population pBr1. However, we cannot rule out the possibility that Notch contributes to segregating variation for SBN in males as the genotype information around Notch in the _X_-tip region is somewhat low (Figures 3 and 5E), and the LOD score at Notch for SBN in pAr1 males is high (LOD = 6.0, Figure 5A). The broad QTL1 peak in pAr1 males may actually represent two QTL that we have insufficient power to resolve. Since we did not fine map the QTL identified at the tip of the X chromosome in females, we are unable to suggest whether ASC or Notch harbor factors affecting female bristle number.
X-middle fine mapping:
The coarse mapping revealed a strong QTL for male ABN in the middle of the X chromosome in the pBr1+2 population and a suggestive peak (LOD < 4) for male SBN in a similar position (Figure 4D). The fine-mapping experiment almost perfectly replicated these observations (Figure 5, B and D), aside from a slight shifting of the QTL maxima relative to the flanking markers (compare Figures 4D and 5D). The pair of _X_-middle fine-mapped QTL were resolved to intervals of 0.9 cM (QTL4) and 1.7 cM (QTL5), down from 9 and 41.1 cM in the coarse mapping. The effect of QTL4 is maintained between the coarse-mapping (effect = 0.91) and fine mapping (effect = 0.97), while the effect of QTL5 increases (coarse-mapping effect = 0.58, fine-mapping effect = 1.31). We looked for evidence that either of these _X_-middle QTL had been identified in other mapping studies of Drosophila bristle number variation. We found no evidence of similarly positioned bristle number QTL in Long et al. (1995), Gurganus et al. (1998), or Dilda and Mackay (2002), and evidence only of weak QTL for female ABN in Gurganus et al. (1999; QTL between 5D and 8E) and Nuzhdin et al. (1999; QTL between 7D and 8E), suggesting we have identified novel QTL for both male ABN and male SBN. The intervals within which QTL4 and QTL5 reside are genetically short (0.9 and 1.7 cM, respectively), physically short (204-kb and 408-kb, respectively), and harbor few genes (QTL4 = 13 genes, QTL5 = 26 genes, of which 13 overlap with those under QTL4). None of the 26 genes would be considered a priori classic bristle number candidate genes: genes in both QTL4 and QTL5 intervals (oc, CG12772, CG11284, Ppt1, Ogg1, CG11294, Hexo2, CG2004, CG1785, l(1)G0020, CG1789, Lim1, and CG32710) and genes in only QTL5 interval (CG12075, Moe, CG1885, CG10648, e(r), CG15352, CG12660, CG3898, CG12661, rdgA, CG10962, CG12662, and mir-31b). Nevertheless, for two of the genes under both QTL4 and QTL5, oc and Lim1, there is reported evidence of bristle defects in mutant flies: oc (ocelliless) mutants affect interocellar, ocellar, and postvertical bristles (Royet and Finkelstein 1995), and Lim1 (Lim kinase) mutants affect sternopleural and vibrissae bristles (Pueyo et al. 2000). These two genes may be the best candidates underlying the two novel QTL we identify in the middle of the X chromosome.
Frequency of _X_-linked bristle number QTL:
Since the synthetic recombinant populations we employ are derived from multiple inbred lines, it is possible to estimate the phenotypic mean for each founder at every position along the chromosome. In turn—under the assumption that an identified QTL is biallelic—founders can be probabilistically assigned to “high” or “low” QTL allele classes. This permits an estimate of the frequency of the QTL. Figure 6 shows, for all five fine-mapped male bristle number QTL and the corresponding coarse-mapped regions, the estimated founder phenotype means, and the probable QTL allele present in each founder. Founder means appear to be estimated well, and as expected estimates are more robust when the sample size is larger: The errors bars are wider for the coarse-mapping pAr1 data (Figure 6A, left) than for the other data sets. Also, those sporadic cases of large standard errors, e.g., line B6 for fine mapping of QTL2 (Figure 6B), are due to a comparatively small number of experimental individuals consistent with harboring this founder chromosome at the QTL.
Figure 6.—
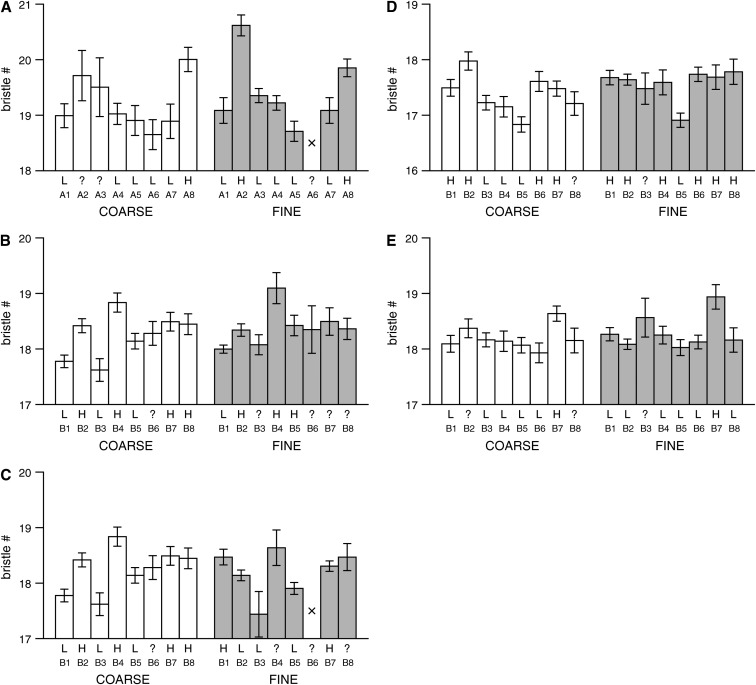
Estimated phenotypic means for each of the founder chromosomes at QTL. Each plot represents a single male bristle number QTL (see Figure 5 and Tables 4 and 5 for details) and shows the estimated phenotypic mean (standard error) at the QTL peak for each of the eight lines used to found the particular synthetic population. The line numbers, A1–A8 and B1–B8, refer to the lines described in Table 1. For comparison the means estimated at the QTL peak are presented for both the coarse- (open bars) and fine-mapping (shaded bars) panels. Bars are presented only if the estimated number of experimental individuals consistent with having a given founder chromosome is >10; otherwise a cross is plotted. Below the bars we give the most probable QTL allele harbored by the founder (L, low allele; H, high allele), under the assumption that the QTL is biallelic. If the founder cannot be confidently (probability > 0.95) assigned an allele, a ? is applied. (A) QTL1 for pA male SBN mapped to the _X_-tip region in population pAr1, (B) QTL2 for pB male SBN mapped to the _X_-tip region in pBr1+2 (coarse mapping) and pBr1 (fine mapping), and (C) QTL3 for pB male SBN mapped to the _X_-tip region in pBr1+2 (coarse mapping) and pBr1 (fine mapping). The coarse-mapping information for QTL2 and QTL3 is identical, as these are the two fine-mapped QTL we detected under a single coarse-mapped peak. (D) QTL4 for pB male ABN mapped to the _X_-middle region in pBr1+2 (coarse mapping) and pBr1 (fine mapping), and (E) QTL5 for pB male SBN mapped to the _X_-middle region in pBr1+2 (coarse mapping) and pBr1 (fine mapping).
There are marked similarities in the overall pattern of estimated founder phenotype means in the coarse- and fine-mapping experiments. For instance, for QTL1 (Figure 6A) the pair of lines with the highest phenotypic means (A2 and A8) are the same in both the coarse and fine mapping. The similarity in founder means for this QTL is particularly encouraging as the sample size, and hence the power, was low in the coarse mapping of population pAr1. The pair of fine-mapped QTL2 and QTL3 were resolved from a single coarse-mapped peak. For QTL2 the overall pattern of line means is concordant between coarse and fine mapping (Figure 6B), but this is not the case for QTL3 (Figure 6C). This observation likely reflects the separation of the two QTL – the founder means for these QTL need not necessarily recapitulate those of the coarse-mapped region. The three identified _X_-tip QTL may be somewhat common. From our analysis we estimate that the high QTL allele is present in  ,
,  , and
, and  founders for QTL1, QTL2, and QTL3, respectively (founders not assigned to either allelic class are ignored). An important caveat is that this analysis rests on the assumption that the QTL are biallelic, which is not necessarily supported for the _X_-tip QTL. For instance, while founders A2 and A8 are considered the “high” lines for QTL1 (Figure 6A), there is a difference of nearly 0.8 bristles in the estimated phenotype mean of this pair of lines, and the standard errors do not overlap. Also, the error bar around “low” line A5 does not overlap those of “low” lines A3 and A4. Similar inconsistencies within assigned biallelic classes for the other two fine-mapped _X_-tip QTL (QTL2 and QTL3) also do not give any strong indication that only two QTL alleles segregate (Figure 6, B and C).
founders for QTL1, QTL2, and QTL3, respectively (founders not assigned to either allelic class are ignored). An important caveat is that this analysis rests on the assumption that the QTL are biallelic, which is not necessarily supported for the _X_-tip QTL. For instance, while founders A2 and A8 are considered the “high” lines for QTL1 (Figure 6A), there is a difference of nearly 0.8 bristles in the estimated phenotype mean of this pair of lines, and the standard errors do not overlap. Also, the error bar around “low” line A5 does not overlap those of “low” lines A3 and A4. Similar inconsistencies within assigned biallelic classes for the other two fine-mapped _X_-tip QTL (QTL2 and QTL3) also do not give any strong indication that only two QTL alleles segregate (Figure 6, B and C).
Of all the QTL, QTL4 for male ABN was fine mapped to the smallest region (0.9 cM), and for this QTL the pattern of founder means alters between the coarse and fine mapping (Figure 6D). In the coarse mapping, while it is difficult to visualize two clear allelic categories, under the assumption that the QTL is indeed biallelic,  founders have the low allele. In contrast, the fine mapping quite clearly reveals two classes, with the low allele in
founders have the low allele. In contrast, the fine mapping quite clearly reveals two classes, with the low allele in  founders. One explanation for the change is that the information content of the genotype data is much greater in the _X_-middle fine mapping (H = 0.187) than in the coarse scan of the entire X chromosome (H = 0.374). The increased information may have led to greater accuracy in estimating the ancestry of recombinant chromosomal segments, and more accurate estimates of the founder means in the fine mapping. Alternatively, there might be additional bristle number factors close to the mapped QTL that interfere with founder mean estimation in the coarse-mapping scan. Expansion of the genetic map in the fine-mapping panel would reduce the effect of any such interference. We note that if marker informativeness is the sole issue, the pattern of founder means for QTL4 observed in the fine-mapping experiment should be seen in the coarse-mapping panel simply by genotyping additional markers.
founders. One explanation for the change is that the information content of the genotype data is much greater in the _X_-middle fine mapping (H = 0.187) than in the coarse scan of the entire X chromosome (H = 0.374). The increased information may have led to greater accuracy in estimating the ancestry of recombinant chromosomal segments, and more accurate estimates of the founder means in the fine mapping. Alternatively, there might be additional bristle number factors close to the mapped QTL that interfere with founder mean estimation in the coarse-mapping scan. Expansion of the genetic map in the fine-mapping panel would reduce the effect of any such interference. We note that if marker informativeness is the sole issue, the pattern of founder means for QTL4 observed in the fine-mapping experiment should be seen in the coarse-mapping panel simply by genotyping additional markers.
Both QTL4 and QTL5 appear rare in population pB, with the minor allele present in  founders (Figure 6, D and E), and the eighth founder (line B3) being ambiguous. Since there is no evidence for equivalent QTL in the pA population (Figures 4C and 5B), if we make the reasonable assumption that the pA lines are fixed for the major QTL allele, QTL4 and QTL5 may each have a frequency of
founders (Figure 6, D and E), and the eighth founder (line B3) being ambiguous. Since there is no evidence for equivalent QTL in the pA population (Figures 4C and 5B), if we make the reasonable assumption that the pA lines are fixed for the major QTL allele, QTL4 and QTL5 may each have a frequency of  (or
(or 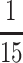 ) in our lines. We use Monte Carlo simulation to estimate the fraction of segregating bristle number variation due to these male-specific QTL in our mapping (synthetic recombinant × sequenced strain _trans_-heterozygote) population (see materials and methods). QTL4 (effect = 0.97 abdominal bristles, SE = 0.160) was detected in males of panel pBr1, a population which shows an ABN variance in the fine-mapping panel of 3.03 (Table 3). If we assume the rare allele is present in
) in our lines. We use Monte Carlo simulation to estimate the fraction of segregating bristle number variation due to these male-specific QTL in our mapping (synthetic recombinant × sequenced strain _trans_-heterozygote) population (see materials and methods). QTL4 (effect = 0.97 abdominal bristles, SE = 0.160) was detected in males of panel pBr1, a population which shows an ABN variance in the fine-mapping panel of 3.03 (Table 3). If we assume the rare allele is present in  lines, the average variance explained by QTL4 is 1.9% (95% confidence interval, 0.84–3.22%). Similarly, QTL5 explains 4.1% (1.26–8.11%) of male SBN variation. Notwithstanding Beavis effects (Beavis 1994), our data imply these QTL contribute 2–4% to the total variation for bristle number in our mapping panel.
lines, the average variance explained by QTL4 is 1.9% (95% confidence interval, 0.84–3.22%). Similarly, QTL5 explains 4.1% (1.26–8.11%) of male SBN variation. Notwithstanding Beavis effects (Beavis 1994), our data imply these QTL contribute 2–4% to the total variation for bristle number in our mapping panel.
Given that QTL4 and QTL5 reside in very small, and overlapping intervals one might conclude that we have mapped a single pleiotropic QTL contributing to variation in both male ABN and male SBN. Figure 6 (D and E) shows this is not the case. The rare low allele for QTL4 is present in line B5, while the rare high allele for QTL5 is present in line B7 (and perhaps line B3): a single QTL affecting both traits would show the same pattern of alleles across the founders. Thus, QTL4 and QTL5 represent independent mutations that are very tightly linked, perhaps even residing in the same gene. Our ability to distinguish tight linkage from pleiotropy is a consequence of mapping QTL in an eight-way cross and estimating founder mean phenotypes at each QTL.
DISCUSSION
Capturing experimental reality by simulation:
We performed simulations to examine our ability to map and characterize QTL in eight-way recombinant populations. Our intent was not to fully explore the parameter space, but rather to inform our experimental work to ensure we carried out a study of sufficient power. Results suggest that we have considerable power to detect QTL contributing 5% to variation in phenotype with the sample sizes and scale of genotyping we eventually employed. Furthermore, the false positive rate is very low with the critical LOD threshold applied. As with any simulation approach, we make various simplifying assumptions. Of potential concern is that we simulated just one QTL on the chromosome. In reality, there could be interference from linked QTL that may affect both our ability to detect QTL and to estimate founder phenotype means. Many QTL mapping algorithms have agreeable properties in the absence of “traffic” from nearby QTL, but are prone to errors in inference with linked QTL (Wright and Kong 1997; Cornforth and Long 2003). An important feature of the recombinant populations we employ is that the negative effects of “traffic” on mapping inference are evaded by genetic map expansion rather than by some form of statistical correction. Fine-mapping QTL should eliminate any problems associated with other nearby factors, implying that our method can ultimately cope with problems arising from linked QTL. Nevertheless, one could envisage scenarios under which linked factors might prevent initial QTL detection in a coarse scan of the genome.
In the simulations we also assume that the recombinant population is not subject to drift or selection, and that the expected frequency of genetic material derived from each founder at every point along the chromosome is  . Deviation from this neutral marker/infinite population size assumption may reduce our ability to detect QTL and accurately assign founders to allelic classes. In an extreme case the population could fix for one of the founder haplotypes, rendering QTL undetectable at that position. The likelihood of this occurrence increases as the population is subject to more genetic drift, for example by passing the population through a bottleneck or by maintaining the population for many generations. We deliberately maintained each of our synthetic populations as a large cohort to minimize the effect of drift. Nevertheless, it is clear from fine mapping at the tip of the X chromosome that the genetic material from certain founders can be largely eradicated from the population (Figure 6). It is unclear if the observed loss of some founder alleles is more consistent with random genetic drift or perhaps purifying selection against a disadvantageous chromosomal segment in our populations. The degree to which founder drop-out is a genomewide problem will require further genotyping of the fine-mapping panels across the five major chromosome arms of Drosophila. Further simulation of mapping performance using eight-way recombinant populations subject to many generations of maintenance will build on the work of Valdar et al. (2006a), and incorporate drift, selection, and more complex, realistic genetic architectures.
. Deviation from this neutral marker/infinite population size assumption may reduce our ability to detect QTL and accurately assign founders to allelic classes. In an extreme case the population could fix for one of the founder haplotypes, rendering QTL undetectable at that position. The likelihood of this occurrence increases as the population is subject to more genetic drift, for example by passing the population through a bottleneck or by maintaining the population for many generations. We deliberately maintained each of our synthetic populations as a large cohort to minimize the effect of drift. Nevertheless, it is clear from fine mapping at the tip of the X chromosome that the genetic material from certain founders can be largely eradicated from the population (Figure 6). It is unclear if the observed loss of some founder alleles is more consistent with random genetic drift or perhaps purifying selection against a disadvantageous chromosomal segment in our populations. The degree to which founder drop-out is a genomewide problem will require further genotyping of the fine-mapping panels across the five major chromosome arms of Drosophila. Further simulation of mapping performance using eight-way recombinant populations subject to many generations of maintenance will build on the work of Valdar et al. (2006a), and incorporate drift, selection, and more complex, realistic genetic architectures.
Information content of markers:
Each marker is composed of a set of genotyped SNPs within a 1-kb PCR amplicon and has the potential to completely distinguish among a set of eight chromosomes. In practice, we find that developed markers are not completely informative. This is the combined result of marker sequence identity among two or more founders, genotyping only a subset of the available SNPs, genotyping assay failure, and residual segregating variation within founders. Despite the non-fully informative nature of the markers we have power to detect QTL because the HMM employed incorporates data from linked markers (Broman 2005). Unlinked markers only provide information on the specific marked segment of the chromosome, whereas a set of linked markers provide information across the linkage group. The level of the information increases with marker density (relative to the average distance between recombination breakpoints) even if the markers remain only partially informative. By extension, instead of attempting to develop highly informative markers, it is possible to apply the HMM to a relatively dense genomewide set of genotyped biallelic SNPs. Future studies of eight-way recombinant Drosophila populations could take advantage of this possibility, but such an approach awaits the development a genomewide bank of intermediate-frequency SNPs for D. melanogaster, as well as some means of inexpensively genotyping those SNPs.
_X_-linked bristle number QTL:
Drosophila bristle number is arguably the best studied quantitative trait, and coupled with its easy and accurate scoring, permitted a rigorous test of our mapping methodology. A strong expectation was that we would identify bristle number QTL at the distal tip of the X chromosome, as factors influencing both sternopleural and abdominal bristle number have been identified in this region in previous studies (Long et al. 1995; Gurganus et al. 1998, 1999; Nuzhdin et al. 1999; Dilda and Mackay 2002). In a coarse-mapping experiment we identified QTL at the tip of the X for sternopleural bristle number (SBN) for both sexes in both synthetic populations, and for female abdominal bristle number (ABN) in just the pB population (Figure 4). Additionally, we found a QTL for male ABN in population pB in the middle of the X chromosome, but no corresponding QTL in the pA population, and a suggestive peak for male SBN in a similar position (Figure 4D). The limited resolution of the significant factors (8.3 cM on average) in the coarse-mapping experiment bars identification of the underlying molecular basis of mapped QTL—a commonly observed shortcoming associated with standard inbred line QTL mapping strategies (Mackay 2001). Therefore, we took advantage of the increased mapping resolution we can achieve by maintaining our synthetic population for many generations, and chose to fine map two interesting QTL regions (the tip of the X and the middle of the X) in males only. This prevented comparison of any fine-mapped QTL between the sexes, however the sex-specific nature of bristle number QTL/QTN is well established (Lai et al. 1994; Long et al. 1995, 1998, 2000; Lyman et al. 1999).
On average, fine-mapped QTL were resolved to 1.3 cM, with the large male pB ABN QTL resolved to just 0.9 cM. These intervals implicate genetically tractable physical distances, and suggest a handful of genes for further study. The best bristle number candidate genes at the tip of the X chromosome are the achaete-scute complex (ASC) and Notch. Association between polymorphisms at ASC and bristle number variation were first seen by Mackay and Langley (1990), extended and confirmed by Long et al. (2000), and more fully explored by Gruber et al. (2007). ASC is located under QTL peaks QTL1 and QTL2, and segregating loci at ASC might plausibly be involved in the expression of these QTL. Unfortunately, the very tip of the X chromosome in Drosophila has a markedly reduced crossover rate relative to physical distance compared to the rest of the chromosome, and LD extends over large physical distances (Aguadé et al. 1989). Thus, the prospect for identifying the actual causal locus, rather than a locus in strong LD with the causal site, contributing to QTL1 and QTL2 is somewhat bleak. The Notch pathway is involved in the cell fate decisions that lead to bristle specification, and mutations of the component genes alter bristle patterning and spacing (reviewed by Artavanis-Tsakonas et al. 1999; Lai 2004). Thus, Notch is considered a viable candidate gene for bristle number variation, although no formal association mapping-style experiment has been performed across the region. The fine-mapping experiment presented here suggests that Notch is unlikely to contribute to segregating variation for male ABN, but we cannot completely rule out an effect of Notch on SBN.
The two QTL mapped to the middle of the X chromosome are particularly interesting as we could find no good evidence for similar QTL in other studies that have scanned the X chromosome (Long et al. 1995; Gurganus et al. 1998, 1999; Nuzhdin et al. 1999; Dilda and Mackay 2002). This is probably because for both QTL the minor allele is rare in our experiment ( ), therefore it is not likely that these QTL segregated between pairs of inbred lines studied previously. Together the two QTL intervals harbor 26 genes (just 13 under the smaller QTL4 interval), and none of these represent classic bristle number candidate genes, although two genes—ocelliless and _Lim kinase_—have mutants that exhibit bristle defects (Royet and Finkelstein 1995; Pueyo et al. 2000). Despite overlap in the regions harboring the two QTL, our data show that while QTL4 and QTL5 are tightly linked, they are independent: the alleles for the two QTL are not in phase across the pB founder lines. Thus, they do not represent a single genetic factor having pleiotropic effects on the two bristle characters. Distinguishing independent factors that are within ∼1 cM highlights the power of our approach compared to standard QTL mapping between pairs of inbred lines. Since QTL4 and QTL5 map to a small region in the middle of the X chromosome having a high rate of recombination relative to physical distance, there is the potential to identify the actual causal sites involved.
), therefore it is not likely that these QTL segregated between pairs of inbred lines studied previously. Together the two QTL intervals harbor 26 genes (just 13 under the smaller QTL4 interval), and none of these represent classic bristle number candidate genes, although two genes—ocelliless and _Lim kinase_—have mutants that exhibit bristle defects (Royet and Finkelstein 1995; Pueyo et al. 2000). Despite overlap in the regions harboring the two QTL, our data show that while QTL4 and QTL5 are tightly linked, they are independent: the alleles for the two QTL are not in phase across the pB founder lines. Thus, they do not represent a single genetic factor having pleiotropic effects on the two bristle characters. Distinguishing independent factors that are within ∼1 cM highlights the power of our approach compared to standard QTL mapping between pairs of inbred lines. Since QTL4 and QTL5 map to a small region in the middle of the X chromosome having a high rate of recombination relative to physical distance, there is the potential to identify the actual causal sites involved.
One of the purported advantages of the bristle number paradigm is that we have a good idea of the likely candidate genes underlying the phenotype (Mackay 1995). Clear QTL in regions without such candidates might appear to cast some doubt on this assumption. However, aside from ASC and Notch, many (if not most) of the best bristle number candidate genes reside on the autosomes (e.g., Suppressor of Hairless, daughterless, and scabrous on chromosome 2, and extra macrochaetae, quemao, hairy, Delta, Hairless, and Enhancer of split on chromosome 3), and there is some evidence for quantitative effects on bristle number residing at scabrous (Lai et al. 1994; Lyman et al. 1999), hairy (Robin et al. 2002), and Delta (Long et al. 1998; Lyman and Mackay 1998).
The frequency of bristle number QTL:
There has been a long-running debate in the quantitative genetics community over the mechanisms by which genetic variation is maintained in natural populations (see Lewontin 1974). Many traits are under either apparent or actual stabilizing selection (e.g., bristle number, Linney et al. 1971; Nuzhdin et al. 1995; García-Dorado and González 1996), yet paradoxically there is substantial genetic variation segregating for these traits. Two broad types of model that attempt to explain this paradox are MSB models and balancing selection models (reviewed by Barton and Turelli 1989; Barton and Keightley 2002; Johnson and Barton 2005). MSB models predict that the bulk of standing genetic variation is due to rare alleles of large effect that are unconditionally deleterious (Johnson and Barton 2005). In contrast, balancing selection models suggest that variation is due to intermediate frequency variants of more modest effect. These balanced polymorphisms might be maintained by heterozygote advantage (overdominance), variation in allelic effects via genotype-by-environment interaction (Gillespie and Turelli 1989; Turelli and Barton 2004), frequency-dependent selection (Hedrick 1972), or antagonistic pleiotropy (Rose 1982). Since mutations obviously occur, at least a portion of the segregating variation we see must be due to the effects of MSB. The relevant question then becomes what proportion of segregating variation is due to intermediate-frequency sites of modest effect.
QTL mapping is routinely used for the genetic analysis of complex traits within and between various species. These works have yielded a staggering number of QTL, yet we have accumulated almost no information regarding the molecular genetic architecture of alleles at QTL or their population frequencies. There have been some attempts to combine the results of different mapping studies for the same trait, carried out in panels derived from different genetic material (e.g., Gurganus et al. 1999): overlap in the QTL identified across experiments can be taken as a loose surrogate for QTL frequency. From this Gurganus et al. (1999) suggest that some Drosophila bristle number QTL may be at intermediate frequency. A difficulty with such a “meta-analysis” approach, aside from the obvious lack of multiple QTL studies for the majority of traits, is that it may not be trivial to compare likelihood profiles generated across different genetic maps. Furthermore, the low resolution of most QTL mapping experiments will not allow confidence in the assertion that different QTL represent the same segregating factor. A much better approach to estimate QTL frequency is to utilize a mapping population that encompasses more than two haploid genomes. Nuzhdin et al. (2005) use a large set of inbred lines derived from a pair of heterozygous flies, such that the panel segregates for four haplotypes (three for the X chromosome), and use the data to assess the effect on mortality of lower-frequency alleles. Here, we take this idea further by taking a much larger sample of haplotypic variation, allowing us to generate a more robust estimate of the frequency for each mapped QTL.
The three _X_-tip QTL appear to be somewhat frequent, with minor QTL frequencies between 0.25–0.4, although these QTL do not obviously appear to be biallelic (Figure 6). The causal gene underlying each of these QTL might by multi-allelic, but it is also possible that the QTL are each due to the action of a haplotype extending across several genes. Particularly at the tip of the _X_—a relatively inert region with respect to recombination (Aguadé et al. 1989)—it is not inconceivable that we are seeing the action of long haplotypes of linked genes. In the case of the two QTL detected in males of population pB in the middle of the X chromosome, it appears that these QTL are biallelic, rare (frequency =  ), but with reasonably large effects on bristle number (0.97 and 1.31 bristles for QTL4 and QTL5, respectively). These QTL contribute 2–4% to the total variation for bristle number within our synthetic mapping panel. Since heritability for bristle number is estimated to be ∼50% (Riska et al. 1989), autosomal bristle number factors clearly remain to be identified.
), but with reasonably large effects on bristle number (0.97 and 1.31 bristles for QTL4 and QTL5, respectively). These QTL contribute 2–4% to the total variation for bristle number within our synthetic mapping panel. Since heritability for bristle number is estimated to be ∼50% (Riska et al. 1989), autosomal bristle number factors clearly remain to be identified.
There are two important points to be made concerning our estimates of the amount of variation explained by the rare QTL4 and QTL5. First, rather than being rare, naturally occurring alleles, these QTL may represent mutations that arose in the founder lines in the laboratory. Identifying such mutations, rather than naturally segregating allelic variation, is a general concern with inbred line QTL mapping approaches. The advantage of our strategy is that such mutations will always be identified as singletons (one founder having a different QTL allele from all others), and a researcher can weigh the costs of further characterization of the causal locus against the possibility that the site may not contribute to natural variation of the trait. Second, our estimates of QTL effect/frequency are derived in a panel of D. melanogaster lines of worldwide distribution. Thus, our estimates of the contribution of each QTL to natural bristle number variation are worldwide estimates. If the frequency (or even the effect) of QTL differ across populations, our worldwide estimate may underestimate the variance explained in some populations, while overestimate it in others. In general there does not appear to be a great deal of population structure in D. melanogaster (Kreitman and Aguadé 1986; Hale and Singh 1991; Begun and Aquadro 1993), although there are some cases of strong geographic variation in allele frequency (e.g., clinal variation at Adh, Berry and Kreitman 1993), and an apparent population-specific effect has been observed at an identified wing-shape QTN (Palsson et al. 2005). We do not yet know the extent of among-population heterogeneity in the genetic control of complex traits in Drosophila.
The five QTL we fine map were identified on the hemizygous X in males and, as such, contribute no dominance genetic variance. Our detection of these QTL was not predicated on the particular allele harbored by the sequenced strain of D. melanogaster, since none of the experimental males receive a sequenced strain X. We note that a fully recessive autosomal or female-specific _X_-linked QTL segregating in our worldwide sample of lines could be detected only if the sequenced strain harbors the recessive allele. The power to detect nonadditive autosomal or female _X_-linked QTL will depend both on the magnitude of the departure from additivity, and on the particular allele present in the isogenic standard line. Some combinations will increase power, and some will decrease power relative to detecting a fully additive QTL.
From a strategic point of view it would be advantageous to be able to accurately estimate QTL frequency from coarse-mapping data alone. We demonstrate that the presence of coarse-mapped QTL is preserved on fine mapping, but it is not clear that founder means are always similar between the coarse and fine-mapping studies. At least in one case (QTL4—Figure 6D) the coarse- and fine-mapping founder mean estimates are qualitatively different, and give a different idea of the QTL minor allele frequency ( vs.
vs.  in the coarse and fine mapping, respectively). We suspect that the estimates from the coarse-mapping data reflect interference between QTL4 and nearby linked factors. In the fine-mapping population these loci are (genetically) further apart and do not cause interference. With isolated QTL it should be possible to obtain an accurate frequency estimate from the coarse-mapping data (provided the genotype information is high), but linked QTL may require fine mapping for accurate frequency estimation.
in the coarse and fine mapping, respectively). We suspect that the estimates from the coarse-mapping data reflect interference between QTL4 and nearby linked factors. In the fine-mapping population these loci are (genetically) further apart and do not cause interference. With isolated QTL it should be possible to obtain an accurate frequency estimate from the coarse-mapping data (provided the genotype information is high), but linked QTL may require fine mapping for accurate frequency estimation.
Amount of natural variation in bristle number explained:
The eventual goal of our work is to identify all loci that contribute to natural variation in bristle number. If we assume additivity among mapped QTL, assume that the QTL represent naturally segregating biallelic polymorphisms (i.e., are not the result of mutation accumulation in the founder lines) and further assume our estimated effects translate to nature, we can estimate the fraction of the variation explained by the X chromosome QTL mapped here. In nature, ABN variation in males is 5.50 and SBN variation in males is 4.67 (Macdonald et al. 2005a). For male ABN, we need only consider QTL4 and estimate that we have explained 1.0% of the total phenotypic variation in ABN with this single QTL (95% confidence interval, 0.03–3.41%). The situation is more difficult for male SBN as we identify multiple QTL for this trait (QTL1, QTL2, QTL3, and QTL5). QTL1 (identified in pAr1) and QTL2 (identified in pBr1) may be equivalent, but this is unclear. To be conservative we ignore QTL2 as it barely achieves our LOD threshold. If QTL1 and QTL2 represent the same segregating factor, only considering QTL1 increases the Monte Carlo variance in allele frequency (as frequency is estimated from 8 rather than 16 alleles), and if the QTL are indeed independent we ignore the contribution of one of them. Similarly, the allele frequency estimate of QTL3 is taken just from pBr1, as although we do not formally identify an equivalent QTL in pAr1, the likelihood curve is only slightly less than our LOD threshold at the equivalent position in pAr1. If we consider that QTL1, QTL3, and QTL5 contribute to male SBN variation, the amount of total natural variation in SBN they collectively explain is 8.7% (95% confidence interval, 3.54–16.04%). Together with the other assumptions made, the caveat with the SBN variance calculation is that we include potentially nonbiallelic QTL at the tip of the X chromosome. This may have unpredictable effects on the accuracy of our estimate. Despite the suite of potential difficulties, mapping in synthetic populations derived from several founders allows for estimates of the total variance explained in nature by identified QTL.
Prospects to resolve QTN from QTL mapped in eight-way populations:
The methodology we outline provides an integrated system with which to map QTL to ∼1 cM, estimate their effects, and identify the most likely allelic configuration at the QTL across the founder lines. Ultimately we wish to identify the underlying QTN, but even our most finely mapped QTL interval (QTL4) encompasses 204 kb of sequence. Since mapping resolution does not increase linearly with each additional generation of recombination (Valdar et al. 2006a), only a very large number of extra maintenance generations would provide a marked increase in mapping resolution. This advantage might well be outweighed by the impact of drift on the founder composition of the recombinant population. One way to confirm the presence of a QTL is to conduct some form of association study across the implicated QTL interval. Assuming one had access to a genomewide database of D. melanogaster polymorphisms, the obvious strategy would be to genotype every common SNP across the entire QTL region, either directly or indirectly via strong LD with a genotyped site. However, extrapolating from previous high-power association mapping work in Drosophila (Palsson and Gibson 2004; Macdonald et al. 2005a), this would entail genotyping several hundred to a few thousand SNPs. It would be possible to reduce the genotyping effort by focusing on likely candidate genes present in the QTL interval. However, as in the case of QTL4 and QTL5, or for those traits that are less well understood than bristle number, no clear a priori candidates may be present. A considerable reduction in genotyping effort could also be achieved by genotyping a subset of the available SNPs expected to be enriched for functional polymorphisms. For instance, one could genotype only nonsynonymous coding SNPs or only those sites in sequence regions tagged as nonneutrally evolving (Boffelli et al. 2003; Boffelli et al. 2004; Macdonald and Long 2005). Unfortunately, given so little is known about the nucleotide-level genetic control of complex traits, it is not clear if a strategy based on genotyping specific sets of putatively functional SNPs will work.
QTL information derived from an eight-way synthetic population provides a different mechanism for identifying likely causal SNPs that is independent of their sequence context. The set of founder means allows us to estimate the QTL allele present in each founder: if the sequence for the QTL region was available from all 16 founders, the most likely causal SNPs are those completely in phase with the predicted QTL allele configuration. We have carried out coalescent simulations that show that, for a common QTL, the number of SNPs in phase with the QTL alleles is expected to be very small, even for large regions of the Drosophila genome (data not shown). Yalcin et al. (2005) explore a similar strategy that, in combination with a statistic reflecting the between-species conservation of the sequence surrounding each SNP, also dramatically reduces the number of segregating sites that may represent the QTN. Testing the small set of implicated sites by association mapping would be relatively trivial. All that is required is to sequence a QTL interval of perhaps 200 kb in 16 lines. Although such an experiment remains prohibitively costly today, emerging technologies suggest that just such a strategy could make sense in a few years (Frazer et al. 2004; Hinds et al. 2005; Margulies et al. 2005; Shendure et al. 2005; reviewed by Shendure et al. 2004; Metzker 2005).
Acknowledgments
We thank V. Bauer DuMont and C. F. Aquadro for access to prepublication Notch resequencing data and L. Ometto for providing DNA sequence alignments. All data from this work are available from http://www.people.ku.edu/∼sjmac/pubs.html. This work was supported by National Science Foundation grant DEB-0614429 to A.D.L.
Sequence data from this article have been deposited with the EMBL/GenBank Data Libraries under accession nos. DQ450201–DQ450355.
References
- Adams, M. D., S. E. Celniker, R. A. Holt, C. A. Evans, J. D. Gocayne_et al_., 2000. The genome sequence of Drosophila melanogaster. Science 287 2185–2195. [DOI] [PubMed] [Google Scholar]
- Aguadé, M., N. Miyashita and C. H. Langley, 1989. Reduced variation in the yellow–achaete–scute region in natural populations of Drosophila melanogaster. Genetics 122 607–615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Artavanis-Tsakonas, S., M. D. Rand and R. J. Lake, 1999. Notch signaling: cell fate control and signal integration in development. Science 284 770–776. [DOI] [PubMed] [Google Scholar]
- Barton, N. H., and M. Turelli, 1989. Evolutionary quantitative genetics: How little do we know? Annu. Rev. Genet. 23 337–370. [DOI] [PubMed] [Google Scholar]
- Barton, N. H., and P. D. Keightley, 2002. Understanding quantitative genetic variation. Nat. Rev. Genet. 3 11–21. [DOI] [PubMed] [Google Scholar]
- Baum, L. E., E. T. Petri, G. Soules and N. Weiss, 1970. A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains. Ann. Math. Stat. 41 164–171. [Google Scholar]
- Beavis, W. D., 1994. The power and deceit of QTL experiments: lessons from comparative QTL studies. Proceedings of the 49th Annual Corn & Sorghum Industry Research Conference. American Seed Trade Association, Washington, DC, pp. 250–266.
- Begun, D. J., and C. F. Aquadro, 1993. African and North American populations of Drosophila melanogaster are very different at the DNA level. Nature 365 548–550. [DOI] [PubMed] [Google Scholar]
- Berry, A., and M. Kreitman, 1993. Molecular analysis of an allozyme cline: alcohol dehydrogenase in Drosophila melanogaster on the East coast of North America. Genetics 134 869–893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boffelli, D., J. McAuliffe, D. Ovcharenko, K. D. Lewis, I. Ovcharenko_et al_., 2003. Phylogenetic shadowing of primate sequences to find functional regions of the human genome. Science 299 1391–1394. [DOI] [PubMed] [Google Scholar]
- Boffelli, D., C. V. Weer, L. Weng, K. D. Lewis, M. I. Shoukry_et al_., 2004. Intraspecies sequence comparisons for annotating genomes. Genome Res. 14 2406–2411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broman, K. W., 2005. The genomes of recombinant inbred lines. Genetics 169 1133–1146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broman, K. W., 2006. Use of hidden Markov models for QTL mapping (Johns Hopkins University, Department of Biostatistics Working Papers). Working Paper 125 (http://www.bepress.com/jhubiostat/paper125).
- Broman, K. W., H. Wu, S. Sen and G. A. Churchill, 2003. R/qtl: QTL mapping in experimental crosses. Bioinformatics 19 889–890. [DOI] [PubMed] [Google Scholar]
- Cargill, M., D. Altshuler, J. Ireland, P. Sklar, K. Ardlie_et al_., 1999. Characterization of single-nucleotide polymorphisms in coding regions of human genes. Nat. Genet. 22 231–238. [DOI] [PubMed] [Google Scholar]
- Celniker, S. E., D. A. Wheeler, B. Kronmiller, J. W. Carlson, A. Halpern_et al_., 2002. Finishing a whole-genome shotgun: release 3 of the Drosophila melanogaster euchromatic genome sequence. Genome Biol. 3 RESEARCH0079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Churchill, G. A., D. C. Airey, H. Allayee, J. M. Angel, A. D. Attie_et al_., 2004. The Collaborative Cross, a community resource for the genetic analysis of complex traits. Nat. Genet. 36 1133–1137. [DOI] [PubMed] [Google Scholar]
- Cornforth, T. W., and A. D. Long, 2003. Inferences regarding the numbers and locations of QTLs under multiple-QTL models using interval mapping and composite interval mapping. Genet. Res. 82 139–149. [DOI] [PubMed] [Google Scholar]
- Demarest, K., J. Koyner, J. McCaughran, Jr., L. Cipp and R. Hitzemann, 2001. Further characterization and high-resolution mapping of quantitative trait loci for ethanol-induced locomotor activity. Behav. Genet. 31 79–91. [DOI] [PubMed] [Google Scholar]
- Dilda, C. L., and T. F. C. Mackay, 2002. The genetic architecture of Drosophila sensory bristle number. Genetics 162 1655–1674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DuMont, V. B., and C. F. Aquadro, 2005. Multiple signatures of positive selection downstream of Notch on the X chromosome in Drosophila melanogaster. Genetics 171 639–653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falconer, D. S., and T. F. C. Mackay, 1996. Introduction to Quantitative Genetics. Longman Group, Harlow, England.
- Florez, J. C., S. Wiltshire, C. M. Agapakis, N. P. Burtt, P. I. de Bakker_et al_., 2006. High-density haplotype structure and association testing of the insulin-degrading enzyme (IDE) gene with type 2 diabetes in 4,206 people. Diabetes 55 128–135. [PubMed] [Google Scholar]
- Frazer, K. A., C. M. Wade, D. A. Hinds, N. Patil, D. R. Cox_et al_., 2004. Segmental phylogenetic relationships of inbred mouse strains revealed by fine-scale analysis of sequence variation across 4.6 Mb of mouse genome. Genome Res. 14 1493–1500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Dorado, A., and J. A. González, 1996. Stabilizing selection detected for bristle number in Drosophila melanogaster. Evolution 50 1573–1578. [DOI] [PubMed] [Google Scholar]
- Genissel, A., T. Pastinen, A. Dowell, T. F. C. Mackay and A. D. Long, 2004. No evidence for an association between common nonsynonymous polymorphisms in Delta and bristle number variation in natural and laboratory populations of Drosophila melanogaster. Genetics 166 291–306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie, J. H., and M. Turelli, 1989. Genotype-environment interactions and the maintenance of polygenic variation. Genetics 121 129–138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gruber, J. D., A. Genissel, S. J. Macdonald and A. D. Long, 2007. How repeatable are associations between polymorphisms in achaete–scute and bristle number variation in Drosophila? Genetics 175 1987–1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurganus, M. C., J. D. Fry, S. V. Nuzhdin, E. G. Pasyukova, R. F. Lyman_et al_., 1998. Genotype-environment interaction at quantitative trait loci affecting sensory bristle number in Drosophila melanogaster. Genetics 149 1883–1898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gurganus, M. C., S. V. Nuzhdin, J. W. Leips and T. F. C. Mackay, 1999. High-resolution mapping of quantitative trait loci for sternopleural bristle number in Drosophila melanogaster. Genetics 152 1585–1604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hale, L.R., and R. S. Singh, 1991. A comprehensive study of genic variation in natural populations of Drosophila melanogaster. IV. Mitochondrial DNA variation and the role of history vs. selection in the genetic structure of geographic populations. Genetics 129 103–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harr, B., M. Kauer and C. Schlötterer, 2002. Hitchhiking mapping: a population-based fine-mapping strategy for adaptive mutations in Drosophila melanogaster. Proc. Natl. Acad. Sci. USA 99 12949–12954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hedrick, P. W., 1972. Maintenance of genetic variation with a frequency-dependent selection model as compared to the overdominant model. Genetics 72 771–775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinds, D. A., L. L. Stuve, G. B. Nilsen, E. Halperin, E. Eskin_et al_., 2005. Whole-genome patterns of common DNA variation in three human populations. Science 307 1072–1079. [DOI] [PubMed] [Google Scholar]
- Hirschhorn, J. N., and M. J. Daly, 2005. Genome-wide association studies for common diseases and complex traits. Nat. Rev. Genet. 6 95–108. [DOI] [PubMed] [Google Scholar]
- Johnson, T., and N. Barton, 2005. Theoretical models of selection and mutation on quantitative traits. Phil. Trans. R. Soc. B 360 1411–1425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kidwell, M. G., T. Frydryk and J. B. Novy, 1983. The hybrid dysgenesis potential of Drosophila melanogaster strains of diverse temporal and geographical natural origins. Drosoph. Inf. Serv. 59 63–69. [Google Scholar]
- Kreitman, M., and M. Aguadé, 1986. Genetic uniformity in two populations of Drosophila melanogaster as revealed by filter hybridization of four-nucleotide-recognizing restriction enzyme digests. Proc. Natl. Acad. Sci. USA 83 3562–3566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruglyak, L., 1999. Prospects for whole-genome linkage disequilibrium mapping of common disease genes. Nat. Genet. 22 139–144. [DOI] [PubMed] [Google Scholar]
- Lai, E. C., 2004. Notch signaling: control of cell communication and cell fate. Development 131 965–973. [DOI] [PubMed] [Google Scholar]
- Lai, C., R. F. Lyman, A. D. Long, C. H. Langley and T. F. C. Mackay, 1994. Naturally occurring variation in bristle number and DNA polymorphism at the scabrous locus of Drosophila melanogaster. Science 266 1697–1702. [DOI] [PubMed] [Google Scholar]
- Lander, E. S., and D. Botstein, 1989. Mapping Mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121 185–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander, E. S., and P. Green, 1987. Construction of multilocus genetic linkage maps in humans. Proc. Natl. Acad. Sci. USA 84 2363–2367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewontin, R. C., 1974. The Genetic Basis of Evolutionary Change. Columbia University Press, New York.
- Lincoln, S. E., and E. S. Lander, 1992. Systematic detection of errors in genetic linkage data. Genomics 14 604–610. [DOI] [PubMed] [Google Scholar]
- Linney, R., B. W. Barnes and M. J. Kearsey, 1971. Variation for metrical characters in Drosophila populations. III. The nature of selection. Heredity 27 163–174. [DOI] [PubMed] [Google Scholar]
- Long, A. D., and C. H. Langley, 1999. The power of association studies to detect the contribution of candidate genetic loci to variation in complex traits. Genome Res. 9 720–731. [PMC free article] [PubMed] [Google Scholar]
- Long, A. D., S. L. Mullaney, L. A. Reid, J. D. Fry, C. H. Langley_et al_., 1995. High resolution mapping of genetic factors affecting bristle number in Drosophila melanogaster. Genetics 139 1273–1291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long, A. D., R. F. Lyman, C. H. Langley and T. F. C. Mackay, 1998. Two sites in the Delta gene region contribute to naturally occurring variation in bristle number in Drosophila melanogaster. Genetics 149 999–1017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Long, A. D., R. F. Lyman, A. H. Morgan, C. H. Langley and T. F. C. Mackay, 2000. Both naturally occurring insertions of transposable elements and intermediate frequency polymorphisms at the achaete-scute complex are associated with variation in bristle number in Drosophila melanogaster. Genetics 154 1255–1269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyman, R. F., and T. F. C. Mackay, 1998. Candidate quantitative trait loci and naturally occurring phenotypic variation for bristle number in Drosophila melanogaster: the Delta-Hairless gene region. Genetics 149 983–998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyman, R. F., C. Lai and T. F. Mackay, 1999. Linkage disequilibrium mapping of molecular polymorphisms at the scabrous locus associated with naturally occurring variation in bristle number in Drosophila melanogaster. Genet Res. 74 303–311. [DOI] [PubMed] [Google Scholar]
- Macdonald, S. J., and A. D. Long, 2004. A potential regulatory polymorphism upstream of hairy is not associated with bristle number variation in wild-caught Drosophila. Genetics 167 2127–2131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macdonald, S. J., and A. D. Long, 2005. Prospects for identifying functional variation across the genome. Proc. Natl. Acad. Sci. USA 102 6614–6621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macdonald, S. J., T. Pastinen and A. D. Long, 2005. a The effect of polymorphisms in the Enhancer of split gene complex on bristle number variation in a large wild-caught cohort of Drosophila melanogaster. Genetics 171 1741–1756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macdonald, S. J., T. Pastinen, A. Genissel, T. W. Cornforth and A. D. Long, 2005. b A low-cost open-source SNP genotyping platform for association mapping applications. Genome Biol. 6 R105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mackay, T. F. C., 1995. The genetic basis of quantitative variation: numbers of sensory bristles of Drosophila melanogaster as a model system. Trends Genet. 11 464–470. [DOI] [PubMed] [Google Scholar]
- Mackay, T. F., 2001. The genetic architecture of quantitative traits. Annu. Rev. Genet. 35 303–339. [DOI] [PubMed] [Google Scholar]
- Mackay, T. F. C., and C. H. Langley, 1990. Molecular and phenotypic variation in the achaete-scute region of Drosophila melanogaster. Nature 348 64–66. [DOI] [PubMed] [Google Scholar]
- Margulies, M., M. Egholm, W. E. Altman, S. Attiya, J. S. Bader_et al_., 2005. Genome sequencing in microfabricated high-density picolitre reactors. Nature 437 376–380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzker, M. L., 2005. Emerging technologies in DNA sequencing. Genome Res. 15 1767–1776. [DOI] [PubMed] [Google Scholar]
- Mott, R., C. J. Talbot, M. G. Turri, A. C. Collins and J. Flint, 2000. A method for fine mapping quantitative trait loci in outbred animal stocks. Proc. Natl. Acad. Sci. USA 97 12649–12654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuzhdin, S. V., J. D. Fry and T. F. C. Mackay, 1995. Polygenic mutation in Drosophila melanogaster: the causal relationship of bristle number to fitness. Genetics 139 861–872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuzhdin, S. V., C. L. Dilda and T. F. C. Mackay, 1999. The genetic architecture of selection response: inferences from fine-scale mapping of bristle number quantitative trait loci in Drosophila melanogaster. Genetics 153 1317–1331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nuzhdin, S. V., A. A. Khazaeli and J. W. Curtsinger, 2005. Survival analysis of life span quantitative trait loci in Drosophila melanogaster. Genetics 170 719–731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ometto, L., S. Glinka, D. De Lorenzo and W. Stephan, 2005. Inferring the effects of demography and selection on Drosophila melanogaster populations from a chromosome-wide scan of DNA variation. Mol. Biol. Evol. 22 2119–2130. [DOI] [PubMed] [Google Scholar]
- Orengo, D. J., and M. Aguadé, 2004. Detecting the footprint of positive selection in a European population of Drosophila melanogaster: multilocus pattern of variation and distance to coding regions. Genetics 167 1759–1766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palsson, A., and G. Gibson, 2004. Association between nucleotide variation in Egfr and wing shape in Drosophila melanogaster. Genetics 167 1187–1198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palsson, A., J. Dodgson, I. Dworkin and G. Gibson, 2005. Tests for the replication of an association between Egfr and natural variation in Drosophila melanogaster wing morphology. BMC Genet. 6 44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paterson, A. H., E. S. Lander, J. D. Hewitt, S. Peterson, S. E. Lincoln_et al_., 1988. Resolution of quantitative traits into Mendelian factors by using a complete linkage map of restriction fragment length polymorphisms. Nature 335 721–726. [DOI] [PubMed] [Google Scholar]
- Presgraves, D. C., 2005. Recombination enhances protein adaptation in Drosophila melanogaster. Curr. Biol. 15 1651–1656. [DOI] [PubMed] [Google Scholar]
- Press, W. H., S. A. Teukolsky, W. T. Vetterling and B. P. Flannery, 1996. Numerical Recipes in C, Ed. 2. Cambridge University Press, New York.
- Pritchard, J. K., 2001. Are rare variants responsible for susceptibility to complex diseases? Am. J. Hum. Genet. 69 124–137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pritchard, J. K., and N. J. Cox, 2002. The allelic architecture of human disease genes: Common disease-common variant … or not? Hum. Mol. Genet. 11 2417–2423. [DOI] [PubMed] [Google Scholar]
- Pueyo, J. I., M. I. Galindo, S. A. Bishop and J. P. Couso, 2000. Proximal-distal leg development in Drosophila requires the apterous gene and the Lim1 homologue dlim1. Development 127 5391–5402. [DOI] [PubMed] [Google Scholar]
- Reich, D. E., and E. S. Lander, 2001. On the allelic spectrum of human disease. Trends Genet. 17 502–510. [DOI] [PubMed] [Google Scholar]
- Risch, N., and K. Merikangas, 1996. The future of genetic studies of complex human diseases. Science 273 1516–1517. [DOI] [PubMed] [Google Scholar]
- Riska, B., T. Prout and M. Turelli, 1989. Laboratory estimates of heritabilities and genetic correlations in nature. Genetics 123 865–871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robin, C., R. F. Lyman, A. D. Long, C. H. Langley and T. F. C. Mackay, 2002. hairy: a quantitative trait locus for Drosophila sensory bristle number. Genetics 162 155–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose, M. R., 1982. Antagonistic pleiotropy, dominance, and genetic variation. Heredity 48 63–78. [Google Scholar]
- Royet, J., and R. Finkelstein, 1995. Pattern formation in Drosophila head development: the role of the orthodenticle homeobox gene. Development 121 3561–3572. [DOI] [PubMed] [Google Scholar]
- Shendure, J., R. D. Mitra, C. Varma and G. M. Church, 2004. Advanced sequencing technologies: methods and goals. Nat. Rev. Genet. 5 335–344. [DOI] [PubMed] [Google Scholar]
- Shendure, J., G. J. Porreca, N. B. Reppas, X. Lin, J. P. McCutcheon_et al_., 2005. Accurate multiplex polony sequencing of an evolved bacterial genome. Science 309 1728–1732. [DOI] [PubMed] [Google Scholar]
- Talbot, C. J., A. Nicod, S. S. Cherny, D. W. Fulker, A. C. Collins_et al_., 1999. High-resolution mapping of quantitative trait loci in outbred mice. Nat. Genet. 21 305–308. [DOI] [PubMed] [Google Scholar]
- Threadgill, D. W., K. W. Hunter and R. W. Williams, 2002. Genetic dissection of complex and quantitative traits: from fantasy to reality via a community effort. Mamm. Genome 13 175–178. [DOI] [PubMed] [Google Scholar]
- Todd, J. A., 2006. Statistical false positive or true disease pathway? Nat. Genet. 38 731–733. [DOI] [PubMed] [Google Scholar]
- Turelli, M., and N. H. Barton, 2004. Polygenic variation maintained by balancing selection: pleiotropy, sex-dependent allelic effects and G × E interactions. Genetics 166 1053–1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valdar, W., J. Flint and R. Mott, 2006. a Simulating the collaborative cross: power of quantitative trait loci detection and mapping resolution in large sets of recombinant inbred strains of mice. Genetics 172 1783–1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valdar, W., L. C. Solberg, D. Gauguier, S. Burnett, P. Klenerman_et al_., 2006. b Genome-wide genetic association of complex traits in heterogeneous stock mice. Nat. Genet. 38 879–887. [DOI] [PubMed] [Google Scholar]
- Wang, W. Y. S., B. J. Barratt, D. G. Clayton and J. A. Todd, 2005. Genome-wide association studies: theoretical and practical concerns. Nat. Rev. Genet. 6 109–118. [DOI] [PubMed] [Google Scholar]
- Weiss, K. M., and J. D. Terwilliger, 2000. How many diseases does it take to map a gene with SNPs? Nat. Genet. 26 151–157. [DOI] [PubMed] [Google Scholar]
- Wright, F. A., and A. Kong, 1997. Linkage mapping in experimental crosses: the robustness of single-gene models. Genetics 146 417–425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yalcin, B., J. Flint and R. Mott, 2005. Using progenitor strain information to identify quantitative trait nucleotides in outbred mice. Genetics 171 673–681. [DOI] [PMC free article] [PubMed] [Google Scholar]