PLINK: A Tool Set for Whole-Genome Association and Population-Based Linkage Analyses (original) (raw)
Abstract
Whole-genome association studies (WGAS) bring new computational, as well as analytic, challenges to researchers. Many existing genetic-analysis tools are not designed to handle such large data sets in a convenient manner and do not necessarily exploit the new opportunities that whole-genome data bring. To address these issues, we developed PLINK, an open-source C/C++ WGAS tool set. With PLINK, large data sets comprising hundreds of thousands of markers genotyped for thousands of individuals can be rapidly manipulated and analyzed in their entirety. As well as providing tools to make the basic analytic steps computationally efficient, PLINK also supports some novel approaches to whole-genome data that take advantage of whole-genome coverage. We introduce PLINK and describe the five main domains of function: data management, summary statistics, population stratification, association analysis, and identity-by-descent estimation. In particular, we focus on the estimation and use of identity-by-state and identity-by-descent information in the context of population-based whole-genome studies. This information can be used to detect and correct for population stratification and to identify extended chromosomal segments that are shared identical by descent between very distantly related individuals. Analysis of the patterns of segmental sharing has the potential to map disease loci that contain multiple rare variants in a population-based linkage analysis.
In spite of a substantial body of research that spans decades, we have largely failed to elucidate the molecular genetic basis of most common, complex human traits and diseases. The genetic epidemiology of these outcomes has often convincingly demonstrated only two facts: that genetic factors play an important role, and that the genetic variation is not due to a single, Mendelian mutation. With this implication of polygenic effects (many genes of small effect) in mind, researchers have become increasingly aware of the need to design larger linkage and association studies that have adequate power.1,2 However, the strategies of the past decade have met with limited success.3,4 One possible reason for the lack of identified complex-trait disease genes is that studies have still been lacking in sample size and genome coverage.
Modern whole-genome association studies (WGAS) represent a direct attempt to address these problems. On the basis of advances arising from large-scale genomic projects—including the human genome sequence, SNP discovery efforts, and the HapMap project, as well as new genotyping technology—it has been only in the past 1 or 2 years that our understanding of variation and our technical ability to assess it have enabled association to move from candidate-gene to unbiased whole-genome searches. The standard logic of the WGAS design implicitly assumes that common variants with modest effects on disease frequently exist and explain substantial proportions of variation (i.e., the common disease/common variant [CD/CV] hypothesis)5; this implies that previous studies either have not looked at them at all (i.e., not enough genetic markers tested) or have been underpowered to find significant associations (i.e., not enough samples). Eventually, WGAS should provide a powerful and comprehensive test of the CD/CV hypothesis for any given disease. In this report, we introduce a new analytic tool for WGAS and discuss some crucial analytic-design considerations, such as multiple testing, bias due to confounding, and the possibility that rare genetic variation underlies common disease.
New SNP genotyping technologies have enabled the next generation of genetic studies, with many WGAS either planned, under way, or already completed. A typical WGAS, currently with hundreds of thousands of SNPs genotyped for thousands of individuals, represents a data set that is several orders of magnitude larger than previous linkage and association studies. As such, WGAS present new computational and statistical challenges. Perhaps the most apparent challenge is from the increased multiple-testing burden: the concern that, from a set of hundreds of thousands of tests, many highly significant results are expected by chance alone, making it hard to distinguish signal from noise. To a large extent, this problem can be assuaged by moderate increases in sample size: basic power calculations show that maintaining the same power when performing an exponentially larger number of Bonferroni-corrected tests requires only a linear increase in sample size. For example, if 500 individuals are needed to test a single SNP with adequate power, ∼2,000 individuals will be required to test 500,000 SNPs, even after Bonferroni correction. So, although increased sample sizes are certainly required, even with the most conservative statistical approaches, these will often be achievable, rather than order-of-magnitude, increases.
The size of these data sets will present a computational as well as statistical testing burden, since many existing genetic-analysis software programs were not designed with WGAS in mind. We have therefore developed a user-friendly software tool, PLINK, to facilitate the analysis of whole-genome data in a number of ways: by addressing the mundane but important need for easy ways to manage such data, by making routine analyses computationally efficient, and by offering new analyses that take advantage of whole-genome coverage. When a relatively small WGAS data set of 100,000 SNPs genotyped for 350 individuals is considered, for example, PLINK takes ∼10 s to load, filter, and perform association analysis for all SNPs; straightforward handling of much larger data sets is also possible.
Aside from computational challenges, larger data sets also exacerbate the problem of confounding in genetic association studies. With increased power to detect true effects comes increased potential for bias to affect results (i.e., the “power to detect” departure from the null hypothesis due to unaccounted confounders will also increase). One well-acknowledged source of confounding in population-based association studies is population stratification.6 However, in the context of WGAS, this perhaps presents less of a problem, given the availability of hundreds of thousands of markers across the genome, which allows for a very accurate empirical assessment of stratification via genomic control7 and structured association methods.8–10 Augmenting this set of approaches, we describe below our approach to stratification, implemented within PLINK and designed to work with whole-genome data.
Another arguably more insidious source of confounding in WGAS is from nonrandom genotyping failure,11,12 which involves an individual’s SNP genotype that is either incorrectly called or (more commonly) not called at all. If this failure is nonrandom with respect to genotype (e.g., some genotypes are more likely to be uncalled) and to phenotype (e.g., cases have lower genotyping rates than do controls, on average), then false-positive associations can occur. That certain genotypes for a given SNP are more likely than others to fail is almost certainly the rule rather than the exception for any genotyping technology. Furthermore, it is probably also the exception rather than the rule that cases and controls are collected at exactly the same time and place and are handled similarly throughout the laboratory process; indeed, control data may come from a completely different study, having been genotyped in a different laboratory and called with a different algorithm.
Even though genotyping rates might be very high in general, in large samples, even a small proportion of nonrandom genotyping failure could induce a false-positive association (especially if it occurs for one of the many SNPs already showing a high level of association by chance). Because normal screening procedures based on measures such as overall genotyping rate and Hardy-Weinberg equilibrium will often not detect these biased SNPs, it is important to look closely at patterns of genotyping failure for nonrandom effects (as well as to visually inspect the raw data before calling genotypes). In PLINK, genotyping failure can be examined with respect to both phenotype and (potentially unobserved) genotype.
For some complex traits and diseases, an alternate hypothesis for the lack of identified genes is that common variants do not explain a substantial proportion of the phenotypic variation. Under this model, the considerable levels of heritability could reflect aggregates of very many, very rare variants (each potentially of moderate effect but accounting for virtually none of the variation at the population level), which we refer to as the “multiple rare variant” (MRV) hypothesis.13 Standard association approaches will likely fail when the MRV hypothesis holds (power will be low even before multiple-testing corrections, even for high genotypic relative risks, e.g., >5, if the frequency is very low, e.g., ∼1/10,000). Importantly, though, the same data collected for WGAS (in particular, panels of common SNPs genotyped in population-based samples) can potentially be analyzed using different approaches that do not assume that common variation underlies disease. In particular, if multiple rare disease variants exist within the same gene or genomic region, then, instead of standard association, one might consider an approach more akin to linkage analysis but performed in population-based samples of unrelated individuals. Rather than directly test frequency differences of a variant, we propose examining ancestral sharing at a locus, following ideas from previous work on haplotype sharing methods.14,15 That is, given ascertainment based on disease, we might expect to see multiple copies of even very rare variants that are moderately or highly penetrant among the descendants of the founder in whom the mutational events occurred.
In standard association analysis, undocumented relatedness can be another source of bias, although, with whole-genome data and analytic tools such as those described below, one can unambiguously detect closely related individuals. However, more-distant relatedness between individuals who share the same disease may convey additional information for gene mapping. Analyses of the type we propose here might be able to leverage this information to provide a complementary approach to standard association analysis, with use of the same data already being collected for single-SNP association studies.
If two individuals share the same rare variant, we would also expect that they share not just that variant but also the surrounding chromosomal region, particularly because rarer variants are more likely to be relatively recent. We propose the use of panels of common SNPs to look for these regions of extended sharing (regions that are inherited identical by descent [IBD] between seemingly unrelated individuals). If a particular region harbors multiple rare variants, we would expect to see inflated levels of segmental sharing between case/case pairs at that locus, compared with case/control and control/control pairs. A procedure for detecting shared segments and testing for correlation between sharing and phenotypic similarity forms the basis of a population-based linkage analysis, which is intended as an approach complementary to standard association analysis. This approach differs from standard haplotype analysis, in that we do not try to infer phase explicitly or estimate haplotype frequencies, so we can accurately assess sharing of very rare, very long regions; in addition, the subsequent unit of analysis is sharing at the locus rather than the frequency of one or more haplotypic variants.
In summary, given the issues raised above, we designed the PLINK WGAS tool set to meet the following requirements: (a) to provide a simple way to handle large WGAS data sets, (b) to assess confounding due to stratification and nonrandom genotyping failure and to produce a range of other summary statistics, (c) to perform a variety of standard association tests efficiently on very large data sets (in populations or families, for disease or quantitative outcomes, allowing for covariates, haplotypic tests, etc.), and (d) to provide a means of assaying rare variation with the use of common SNP panels, thereby providing a mapping method that might perform better when the MRV model holds. In the rest of this report, we highlight some of PLINK’s main features, briefly describing five domains of functions: data management, summary statistics, assessment of population stratification, association analysis, and IBD estimation. All these methods are applicable to whole-genome data sets. Below, we either describe or provide references for the tests implemented; these methods and other new ones being added are described in more detail in the online technical documentation being added to the PLINK Web site.
Data management.—We have developed a compact binary file format to represent SNP data, as well as tools to transform the binary format to standard text-based formats (including both a one-row-per-individual and a transposed one-row-per-SNP format). A simple interface is provided for reordering, recoding, and filtering genotype information (i.e., extracting individuals and/or SNPs on the basis of certain criteria, such as physical position, genotyping rate, or covariate values). It is also possible to merge two or more data sets that can partially overlap, in terms of both individuals and markers, and produce reports of discrepancies between overlapping data sets.
Summary statistics.—Standard summary measures are available: genotyping rates, allele and genotype frequencies, Hardy-Weinberg equilibrium tests using asymptotic and exact16 procedures, and single-SNP Mendelian error summaries for family data. PLINK also estimates individual heterozygosity rates and provides an automatic sex-check facility based on X-chromosome heterozygosity. We employ a per-SNP test of nonrandom genotyping failure with respect to phenotypic status, which is based on a simple χ2 test of different rates of genotyping failure in cases versus controls.
We also test whether missingness at a site can be predicted by the local haplotypic background, to spot nonrandom genotyping failure with respect to genotype. Taking each SNP that has an above-threshold level of genotyping failure as the reference SNP, we ask whether the haplotypes formed by the two (or more) flanking SNPs can predict which individuals are missing at the reference SNP. The test is a simple haplotypic case/control test, where the phenotype is the presence or absence of a called genotype at the reference SNP. If missingness at the reference SNP is not random with respect to the true (unobserved) genotype, we will often expect to see an association between missingness and flanking haplotypes. This test will often have higher specificity than sensitivity: it relies on linkage disequilibrium (LD) patterns to make an inference about the potentially unobserved reference allele, so it might miss many SNPs showing high, nonrandom levels of genotyping failure. However, used as a screening tool, SNPs that show highly nonrandom patterns of missing data could obviously be problematic and should be treated with caution.
For an example, we consider an Illumina whole-genome SNP data set, available free of charge from the National Institute of Neurological Disorders and Stroke (NINDS) Repository at Coriell (see the Acknowledgments for full details), comprising 276 amyotrophic lateral sclerosis cases and 271 controls. We illustrate the above tests for one particular SNP, rs5742981. Genotyping failure for this SNP was not randomly distributed with respect to phenotype (10.5% in cases and 0.7% in controls, _P_=2×10-7) or genotype. Flanking haplotypes (formed by SNPs rs1899025 and rs5743030) are very strongly associated with genotyping status at rs5742981 (e.g., the GA haplotype is associated with the missing rs5742981 genotype at _P_=9×10-56). In fact, if we divide the sample into individuals who are heterozygous for the background haplotype (_N_=213) and those who are not (_N_=333), then all instances of genotyping failure at rs5742981 fall into the smaller, heterozygous group (_P_=7.6×10-13). It would seem that, in this particular case, heterozygosity for the haplotypic background predicts heterozygosity at the reference SNP and that heterozygotes are preferentially dropped in cases only. This would also seem to generate the association between allele count at rs5742981 with disease (_P_=.0043; minor-allele frequency [MAF] 0.4% in cases and 2.6% in controls). Of course, such problems can often, but not always, be avoided by imposing appropriate limits on allele frequency, genotyping rate, and Hardy-Weinberg threshold. In this case, most Hardy-Weinberg filters would not have excluded this SNP (in controls, _P_=1; in the total sample, _P_=.11), although a missing-data threshold of 5% would have excluded this SNP. In any case, having additional simple quality-control (QC) metrics, including the two presented here, being automatically and quickly calculated by PLINK will often help to flag problematic SNPs.
Population stratification.—On the basis of the genomewide average proportion of alleles shared identical by state (IBS) between any two individuals, PLINK offers tools to (a) cluster individuals into homogeneous subsets, (b) perform classical multidimensional scaling (MDS) to visualize substructure and provide quantitative indices of population genetic variation, and (c) identify outlying individuals. PLINK uses complete-linkage hierarchical clustering to assess population stratification, with the use of whole-genome SNP data. This agglomerative procedure starts by considering every individual as a separate cluster of size 1, then repeatedly merges the two closest clusters. Complete-linkage clustering specifies that clusters are compared on the basis of their two most dissimilar members; clustering stops either when all individuals belong to one cluster or on the basis of prespecified constraints (stopping rules).
Various optional constraints can be applied with the specific goal of subsequent association analysis in mind, rather than an accurate description of population genetic variation per se. That is, we aim to ensure that all members of any derived cluster belong to the same subpopulation, rather than attempting to ensure that all members of the same subpopulation belong to the same cluster. The purpose of the constraints is to select which solution to accept from the distance-based clustering approach—that is, with no constraints, all solutions are considered (i.e., for N individuals, from N clusters, each of size 1, to 1 cluster of size N).
One constraint PLINK applies is called the “pairwise population concordance” (PPC) test, similar to a method used by Lee,17 such that for any putative new cluster, all pairs of individuals pass this test. For a given pair, we expect to see autosomal SNPs with two copies of each allele occur in a 2:1 ratio of IBS 2 {Aa,Aa} to IBS 0 {AA,aa} SNP pairs if both members of the pair come from the same random-mating population. For SNPs selected far enough apart to be approximately independent (e.g., 500 kb), a test of binomial proportions can suggest concordant or discordant ancestry for each pair of individuals. A pair from different populations is expected to show relatively more IBS 0 SNPs; a one-sided test for departure from a 2:1 ratio is given by the normal approximation to the binomial: for a particular pair, if L is the total number of informative, independent SNP pairs and _L_2 is the IBS 2 subset,
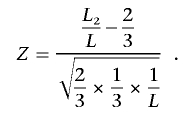
One can choose to merge clusters only if no between-cluster pairs have a statistically significant PPC result at a given significance threshold. In addition to the PPC test, we have incorporated other constraints in the clustering procedure. As mentioned above, nonrandom genotyping failure is a possible source of confounding in genetic association studies. One possible constraint is to cluster only individuals who have similar profiles of missing data, or “identity by missingness,” in which we specify a threshold for the maximum permissible proportion of sites for which two individuals are discordant in genotyping status (genotyped versus missing). For case/control samples, another possible constraint is that each cluster of two or more individuals has at least one case and one control (and so is informative for association analysis that conditions on cluster). Alternatively, the maximum cluster size or the number of clusters can be fixed. It is also possible to combine phenotype and cluster size constraints, by specifying that a cluster contains no more than one case and three controls, for example. Finally, one can also combine multiple external categorical and quantitative matching criteria (such as age, sex, other environmental variables, or QC measures such as the genotype call rate for each individual) alongside the genetic matching. Categorical criteria can be either “positive” or “negative,” such that only similarly categorized or differently categorized individuals can be merged. It is also possible to select only a single individual from a particular prespecified group. The complete algorithm is as follows: the IBS distance between individual k (belonging to cluster i) and individual l (belonging to cluster j) is denoted d ijkl; the between-cluster distances are denoted D ij.
- 1.
START: Find valid i,j for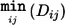 , where
, where 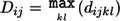 .
. - 2.
Test (optional) constraints for this potential new cluster:- →
New cluster contains both cases and controls? - →
Merged i+j cluster smaller than maximum cluster size constraint? - →
Maximum number of cases or controls exceeded?
- →
- 3.
For every pair between i and j, test the following (optional) constraints:- →
Pairable based on external constraints? - →
Nonsignificant PPC test? - →
Pass identity-by-missingness threshold? - →
Already selected an individual from this group?
- →
- 4.
Satisfies constraints? → Merge clusters. - 5.
No remaining pairable clusters? → STOP. - 6.
Return to START for next best pair of clusters.
PLINK also provides an alternate way to look at population stratification: rather than clustering into discrete groups, it can use the data-reduction technique of classical MDS to produce a _k_-dimensional representation of any substructure. Although the primary use of this approach is for visualization, the values for each of the k dimensions, instead of discrete clusters, can be used as covariates in subsequent association analysis to control for stratification. There is an option to use a Euclidean IBS distance metric in place of the standard metric of proportional sharing; classical MDS based on a Euclidean distance metric is numerically identical to principal-components analysis, which forms the basis of other methods.10
Finally, PLINK also supports an IBS-based “nearest-neighbor” analysis to detect outlying individuals who do not belong with any major cluster in the sample. For each individual, the distance to its nearest neighbor is calculated; this distribution is standardized (by the sample mean and variance of nearest-neighbor distances) and can be inspected for outliers. The same procedure can also be applied to individuals’ _n_th-nearest neighbor.
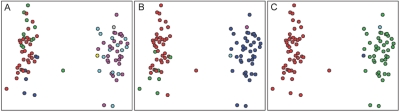
Here, we illustrate how these methods can differentiate between two quite similar populations and can control for between-population differences in tests of association, with the use of available HapMap data. From the 90 Asian individuals (45 unrelated Han Chinese from Beijing labeled “CHB,” and 45 unrelated Japanese from Tokyo labeled “JPT”) in the phase II data set, we extracted the set of autosomal SNPs on the Affymetrix GeneChip 500K Mapping Array. Figure 1 shows the results of an MDS analysis, which clearly separates two clusters (the left and right clusters correspond to CHB and JPT, respectively). The color coding in the three panels shows the classification of individuals according to increasingly liberal PPC thresholds: 0.01, 0.001, and 0.0001 (from left to right), which result in 7, 5, and 4 classes, respectively. In all solutions, two of the classes represent two single Japanese individuals: the nearest-neighbor diagnostics identified these two individuals (NA18987 and NA18992) as clear outliers >3 SDs below the mean.
Figure 1. .
MDS and classification of Asian HapMap individuals. MDS reveals in each panel two clear clusters that correspond to CHB (left) and JPT (right) HapMap populations. The figure’s three panels differ only in the color scheme, which represents classification according to PPC thresholds of 0.01 (A), 0.001 (B), and 0.0001 (C).
To mimic a data set showing stratification effects, we next created a dummy phenotype to represent genotype at rs2976396, a SNP that shows strong (_P_=2.7×10-8) allele-frequency differences between CHB (frequency of the A allele is 0.24) and JPT (frequency of the A allele is 0.66) populations. Specifically, individuals with the GG genotype are designated cases, and AA and AG individuals are designated controls. The dummy phenotype therefore shows a marked difference in prevalence between CHB and JPT populations. When a standard association analysis is performed (methods described below) for all 500,000 SNPs with this phenotype, the genomic-control inflation factor is 1.163, which is indicative of some inflation (importantly, this would be sufficient to impact the tail of the test statistic distribution, perhaps pushing what would have been marginally significant results to genomewide-significant results). Performing tests of association, with between-strata effects controlled for, reduced the genomic-control inflation factor to virtually 1 for all three solutions (1.00474, 1.00315, and 1.00098 for PPC 0.01, 0.001, and 0.0001 solutions, respectively; when actual population membership, CHB versus JPT, was used instead of the empirically derived classification, the inflation factor was 1.00044).
Given the range of methods and options for detecting and correcting for population stratification (in addition to a genomic-control procedure7 implemented in PLINK), further work is clearly required to determine and quantify the typical performance of these approaches, in terms of the type I and type II error rates in subsequent association analysis. Further work is also needed to assess how to best apply these types of genetic-matching procedures when controls are selected from large, preexisting panels (i.e., as opposed to cases and controls being collected and genotyped together). Toward this goal, we are involved in work that provides direct comparisons of PLINK with other methods for real whole-genome data18 (R. Plenge, C. Cotsapas, L. Davies, A. L. Price, P. I. W. de Bakker, J. Maller, I. Pe’er, N. Burtt, B. Blumenstiel, M. DeFelice, et al., unpublished data).
Association analysis.—As well as the standard case/control allelic test, PLINK offers a Cochran-Armitage trend test, Fisher’s exact test, genotypic tests (general, dominant, and recessive models), and Cochran-Mantel-Haenszel tests for stratified tables,19 which allow for tests of association conditional on any cluster solution or other categorization of samples. The Breslow-Day19 and homogeneity of odds ratio20 tests are supported, as are tests for quantitative traits that use a standard linear regression of phenotype on allele dosage. The standard disease- and quantitative-trait association tests are implemented for speed; the same analyses are also framed as more general linear- and logistic-regression models that allow for multiple binary or continuous covariates having both main effects and interactions. One can test for joint effects or perform a scan conditional on a given SNP or set of SNPs, for example; also, gene-gene and gene-environment interaction tests for quantitative and disease traits can be performed.
For family data, the standard transmission/disequilibrium test (TDT)21 is provided. The permutation procedure applied to the TDT flips the transmitted and untransmitted alleles of all individuals in a nuclear family for all SNPs per permutation, thereby preserving in each permuted data set the possible nonindependence of transmissions across SNPs and across multiple offspring due to LD and linkage. We also implement the sib-TDT22 for nuclear families, to include sibships without parents as well as unrelated individuals (called the “DFAM test” within PLINK). We break pedigrees into nuclear families and classify them as those in which both parents are genotyped and those in which they are not. For the first class of families, we obtain the allele count of the minor allele (A; major allele is a) among affected children in family f, labeled S f. Under the null hypothesis of no association, the binomial distribution gives the expected value and variance of S f, given the parental genotypes (i.e., sampling parental transmissions with replacement). If family f contains D affected offspring, then E(S f)=DP, where P is 1/2, 1, or 1 1/2 for aa×Aa, Aa×Aa, and AA×Aa parental mating types, respectively, and Var(S f)=D/4 unless both parents are heterozygous, in which case Var(S f)=D/2. For the second class of families, we also obtain S f, the count of minor alleles in affected offspring and its expected value and variance (under H_0, based on the genotypes of all siblings in the family); these are given by the multivariate hypergeometric distribution (i.e., sampling genotypes without replacement). The use of the genotype-based multivariate hypergeometric distribution in sibships accounts for the fact that not all allelic combinations are possible within a sibship (e.g., an individual cannot have two paternal alleles). The number of all offspring with genotypes AA, Aa, and aa in family f are labeled N AA, N Aa, and N aa, respectively (which sum to N); the equivalent numbers in affected offspring are D AA, D Aa, and D aa, which sum to D; therefore, S f_=2_D AA+D Aa. The expected allele count in affected individuals in family f under the null hypothesis is E(S f)=2_E(D AA)+E(D Aa)=(2_N_ AA+N Aa)(D/N), and the variance, obtained using the multivariate hypergeometric distribution, is
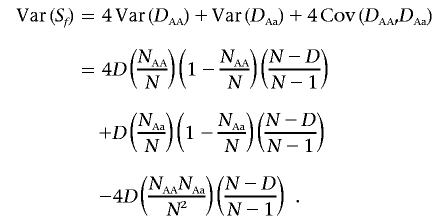
Summing over families, a test statistic is
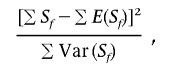
which follows a χ21 distribution under the null hypothesis. Additional unrelated cases and controls, potentially stratified into clusters, can be included within this framework if they are treated as sibships and the standard hypergeometric distribution is used (i.e., sampling alleles without replacement), which is equivalent to the standard Cochran-Mantel-Haenszel test mentioned above.
For quantitative traits, PLINK provides an implementation of the between/within model,23,24 which uses a permutation procedure (permuting genotype rather than phenotype) to control for the nonindependence of individuals within the same family (the QFAM test). The analysis of phenotype-genotype association is a standard regression of phenotype on genotype that ignores family structure. Significance is based on the following permutation procedure: genotypes are decomposed into between- and within-family components, following the models referenced above; these two components are then permuted independently at the level of the family and are summed to form new pseudogenotype scores for each individual. That is, between components are swapped between families; within components have their sign swapped, with a 50% chance (similar for all members of the same family). This approach provides tests that give correct type I error rates accounting for the relatedness between individuals. Despite the necessity of permutation, one advantage is that nonnormal and dichotomous phenotypes can be appropriately analyzed. Whereas the basic test is of total association, the between and within components can also be tested separately. Information about parental phenotypes can also be combined in these analyses.25,26
There is support for haplotype-based case/control and quantitative trait tests and TDTs based on the expected haplotype distribution for each individual obtained from expectation-maximization phasing. Either prespecified lists or sliding windows are used to specify the particular haplotype tests; precomputed lists of efficient sets of tests for common WGAS products based on HapMap,27 are available from the PLINK Web site and can be immediately applied to these data sets. Also, two nonhaplotypic multilocus “gene-based” or “set-based” tests are available: sum-statistics28 and, for case/control samples, Hotelling’s _T_2.
For many tests, a number of permutation procedures are available: “adaptive” permutations, which give up early on clearly nonsignificant results29; a “max(T)” permutation to correct for multiple tests30; a rank-ordered permutation in which the _n_th-best original result is compared against the _n_th best in each permuted data set; gene-dropping for family-based tests; and, finally, the between/within permutation scheme described above. A range of multiple-test corrections are also available, including those based on Bonferroni correction and false-discovery rate.31
_IBD estimation._—The final domain of function concerns IBD estimation. In homogeneous samples, PLINK provides options to estimate genomewide IBD-sharing coefficients between seemingly unrelated individuals from whole-genome data.32 These metrics (probabilities of sharing 0, 1, or 2 alleles IBD) can be particularly useful for QC, by diagnosing pedigree errors, undetected relationships, and sample swap, duplication, and contamination events.
PLINK has a simple procedure to find extended stretches of homozygosity in whole-genome data (regions spanning more than a certain number of SNPs and/or kilobases, allowing for a certain amount of missing genotypes and/or occasional heterozygote calls) that occur relatively frequently, and it can provide a powerful approach to map recessive disease genes.33,34 Via permutation, an empirical P value can be calculated for each SNP on the basis of a test for whether there is a higher rate of homozygous segments spanning that position in cases versus controls. PLINK also has options to determine distinct sets of overlapping (and, optionally, allelically matching) segments, thereby allowing for further inspection of the data.
PLINK also calculates inbreeding coefficients for each individual. Specifically, for a particular SNP with known allele frequencies p and q, the probability that individual i is homozygous equals f i+(1-f i)(_p_2+_q_2), or the probability of being autozygous (homozygous by descent) (f i) plus the probability of being homozygous by chance. If individual i has L i genotyped autosomal SNPs, let O i be the number of observed homozygotes and E i be the number expected by chance; then, O _i_=f i_×_L i+(1-f i)E i, which gives f _i_=(O _i_-E i)/(L _i_-E i). When allele frequencies are not known but are estimated from the sample, an unbiased estimator of E i is based on the sum over all SNPs not missing for individual i: 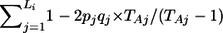 , where T Aj is twice the number of nonmissing genotypes for SNP j.
, where T Aj is twice the number of nonmissing genotypes for SNP j.
We have also implemented a novel method to detect extended chromosomal segmental IBD sharing between pairs of distantly related individuals by use of a hidden Markov model (HMM), in which the underlying hidden IBD state is estimated given the observed IBS sharing and genomewide level of relatedness between the pair. We also provide a test for correlation between segmental chromosomal sharing and phenotypic sharing. This test, a population-based linkage analysis, potentially offers a complementary approach to whole-genome data that does not assume the common variant hypothesis of disease-related genetic variation. We describe our approach in three steps: estimation of genomewide relatedness, estimation of local segmental sharing, and relating pairwise segmental sharing to phenotypic similarity.
We use a method-of-moments approach to estimate the probability of sharing 0, 1, or 2 alleles IBD for any two individuals from the same homogeneous, random-mating population. If we denote IBS states as I and IBD states as Z (in both cases, the possible states being 0, 1, and 2), then we can express the prior probability of IBS sharing as
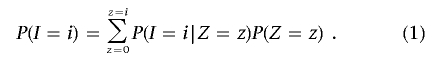
As described in detail below, for each SNP, we specify P(I|Z) in terms of the allele frequency; averaging over all SNPs, we obtain the expected value for P(I|Z). Then, rearranging the three equations implied by equation (1), we solve for P(_Z_=0), P(_Z_=1), and P(_Z_=2) and calculate
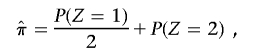
the proportion of alleles shared IBD.
For all SNPs, we calculate allele frequencies (on the basis of only founders if family information is present). For any one marker, P(I|Z) is a function of allele frequency (for alleles A and a, these are p and _q_=1-p, respectively). If p and q were known with certainty, then 2_p_2_q_2 would, for example, be an unbiased estimator of P(_I_=0|_Z_=0) (i.e., this requires that both individuals have opposite homozygotes, either {AA/aa} with probability _p_2×_q_2 or {aa/AA} with probability _q_2×_p_2). However, because p and q are estimated only from a finite sample, there is a bias that we take into account as follows. Let X and Y equal the counts of the two alleles in the sample for a particular SNP, so that _p_=X/T A and _q_=Y/T A, where T A is twice the number of nonmissing genotypes. There are T A(T _A_-1)(T _A_-2)(T _A_-3) possible ways of selecting four distinct alleles from T A alleles; of these, X(_X_-1)Y(_Y_-1) will be {AA/aa} genotype pairs and Y(_Y_-1)X(_X_-1) will be {aa/AA}. Therefore,
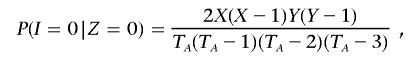
which, reexpressed in terms of the original probabilities and a correction factor based on allele counts, equals
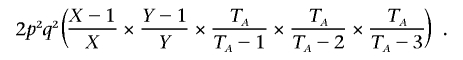
Following a similar logic, the full set of P(I|Z) is given in table 1.
Table 1. .
Calculation of P(I|Z)[Note]
Conditional on IBD state _Z_=z for the entire genome, the expected count of SNPs with IBS state _I_=i is given as 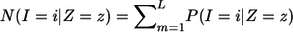 , where the summation is over all SNPs with genotype data on both individuals. Then, from equation (1), we can obtain global IBD estimates of P(Z) for that pair by the method of moments, substituting into
, where the summation is over all SNPs with genotype data on both individuals. Then, from equation (1), we can obtain global IBD estimates of P(Z) for that pair by the method of moments, substituting into
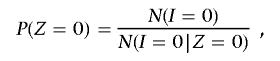
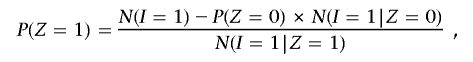
and
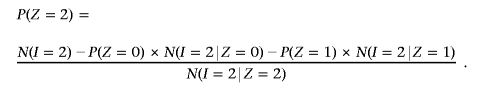
These estimates of P(Z) are not bounded 0⩽_x_⩽1 and are also not constrained to biologically plausible values (e.g., 0.5, 0, and 0.5 are not plausible values for IBD states 0, 1, and 2, respectively). In practice, we bound these estimates as follows. If P(_Z_=0)>1, then P(_Z_=0) is set to 1 and P(_Z_=1) and P(_Z_=2) are set to 0. If P(_Z_=0)<0, then P(_Z_=0) is set to 0 and P(_Z_=1) and P(_Z_=2) are set to P(_Z_=1)/S and P(_Z_=2)/S, respectively, where _S_=P(_Z_=1)+P(_Z_=2).
If π2⩽P(_Z_=2), where
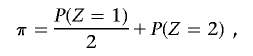
to constrain IBD estimates to biologically plausible values (assuming a homogeneous, random-mating population), we find a new value for P(_Z_=1), which we label P*(_Z_=1), which satisfies the equation
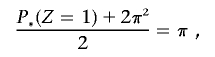
which gives P*(_Z_=1)=2π(1-π). The transformed IBD probabilities, used in all subsequent calculations, are therefore
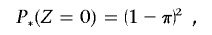
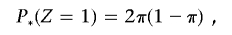
and
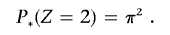
When not constrained to biologically plausible values, genomewide IBD sharing estimates can be used for QC and to indicate and diagnose sample and genotyping errors, including swaps, duplications, and contamination events, as well as misspecified or undetected familial relationships. For example, values of P(_Z_=2) near 1 clearly indicate duplicated samples (or MZ twins). Alternatively, if an experiment is conducted on two separate chips (e.g., two 250K SNP arrays comprising a 500K array), values near 0.5, 0, and 0.5 might represent an individual duplicated for one 250K array only.
If DNA from one or more individual contaminates other samples, this can lead to a distinctive pattern of contaminated samples showing high IBD with all other individuals. This is because contamination induces false heterozygote calls (e.g., AA pooled with CC may well be typed as AC), and heterozygotes cannot be IBS 0 with any other SNP genotype, which artificially inflates IBD estimates. Furthermore, contaminated samples will show strong, negative inbreeding coefficients, indicating more heterozygotes than expected.
In analogy to the traditional Lander-Green algorithm for multilocus analysis,35 we use an HMM approach to provide multipoint estimates of allele-sharing IBD for each pair of individuals in a homogeneous sample at any arbitrary position along the chromosome, given the observed pattern of IBS sharing. Note that, unlike full inheritance vectors, IBD states along the chromosome do not actually satisfy the Markov property. Nevertheless, we used an HMM because it is computationally tractable and likely to give a good approximation.
We require the conditional probability of IBD for _z_=0, 1, or 2 at a particular position, given the marker genotypes M of all K markers on a chromosome, P(_Z_=z|M). This can be reexpressed, using the Bayes theorem, as
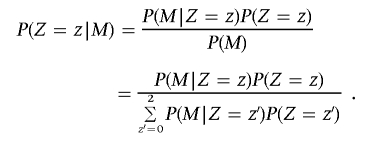
Here, P(_Z_=z) is the global IBD sharing probability for the whole genome, and the summation is over the three possible IBD states. Because of the Markov property, the probability P(M|_Z_=z) can be factorized as the product P(M L|Z_=z)×_P(M R|_Z_=z), where M L and M R are the marker genotypes to the left and to the right, respectively, of the position. Suppose the position is between markers l and l+1; then, the Markov property ensures that
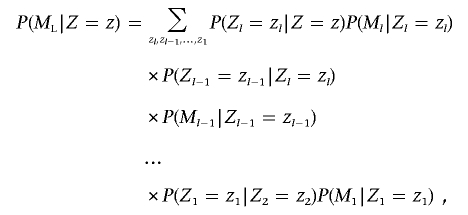
where the summation is over all possible IBD states for all markers. Writing the 3×3 diagonal matrix of marker genotype probabilities conditional on IBD state for marker l as M l and the 3×3 transition matrix between marker l and l+1 as T l (where element t ij is the conditional probability of marker l having IBD state j, given that marker l+1 has IBD state i), this summation can be written in matrix form as
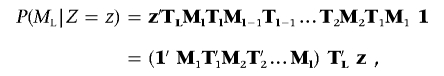
where T L is the transition matrix between marker l and the position, 1 is a 3×1 vector of 1s, and z is a 3×1 column vector that has value 1 for element z and value 0 for the others. The elements of M and T are given in tables 2 and 3, respectively, and are described in the section below.
Table 2. .
Calculation of Genotypic State M[Note]
| Genotypic-IBDState | ||
|---|---|---|
| _M_=_G_1,_G_2 | Z | P(M|Z) |
| AA, AA | 0 | 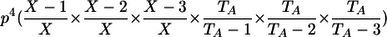 |
| AA, Aa | 0 | 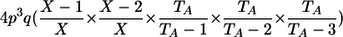 |
| AA, aa | 0 | 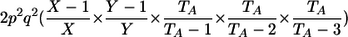 |
| Aa, Aa | 0 | 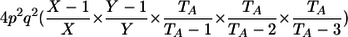 |
| Aa, aa | 0 | 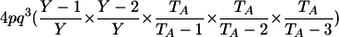 |
| aa, aa | 0 | 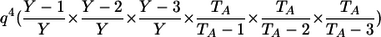 |
| AA, AA | 1 | 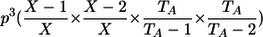 |
| AA, Aa | 1 | 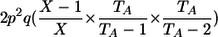 |
| AA, aa | 1 | 0 |
| Aa, Aa | 1 | 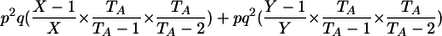 |
| Aa, aa | 1 | 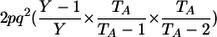 |
| aa, aa | 1 | 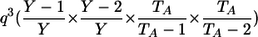 |
| AA, AA | 2 | 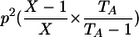 |
| AA, Aa | 2 | 0 |
| AA, aa | 2 | 0 |
| Aa, Aa | 2 | 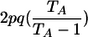 |
| Aa, aa | 2 | 0 |
| aa, aa | 2 | 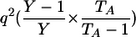 |
Table 3. .
Full Transition Matrix T Specifying P(Z l+1|Z l) for Diploid IBD State from Locus l to Locus l+1[Note]
The expression P(M L|Z) represents the “left conditional” probability based on markers 1 through l; the same procedure is used to calculate the chain of right-conditional probabilities for markers K back through l+1:
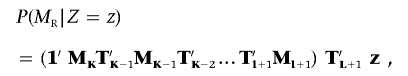
where T L+1 is the transition matrix between marker l+1 and the position.
For computational efficiency, the left conditionals (M_1_T_′1_M_2_T_′2…_M l) and right conditionals (M K T_′_K_-1_M K_-1_T_′_K_-2…_T_′_l+1_M_ l+1) are precomputed for different values of l and are used in the computation for conditional IBD probabilities of all positions. In practice, normalization steps must be performed at intervals to avoid underflow.
On the basis of these estimates of P(_Z_=z|M), shared segments are defined as any contiguous region having a >50% chance of having at least one pair of chromosomes shared IBD (we can ignore the negligible probability of distantly related individuals sharing two segments IBD). Please see appendix A for a detailed description of the HMM emission and transition parameters.
One requirement of this approach is that SNPs are in approximate linkage equilibrium in the population; otherwise, many small regions of high LD will be called as shared IBD segments. One approach is to prune the SNP panel to a reduced subset of approximately independent SNPs. As outlined in the next section, for the purpose of population-based linkage analysis, we expect most segments surrounding shared rare, recent variants to be relatively large, and therefore detectable, with a less dense SNP panel. We use a repeated sliding-window procedure, recursively pruning SNPs on the basis of pairwise SNP _r_2 values and/or the variance inflation factor, which is defined as 1/(1-_R_2), where _R_2 is the multiple correlation coefficient between a SNP and all other SNPs in the window based on allele counts. In the context of the population-based linkage test described below, failure to completely prune all sample-level LD should not be particularly troublesome. At worst, it will simply mean that a number of more common extended segments (that are perhaps better tested in a standard association design) will be included in the analysis, possibly reducing efficiency.
The results of applying this method to phase II HapMap data, in terms of the typical distribution and extent of extended segmental sharing and its relationship to rare variation, are described in the International HapMap Consortium phase II analysis manuscript (International HapMap Consortium, unpublished data). Here, we apply the method to CEU (Utah residents with European ancestry from the CEPH collection) HapMap individuals. For illustrative purposes, we focus here only on a particular region of chromosome 9 shared between two families (parent-offspring trios). Genomewide data about the full CEU panel were still used to calculate allele frequencies (founders only) and global IBD-sharing estimates. We selected SNPs with complete genotyping and MAF >1% and then iteratively removed SNPs showing local LD; the final chromosome 9 data set comprised 6,513 SNPs (∼1 per 20 kb). In the CEU sample as a whole, there is virtually no LD in the pruned data set: for the entire chromosome 9, only six LD blocks are identified, comprising 15 SNPs in total (three blocks containing 2 SNPs and three blocks containing 3 SNPs).
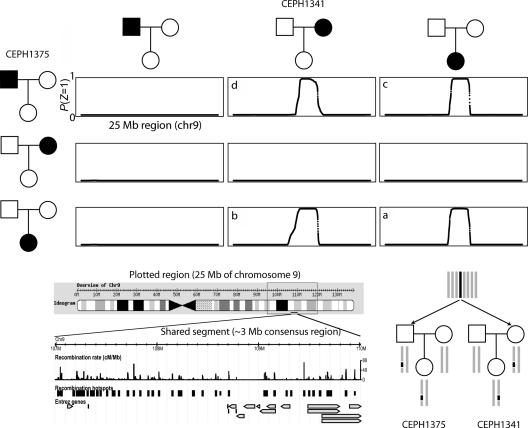
We present here a single segment shared between two CEU offspring, NA10863 and NA06991. This segment spans ∼3.7 Mb and, in the pruned data set, 272 SNPs. The phase II HapMap has >4,500 SNPs in this region (CEU panel) and dozens of estimated recombination hotspots. We selected a segment shared between two offspring for illustrative purposes: given that the region is shared IBD, we would also expect to see a pattern of sharing consistent with transmission from one and only one parent in each family, as illustrated in figure 2. That is, we also observe the same segment shared between each offspring and one parent of the other family and also between these two parents. (Naturally, parent-offspring pairs within the same family are always IBD 1; these basic intrafamilial relationships are not shown in fig. 2).
Figure 2. .
Example segment shared IBD between two HapMap CEU offspring individuals and their parents. The main set of plots show the multipoint estimate of IBD sharing, P(_Z_=1), for a 25-Mb region of chromosome 9, for the pairs of individuals between two families (CEPH1375 and CEPH1341). The region was selected because the two offspring (NA10863 and NA06991) showed sharing in this region, shown in plot a. The three other segments shared between seemingly unrelated individuals are shown—that is, between the offspring in one family and a parent in the other family (two plots labeled b and c) and between those two parents (plot d). The lower-left diagram illustrates the region shared; this extended haplotype spans multiple haplotype blocks and recombination hotspots in the full phase II data. The lower-right diagram depicts the pattern of gene flow for this particular region—that is, a segment of the original common chromosome (dark rectangles) appears in the two families as shown.
No other pairs of individuals show any extended segmental sharing in this same region. This type of rare, extended segment is an example of shared genetic variation that is outside the standard heuristic and analytic framework of LD involving only short, common “haplotype blocks” separated by recombination hotspots. Naturally, this approach can also be applied to detection of the much longer segments shared between very closely related individuals. There are, in fact, a number of close relationships between HapMap founders: in the CEU and YRI (Yoruba individuals from Ibadan, Nigeria) panels, there are a number of cousins and individuals with closer relationships (excluding known parent-offspring relationships, of course). For example, two CEU individuals, NA12154 and NA12264, have a global P(_Z_=1) of .14; shared segment analysis reveals at least 33 segments >1 Mb for this single pair. Six segments are >10 Mb, and the longest is 128 Mb (they share virtually all of one copy of chromosome 11). For this pair, the total proportion of the autosomes spanned by these segments (in terms of physical distance) is ∼0.12, which is close to the global probability of sharing one copy IBD of .14.
In a population-based sample of cases and controls, having determined the extent and location of pairwise segmental sharing with use of the approach described above, one might also want to inquire whether patterns of segmental sharing are related to phenotypic similarity between individuals. In this section, we describe a test based on the premises that (a) shared rare variants will typically reside on shared extended segments and (b) there will be an inflation in the rate of segmental sharing at the disease locus in case/case pairs if rare variants influence disease risk. This represents a first-generation approach that can no doubt be extended and improved in numerous ways—for example, by considering other statistics based on segmental sharing.37,38
A sample of N A cases and N U controls contains N _AA_=N A(N _A_-1)/2 case/case pairs and N!_AA_=N A N U+N U(N _U_-1)/2 case-control and control/control pairs. At a particular position p, the number of segments shared at a particular locus (i.e., spanning that position) is denoted S p for all case/case pairs and T p for case/control and control/control pairs. A standard test for a difference in rate of sharing between these two groups is complicated by the fact that not all pairs are independent (since the same individuals will possibly feature in multiple pairs); also, not all pairs have similar degrees of global relatedness. To account for the dependence, we use permutation to generate empirical significance values by label-swapping individuals’ phenotypes and recalculating the pairwise phenotypic concordance metrics (i.e., rather than permuting the pairwise concordance terms directly). The test statistic is framed as a one-sided test (i.e., greater sharing in case/case pairs) and adjusts for the average level of global sharing in the two categories; for position p of L positions,
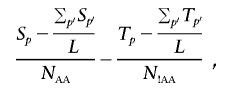
which is bounded at 0 (in addition,
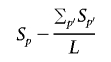
and
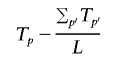
are also bounded at 0). The permutation procedure is computationally feasible, since the IBD segments do not need to be recomputed for each replicate.
Given regions that show statistically significant levels of increased sharing among cases, one can use PLINK to determine the allelic identity of the specific sets of overlapping segments present (although without inferring phase when both individuals are heterozygous). The results of such an analysis should be similar in principle to those from a linkage analysis, except that signals will be localized on a finer scale.
Performance.—Very large WGAS data sets can be analyzed using fairly standard hardware, and there are no fixed limits on the number of samples or SNPs. For example, a Linux workstation with 2 GB random-access memory and a 3.6-GHz dual processor can handle >5,000 individuals genotyped for 500,000 SNPs. On the same machine, one can load (using a binary format file set) the entire phase II HapMap (3.6 million SNPs for 270 individuals), filter on genotyping rate, and then calculate and output allele frequencies for all SNPs in <6 min.
Although analyses that involve pairwise comparisons between all individuals can take a long time in large samples (in particular, calculating genomewide IBD and IBS for all individuals), if a cluster-computing environment is available, such jobs are easily parallelized, and PLINK provides some options to facilitate this, potentially reducing analyses that might take days to 1 or 2 h with little extra work on the part of the user.
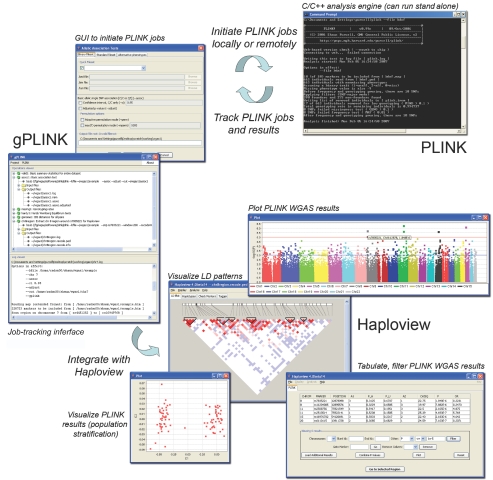
Graphical user interface.—We have also developed a separate, optional Java-based graphical user interface, gPLINK, to initiate, track, and record PLINK jobs. In addition, gPLINK provides integration with Haploview,39; version 4 of Haploview offers extensive tools for tabulating, filtering, sorting, merging, and visualizing PLINK WGAS output files in the context of HapMap LD and genomic information. gPLINK can also extract filtered subsets of WGAS data for viewing in Haploview with just a few mouse clicks. gPLINK either can be used to direct local analyses (with data and computation residing on the same local machine) or can remotely use secure shell networking (with data and computation performed by the remote server, but with initiation and viewing of results done locally). Figure 3 illustrates the relationship among PLINK, gPLINK, and Haploview.
Figure 3. .
Schema of integration of PLINK, gPLINK, and Haploview. PLINK is the main C/C++ WGAS analytic engine that can run either as a stand-alone tool (from the command line or via shell scripting) or in conjunction with gPLINK, a Java-based graphical user interface (GUI). gPLINK also offers a simple project management framework to track PLINK analyses and facilitates integration with Haploview. It is easy to configure these tools, such that the whole-genome data and PLINK analyses (i.e., the computationally expensive aspects of this process) can reside on a remote server, but all initiation and viewing of results is done locally—for example, on a user’s laptop, connected to the whole-genome data via the Internet, by use of gPLINK’s secure shell networking.
In summary, PLINK offers a powerful, user-friendly tool for performing many common analyses with whole-genome data. There is comprehensive Web-based documentation, including a tutorial, an e-mail list, and a Web-based version-check to inform users of updates and problems. As methods for WGAS evolve, we expect that PLINK will be updated. For example, as of this report going to press, newly added features include support for R plug-ins to extend the basic functionality of PLINK, a Web-based SNP annotation look-up tool, and a set of “proxy association” methods, designed to explore single SNP associations in their local haplotypic context. The proxy association tools provide, among other things, a haplotype-based single-SNP test that can often be more robust to nonrandom missing genotype data. Future directions include enhanced tools for browsing annotated WGAS results in their full genomic context and the incorporation of copy-number–variation data.
We have also implemented an approach based on the MRV hypothesis that is designed to be a complement, rather than an alternative, to association analysis. In this report, we have outlined our analytic approach and have described an implementation of the method that is appropriate for whole-genome SNP data. Following decades of work mapping Mendelian disease genes, this approach uses haplotypes of common alleles to measure very rare variation. This is an example of how one can take multiple approaches to existing high-density SNP array data, rather than needing to embark on a completely orthogonal data collection to execute a MRV-oriented test.
Standard association will be much more powerful when a single common causal variant is directly assayed or well captured by a tag SNP. When the CD/CV hypothesis does not hold, however, we hope that this approach will perform better. In this case, straightforward association approaches are unlikely to succeed, since the rare variants will most likely not be identified, genotyped, or tagged with sufficient precision; in any case, there will typically be too few observations to provide adequate statistical power for standard association tests of any one rare variant.
We are currently embarking on the next step—to determine the potential power of such an approach under a range of scenarios and to determine the best way to apply this method to real data. Possible extensions of this approach include allowing for LD between SNPs, genotyping error, and inbreeding in the IBD estimation. This approach could also be applied to detecting autozygous segments within a single individual, allowing for population-based homozygosity mapping to map recessive disease loci.
Acknowledgments
We acknowledge support from the National Institutes of Health (NIH) National Heart, Lung, and Blood Institute ENDGAME project grant U01 HG004171 (to S.P., M.J.D., and P.I.W.d.B.), from NIH grant EY-12562 (to S.P. and P.C.S.), from The Research Grants Council of Hong Kong, Project Number HKU 7669/06M (to S.P. and P.C.S.), from The University of Hong Kong Strategic Research Theme on Genomics, Proteomics and Bioinformatics (to P.C.S.), from National Health and Medical Research Council of Australia Sidney Sax fellowship 389927 (to M.A.R.F.), and from NIH/National Institute of Mental Health grant R03 MH73806-01A1 (to S.P.). We also thank the NINDS Repository at Coriell for making the data from the Laboratory of Neurogenetics (part of the intramural program of the National Institute on Aging, NIH) available free of charge. These data were deposited by John Hardy and Andrew Singleton; we accessed the data (upload identification numbers 7 and 8) at the Queue portal at the Coriell Institute. Finally, we thank PLINK users, both within the Broad Institute Medical and Population Genetics Program and elsewhere, for all feedback.
Appendix A: Description of HMM Emission and Transition Parameters, M and T
The elements of M_—the probability of the pair’s genotypes for that SNP conditional on IBD state—_P(M|Z)) are calculated according to table 2. These values are a function of allele frequency, including an ascertainment correction term, which follows the procedure described above in the calculation of global IBD probabilities. Markers with missing genotypes are assigned an identity matrix M.
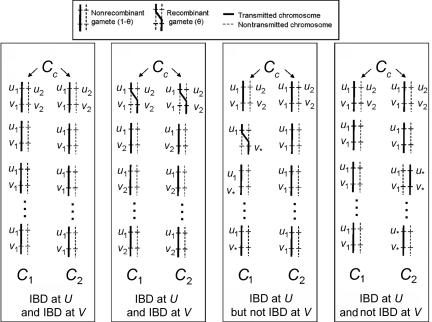
The elements of T, the transition probabilities between two IBD states at neighboring loci, are precalculated in terms of the recombination fraction estimated from a specified genetic map and global relatedness for that pair, P(Z). With dense SNP maps, the method is not particularly sensitive to the precise genetic map used: in practice, a basic 1 _cM_=1 Mb approximation appears to work well, although one could also use the fine-scale recombination map.36 For each pair of individuals, we estimate the least number of meioses that separate the two genomes and use these estimates to specify a transition matrix for unobserved IBD states along the chromosome. Specifically, we consider two chromosomes, or haploid genomes (_C_1 and _C_2), that share a common ancestor (C C, a diploid genome), with _C_1 and _C_2 separated by m meioses. If _C_1 and _C_2 are present in distinct individuals, then _m_⩾2, whereas, if _C_1 and _C_2 are in the same person, then _m_⩾3. At a particular locus, U, the probability that _C_1 and _C_2 are IBD is (1/2)(_m_-1). That is, if we label the allele transmitted in the first meiosis from C C as “_u_1,” there is probability (1/2)(_m_-1) that all the other _m_-1 meioses also transmit _u_1. Now, consider a second locus, V, that is linked to U with recombination fraction θ. Let the alleles at V present in C C be _v_1 and _v_2, with allele _v_1 in coupling phase with allele _u_1. Figure A1 shows some examples of possible transmission patterns and the corresponding IBD states for _C_1 and _C_2, which we outline here.
Figure A1. .
Example transmissions and corresponding IBD states. For two haploid genomes, _C_1 and _C_2, the figure illustrates four (of many) possible patterns of transmission and the corresponding IBD states at two positions, U and V. The text describes how consideration of these possible scenarios leads to the specification of transition matrices for IBD state along the chromosome.
For _C_1 and _C_2 to be IBD at V, they must either both share allele _v_1 or allele _v_2. For _C_1 and _C_2 to both share allele _v_1, given that _C_1 and _C_2 are IBD at U for allele _u_1, which is in coupling phase with _v_1 in the common ancestor C C, all the m meioses must be nonrecombinants, so that _v_1 is cotransmitted with _u_1 all the way down to _C_1 and _C_2. The probability of this is (1-θ)m. For _C_1 and _C_2 to both share allele _v_2, given that _C_1 and _C_2 are IBD at U for allele _u_1, which is in repulsion phase with _v_2 in the common ancestor C C, the two meioses of C C must both be recombinants (so that _v_2 crosses over to be cotransmitted with _u_1), and all the remaining _m_-2 meioses must be nonrecombinants, so that _v_2 is cotransmitted with _u_1 all the way down to _C_1 and to _C_2. The probability of this is θ2(1-θ)(_m_-2). If these two possibilities are taken together, the probability that _C_1 and _C_2 are IBD at V, given that they are IBD at U, is

which can be rewritten as (1-θ)(_m_-2)[θ2+(1-θ)2]. The probability that _C_1 and _C_2 are IBD at V, given that they are not IBD at U, is given by the Bayes theorem:
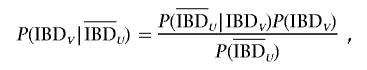
which simplifies to
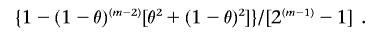
This equation involves two parameters, θ and m. Because of the assumption of very closely spaced markers, we use the Morgan map function θ=d, where d is the genetic distance between the loci in Morgans. For m, we consider the two pairs of haploid genomes (each pair containing a haploid genome from each individual) that may have common ancestry and estimate the numbers of meioses (m A and m B) that separate the two pairs. If x A and x B are the probabilities that the two pairs of haploid genomes are IBD, then
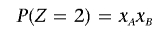
and
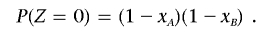
Substituting x _B_=P(_Z_=2)/x A into the second expression, we obtain
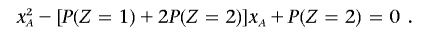
Solving this equation gives x A and x B. These IBD probabilities (x) are related to the number of meioses separating the haploid genomes (m) by _x_=(1/2)(_m_-1). Therefore, if P(_Z_=2)=0, then
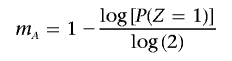
and m _B_=0; otherwise,
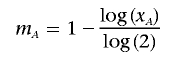
and
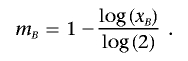
Note that the quadratic equation
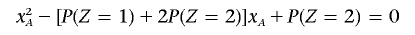
has real roots only if
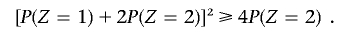
This gives rise to the inequality P(_Z_=2)⩽π2 in the previous section on constraining global IBD estimates to biologically plausible values. The form of the transition matrix for pairs of haploid genomes (denoted A and B) is given in table A1; these are combined to form the full transition matrix for a diploid genome in table 3.
Table A1. .
Structure of Transition Submatrices A (where _m_=m A) and B (where _m_=m B) for Two Haploid Genomes[Note]
Web Resources
The URLs for data presented herein are as follows:
- Haploview, http://www.broad.mit.edu/mpg/haploview/
- HapMap, http://www.hapmap.org/
- PLINK and gPLINK, http://pngu.mgh.harvard.edu/purcell/plink/
- Queue portal at the Coriell Institute, https://queue.coriell.org/q/
References
- 1.Lander ES, Schork NJ (1994) Genetic dissection of complex traits. Science 265:2037–2048 (erratum 266:353) 10.1126/science.8091226 [DOI] [PubMed] [Google Scholar]
- 2.Risch N, Merikangas K (1996) The future of genetic studies of complex human diseases. Science 273:1516–1517 10.1126/science.273.5281.1516 [DOI] [PubMed] [Google Scholar]
- 3.Hirschhorn JN, Lohmueller K, Byrne E, Hirschhorn K (2002) A comprehensive review of genetic association studies. Genet Med 4:45–61 [DOI] [PubMed] [Google Scholar]
- 4.Ioannidis JP, Trikalinos TA, Khoury MJ (2006) Implications of small effect sizes of individual genetic variants on the design and interpretation of genetic association studies of complex diseases. Am J Epidemiol 164:609–614 10.1093/aje/kwj259 [DOI] [PubMed] [Google Scholar]
- 5.Reich DE, Lander ES (2001) On the allelic spectrum of human disease. Trends Genet 17:502–510 10.1016/S0168-9525(01)02410-6 [DOI] [PubMed] [Google Scholar]
- 6.Freedman ML, Reich D, Penney KL, McDonald GJ, Mignault AA, Patterson N, Gabriel SB, Topol EJ, Smoller JW, Pato CN, et al (2004) Assessing the impact of population stratification on genetic association studies. Nat Genet 36:388–393 10.1038/ng1333 [DOI] [PubMed] [Google Scholar]
- 7.Devlin B, Roeder K (1999) Genomic control for association studies. Biometrics 55:997–1004 10.1111/j.0006-341X.1999.00997.x [DOI] [PubMed] [Google Scholar]
- 8.Pritchard JK, Stephens M, Donnelly PJ (2000) Inference of population structure using multilocus genotype data. Genetics 155:945–959 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Purcell S, Sham PC (2004) Properties of structured association approaches to detecting population stratification. Hum Hered 58:93–107 10.1159/000083030 [DOI] [PubMed] [Google Scholar]
- 10.Price AL, Patterson NJ, Plenge RM, Weinblatt ME, Shadick NA, Reich D (2006) Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet 38:904–909 10.1038/ng1847 [DOI] [PubMed] [Google Scholar]
- 11.Clayton DG, Walker NM, Smyth DJ, Pask R, Cooper JD, Maier LM, Smink LJ, Lam AC, Ovington NR, Stevens HE, et al (2005) Population structure, differential bias and genomic control in a large-scale, case-control association study. Nat Genet 37:1243–1246 10.1038/ng1653 [DOI] [PubMed] [Google Scholar]
- 12.Hirschhorn JN, Daly MJ (2005) Genome-wide association studies for common diseases and complex traits. Nat Rev Genet 6:95–108 10.1038/nrg1521 [DOI] [PubMed] [Google Scholar]
- 13.Pritchard JK (2001) Are rare variants responsible for susceptibility to complex diseases? Am J Hum Genet 69:124–137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Houwen RH, Baharloo S, Blankenship K, Raeymaekers P, Juyn J, Sandkuijl LA, Freimer NB (1994) Genome screening by searching for shared segments: mapping a gene for benign recurrent intrahepatic cholestasis. Nat Genet 8:380–386 10.1038/ng1294-380 [DOI] [PubMed] [Google Scholar]
- 15.te Meerman GJ, van der Meulen MA, Sandkuijl LA (1995) Perspectives of identity by descent (IBD) mapping in founder populations. Clin Exp Allergy 25:97–102 10.1111/j.1365-2222.1995.tb00433.x [DOI] [PubMed] [Google Scholar]
- 16.Wigginton JE, Cutler DJ, Abecasis GR (2005) A note on exact tests of Hardy-Weinberg equilibrium. Am J Hum Genet 76:887–893 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lee WC (2003) Detecting population stratification using a panel of SNPs. Int J Epidemiol 32:1120 10.1093/ije/dyg301 [DOI] [PubMed] [Google Scholar]
- 18.Diabetes Genetics Initiative of Broad Institute of Harvard and MIT, Lund University, and Novartis Institutes for BioMedical Research (2007) Genome-wide association analysis identifies novel loci for type 2 diabetes and triglyceride levels. Science 316:1331–1336 10.1126/science.1142358 [DOI] [PubMed] [Google Scholar]
- 19.Agresti A (1990) Categorical data analysis. John Wiley, New York, pp 100–102 [Google Scholar]
- 20.Fleiss JL (1981) Statistical methods for rates and proportions, 2nd ed. Wiley, New York [Google Scholar]
- 21.Ewens WJ, Spielman RS (1995) The transmission/disequilibrium test: history, subdivision, and admixture. Am J Hum Genet 57:455–465 [PMC free article] [PubMed] [Google Scholar]
- 22.Spielman RS, Ewens WJ (1998) A sibship test for linkage in the presence of association: the sib transmission/disequilibrium test. Am J Hum Genet 62:450–458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fulker DW, Cherny SS, Sham PC, Hewitt JK (1999) Combined linkage and association sib-pair analysis for quantitative traits. Am J Hum Genet 64:259–267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Abecasis GR, Cardon LR, Cookson WO (2000) A general test of association for quantitative traits in nuclear families. Am J Hum Genet 66:279–292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Purcell S, Sham PC, Daly MJ (2005) Parental phenotypes in family-based association analysis. Am J Hum Genet 76:249–259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ferreira MAR, Sham PC, Daly MJ, Purcell S (2007) Ascertainment through family history of disease often decreases the power of family-based association studies. Behav Genet 37:631–636 10.1007/s10519-007-9149-0 [DOI] [PubMed] [Google Scholar]
- 27.Pe’er I, de Bakker PI, Maller J, Yelensky R, Altshuler D, Daly MJ (2006) Evaluating and improving power in whole-genome association studies using fixed marker sets. Nat Genet 38:605–606 10.1038/ng1816 [DOI] [PubMed] [Google Scholar]
- 28.Hoh J, Wille A, Ott J (2001) Trimming, weighting, and grouping SNPs in human case-control association studies. Genome Res 11:2115–2119 10.1101/gr.204001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Besag J, Clifford P (1991) Sequential Monte Carlo p-values. Biometrika 78:301–304 [Google Scholar]
- 30.Churchill GA, Doerge RW (1996) Empirical threshold values for quantitative trait mapping. Genetics 142:285–294 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Benjamini Y, Hochberg Y (1995) Controlling the false discovery rate—a practical and powerful approach to multiple testing. J R Stat Soc Ser B 57:289–300 [Google Scholar]
- 32.Milligan BG (2003) Maximum-likelihood estimation of relatedness. Genetics 163:1153–1167 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Broman KW, Weber JL (1999) Long homozygous chromosomal segments in reference families from the Centre d’Étude du Polymorphisme Humain. Am J Hum Genet 65:1493–1500 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Puffenberger EG, Hu-Lince D, Parod JM, Craig DW, Dobrin SE, Conway AR, Donarum EA, Strauss KA, Dunckley R, Cardenas JF, et al (2004) Mapping of sudden infant death with dysgenesis of the testes syndrome (SIDDT) by a SNP genome scan and identification of TSPYL loss of function. Proc Natl Acad Sci USA 101:11689–11694 10.1073/pnas.0401194101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Lander ES, Green P (1987) Construction of multilocus genetic linkage maps in humans. Proc Natl Acad Sci USA 84:2363–2367 10.1073/pnas.84.8.2363 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Myers S, Bottolo L, Freeman C, McVean G, Donnelly P (2005) A fine-scale map of recombination rates and hotspots across the human genome. Science 310:321–324 10.1126/science.1117196 [DOI] [PubMed] [Google Scholar]
- 37.Wang Y, Zhao LP, Dudoit S (2006) A fine-scale linkage-disequilibrium measure based on length of haplotype sharing. Am J Hum Genet 78:615–628 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Beckmanna L, Thomas DC, Fischer C, Chang-Claudea J (2005) Haplotype sharing analysis using Mantel statistics. Hum Hered 59:67–78 10.1159/000085221 [DOI] [PubMed] [Google Scholar]
- 39.Barrett JC, Fry B, Maller J, Daly MJ (2005) Haploview: analysis and visualization of LD and haplotype maps. Bioinformatics 21:263–265 10.1093/bioinformatics/bth457 [DOI] [PubMed] [Google Scholar]