The evolution of genome compression and genomic novelty in RNA viruses (original) (raw)
Abstract
The genomes of RNA viruses are characterized by their extremely small size and extremely high mutation rates (typically 10 kb and 10−4/base/replication cycle, respectively), traits that are thought to be causally linked. One aspect of their small size is the genome compression caused by the use of overlapping genes (where some nucleotides code for two genes). Using a comparative analysis of all known RNA viral species, we show that viruses with larger genomes tend to have less gene overlap. We provide a numerical model to show how a high mutation rate could lead to gene overlap, and we discuss the factors that might explain the observed relationship between gene overlap and genome size. We also propose a model for the evolution of gene overlap based on the co-opting of previously unused ORFs, which gives rise to two types of overlap: (1) the creation of novel genes inside older genes, predominantly via +1 frameshifts, and (2) the incremental increase in overlap between originally contiguous genes, with no frameshift preference. Both types of overlap are viewed as the creation of genomic novelty under pressure for genome compression. Simulations based on our model generate the empirical size distributions of overlaps and explain the observed frameshift preferences. We suggest that RNA viruses are a good model system for the investigation of general evolutionary relationship between genome attributes such as mutational robustness, mutation rate, and size.
The two most striking attributes of RNA viruses are their small size and their high mutation rate. The average genome length of a family is only 9 kb, with the longest being the Coronaviridae at 29 kb. Viral polymerases (RNA-dependent RNA replicases and reverse transcriptases) have a high misincorporation frequency and lack a proofreading 3′ to 5′ exonuclease domain (Steinhauer et al. 1992); there is also no mismatch repair, even in double-stranded RNA viruses. This leads to mutation rates in the order of 10−4 per base per round of replication (Drake and Holland 1999; Mansky 2000; Crotty et al. 2001), several orders of magnitude higher than those found in DNA-based life forms (Drake et al. 1998). The deleterious effects of most mutations in RNA viruses are well studied (Sanjuan et al. 2004; Elena et al. 2006).
These two attributes have been linked most recently by Holmes (2003), who suggests that the genome size of an RNA virus is limited by its mutation rate. This argument is derived from the inverse relationship, first identified by Eigen (1971), expected between the size of any replicating molecule (its information content) and its mutation (error) rate. For example, a hypothetical 1-Mb RNA virus (the size of the largest DNA virus) with a mutation rate similar to that of known RNA viruses would be unable to replicate without incurring lethal mutations. Indeed, the idea that RNA viruses exist near a so-called error threshold, determined by a function of their genome size and mutation rate (Nowak 1992), lies behind the development of drug therapies that artificially elevate the viral mutation rate—referred to as lethal mutagenesis (Crotty et al. 2001). Consistent with this theoretically predicted relationship, RNA viral substitution rates do indeed appear to be negatively related to genome size (Jenkins et al. 2002), although substitution rates may not always reflect mutation rates. Thus, larger viruses may have evolved lower per site mutation rates in order to avoid an excessively high genomic mutation rate. These arguments have also been extended to various DNA-based microbes (several DNA viruses, Escherichia coli, Saccharomyces cerevisiae, and Neurospora crassa) with the observation that, across a wide range of genome sizes and per base mutation rates, the genomic mutation rate remains approximately constant (at ∼0.003 per round of replication) (Drake et al. 1998).
One aspect of the small size of RNA viruses is the genome compression resulting from gene overlap, i.e., where some nucleotides code for more than one protein as a result of being simultaneously in two translated ORFs (open reading frames). Many RNA virus species are known to exhibit some gene overlap, which can be caused by several unrelated molecular mechanisms: ribosomal frameshifting, RNA splicing, formation of subgenomic mRNAs, the use of non-AUG start codons, and RNA editing (the facultative addition of bases during transcription) (Lower et al. 1995; Hausmann et al. 1999; Baril and Brakier-Gingras 2005).
Gene overlap is an aspect of genome compression that can be readily quantified. Here we analyze the genome structure of all known RNA viruses and investigate the relationship between overlap and genome length. We find that there tends to be less gene overlap in viruses with larger genomes. We show how a high mutation rate could drive the evolution of gene overlap, and we discuss various explanations for this relationship between overlap and genome size.
We also investigate how gene overlap may have evolved and propose an evolutionary model involving two distinct processes: new genes being created in other frames within existing genes, and incremental overlap between originally contiguous genes that happen to be in different frames. The model involves the translation of new, previously “unused” ORFs derived from the gain and loss of start and stop codons, respectively, and the gradual acquisition of function by these novel proteins. Simulations based on this model both reproduce the empirical distributions of gene overlap sizes and explain the observed frameshift preferences. We suggest that both these processes allow for the gain of genomic function while under selection pressure for genome compression.
Results
Gene overlap and genome length
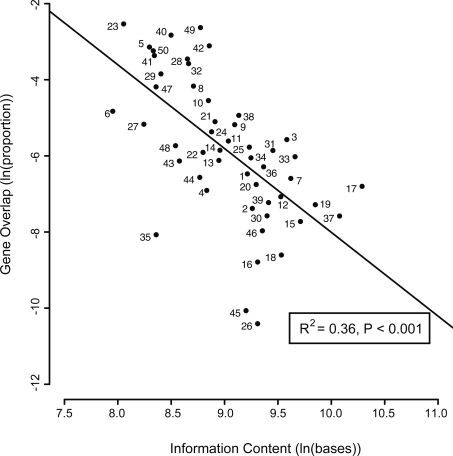
Our analysis shows 819 instances of gene overlap among the 701 reference RNA viral genomes, with 56% of the viruses having some gene overlap. After calculating, for each viral family, the mean overlap as a proportion of its total information content (which we define here as genome length plus overlap length; see Methods), we find that viruses with larger genomes tend to have proportionately less gene overlap (linear regression, P < 0.001, _R_2 = 0.36; Fig. 1). This relationship is also significant using untransformed data that retain the zero overlap values—such zero values representing 16 of the 66 families (Spearman rank correlation, P = 0.012). The mean overlap across all virus families represents only 1% of their genome length, but the relationship with genome size results in mean overlap being 2% in families with genomes smaller than the median length, and 0.1% in families with larger genomes.
Figure 1.
Relationship between gene overlap (as a proportion of information content) and information content, both expressed as natural logarithms. Points are means for the following taxa. 1, Acyrthosiphon pisum virus (n = 1); 2, Arenaviridae (n = 11); 3, Arteriviridae (n = 4); 4, Astroviridae (n = 6); 5, Barnaviridae (n = 1); 6, Beet western yellows ST9 associated virus (n = 1); 7, Benyvirus (n = 2); 8, Birnaviridae (n = 5); 9, Bornaviridae (n = 1); 10, Botrytis virus X (n = 1); 11, Bromoviridae (n = 22); 12, Bunyaviridae (n = 20); 13, Caliciviridae (n = 13); 14, Caulimoviridae (n = 23); 15, Closteroviridae (n = 16); 16, Comoviridae (n = 18); 17, Coronaviridae (n = 12); 18, Cystoviridae (n = 4); 19, Filoviridae (n = 4); 20, Flaviviridae (n = 34); 21, Flexiviridae (n = 52); 22, Fusarium graminearum dsRNA mycovirus 1 (n = 1); 23, Hepadnaviridae (n = 10); 24, Hepeviridae (n = 1); 25, Hordeivirus (n = 1); 26, Hypoviridae (n = 4); 27, Leviviridae (n = 8); 28, Luteoviridae (n = 17); 29, Nodaviridae (n = 8); 30, Ophiovirus (n = 3); 31, Orthomyxoviridae (n = 5); 32, Oyster mushroom spherical virus (n = 1); 33, Paramyxoviridae (n = 28); 34, Pecluvirus (n = 2); 35, Picobirnavirus (n = 1); 36, Pomovirus (n = 4); 37, Reoviridae (n = 21); 38, Retroviridae (n = 40); 39, Rhabdoviridae (n = 17); 40, Sclerophthora macrospora virus A (n = 1); 41, Sobemovirus (n = 9); 42, Tetraviridae (n = 4); 43, Thielaviopsis basicola dsRNA virus 1 (n = 1); 44, Tobamovirus (n = 15); 45, Tobravirus (n = 3); 46, Togaviridae (n = 16); 47, Tombusviridae (n = 35); 48, Totiviridae (n = 20); 49, Tymoviridae (n = 12); 50, Umbravirus (n = 4). The following taxa are excluded because of zero overlap: Botrytis virus F (n = 1), Cheravirus (n = 2), Chrysoviridae (n = 1), Diaporthe ambigua RNA virus 1 (n = 1), Dicistroviridae (n = 12), Endornavirus (n = 1), Furovirus (n = 5), Idaeovirus (n = 1), Iflavirus (n = 7), Marnaviridae (n = 1), Narnaviridae (n = 8), Partitiviridae (n = 14), Picornaviridae (n = 31), Potyviridae (n = 54), Sequiviridae (n = 6), and Tenuivirus (n = 2).
Characteristics of gene overlap
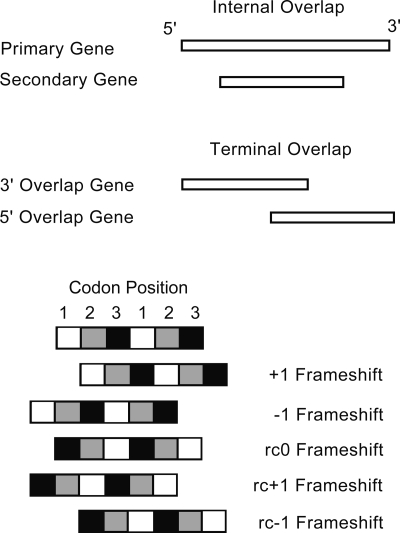
Of the 819 instances of gene overlap that we observe among RNA viruses (Table 1), almost all involve either a simple +1 (forward) frameshift or a simple −1 (backward) frameshift (Fig. 2). We can place these overlaps into two categories. Some genes are entirely within a second gene but in a different reading frame, and we call these “Internal Overlaps.” A majority of gene overlaps, however, involve only the 3′ end of one gene and the 5′ end of another, and we call these “Terminal Overlaps.” Both categories of overlap are significantly less common in viruses with larger genomes (linear regression; P < 0.001), although the relationship is more marked among Internal Overlaps (_R_2 = 0.65). We observe several differences between these two categories of overlap.
Table 1.
Summary of overlaps among reference RNA genomes
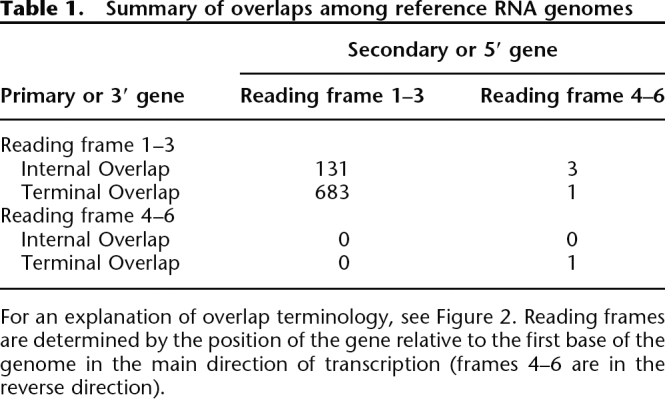
Figure 2.
Explanation of terminology used to describe gene overlaps. (Note that some other investigators use a +2 notation to represent our −1 frameshift.)
Length
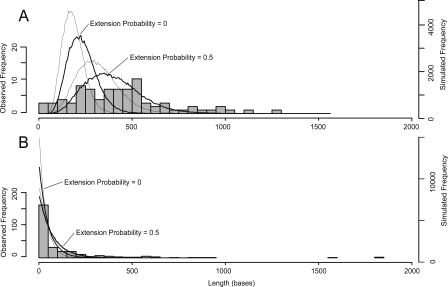
The frequency distributions of the sizes of these two categories of overlap are shown in Figure 3, with each data point being the mean of a homologous group of overlaps (see Methods). Internal Overlaps tend to be longer, with a mean length of 466 bases compared with only 137 bases for Terminal Overlaps. There are, however, three outlying very long Terminal Overlaps (>1500 bases in length). We suspect that these may have arisen as internals and then extended to become terminals (see Discussion), and, if we exclude these, the mean length of Terminal Overlaps is reduced to 105 bases.
Figure 3.
Frequency distribution of observed overlap lengths and the lengths of ORFs recovered by our simulation. (A) Internal Overlaps: observed and simulated data. (B) Terminal Overlaps: observed and simulated data. Observed overlap lengths are shown as histograms with each value being the mean of a homologous group. Simulated ORF lengths are shown as lines that connect the mid points of a hidden histogram: The thick lines show the +1 frameshift, and the thin line shows the −1 frameshift; the effect of including an extension probability of 0.5 in the simulation is also indicated.
Frameshift
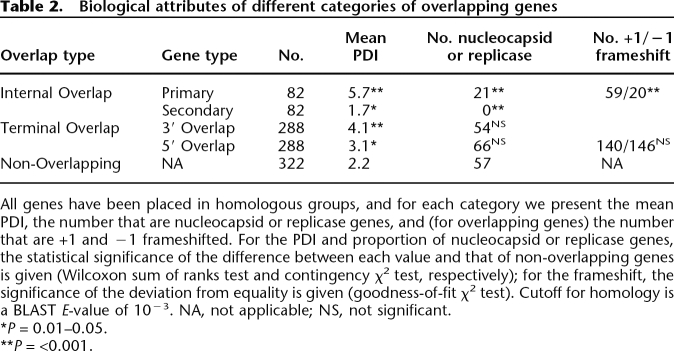
Among the observed Internal Overlaps, +1 frameshifts are significantly more common than −1 frameshifts: 59 and 20 instances of each, respectively (goodness-of-fit χ2 test, P < 0.001) (Table 2). In contrast, among Terminal Overlaps they are equally common: 140 and 146, respectively.
Table 2.
Biological attributes of different categories of overlapping genes
Age
Among Internal Overlaps, we call the longer gene the “Internal Primary” gene and the shorter gene that is overlapped the “Internal Secondary” gene (Fig. 2). Using our estimate of relative age, the PDI (phylogenetic dispersion index; see Methods), we find that Internal Primaries tend to be older than non-overlapping genes, as determined by their high PDI, while the Internal Secondaries tend to be younger (Table 2). In contrast, all the genes involved in Terminal Overlaps, whether overlapping at their 3′ or 5′ ends (Fig. 2) tend to be older than non-overlapping genes. Considering those genes that are either nucleocapsids or replicases, which we consider a priori to be older and less likely to be acquired secondarily than any other functional category (see Methods), we find a significantly higher proportion among Internal Primaries but a significantly lower proportion among Internal Secondaries, compared with non-overlapping genes (both nucleocapids and replicases separately show this trend; data not shown). The genes involved in Terminal Overlaps have a similar proportion of nucleocapsids or replicases compared with non-overlapping genes.
Why does gene overlap evolve?
Given the likely role of the high mutation rate of RNA viruses in constraining genome size, gene overlap may be a way of acquiring genomic novelty, in the form of new or longer genes, while under this constraint. If most mutations are deleterious and the rate of mutation per base is constant, gene overlap will have two conflicting effects on individual fitness: It will reduce the number of mutations that occur per replication because the number of nucleotides necessary to encode the viral genes is smaller, but it will increase the deleterious effect of those mutations because some will affect more than one gene. The interaction between these two effects is neither intuitively obvious nor easily represented by a simple analytical model. We can, however, readily simulate them, and estimates exist for the values of the necessary parameters. A summary of studies using 14 RNA viruses (Burch et al. 2003) found no strong evidence for epistasis, with most fitting a standard multiplicative model for fitness of e_−sn_, where s is the selection coefficient and n is the number of mutations (Elena and Lenski 1997). We have reasonable estimates for these values: The median value of s across RNA viruses is 0.1 (Elena et al. 2006), and n can be calculated from a typical viral genome length of 104 bases and per base mutation rate of 10−4 (Drake and Holland 1999).
We therefore simulated the interaction between the effect on fitness of mutation and overlap by representing the number of mutations in viral progeny by a Poisson distribution (with mean equal to the per base mutation rate multiplied by genome length). The proportion of these mutations that occur in regions of gene overlap is given by a binomial distribution, and these are treated as two mutations. The mean fitness of progeny is then calculated using e_−sn_.
We then changed the proportion (p) of the genome that is involved in a gene overlap from zero to one: The information content (as defined earlier) thus remains constant while the genome length (the number of nucleotides) is reduced incrementally to a minimum of one-half of its starting value, at which point we have an overlap proportion of one and every nucleotide codes for two genes. Under this scheme, the fitness of progeny with a single mutation is [p × e−2_s_ + (1 − p) × e–_s_].
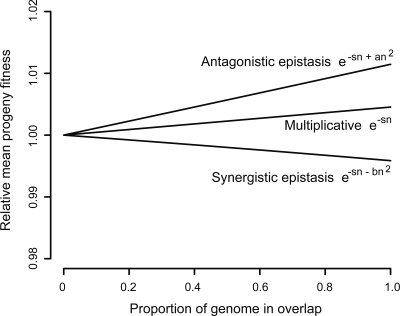
This simulation, coded in R and given in the Supplemental material, shows that fitness increases with the proportion of gene overlap (Fig. 4). This effect becomes stronger (the slope increases) if the mutation rate is increased. These findings are not affected by using an alternate model for multiplicative fitness, (1 − s)n (Wade et al. 2001) or by assuming antagonistic epistastic interactions, where multiple mutations have less than a multiplicative effect on fitness, as found in three of five other studies on RNA viruses (Sanjuan and Elena 2006). Only synergistic epistasis between mutations, where multiple mutations have greater than a multiplicative effect, results in gene overlap reducing fitness (an additive model leads to it having no effect).
Figure 4.
Simulation results showing effect of increasing gene overlap on the fitness effect of mutations, given different models for the interactions between mutations. Fitness is shown relative to the value for that model of fitness interaction at zero overlap. For epistatic interactions, taken from Elena and Lenski (1997), the additional fitness parameter values of a = 0.01 and b = 0.02 have been chosen for illustrative purposes only.
We do not, however, expect to see viruses with complete gene overlap because there is a cost to overlap not included in the model. This cost is the constraint on adaptation of the overlapping genes: both genes cannot be optimally adapted (see Discussion). Incorporating a cost to overlap in the model to represent this constraint, where this cost is an increasing function of the proportion of the genome that is overlapped, would lead to an intermediate optimum fitness. Unfortunately, there are no estimates of values for this parameter.
Thus the deleterious effect of the high mutation rate in RNA viruses may have led to the evolution of gene overlap, but there are other selective forces that may be involved. If we assume that a smaller genome will be quicker to copy, gene overlap will increase the rate of viral replication. Using a quasispecies model of viral population fitness, stable levels of gene overlap can be obtained given an increase in fitness caused by faster replication and an exponential cost of the evolutionary constraint that we discuss above (Krakauer 2000). A smaller genome will also require fewer resources from the host cell, and thus, the burst size would be larger.
Why do viruses with larger genomes have less gene overlap?
The simple model we describe above, using only mutation rate, does not explain this finding. Indeed, unless larger viruses have evolved a lower per base mutation rate as suggested in the Introduction, they would experience a higher mean number of mutations. In such a situation, we might even expect them to be more likely to evolve gene overlap.
A possible answer is provided by classical population genetic theory, but we are unsure how applicable this is to RNA viruses. Theory suggests that mean population fitness is determined by the mutation rate and not the degree to which those mutations are harmful (the Haldane-Muller principle). Briefly, the more harmful the mutation, the more quickly it should be removed from the population by selection (Haldane 1937; Kimura and Maruyama 1966). If we consider a virus composed of only two genes that are initially separated and that each have a rate of deleterious mutation m, its equilibrium mutation load is 2_m_ and its equilibrium fitness is thus 1 − 2_m_. If the virus were to overlap fully its two genes, this would reduce its mutation rate to m, giving an equilibrium mutation load m. If we now incorporate the cost of the evolutionary constraint, c, viral fitness becomes 1 − m − c. We might therefore expect overlap to evolve when (1 − m − c) > (1 − 2_m_), that is, when m > c. If the reduced substitution rate of larger RNA viruses does reflect a reduced per base mutation rate, then the above equations do predict the observed relationship between overlap and genome size—in larger viruses m is smaller while c is the same. These models assume that the mutation rate is low and that populations are at equilibrium. RNA viruses fit neither of these assumptions, and we believe that the explanation of why larger viruses have less overlap may await a more detailed analysis of the costs and benefits of overlap to individual fitness that we outline above.
How does gene overlap evolve?
Although gene overlaps are created by a range of very different molecular mechanisms, they all rely on the presence of ORFs in both frames. We therefore propose the following model for their origin. Internal Overlaps begin with the translation of a +1 or −1 frameshifted ORF within an existing gene, while Terminal Overlaps begin with the replacement of the terminating stop codon by one downstream that is in another gene, or the replacement of a start codon by one upstream that is in another gene, i.e., contiguous (immediately adjacent) genes extending over each other. We call these “unused ORFs” (they have also been referred to as “shadow,” ”redundant,” “off-frame,” or “out-of-phrase ORFs”). Translation of such unused ORFs could provide a pool of genomic novelty, some of which may acquire function and so become fixed in the population. By simulating the origin of genes via these unused ORFs we can account for some of the observed differences between Internal and Terminal Overlaps.
Length
We can recover the observed overlap lengths reasonably easily. For example, the unused ORF lengths in our simulation of Internal Overlaps are shorter than the observed overlaps: mean lengths 234 and 186 bases for +1 and −1 frameshifts, respectively (Fig. 3A); however, if we include in our simulation an extension probability of 0.5—representing the chance of another stop codon being acquired further downstream—this reproduces the observed distribution reasonably closely. The very small observed overlaps, which are not present in the simulated distribution, are all fragments of larger spliced genes (Supplemental Fig. S2). With a mean length of only ∼500 bases, these new genes in the form of Internal Secondaries are still small—the mean of an RNA viral ORF is ∼2000 bases. The unused ORF lengths in our simulation of Terminal Overlaps are also shorter than the observed overlaps, but incorporating an extension probability of 0.5 into the simulation also improves the match to the observed size distribution (Fig. 3B).
Frameshifts
For Internal Overlaps, our simulation shows that the underlying genetic code results in unused +1 ORFs being significantly longer than unused −1 ORFs (P < 0.001; Fig. 3A). If we assume that the creation of new genes via these unused ORFs involves a threshold minimum length, the majority of new genes created would be +1 frameshifted—which is what we observe. In contrast, our model for the evolution of Terminal Overlaps would not require a minimum threshold size to such overlaps (they are extensions to pre-existing genes), and hence we would not expect any bias toward +1 frameshifts. Our simulation also shows that unused +1 frameshifted ORFs are significantly longer (49 compared with 37 bases) but, consistent with our expectation, +1 and −1 frameshifts are equally common among observed Terminal Overlaps (Table 2).
Age
Our model can also account for some of the observed differences in relative age of genes involved in different types of overlap. The absence of replicases or nucleocapsids among Internal Secondary genes would reflect their relatively recent origin; in contrast, Terminal Overlaps represent the extension of existing genes that will already belong within functional groups, and hence the proportion of nucleocapsids or replicases would be similar. We might, nevertheless, expect genes involved in Terminal Overlaps on average to be older than non-overlapping genes if the overlaps have occurred gradually through time.
Discussion
We suspect that the deleterious effect of the high mutation rate in RNA viruses has led to the evolution of gene overlap. Peleg et al. (2004) came to the same conclusion using an analytical model based on individual fitness (although this model required assumptions about the probability of lethal mutations occurring in overlapping compared with nonoverlapping regions). A putative increase in the replication rate as a result of gene overlap may also be involved. One other factor is that the frameshift may produce a shift in the chemical properties of the new protein via a changed codon bias: e.g., if a gene has a biased nucleotide composition in its third codon position, then an overlapping second gene in a +1 frameshift will have this bias in its second codon position. Such overlaps might be a source of evolutionary novelty in the form of new proteins whose chemical properties differ from those of existing ones (Normark et al. 1983; Keese and Gibbs 1992).
We should point out that the observed preponderance of +1 frameshifts among Internal Overlaps cannot be explained by differences in selective constraint. As pointed out above, in an overlap there is likely to be conflicting selective pressures because nucleotides code for two genes. The extent of this constraint will depend upon how the codon positions overlie each other, and certain frameshifts will constrain the evolution of the two genes more than others. For example, there is a preponderance of rc − 1 frameshifts compared with rc0 and rc + 1 (Fig. 2) among prokaryote overlapping genes (Rogozin et al. 2002): This particular overlap has the least selective constraint because third codon positions overlay second codon positions. However, +1 and −1 frameshifts, which account for almost all the overlaps in RNA viruses, are identical in the extent to which they allow selective independence of the two genes (Krakauer 2000). The reason why +1 frameshifts tend to produce longer ORFs than −1 frameshifts lies in the observation that a wide range of organisms have a tendency to use a repeated RNY triplet in their coding sequences (Shepherd 1981; Jukes 1996). Therefore, frameshifts in the +1 and −1 directions will tend to result in a preponderance of NYR and YRN triplets, respectively, and we would expect to find more stop codons sequences (TAA,TAG, and TGA) by chance in a YRN-rich (−1 frameshifted) sequence than in a NYR-rich (+1 frameshifted) sequence. In our data set, the most frequently represented nucleotides at the three codon positions are G, A, and T, respectively (Supplemental Table S1). The +1 frameshift would thus make ATG (the start codon) the commonest triplet, while the −1 frameshift would make TGA (the Opal stop codon) the commonest. Clearly, we would therefore expect longer ORFs in a +1 shifted sequence. We note here that this triplet tendency overrides the fact that more of the 64 possible codons could potentially contribute to stop codons following a +1 rather than a −1 frameshift—36 compared with 22, respectively (Seligmann and Pollock 2004). Hence we might expect a protein-coding sequence that is randomly generated from the 64 possible codons to have shorter unused ORFs in +1 compared with −1 frameshifts. Seligmann and Pollock suggest that, across a range of taxa, particular codon usage biases have evolved so as to increase the frequency of stop codons in unused ORFs and hence reduce the wastage caused by the translation of accidentally frameshifted genes.
Our model for the evolution of gene overlap in RNA viruses comprises two separate processes, one of which—the evolution of Internal Secondaries—represents the creation of new genes. This process corresponds to an earlier general theory for the origin of new genes called overprinting (Keese and Gibbs 1992). These investigators also predict several of our findings: the importance of long unused ORFs, the restricted phylogenetic distribution of such new genes, and their tendency to have derived functions. We stress that both types of gene overlap may be viewed as the gain of genomic novelty without increasing the size of the genome, i.e., while under selective pressure for genomic compression. It has even been suggested that novel eukaryote genes may have appeared first as what we call Internal Secondaries, but the overlap was subsequently lost through gene duplication events, followed by loss of one function in each of the copies (Keese and Gibbs 1992). We do not know if there have been general trends in genome size of RNA viruses over evolutionary time; however, we assume that, as in all lineages, there have been processes of gain and loss of genetic functions: Gene overlap may thus be a way of increasing information content (gaining genomic novelty) without increasing genome size, or reducing genome size without losing information content. There appears to us to be no intrinsic reason why RNA viruses could not have acquired new genes by simply increasing their genome size; e.g., certain retroviruses have acquired oncogenes via horizontal transfer from their host (Swanstrom et al. 1983), and the recombination commonly seen would provide routes for gene duplication.
Some gene overlaps in RNA viruses that have been studied in detail illustrate our view of them as a source of genomic novelty, i.e., new functions being acquired that become increasingly important to the virus through time. Within the Retroviridae, some genes are overlapped by the ancestral env gene: rev is essential for viral replication and is found within all lentiviruses (a subgroup of Retroviridae), while vpu is dispensable and is restricted to HIV-1. Thus, rev and vpu appear to represent new genes of differing age and corresponding importance (Keese and Gibbs 1992). Another example is the recently reported F protein of hepatitis C virus. The function of this internal +1 frameshifted protein is unknown and it is not essential for viral replication (Baril and Brakier-Gingras 2005); analysis of its sequence suggests that molecular change in the gene is dominated by purifying selection on the primary gene which overlaps it—an essential polyprotein (Cristina et al. 2005). If, as seems likely, the F protein does not yet have a function but its ORF has a tendency to be expressed in error, then this opens the opportunity for it to acquire a function in the future. One of the few potentially misclassified Terminal Overlaps is in Tymovirus. This is the longest Terminal Overlap, with the long so-called Overlapping or Movement protein completely within the viral replicase ORF except for seven bases at its 5′ end. This has all the characteristics of an Internal Overlap: the Overlapping protein is thought to be younger than the much longer replicase (Keese and Gibbs 1992)—which we can confirm with our PDI measures for the two genes—and the overlap has arisen via a +1 frameshift. In bacteria, a comparative analyses of the genomes of Mycoplasma genitalium and Mycoplasma pneumoniae found some relatively long Terminal Overlaps, which appeared to be incidental elongations of the coding region by loss of the 3′ stop codon (Fukuda et al. 1999). The investigators found poor conservation of these elongated regions compared with homologs in other taxa, and suggested that these regions had little or no functional role at present; they appear to us to be other examples of gene overlap in the process of acquiring function. Examining overlaps from an evolutionary perspective may help molecular biologists in investigating the potential function of viral proteins. For example, the proportion of conserved amino acids in different overlapped regions of the P gene in hepatitis B virus can be explained by how essential that region of the gene is to viral replication (Mizokami et al. 1997).
We have used estimates of age (PDI) and broad categories of gene function to infer something of the evolutionary processes behind gene overlaps, but there are other methods that can be used to investigate the process in more detail. Studies have compared ratios of nonsynonymous to synonymous changes, retention of the RNY triplet pattern discussed above, or the rates of change at different codon positions, to infer which gene was “dominating” the evolution at the overlap (Normark et al. 1983; Firth and Brown 2005). The information content of the overlap, defined here as the degree to which the nucleotide sequence differs from random compared with non-overlapping regions, has also been used to infer different types of evolutionary outcome following overlap (Pavesi et al. 1997). We predict that a comparative application of these methods to gene overlaps in RNA viruses, similar to our approach, would support our model of the evolution of gene overlap.
Bacteria also have many gene overlaps, corresponding to our terminal category, which have been analyzed recently (Johnson and Chisholm 2004). In contrast to RNA viruses, these overlaps tend to be both short and involve −1 frameshifts. Among 198 bacterial genomes, only 15% of the gene overlaps are more than 30 bases in length (compared with 56% among RNA viruses). Also, 69% of the non-reverse complemented frameshifts are −1 rather than +1. For example, there is a common shared use of the “A” or “TG” motif in overlapping start and stop codons, which would represent a −1 frameshift leading to an overlap of one or four bases, respectively, between previously contiguous genes. The primary purpose of gene overlaps in Bacteria is thought to be regulatory (achieved via the translational coupling of genes); we see no evidence of this in RNA viruses. Gene overlap also occurs among DNA viruses, but it has not been investigated across a range of taxa. Although on average much larger, the size distribution of DNA viruses overlaps that of RNA viruses, with the very small DNA viruses, such as parvoviruses and some bacteriophages (e.g., ΦX174), using a host polymerase for their replication (Shackelton et al. 2005)—a route not possible for RNA viruses. It will be interesting to see if the relationship between gene overlap and genome size will be found to apply to DNA viruses, or whether it is a consequence of the uniquely high mutation rate of RNA viruses.
Finally, it has recently been argued that RNA viruses are at one end of a continuum that links genome complexity, epistasis, and mutational robustness, with RNA viruses exhibiting antagonistic epistasis as a result, the investigators suggest, of a less complex genome tending to be less mutationally robust (Sanjuan and Elena 2006). Gene overlap has been assumed to lower mutational robustness and has been described as a type of anti-redundancy (Krakauer and Plotkin 2002), because of the increased effect of mutation in nucleotides that code for more than one gene. The preponderance of gene overlap among the smaller RNA viruses might then agree with models in which robustness increases with genome size and/or complexity. However, we believe that the effect of gene overlap on mutational robustness is not intuitively clear. Gardner and Kalinka (2006) also propose on theoretical grounds that recombination may play a key role in the evolution of mutational robustness, and recombination varies widely among RNA viruses (Chare et al. 2003). There may well be a relationship between mutational robustness and mutation rate: in silico, digital organisms evolve higher mutational robustness under high mutation rates (Wilke et al. 2001). This is the so-called survival of the flattest phenomenon, where mutational robustness is considered as the local gradient of the fitness landscape around its peak—sharper peaks representing less mutationally robust genomes where mutations have a proportionately greater negative effect on fitness (Wilke and Adami 2003). Montville et al. (2005) have been able to manipulate the mutational robustness of an RNA virus using coinfection. Under high mutation rates, we may expect a more mutationally robust virus to outcompete one with a higher rate of replication, and there is now some experimental evidence for this (Codoñer et al. 2006; Sanjuan et al. 2007). These findings highlight that genomic evolution, at present, lacks a well-developed body of theory comparable to that developed for population genetics. Far from being an aberrant taxon of interest only because of their medical importance, RNA viruses, with their simple—and experimentally malleable—genomes, may be a good group from which to develop such theory.
Methods
Collation of genome sequences
The reference sequence for all available 701 RNA viruses were taken from the NCBI Genome Web site (http://www.ncbi.nlm.nih.gov), which classifies them into 66 families or unassigned genera or species. Eleven viruses were excluded due to being either replication deficient or lacking ORF definitions. Hepadnaviruses and caulimoviruses are traditionally classified as DNA viruses because their mature virion contains DNA; however, we consider that their use of the (error-prone) reverse transcriptase, a feature that they share with retroviruses, means that their evolution is likely to resemble that of RNA viruses. We exclude all the subviral RNA-based pathogens, which lack multiple genes to overlap. Gene overlaps were calculated using Perl scripts from the coordinates given in the GenBank entries. All genomes used in this article may be inspected at our Web site at http://virus.zoo.ox.ac.uk/virus/index.html, with the coordinates of all overlaps available in mySQL format upon request from the corresponding author.
Determining the relationship between gene overlap and genome size
The paucity of sequence homology across viral families has prevented the establishment of a reliable phylogeny of RNA viruses (Zanotto et al. 1996); therefore, we correct for phylogenetic non-independence (Felsenstein 1985) by using the means of the families, which are relatively well defined taxonomic units in RNA viruses. For this analysis, we treated each family (or unassigned genus or species) as independent and calculated mean values for their gene overlap and genome length.
One way of quantifying gene overlap would be to measure the proportion of nucleotides that code for two proteins in different reading frames. However, even under the null hypothesis (that overlaps are distributed among genomes independently of genome length), there would be some form of negative relationship because the overlap itself would shorten genome length, and any overlap would be a smaller proportion of a larger genome than of a smaller genome. Therefore, to correct for this, we test the relationship between gene overlap and the information content of the virus, which we define here as genome length plus the overlap (i.e., we count each overlapped base twice; triple gene overlaps being very rare).
There is a positive skew in the distributions of both overlap and information content. The distribution of variance of both variables can be made symmetrical by logarithmic transformation excluding zero values (cases of no gene overlap). Some zero values can legitimately be excluded as they appear to represent missing data, e.g., in Iflavirus there is only a single polyprotein and the cleavage coordinates are unknown. Other zero values, however, do represent a genuine absence of overlap, e.g., Picornaviridae. It could be argued, however, that these zero values should also be excluded as they may reflect merely the absence of a molecular mechanism in that viral taxon that could allow gene overlap (see Introduction). Following this line of reasoning, we should expect a linear relationship between overlap and information content only between taxa where such a mechanism is known to exist. We present the results of this logarithmically transformed analysis, but we also present the results of analyses where zero values are not excluded: using either untransformed overlap values in a nonparametric ranking test or those from an alternate transformation, the arcsine-square root. In the arcsine-square root transformation, gene overlap is expressed as the angle whose sine is the square root of the overlap (the natural logarithm of the information content is used as before). This transformation fails to remove completely the skew in overlap distribution, but a linear regression shows a significant relationship (Supplemental Fig. S1; P < 0.001).
Placing gene overlaps into homologous groups
In order to minimize phylogenetic non-independence, we classified all gene overlaps into homologous groups, and the mean value of each of these homologous groups was treated as a single data point. Our procedure is as follows. We used NCBI BLAST to compare each gene against every other, and we defined as homologous those pairs of genes with an _E_-value greater than 10−3. We repeated analyses with threshold values of 10−2 and 10−5, but this only had a very small effect and did not affect our conclusions. For example, reducing the value to 10−5 has the effect of creating three additional homologous groups of terminal overlaps (changing from 76 to 79 groups), while increasing the value to 10−2 has the effect of reducing the number of homologous groups by two (from 76 to 74 groups in the smaller dataset; see below). Thus, instances of internal overlap were treated as homologous if (1) the primaries were homologs of each other, (2) the secondaries were homologs of each other, and (3) the frameshift was the same. Similarly, instances of terminal overlap were treated as homologous if (1) the genes with their 3′ end overlapped were homologs of each other, (2) the genes with their 5′ end overlapped were homologs of each other, and (3) the frameshift was the same. Non-overlapping genes were placed into homologous groups simply using the BLAST _E_-values.
In the analyses presented, we used all the genes, but our results are the same if we restricted the analyses to a smaller data set consisting only of genes with no potentially complicating factors such as splicing, internal frameshifting, or multiple overlaps (shown in Supplemental Table S2 and Fig. S2).
Determining gene age and functional group
We approximate the relative age of a gene by determining how dispersed its homologs are among the other virus families, quantified as the PDI of the gene. The PDI of a gene is the number of other families that contain a homolog to that gene as defined by the above BLAST _E_-values, and the PDI of a category of genes is the mean of its constituent values.
We were able to place 95% of all genes into functional groups using a keyword search of the GenBank entry, supplemented with reference to a standard reference work (van Regenmortel et al. 2000) when no result was returned. These groups were as follows: capsid nucleoproteins; surface proteins; replicases; helicases; proteases and RNases; methytransferases; integrases; other nonstructural and accessory proteins; nucleic acid binding proteins, including transcription factors; movement proteins such as gene-block; and hypothetical proteins. Polyproteins were given multiple relevant functions, and for each homologous group of genes, we found the single most common function.
Simulations
Our simulation of unused ORFs involved drawing codons at random from the observed codon frequency distribution across all viruses in our database. For Internal Overlaps, we drew a gene length from the observed length frequency distribution and then drew codons (excluding stop codons) for the primary reading frame up to that length. We then found the longest ORF, defined here as the number of nucleotides between start and stop codons, in both the +1 and −1 frames, performing 100,000 replications. For Terminal Overlaps, we drew codons at the notional start of the adjacent gene and noted the length to the first stop codon in the +1 and −1 frame. To represent the proposed gradual extension of an existing overlap by mutation (and hence loss) of the new start and/or stop codon, we modified the above simulation by incorporating a single probability that any drawn start or stop codon would be lost and translation would continue to the next start or stop codon. This is termed the extension probability (thus, in our basic simulation of unused ORFs described above the extension probability is zero). For Terminal Overlaps, the results presented are for downstream extensions to a stop codon; the results for upstream extension to a start codon (without interruption by a stop codon) are very similar and are not shown. The JAVA files for the simulations are available in the Supplemental material (Archive.tar.zip).
Acknowledgments
We thank Andy Gardner, Eddie Holmes, Aris Katzourakis, and Joe Parker for discussions. This work was funded by the Wellcome Trust. A.R. and O.G.P. were funded by the Royal Society.
Footnotes
References
- Baril M., Brakier-Gingras L., Brakier-Gingras L. Translation of the F protein of hepatitis C virus is initiated at a non-AUG codon in a +1 reading frame relative to the polyprotein. Nucleic Acids Res. 2005;33:1474–1486. doi: 10.1093/nar/gki292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burch C.L., Turner P.E., Hanley K.A., Turner P.E., Hanley K.A., Hanley K.A. Patterns of epistasis in RNA viruses: A review of the evidence from vaccine design. J. Evol. Biol. 2003;16:1223–1235. doi: 10.1046/j.1420-9101.2003.00632.x. [DOI] [PubMed] [Google Scholar]
- Chare E.R., Gould E.A., Holmes E.C., Gould E.A., Holmes E.C., Holmes E.C. Phylogenetic analysis reveals a low rate of homologous recombination in negative-sense RNA viruses. J. Gen. Virol. 2003;84:2691–2703. doi: 10.1099/vir.0.19277-0. [DOI] [PubMed] [Google Scholar]
- Codoñer F.M., Daròs J.A., Solé R.V., Elena S.F., Daròs J.A., Solé R.V., Elena S.F., Solé R.V., Elena S.F., Elena S.F. The fittest versus the flattest: Experimental confirmation of the quasispecies effect with subviral pathogens. PLoS Pathog. 2006;2:e136. doi: 10.1371/journal.ppat.0020136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cristina J., Lopez F., Moratorio G., Lopez L., Vasquez S., Garcia-Aguirre L., Chunga A., Lopez F., Moratorio G., Lopez L., Vasquez S., Garcia-Aguirre L., Chunga A., Moratorio G., Lopez L., Vasquez S., Garcia-Aguirre L., Chunga A., Lopez L., Vasquez S., Garcia-Aguirre L., Chunga A., Vasquez S., Garcia-Aguirre L., Chunga A., Garcia-Aguirre L., Chunga A., Chunga A. Hepatitis C virus F protein sequence reveals a lack of functional constraints and a variable pattern of amino acid substitution. J. Gen. Virol. 2005;86:115–120. doi: 10.1099/vir.0.80510-0. [DOI] [PubMed] [Google Scholar]
- Crotty S., Cameron C.E., Andino R., Cameron C.E., Andino R., Andino R. RNA virus error catastrophe: Direct molecular test by using ribavirin. Proc. Natl. Acad. Sci. 2001;98:6895–6900. doi: 10.1073/pnas.111085598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake J.W., Holland J.J., Holland J.J. Mutation rates among RNA viruses. Proc. Natl. Acad. Sci. 1999;96:13910–13913. doi: 10.1073/pnas.96.24.13910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake J.W., Charlesworth B., Charlesworth D., Crow J.F., Charlesworth B., Charlesworth D., Crow J.F., Charlesworth D., Crow J.F., Crow J.F. Rates of spontaneous mutation. Genetics. 1998;148:1667–1686. doi: 10.1093/genetics/148.4.1667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eigen M. Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften. 1971;58:465–523. doi: 10.1007/BF00623322. [DOI] [PubMed] [Google Scholar]
- Elena S.F., Lenski R.E., Lenski R.E. Test of synergistic interactions among deleterious mutations in bacteria. Nature. 1997;390:395–398. doi: 10.1038/37108. [DOI] [PubMed] [Google Scholar]
- Elena S.F., Carrasco P., Daros J.A., Sanjuan R., Carrasco P., Daros J.A., Sanjuan R., Daros J.A., Sanjuan R., Sanjuan R. Mechanisms of genetic robustness in RNA viruses. EMBO Rep. 2006;7:168–173. doi: 10.1038/sj.embor.7400636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. Phylogenies and the comparative method. Am. Nat. 1985;125:1–15. [Google Scholar]
- Firth A.E., Brown C.M., Brown C.M. Detecting overlapping coding sequences with pairwise alignments. Bioinformatics. 2005;21:282–292. doi: 10.1093/bioinformatics/bti007. [DOI] [PubMed] [Google Scholar]
- Fukuda Y., Washio T., Tomita M., Washio T., Tomita M., Tomita M. Comparative study of overlapping genes in the genomes of Mycoplasma genitalium and Mycoplasma pneumoniae. Nucleic Acids Res. 1999;27:1847–1853. doi: 10.1093/nar/27.8.1847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner A., Kalinka A.T., Kalinka A.T. Recombination and the evolution of mutational robustness. J. Theor. Biol. 2006;241:707–715. doi: 10.1016/j.jtbi.2006.01.011. [DOI] [PubMed] [Google Scholar]
- Haldane J.B.S. The effect of variation on fitness. Am. Nat. 1937;71:337–349. [Google Scholar]
- Hausmann S., Garcin D., Delenda C., Kolakofsky D., Garcin D., Delenda C., Kolakofsky D., Delenda C., Kolakofsky D., Kolakofsky D. The versatility of paramyxovirus RNA polymerase stuttering. J. Virol. 1999;73:5568–5576. doi: 10.1128/jvi.73.7.5568-5576.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes E.C. Error thresholds and the constraints to RNA virus evolution. Trends Microbiol. 2003;11:543–546. doi: 10.1016/j.tim.2003.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jenkins G.M., Rambaut A., Pybus O.G., Holmes E.C., Rambaut A., Pybus O.G., Holmes E.C., Pybus O.G., Holmes E.C., Holmes E.C. Rates of molecular evolution in RNA viruses: A quantitative phylogenetic analysis. J. Mol. Evol. 2002;54:156–165. doi: 10.1007/s00239-001-0064-3. [DOI] [PubMed] [Google Scholar]
- Johnson Z.I., Chisholm S.W., Chisholm S.W. Properties of overlapping genes are conserved across microbial genomes. Genome Res. 2004;14:2268–2272. doi: 10.1101/gr.2433104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jukes T.H. On the prevalence of certain codons (“RNY”) in genes for proteins. J. Mol. Evol. 1996;42:377–381. doi: 10.1007/BF02498631. [DOI] [PubMed] [Google Scholar]
- Keese P.K., Gibbs A., Gibbs A. Origins of genes: “Big bang” or continuous creation. Proc. Natl. Acad. Sci. 1992;89:9489–9493. doi: 10.1073/pnas.89.20.9489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M., Maruyama T., Maruyama T. The mutational load with epistatic gene interactions in fitness. Genetics. 1966;54:1337–1351. doi: 10.1093/genetics/54.6.1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krakauer D.C. Stability and evolution of overlapping genes. Evolution. 2000;54:731–739. doi: 10.1111/j.0014-3820.2000.tb00075.x. [DOI] [PubMed] [Google Scholar]
- Krakauer D.C., Plotkin J.B., Plotkin J.B. Redundancy, antiredundancy, and the robustness of genomes. Proc. Natl. Acad. Sci. 2002;99:1405– 1409. doi: 10.1073/pnas.032668599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lower R., Tonjes R.R., Korbmacher C., Kurth R., Lower J., Tonjes R.R., Korbmacher C., Kurth R., Lower J., Korbmacher C., Kurth R., Lower J., Kurth R., Lower J., Lower J. Identification of a Rev-related protein by analysis of spliced transcripts of the human endogenous retroviruses HTDV/HERV-K. J. Virol. 1995;69:141–149. doi: 10.1128/jvi.69.1.141-149.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mansky L.M. In vivo analysis of human T-cell leukemia virus type 1 reverse transcription accuracy. J. Virol. 2000;74:9525–9531. doi: 10.1128/jvi.74.20.9525-9531.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizokami M., Orito E., Ohba K., Ikeo K., Lau J.Y., Gojobori T., Orito E., Ohba K., Ikeo K., Lau J.Y., Gojobori T., Ohba K., Ikeo K., Lau J.Y., Gojobori T., Ikeo K., Lau J.Y., Gojobori T., Lau J.Y., Gojobori T., Gojobori T. Constrained evolution with respect to gene overlap of hepatitis B virus. J. Mol. Evol. 1997;44:S83–S90. doi: 10.1007/pl00000061. [DOI] [PubMed] [Google Scholar]
- Montville R., Froissart R., Remold S.K., Tenaillon O., Turner P.E., Froissart R., Remold S.K., Tenaillon O., Turner P.E., Remold S.K., Tenaillon O., Turner P.E., Tenaillon O., Turner P.E., Turner P.E. Evolution of mutational robustness in an RNA virus. PLoS Biol. 2005;3:e381. doi: 10.1371/journal.pbio.0030381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Normark S., Bergstrom S., Edlund T., Grundstrom T., Jaurin B., Lindberg F.P., Olsson O., Bergstrom S., Edlund T., Grundstrom T., Jaurin B., Lindberg F.P., Olsson O., Edlund T., Grundstrom T., Jaurin B., Lindberg F.P., Olsson O., Grundstrom T., Jaurin B., Lindberg F.P., Olsson O., Jaurin B., Lindberg F.P., Olsson O., Lindberg F.P., Olsson O., Olsson O. Overlapping genes. Annu. Rev. Genet. 1983;17:499–525. doi: 10.1146/annurev.ge.17.120183.002435. [DOI] [PubMed] [Google Scholar]
- Nowak M.A. What is a quasispecies? Trends Ecol. Evol. 1992;7:118–121. doi: 10.1016/0169-5347(92)90145-2. [DOI] [PubMed] [Google Scholar]
- Pavesi A., DeIaco B., Granero M.I., Porati A., DeIaco B., Granero M.I., Porati A., Granero M.I., Porati A., Porati A. On the informational content of overlapping genes in prokaryotic and eukaryotic viruses. J. Mol. Evol. 1997;44:625–631. doi: 10.1007/PL00006185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peleg O., Kirzhner V., Trifonov E., Bolshoy A., Kirzhner V., Trifonov E., Bolshoy A., Trifonov E., Bolshoy A., Bolshoy A. Overlapping messages and survivability. J. Mol. Evol. 2004;59:520–527. doi: 10.1007/s00239-004-2644-5. [DOI] [PubMed] [Google Scholar]
- Rogozin I.B., Spiridonov A.N., Sorokin A.V., Wolf Y.I., Jordan I.K., Tatusov R.L., Koonin E.V., Spiridonov A.N., Sorokin A.V., Wolf Y.I., Jordan I.K., Tatusov R.L., Koonin E.V., Sorokin A.V., Wolf Y.I., Jordan I.K., Tatusov R.L., Koonin E.V., Wolf Y.I., Jordan I.K., Tatusov R.L., Koonin E.V., Jordan I.K., Tatusov R.L., Koonin E.V., Tatusov R.L., Koonin E.V., Koonin E.V. Purifying and directional selection in overlapping prokaryotic genes. Trends Genet. 2002;18:228–232. doi: 10.1016/s0168-9525(02)02649-5. [DOI] [PubMed] [Google Scholar]
- Sanjuan R., Elena S.F., Elena S.F. Epistasis correlates to genomic complexity. Proc. Natl. Acad. Sci. 2006;103:14402–14405. doi: 10.1073/pnas.0604543103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanjuan R., Moya A., Elena S.F., Moya A., Elena S.F., Elena S.F. The distribution of fitness effects caused by single-nucleotide substitutions in an RNA virus. Proc. Natl. Acad. Sci. 2004;101:8396–8401. doi: 10.1073/pnas.0400146101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanjuan R., Cuevas J.M., Furió V., Holmes E.C., Moya A., Cuevas J.M., Furió V., Holmes E.C., Moya A., Furió V., Holmes E.C., Moya A., Holmes E.C., Moya A., Moya A. Selection for robustness in mutagenized RNA viruses. PLoS Genet. 2007;3:e93. doi: 10.1371/journal.pgen.0030093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seligmann H., Pollock D.D., Pollock D.D. The ambush hypothesis: Hidden stop codons prevent off-frame gene reading. DNA Cell Biol. 2004;23:701–705. doi: 10.1089/dna.2004.23.701. [DOI] [PubMed] [Google Scholar]
- Shackelton L.A., Parrish C.R., Truyen U., Holmes E.C., Parrish C.R., Truyen U., Holmes E.C., Truyen U., Holmes E.C., Holmes E.C. High rate of viral evolution associated with the emergence of carnivore parvovirus. Proc. Natl. Acad. Sci. 2005;102:379–384. doi: 10.1073/pnas.0406765102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepherd J.C.W. Periodic correlations in DNA sequences and evidence suggesting their evolutionary origin in a comma-less genetic code. J. Mol. Evol. 1981;17:94–102. doi: 10.1007/BF01732679. [DOI] [PubMed] [Google Scholar]
- Steinhauer D.A., Domingo E., Holland J.J., Domingo E., Holland J.J., Holland J.J. Lack of evidence for proofreading mechanisms associated with an RNA virus polymerase. Gene. 1992;122:281–288. doi: 10.1016/0378-1119(92)90216-c. [DOI] [PubMed] [Google Scholar]
- Swanstrom R., Parker R.C., Varmus H.E., Bishop J.M., Parker R.C., Varmus H.E., Bishop J.M., Varmus H.E., Bishop J.M., Bishop J.M. Transduction of a cellular oncogene—the genesis of Rous sarcoma virus. Proc. Natl. Acad. Sci. 1983;80:2519–2523. doi: 10.1073/pnas.80.9.2519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Regenmortel M.H.V., Fauquet C.M., Bishop D.H.L., Carstens E.B., Estes M.K., Lemon S.M., Maniloff J., Mayo M.A., McGeoch D.J., Pringle C.R., Fauquet C.M., Bishop D.H.L., Carstens E.B., Estes M.K., Lemon S.M., Maniloff J., Mayo M.A., McGeoch D.J., Pringle C.R., Bishop D.H.L., Carstens E.B., Estes M.K., Lemon S.M., Maniloff J., Mayo M.A., McGeoch D.J., Pringle C.R., Carstens E.B., Estes M.K., Lemon S.M., Maniloff J., Mayo M.A., McGeoch D.J., Pringle C.R., Estes M.K., Lemon S.M., Maniloff J., Mayo M.A., McGeoch D.J., Pringle C.R., Lemon S.M., Maniloff J., Mayo M.A., McGeoch D.J., Pringle C.R., Maniloff J., Mayo M.A., McGeoch D.J., Pringle C.R., Mayo M.A., McGeoch D.J., Pringle C.R., McGeoch D.J., Pringle C.R., Pringle C.R., et al. Virus taxonomy: Classification and nomenclature of viruses. Academic Press; San Diego: 2000. [Google Scholar]
- Wade M.J., Winther R.G., Agrawal A.F., Goodnight C.J., Winther R.G., Agrawal A.F., Goodnight C.J., Agrawal A.F., Goodnight C.J., Goodnight C.J. Alternative definitions of epistasis: Dependence and interaction. Trends Ecol. Evol. 2001;16:498–504. [Google Scholar]
- Wilke C.O., Adami C., Adami C. Evolution of mutational robustness. Mutat. Res. 2003;522:3–11. doi: 10.1016/s0027-5107(02)00307-x. [DOI] [PubMed] [Google Scholar]
- Wilke C.O., Wang J.L., Ofria C., Lenski R.E., Adami C., Wang J.L., Ofria C., Lenski R.E., Adami C., Ofria C., Lenski R.E., Adami C., Lenski R.E., Adami C., Adami C. Evolution of digital organisms at high mutation rates leads to survival of the flattest. Nature. 2001;412:331–333. doi: 10.1038/35085569. [DOI] [PubMed] [Google Scholar]
- Zanotto P.M.D., Gibbs M.J., Gould E.A., Holmes E.C., Gibbs M.J., Gould E.A., Holmes E.C., Gould E.A., Holmes E.C., Holmes E.C. A reevaluation of the higher taxonomy of viruses based on RNA polymerases. J. Virol. 1996;70:6083–6096. doi: 10.1128/jvi.70.9.6083-6096.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]