Prediction of individual genetic risk to disease from genome-wide association studies (original) (raw)

Abstract

Empirical studies suggest that the effect sizes of individual causal risk alleles underlying complex genetic diseases are small, with most genotype relative risks in the range of 1.1–2.0. Although the increased risk of disease for a carrier is small for any single locus, knowledge of multiple-risk alleles throughout the genome could allow the identification of individuals that are at high risk. In this study, we investigate the number and effect size of risk loci that underlie complex disease constrained by the disease parameters of prevalence and heritability. Then we quantify the value of prediction of genetic risk to disease using a range of realistic combinations of the number, size, and distribution of risk effects that underlie complex diseases. We propose an approach to assess the genetic risk of a disease in healthy individuals, based on dense genome-wide SNP panels. We test this approach using simulation. When the number of loci contributing to the disease is >50, a large case-control study is needed to identify a set of risk loci for use in predicting the disease risk of healthy people not included in the case-control study. For diseases controlled by 1000 loci of mean relative risk of only 1.04, a case-control study with 10,000 cases and controls can lead to selection of ∼75 loci that explain >50% of the genetic variance. The 5% of people with the highest predicted risk are three to seven times more likely to suffer the disease than the population average, depending on heritability and disease prevalence. Whether an individual with known genetic risk develops the disease depends on known and unknown environmental factors.

An important benefit from the study of the genetics of human disease is to predict the risk that individuals may have of succumbing to a particular disease. Knowledge of this risk can then be used by the clinician in prevention, diagnosis, prognosis, and treatment. Currently, clinicians use the family history of a patient to help assess their risk of a disease with a known genetic component, with family history formally included in standard international disease classification systems. With modern molecular tools, can we improve on the use of family history to assess genetic risk of disease? For diseases caused by single genes, the answer is obviously “yes,” but for diseases with complex inheritance, the best method to use and the success that might be expected are unclear. The dominant paradigm in human complex-trait genetics has been to map loci affecting disease risk and then to identify the causative mutations. Complex traits are likely to be affected by many genes and mutations, most of which have a small effect on disease risk. The relative risk of disease due to one allele is typically of the order of 1.1 to 2.0 (Ioannidis et al. 2006; Bertram et al. 2007), but observed effect sizes may still represent the upper tail of true effect size. These findings are consistent with the expectation that quantitative complex traits in general are affected by a large number of loci. In species where it is possible to measure the number of loci influencing a trait, around 10–50 loci have been identified, most individually counting for only a few percent, and together accounting for <50% of the genetic variation (Henderson et al. 2004; Jacobsson et al. 2005; Valdar et al. 2006). The number of risk loci underlying complex disease and their effect size must be constrained by the disease parameters of prevalence and heritability, yet, to our knowledge, this relationship has not been explored.

Identification of causal variants and elucidating disease pathways through genetic and functional studies is difficult and time-consuming, particularly if there are many risk loci with small effects. However, knowledge of all risk loci or knowledge of causal variants at any one risk locus is not necessary for the prediction of the risk to disease of individuals in the population. The recent advances in high-density single-nucleotide polymorphism (SNP) technology (Kennedy et al. 2003) have made it possible to conduct genome-wide association studies (Hirschhorn and Daly 2005). These studies have been considered as only a first step to identifying the causal mutations, but the SNPs used in the association study could be useful to create genome-wide predictors of disease or a “genomic profile” (Khoury et al. 2004) for disease risk. Janssens et al. (2006) have investigated predictive testing for complex diseases using multiple genes by simulation. They examined diseases controlled by up to 400 risk loci, but, although they considered a range of risk effects and allele frequencies, they did not consider distributions of risk effects that relate to models of the genetic architecture underlying complex diseases. More importantly, the model that Janssens et al. used implicitly assumed that an individual’s true genetic risk is known without error, so that the correlation between genetic risk and disease status is simply the square root of the broad-sense heritability on the observed scale. That is, their study does not deal with the key problem, which is to predict the genetic risk faced by each individual. Pharoah et al. (2002) quantified the proportion of cases in subsets of the population that are at highest genetic risk of disease, assuming a polygenic model for which risk was log-normally distributed, without modeling or estimating the effects of individual risk loci.

The objective of this study is to quantify the accuracy of risk prediction from genome-wide association studies and to quantify the true disease risk faced by the people predicted to be most at risk in subsequent samples from the population. To do this we consider models of the underlying genetic architecture assuming realistic distributions of the frequencies and effect sizes of risk loci, constraining the number of risk loci and the mean effect size to be consistent with disease prevalence and heritability. Using these models, we estimate the genetic risk of individuals based on a simulated genome-wide association study (GWAS).

Results

The success of association studies, and also of genomic profiling, depends on the genetic architecture underlying complex diseases. First, we investigate the relationship between the relative risk (RR) of genetic loci and the number of loci that contribute to risk of a disease under constraints of known disease prevalence and heritability. We model the genetic architecture of complex disease by allowing the effect size and frequency of risk allele to vary across loci. We go on to use these results to investigate the possibilities of using multiple risk loci identified in a GWAS to predict risk of disease in a new population cohort.

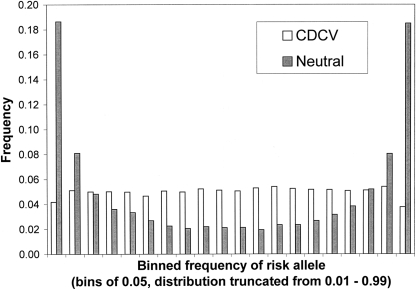
We consider four disease scenarios based on realistic combinations of disease prevalence, K = 0.05 or 0.10, and heritabilities of the disease on the observed scale, _h_2 = 0.1 or 0.2. We consider two distributions of frequency of risk alleles underlying the disease (Fig. 1): A uniform distribution of allele frequencies that broadly corresponds to the common-disease common-variant (CDCV) hypothesis in which the frequency of the increasing risk allele was simulated as pi ∼ Uniform(0.01,0.99) or a U-shaped distribution, which broadly corresponds the neutral allele hypothesis (Pritchard 2001).

Figure 1.

Figure 1.

Distribution of allele frequencies under the neutral and common-disease common-variant (CDCV) models from 10,000 simulated loci.

Number of loci underlying complex diseases

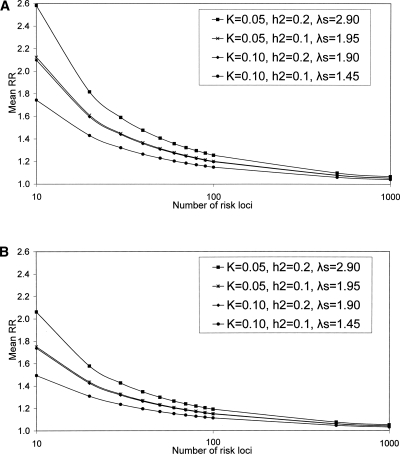
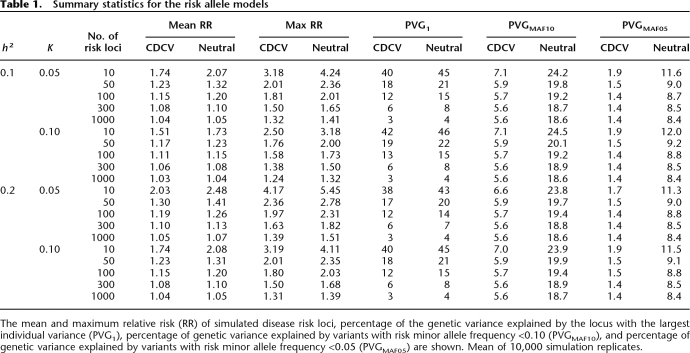
For a given number of disease loci we force the effect sizes to be consistent with the disease prevalence and heritability parameters. The average relative risks for fixed numbers of disease loci for the four disease scenarios are given in Figure 2. Summary statistics of the mean and maximum RR, the maximum percentage of genetic variance explained by a single locus, and the percentage of genetic variance explained by extreme frequency risk variants describe the properties and differences of the models (Table 1). For the CDCV model, an average RR of 1.2 corresponds to 40 or more loci. As expected, fewer loci imply larger average RR, and the average risk of loci for the approximate neutral model of evolution is always larger than that for the CDCV model for the same number of loci. Similarly, the maximum percentage of genetic variance explained by a single locus is always larger for the neutral model compared to the CDCV model when the number of risk loci is the same. However, the relationship between the number of disease loci and their average RR is broadly similar for the two models. When 1000 risk loci influence a disease, the maximum contribution to genetic variance of any single locus is only 3%–4%. As expected, as the sibling risk increases, the average RR increases if the number of risk loci is fixed; or, the number of risk loci required increases if the mean RR is held constant.

Figure 2.

Figure 2.

Relationship between the number of susceptibility or risk loci and their average relative risk (RR) for common disease; K is the population prevalence of the disease; _h_2 is the heritability on the observed scale; λs is the RR for full-siblings based on the heritability and prevalence parameters. Distribution of effects of risk loci under neutral (A) and CDCV (B) models. The mean RR are the mean of 10,000 simulated samples.

Table 1.

Summary statistics for the risk allele models

graphic file with name 1520tbl1.jpg

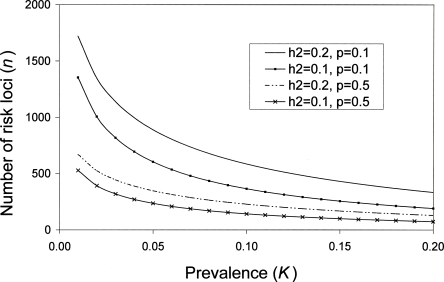
We derived an analytic expression for number of loci when RR and allele frequency are fixed for all loci (Equation 3), which agrees well with the results of the CDCV model when p = 0.5 and with the neutral model when allele frequency p = 0.1; e.g., for K = 0.05 and _h_2 = 0.2, then for p = 0.5, the number of loci for fixed relative risks of 1.1, 1.2, 1.4, and 1.6 are 346, 95, 29, and 15, respectively; and for p = 0.1, the corresponding number of loci are 889, 227, 59, and 28. Different combinations of K and _h_2 can lead to the same sibling (sib) relative risk (Fig. 2); it is this combined parameter that drives the results. Equation 3 can be used to investigate the impact of K or _h_2 on the number of loci underlying complex diseases (Fig. 3).

Figure 3.

Figure 3.

Relationship between disease prevalence (K) and heritability (_h_2) on number of risk loci contributing to a disease, assuming a fixed frequency of risk alleles (p) and fixed RR of 1.1 (Equation 3). Based on results from Figure 1, p = 0.1 approximates to the neutral model and p = 0.5 approximates to the CDCV model.

Use of GWAS to predict disease risk

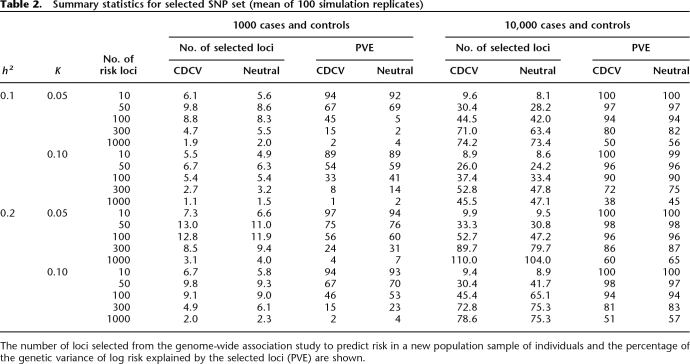
Using our models for the genetic architecture of complex diseases, we go on to investigate prediction of genetic risk to disease from multiple risk loci identified in a GWAS. To do this we simulated a case-control study assuming a single-stage genome-wide association screen with 500,000 SNPs. The number of disease risk loci was fixed at 10, 20, 50, 100, 300, or 1000, and allele frequencies were simulated from either the U-shaped (neutral) or uniform distribution (CDCV). Table 2 summarizes the number of loci selected for prediction of genetic risk and the proportion of variance in log risk that they explain in an independent sample of people.

Table 2.

Summary statistics for selected SNP set (mean of 100 simulation replicates)

graphic file with name 1520tbl2.jpg

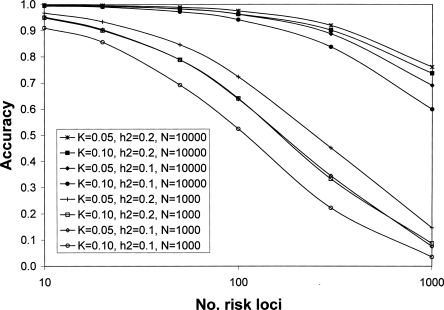
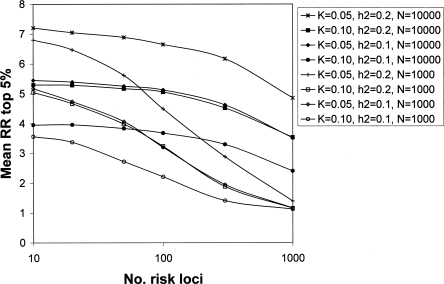
For all simulated scenarios, when 10,000 cases and controls were used, the accuracy with which the genetic risk of disease was predicted in a new random sample of the population of 1000 individuals was very high (Fig. 4 for CDCV model; results for the neutral model were similar but less conservative). For example, for the CDCV model of a disease with prevalence 0.05 and heritability 0.1 caused by 100 risk loci with average RR of 1.15 (Table 1), the accuracy of prediction was 0.97 (Fig. 4). The prediction equation used 45 loci that explained 94% of the genetic variance (Table 2). As the number of risk loci increases from 100 to 300 to 1000, the accuracy remains above 0.70, even though the average genotype relative risk falls below 1.1 (Fig. 4). The number of loci included in the prediction profile continues to increase as the total number of risk loci increases (Table 1), although the percentage of genetic variation they explain decreases. Even when only 1000 cases and controls were used, the accuracy of prediction was high (>0.7) unless the number of disease loci was >50, corresponding to average RR of disease alleles of <1.2. A GWAS of this size does not have sufficient power to detect risk loci with low average RR, and hence the number of loci selected for inclusion in the prediction profiles and the percentage of genetic variation they explain drops off (Table 1). The results are broadly similar for the CDCV and neutral disease models. The power of our approach is demonstrated in Figure 5 for CDCV, where the true RR of disease for the individuals with the highest 5% of predicted risk in a new sample is shown relative to the mean empirical population risk (∼0.05 or 0.10 when population prevalence K = 0.05 or 0.10, respectively). Case-control samples of 1000 can generate SNP risk profile sets that identify individuals who have risk of disease three times higher than the population average when the number of disease loci is <50.When the case-control sample is 10,000, individuals in the population that have a three to seven times increased risk of disease can be identified even when the number of disease loci is very large (1000). That is, individuals that have an absolute risk of disease of 15%–70% can be identified. The results are broadly similar for the CDCV and neutral disease models; the accuracy was slightly higher under the neutral model except when the number of risk loci was small. The high accuracy of prediction is not explained by the presence of a few loci of very large effect (the mean maxima RR are listed in Table 1). Under the null hypothesis, one marker is expected, by chance, to have a test statistic that exceeds the threshold of 22.59. Selection of, on average, one false positive was confirmed in the simulations. When the number of true risk loci is small, their mean RR is higher for the same heritability of the disease, so that even with only 1000 cases and 1000 controls in the association study, most of the true disease loci are selected. When the number of risk loci is high, the mean RR is low, but the distribution of RR means that almost all the genetic variance is explained by a fraction of the risk loci.

Figure 4.

Figure 4.

Accuracy of risk prediction of disease risk in a population sample using a set of predictive SNPs selected after a genome-wide association study of N each of cases and controls. A CDCV disease model is assumed with population prevalence (K) and heritability (_h_2) of the disease. Results for the neutral model were similar. Mean of 100 simulation replicates. The legend lists the data series in their order at 1000 risk loci.

Figure 5.

Figure 5.

Relative risk of disease for the estimated top 5% of individuals at risk of a new sample of 1000 people following a case-control study with sample size of N each of cases and controls. A CDCV disease model is assumed with population prevalence (K) and heritability (_h_2) of the disease. Results for the neutral model were similar. Mean of 100 simulation replicates. The legend lists the data series in their order at 1000 risk loci.

Discussion

We have quantified the number of disease loci underlying common disease using realistic parameters and have shown that results from GWAS can be used to identify healthy individuals in the population who are at a substantially increased risk of developing disease, even when individual risk loci confer small relative risks. From our model we first determined the relationship between the number of susceptibility loci underlying a complex disease and their average RR, given the allele frequency distribution of risk alleles, the population prevalence, and the heritability. Our results are robust to the distribution of risk allele frequencies assumed (approximating the CDCV or neutral model). We assume additive gene action on the log risk scale (multiplicative gene action on the risk scale), that loci act independently and that there is no linkage disequilibrium between disease predisposition loci. Four disease scenarios were considered that are representative of complex diseases, such as major depression, hypertension, heart disease, or type II diabetes; a population prevalence of 5% or 10%; and heritability on the observed disease scale of 10% or 20%. These choices of parameters translate to diseases with relative risks for full-sibs of affected probands (λs) ranging from 1.45 to 2.90. The analytic formula for the number of loci, assuming all loci to have the same effect and the same allele frequency, was found to be a robust predictor of the number of loci estimated by simulation when frequencies and effect sizes were sampled from a distribution; using Equation 3 with allele frequency, p = 0.5 or 0.1, gave results that agreed well with the CDCV or neutral model simulation, respectively. The analytic result is a convenient way to investigate the impact of disease prevalence and heritability on the number of loci underlying disease (Fig. 3). The number of disease risk loci that underlie complex disease have previously been investigated (Yang et al. 2005) based on an epidemiological parameterization using population-attributable fractions (rather than heritability), assuming equal frequencies and effects of risk loci. In Appendix A we derive closed-form solutions for the number of disease risk loci based on their parameterization.

In addition to the simulations reported here, we also simulated a disease with prevalence K = 0.01 and heritability _h_2 = 0.05 (corresponding to a sibling RR of 3.48) and found results similar to those for a disease with similar relative sibling RR, e.g., K = 0.05, _h_2 = 0.25. As with the other disease scenarios, we were able to identify individuals who had an increased risk of disease that was three to five times higher than average, but when prevalence is so low this still translates to a small absolute risk of disease, and so genomic profiling may be less useful for rare diseases. However, we note that low-prevalence diseases often show evidence for nonadditive genetic effects (monozygotic twin concordance rates several fold higher than dizygotic twin concordance rates, e.g., schizophrenia, type 1 diabetes, Crohn’s disease), implying that models that include nonadditive genetic effects may be more relevant to these disorders.

Our results show that, even for diseases controlled by 1000 loci with mean RR of only 1.04, a case-control study with 10,000 cases and controls can lead to selection of ∼75 loci that explain >50% of the genetic variance, resulting in accuracy of risk prediction of >0.75. Prediction of increased risk to disease will be more successful for diseases with a high sibling risk. However, for diseases of low prevalence, the increased RR may translate into only a small absolute risk to disease. In contrast, for a disease of higher prevalence, the increase in RR for the top proportion of a population based on estimated risk may be small but may translate into a substantial absolute risk of disease. Examination of the true RR of disease for the individuals with the highest 5% of predicted risk in a new sample relative to the mean empirical population risk (Fig. 5) shows that, even with a case-control samples of 1000 for generation of risk profile SNPs, individuals who have risk of disease three times higher than the population average can be identified when the number of disease loci is <50. When the case-control sample is 10,000, individuals in the population that have a three to seven times increased risk of disease can be easily identified even when the number of disease loci is very large (1000). That is, individuals that have an absolute risk of disease of 15%–70% can be identified for the prevalences we have considered. Therefore, following a single large case-control study and the selection of a small set of SNPs, 100,000s to millions of individuals could be identified subsequently that are at substantial increased risk of disease relative to the population average. Genomic profiles can be viewed as a more accurate predictor of genetic predisposition than family history. The accuracy of prediction that we report can be compared with that achieved from a family history consisting of the disease status of a person’s mother and father, which is only 0.2–0.3 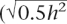Inline graphic; Falconer and Mackay 1996) for the disease scenarios considered. Whereas all sibs within a nuclear family will have the same risk based on family history, a genomic profile will provide individual risk profiles utilizing information from inherited risk loci (after all, half of the genetic variation occurs within families), even if disease has not been expressed in family members.

The accuracy of prediction 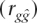Inline graphic is the correlation between true and predicted genetic risk. This measure is appropriate to evaluate the utility of genetic profiling because it is the precision with which we can predict genetic risk. Whether an individual with known genetic risk goes on to develop the disease is dependent on known and unknown environmental risk factors. In practice, genomic profiling would be used in combination with information of known environmental risk factors (Lyssenko et al. 2005). Without any such information, the accuracy of predicting disease status is simply 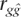Inline graphich. Janssens et al. (2006) suggest that the ROC (receiver operator curve)-based measure of discriminative accuracy, the area under the curve (AUC), is an appropriate measure for evaluating efficiency of genetic profiling, although others have disagreed (Lyssenko et al. 2006). A predictor of genetic risk cannot do better than predict the true genetic risk with an accuracy of 100%. Yet even in this situation, Janssens et al. (2006) noted that AUC accuracy is a function of heritability and disease prevalence. 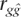Therefore, AUC seems to us to be a confusing statistic, and it is preferable to quote the accuracy of the prediction, Inline graphic.

To investigate the use of high-density genome-wide genetic markers for prediction of genetic risk of disease, we have made some simplifying assumptions. We assumed that the true causal SNPs were always included in the GWAS, and we ignored linkage disequilibrium (LD) between simulated SNPs. If all of our SNPs are viewed as “tag-SNPs” (Carlson et al. 2004) that are selected to tag ungenotyped SNPs with a minimum _r_2 value of 0.8, then 500,000 carefully selected SNPs will capture nearly all of the common variation in the genome (Barrett and Cardon 2006). In this case, our accuracy of prediction may be less than that calculated in our study, by a factor of at most r = 0.9. We chose a simple method to select SNPs based upon a predetermined number of false positives (∼1 out of 500,000) and a stringent type I error rate of 2 × 10−6. More complex methods could be used to select SNPs and to ensure unbiased estimates of effect size of variants contributing to the genomic profile (e.g., Meuwissen et al. 2001; Tibshirani et al. 2002; Storey and Tibshirani 2003; Zollner and Pritchard 2007), and such methods could be adapted to account for LD between the SNPs. However, our demonstration that a simple method performs adequately suggests that improvements from applying other SNP selection algorithms are not going to change the overall conclusions. We also ignored dominance and epistasis in the genetic model for disease because there is overwhelming evidence that most genetic variation is additive by nature, even when genes interact at a mechanistic level (Barton and Keightley 2002). Evidence that highly associated variants act additively (with disease risks of associated variants combining multiplicatively) in the same way as we have modeled has been shown recently for age-related macular degeneration (Maller et al. 2006). Nonetheless, evidence from experimental organisms suggests that gene × gene interactions are likely to be important in some complex traits (Mackay 2004). We also did not consider gene × environment interactions; just as knowledge of environmental risk factors can be included into association studies, so can they be included in prediction of genetic risk to disease. Although many specific models could be defined, we believe the results given here will apply in general terms to a wide range of model assumptions. The high accuracy of prediction of risk that we achieve is partly attributable to the large case-control study samples that we have assumed, but large sample sizes are recognized as necessary for GWAS, and samples of >1000 cases and 1000 controls are already being genotyped (http://www.ncbi.nlm.nih.gov/WGA/programs/GAIN/data/; http://www.wtccc.org.uk/), with even larger samples used for replication studies (Cox et al. 2007; Sladek et al. 2007).

In the past, lack of replication has been a recurring problem for genetic association studies, which must, in part at least, be attributable to lack of power resulting from small sample sizes. In contrast, GWAS and their subsequent replication studies are characterized by large study samples. Time will tell if nonreplication of results and identification of large numbers of false positives is a characteristic of large-scale GWAS. Nonreplication of results may remain a problem if there are, as yet, undetermined methodological problems in genotyping, subtle population stratification effects, or important gene × environment interaction effects. If such problems exist, then our predictions for genetic risk provide an upper bound on the potential for prediction of genetic risk. GWAS for type 2 diabetes have just been published (Saxena et al. 2007; Scott et al. 2007; Zeggini et al. 2007), and no evidence of confounding from population substructure and genotyping biases was found. In the Wellcome Trust Case Control Consortium study (Zeggini et al. 2007) of 459,448 polymorphic SNPs genotyped on 1924 cases and 2938 controls, 30 SNPs from nine regions with P < 10−5 were genotyped on independent replication samples. Variants from three of the nine regions survived replication and showed RR of 1.1–1.4. Prevalence and heritability of type 2 diabetes approximately corresponds our disease scenario of K = 0.05 and _h_2 = 0.2. In this situation, we predict that ∼500 risk loci underlie the disease with mean RR of 1.1 (Fig. 2). In this case, our results show that larger case-control studies are needed to generate accurate predictions of genetic risk from a single study (Fig. 4).

We considered two models for the distribution of risk effects, and we assumed that all genetic variance was attributable to variants of frequency 0.01 to 0.99. If the true genetic architecture underlying complex diseases means that the majority of genetic variance is explained by variants with minor allele frequency <0.01 (the rare variants model; Pritchard 2001), then GWAS will fail to detect risk variants that explain much of the genetic variance because of lack of power and because very rare variants will not be tagged in a set of 500,000 SNPs. If GWAS fail to detect risk variants, then prediction of genetic risk will also fail if it is solely based upon the results from the GWAS. If only part of the genetic variance is available for detection, _h_2available, then accuracy of prediction will decrease by a factor of _h_available/h. Under the neutral model we have simulated ∼50% of the risk variants have minor allele frequency <0.10 (Fig. 1), and these variants explain ∼20% of the genetic variance (Table 1). The first results of the Wellcome Trust Case Control Consortium (2007) have been published and have shown that the number of risk loci that they detect, the proportion of variance they explain, and the conclusion that larger sample sizes are needed are all in line with the models we have used.

Our simulation model allows direct investigation of the most important underlying factors that drive whether genomic profiling is feasible. Our results provide a foundation stone upon which further layers of complexity can be added, but such an exercise is only worthwhile if the foundation is sufficiently solid. All the caveats that apply to GWAS and their replication apply to the derivation of a SNP set that together predict genetic risk and its validation, ensuring that discovery, validation, and application populations are the same.

The need for new methodology for prediction of genetic risk has been recognized (Collins et al. 2003; Bell 2004; Khoury et al. 2006). Implementation of risk prediction in a clinical context has serious ethical and social implications (Grosse and Khoury 2006; Khoury et al. 2006) but has the potential to be of major economic benefit to population health (Khoury et al. 2006). Our study shows that prediction of genetic risk is possible, even if there are hundreds of risk variants each of small effect. Following a large single-stage GWAS (probably larger than those that are currently taking place worldwide), a set of SNPs can be selected that can accurately predict risk of disease in the population. For our prediction, it does not matter (assuming no population stratification), as long as the selected SNPs are true positives, whether they are in linkage disequilibrium with causal variants or causal themselves. The value of these predictive SNPs could be reaped long before the causal mechanism of each contributing variant can be determined.

Methods

The success of association studies and also of genomic profiling depends on the genetic architecture underlying complex diseases. Our first aim is to investigate the relationship between the RR of genetic loci and the number of loci that contribute to risk of a disease under constraints of known disease prevalence and heritability. Ultimately, we will model the genetic architecture of complex disease by allowing the effect size and frequency of risk allele to vary across loci. However, to give insight into our results we first derive an analytical expression for the number of loci that contribute to a disease when the RR (λ) and the allele frequency (p) of the risk alleles are both fixed. We will go on to use these results to investigate the possibilities of using multiple risk loci identified in a genome-wide association study to predict risk of disease in a new population cohort.

We introduce the following notations:

Number of loci underlying complex disease when frequency and RR of risk loci are fixed across all loci

To model the underlying genetic control of complex diseases, we build upon the disease model suggested by Risch (Risch 1990; Risch and Merikangas 1996). We assume that all genotypes are in Hardy–Weinberg equilibrium, so that the probabilities of wild-type, carrier, and homozygous risk genotypes are (1 − p)2, 2_p_(1 − p), and _p_2, respectively. The relative risk of the carrier and homozygous risk genotypes are assumed to be λ and λ2, respectively.

Let g = Prob(affected | genotype) = f_0λ_x, where x is the total number of risk alleles across all loci. Since we assume Hardy–Weinberg equilibrium, x is distributed binomial (2_n_,p). Given the population parameters K, p, and _h_2, we can derive the number of loci, using the mean and genetic variance of the probability of an individual being affected.

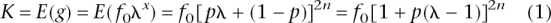
graphic file with name 1520equ1.jpg

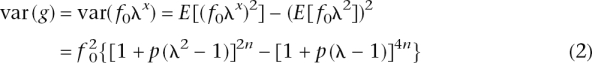
graphic file with name 1520equ2.jpg

For n = 1, the population mean and the genetic variance reduce to those derived by Risch (1990). The variance of disease prevalence due to genetic factors is h_2_K(1 − K). Hence, using this expression and Equations 1 and 2, we can solve for n. After some algebra,

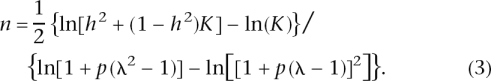
graphic file with name 1520equ3.jpg

Number of loci underlying a complex disease when frequency and RR of risk alleles vary across loci

Next we investigate the number of loci underlying complex disease of given disease prevalence and heritability when the frequency and RR of risk alleles vary. In this situation there is no simple analytical method to derive the number of loci (n), and so we use simulation to determine the mean RR needed to explain the genetic variance of disease for a given number of loci. For n loci with allele frequency pi and relative risk parameter λ_i_, the mean and variance of risk (R) are defined as

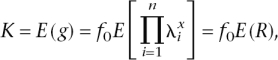
graphic file with name 1520equ4.jpg

with x the number of susceptibility alleles (0, 1, 2) at the _i_th locus.

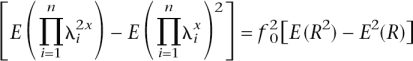
graphic file with name 1520equ5.jpg

and _CV_2 = var(g)/_K_2 = [E(_R_2) − _E_2(R)]/_E_2(R) = E(_R_2)/E(R) − 1], where CV is the coefficient of variation. If we make the following approximations:

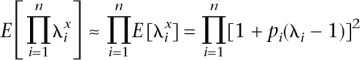
graphic file with name 1520equ6.jpg

and

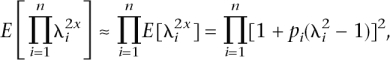
graphic file with name 1520equ7.jpg

then the genetic variance can be calculated conditionally on the allele frequencies and relative risks, without the need to sample genotypes for multiple individuals. The approximation was checked by simulation and was found to work well. Two distributions of frequency of risk alleles were considered: A uniform distribution of allele frequencies that broadly corresponds to the common-disease common-variant (CDCV) hypothesis (Chakravarti 1999; Reich and Lander 2001), in which the frequency of the increasing risk allele was simulated as pi ∼ Uniform(0.01,0.99), or a U-shaped distribution that broadly corresponds the neutral allele hypothesis (Pritchard 2001). In this case, the density function of p is f(p) = C/[p(1 − p)], and the cumulative density function is 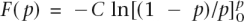Inline graphic with C a constant. To force the cumulative density to 1, we integrate from 0 + δ to 1 − δ, with δ a small number. Solving 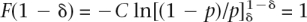Inline graphic for C gives C = 0.5/ln[(1 − δ)/δ]. To simulate an allele frequency from this distribution, we first draw a random number r ∼ Uniform(0,1), which is a draw from the cumulative density function F(p), and then solve for p, as p = 1/{1 + exp[−(r − 1/2)/C_]}. To avoid the simulation of many allele frequencies that are close to 0 or 1 (with resulting finite samples that would be monomorphic), we truncated the allele frequencies at 0.01 and 0.99. To truncate the allele frequencies at pt and 1−_pt, δ satisfies the relationship, 1/pt − 1 = exp[(1/2 − δ)/C_], which can be solved iteratively. For pt = 0.01, δ = 0.009183. For each of the n risk loci, RR was simulated as λ_i = 1 + x(λ0 − 1), with x ∼ Exponential(1). This results in λ_i_ always being larger than 1.0, provided that λ0, an arbitrary input parameter is >1.0. The mean of the simulated RR is E(λ) = λ0. The λ_i_ are transformed so that all the genetic variance is explained by the n loci as 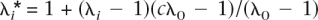Inline graphic, and the adjustment factor c was found iteratively so that it satisfies

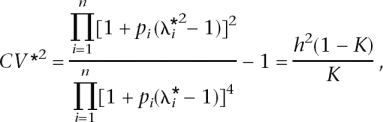
graphic file with name 1520equ8.jpg

or

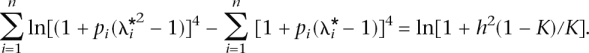
graphic file with name 1520equ9.jpg

The mean RR of the n simulated loci is λ* = 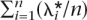Inline graphic, and the 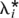Inline graphic are distributed 1 + x(λ* − 1) with x ∼ Exponential(1). This procedure of simulating and transforming relative risks for a fixed number of loci was implemented to force the set of simulated risk alleles to be consistent with a given heritability and disease prevalence, while keeping the distribution of the effects exponential.

Analysis of case-control data for identification of multiple risk loci

Using our models for the genetic architecture of complex diseases, we go on to investigate prediction of genetic risk to disease from multiple risk loci identified in a GWAS. To do this we simulated a case-control study assuming a single-stage genome-wide association screen with 500,000 SNPs. The number of risk loci was fixed at 10, 20, 50, 100, 300, or 1000, and allele frequencies were simulated from either the U-shaped (neutral) or uniform distribution (CDCV). RR of disease loci were simulated from an exponential distribution, forcing the mean RR to be consistent with the heritability, population prevalence, and sampled allele frequencies (as described above). For all other nonsusceptibility loci, the RR was 1.0 and the allele frequencies were sampled as described for the risk loci. Using the sampled allele frequencies, genotypes for each independent locus for each simulated individual resulted from two independent draws from a Bernoulli distribution, which implies Hardy–Weinberg equilibrium. Disease status was simulated from the genotypes at the true n susceptibility loci using a Bernoulli distribution with probability

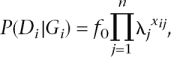
graphic file with name 1520equ10.jpg

where xij is the number of susceptibility alleles for individual i at locus j (xij = 0, 1, 2). A case-control study of 1000 or 10,000 cases and controls was simulated. For each SNP the RR was estimated by maximum likelihood for a logistic model

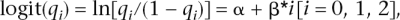
graphic file with name 1520equ11.jpg

with qi the proportion of cases of genotype i (e.g., aa, Aa, and AA, for i = 0, 1, 2) who were diseased. The estimate of the RR in the population (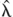Inline graphicj for locus j) was e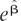Inline graphic, with 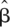Inline graphic the estimate of the regression parameter from the logistic model. Since it is arbitrary which of the alleles the risk is calculated for, 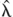Inline graphicj can be >1 or <1. A Newton–Raphson algorithm was applied, which converged in approximately four iterations. In the rare cases where the count for a genotype was zero, the count was set to 1/2. Loci were selected for subsequent prediction of risk if the test statistic (a χ2 test) for association was above a predetermined threshold of 22.59, which corresponds to an expected number of one false positive from 500,000 tests and a nominal _P_-value of 2 × 10−6.

Risk prediction in a new sample from the same population

Next we used the SNPs selected from the simulated case-control study to see how accurately they could predict risk of disease in a randomly identified population sample. Therefore, we simulated a new independent sample of multilocus genotypes of 1000 individuals using the same properties of the multiple simulated risk loci. We assumed that disease status was unknown at the time of predictive testing but that subsequently disease status was known. Disease status for an individual was simulated conditionally on the simulated genotype (G). For each of these individuals, we knew the true disease probability and estimated disease probability from the selected SNPs, calculated as,

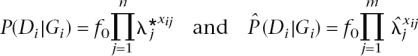
graphic file with name 1520equ12.jpg

with n the total number of true risk loci, m the number of selected loci (both true and false), 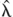Inline graphicj the estimated RR for locus j from the case-control study, and xij the number of risk alleles for individual i at locus j. Note that the estimated risk will deviate from 1.0 only for the selected loci. Probabilities of disease based upon observed genotypes at the selected SNP loci were estimated for all 1000 individuals and were ranked to identify those individuals that were predicted to be at most risk. The number of people with disease (simulated from the genotypes at all true susceptibility loci) was counted among the top 5% of these ranked probabilities. The ratio of the disease risk among the top 5% relative to the disease risk in the entire sample was calculated. This is the observed risk of the identified 5% of people that are most at risk. The accuracy of prediction was quantified by calculating the correlation between the logarithms of the true and predicted probability of disease.

Disease parameters

We considered two disease prevalences, K = 0.05 or 0.10, and two heritabilities on the observed disease scale, h_2 = 0.1 or 0.2. A total of 100 replicates were simulated for each scenario. Note that we assume additive gene action on the log risk scale (multiplicative gene action on the risk scale), that loci act independently, and that there is no linkage disequilibrium between disease predisposition loci. Additive gene action on the log risk scale approximates to having additive action on an underlying liability scale (Lynch and Walsh 1998). The heritability and prevalence parameters that we used can be interpreted in terms of the relative risk of a full-sib of an affected individual λ_s ≈ 1 + 0.5_h_2(1 − K)/K (Lynch and Walsh 1998). This approximation assumes additivity on the risk scale, whereas we have additivity on the log risk scale. For a fixed number of loci, the mean RR is proportional to _h_2(1 − K)/K, that is, proportional to 1 − λs.

Acknowledgments

We thank Stuart Macgregor and Bill Hill for commenting on the manuscript and three reviewers for many helpful comments and suggestions. This work was supported by the Australian National Health and Medical Research Council grants 389892, 442915, 339450, and 443011 and Australian Research Council grant DP0770096.

Footnotes

Appendix A

Closed solutions for number of risk loci for parameterization of Yang et al. (2005)

Yang et al. (2005) investigated the number of genes underlying complex disease by using an epidemiological framework. They consider an additive-effects (on the risk scale) model for which disease prevalence (using our notation for their Equation 1) is

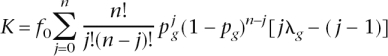
graphic file with name 1520equ13.jpg

where _p_g is the frequency of risk genotype at a risk locus and λg is the RR of the risk genotype. Using the expected value of the number of risk genotypes n in the population of _p_g, this equation reduces to a closed form of K = _f_0[1 + _np_g(λg − 1)]. Defining population-attributable fraction (PAF), as PAF = (K − _f_0)/K, a closed solution for the number of risk loci is

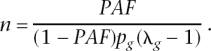
graphic file with name 1520equ14.jpg

They also consider a multiplicative-effects model (on the risk scale, additive on the log risk scale); their Equation 3, in our notation, is \

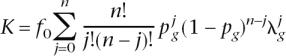
graphic file with name 1520equ15.jpg

which, using the expected value of 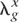Inline graphic = [1 + _p_g(λg − 1)], with x = 1 with probability _p_g and x = 0 with probability (1 − _p_g), reduces to a closed form of K = _f_0[1 + _p_g(λg − 1)]n; solving for n gives

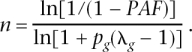
graphic file with name 1520equ16.jpg

References

  1. Barrett J.C., Cardon L.R., Cardon L.R. Evaluating coverage of genome-wide association studies. Nat. Genet. 2006;38:659–662. doi: 10.1038/ng1801. [DOI] [PubMed] [Google Scholar]
  2. Barton N.H., Keightley P.D., Keightley P.D. Understanding quantitative genetic variation. Nat. Rev. Genet. 2002;3:11–21. doi: 10.1038/nrg700. [DOI] [PubMed] [Google Scholar]
  3. Bell J. Predicting disease using genomics. Nature. 2004;429:453–456. doi: 10.1038/nature02624. [DOI] [PubMed] [Google Scholar]
  4. Bertram L., McQueen M.B., Mullin K., Blacker D., Tanzi R.E., McQueen M.B., Mullin K., Blacker D., Tanzi R.E., Mullin K., Blacker D., Tanzi R.E., Blacker D., Tanzi R.E., Tanzi R.E. Systematic meta-analyses of Alzheimer disease genetic association studies: The AlzGene database. Nat. Genet. 2007;39:17–23. doi: 10.1038/ng1934. [DOI] [PubMed] [Google Scholar]
  5. Carlson C.S., Eberle M.A., Kruglyak L., Nickerson D.A., Eberle M.A., Kruglyak L., Nickerson D.A., Kruglyak L., Nickerson D.A., Nickerson D.A. Mapping complex disease loci in whole-genome association studies. Nature. 2004;429:446–452. doi: 10.1038/nature02623. [DOI] [PubMed] [Google Scholar]
  6. Chakravarti A. Population genetics—Making sense out of sequence. Nat. Genet. 1999;21:56–60. doi: 10.1038/4482. [DOI] [PubMed] [Google Scholar]
  7. Collins F.S., Green E.D., Guttmacher A.E., Guyer M.S., Green E.D., Guttmacher A.E., Guyer M.S., Guttmacher A.E., Guyer M.S., Guyer M.S. A vision for the future of genomics research. Nature. 2003;422:835–847. doi: 10.1038/nature01626. [DOI] [PubMed] [Google Scholar]
  8. Cox A., Dunning A.M., Garcia-Closas M., Balasubramanian S., Reed M.W., Pooley K.A., Scollen S., Baynes C., Ponder B.A., Chanock S., Dunning A.M., Garcia-Closas M., Balasubramanian S., Reed M.W., Pooley K.A., Scollen S., Baynes C., Ponder B.A., Chanock S., Garcia-Closas M., Balasubramanian S., Reed M.W., Pooley K.A., Scollen S., Baynes C., Ponder B.A., Chanock S., Balasubramanian S., Reed M.W., Pooley K.A., Scollen S., Baynes C., Ponder B.A., Chanock S., Reed M.W., Pooley K.A., Scollen S., Baynes C., Ponder B.A., Chanock S., Pooley K.A., Scollen S., Baynes C., Ponder B.A., Chanock S., Scollen S., Baynes C., Ponder B.A., Chanock S., Baynes C., Ponder B.A., Chanock S., Ponder B.A., Chanock S., Chanock S., et al. A common coding variant in CASP8 is associated with breast cancer risk. Nat. Genet. 2007;39:352–358. doi: 10.1038/ng1981. [DOI] [PubMed] [Google Scholar]
  9. Falconer D., Mackay T., Mackay T. Introduction to quantitative genetics. Longman; London: 1996. [Google Scholar]
  10. Grosse S.D., Khoury M.J., Khoury M.J. What is the clinical utility of genetic testing? Genet. Med. 2006;8:448–450. doi: 10.1097/01.gim.0000227935.26763.c6. [DOI] [PubMed] [Google Scholar]
  11. Henderson N.D., Turri M.G., DeFries J.C., Flint J., Turri M.G., DeFries J.C., Flint J., DeFries J.C., Flint J., Flint J. QTL analysis of multiple behavioral measures of anxiety in mice. Behav. Genet. 2004;34:267–293. doi: 10.1023/B:BEGE.0000017872.25069.44. [DOI] [PubMed] [Google Scholar]
  12. Hirschhorn J.N., Daly M.J., Daly M.J. Genome-wide association studies for common diseases and complex traits. Nat. Rev. Genet. 2005;6:95–108. doi: 10.1038/nrg1521. [DOI] [PubMed] [Google Scholar]
  13. Ioannidis J.P., Trikalinos T.A., Khoury M.J., Trikalinos T.A., Khoury M.J., Khoury M.J. Implications of small effect sizes of individual genetic variants on the design and interpretation of genetic association studies of complex diseases. Am. J. Epidemiol. 2006;164:609–614. doi: 10.1093/aje/kwj259. [DOI] [PubMed] [Google Scholar]
  14. Jacobsson L., Park H.B., Wahlberg P., Fredriksson R., Perez-Enciso M., Siegel P.B., Andersson L., Park H.B., Wahlberg P., Fredriksson R., Perez-Enciso M., Siegel P.B., Andersson L., Wahlberg P., Fredriksson R., Perez-Enciso M., Siegel P.B., Andersson L., Fredriksson R., Perez-Enciso M., Siegel P.B., Andersson L., Perez-Enciso M., Siegel P.B., Andersson L., Siegel P.B., Andersson L., Andersson L. Many QTLs with minor additive effects are associated with a large difference in growth between two selection lines in chickens. Genet. Res. 2005;86:115–125. doi: 10.1017/S0016672305007767. [DOI] [PubMed] [Google Scholar]
  15. Janssens A.C., Aulchenko Y.S., Elefante S., Borsboom G.J., Steyerberg E.W., van Duijn C.M., Aulchenko Y.S., Elefante S., Borsboom G.J., Steyerberg E.W., van Duijn C.M., Elefante S., Borsboom G.J., Steyerberg E.W., van Duijn C.M., Borsboom G.J., Steyerberg E.W., van Duijn C.M., Steyerberg E.W., van Duijn C.M., van Duijn C.M. Predictive testing for complex diseases using multiple genes: Fact or fiction? Genet. Med. 2006;8:395–400. doi: 10.1097/01.gim.0000229689.18263.f4. [DOI] [PubMed] [Google Scholar]
  16. Kennedy G.C., Matsuzaki H., Dong S., Liu W.M., Huang J., Liu G., Su X., Cao M., Chen W., Zhang J., Matsuzaki H., Dong S., Liu W.M., Huang J., Liu G., Su X., Cao M., Chen W., Zhang J., Dong S., Liu W.M., Huang J., Liu G., Su X., Cao M., Chen W., Zhang J., Liu W.M., Huang J., Liu G., Su X., Cao M., Chen W., Zhang J., Huang J., Liu G., Su X., Cao M., Chen W., Zhang J., Liu G., Su X., Cao M., Chen W., Zhang J., Su X., Cao M., Chen W., Zhang J., Cao M., Chen W., Zhang J., Chen W., Zhang J., Zhang J., et al. Large-scale genotyping of complex DNA. Nat. Biotechnol. 2003;21:1233–1237. doi: 10.1038/nbt869. [DOI] [PubMed] [Google Scholar]
  17. Khoury M.J., Jones K., Grosse S.D., Jones K., Grosse S.D., Grosse S.D. Quantifying the health benefits of genetic tests: The importance of a population perspective. Genet. Med. 2006;8:191–195. doi: 10.1097/01.gim.0000206278.37405.25. [DOI] [PubMed] [Google Scholar]
  18. Khoury M.J., Yang Q., Gwinn M., Little J., Dana Flanders W., Yang Q., Gwinn M., Little J., Dana Flanders W., Gwinn M., Little J., Dana Flanders W., Little J., Dana Flanders W., Dana Flanders W. An epidemiologic assessment of genomic profiling for measuring susceptibility to common diseases and targeting interventions. Genet. Med. 2004;6:38–47. doi: 10.1097/01.gim.0000105751.71430.79. [DOI] [PubMed] [Google Scholar]
  19. Lynch M., Walsh B., Walsh B. Genetics and analysis of quantitative traits. Sinauer Associates, Inc.; Sunderland, MA: 1998. [Google Scholar]
  20. Lyssenko V., Almgren P., Anevski D., Orho-Melander M., Sjögren M., Saloranta C., Tuomi T., Groop L., Almgren P., Anevski D., Orho-Melander M., Sjögren M., Saloranta C., Tuomi T., Groop L., Anevski D., Orho-Melander M., Sjögren M., Saloranta C., Tuomi T., Groop L., Orho-Melander M., Sjögren M., Saloranta C., Tuomi T., Groop L., Sjögren M., Saloranta C., Tuomi T., Groop L., Saloranta C., Tuomi T., Groop L., Tuomi T., Groop L., Groop L. Genetic prediction of future type 2 diabetes. PLoS Med. 2005;2:e345. doi: 10.1371/journal.pmed.0020345.. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Lyssenko V., Anevski D., Almgren P., Groop L., Anevski D., Almgren P., Groop L., Almgren P., Groop L., Groop L. Authors’ reply. PLoS Med. 2006;3:e127. doi: 10.1371/journal.pmed.0030127. [DOI] [Google Scholar]
  22. Mackay T.F. The genetic architecture of quantitative traits: Lessons from Drosophila. Curr. Opin. Genet. Dev. 2004;14:253–257. doi: 10.1016/j.gde.2004.04.003. [DOI] [PubMed] [Google Scholar]
  23. Maller J., George S., Purcell S., Fagerness J., Altshuler D., Daly M.J., Seddon J.M., George S., Purcell S., Fagerness J., Altshuler D., Daly M.J., Seddon J.M., Purcell S., Fagerness J., Altshuler D., Daly M.J., Seddon J.M., Fagerness J., Altshuler D., Daly M.J., Seddon J.M., Altshuler D., Daly M.J., Seddon J.M., Daly M.J., Seddon J.M., Seddon J.M. Common variation in three genes, including a noncoding variant in CFH, strongly influences risk of age-related macular degeneration. Nat. Genet. 2006;38:1055–1059. doi: 10.1038/ng1873. [DOI] [PubMed] [Google Scholar]
  24. Meuwissen T.H., Hayes B.J., Goddard M.E., Hayes B.J., Goddard M.E., Goddard M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics. 2001;157:1819–1829. doi: 10.1093/genetics/157.4.1819. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Pharoah P.D.P., Antoniou A., Bobrow M., Zimmern R.L., Easton D.F., Ponder B.A.J., Antoniou A., Bobrow M., Zimmern R.L., Easton D.F., Ponder B.A.J., Bobrow M., Zimmern R.L., Easton D.F., Ponder B.A.J., Zimmern R.L., Easton D.F., Ponder B.A.J., Easton D.F., Ponder B.A.J., Ponder B.A.J. Polygenic susceptibility to breast cancer and implications for prevention. Nat. Genet. 2002;31:33–36. doi: 10.1038/ng853. [DOI] [PubMed] [Google Scholar]
  26. Pritchard J.K. Are rare variants responsible for susceptibility to complex diseases? Am. J. Hum. Genet. 2001;69:124–137. doi: 10.1086/321272. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Reich D.E., Lander E.S., Lander E.S. On the allelic spectrum of human disease. Trends Genet. 2001;17:502–510. doi: 10.1016/s0168-9525(01)02410-6. [DOI] [PubMed] [Google Scholar]
  28. Risch N. Linkage strategies for genetically complex traits. I. Multilocus models. Am. J. Hum. Genet. 1990;46:222–228. [PMC free article] [PubMed] [Google Scholar]
  29. Risch N., Merikangas K., Merikangas K. The future of genetic studies of complex human diseases. Science. 1996;273:1516–1517. doi: 10.1126/science.273.5281.1516. [DOI] [PubMed] [Google Scholar]
  30. Saxena R., Voight B.F., Lyssenko V., Burtt N.P., de Bakker P.I., Chen H., Roix J.J., Kathiresan S., Hirschhorn J.N., Daly M.J., Voight B.F., Lyssenko V., Burtt N.P., de Bakker P.I., Chen H., Roix J.J., Kathiresan S., Hirschhorn J.N., Daly M.J., Lyssenko V., Burtt N.P., de Bakker P.I., Chen H., Roix J.J., Kathiresan S., Hirschhorn J.N., Daly M.J., Burtt N.P., de Bakker P.I., Chen H., Roix J.J., Kathiresan S., Hirschhorn J.N., Daly M.J., de Bakker P.I., Chen H., Roix J.J., Kathiresan S., Hirschhorn J.N., Daly M.J., Chen H., Roix J.J., Kathiresan S., Hirschhorn J.N., Daly M.J., Roix J.J., Kathiresan S., Hirschhorn J.N., Daly M.J., Kathiresan S., Hirschhorn J.N., Daly M.J., Hirschhorn J.N., Daly M.J., Daly M.J., et al. Genome-wide association analysis identifies loci for type 2 diabetes and triglyceride levels. Science. 2007;316:1331–1336. doi: 10.1126/science.1142358. [DOI] [PubMed] [Google Scholar]
  31. Scott L.J., Mohlke K.L., Bonnycastle L.L., Willer C.J., Li Y., Duren W.L., Erdos M.R., Stringham H.M., Chines P.S., Jackson A.U., Mohlke K.L., Bonnycastle L.L., Willer C.J., Li Y., Duren W.L., Erdos M.R., Stringham H.M., Chines P.S., Jackson A.U., Bonnycastle L.L., Willer C.J., Li Y., Duren W.L., Erdos M.R., Stringham H.M., Chines P.S., Jackson A.U., Willer C.J., Li Y., Duren W.L., Erdos M.R., Stringham H.M., Chines P.S., Jackson A.U., Li Y., Duren W.L., Erdos M.R., Stringham H.M., Chines P.S., Jackson A.U., Duren W.L., Erdos M.R., Stringham H.M., Chines P.S., Jackson A.U., Erdos M.R., Stringham H.M., Chines P.S., Jackson A.U., Stringham H.M., Chines P.S., Jackson A.U., Chines P.S., Jackson A.U., Jackson A.U., et al. A genome-wide association study of type 2 diabetes in Finns detects multiple susceptibility variants. Science. 2007;316:1341–1345. doi: 10.1126/science.1142382. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Sladek R., Rocheleau G., Rung J., Dina C., Shen L., Serre D., Boutin P., Vincent D., Belisle A., Hadjadj S., Rocheleau G., Rung J., Dina C., Shen L., Serre D., Boutin P., Vincent D., Belisle A., Hadjadj S., Rung J., Dina C., Shen L., Serre D., Boutin P., Vincent D., Belisle A., Hadjadj S., Dina C., Shen L., Serre D., Boutin P., Vincent D., Belisle A., Hadjadj S., Shen L., Serre D., Boutin P., Vincent D., Belisle A., Hadjadj S., Serre D., Boutin P., Vincent D., Belisle A., Hadjadj S., Boutin P., Vincent D., Belisle A., Hadjadj S., Vincent D., Belisle A., Hadjadj S., Belisle A., Hadjadj S., Hadjadj S., et al. A genome-wide association study identifies novel risk loci for type 2 diabetes. Nature. 2007;445:881–885. doi: 10.1038/nature05616. [DOI] [PubMed] [Google Scholar]
  33. Storey J.D., Tibshirani R., Tibshirani R. Statistical significance for genomewide studies. Proc. Natl. Acad. Sci. 2003;100:9440–9445. doi: 10.1073/pnas.1530509100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Tibshirani R., Hastie T., Narasimhan B., Chu G., Hastie T., Narasimhan B., Chu G., Narasimhan B., Chu G., Chu G. Diagnosis of multiple cancer types by shrunken centroids of gene expression. Proc. Natl. Acad. Sci. 2002;99:6567–6572. doi: 10.1073/pnas.082099299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Valdar W., Solberg L.C., Gauguier D., Burnett S., Klenerman P., Cookson W.O., Taylor M.S., Rawlins J.N., Mott R., Flint J., Solberg L.C., Gauguier D., Burnett S., Klenerman P., Cookson W.O., Taylor M.S., Rawlins J.N., Mott R., Flint J., Gauguier D., Burnett S., Klenerman P., Cookson W.O., Taylor M.S., Rawlins J.N., Mott R., Flint J., Burnett S., Klenerman P., Cookson W.O., Taylor M.S., Rawlins J.N., Mott R., Flint J., Klenerman P., Cookson W.O., Taylor M.S., Rawlins J.N., Mott R., Flint J., Cookson W.O., Taylor M.S., Rawlins J.N., Mott R., Flint J., Taylor M.S., Rawlins J.N., Mott R., Flint J., Rawlins J.N., Mott R., Flint J., Mott R., Flint J., Flint J. Genome-wide genetic association of complex traits in heterogeneous stock mice. Nat. Genet. 2006;38:879–887. doi: 10.1038/ng1840. [DOI] [PubMed] [Google Scholar]
  36. Wellcome Trust Case Control Consortium Genome-wide association study of 14,000 cases of seven common diseases and 3,000 shared controls. Nature. 2007;447:661–678. doi: 10.1038/nature05911. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Yang Q., Khoury M.J., Friedman J., Little J., Flanders W.D., Khoury M.J., Friedman J., Little J., Flanders W.D., Friedman J., Little J., Flanders W.D., Little J., Flanders W.D., Flanders W.D. How many genes underlie the occurrence of common complex diseases in the population? Int. J. Epidemiol. 2005;34:1129–1137. doi: 10.1093/ije/dyi130. [DOI] [PubMed] [Google Scholar]
  38. Zeggini E., Weedon M.N., Lindgren C.M., Frayling T.M., Elliott K.S., Lango H., Timpson N.J., Perry J.R., Rayner N.W., Freathy R.M., Weedon M.N., Lindgren C.M., Frayling T.M., Elliott K.S., Lango H., Timpson N.J., Perry J.R., Rayner N.W., Freathy R.M., Lindgren C.M., Frayling T.M., Elliott K.S., Lango H., Timpson N.J., Perry J.R., Rayner N.W., Freathy R.M., Frayling T.M., Elliott K.S., Lango H., Timpson N.J., Perry J.R., Rayner N.W., Freathy R.M., Elliott K.S., Lango H., Timpson N.J., Perry J.R., Rayner N.W., Freathy R.M., Lango H., Timpson N.J., Perry J.R., Rayner N.W., Freathy R.M., Timpson N.J., Perry J.R., Rayner N.W., Freathy R.M., Perry J.R., Rayner N.W., Freathy R.M., Rayner N.W., Freathy R.M., Freathy R.M. Replication of genome-wide association signals in U.K. samples reveals risk loci for type 2 diabetes. Science. 2007;316:1336–1341. doi: 10.1126/science.1142364. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Zollner S., Pritchard J.K., Pritchard J.K. Overcoming the winner’s curse: Estimating penetrance parameters from case-control data. Am. J. Hum. Genet. 2007;80:605–615. doi: 10.1086/512821. [DOI] [PMC free article] [PubMed] [Google Scholar]