Microtubules can bear enhanced compressive loads in living cells because of lateral reinforcement (original) (raw)
Abstract
Cytoskeletal microtubules have been proposed to influence cell shape and mechanics based on their ability to resist large-scale compressive forces exerted by the surrounding contractile cytoskeleton. Consistent with this, cytoplasmic microtubules are often highly curved and appear buckled because of compressive loads. However, the results of in vitro studies suggest that microtubules should buckle at much larger length scales, withstanding only exceedingly small compressive forces. This discrepancy calls into question the structural role of microtubules, and highlights our lack of quantitative knowledge of the magnitude of the forces they experience and can withstand in living cells. We show that intracellular microtubules do bear large-scale compressive loads from a variety of physiological forces, but their buckling wavelength is reduced significantly because of mechanical coupling to the surrounding elastic cytoskeleton. We quantitatively explain this behavior, and show that this coupling dramatically increases the compressive forces that microtubules can sustain, suggesting they can make a more significant structural contribution to the mechanical behavior of the cell than previously thought possible.
Introduction
Microtubules are hollow nanoscale biopolymers (Nogales, 2000) that, together with actomyosin filaments and intermediate filaments, form the composite cytoskeleton that controls cell shape and mechanics (Alberts et al., 2005). Microtubules are the most rigid of the cytoskeletal biopolymers, with a bending rigidity ∼100 times that of actin filaments and a persistence length on the order of millimeters (Gittes et al., 1993). Cytoplasmic microtubules are particularly critical for stabilization of long cell extensions, such as nerve cell processes (Zheng et al., 1993), and their disruption results in process retraction and production of regular polygonal cell forms (Omelchenko et al., 2002). Microtubules also orient vertically in cells when they become columnar, as observed during neurulation in the embryo (Burnside, 1971), and they can physically interfere with cardiac myocyte contractility in certain heart conditions (Tsutsui et al., 1993, 1994; Tagawa et al., 1997). Despite their long persistence length, microtubules are also often highly curved in cultured cells, suggesting that they experience large forces within the cytoplasm. Indeed, both slow retrograde flow of the actin cytoskeleton at the cell periphery and stimulation of cell contraction appear to cause compressive buckling of microtubules (Wang et al., 2001; Gupton et al., 2002; Schaefer et al., 2002), whereas disruption of microtubules results in increased transfer of cytoskeletal contractile stress to extracellular matrix adhesions (Stamenovic et al., 2002).
These observations suggest that microtubules can bear compressive loads, which is consistent with models for cellular mechanics in which microtubule compression helps stabilize cell shape by balancing tensional forces within a prestressed cytoskeleton (Wang et al., 1993; Ingber et al., 2000, 2003; Wang et al., 2001; Stamenovic et al., 2002). However, other biophysical studies suggest that individual microtubules cannot bear the large-scale compressive forces generated by the surrounding cytoskeleton in a whole living cell. Moreover, under compressive loading, isolated microtubules exhibit a classic Euler buckling instability, resulting in the formation of a single long-wavelength arc that is completely unlike the highly curved appearance of microtubules observed in living cells (Gittes et al., 1996; Dogterom and Yurke, 1997). These results suggest that microtubules may not support compressive loads because they should buckle at much larger wavelengths and should be unstable to very small forces (Dogterom et al., 2005; Deguchi et al., 2006). The structural role of microtubules in whole living cells thus remains highly controversial.
Despite the importance of understanding the forces associated with the microtubule cytoskeleton for control of cell shape and mechanics, there have been very few studies that quantitatively measure these forces, and the precise physical basis of the microtubule bending seen throughout the cytoplasm remains unknown (Heidemann et al., 1999; Ingber et al., 2000). In this paper, we address the question of whether or not microtubules bear large-scale compressive forces in living cells. Our results reveal that individual microtubules can and do bear levels of compressive force that are one hundred times greater in whole cells than in vitro. This is possible because of lateral mechanical reinforcement by the surrounding elastic cytoskeleton. To illustrate this principle, we present a macroscale model composed of a plastic rod embedded in an elastic gel, which mimics the short-wavelength curvature observed in microtubules in living cells. We show that a reinforced buckling theory accounting for the surrounding elastic network can quantitatively predict the wavelengths of buckling induced by compression at both the macro- and microscales. This simple reinforcement principle, which appears to be widely used by nature to enhance the structural stability of cells, provides an explanation for how microtubules can bear large compressive forces within the cytoskeleton of living cells.
Results
Buckling of microtubules polymerizing at the cell periphery
We first explored whether microtubules bear large-scale compressive loads in living cells by addressing the question of why cytoplasmic microtubules exhibit highly curved forms, whereas isolated microtubules undergo single long-wavelength Euler buckling. The Euler buckling instability observed in vitro with isolated microtubules occurs at a critical compression force given by
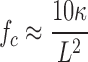
(see supplemental discussion, available at http://www.jcb.org/cgi/content/full/jcb.200601060/DC1), where κ is the bending rigidity and L is the length of the microtubule (Landau and Lifshitz, 1986; Dogterom and Yurke, 1997). Within a cell, microtubules are typically even longer than those studied in vitro, suggesting that they should buckle easily under small loads of order 1 pN; forces larger than this can be generated by even a single kinesin or myosin motor protein (Gittes et al., 1996).
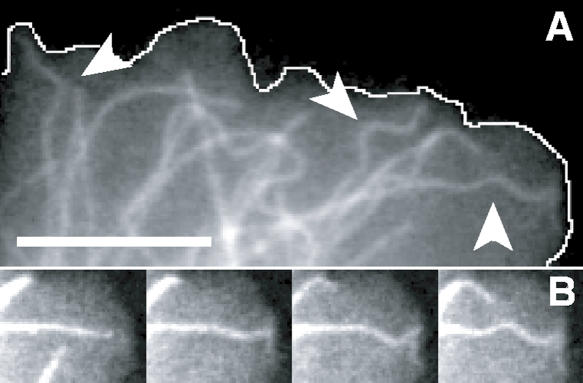
To investigate the response of microtubules to endogenous polymerization forces, Cos7 epithelial cells and bovine capillary endothelial cells were either transfected with tubulin labeled with EGFP or microinjected with rhodaminated tubulin and then analyzed using real-time fluorescence microscopy. The dynamic ends of growing microtubules that polymerized toward the edge of the cell consistently buckled when they hit the cell cortex (Fig. 1 and Videos 1 and 2, available at http://www.jcb.org/cgi/content/full/jcb.200601060/DC1), as observed in a previous study (Wang et al., 2001). Given the well defined (end-on) loading conditions that were visualized with this real-time imaging technique, these results strongly suggest that these particular microtubules are compressively loaded. These microtubules did not, however, exhibit the expected long-wavelength Euler buckling, but, instead, consistently formed multiple short-wavelength (λ ≈ 3 μm) arcs near the site of contact (Fig. 1 and Videos 1 and 2), which were similar to the microtubule shapes that were previously observed in various different cell types (Kaech et al., 1996; Wang et al., 2001; Gupton et al., 2002; Schaefer et al., 2002).
Figure 1.
Structural dynamics of fluorescently labeled microtubules in living cells. (A) Fluorescence micrograph of a Cos7 cell expressing EGFP-labeled microtubules that frequently display sinusoidal shapes (arrowheads) at their ends, which is where they hit end-on at the cell periphery (white line indicates cell periphery). (B) Time sequence (left to right; 5 s between images) showing one microtubule from A at higher magnification as it buckles into a sinusoidal shape when it hits the cell edge (Video 1). Bar, 5 μm. Video 1 is available at http://www.jcb.org/cgi/content/full/jcb.200601060/DC1.
Microtubule buckling induced by exogenous compressive forces
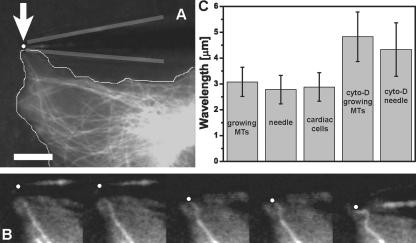
Short-wavelength buckling has not been reported in studies with isolated microtubules under compression (Dogterom and Yurke, 1997). Therefore, we directly tested whether compressive forces are indeed the cause by imposing an exogenous compressive load on intracellular microtubules in living cells. To accomplish this, a glass microneedle controlled by a micromanipulator was used to compress the cell membrane and underlying microtubules at the cell periphery, while simultaneously analyzing their structural response (Fig. 2 A). When initially straight microtubules that were aligned along the main axis of force application were compressed in this way, their proximal regions buckled with a short wavelength (2.8 ± 0.5 μm; mean ± SD) that was nearly identical to that naturally exhibited by the ends of growing microtubules (3.1 ± 0.6 μm; Fig. 2 B and Videos 3 and 4, available at http://www.jcb.org/cgi/content/full/jcb.200601060/DC1). Therefore, we conclude that the short-wavelength buckling of microtubules is indeed a mechanical response to compressive loading caused by axial forces.
Figure 2.
Deformation response of initially straight microtubules compressively loaded by a microneedle. (A) To determine if microtubules in cells buckle into short-wavelength shapes when artificially compressed by an exogenous force, we used a fine glass microneedle to push on initially straight microtubules at the cell periphery (white dot, needle tip position; gray lines, needle outline) Bar, 10 μm. (B) Time sequence of the microtubule in A compressed by the needle as it is moved from top to bottom (left to right; 1.1 s between images; Video 3). The microtubule buckles into a sinusoidal shape similar to that of naturally buckling microtubules. (C) The wavelength of microtubules buckled by the needle is the same as that of microtubules buckled as they polymerize into the cell cortex and that of microtubule buckling caused by actomyosin contractility in beating cardiac myocytes. When the actin cytoskeleton was disrupted in Cos7 cells treated with cytochalasin D, the wavelength of both naturally buckled and needle-buckled microtubules increased. MTs, microtubules. Error bars are ± SD. Video 3 is available at http://www.jcb.org/cgi/content/full/jcb.200601060/DC1.
Microtubule buckling caused by actomyosin contractility
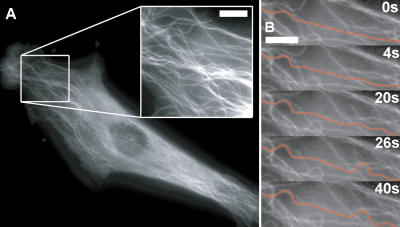
Short-wavelength buckling forms are also observed in microtubules located deep within the cytoplasm of these same cells (Fig. 3, A and B). Hypercontraction of the cytoskeleton in nonmuscle cells can induce buckling of cytoplasmic microtubules, and normally curved microtubules straighten when tension is released (Wang et al., 2001). Myosin-based force generation also appears to drive microtubule compression under retrograde flow of the lamellar actin network (Gupton et al., 2002), and overproduction of microtubules can impair cardiac cell contraction in dilated heart muscle (Tsutsui et al., 1994). These observations suggest that the contractile actin cytoskeleton may also compressively load and buckle cytoplasmic microtubules (Ingber, 2003).
Figure 3.
Microtubule buckling caused by cell contractility. (A) Fluorescence micrograph of a capillary cell expressing EGFP-tubulin and low and high (inset) magnification showing that microtubule buckling occurs throughout the cytoplasm with similar short-wavelength forms as observed at the periphery. (B) Time sequence of a movie of the cell shown in A, with a single microtubule highlighted in orange for clarity, demonstrated that high curvature buckling occurs in localized regions separated by straight regions of the same microtubule. Bars, 5 μm. Video 8. Video 8 is available at http://www.jcb.org/cgi/content/full/jcb.200601060/DC1.
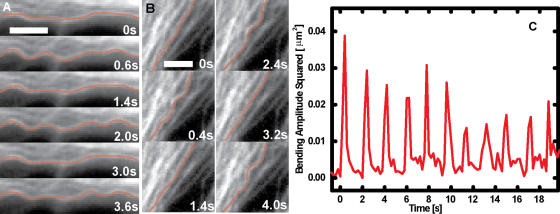
To test this possibility under physiological conditions, we analyzed microtubule behavior in beating cardiac myocytes where actomyosin-based contraction is temporally periodic and well defined. Microtubules in these cells cyclically buckled and unbuckled with each wave of contraction (systole) and relaxation (diastole) of the cardiac muscle cell (Fig. 4 and Videos 5 and 6, available at http://www.jcb.org/cgi/content/full/jcb.200601060/DC1). The wavelength was again short; λ ≈ 2.9 ± 0.6 μm (Fig. 2 C). Thus, in addition to polymerization forces and external loads, internally generated actomyosin contractile forces can also compressively load microtubules under physiological conditions. The microtubules buckle at identical short wavelengths in each case, suggesting that the same physics governs their behavior.
Figure 4.
Periodic microtubule buckling caused by contractile beating of heart cells. (A) Time sequence of a microtubule buckling in a beating cardiac myocyte. The microtubule can be seen to buckle and unbuckle successively three times (Video 5). (B) Time sequence of a microtubule buckling and unbuckling in a beating cardiac myocyte, while neighboring microtubules remain straight. The microtubule buckles in a specific spot in each of the successive buckling events (Video 6). (C) Fourier mode analysis of the microtubule shown in B demonstrates that the amplitude of the bending on wavelengths of ∼3 μm shows periodic spikes caused by periodic buckling of the microtubule under successive contractile beats. The amplitude of this periodic buckling decreases with time as the intensity of the contractile force decreases with time because of photodamage. Bars, 3 μm. Videos 5 and 6 are available at http://www.jcb.org/cgi/content/full/jcb.200601060/DC1.
Origin of short-wavelength buckling response
A clue to the origin of this high-curvature buckling comes from observations of the dense microtubule network in beating cardiac myocytes, where we found that neighboring microtubules often buckled in a coordinated manner, both temporally and spatially in phase (Video 7, available at http://www.jcb.org/cgi/content/full/jcb.200601060/DC1). This suggests that they are mechanically coupled to each other because of the intervening elastic cytoplasm. Thus, the short-wavelength buckling of individual microtubules could reflect constraints on microtubule bending that are caused by the need to deform lateral structural reinforcements. This mechanical coupling likely reflects the fact that microtubules in eukaryotic cells are embedded in a surrounding elastic network of cytoskeletal actin microfilaments and intermediate filaments, as demonstrated by high-resolution microscopy (Svitkina et al., 1995; Waterman-Storer and Salmon, 1997). This composite network of cytoskeletal filaments is largely responsible for the elastic response of the cytoplasm (Wang et al., 1993), and may also act as a reinforcing lateral constraint that prevents long-wavelength buckling of microtubules (Brodland and Gordon, 1990).
To test the biophysical hypothesis that lateral mechanical constraints lead to short-wavelength buckling in microtubules within living cytoplasm, we first performed studies using a macroscopic model system in which a thin plastic rod (∼0.1-mm-diam) was used to mimic a single microtubule. When this rod was compressed in aqueous solution, it yielded the expected long-wavelength Euler buckling mode (Fig. 5 A). To mimic the effect of a surrounding elastic network, we embedded the rod in gelatin: when the rod was compressed, the long-wavelength mode was suppressed. Instead, shorter-wavelength buckling resulted (Fig. 5 B), which was strikingly similar to that displayed by microtubules in living cells (Figs. 1–4). This finding suggests that similar lateral constraints may lead to the short-wavelength buckling behavior observed in living cells.
Figure 5.
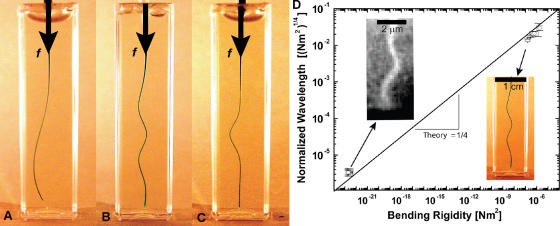
Macroscopic buckling with a plastic rod. (A) When a thin (∼0.2-mm-diam) plastic rod was compressed in a 1-cm-wide rectangular chamber filled with water it underwent classic long-wavelength Euler buckling. (B) When this experiment was repeated with a rod embedded in an elastic gelatin network, short wavelength buckling (λ = 1.1 cm) was observed. (C) A local region of the gelatin network was first disrupted by overcompression of the rod. When the rod was subsequently released and then compressed again, local short-wavelength buckling was limited to this same disrupted region, even while the rest of the rod remained straight. (D) When this experiment was repeated with plastic rods of differing stiffness, there was good agreement with theory in all cases (top right data points). The data from microtubules buckled because of exogenous forces, polymerization forces, and actomyosin contractile forces also show good agreement with this theory (bottom left data points). Vertical error bars are ± SD. Horizontal error bars (bottom left cell MT data) are an estimate of the uncertainty in MT bending rigidity.
This short-wavelength buckling behavior can be described quantitatively using a constrained buckling theory. For a constrained rod to bend, it must push into and deform the surrounding network. Because of the energetic cost of this deformation, short-wavelength buckling will be preferred because the same degree of end-to-end compression is possible with smaller lateral motion (smaller deformation). This can be described with the following equation showing the total energy of deformation, which is a sum of integrals along the length of the rod (Landau and Lifshitz, 1986; Skotheim and Mahadevan, 2004):
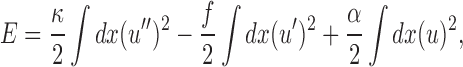
where u(x) is the transverse displacement of the rod as a function of the axial coordinate x, and α is proportional to the elastic modulus G (see supplemental discussion). The first term represents the bending energy of the rod, the second term expresses the axial compression energy released by the buckling, f_Δ_L, where Δ_L_ is the change in axial length of the rod, and the third term is the elastic deformation energy associated with pushing laterally into the surrounding medium. The Euler buckling theory comprises the first two terms; in contrast to the long wavelength Euler buckling result, the additional deformation energy represented by the third term leads to buckling on a short wavelength. The wavelength is set by the ratio of the bending rigidity of the rod and the elastic modulus of the surrounding network in the following equation:
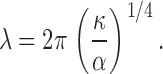
This constrained buckling theory provides a quantitative description of our macroscopic observation. Using measured values of the elastic modulus of the gelatin (G = 1.5 kPa), and the bending rigidity of the plastic rod (κ ≈ 10−7 Nm2), the theory predicts a buckling wavelength of λ ≈ 1 cm, which is in excellent agreement with the experimental result (λ ≈ 1.1 cm). Moreover, by using an array of plastic rods with bending rigidities varying by over an order of magnitude, we confirmed that the theoretical predictions closely matched the measured wavelengths in all cases (Fig. 4 D).
The biological relevance of this theory was also examined quantitatively by testing its ability to predict the buckling wavelength of microtubules in living cells. Using the reported microtubule bending rigidity (Gittes et al., 1993), κ ≈ 2 × 10−23 Nm2, and the elastic modulus of the surrounding cytoskeletal network (Mahaffy et al., 2000; Fabry et al., 2001), G ≈ 1 kPa, the theory predicts that compressively loaded microtubules should buckle with a wavelength of λ ≈ 2 μm; this is in good agreement with the measured wavelength λ ≈ 3 μm (Fig. 2 C). We note that the effect of intracellular microtubule-associated proteins on the microtubule bending rigidity is unclear (Felgner et al., 1997), and the rigidity also appears to depend on the speed of their polymerization (Janson and Dogterom, 2004); indeed, measurements of microtubule bending rigidity have varied by an order of magnitude. The elastic modulus of the cytoskeleton is also locally heterogeneous within the same cell, and measurements of this quantity have varied. However, the one-quarter power dependence of the wavelength on both the bending rigidity and the elastic modulus makes the predicted wavelength relatively insensitive to uncertainty in these values. The close agreement between the predicted and observed wavelengths shows that this constrained buckling theory can quantitatively explain both the macroscale model and the microscale buckling of microtubules in living cells (Fig. 5 D). Despite the fact that these two systems differ by more than four orders of magnitude in spatial scale, with bending rigidity differing by over 16 orders of magnitude, the same physics governs their behavior.
A central component of the elastic cytoskeleton of the cell is the actin filament network (Wang et al., 1993; Fabry et al., 2001; Gardel et al., 2006), which surrounds and is connected to intracellular microtubules (Svitkina et al., 1995; Waterman-Storer and Salmon, 1997); therefore, we hypothesize that this actin network plays an important role in microtubule reinforcement. To test this hypothesis, we pretreated Cos7 cells with 2 μM cytochalasin D for 30 min to disrupt the surrounding actin filament network, and used a microneedle to compress microtubules. We found that the wavelength increased to 4.3 ± 1.0 μm in cytochalasin-treated cells, compared with 2.8 ± 0.5 μm in untreated cells (P < 0.0005; paired t test; Fig. 2 C). The wavelength of naturally buckled microtubules also increased to a similar degree in these cells. This increase, albeit small, supports the hypothesis that the actin network plays a role in reinforcing microtubules. The relatively small change is consistent with the weak dependence of the buckling wavelength on the elasticity of the surrounding cytoskeleton (λ ≈ G −1/4). Indeed, the larger buckling wavelength corresponds to a decrease in the elastic modulus of the surrounding cytoskeleton by a factor of ∼5, which is consistent with previous measurements of cytochalasin-treated cells (Wang et al., 1993; Fabry et al., 2001). Thus, the lateral structural reinforcement of microtubules responsible for their enhanced compressive load-bearing capacity appears to be at least partly attributable to the surrounding actin cytoskeleton in living cells.
Effect of local mechanical properties on location and extent of buckling
In studies with both muscle and nonmuscle cells, we found that localized regions of single microtubules repeatedly underwent short-wavelength buckling at the same sites when analyzed over many minutes, whereas intervening regions of the same microtubule, and also neighboring microtubules, remained straight (Figs. 3 and 4; and Videos 6 and 8, available at http://www.jcb.org/cgi/content/full/jcb.200601060/DC1). Nonbuckled microtubules in cells may experience a large, but subcritical compressive force, even when other regions of the same microtubule exhibit short-wavelength buckling, perhaps because of local weak spots in the surrounding elastic network. We observed similar behavior in the macroscopic experiment when a localized region of the surrounding gelatin network was disrupted; the rod preferentially buckled in this same localized region when it was compressed a second time, even though adjacent segments of the same rod remained straight (Fig. 5 C). These observations suggest that the location of high curvature microtubule buckling may be linked to local variations in the stiffness of the surrounding cytoskeletal network.
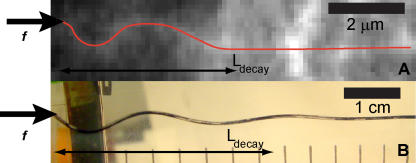
Interestingly, when microtubules were compressed by forces acting at their tips, the buckling typically did not extend along the entire microtubule; instead, the buckling was localized to a region close to the site of force application (Figs. 1, 2, and 6). We found similar behavior when we performed the macroscopic buckling experiment in tall sample chambers; the amplitude of the short-wavelength buckling decayed with distance from the site of force application (Fig. 6 B). This localization of the buckling results from longitudinal mechanical coupling (sticking) of the rod to the network; this attenuates the compressive force along the axis of the rod (see supplemental discussion). Thus, there is likely a similar coupling of the microtubule to the surrounding network, causing the attenuation of its buckling. This is consistent with studies showing that microtubules are physically linked to the surrounding cytoskeleton through protein cross-linkers (Svitkina et al., 1995; Gupton et al., 2002). Thus, the strength and kinetics of these cross-linkers determine the distance over which forces are mechanically transmitted through the cell.
Figure 6.
Decay of transmission of the compressive force. (A) In microtubules compressed by force application at their tips (Figs. 1 and 2), the buckling amplitude decays along the length of the microtubule, reflecting an attenuation of the compressive force by the surrounding network. (B) Similar behavior was seen in the macroscopic experiments using plastic rods embedded in elastic gelatin.
Discussion
The structural organization and mechanical behavior of microtubules are believed to play a central role in the determination of polarized cell shape and directional motility that are critical for tissue development. Microtubules also appear to contribute to some heart diseases by physically interfering with the contraction of hypertrophied cardiac muscle cells (Tsutsui et al., 1993, 1994). Yet, studies of isolated microtubules suggest that they should not be able to bear more than ∼1 pN of compressive force, and thus, they should not contribute significantly to the mechanical stability of the whole cell. This apparent discrepancy reflects the lack of information about the mechanical behavior of microtubules within the normal physical context of the living cytoplasm. In this study, we directly addressed the question of whether individual microtubules can bear the levels of compressive forces necessary to influence overall cell mechanical behavior by studying and modeling microtubule buckling behavior in the living cytoplasm. Our results show that microtubules exhibit similar buckling responses, with nearly identical short wavelengths and correspondingly high curvature, whether compressed by endogenous polymerization or contractile forces or by direct application of end-on compression using a micropipette. This buckling wavelength could be increased by weakening the reinforcement provided by the cytoskeletal actin network. Moreover, similar buckling behavior can be mimicked using a macroscale model of a plastic rod embedded in an elastic gelatin network. A constrained buckling theory provides a quantitative description of this behavior at all size scales.
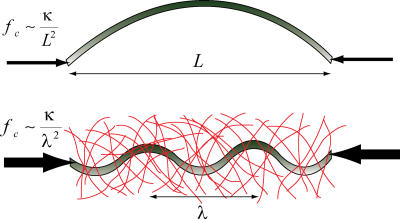
The finding that microtubules buckle in the living cytoplasm implies that they are under a minimum level of compressive loading because buckling is a threshold phenomenon; it only occurs once the compressive force reaches a critical value. However, lateral reinforcement ensures that a microtubule can remain structurally stable and continue to support a compressive load even after it buckles. Within this picture, we can calculate the critical force using
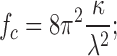
this expression is similar to that for Euler buckling, except that the relevant length scale is now λ, which is the shorter wavelength of buckling (see supplemental discussion). This critical force depends linearly on the bending rigidity and, therefore, is sensitive to the large uncertainties in the microtubule bending rigidity. Nevertheless, using the measured wavelength, which is λ ≈ 3 μm, and the bending rigidity of microtubules, the minimum compressive force experienced by microtubules that exhibit short-wavelength buckling can be estimated, and we obtain fc ≈ 100 pN. Interestingly, this is about 10 times larger than the microtubule polymerization forces measured in vitro (Dogterom and Yurke, 1997), which could reflect larger forces in the cell caused by the complex molecular environment at the microtubule tip (Schuyler and Pellman, 2001; Dogterom et al., 2005).
Short-wavelength shapes similar to those we describe have also been seen in microtubules that were buckled by retrograde flow of the actin network (Gupton et al., 2002; Schaefer et al., 2002), and can be seen in microtubules in various other cell types and species (Kaech et al., 1996; Heidemann et al., 1999; Wang et al., 2001). Some of this high curvature microtubule bending may result from transverse shear stresses (Heidemann et al., 1999). For example, the active viscoelastic flow of the cytoplasm generates a slowly evolving stress field (Lau et al., 2003) that can cause both longitudinal compression and transverse shear stresses, depending on the details of the local stress field. Indeed, microtubules also display bending on longer length scales that appears to result from this complex stress field (Figs. 1 and 2). However, it is highly unlikely that the observed multiple short-wavelength bending could be caused by effects of transverse stresses alone. Instead, our results suggest that this ubiquitous highly curved form of microtubule deformation reflects the generic nature of reinforced microtubule compression in living cytoplasm.
Our results suggest that microtubules can be used to probe the local mechanical environment within cells. Although we have focused on the cytoskeleton of interphase cells, the mitotic spindle is another important microtubule-based structure. This may provide additional insight into the poorly understood mechanical behavior of mitotic spindles (Pickett-Heaps et al., 1984; Maniotis et al., 1997; Kapoor and Mitchison, 2001; Scholey et al., 2001). Microtubules within spindles have been observed to buckle at somewhat longer wavelengths under natural conditions (Aist and Bayles, 1991), or after mechanical or pharmacological perturbations (Pickett-Heaps et al., 1997; Mitchison et al., 2005), which suggests that spindle microtubules also experience compressive forces. This long-wavelength buckling may reflect an increased effective stiffness of microtubules caused by reinforcement by intermicrotubule bundling connections within the complex structure of the spindle. However, in the absence of bundling, these results suggest that the elasticity of any surrounding matrix cannot be very large. Another cell in which longer-wavelength buckling is observed is the fission yeast, where nuclear positioning is thought to occur by compressive loading of microtubules (Tran et al., 2001). This again suggests that the elasticity of any surrounding network must be considerably less than that of the interphase animal cells we studied. Thus, in these particular microtubule arrays, structural reinforcement may be either unnecessary, or mediated by other mechanisms, such as microtubule bundling.
An important implication of this work is the demonstration that cytoplasmic microtubules are effectively stiffened when embedded in even a relatively soft (elastic modulus ∼1 kPa) cytoskeletal network; e.g., a reinforced 20-μm-long cytoplasmic microtubule can withstand a compressive force (>100 pN) >100 times larger than a free microtubule before buckling. Consequently, individual microtubules can withstand much larger compressive forces in a living cell than previously considered possible (Fig. 7). Moreover, as demonstrated by our results with cytochalasin-treated cells, the lateral reinforcement is robust; even disruption of the surrounding actin network only slightly increases the buckling wavelength, with a corresponding decrease in the critical force by a factor of ∼2. This is likely caused by the presence of other sources of elasticity, such as intermediate filaments, which have been previously shown to both connect laterally to microtubules (Bloom et al., 1985), and to contribute to whole cytoskeletal mechanics (Wang et al., 1993). As illustrated with the macroscopic model, this reinforcement is a robust phenomenon that is insensitive to the specific molecular details; the only requirement is that the surrounding matrix must be elastic.
Figure 7.
Schematic summarizing how the presence of the surrounding elastic cytoskeleton reinforces microtubules in living cells. Free microtubules in vitro buckle on the large length scale of the filament, at a small critical buckling force. Microtubules in living cells are surrounded by a reinforcing cytoskeleton. This leads to a larger critical force, and buckling on a short wavelength.
Mechanical reinforcement by the surrounding cytoskeleton may therefore provide a physical basis by which the microtubule network can bear the large loads required to stabilize the entire cytoskeleton and thereby control cell behavior that is critical for tissue development, including polarized cell spreading, vesicular transport, and directional motility. These data also suggest that these are often large compressive forces; this is consistent with mechanical models of the cell that incorporate compression-bearing microtubules which balance tensional forces present within a prestressed cytoskeleton (Wang et al., 1993; Stamenovic et al., 2002; Ingber, 2003). Compressive loading of reinforced microtubules may also have important implications for specialized cell functions, such as in cardiac myocytes, where elastic recoil of compressed microtubules may contribute to diastolic relaxation or interfere with normal contractility in diseased tissue. These results represent a first step toward a quantitative understanding of how living cells are constructed as composite materials and mechanically stabilized at the nanometer scale.
Materials and methods
Cell culture and transfection
Cos7 cells (African green monkey kidney–derived) were obtained from the American Type Culture Collection and cultured in 10% FBS DME. Bovine capillary endothelial cells were cultured as previously described (Parker et al., 2002). For EGFP studies, confluent monolayers of cells were incubated for 24–48 h with an adenoviral vector encoding EGFP-tubulin (Wang et al., 2001). Cells were sparsely plated onto glass-bottomed 35-mm dishes (MatTek Corp.) and allowed to adhere and spread overnight. For some studies, cells were microinjected with ∼1 mg/ml rhodamine-labeled tubulin (Cytoskeleton, Inc.) using a Femtojet microinjection system (Eppendorf) and allowed to incorporate fluorescent tubulin for at least 2 h. For some experiments, cells were incubated with 2 μM cytochalasin D (Sigma-Aldrich) for 30 min before imaging. Microtubules were buckled using Femtotip needles controlled with a micromanipulator (both Eppendorf).
Cardiac myocytes
Cardiac myocytes were isolated from 2-d-old Sprague-Dawley rats (Charles River Laboratories). In brief, whole hearts were removed from killed animals and subsequently homogenized and washed in HBSS, followed by trypsin and collagenase digestion for 14 h at 4°C with agitation. Once trypsinized, cells were resuspended in M199 culture medium supplemented with 10% heat-inactivated FBS, 10 mmol/liter Hepes, 3.5 g/liter glucose, 2 mmol/liter l-glutamine, 2 mg/liter vitamin B-12, and 50 U/ml penicillin at 37°C and agitated. Immediately after purification, cells were plated on glass-bottomed Petri dishes (MatTek Corp.). For some studies, the dishes were spin coated with polydimethylsiloxane silicone elastomer (Sylgard; Dow Corning) that was treated with 25 μg/ml human fibronectin in ddH20 for 1 h. Immediately before incubation with the protein solution, culture substrates were treated in a UVO cleaner for 8 min (Jelight Company, Inc.). Cells were kept in culture at 37°C with a 5% CO2 atmosphere. Medium was changed 24 h after plating to remove unattached and dead cells, followed by changes with supplemented M199 medium containing 2% FBS 48 and 96 h after plating. Cells were transfected with EGFP-tubulin or microinjected with fluorescent tubulin, as with nonmuscle cells. For some studies, beating was stimulated with 1 μmol/liter epinephrine immediately before imaging.
Microscopy and image analysis
Fluorescent images were acquired on an inverted microscope (DM-IRB; Leica) equipped with an intensified charge-coupled device camera (model C7190-21 EB-CCD; Hamamatsu) and automated image acquisition software (MetaMorph; Universal Imaging Corp.). Images were analyzed using custom-built filament tracking software to extract the contours of single microtubules as a function of time. The shape at each time point was then analyzed using a Fourier decomposition (Gittes et al., 1993).
Macroscopic buckling
The macroscopic rods were either hollow capillary-loading pipette tips (Eppendorf) or solid fishing line (Stren). The rods were placed in a 1-cm cuvette cell that was then filled with liquid gelatin (Sigma-Aldrich) and allowed to gel before applying a compressive force from the top. For the capillary-loading pipette tips, we used tabulated values for the elastic modulus of the polypropylene plastic (E = 1.9 GPa) and measured the outer (ro ≈ 116 μm) and inner radius (ri ≈ 93 μm) of the rod. For the fishing line, we determined the elastic modulus using a tensile test (E = 0.9 GPa) and measured the radius. We tested samples in the range r ≈ 103–227 μm. We estimated the bending rigidity (Landau and Lifshitz, 1986) using the following equation:
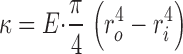
The elastic modulus of the gelatin was determined using a stress-controlled rheometer (model CVOR; Bohlin Instruments) equipped with a 4°C 40-mm cone and plate tool.
Online supplemental material
Video 1 shows EGFP microtubules buckling into sinusoidal shapes when they polymerize into the edge of a Cos7 cell. Video 2 shows an EGFP microtubule buckling into a sinusoidal shape as it polymerizes against the edge of a capillary endothelial cell. Video 3 shows an initially straight EGFP microtubule at the edge of a Cos7 cell that is compressively loaded with a glass microneedle and undergoes buckling. Video 4 shows another example of an EGFP microtubule compressively loaded with a microneedle at the edge of a Cos7 cell. Video 5 shows a rhodamine-labeled microtubule repeatedly buckling into a short-wavelength shape with each cycle of contraction in a beating cardiac myocyte. Video 6 shows an example of a rhodamine-labeled microtubule in a beating cardiac myocyte that repeatedly buckles in the same spot, even while adjacent microtubules remain straight. Video 7 shows two microtubules within an EGFP-tubulin–transfected cardiac myocyte that can be seen to cyclically buckle in a coordinated manner with each contractile beat. Video 8 shows a microtubule locally buckling within the cytoplasm of an EGFP-tubulin–transfected capillary cell, whereas adjacent regions of the same microtubule remain straight. Online supplemental materials are available at http://www.jcb.org/cgi/content/full/jcb.200601060/DC1.
Supplementary Material
[Supplemental Material Index]
Acknowledgments
We wish to thank Sean Sheehy for harvesting cardiac myocytes and Dan Needleman for helpful discussions.
This work was supported by the National Science Foundation (NSF) through the Harvard Materials Research Science and Engineering Center (DMR-0213805). C.P. Brangwynne was supported by the NSF through the Integrated Training Program in Biomechanics (DGE-0221682). D.A. Weitz was supported by the NSF (DMR-0243715). D.E. Ingber and S. Kumar were supported by grants from the National Aeronautics and Space Administration (NN-A04CC96G) and a National Institutes of Health postdoctoral fellowship (F32-NS048669). F.C. MacKintosh was supported by the Foundation for Fundamental Research on Matter. J. Talbot was supported by the Research Experience for Undergraduates/Research Experience for Teachers in Materials Research programs from the NSF (DMR-0353937).
S. Kumar's present address is Dept. of Bioengineering, University of California, Berkeley, Berkeley, CA 94720.
References
- Aist, J.R., and C.J. Bayles. 1991. Detection of spindle pushing forces in vivo during anaphase b in the fungus _Nectria haematococca._Cell Motil. Cytoskeleton. 19:18–24. [Google Scholar]
- Alberts, B., A. Johnson, J. Lewis, M. Raff, K. Roberts, and P. Walter. 2005. Molecular Biology of the Cell. Fourth edition. Garland Science, New York. 1463 pp.
- Bloom, G.S., F.C. Luca, and R.B. Vallee. 1985. Cross-linking of intermediate filaments to microtubules by microtubule-associated protein 2. Ann. N. Y. Acad. Sci. 455:18–31. [DOI] [PubMed] [Google Scholar]
- Brodland, G.W., and R. Gordon. 1990. Intermediate filaments may prevent buckling of compressively loaded microtubules. J. Biomech. Eng. 112:319–321. [DOI] [PubMed] [Google Scholar]
- Burnside, B. 1971. Microtubules and microfilaments in newt neuralation. Dev. Biol. 26:416–441. [DOI] [PubMed] [Google Scholar]
- Deguchi, S., T. Ohashi, and M. Sato. 2006. Tensile properties of single stress fibers isolated from cultured vascular smooth muscle cells. J. Biomech. 10.1016/j.jbiochem.2005.08.026. [DOI] [PubMed]
- Dogterom, M., and B. Yurke. 1997. Measurement of the force-velocity relation for growing microtubules. Science. 278:856–860. [DOI] [PubMed] [Google Scholar]
- Dogterom, M., J.W.J. Kerssemakers, G. Romet-Lemonne, and M.E. Janson. 2005. Force generation by dynamic microtubules. Curr. Opin. Cell Biol. 17:67–74. [DOI] [PubMed] [Google Scholar]
- Fabry, B., G.N. Maksym, J.P. Butler, M. Glogauer, D. Navajas, and J.J. Fredberg. 2001. Scaling the microrheology of living cells. Phys. Rev. Lett. 87:148102. [DOI] [PubMed] [Google Scholar]
- Felgner, H., R. Frank, J. Biernat, E.-M. Mandelkow, E. Madelkow, B. Ludin, A. Matus, and M. Schliwa. 1997. Domains of neuronal microtubule-associated proteins and flexural rigidity of microtubules. J. Cell Biol. 138:1067–1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardel, M.L., F. Nakamura, J.H. Hartwig, J.C. Crocker, T.P. Stossel, and D.A. Weitz. 2006. Prestressed F-actin networks cross-linked by hinged filamins replicate mechanical properties of cells. Proc. Natl. Acad. Sci. USA. 103:1762–1767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gittes, F., B. Mickey, J. Nettleton, and J. Howard. 1993. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 120:923–934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gittes, F., E. Meyhofer, S. Baek, and J. Howard. 1996. Directional loading of the kinesin motor molecule as it buckles a microtubule. Biophys. J. 70:418–429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupton, S.L., W.C. Salmon, and C.M. Waterman-Storer. 2002. Converging populations of f-actin promote breakage of associated microtubules to spatially regulate microtubule turnover in migrating cells. Curr. Biol. 12:1891–1899. [DOI] [PubMed] [Google Scholar]
- Heidemann, S.R., S. Kaech, R.E. Buxbaum, and A. Matus. 1999. Direct observations of the mechanical behaviors of the cytoskeleton in living fibroblasts. J. Cell Biol. 145:109–122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ingber, D.E. 2003. Tensegrity I. Cell structure and hierarchical systems biology. J. Cell Sci. 116:1157–1173. [DOI] [PubMed] [Google Scholar]
- Ingber, D.E., S.R. Heidemann, P. Lamoureux, and R.E. Buxbaum. 2000. Opposing views on tensegrity as a structural framework for understanding cell mechanics. J. Appl. Physiol. 89:1663–1678. [DOI] [PubMed] [Google Scholar]
- Janson, M.E., and M. Dogterom. 2004. A bending mode analysis for growing microtubules: evidence for a velocity-dependent rigidity. Biophys. J. 87:2723–2736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaech, S., B. Ludin, and A. Matus. 1996. Cytoskeletal plasticity in cells expressing neuronal microtubule-associated proteins. Neuron. 17:1189–1199. [DOI] [PubMed] [Google Scholar]
- Kapoor, T.M., and T.J. Mitchison. 2001. Eg5 is static in bipolar spindles relative to tubulin: evidence for a static spindle matrix. J. Cell Biol. 154:1125–1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landau, L.D., and E.M. Lifshitz. 1986. Theory of Elasticity. Pergamon Press, Oxford. 187 pp.
- Lau, A.W., B.D. Hoffman, A. Davies, J.C. Crocker, and T.C. Lubensky. 2003. Microrheology, stress fluctuations, and active behavior of living cells. Phys. Rev. Lett. 91:198101. [DOI] [PubMed] [Google Scholar]
- Mahaffy, R.E., C.K. Shih, F.C. MacKintosh, and J. Kas. 2000. Scanning probe-based frequency-dependent microrheology of polymer gels and biological cells. Phys. Rev. Lett. 85:880–883. [DOI] [PubMed] [Google Scholar]
- Maniotis, A.J., K. Bojanowski, and D.E. Ingber. 1997. Mechanical continuity and reversible chromosome disassembly within intact genomes removed from living cells. J. Cell. Biochem. 65:114–130. [PubMed] [Google Scholar]
- Mitchison, T.J., P. Maddox, J. Gaetz, A. Groen, M. Shirasu, A. Desai, E.D. Salmon, and T.M. Kapoor. 2005. Roles of polymerization dynamics, opposed motors, and a tensile element in governing the length of Xenopus extract meiotic spindles. Mol. Biol. Cell. 16:3064–3076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nogales, E. 2000. Structural insights into microtubule function. Annu. Rev. Biochem. 69:277–302. [DOI] [PubMed] [Google Scholar]
- Omelchenko, T., J.M. Vasiliev, I.M. Gelfand, H.H. Feder, and E.M. Bonder. 2002. Mechanisms of polarization of the shape of fibroblasts and epitheliocytes: separation of the roles of microtubules and Rho-dependent actin-myosin contractility. Proc. Natl. Acad. Sci. USA. 99:10452–10457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parker, K.K., A.L. Brock, C. Brangwynne, R.J. Mannix, N. Wang, E. Ostuni, N.A. Geisse, J.C. Adams, G.M. Whitesides, and D.E. Ingber. 2002. Directional control of lamellipodia extension by constraining cell shape and orienting cell tractional forces. FASEB J. 16:1195–1204. [DOI] [PubMed] [Google Scholar]
- Pickett-Heaps, J., T. Spurck, and D. Tippit. 1984. Chromosome motion and the spindle matrix. J. Cell Biol. 99:137s–143s. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickett-Heaps, J.D., A. Forer, and T. Spurck. 1997. Traction fibre: toward a “tensegral” model of the spindle. Cell Motil. Cytoskeleton. 37:1–6. [DOI] [PubMed] [Google Scholar]
- Schaefer, A.W., N. Kabir, and P. Forscher. 2002. Filopodia and actin arcs guide the assembly and transport of two populations of microtubules with unique dynamics parameters in neuronal growth cones. J. Cell Biol. 158:139–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scholey, J.M., G.C. Rogers, and D.J. Sharp. 2001. Mitosis, microtubules, and the matrix. J. Cell Biol. 154:261–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuyler, S.C., and D. Pellman. 2001. Microtubule “plus-end-tracking proteins”: the end is just the beginning. Cell. 105:421–424. [DOI] [PubMed] [Google Scholar]
- Skotheim, J.M., and L. Mahadevan. 2004. Dynamics of poroelastic filaments. Proc. R. Soc. Lond. A. 460:1995–2020. [Google Scholar]
- Stamenovic, D., S.M. Mijailovich, I.M. Tolic-Norrelykke, J. Chen, and N. Wang. 2002. Cell prestress. II. Contribution of microtubules. Am. J. Physiol. Cell Physiol. 282:C617–C624. [DOI] [PubMed] [Google Scholar]
- Svitkina, T.M., A.B. Verkhovsky, and G.G. Borisy. 1995. Improved procedures for electron microscopic visualization of the cytoskeleton of cultured cells. J. Struct. Biol. 115:290–303. [DOI] [PubMed] [Google Scholar]
- Tagawa, H., N. Wang, T. Narishige, D.E. Ingber, M.R. Zile, and G. Cooper. 1997. Cytoskeletal mechanics in pressure-overload cardiac hypertrophy. Circ. Res. 80:281–289. [DOI] [PubMed] [Google Scholar]
- Tran, P.T., L. Marsh, V. Doye, S. Inoue, and F. Chang. 2001. A mechanism for nuclear positioning in fission yeast based on microtubule pushing. J. Cell Biol. 153:397–412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsutsui, H., K. Ishihara, and G. Cooper. 1993. Cytoskeletal role in the contractile dysfunction of hypertrophied myocardium. Science. 260:682–687. [DOI] [PubMed] [Google Scholar]
- Tsutsui, H., H. Tagawa, R.L. Kent, P.L. McCollam, K. Ishihara, M. Nagatsu, and G. Cooper. 1994. Role of microtubules in contractile dysfunction of hypertrophied cardiocytes. Circulation. 90:533–555. [DOI] [PubMed] [Google Scholar]
- Wang, N., J.P. Butler, and D.E. Ingber. 1993. Mechanotransduction across the cell surface and through the cytoskeleton. Science. 260:1124–1127. [DOI] [PubMed] [Google Scholar]
- Wang, N., K. Naruse, D. Stamenovic, J.J. Fredberg, S.M. Mijailovich, I.M. Tolic-Norrelykke, T. Polte, R. Mannix, and D.E. Ingber. 2001. Mechanical behavior in living cells consistent with the tensegrity model. Proc. Natl. Acad. Sci. USA. 98:7765–7770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waterman-Storer, C.M., and E.D. Salmon. 1997. Actomyosin-based retrograde flow of microtubules in the lamella of migrating epithelial cells influences microtubule dynamic instability and turnover and is associated with microtubule breakage and treadmilling. J. Cell Biol. 139:417–434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng, J., R.E. Buxbaum, and S.R. Heidemann. 1993. Investigation of microtubule assembly and organization accompanying tension-induced neurite initiation. J. Cell Sci. 104:1239–1250. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
[Supplemental Material Index]