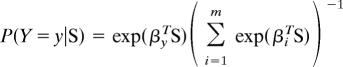Statistical evaluation of alternative models of human evolution (original) (raw)

Abstract

An appropriate model of recent human evolution is not only important to understand our own history, but it is necessary to disentangle the effects of demography and selection on genome diversity. Although most genetic data support the view that our species originated recently in Africa, it is still unclear if it completely replaced former members of the Homo genus, or if some interbreeding occurred during its range expansion. Several scenarios of modern human evolution have been proposed on the basis of molecular and paleontological data, but their likelihood has never been statistically assessed. Using DNA data from 50 nuclear loci sequenced in African, Asian and Native American samples, we show here by extensive simulations that a simple African replacement model with exponential growth has a higher probability (78%) as compared with alternative multiregional evolution or assimilation scenarios. A Bayesian analysis of the data under this best supported model points to an origin of our species ≈141 thousand years ago (Kya), an exit out-of-Africa ≈51 Kya, and a recent colonization of the Americas ≈10.5 Kya. We also find that the African replacement model explains not only the shallow ancestry of mtDNA or Y-chromosomes but also the occurrence of deep lineages at some autosomal loci, which has been formerly interpreted as a sign of interbreeding with Homo erectus.

Keywords: Bayesian analysis, DNA nuclear data, multiregional hypothesis, out of Africa hypothesis

Recent international efforts have produced a large amount of genetic data (1) to identify loci involved in complex diseases or genomic regions with unusual patterns of polymorphism that could be indicative of recent selective events (2). However, because past demographic events are likely to have greatly affected current patterns of genetic diversity, genetic data are difficult to interpret without a general demographic model that can explain neutral variability (3). A global scenario of human evolution is also important to understand our origins and how and when human populations have colonized the globe, a question that has fascinated physical and molecular anthropologists over the past decades (4).

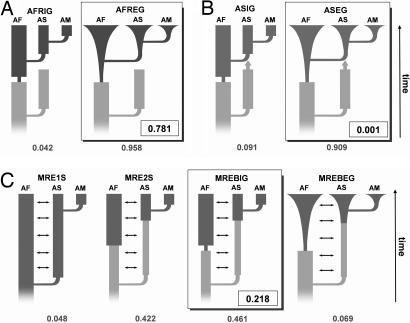
Many general scenarios of human evolution have been proposed based on paleontological, archeological, or genetic data (5, 6), and their fit to various aspects of our genetic diversity has been investigated (3, 7–9). The current debate over recent human evolution can be simplified by considering the alternative scenarios shown in Fig. 1(5). The African replacement scenarios (Fig. 1A), which posit a single and recent African origin for all modern humans, are mainly supported by mitochondrial DNA (mtDNA) and Y-chromosome polymorphisms (4), by the current lack of Neanderthal mtDNA genes in modern humans (10), and by gradients of nuclear genetic diversity from Africa toward the Americas (4, 11). Recent examination of nuclear DNA has, however, revealed some polymorphism patterns that were judged incompatible with a pure African replacement scenario (7, 12–17). For instance, the presence of very old lineages in Africa and Asia raised claims for some degree of interbreeding between modern and archaic Homo forms (13, 14, 16, 17). Such interbreeding can occur under assimilation scenarios (Fig. 1B), where modern humans migrating out of Africa would have hybridized with local Homo erectus and incorporated old lineages (15, 18) or under multiregional scenarios (Fig. 1C), where migrants would have been continuously exchanged between Africa and Asia, leading to a synchronized emergence of modern anatomy. Note that these simple scenarios are somewhat arbitrary and that human evolution has certainly been more complex, but they certainly incorporate key debated features of human evolution, such as population expansions within continents, intercontinental migrations, and potential hybridization with archaic forms.

Fig. 1.

Fig. 1.

Alternative scenarios of human evolution. (A) African replacement models: AFRIG, African replacement with instantaneous population growth; AFREG, African replacement with exponential population growth. (B) Assimilation models: ASIG, assimilation with instantaneous population growth; ASEG, assimilation with exponential population growth. (C) Multiregional evolution (MRE) models: MRE1S, MRE with constant population size in Africa/Asia; MRE2S, MRE with two population sizes in Africa/Asia; MREBIG, MRE with bottleneck and instantaneous population growth; MREBEG, MRE with bottleneck and exponential population growth. For all models, the dark grays represent modern human populations, and lighter grays represent archaic populations. AF, Africa; AS, Asia; AM, Americas. A more detailed description of these models is provided in Materials and Methods and in SI Fig. 3. The posterior probability of different models within each major scenario is given below each model. The posterior probabilities of the best model selected under each scenario are reported within boxes.

Previous approaches to understand human evolution using genetic data have not attempted to compare directly alternative scenarios within a global statistical framework, and the posterior probability of the models presented above has never been evaluated. In principle, alternative models can be directly compared if their likelihood can be computed. Even though these likelihoods can now be computed for relatively simple scenarios involving a few parameters (19), the likelihood function of complex demographic scenarios may be very difficult, or even impossible, to solve analytically (20). In this article, we overcome this problem by taking an approximate Bayesian computation (ABC) approach (21) to compare models and estimate the parameters of interest. The ABC approach is a convenient way of dealing with such situations because it is possible to compare the probability of obtaining the observed data (or summary statistics computed from them) under alternative scenarios, marginal to (i.e., irrespective of) the parameter values. Complex models can thus be compared even though they depend on many parameters, the true values of which are very uncertain.

Results

We first evaluated the posterior probabilities of different models within each class of the three scenarios considered here, which are the African replacement, multiregional evolution, and assimilation scenarios (see Fig. 1 and Materials and Methods for further information on the models). Under the African replacement and assimilation scenarios, models with exponential growth [African replacement with exponential population growth (AFREG) and assimilation with exponential population growth (ASEG)] were found to have the largest posterior probabilities (0.958 for AFREG and 0.909 for ASEG, Fig. 1 A and B), suggesting that both the emergence of modern humans in Africa and their spread into other continents are better modeled as a gradual rather than an instantaneous process. Among the multiregional evolution (MRE) models, the MRE with bottleneck and instantaneous population growth (MREBIG) model (Fig. 1C) is slightly favored, with a posterior probability of 0.461 over MRE with two population sizes in Africa/Asia (MRE2S) (0.422). The MREBIG model implements a bottleneck in Africa with an instantaneous recovery, a recent population growth in Asia, and it allows for different migration rates between Africa and Asia at different periods.

We then compared the best model of each scenario. We find that AFREG has the highest posterior probability (_P_AFREG = 0.781), followed by the best MRE (_P_MREBIG = 0.218) and ASEG (_P_ASEG = 0.001) models (Fig. 1). Neutral nuclear sequence data thus give strong support to a recent African origin of modern humans without interbreeding with archaic Homo forms, at least in Asia. To study the power of our model choice procedure in the context of human evolution, we simulated 1,000 random data sets under the best model for African replacement (AFREG), assimilation (ASEG), and multiregional (MREBIG) models and each time estimated the posterior probability of the three models. We find that the AFREG and MREBIG models are correctly recovered (have the highest posterior probability) in 79.3% and 80.1% of the cases, respectively, but the ASEG model is correctly identified in only 50.3% of the cases [supporting information (SI) Fig. 3] and, thus, seems to be the model most difficult to identify. Assuming that the three models have the same prior probability, we can compute the probability that AFREG is the correct model given our observation that _P_AFREG = 0.78 as Pr(_P_AFREG = 0.78|AFREG)/[Pr(_P_AFREG = 0.78|AFREG) + Pr(_P_AFREG = 0.78|ASEG) + Pr(_P_AFREG = 0.78|MREBIG)] = 0.817 (see SI Fig. 4). Similarly, we obtain Pr(ASEG|_P_AFREG = 0.78) = 0.147 and Pr(MREBIG|_P_AFREG = 0.78) = 0.036. Because the ASEG model is generally difficult to identify (SI Fig. 3), a large posterior probability of the AFREG model is relatively likely under this scenario but not under the MREBIG model, which explains the low probability of <4% for the MREBIG model.

We then estimated the parameters of the overall best African replacement model (AFREG, Table 1 and SI Fig. 5) under an ABC framework based from 5 million simulations. Under this model, we find that an archaic African population of ≈12,800 effective individuals gave rise to modern humans ≈141 thousand years ago (Kya) after a bottleneck involving ≈600 effective individuals. The Out-of-Africa migration, initially involving only ≈450 effective individuals would have occurred some 51 Kya, and the Americas would have been colonized only ≈10.5 Kya by ≈450 individuals.

Table 1.

Demographic and historical parameters estimated under the favored AFREG model

Parameters† Median‡ 95% HPD§
Speciation time for modern human, yr (TMH) 141,455 103,535–185,642
Exit out of Africa, yr (TAS) 51,102 40,135–70,937
Colonization of the Americas, yr (TAM) 10,280 7,647–15,945
Size of archaic African population (NA-AF) 12,772 6,604–20,211
Bottleneck size during speciation (NbMH) 600 76–1,620
Bottleneck size when leaving Africa (NbAS) 462 64–1,224
Bottleneck size when leaving Asia (NbAM) 452 71–1,280
Current African population size (NAF) 206,920 23,535–801,895
Current Asian population size (NAS) 20,262 1,938–62,726
Current American population size (NAM) 5,606 757–13,740

Discussion

The demographic and time estimates (Table 1) are in overall good agreement with those obtained previously from fossil or genetic data. The date for the emergence of modern humans is indeed well consistent with paleontological record suggesting dates of 130–200 Kya (5, 22), and with previous genetic estimates (120–160 Kya) (23). The size of the archaic modern human population is also close to recent estimates of the ancestral size for modern humans of ≈12,500 individuals (3, 7). The size and timing of the exit out of Africa are in excellent agreement with recent molecular and archeological studies suggesting that this migration resulted in a limited number of lineages having left Africa only ≈55–65 Kya (6, 11, 24). Finally, the estimates for the current effective continental population sizes show a net decrease from Africa to America compatible with a series of spatial expansions and founder effects during the colonization of the world (4, 11).

Our estimated date for the colonization of the Americas (10.3 Kya) is more recent than usually considered, but the upper limit of the 95% highest posterior density includes the dates of the oldest archaeological sites of ≈14 Kya (25). This young settlement time could result in part from the sole sampling of Central and South American individuals. It is indeed known from the study of mtDNA and the Y chromosome that some rare alleles (haplogroups) were found only in North America (26). Therefore, the inclusion of northern Native Americans could lead to increased genetic diversity and colonization time estimates. This result nevertheless suggests a late, postglacial maximum colonization of the Americas, which is in better agreement with the estimates of ≈14 Kya based on the Y chromosome (27) than on those of ≈30 Kya based on mtDNA control region (28). The estimated founder population size for America is about six times larger than that recently proposed by Hey (29), who suggested that <80 effective individuals would have colonized the Americas, but a moderate bottleneck for the settlement of the New World agrees with recent results from nuclear loci (30) and with previous mtDNA studies (28). Differences in sampling design and marker choice between studies could explain this discrepancy: Although our study is based on a homogeneous set of 50 nuclear loci genotyped in the same individuals, the former study (29) used a mixture of fewer autosomal, X-linked, and uniparentally inherited markers assessed on a very heterogeneous set of individuals and sample sizes.

Even though the ASEG model is clearly not supported by our analysis, it is interesting to see that the archaic contribution to the current Asian gene pool estimated under this model is extremely small (median: 0.007; 95% highest posterior density: 6.3 × 10−5 − 0.023, SI Table 2). It shows that the observed data are only compatible with minute or virtually no admixture with previous members of the Homo genus, at odds with recent studies of nuclear diversity suggesting a substantial contribution of archaic genes to the modern gene pool (7, 15), but in keeping with analyses of mitochondrial DNA (31–33). Despite its convergence to the AFREG model, which assumes no admixture, the ASEG model has a much lower posterior probability, probably because the prior for the admixture proportion was chosen to be uniform between 0 and 1, to include potentially high levels of admixture (15). Note that an ASEG model with a narrower or a negative exponential prior for an archaic contribution would certainly be better supported. In contrast to the ASEG model, the MRE model most compatible with our data set (MREBIG), however, does not show any convergence toward an African replacement model, or toward previous implementations of a multiregional model (e.g., refs. 8 and 34), where a large archaic African population would send more migrants to Asia than the reverse. The median estimates of the MREBIG model (SI Table 2) rather suggest small archaic population sizes in both continents (<600 effective individuals) and recent migration rates between continents being very small but still larger than between the two archaic populations.

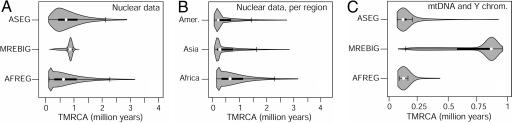
Because the occurrence of deep lineages in modern humans has sometimes been taken as evidence against replacement models (e.g., refs. 13 and 16), we have computed the empirical distribution of the times to the most recent common ancestors (TMRCAs) for the best model under each of the three scenarios (Fig. 2A and SI Table 3). We see that the multiregional model has the narrowest and shortest distribution because of the small estimated archaic population size that promotes coalescent events as soon as archaic Asian lineages are brought back (looking backward in time) to Africa ≈800 Kya in our model. On the other hand, very old TMRCAs exceeding several millions of years can be readily obtained under the African replacement models (in agreement with previous expectations, see, e.g., ref. 35), because the larger ancestral size in Africa prevents a rapid coalescence of the lineages that passed through the speciation bottleneck. When computing continent-specific TMRCAs under the overall best African replacement model (AFREG) (Fig. 2B and SI Table 4), we see that very ancient TMRCAs are not restricted to African samples but that they are also found for Asian and Amerindian samples. Our results therefore question the hypothesis that very old TMRCAs should be taken as evidence for interbreeding events between modern humans and individuals of other Homo species (13). Unexpectedly, we find that ≈10% of autosomal loci should have TMRCAs younger than 140 Kya. This is at odds with a recent review reporting no TMRCA younger than 600 Ky among 27 autosomal genes (13), even though we cannot exclude the possibility that loci with little or no variation are underrepresented in the published literature. However, in keeping with these results, we note that 4 of our 50 loci (8%) are entirely monomorphic in the three samples and, therefore, indicative of a shallow ancestry.

Fig. 2.

Fig. 2.

Empirical TMRCA distribution obtained by simulation under different models. Parameter values were set to the median of the estimated marginal posterior distributions. Each distribution combines a mirrored estimated density surface in gray with a standard boxplot representation. Boxplots display the median of the distribution as a white dot, the interquartile range (IQR, 25–75%) as a thick line, and the region of ±1.5 IQR as a thin line ending with vertical whiskers. To facilitate the comparison among models, all distributions (apart those from MREBIG model) were cut after the 99th percentile (full distributions are available in SI Tables 6, 7, and 8). (A) Autosomal loci. (B) Autosomal loci under the best model (AFREG), where only the samples of each of the three regions are considered. (C) mtDNA and Y-chromosome. For these markers, simulations were performed by using estimates of effective sizes four times smaller than those obtained for autosomal loci to reflect the smaller population sizes of these uniparentally inherited markers.

Although our models were fitted to autosomal DNA, they should also be able to explain the observed features of mtDNA and Y-chromosome polymorphism, such as their more recent TMRCAs or very negative Tajima's D values. We have therefore simulated TMRCAs and Tajima's D values for these uniparentally inherited loci using effective sizes four times smaller than for nuclear loci. We find (Fig. 2C and SI Table 5) that the African replacement and assimilation models are fully compatible with TMRCAs <250 Kya such as those found with mtDNA or Y-chromosome data (e.g., ref. 4), whereas TMRCAs are found mostly >400 Kya for the best multiregional model, which seems therefore fully incompatible with these uniparentally inherited markers. Indeed, the very large TMRCAs obtained for the MREBIG model occur because, most of the time, Asian and African lineages do not coalesce after the initial exit out of Africa. Tajima's D distributions for autosomal markers are quite similar under the three best models (SI Fig. 6) and show more negative values for African than for non-African populations, in keeping with previous reports (7, 13, 36, 37). On the other hand, simulated uniparentally inherited loci show positive Tajima's D values for Africa under the MREBIG model, at odds with most reports (e.g., ref. 38) and with the AFREG and the ASEG models.

Our model choice framework relies on massive computer simulations and makes it now possible to estimate the posterior probability of relatively realistic (but still debated) models of human evolution. The ability to assign probabilities to various competing scenarios without need to estimate parameters seems much more satisfying than previous approaches based on goodness-of-fit statistics (e.g., refs. 7–9). However, this probabilistic approach still does not guarantee that the best supported scenario is the correct one, which could be an untested model. Although we considered a variety of alternative scenarios, we did not specifically attempt to design models of human evolution that would maximize the fit between observed and simulated data. However, these very simple models capture the basic differences between proposed alternative scenarios of human evolution (see, e.g., ref. 5). More elaborate models incorporating intracontinental population subdivisions, long-distance dispersal, or spatially explicit information (8) could be implemented, and the current model choice framework could be used to evaluate their respective merits, which would be impossible under a likelihood framework. An additional improvement would be to account for the spatial and population structure of the sampling. We have indeed performed here all simulations assuming random mating, whereas sampled individuals from different continents were each drawn from different subpopulations. The coalescent process in a structured population is similar to the coalescent in an unsubdivided population if one samples a single gene by subpopulation (39). Because we sampled two genes per subpopulation, we may have underestimated the frequency of recent coalescent events within subpopulations, which could, for instance, lead to some underestimation of divergence time between continents, potentially explaining the recent colonization time we find for the Americas. The choice of summary statistics may have an influence on our results, and we used only statistics that do not require information on the gametic phase (haplotypic information). It is likely that additional information could lead to a better discrimination among models. The analysis of larger data sets, such as genome-wide resequencing data (e.g., ref. 40) or STR data on population samples from various continents (41) would be helpful to confirm our results, and it could also lead to increased power for our model choice procedure. However, these much larger data sets would require much more computer power than that used in our study, which already exceeded 10 CPU-months of computations on a Linux cluster.

In conclusion, although our best supported model (AFREG) certainly does not represent the exact history of modern humans, we show here that it is much better supported by a random set of neutral loci than any other models involving interbreeding with other Homo species. Although we cannot exclude that any interbreeding ever occurred between modern and archaic humans or that any favorably selected H. erectus genes could have spread into modern humans (see, e.g., ref. 18), our results suggest that this archaic contribution, if present, should be very small. Our results therefore confirm that our modern gene pool has a recent and predominant African origin, and they offer a neutral demographic scenario that could be used to detect ancient admixture for specific gene regions. Moreover, the best African replacement model explains key features of other data sets, such as recent TMRCAs for mtDNA or Y-chromosome loci, as well as occasional deep lineages of nuclear loci, previously thought to be indicative of balancing selection or interbreeding with H. erectus or Neanderthals (7, 13). The demographic parameters of this model should prove useful to improve our ability to detect loci involved in complex diseases or in past adaptive events by providing better null distributions of various statistics used in genome scans or linkage disequilibrium mapping studies.

Materials and Methods

Samples, Loci, and Laboratory Methods.

We sequenced 50 independent autosomal noncoding loci of ≈500 bp each, providing a total of ≈25,000 bp for each individual (see SI Table 6). These loci have been studied in human and chimpanzee populations (42–44). Additionally, each locus is short enough so that it can be considered as a nonrecombining segment. Because these data have been generated through DNA sequencing, they are not likely to be affected by ascertainment bias.

To complement a first data set consisting of 10 African, and 8 Asian individuals previously analyzed (43), we sequenced here 12 Native American individuals, each affiliated to a different tribe. This sampling scheme is similar to that used for Africa and Asia (43) (see also SI Text).

We performed PCR amplification using primers and conditions described in ref. 43, except for five loci for which we designed new primers whose sequence is available in SI Text. Sequencing was performed in a MegaBACE1000 system (GE Healthcare, Chalfont St. Giles, U.K.). Individual reads were assembled in the PhredPhrap package (45), together with a reference containing the known variants for each locus. Assemblies were visually inspected by using Consed (46), and all possible heterozygous sites have been rechecked sequencing a new PCR product. Mutation rates at all loci were estimated after gametic phase estimation and comparison with chimpanzee sequences, as explained in SI Table 6.

Tested Evolutionary Scenarios.

We modeled three different sets of scenarios constructed to capture most of the current debate concerning modern human evolution (see, e.g., refs 5 and 47 for a general account on different models of human evolution). Because there is still some uncertainty on the exact details of past human demography (48), we chose to evaluate several alternative models within each class of scenarios. For example, previous attempts of fitting molecular data to the African replacement scenario have used different demographic growth models (instantaneous, exponential, linear, or logistic) (3, 7–9, 23), but it is still unclear whether one of these models has better properties than others.

A general representation of the models contrasted in this study is shown in Fig. 1, and a detailed schematic representation is shown in SI Fig. 7, where we list the parameters of all models. The African replacement models (SI Fig. 7_A_) are simulated with instantaneous (AFRIG) or exponential (AFREG) growth after bottlenecks. Looking forward in time, both models start with an ancestral (archaic) population in Africa that passes through a bottleneck and gives rise to a population of modern humans. After the bottleneck, the population is allowed to grow to its current size, either instantaneously or exponentially, depending on the model. After this event, a migration occurs from Africa to Asia and, finally, from Asia to the Americas. In both cases, after a few generations, the founding population is allowed to expand to its current size.

Multiregional evolution generally refers to a class of models in which the transition toward modern morphology occurs simultaneously because of ongoing gene flow between continents (17, 48). We simulated four different models (see SI Fig. 7_C_) that differ in the way population sizes change over time and whether population growth has been instantaneous or exponential. Forward in time, all models start with an archaic African population that moves out of Africa in an event that attempts to model the peopling of Asia by H. erectus. Since then, and up to the present, Africa and Asia exchange migrants. Another major migration event takes place only from Asia to the Americas. In model MRE1S, African and Asian population sizes and migration rates are held constant over the whole simulated period. In model MRE2S, there is a transition between an “archaic” and “modern” population size that occurs independently first in Africa and then in Asia, with new migration rates occurring after the demographic transition in Africa. The remaining models implement a bottleneck in Africa during the emergence of modern humans: In model MREBIG, all populations grow instantaneously, whereas in model MREBEG, all “modern” populations grow exponentially.

Finally, the African origin with assimilation (see SI Fig. 7_B_) is a “hybrid” model that includes an early dispersal of H. erectus out of Africa, but it differs from MRE in two major aspects: There is no migration between continents, and a fraction of “modern” Asian lineages have originated recently from Africa, like in the African replacement model. However, another fraction of the “modern” Asian lineages come from the archaic Asian population. The ASIG and ASEG models differ by implementing instantaneous or exponential growth, respectively, after the bottlenecks associated with the founding of each continent by “modern” humans. These scenarios have been adapted from the models reviewed in Stringer (47). The prior distributions of the parameters of the eight tested models are described in SI Table 7 (see next section).

Approximate Bayesian Computations.

Parameter estimation and model evaluation were done under an ABC framework (21). The different steps of the ABC parameter estimation procedure are described in detail (see refs. 21 and 49), but we briefly outline them below. For each model, we first perform a large number of genetic simulations based on a demographic history that describes the model using the program SIMCOAL ver. 2 (50). Some or all parameters that define the model (e.g., population sizes, migration rates, timing of the demographic events, mutation rates) are considered as random variables for which some prior distribution must be defined, as shown in SI Table 7. For each simulation, the parameter values are drawn from their prior distributions defining a demographic history that is used to build a specific input file for the SIMCOAL program. SIMCOAL then performs coalescent-based (51) simulations to generate the genetic diversity of samples, with the same number of gene copies and loci than those observed. Summary statistics (S) identical to those computed on the observed data (S*) are then calculated for the simulated data set. As in any coalescent approach, our simulations were performed considering haploid individuals and with time scaled in generations. Following Beaumont et al. (21), a Euclidean distance δ is calculated between normalized S and S* for each simulated data set.

Prior Distributions.

The prior distributions of the parameters of all eight models are shown in SI Table 7.

Summary Statistics.

Summary statistics of genetic diversity were calculated by using the program Arlequin ver 3.1 (52). The following summary statistics were computed: total and per population number of segregating sites (S), nucleotide diversity (π) for each population, and total and pairwise _F_STs (53). Because there is some uncertainty associated with the phasing procedure, we used only summary statistics that do not depend on phase information. Summary statistics calculated for the 50 loci are reported in SI Table 8.

Model Choice.

The posterior probability of each model is estimated by an approach based on a weighted multinomial logistic regression procedure (54). This approach is an extension of ordinary logistic regression to more than two categories, and it is explained in more detail in SI Text and SI Fig. 8. Briefly, Beaumont (54) has suggested that one can sample the model indicator (i.e., {1, …, m} for models _M_1, …, M m) from the prior, π(M) and treat it as a categorical random variable, Y, in the ABC simulations. We can then apply categorical regression to estimate P(Y = y|S = S*), where y = 1… m is the indicator for model M y, and S* is the vector of observed summary statistics. Specifically, we estimate the coefficients β in

graphic file with name zpq04507-7960-m01.jpg

using the VGAM package implemented in R. We make the regression estimate locally around S* in the same way as in the standard regression approach, i.e., only the 5,000 simulations closest to the observations are retained, and these are weighted by an Epanechnikov kernel that has a maximum when S = S* (see SI Text for details). This procedure has been shown (54) to substantially improve on a previous method (55, 56) for selecting models by using ABC, and its application to a mixture model shows that it performs almost as well as a reversible jump Markov Chain Monte Carlo method using the full data (57). Model selection within each set of scenarios was based on 2 million simulations for each model. We performed an additional 3 million simulations for each of the best African replacement, multiregional, and assimilation models to obtain their posterior probability based on a total of 5 millions simulations for each model.

Parameter Estimation.

For the best model within each set of scenarios, we retained the 5,000 simulations with smallest associated Euclidean distance δ computed on a total of 5 million simulations. Then posterior distributions of the parameters were obtained by means of a locally weighted multivariate regression (see ref. 21 for more details). Parameters (x) were transformed as z = log[tan(x)−1] before regression to prevent estimations from exceeding distribution limits (58). Although several point estimators can be computed from these distributions, we report only the median in Table 1 because it has been shown to have the overall lowest associated mean square error (59), but we also report the mode of the parameter distributions for all models in SI Table 2.

TMRCA Simulations.

We generated for each model the expected distribution of the TMRCA by performing 5,000 simulations of 50 loci, using as fixed parameter values the median estimates obtained under our ABC approach, which is a reasonably good point in the parameter space. In the same way, we generated the distribution of TMRCAs for uniparentally inherited markers by dividing the population sizes by four because the effective size for these markers is four times less than for nuclear loci.

Supplementary Material

Supporting Information

Acknowledgments

We thank the Fundação de Amparo à Pesquisa do Estado do Rio Grande do Sul and Institutos do Milênio and PRONEX for extra support and to the EGEE2 European project for providing access to its computing grid infrastructure and for user assistance. We thank Pierre Berthier for computational services; Johan Montagnat and Cladinara Sarturi for technical help; Wen-Hsiung Li (University of Chicago, Chicago) for the primers; Kim Hill, (University of Arizona, Tucson, AZ), A. Magdalena Hurtado (Arizona State University, Tempe, AZ), Ramiro Barrantes (University of Costa Rica, San Pedro, Costa Rica), Francisco R. Carnese (University of Buenos Aires, Buenos Aires, Argentina), and Eduardo Tarazona-Santos (Federal University of Minas Gerais, Minas Gerais, Brazil) for sample donations; all individuals who, by contributing their own samples, made this study possible; Montgomery Slatkin and Paul Mellars for their comments on a previous version of this manuscript; Gerald Heckel for helpful discussions; and Lounès Chikhi for insightful and constructive comments. This work was supported by a University of Bern grant (to N.J.R.F.), Swiss National Foundation Grant 3100A0-112072 (to L.E.), and CNPq (Brazil) Grant 477780/2003-2 (to S.L.B.). N.J.R.F. was partially supported by Coordenação de Aperfeiçoamento de Pessoal de Nivel Superior (CAPES) (Brazil) Scholarship 3624-05-6.

Abbreviations

ABC

approximate Bayesian computation

AFREG

African replacement with exponential population growth

ASEG

assimilation with exponential population growth

Kya

thousand years ago

MRE

multiregional evolution

MREBIG

MRE with bottleneck and instantaneous population growth

TMRCA

time to the most recent common ancestor.

Footnotes

The authors declare no conflict of interest.

Data deposition: Sequences reported in this paper have been deposited in the GenBank database (accession nos. EU105474–EU106045).

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information