Mechanisms of Laser-Induced Dissection and Transport of Histologic Specimens (original) (raw)
Abstract
Rapid contact- and contamination-free procurement of histologic material for proteomic and genomic analysis can be achieved by laser microdissection of the sample of interest followed by laser-induced transport (laser pressure catapulting). The dynamics of laser microdissection and laser pressure catapulting of histologic samples of 80 _μ_m diameter was investigated by means of time-resolved photography. The working mechanism of microdissection was found to be plasma-mediated ablation initiated by linear absorption. Catapulting was driven by plasma formation when tightly focused pulses were used, and by photothermal ablation at the bottom of the sample when defocused pulses producing laser spot diameters larger than 35 _μ_m were used. With focused pulses, driving pressures of several hundred MPa accelerated the specimen to initial velocities of 100–300 m/s before they were rapidly slowed down by air friction. When the laser spot was increased to a size comparable to or larger than the sample diameter, both driving pressure and flight velocity decreased considerably. Based on a characterization of the thermal and optical properties of the histologic specimens and supporting materials used, we calculated the evolution of the heat distribution in the sample. Selected catapulted samples were examined by scanning electron microscopy or analyzed by real-time reverse-transcriptase polymerase chain reaction. We found that catapulting of dissected samples results in little collateral damage when the laser pulses are either tightly focused or when the laser spot size is comparable to the specimen size. By contrast, moderate defocusing with spot sizes up to one-third of the specimen diameter may involve significant heat and ultraviolet exposure. Potential side effects are maximal when samples are catapulted directly from a glass slide without a supporting polymer foil.
INTRODUCTION
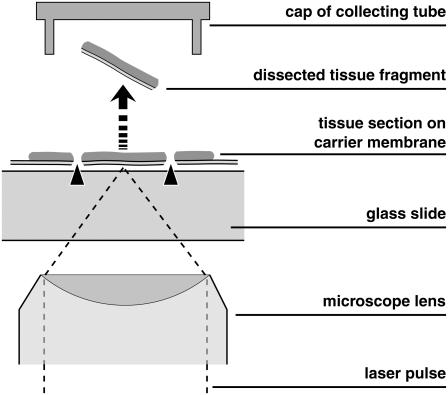
Procurement of defined samples of histologic material for proteomic and genomic analysis has become important with the increasing refinement of analytic techniques. Moreover, separation and transport of living cells is of interest for stem cell research, organ culture, and tissue engineering. Mechanical separation techniques are tedious, time-consuming, and bear the risk of contamination. Therefore, faster laser-based processes have been developed (1–3), and several companies are active in this field. A widespread, rapid, contact- and contamination-free separation method consists in laser microdissection (LMD) of the sample of interest and subsequent laser-induced forward transport of the dissected material into a vial which is used for further analysis (4,5). For the transport process, the expression “laser pressure catapulting” (LPC) has been coined, and the combined separation and procurement procedure is often termed “laser microdissection and pressure catapulting” (LMPC). The principle is illustrated in Fig. 1. The scheme in Fig. 1 shows a setup based on an inverted microscope, with the specimen located on a polymer foil backed by a transparent substrate (glass slide). The same principle, with opposite direction of material transport, has been incorporated also in upright microscopes (6).
FIGURE 1.
Principle of separation of small biological objects, exemplified by the isolation of parts of a histologic section. The section is placed on a thin, UV-absorbing polymer foil that is mounted on a routine microscope glass slide. A region of interest is dissected from the section using a series of focused UV-A laser pulses (LMD, marked by arrowheads) and subsequently catapulted (LPC, marked by an arrow) into the cap of a microfuge tube by a final, typically more energetic, laser pulse. The catapulting pulse can be directed either in the center or in the periphery of the dissected specimen.
Historical roots of the individual steps of the process date ∼30–40 years back. Laser microdissection of histologic material using a nitrogen laser (λ = 337 nm, pulse duration 3 ns) was introduced in 1976, but the harvesting still had to be done with mechanical tools (7,8). Ten years later, high-energy laser pulses were used to accelerate small metallic disks to velocities >2.5 km/s for impact studies (9), and the underlying physical processes were analyzed in several studies (10–12). In the late 1990s, Schütze and co-workers discovered that a combination of LMD and LPC with focused low-energy nitrogen laser pulses can be used to isolate minute amounts of biologic material (4,5). At the same time, a polymer carrier foil absorbing ultraviolet (UV) light was introduced to enhance the laser light absorption in the specimen and to maintain its mechanical integrity during LPC (4). These advancements, together with an increased demand for separation techniques due to the refinements of proteomic and genomic analysis, and the proof that the combination of LMD and LPC is compatible with recovery of ribonucleic acid (RNA) and deoxyribonucleic acid (DNA) (4,13) paved the way of LMPC into the laboratories, with several hundred devices installed to date.
LMPC has been developed largely on an empirical basis. The inventors speculated that LMD at the nitrogen laser wavelength (337 nm) is based on photochemical dissociation and that LPC relies on the photon pressure of the incident light (4). Others conjectured that microdissection with pulse durations of nanoseconds (ns) or shorter is plasma-mediated (8,14). The latter hypothesis was experimentally proven for infrared (IR) and visible nanosecond pulses in 2002 (15), and a detailed theory of plasma-mediated nanosurgery of cells and tissues with femtosecond (fs) pulses was presented in 2005 (16). However, systematic investigations of the mechanisms of dissection and catapulting of biological samples using nanosecond pulses at UV-A wavelengths (320 < λ < 400 nm) are still lacking, and this study is intended to fill this gap. We elucidate the mechanisms and potential side effects of LMPC for histologic specimens and, based on this analysis, discuss strategies for an improvement of dissection and catapulting.
To provide a basis for the analysis of the physical mechanisms, we first characterize relevant parameters of the apparatus and of the optical and thermal properties of all materials involved in the dissection and laser-induced transport process. We then determine the thresholds for thermal ablation based on linear absorption of the respective targets and for plasma formation. Laser-induced plasma formation (optical breakdown) is a nonlinear absorption process via multiphoton and avalanche ionization that, for nanosecond pulses, results in large energy densities far above the vaporization enthalpy of the target medium, high temperatures of several thousand Kelvin, and large pressures in the focal volume (15,16). The dynamics of the catapulting process are investigated by means of time-resolved photography. A similar method has been previously employed to study laser “printing” of cells in suspension with 1 _μ_s time resolution (17), while the transport of histologic samples driven by laser pulses focused through an upright microscope has been documented by high-speed cinematography with 1 ms interframing time (6). We achieved a temporal resolution better than 20 ns by using single frame photography with increasing time delay between the catapulting laser pulse and the instant at which the photograph was exposed. The photographic technique is also used to investigate the dependence of catapulting velocity on various process parameters such as laser pulse energy, diameter of the laser spot on the specimen, and backing of the specimen (confined versus nonconfined ablation). Catapulted specimens are, for different laser spot sizes, examined by scanning electron microscopy (SEM).
The experimental results are analyzed to identify the mechanisms of laser microdissection and the driving forces of laser-induced transport for different laser spot sizes (i.e., radiant exposures) at the catapulted sample. Microdissection was found to rely on plasma formation initiated by linear absorption. Catapulting with focused laser pulses also relies on plasma formation, while for defocused pulses it is driven by confined thermal ablation. For very large spot sizes for which the average radiant exposure remains below the ablation threshold, thermoelastic forces may also come into play.
Based on the characterization of the thermal and optical properties of the histologic specimens and supporting materials used, and on the measured data of specimen velocity and acceleration, we discuss potential side effects originating from the exposure of the biological sample to heat, UV irradiation, and mechanical forces and assess their consequences on the accuracy of the subsequent molecular analysis. Catapulting with tightly focused pulses or strongly defocused pulses (spot size comparable to the sample diameter) was found to result in very little collateral damage. By contrast, moderate defocusing with spot sizes up to approximately one-third of the specimen diameter involves significant heat and UV exposure of a considerable fraction of the specimen volume. The same problems arise, if samples are catapulted directly from a glass slide without a preceding dissection step because in that case the size of the specimen fractions transported by each individual pulse is not much larger than the area irradiated by that pulse. We conclude with a discussion of possible strategies for an improvement of microdissection and catapulting.
METHODS AND MATERIALS
Apparatus for microdissection and laser-induced transport
We used a microbeam system equipped with an N2 laser (λ = 337 nm) emitting pulses of 3 ns duration (PALM Microlaser Technologies, Bernried, Germany). In this system, the laser beam is coupled through the beam path for epifluorescence illumination into an inverted microscope (Axiovert 200, Carl Zeiss MicroImaging, Göttingen, Germany) that is equipped with a motorized, computer-controlled stage. The infinity-corrected microscope objectives used in this study were Zeiss LD Plan-Neofluar 40×/0.6 corr, and Fluar 5×/0.25. The UV-absorbing polymer foil mounted on the glass slides carrying the histologic sections (Fig. 1) consists of polyethylene naphthalate (PEN) (Dupont Teijin Films Luxembourg, Luxembourg) and is 1.35-_μ_m thick.
The laser beam is expanded to overfill the rear pupil of the microscope objective. For dissection and focused catapulting, the laser focus is located in the focal plane of the objective. This colocation is adjusted by means of a telescope in the laser beam path in which one lens can be shifted by means of a motorized drive. Focusing is regulated by a potentiometer at the laser control board. Criterion for optimum focusing is the achievement of the smallest cutting width in PEN foil at minimum laser pulse energy. The telescope for focus control can also be used for purposeful defocusing by making the laser beam before the microscope objective slightly divergent or convergent.
The diameter 2_ω_0 of the laser beam in the focal plane of the 40× and 5× microscope objectives was measured using a knife-edge technique (18). The near- and far-field beam profiles of the N2 laser were measured using a commercially available beam analyzer (Spiricon, Grosshansdorf, Germany), and charge-coupled device camera (WinCamD, Laser 2000, Wessling, Germany).
We related the settings at the focus control unit of the microbeam system to the actual spot sizes at the target using the following procedure: The z shifts of the focus corresponding to given settings at the control unit were measured by producing laser effects in microscope glass slides, using the lower surface of the slide as reference. The distance between surface and laser effects was determined from the distance of the positions of the microscope stage for which either plane is in focus, considering the light refraction in the slide. The relation between focus settings and actual z shifts was found to be linear. For defocused catapulting of histologic samples, the microscope was focused at the bottom of the sample lying on the glass slide and the laser focus was always shifted to a position above the microscope slide to avoid breakdown in the glass below the sample. The radius of the irradiated spot at the bottom of the sample microscope was then calculated using the relation
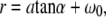 |
(1) |
|---|
where a denotes the distance between the focal plane of the microscope objective and the laser focus, α = arcsin(NA/_n_air) is the focusing angle of the microscope objective in air, and _ω_0 is the focal spot radius of the laser beam.
We performed an energy calibration between the settings at the laser control unit of the microbeam system and the actual energies transmitted through the objectives using detectors with 1 nJ–10 _μ_J and 1 _μ_J–20 mJ measurement range, respectively (PD10 and PE 10, Ophir Optronics, Jerusalem, Israel). The calibration revealed that the relation between energy setting and energy reaching the target is logarithmic. For equal settings, the transmitted energies are approximately four times larger for the 5× objective than for the 40× objective because the 5× objective possesses a larger optical pupil. All energy values quoted in this article refer to the laser energy incident on the target.
Determination of optical and thermal material properties
We determined the optical transmission and scattering properties at λ = 337 nm of histologic material stained with hematoxilin and eosin (H&E), of the PEN polymer foil and of a single, confluent layer of cultured Chinese hamster ovary cells. The heat capacity of the PEN foil and the histologic specimens were determined by differential scanning calorimetry, and the dissociation temperatures were obtained through thermogravimetric analysis. Technical details of these measurements are described in Supplementary Material available online.
Time-resolved photography
The mechanisms of catapulting of histologic specimens were analyzed by time-resolved photography in side view with a temporal resolution better than 20 ns and a spatial resolution of 2 _μ_m. The catapulting dynamics was followed by single-frame photography with increasing time delay between catapulting laser pulse and the instant at which the photograph was exposed. Bright-field images of the catapulted specimen were taken in trans-illumination using the light of a plasma discharge lamp with 18-ns duration. The laser-produced pressure waves were visualized by means of a sensitive dark-field Schlieren technique using pulses from a frequency-doubled Nd:YAG laser with 16-ns duration as light source (19). Details of the photographic techniques are described in the Supplementary Material.
Scanning electron microscopy of dissected and catapulted specimens
To facilitate the analysis of the phase transitions occurring during laser-induced forward transfer, we examined some catapulted specimens by SEM. Histological sections of mouse liver tissue supported on PEN foil were microdissected and catapulted onto SEM specimen holders covered with adhesive film (Plano, Wetzlar, Germany). After sputter-coating with gold, the samples were examined in a Philips 505 scanning electron microscope (Philips, Eindhoven, The Netherlands).
RESULTS
Optical and thermal material parameters
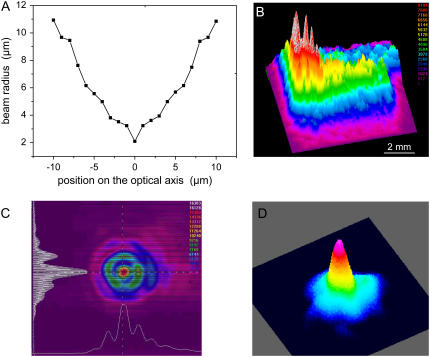
The result of the spot size measurement for the 40× objective (NA = 0.6) is shown in Fig. 2 A. Because of the poor quality of the N2 laser beam (Figs. 2, B and C), the spot diameter (4.2 _μ_m up to 1/_e_2 irradiance values) is more than six times larger than the diffraction-limited focus diameter. Nevertheless, the hot spot visible in the center of the far-field beam profile in Fig. 2 C allows producing relatively fine effects if energies very close to the ablation threshold are employed. In this generation of commercial microbeam systems that has recently been introduced into the market, the N2 laser is replaced by a frequency-tripled Nd:YAG laser emitting at λ = 355 nm that exhibits a much better beam profile, as shown in Fig. 2 D. This makes it possible to achieve a nearly diffraction-limited focal spot size if the laser beam is appropriately coupled into the microscope.
FIGURE 2.
(A) Spot size of the N2 laser beam focused through a 40× objective; (B) near-field and (C) far-field profiles of the N2 laser beam; and (D) far-field beam profile for a frequency-tripled Nd:YAG laser.
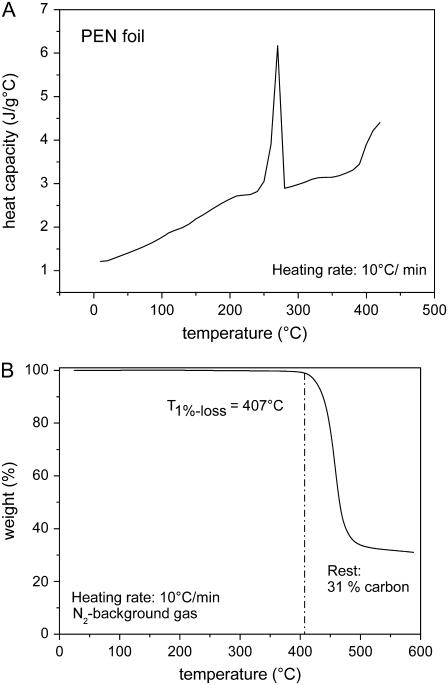
Fig. 3 shows the differential scanning calorimetry and thermogravimetric analysis data for polyethylene naphthalate (PEN) foil, the polymer material that is usually mounted on the microscope glass slides on which the histologic specimens are placed. Table 1 presents a summary of the measurement results for the optical and thermal material properties of materials relevant for LMD and LPC of cells and histologic materials.
FIGURE 3.
Thermal properties of PEN foil. (A) Temperature-dependent heat capacity _c_p. The peak at 269°C indicates an endothermal melting transition, and the rise above 400°C is due to dissociation. (B) Temperature-dependent weight loss for a slow heating rate, with dissociation starting at 407°C and ending at ≈500°C. The dissociation temperature defined by half of the total weight loss is ≈450°C. For very fast heating rates such as in pulsed laser catapulting, it will probably be higher because dissociation is a rate process that depends on both temperature and time.
TABLE 1.
Optical properties at 337 nm and thermal properties of cells, histologic material, polyethylene naphthalate polymer foil, glass, and water
| Material | Sample thickness x (_μ_m) | Transmission (%) | Extinction coefficient _μ_eff (cm−1) | Optical penetration depth δ (_μ_m) | Average heat capacity (kJ K−1 kg−1) | Phase transition temperature (°C) | Heat conductivity (W m−1 K−1) | Density (kg m−3) |
|---|---|---|---|---|---|---|---|---|
| Glass slide | 1000 | 94.7 | 0.55 | 18200 | 0.666 | — | 1.07 | 2500 |
| PEN*-foil | 1.35 | T = 20.5 R = 22.4 | _μ_a = 3520 _μ_′s = 8680 _μ_eff = 11360 | 0.88 | 2.7 | 460 | ≈0.4 | 1.39 |
| H&E† stained histol. specimen | ≈5 | 7–35 (15.7) | 2100–5300 (3700) | 1.9–4.8 (2.7) | 3.2 | 340 | ≈0.5 | ≈1000 |
| CHO‡ cells | ≈5 | 93.8 | 127 | 79 | 4.0 | 150–300 | ≈1000 | |
| Water | 0.0172 | 5.8 × 105 | 4.187 | 300 | 0.598 | 998 |
Thresholds for dissection and forward transfer
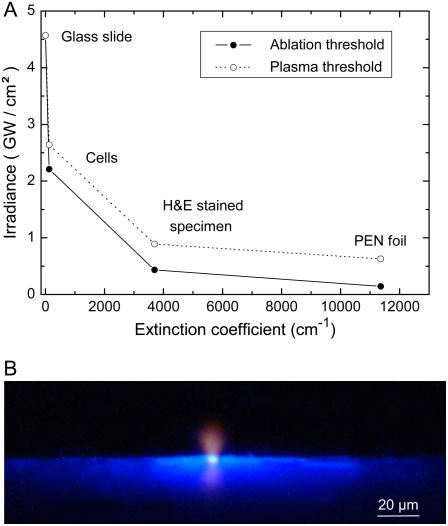
Fig. 4 A presents the thresholds for thermal ablation and plasma formation by 337-nm, 3-ns laser pulses for various materials. All values were determined using tightly focused laser pulses. As threshold criterion for plasma formation we used the observation of bluish plasma luminescence during microscopic inspection of the irradiated sample with dark adapted eyes. For unstained cells the ablation threshold was only slightly smaller than the threshold for the formation of a luminescent plasma. By contrast, for stained histologic specimens and the PEN polymer foil that have a much larger optical absorption coefficient than unstained cells (Table 1), the ablation threshold is considerably lower than the plasma formation threshold.
FIGURE 4.
(A) Thresholds for thermal ablation and plasma formation by 337-nm, 3-ns laser pulses for various materials. All values were determined by focusing the laser pulses through the 40× objective (4.2 _μ_m spot diameter). (B) Image of plasma luminescence and fluorescence of PEN foil during microdissection of histologic specimens by laser pulses focused through the 40× objective. The photograph was taken in side view and integrates over the luminescence produced by six pulses of 4.6-_μ_J incident energy.
Fig. 4 B shows a typical image of plasma luminescence during microdissection of histologic specimens on PEN polymer foil. The plasma luminescence (seen in side view) is blue at the target surface but turns red at larger distances where the temperatures are smaller and the corresponding wavelength of blackbody radiation is longer. The blue light emission adjacent to the laser focus is caused by fluorescence of the PEN foil.
The threshold radiant exposures _φ_th and irradiances _I_th for catapulting determined with different microscope objectives and laser pulse energies are listed in Table 2. The thresholds were measured by varying the spot size at constant laser pulse energy (5 or 10 _μ_J on the target, respectively). The threshold values refer to a catapulting mode in which the laser spot size is comparable to the specimen diameter. In this regime, no plasma luminescence and hole formation in the specimen was observed and the pressure accelerating the specimen is produced by thermal ablation. A decrease of the laser spot size below the specimen diameter corresponds to an increase of the radiant exposure and irradiance required for catapulting, until finally the threshold for plasma formation is exceeded. For 10 _μ_J pulse energy on the target, the largest spot size for which plasma luminescence was observed on the photographic images is 27 _μ_m, and the corresponding plasma formation thresholds are _φ_th = 1.75 J/cm2 and _I_th = 0.58 GW/cm2, respectively. These threshold values are slightly larger than the values given for PEN foil in Fig. 4 A because the detection of plasma luminescence on photographs is less sensitive than by observation with dark adapted eyes.
TABLE 2.
Threshold radiant exposures _φ_th and irradiances _I_th for catapulting using 3-ns, 337-nm laser pulses focused through different microscope objectives
| 40×-objective | 5×-objective | |||||
|---|---|---|---|---|---|---|
| Laser pulse energy (_μ_J) | Spot diameter at catapulting threshold (_μ_m) | _φ_th (J/cm2) | _I_th (MW/cm2) | Spot diameter at catapulting threshold (_μ_m) | _φ_th (J/cm2) | _I_th (MW/cm2) |
| 10 | 210 | 0.03 | 10 | 135 | 0.07 | 23.3 |
| 5 | 85 | 0.09 | 30 | 65 | 0.15 | 50 |
Dynamics of the initial phase of laser-induced transport
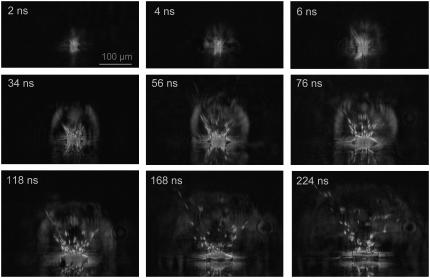
The initial dynamics of laser-induced forward transfer using focused laser pulses aimed centrally below the specimen is shown in Fig. 5. A luminescent plasma at the laser focus is visible in all frames. Immediately after the laser pulse, small debris particles are ejected with high velocity, and after 270 ns, the specimen is already clearly detached from the substrate surface. At the location of plasma formation, a hole is produced in the specimen, which is clearly visible in the image taken after 5.4 _μ_s (arrow). The initial specimen velocity amounts to 180 m/s, and the acceleration required to reach this velocity within 100–200 ns is ∼108 g. Since the catapulting laser pulse does not always hit the specimen exactly at its center, the specimen tumbles statistically after release, and the orientation on the frames differs in each individual case.
FIGURE 5.
(A) Initial phase of the catapulting dynamics of a specimen with 80-_μ_m diameter from a paraffin section. A single laser pulse of 10-_μ_J incident energy was focused at the center of the specimen. 40× objective, NA = 0.6. (B) Enlarged view of the specimen after 1.7 _μ_s showing the luminescent plasma driving the specimen, and the blue fluorescence of the PEN polymer foil.
In commercial microbeam systems, the region of interest is usually dissected in such a way that a small bridge is left at the location where the end of the trajectory of the cut would meet the starting point. A single pulse of larger energy is then aimed at the bridge to complete dissection and, at the same time, catapult the specimen. Since the catapulting laser pulse hits the specimen at its periphery, a fast rotational movement of the specimen is always induced, and the flight trajectories are generally not in line with the optical axis of the microscope but oblique. The initial rotation frequency deduced from photographic picture series (not shown) often exceeds 100,000 rps during the first 2–3 _μ_s. It varies from shot to shot and soon slows down by air friction.
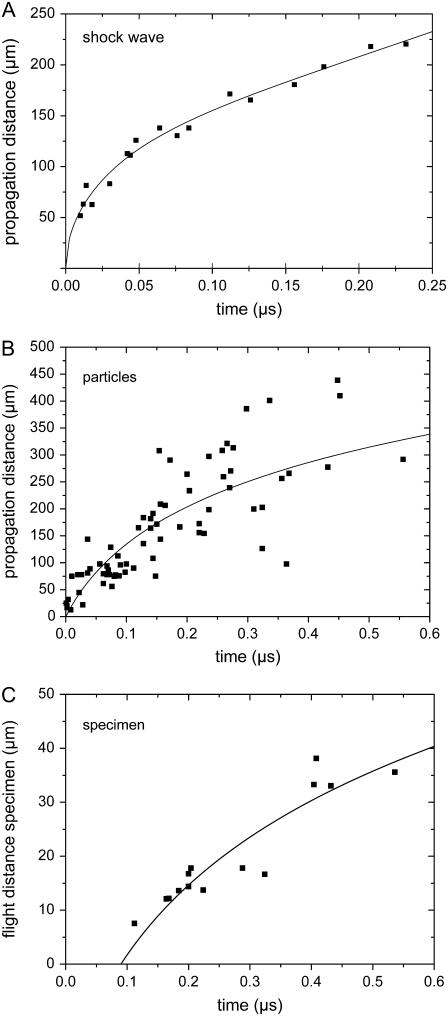
Schlieren photographs of the pressure wave produced by the expansion of the laser plasma are shown in Fig. 6. An evaluation of the photographic series provided quantitative information on the propagation distance of the laser-produced pressure wave, the ejected debris, and the catapulted specimen as a function of time that is presented in Fig. 7. The initial velocity of the pressure wave amounts to 26,000 m/s, which is 76 times larger than the normal sound velocity in air and thus indicative for a strong shock wave. The plasma pressure driving the shock wave can be derived from the initial shock wave velocity _v_s using the relation (20)
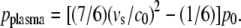 |
(2) |
|---|
Here _c_0 = 345 m/s denotes the normal sound velocity in air, and _p_0 = 0.1 MPa is the atmospheric pressure. The initial laser-produced pressure obtained is 670 MPa.
FIGURE 6.
Dark-field photographic series showing the first 225 ns of the catapulting dynamics. A specimen with 80-_μ_m diameter from a paraffin section was catapulted using a 10-_μ_J pulse focused at the center of the specimen. 40× objective, NA = 0.6. The movement of the ejected particles and the propagation of the laser-induced shock wave can be recognized, followed by the detachment of the specimen after 100–200 ns.
FIGURE 7.
Propagation distance d of the laser-produced shock wave (A), the ejected particulate debris (B), and the catapulted specimen (C) as a function of time. From the slope of the d(t) curves, initial velocities of (A) 26000 m/s, (B) 2200 m/s, and (C) 178 m/s are deduced, which corresponds to (A) 76×, (B) 6.4×, and (C) 0.52×, the sound velocity in air. 40× objective, NA = 0.6, specimen diameter 80 _μ_m, and laser energy on the target E = 10 _μ_J. The laser focus was located at the center of the specimen.
Flight trajectories
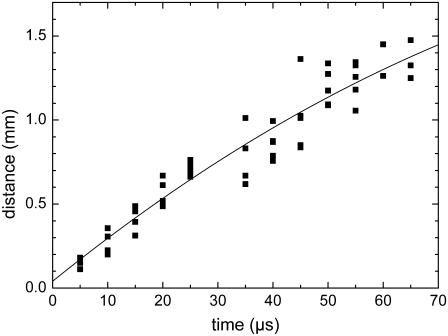
The catapulted specimen has to be accelerated against inertia and hydrodynamic drag. Acceleration ceases when the force exerted by the pressure below the specimen becomes smaller than the resistance originating from the compressed air in front of the specimen and hydrodynamic drag. Afterwards, the specimens are slowed down by the air friction. The trajectory of the dissectats during their flight toward the microfuge cap is presented in Fig. 8.
FIGURE 8.
Slowing of the specimens due to the friction in air. The specimens had 80-_μ_m diameter and were catapulted using a 40×, NA = 0.6 objective, and E = 6.5 _μ_J incident energy. The fitted curve corresponds to Eq. 3.
A theoretical description of the flight trajectory z(t) for the phase dominated by air friction is generally quite complicated (6,21). However, for large particle velocities and sizes, Newtonian friction (related to the inertia of the displaced material) dominates Stokes friction (related to the medium viscosity), and it can be assumed that the hydrodynamic drag is approximately proportional to the square of the velocity. One then obtains the trajectory (21)
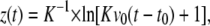 |
(3) |
|---|
where _v_0 is the initial velocity at time _t_0 denoting the duration of the acceleration phase, and K is a constant incorporating all material parameters including its density, cross sectional area, and shape-related properties. Equation 3 was fitted to the measurement points in Fig. 7, B and C, and Fig. 8 to obtain information on _v_0 and _t_0. Generally good agreement between the trend exhibited by the experimental data and the fitted z(t) curves was found. At later times > 1 ms, when the specimen velocities have slowed down to ≤1 m/s, the hydrodynamic drag must be described by a combination of Newtonian friction (∝ _v_2) and Stokes friction (∝ v), which leads to a more complex equation of motion (6).
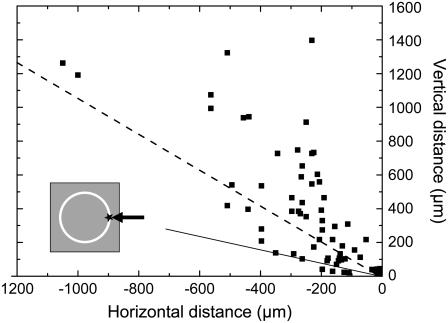
When the catapulting pulses are aimed at the rim of the specimen, the flight trajectories are generally not in line with the optical axis of the microscope but oblique, as shown in Fig. 9. As a consequence, not all catapulted specimens arrive in the cap of the microfuge tube. In our investigations, ∼93% of all dissectats would have arrived within the cap when factory settings are used for the distance between cap and microscope slide. Sixty-five percent would have reached the top part of the cap where the chance of adhesion is usually enhanced by applying a drop of mineral oil before catapulting . The oblique direction of the flight trajectories is related to the fact that plasma formation at the rim of the specimen imparts an impulse not only in upward but also in lateral direction.
FIGURE 9.
Directional distribution of flight directions when the laser pulses are aimed at the rim of the specimen (see inset). Specimen diameter 80 _μ_m, 40× objective, NA = 0.6, E = 5 _μ_J. The specimens were photographed at different times after the catapulting laser pulse, and the data points show their location at these times. The flight trajectories are given by the connection between the laser focus (at 0,0) and the respective data points. The straight line delineates which specimen will reach the cap of the microfuge tube if it is located at a distance of 1 mm from the supporting slide and if the center of the cap is in line with the optical axis of the microscope objective. The dashed line indicates which specimens would reach the top of the cap, which is commonly wetted by a drop of mineral oil to improve adhesion.
Parameter dependence of specimen velocity
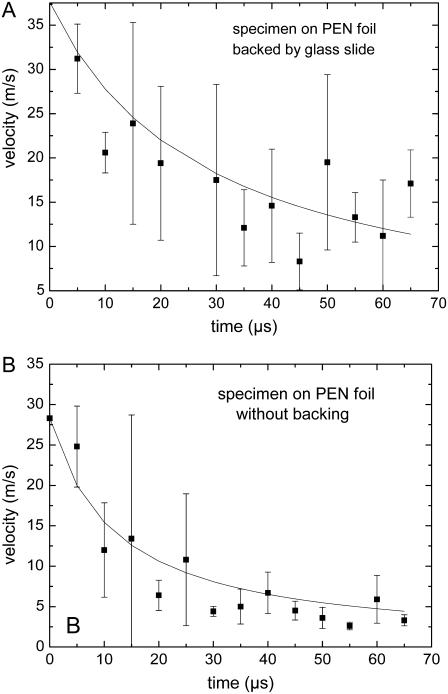
The specimen is usually located on a PEN foil backed by a transparent substrate (glass slide). However, in some cases, the histologic specimens to be catapulted are mounted on a foil without backing by a glass substrate. Without confinement by the glass substrate, the plasma or ablation plume can freely expand, and catapulting relies merely on the force produced by the ablative recoil pressure. This pressure is smaller and ceases faster than the pressure arising from plasma generation or ablation in a confined geometry. As a result, the catapulting velocities are also smaller, as shown in Fig. 10. The impulse coupling efficiency in laser ablation was theoretically analyzed by Phipps et al. (10) and Dingus (22,23). It was predicted to be smaller without confinement of the ablation products, in agreement with our observations and with previous results for aluminum foils (9).
FIGURE 10.
Comparison of the velocities of specimens on a foil (A) with and (B) without backing by a glass substrate. Each data point refers to the average of five measurements. Specimen diameter 80 _μ_m, 40× objective, NA = 0.6, E = 5 _μ_J.
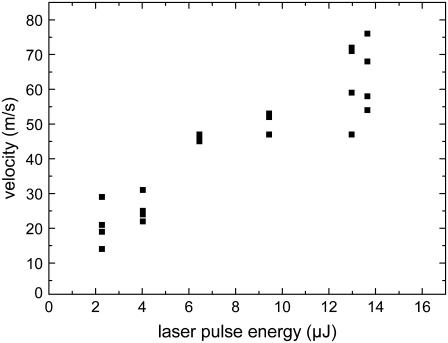
The dependence of the velocity on laser pulse energy for specimens that are backed by a glass slide is shown in Fig. 11. As expected, the specimen velocity increases monotonously with laser energy. In the energy range investigated which is still close to the catapulting threshold, their relation is approximately linear. However, further above threshold we would rather expect a square-root dependence corresponding to a constant conversion efficiency from laser energy into the kinetic energy of the moving specimen.
FIGURE 11.
Dependence of specimen velocity on laser pulse energy (average velocity values during the first 15-_μ_s flight time). Specimens of 80-_μ_m diameter were catapulted using a 40× objective, NA = 0.6.
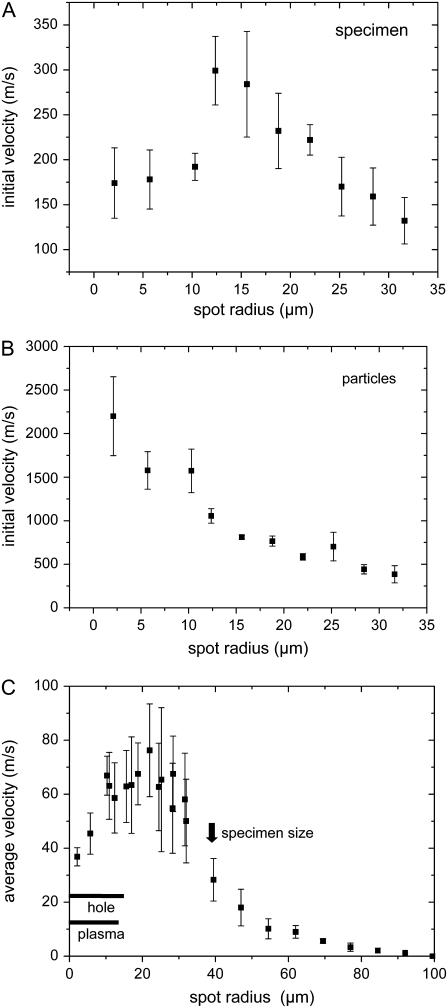
To identify the gentlest and/or most efficient way of catapulting, we investigated how the catapulting behavior depends on the size of the irradiated spot at the bottom of the specimen. The dependence of the initial velocities of the specimen and the ejected particulate debris on spot size is presented in Fig. 12, A and B, and the average velocity during the first 50 _μ_s after the laser pulse is shown in Fig. 12 C. The catapulting velocities first increase and then decrease when the irradiated spot is enlarged.
FIGURE 12.
Catapulting velocity as a function of laser spot size. (A) Initial velocity of the specimens; (B) initial velocity of the particulate debris; (C) average velocity of the specimens during the first 50-_μ_s flight time, with regimes for plasma and hole formation. 40×, objective, NA = 0.6, E = 10 _μ_J. The center of the irradiated spot coincided with the center of the specimen.
For a constant laser energy of 10 _μ_J, the velocity of the dissectats was found to be 2.3 times larger when the laser pulses were focused through a 5× objective instead of a 40× objective. This striking difference is due to the fact that the focal spot size increases with decreasing numerical aperture of the objective. The measured focus radius of the N2 laser beam in the PALM system was 21.4 _μ_m for the 5× objective compared to 2.1 _μ_m for the 40× objective. Because of the large spot size we did not observe holes in the specimens after catapulting with the 5× objective, while 10-_μ_J pulses focused through the 40× objective consistently produced a hole. The better confinement of the ablation products for the 5× objective explains the larger catapulting velocity.
Scanning electron microscopy of dissected specimens
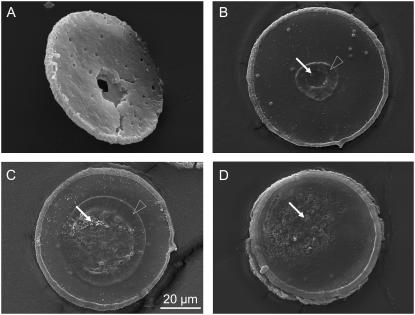
Fig. 13 shows SEM micrographs of specimens catapulted at different irradiated spot sizes. Catapulting with tightly focused laser pulses is associated with the generation of a hole through the entire specimen as visible in Fig. 13 A. With 30 _μ_m spot diameter, a hole was formed in the polymer foil but not in the specimen (Fig. 13 B). In a zone around this hole, the PEN foil was apparently molten and has resolidified. More strongly defocused laser pulses comparable to the specimen size lead to local ablation and melting of the foil, but do not perforate it (Fig. 13 C). Pointlike ablated spots lacking signs of surrounding melting, are also observed when the irradiated spot becomes larger than the specimen size (Fig. 13 D).
FIGURE 13.
Scanning electron micrographs of histologic specimens that were catapulted by irradiating different spot sizes with 10-_μ_J incident energy. The spot diameters were (A) 4 _μ_m, (B) 30 _μ_m, (C) 80 _μ_m, and (D) 136 _μ_m. These values denote the diameter of the geometric cone angle of the laser beam at the location of the specimen. The actual spot size may be smaller if the irradiance distribution has an intensity peak around the optical axis. In panel A, the specimen is viewed from the side of the histologic section, whereas in panels B_–_D it is viewed from the side covered with PEN foil. Solid arrows mark areas where the PEN foil is either entirely or in parts ablated; open arrowheads mark molten and resolidified regions.
DISCUSSION
Mechanism of laser dissection
It has previously been shown that cell surgery using pulsed visible and near infrared (IR) irradiation is plasma mediated, i.e., based on nonlinear absorption via multiphoton and avalanche ionization. The irradiance required for cell surgery with nanosecond laser pulses is ∼109 W/mm2, just as the optical breakdown threshold in water (15). For femtosecond laser pulses, we find the same accordance between the thresholds for optical breakdown and dissection, only that the required irradiance is approximately two orders-of-magnitude larger than for nanosecond pulses while, due to the much shorter pulse duration, the breakdown energy is approximately three orders-of-magnitude smaller (16).
For cell surgery using visible or near-IR wavelengths the dominant role of plasma formation is not surprising because the linear absorption of water and biomolecules in this region of the optical spectrum is very small (24,25). However, this study revealed that plasma formation plays a key role also for the dissection of cells at UV-A wavelengths. Although the absorption increases with decreasing wavelength, it is still fairly small at λ = 337 nm (the optical penetration depth is ∼80 _μ_m, see Table 1), and even smaller at 355 nm. Thus, the ablation threshold in unstained cells was found to be only slightly smaller than the threshold for the formation of luminescent plasma, as shown in Fig. 4 A.
Stained histologic specimens and the PEN polymer foil have a much larger optical absorption coefficient than unstained cells (see Table 1). For those materials, the threshold for ablation based on linear absorption is thus considerably lower than the plasma formation threshold (Fig. 4 A). The threshold for plasma formation is also lowered because the heating through linear absorption results, for sufficiently large temperatures, in thermal ionization that provides start electrons for an ionization avalanche. It has previously been speculated that ablation of biomaterial at the N2 laser wavelength of 337 nm is based on photochemical dissociation (4). However, this is unlikely because indications for a relevant contribution of photochemical effects to tissue ablation have been found only at much shorter wavelengths—for example, with argon fluoride excimer laser pulses at λ = 193 nm, whereas they were completely absent with xenon chloride excimer laser pulses of 308 nm wavelength (24,26). Therefore, we conclude that ablation based on linear absorption at λ = 337 nm is a photothermal process.
Fig. 4 A indicates that dissection of stained histologic specimens by N2 laser pulses could, in principle, be performed by ablation without any contribution of plasma formation because the ablation threshold (0.15 _μ_J as measured with the 40× microscope objective and 4.2 _μ_m spot diameter) is lower than the threshold for plasma formation (0.3 _μ_J). However, because of the small ablation efficiency close to the threshold for material removal, this dissection mode would require very many pulses, which is not viable at the relatively small laser repetition rate of 30 Hz. Therefore, pulse energies of ∼0.5 _μ_J are commonly used. That energy corresponds, for 4.2 _μ_m spot diameter, to a radiant exposure of 3.6 J/cm2 and an irradiance of 1.2 GW/cm2. These values are larger than the threshold for plasma formation, and dissection is thus accompanied by blue plasma luminescence as visible in Fig. 4 B. The slightly disruptive action of the plasma expansion helps to achieve clean cuts without any bridges remaining between the parts to be separated. We conclude that dissection of histologic specimens using UV lasers with low to moderate repetition rate is based on plasma formation initiated by linear absorption.
Driving forces for transport by focused laser pulses
Laser pulse energies commonly used for catapulting are 5–10 _μ_J on the target, corresponding to radiant exposures of 36.1–72.2 J/cm2 and irradiances of 12–24 GW/cm2 for a 40× objective and 4.2 _μ_m spot diameter. These values are larger than the parameters employed for dissection that was already shown to rely on plasma formation. It is thus obvious that catapulting with focused laser pulses must be driven by plasma formation. The plasma luminescence is clearly visible in the photographs of Fig. 5.
Plasma formation creates a large pressure in the space between specimen and substrate that accelerates the specimen. The initial pressure value derived from the shock wave data in Fig. 7 using Eq. 2 is 670 MPa, which is typical for plasmas generated in condensed matter (12,27,28). Similar pressure values are also obtained by analyzing the acceleration of the debris flying off from the laser focus that is visible in the dark-field images of Fig. 6. Using Newton's laws of motion, one can derive the relationship
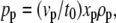 |
(4) |
|---|
between the time-averaged driving pressure _p_p, the time _t_0 during which a particle is accelerated to a final velocity _v_p, and the thickness _x_p, and mass density _ρ_p of the particle. The images in Fig. 6 suggest that the acceleration time for particulate debris is not much longer than the laser pulse duration of 3 ns, i.e., it will be in the order of 5 ns. From the slope of the curve fitted to the data in Fig. 7 B we obtain an initial velocity of ≈2200 m/s for the debris produced by a 10-_μ_J laser pulse. Assuming _ρ_p = 1000 kg/m3 (Table 1) and _x_p = 3 _μ_m (the lower part of the specimen at the laser focus is disintegrated during plasma formation, and only the upper part flies off as debris), we get _p_p = 1320 MPa.
In the early days of LPC, it has been speculated that the specimens are driven by the light pressure (4). We can check the validity of this hypothesis by comparing the measured specimen velocity with the speed that can be imparted by the light pressure
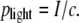 |
(5) |
|---|
Here I is the irradiance in the illuminated laser spot and c is the vacuum velocity of light. The accelerating force exerted by the light pressure acts only within the illuminated region and during the laser pulse duration. The final velocity reached can be calculated considering Newton's laws of motion and the mass of the specimen. The calculation yields v = 0.9 mm/s for a specimen of 80-_μ_m diameter, 7-_μ_m thickness, and a mass density of 1000 kg/m3 that is catapulted by a 10-_μ_J pulse (parameters as in Fig. 7). The actual initial specimen velocity obtained from the data in Fig. 7 C is ≈180 m/s, which is five orders-of-magnitude larger than the value predicted by Eq. 5. The pressure exerted by the photons in the laser pulse, which is the working mechanism in laser tweezers (29–31), thus plays only a negligible role in LPC.
We showed that catapulting with focused pulses relies on the pressure produced by confined plasma formation. However, despite the large pressures involved, the catapulted specimens in Fig. 5 show little bending or other deformations. This is due to the fact that the large pressure at the focus is in vertical direction rapidly released by the hole formation in the specimen. In horizontal direction, the shock wave spreads across the specimen diameter within ∼20 ns (Fig. 6). This way, it produces an approximately homogeneous elevated pressure below the specimen that lifts off from the substrate after ∼100–200 ns (Figs. 5 and 6). In Fig. 5, one can see that parts of the histologic section surrounding the dissected area are transiently lifted from the substrate for a few microseconds. This indicates that the horizontal pressure wave does not stop at the cut but, at least partially, continues to propagate under adjacent parts of the histologic sample. From the initial velocity of the dissectat (180 m/s), we can calculate the average pressure under the entire catapulted specimen during the acceleration phase of ∼100 ns using Eq. 4. For _x_p = 7 _μ_m and _ρ_p = 1000 kg/m3, it amounts to ∼13 MPa, which is considerably less than the peak pressure within the laser plasma of ≈670 MPa.
In LMPC with commercial microbeam systems, a small bridge is left before the selected dissection trajectory is completed, and a single pulse of larger energy is then aimed at the bridge to complete dissection and catapult the specimen. This strategy saves processing time but the flight path is usually oblique (Fig. 9). Moreover, due to the reduced confinement of ablation products, the impulse coupling to the specimen is not as good as with laser pulses aimed at the center of the specimen. To optimize impulse coupling to the specimen, the width of the bridge should be at least equal to the diameter of the laser spot, and the spot size should be as large as possible without compromising the dissection of the bridge at the given pulse energy (6).
Transport mechanisms with defocused laser pulses
Catapulting with laser spot sizes of up to d = 27 _μ_m diameter was associated with plasma formation and the generation of a hole through the entire specimen (Figs. 12 C and 13 A). However, since the radiant exposure drops with increasing laser spot size, both the driving mechanism and the alterations of the specimen change when the pulses are more strongly defocused. For d > 27 _μ_m, plasma formation is replaced by explosive vaporization, and for d ≥ 30 _μ_m, hole formation was only observed in the polymer foil but not in the specimen (Fig. 13 B). In this regime, the catapulting velocities are maximal (Fig. 12) because the ablation products remain confined below the specimen and cannot escape through a hole in the center of the specimen. More strongly defocused laser pulses lead to local ablation without perforation of the foil (Fig. 13, C and D). When the irradiated spot becomes comparable to or larger than the specimen size, catapulting occurs still in a reproducible fashion but the velocities are much smaller than with spot diameters of 30–40 _μ_m (Fig. 12).
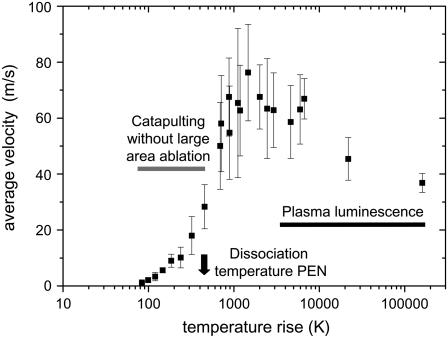
For further analysis of the mechanisms of defocused catapulting, we calculated the average temperature rise within the irradiated spot in a layer with the thickness of the optical penetration depth, assuming a homogeneous light distribution in the irradiated spot. The calculation was based on the measured optical and thermal properties (heat capacity) listed in Table 1. Because of the pronounced scattering of the PEN foil, 22.4% of the incident light are back-scattered. This has been considered in calculating the temperature rise in the PEN foil, as well as the slight transmission loss of 5.3% in the microscope glass slide. The results for the average laser-induced temperature in a PEN layer with the thickness of the optical penetration depth (0.88 _μ_m) are presented in Fig. 14.
FIGURE 14.
Velocity data of Fig. 12 C plotted as a function of the temperature rise at the bottom of the specimen. The average temperature rise in the optically absorbing layer is calculated based on the laser pulse energy on the target (10 _μ_m), the measured optical penetration depth (0.88 _μ_m), and an average value of the heat capacity of the PEN foil (2.7 J/gK, see Fig. 3). Losses by specular reflection at the glass slide, absorption in the glass (together 5.3%), and by backscattering from the PEN foil (22.4%) were taken into account.
The calculated peak temperatures for tightly focused irradiation (≈105 K) are unrealistically large because the calculation does not consider that the plasma expansion and adiabatic cooling already start during the laser pulse. Realistic plasma temperatures are in the order of 5000–10,000 K (32). With defocused irradiation, for which catapulting is driven by ablation without plasma formation, adiabatic cooling by the expansion of the ablation plume reaches a significant level only toward the end of the laser pulse when most of the laser energy has been deposited (33). Therefore, the calculated peak temperatures at the bottom of the specimen are realistic. The calculated temperature rise for the spot radius of 22 _μ_m associated with the maximum catapulting velocity is ∼1400°C. This is considerably larger than the melting temperature of PEN (269°C for slow heating, see Fig. 3 A), and also larger than the dissociation temperature (462°C for slow heating, see Fig. 3 B). At the same time, it is lower than typical plasma temperatures, which is consistent with the fact that no plasma luminescence was observed. A temperature jump of 1400°C within 3 ns will be associated with explosive dissociation of the heated PEN material followed by a very rapid volume expansion. This is a very efficient catapulting mechanism (12).
Interestingly, the specimens can still be catapulted when the average temperature rise in the absorbing layer is less than one-quarter of the dissociation temperature of the PEN foil. The observation that average temperatures well below the dissociation limit are sufficient for catapulting may indicate that the specimen is driven by sudden thermal expansion and deformation (similar to the working mechanism of dry laser cleaning (34,35). Even though the actual surface movement caused by thermal expansion is very small, this expansion is achieved in the laser pulse duration of a few nanoseconds. Therefore, the acceleration by one-dimensional surface expansion is 105–107 times larger than gravitational acceleration, leading to velocities in the order of 1 m/s at the end of the laser pulse (34,36). Moreover, because of the small size of the specimen, thermal expansion can also occur in lateral direction. It is stronger in the lower part of the specimen where higher temperatures are reached than the upper part. This difference results in an upward bending of the peripheral parts of the dissectat that probably contributes to its upward acceleration. However, it is unlikely that these effects alone can account for specimen velocities of up to 20 m/s that were observed with irradiation parameters for which the average temperature in the absorbing layer is below the dissection threshold. We need to consider that the beam profile of the N2 laser is highly irregular (Fig. 2, B and C), that the temperature at the irradiated specimen surface is larger than the average temperature within the optical penetration depth shown in Fig. 14, that the SEM picture in Fig. 13 D) is indicative for scattered pointlike ablation, and that the volume expansion of ablated material in confined geometry is an extremely efficient catapulting mechanism (12). Thus even when the specimen's acceleration by thermal deformation becomes relevant, it is probably still accompanied by the propelling action of ablation in hot spots of the laser beam.
We conclude that catapulting with defocused pulses of 10 _μ_J energy relies on the pressure produced by confined plasma formation for irradiated spot sizes d ≤ 27 _μ_m and on confined thermal ablation for d > 27 _μ_m. For very large spots comparable to the sample diameter, thermal expansion and deformation of the dissectat possibly also contribute to its acceleration. The relative contributions of ablation and thermal expansion need to be further investigated.
Possible side effects and their minimization
Thermal effects
The high temperatures produced during plasma formation or pulsed laser ablation seem to be an obvious source for potential side effects of LMD and LPC. However, one needs to consider that any changes within the material that is disintegrated or vaporized during the cutting process do not affect the accuracy of the subsequent genomic or proteomic analysis because this material is not collected in the vial for analysis. Of interest are only those changes by heat conduction or convection that alter the remaining dissected specimen catapulted into the cap of the microfuge tube.
Let us first consider LMD and LPC with tightly focused laser pulses (4.2 _μ_m spot size): Here the fraction of the specimen exposed to high temperatures is very small, and most of it is disintegrated and does not take part in the subsequent analysis. Because of the fast adiabatic cooling during the rapid expansion of the laser-induced plasma, the time available for heat conduction into adjacent parts of the specimen is extremely short (< 1 _μ_s), and the heat-affected zone next to a cut is therefore very small. The width of the altered region at the rim of the dissectat in the SEM pictures of Fig. 13 amounts to 2–3 μ_m for the bottom side covered with PEN foil (Fig. 13, B–_D) but is smaller (<1 _μ_m) for the upper side, i.e., for the histologic specimen itself. The fact that thermal alterations are most pronounced at the bottom side of the dissectat may partly be attributable to heat diffusion from the plasma through the supporting glass slide, which is a good heat conductor. Partly it may be due to the fact that the ablation products in the confined space below the specimen expand in a two-dimensional geometry, which results in slower cooling than for the unhindered plume expansion above the specimen. The small amount of thermal damage in the histologic specimen is consistent with previous transmission electron microscopical studies of plasma-mediated dissections in ocular tissues performed with IR laser pulses of 6-ns and 40-ps duration in which the heat-affected zone was found to be far below 1 _μ_m (37,38).
The situation is less obvious when a larger fraction of the specimen is exposed to the laser radiation, and when the sample is catapulted directly from a glass slide, without protection by the light-absorbing PEN foil. To assess potential side effects by thermal damage for these cases, we calculated the time evolution of the temperature distribution under different focusing conditions of the laser pulse.
We used an analytical solution of the differential equations for heat diffusion in a multilayer geometry (39), with layers representing glass, PEN-foil, histologic specimen, and air. Glass and air were supposed to be transparent, and the absorption properties of PEN foil and histologic section were assumed to be in accordance with Lambert-Beer's law and taken from Table 1. Calculations were performed for a laser pulse with rectangular temporal shape and 3-ns duration. As analytical solutions for layered geometries with different optical properties are restricted to homogeneous thermal properties of the medium, we had to use the same values for heat capacity, heat conductivity, and mass density for all layers. We employed the measured data for H&E stained specimens listed in Table 1.
We assumed that heat can diffuse from the light absorbing PEN foil and histologic section into the adjacent glass slide until the specimen detaches from the slide during the expansion of the ablation plume, which occurs ∼300 ns after the laser pulse (Fig. 5). Afterwards the calculations were continued for a thermally isolated specimen because heat conduction into the surrounding air is negligible. The adiabatic conditions were simulated by the introduction of appropriate mirror heat sources (40).
For catapulting without plasma formation, the temperature of the sample surface is determined by the ablation temperature _T_abl of the sample material. For polymers, the ablation temperature corresponds to the dissociation temperatures that, for slow heating, are given in Table 1. At very short heat exposure times, dissociation temperatures are higher because dissociation is a chemical rate process (41). In a similar way, the temperature required for protein denaturation increases with decreasing heat exposure time (41–43). This rise of dissociation and denaturation temperatures could not be considered in our calculations because the rate constants for very fast heating are not yet known. To avoid this difficulty, all temperatures in Fig. 15 are not given in absolute values but normalized to the maximum temperature at the sample surface reached at the end of the laser pulse.
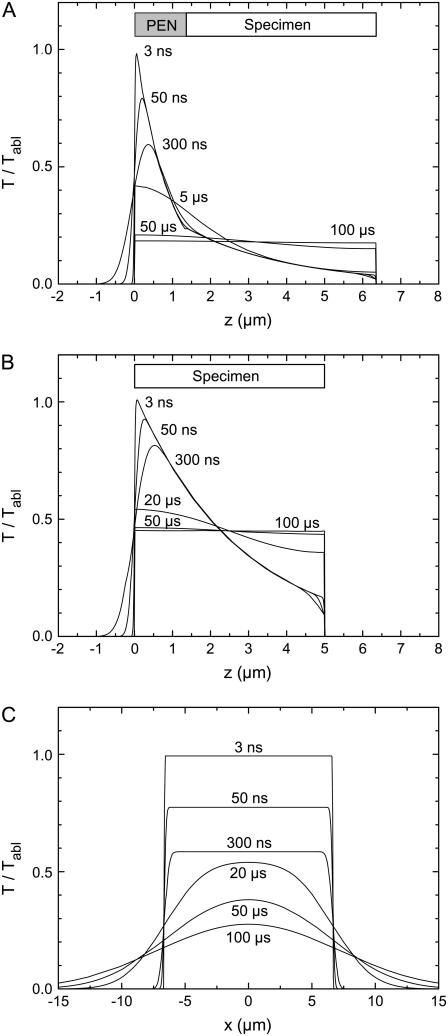
FIGURE 15.
Evolution of the temperature distribution for (A) H&E stained specimen on PEN foil backed by a glass slide, homogeneously irradiated by a defocused laser beam having a diameter equal to or larger than the specimen size; (B) H&E stained specimen on a glass slide, homogeneously irradiated by a defocused laser pulse; and (C) H&E stained specimen on a glass slide, irradiated by a pulse with top-hat distribution of 15-_μ_m diameter. The plots in panels A and B show the temperature distribution in z direction; the distribution in lateral direction is homogeneous. The plots in panel C present the lateral temperature distribution at the surface of the heated area and in its vicinity; the temperature decay in z direction resembles that in panel B and is not shown.
Fig. 15 compares the temperature evolution for cases where an H&E stained specimen is either mounted on PEN foil backed by a glass slide (Fig. 15 A) or directly placed on the glass slide, with different spot sizes used for catapulting (Fig. 15, B and C). In the cases analyzed in Fig. 15, A and B, the samples were assumed to be homogeneously irradiated by a strongly defocused laser beam having a diameter equal to or larger than the specimen size. Therefore, the temperature varies only in z direction, but exhibits a homogenous distribution in lateral direction. When the histologic specimen is mounted on PEN foil, the ablation temperature is reached at the glass-PEN interface, and the specimen itself is well protected by the strong laser light attenuation in the PEN material. The equilibrium temperature reached 50–100 _μ_s after the end of the laser pulse amounts to only 20% of the ablation temperature, and even at the PEN-specimen interface the temperature never exceeds 35% of the PEN ablation temperature (Fig. 15 A). By contrast, when the specimen is placed directly on glass, the specimen's ablation temperature must be reached at the surface of the specimen itself. Moreover, since the laser light penetrates deeper into the specimen material than into PEN, the initial temperature distribution in Fig. 15 B is broader than in Fig. 15 A, and the equilibrium temperature reached 50–100 _μ_s after catapulting is higher; it amounts to 45% of the ablation temperature. Catapulting directly from glass with spatially homogeneous irradiation thus should be avoided if possible. The thermal load from tightly focused laser irradiation is much smaller, as discussed in the beginning of this section, but the amount of material transported per pulse will also be smaller than with homogeneous irradiation if no PEN foil is used.
The modeling results of Fig. 15 A predict that the histologic specimen on top of the 1.35 _μ_m thick PEN foil is hardly affected by heat. This is in good agreement with the SEM results of Fig. 13 D that demonstrate that only the bottom of the polymer foil is ablated when the irradiated spot is larger than the specimen diameter. However, even when PEN foil is used, the specimen is not in all cases protected. The SEM images in Fig. 13 B show that with moderate defocusing corresponding to 30-_μ_m spot diameter, the PEN foil is removed from the irradiated area. A part of the PEN material has been ablated and another part was probably molten and pushed aside by the pressure in the ablation cloud. Therefore, the lower surface of the histologic specimen is exposed to the PEN ablation temperature, and the temperature profiles in z direction will thus resemble those of Fig. 15 B. However, because of the small size of the irradiated spot, lateral heat diffusion now contributes to cooling as shown in Fig. 15 C, and the lateral heat diffusion continues even after the specimen is separated and thus thermally isolated from the glass slide. As a consequence, the temperature at the specimen surface drops to 28% of the ablation temperature within 100 _μ_s, compared to 45% in Fig. 15 B. Nevertheless, for spot sizes up to ∼30–35 _μ_m it cannot be excluded that the nonablated specimen volume above the perforated area and next to the molten foil is subject to thermal changes. However, the potentially heat-affected volume is still relatively small. It comprises, for example, 3% of the entire specimen volume for a spot diameter of 15 _μ_m and a specimen diameter of 80 _μ_m. For 30-_μ_m spot size, the fraction increases to 12%.
Photodamage by UV light
Chemical changes by UV light are, like thermal damage, only relevant for the material remaining after dissection. During dissection and catapulting with focused laser pulses, the dissectat may be irradiated by UV laser light scattered at the laser plasma, and by the UV plasma luminescence. The light scattering by nanosecond-plasmas was found to involve <2% of the incident laser irradiation and to occur mainly in forward and backward direction (44). Therefore, the scattered laser light may, at worst, affect a very thin specimen layer at the edge of the cut that is of little relevance for LMD and LPC. The energy of the plasma radiation stays below 0.1% of the incident laser energy (45) and is thus completely irrelevant.
When the irradiated spot is comparable to the specimen size, a large fraction of the specimen or the entire specimen is exposed to the laser light. However, the histologic section is protected by the PEN polymer foil that transmits only 20.5% of the incident light at 337 nm (Table 1). Furthermore, the N2 laser wavelength of 337 nm is far away from the peak of the action spectrum for DNA damage, and the wavelength of a frequency-tripled Nd:YAG laser (355 nm) is even further away. For both wavelengths, the relative response per photon is four orders-of-magnitude smaller than in the wavelength range between 250 nm and 290 nm (46). This is consistent with investigations on the wavelength dependence of laser-induced DNA damage in lymphocytes using the comet assay (47). For λ = 340 nm, the detection threshold for DNA damage corresponded to a radiant exposure of 1.5 J/cm2 (47). Because of the limited sensitivity of the comet assay, ∼300 strand breaks per cell are necessary to detect DNA damage. Hence, one single DNA strand break per cell is expected to occur after a radiant exposure of 5 mJ/cm2. Other pathways of cell damage in the UV-A/B region of the optical spectrum involve the generation of reactive oxygen species such as H2O2 and OH· radical (48–50). For broadband radiation (305–350 nm) peaking at 325 nm, significant cell killing was observed with light doses ≥1 J/cm2 (49). We use the above threshold data on photodamage of living cells as a reference for the assessment of possible photodamage in LPC of histologic specimens because we are not aware of studies performed specifically on histologic materials.
The dose arriving at the PEN foil when a 10-_μ_J pulse irradiates the entire area of a specimen with 80 _μ_m diameter is 200 mJ/cm2. The dose transmitted through the foil (20%, see Table 1) and arriving at the biologic material is 40 mJ/cm2. This is 25 times below the threshold for cell killing (49) but larger than the dose causing, on average, one DNA single strand break per cell (47).
For smaller spot sizes, for example, 15-_μ_m spot diameter, the dose within the irradiated area increases by a factor of 30, to 6 J/cm2, and the protection by the PEN foil is largely absent because it is ablated by the catapulting laser pulse (Fig. 13 B). In this case, the risk for UV damage directly above the irradiated spot is considerably higher because the radiant exposure exceeds the value of 1 J/cm2 leading to significant cell damage, and largely exceeds the threshold value of 5 mJ/cm2 for sporadic DNA strand breaks in individual cells. This dose will likely affect not only live cells but also the accuracy of genomic analysis of histologic material. However, as already mentioned, the total volume affected by UV irradiation of a spot with 15–30 _μ_m diameter is restricted to 3–12% of the specimen volume when a dissectat of 80-_μ_m diameter is transported.
Mechanical deformation and rupture
In general, purely mechanical rupture and disintegration of a histologic sample during LPC imposes no problem for subsequent genomic or proteomic analysis because only a very small fraction of the biomolecules will be affected even if the dissectat is fragmented into many pieces. Crushing of the samples is even a prerequisite for many analytical techniques in biochemistry and molecular biology (4). However, mechanical forces may affect the viability of live cells (17,51–53).
The specimen is accelerated to a speed of 180–350 m/s within ∼200 ns (Fig. 12 A). The acceleration in the initial phase of catapulting is thus enormous, being ∼108 times larger than the gravitational acceleration. However, this does not affect the specimen's integrity as long as the accelerating forces are homogeneous because only tensile stress and shear forces lead to deformation and tearing. When shear forces or tensile stresses do arise, not only their magnitude but also their duration is important for an assessment of their damage potential because biomaterials usually need to be strained to a certain degree to rupture. Since the acceleration phase of the specimens lasts only 200 ns, the strains produced during this time will not lead to rupture as long as shear forces and tensile stresses remain much smaller than the linear acceleration force.
The main sources of shear forces are pressure gradients, while tensile stresses may also originate from radial expansion movements (54). During focused LPC, the huge pressure gradients produced in the vicinity of the plasma lead to local rupture of the specimen, and the large absolute pressure values in this region result in the immediate ejection of debris at very high velocity. However, once the plasma pressure is partly released through the hole in the center of the specimen, the distribution of the driving forces becomes more homogeneous as the shock wave spreads laterally below the entire specimen. At this stage, the pressure gradients have become too small to cause further rupture or strong deformations, and the dissectat flies off in a disklike shape (Fig. 5).
More significant deformations may arise when laser pulses irradiating a spot of ∼30 _μ_m diameter are used for catapulting. In this case, the spot diameter is still much smaller than the specimen diameter but no hole is produced in the specimen. Therefore, the initial pressure distribution under the specimen is inhomogeneous and the center of the specimen will bulge upwards before it flies off. Such deformation can be avoided by defocusing the laser beam to a degree that a nearly homogeneous irradiance and pressure distribution is created across the specimen. However, because the irradiance is largest in the center of the irradiated spot (Fig. 2), this approach requires a spot size much larger than the specimen and is thus associated with considerable energy loss. Alternatively, a phase mask could be used to create a homogeneously illuminated spot with an appropriate size just matching the specimen diameter.
Influence of side effects on the accuracy of quantitative molecular analysis
LMD was originally developed to facilitate the histochemical analysis of tissue sections (8). Correspondingly, the authors performed enzyme-histotopochemical investigations on N2 laser dissected tissue fragments to assess the quality of the procurement method. They observed a decrease of enzyme activity by 10–20% in a several-microns-thick region bordering the cut when dissection was performed at an energy level four-times larger than that sufficient for cutting. The changes were attributed to heat diffusion from the glass support and characterized as not relevant for subsequent histochemical analysis.
At present, LMD is mostly combined with molecular biological analysis, including polymerase chain reaction (PCR) and micro-arrays for genomic, and mass spectrometry for proteomic, studies. In qualitative and quantitative analysis of gene expression, reverse transcriptase PCR (RT-PCR) plays a prominent role. In principle, the method allows very small numbers of molecules to be detected at extreme sensitivity and high specificity (55), and is therefore the preferred method for the analysis of tiny tissue fragments procured in LMD and LPC. Initially, Schütze and Lahr (4) used formalin-fixed and paraffin-embedded tissue sections supported by a PEN foil, isolated tissue fragments by LMD and LPC, and successfully detected specific messenger-RNA (mRNA) sequences in RT-PCR. Since then, it is known that numerous factors, including fixation, tissue processing, staining and labeling, and probably also laser-dissection, may reduce the content of mRNA in the tissue samples by several orders of magnitude and thus may critically affect quantitative analyses (56,57). A major effect on the mRNA loss can be attributed to chemical fixation in aldehydes and embedding in paraffin, as typically done in histopathology (58,59). As compared to unfixed cryo-sections, this classical tissue processing reduces the mRNA by factors of 85–99% (56,60,61). In addition, conventional staining protocols (e.g., H&E) or immuno-histochemical labeling (e.g., for fluorescence microscopy) also attribute to mRNA loss by factors of up to 99.8% (57). It must be assumed that thermal effects and those evoked by UV light during LMD and LPC can produce some additional damage to the mRNA contained in the isolated samples, but quantitative data on the absolute mRNA loss and on the relative loss compared to the factors mentioned above are still lacking.
The possible extent of thermal and UV light damage depends on the volume fraction of the samples that are exposed to heating or UV irradiation, respectively, and on the degree of exposure. When focused laser pulses are used, this fraction is always small, especially when large specimens are catapulted. When the laser spot size is comparable to the specimen diameter, the biological sample is protected by the supporting polymer foil, as discussed above. However, we saw that moderate defocusing with spot sizes up to one-third of the specimen diameter may involve significant heat and UV exposure even if a polymer foil is used. The maximum likelihood for laser-induced unwanted side effects in both proteomics and genomics arises when histologic material is directly catapulted from glass substrates without supporting polymer foils. This approach is sometimes taken to save processing time or to avoid scattering and fluorescence by the PEN foil that may disturb the identification of the regions of interest. In this case, the dissection step is skipped and a slightly defocused laser beam is scanned across the area to be catapulted, with small distances between the individual laser exposures. Small pieces of the sample are thereby separated from their surroundings and, at the same time, catapulted into the vial for further analysis. With this approach, the area of a piece that can be catapulted by one laser pulse is usually not much larger than the irradiated spot because the ablative pressure at the bottom of the specimen must not only overcome the adhesion of the specimen to the glass slide but also tear the piece off from the rest of the sample. The combination of a large irradiated fraction of the sample volume with the lack of a protecting polymer foil implicates a largely increased exposure to both UV radiation and heat.
Preliminary investigations revealed that mRNA recovery decreases considerably if the material is catapulted from glass without the use of a PEN foil and a preceding dissection step. To compare the two methods, we used cryo-sections which are not altered by fixation, staining, or labeling. Eight samples on PEN foil were processed by dissection of round specimens of 100-μ_m diameter and subsequent catapulting with a single laser pulse, and eight identical samples of the same size were processed without foil in the scanning mode using factory default settings of the instrument. The amount of intact mRNA copies of the housekeeping gene EF1_α remaining in the sample after catapulting was determined using real-time PCR (ABI Prism 7000 Sequence Detection System, Applied Biosystems, Foster City, CA). After catapulting directly from glass, 35.5–40.0 amplification cycles were necessary to achieve a certain signal strength as compared to 26.1–28.2 cycles when a PEN foil was used (unpublished results). Since the amount of genetic material is doubled in each cycle, an increase by one cycle (1 ct unit) corresponds to a loss of 50% specific mRNA in the sample, and an increase of 7–9 ct units indicates a loss of 99.2–99.8% of specific mRNA copies. This value resembles the loss observed otherwise as a consequence of fixation, embedding, and staining.
We conclude that significant side effects may arise when samples are catapulted directly from a glass slide without a supporting polymer foil. Thus there is still a large potential for improving laser-assisted mRNA recovery from cryo-sections.
Potential improvements of microdissection and laser-induced transport
Dissection
Finer dissections than possible with the N2 laser employed in our experiments can be achieved through a reduction of the energy threshold for plasma formation. This can be accomplished by improvements of the laser beam profile and a reduction of the laser pulse duration. The beam profile of diode-pumped frequency-tripled Nd:YAG lasers that are incorporated in the newest generation of most commercial microbeam systems is much better than that of the N2 laser (see Fig. 2). This can lead to a considerable reduction of the focal spot size, optical breakdown energy, and cutting width, provided that the delivery optics to the focusing microscope objective maintains the good beam quality. This goal will not be achieved if the laser beam is simply coupled into the fluorescence beam path that is optimized for homogeneous illumination of the object field but not for focusing of a laser beam. Additional corrections of the spherical aberrations induced in the beam path of the fluorescence illumination are required to provide optimum focusing conditions.
An even larger reduction of the energy threshold for optical breakdown can be reached by employing shorter laser pulse durations (16,62). We observed that a reduction of the pulse duration from 6 ns to 300 fs reduces the breakdown threshold by a factor of ∼100 for UV wavelengths and even more for IR wavelengths. Use of femtosecond lasers thus creates the potential for nanosurgery on a subcellular level ((16) and references therein; (63,64)) and for gentle optotransfection (65). Already a moderate reduction of the laser pulse duration to 500 ps in combination with a good beam profile and the use of UV-A light (λ = 355 nm) made it possible to selectively dissect microtubules in live cells (66).
Especially for pulse durations in the nanosecond range, the use of UV laser pulses seems to be advantageous because the energy threshold for plasma formation decreases with decreasing wavelength. We found that the breakdown threshold for 6-ns pulses measured at NA = 0.9 is 16 times smaller for λ = 355 nm than for λ = 1064 nm (unpublished results). For femtosecond pulses, the breakdown threshold was five-times smaller for λ = 355 nm than for λ = 1064 nm.
When very small single pulse energies are used for dissection, a large number of pulses is necessary to complete a cut of finite length. Therefore, the repetition rate of the laser pulses must be sufficiently large (hundreds of Hertz to kiloHertz) to avoid an impractical prolongation of the processing time.
Laser-induced transport
The use of ultrashort laser pulses may not only improve dissection but also increase the efficiency of catapulting because 1), the linear absorption of the sample is always supplemented by nonlinear mechanisms (photoionization and avalanche ionization); 2), the thermal expansion velocity of a heated sample increases with decreasing laser pulse duration; and 3), for sufficiently short pulses, large thermoelastic stresses are generated, and phase transitions occur at lower temperatures. All mentioned effects reduce the energy threshold for catapulting.
Nonlinear absorption will probably make it easier to catapult specimens directly from a glass slide without the use of a strongly UV absorbing foil, and it permits us to use any desired laser wavelength. Nonlinear absorption eases the energy requirements for catapulting because it reduces the optical penetration depth of the laser light.
We mentioned above that, for catapulting using spot sizes comparable to the specimen size, thermal expansion of the heated specimen may contribute to catapulting. This contribution increases with decreasing pulse duration because the expansion velocity increases (34,36). If the pulse duration becomes sufficiently short for the temperature rise to occur on a timescale shorter than the stress propagation time out of the heated volume (which is also the time required for thermal expansion), large thermoelastic stresses are generated in the layer absorbing the laser energy (24). Under such stress-confinement conditions, part of the laser energy is transformed into elastic energy of the heated sample, and the release of this energy during the subsequent expansion phase results in a considerably larger detachment velocity than mere thermal expansion.
In LPC, the light-absorbing layer is located at the bottom of the specimen that is attached to the supporting glass slide. Therefore, the detachment through thermoelastic mechanisms does not occur immediately but with a certain delay: The compressive wave generated in the absorbing layer first travels to the upper side of the specimen bordered by air. Here it is reflected as a tensile stress wave because the acoustic impedance of air is much smaller than that of the specimen (67). This tensile wave travels back into the sample, and when, after a few nanoseconds, it reaches the interface between sample and supporting substrate, it will induce or facilitate the sample's lift off from the substrate. Moreover, the tensile stress wave will reduce the temperature required for explosive vaporization in the heated layer at the bottom of the sample (16,24). The latter effect increases the driving force of phase transitions involved in catapulting.
For biological materials with a sound velocity similar to that of water (1500 m/s) and for an optical penetration depth of, for example, 1 _μ_m, the stress-confinement condition is fulfilled if the laser pulse duration _t_L ≤ 700 ps. Thus, the degree of stress confinement is small for nanosecond pulses but high for picosecond pulses and very high for femtosecond pulses, and it is therefore expected that the catapulting efficiency is better with picosecond and femtosecond pulses. We were able to catapult histologic specimens 120 _μ_m in diameter using focused IR fs pulses (_t_L = 315 fs, λ = 1040 nm) of only 1.2 _μ_J (unpublished results). The corresponding radiant exposure averaged over the entire specimen area is only 0.01 J/cm2, i.e., one-third of the lowest value achieved with UV nanosecond pulses (Table 2). Laser printing of biomaterial with femtosecond-pulses has been demonstrated (68), and it was shown that the printing process has a better forward directionality with femtosecond-pulses than with nanosecond-pulses (69).
It would be desirable to establish catapulting techniques for histologic samples that do not require a UV absorbing polymer foil because the foil scatters and fluoresces (see Fig. 5 B) and thus impairs histological and fluorescence identification techniques for cells of interest. However, it does not help to simply omit the foil because a narrow grid of laser spots is required to catapult the specimens directly from a glass slide, which considerably increases the amount of UV-light-induced and thermal damage. Therefore, new types of dynamic release layers allowing for gentle catapulting will have to be explored. This research may profit from previous experience gathered in the field of laser color printing (70), laser-induced forward transfer using dynamic release layers (71), laser printing of biomaterials (72), laser cleaning (35), polymers especially designed for laser ablation (73), and other fields of laser-mediated mass transfer (53,74–77).
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
[Supplement]
Acknowledgments
We appreciate stimulating discussions with Karin Schütze and Bernd Sägmüller of PALM-Microlaser Technologies. The laser beam profiles of Fig. 3 were measured by Carsten Lüthy (PALM), and the thermal properties of polymer foils and histologic specimens quoted in Fig. 4 and Table 1 were determined by Christine Mimler (Institut für Werkstoffwissenschaften, Universität Erlangen-Nürnberg). We thank Ingo Apitz, Pieternel Doeswijk, Nadine Steiner, and Reinhard Schulz of the Institute of Biomedical Optics, University of Lübeck, for technical assistance.
This work was sponsored by the German Bundesministerium für Bildung und Forschung under grant No. 13N8461, and, in parts, by US Air Force Office of Scientific Research under grant No. FA8655-02-1-3047. PALM Microlaser Technologies provided the microbeam system used.
References
- 1.Eltoum, I. A., G. P. Siegal, and A. R. Frost. 2002. Microdissection of histologic sections: past, present, and future. Adv. Anat. Pathol. 9:316–322. [DOI] [PubMed] [Google Scholar]
- 2.Thalhammer, S., G. Lahr, A. Clement-Sengewald, W. M. Heckl, R. Burgemeister, and K. Schütze. 2003. Laser microtools in cell biology and molecular medicine. Laser Phys. 13:681–691. [Google Scholar]
- 3.Kehr, J. 2003. Single cell technology. Curr. Opin. Plant Biol. 6:617–621. [DOI] [PubMed] [Google Scholar]
- 4.Schütze, K., and G. Lahr. 1998. Identification of expressed genes by laser-mediated manipulation of single cells. Nat. Biotechnol. 16:737–742. [DOI] [PubMed] [Google Scholar]
- 5.Schütze, K., H. Pösl, and G. Lahr. 1998. Laser micromanipulation systems as universal tools in molecular biology and medicine. Cell. Mol. Biol. 44:735–746. [PubMed] [Google Scholar]
- 6.Elvers, D., L. Remer, N. Arnold, and D. Bäuerle. 2005. Laser microdissection of biological tissues: process optimization. Appl. Phys. A. 80:55–59. [Google Scholar]
- 7.Isenberg, G., W. Bielser, W. Meier-Ruge, and E. Remy. 1976. Cell surgery by laser micro-dissection: a preparative method. J. Microsc. 107:19–24. [DOI] [PubMed] [Google Scholar]
- 8.Meier-Ruge, W., W. Bielser, E. Remy, F. Hillenkamp, R. Nitsche, and R. Unsöld. 1976. The laser in the Lowry technique for microdissection of freeze-dried tissue slices. Histochem. J. 8:387–401. [DOI] [PubMed] [Google Scholar]
- 9.Sheffield, S. A., J. W. Rogers, and J. N. Castaneda. 1986. Velocity measurements of laser-driven flyers backed by high impedance windows. In Shock Waves in Condensed Matter. Y. M. Gupta, editor. Plenum Press, New York and London.
- 10.Phipps, C. R., T. P. Turner, R. F. Harrison, G. W. York, W. Z. Osborne, G. K. Anderson, X. F. Corlis, L. C. Haynes, H. S. Steele, K. C. Spicochi, and T. R. King. 1988. Impulse coupling to targets in vacuum by KrF, HF and CO2 lasers. J. Appl. Phys. 64:1083–1096. [Google Scholar]
- 11.Romain, J. P., and P. Darquey. 1990. Shock waves and acceleration of thin foils by laser pulses in confined plasma interaction. J. Appl. Phys. 68:1926–1928. [Google Scholar]
- 12.Fabbro, R., J. Fournier, P. Ballard, D. Devaux, and J. Virmont. 1990. Physical study of laser-produced plasma in confined geometry. J. Appl. Phys. 68:775–784. [Google Scholar]
- 13.Lahr, G. 2000. RT-PCR from archival single cells is a suitable method to analyze specific gene expression. Lab. Invest. 80:1477–1479. [DOI] [PubMed] [Google Scholar]
- 14.Greulich, K. O., and G. Pilarczyk. 1998. Laser tweezers and optical microsurgery in cellular and molecular biology. Working principles and selected applications. Cell. Mol. Biol. 44:701–710. [PubMed] [Google Scholar]
- 15.Venugopalan, V., A. Guerra, K. Nahen, and A. Vogel. 2002. The role of laser-induced plasma formation in pulsed cellular microsurgery and micromanipulation. Phys. Rev. Lett. 88:078103. [DOI] [PubMed] [Google Scholar]
- 16.Vogel, A., J. Noack, G. Hüttmann, and G. Paltauf. 2005. Mechanisms of femtosecond laser nanosurgery of cells and tissues. Appl. Phys. B. 81:1015–1047. [Google Scholar]
- 17.Hopp, B., T. Smausz, N. Kresz, N. Barna, Z. Bor, L. Kolozsvari, D. B. Chrisey, A. Szabo, and A. Nogradi. 2005. Survival and proliferative ability of various living cell types after laser-induced forward transfer. Tissue Eng. 11:1817–1823. [DOI] [PubMed] [Google Scholar]
- 18.Siegmann, A. E., M. W. Sasnett, and T. F. Johnston, Jr. 1991. Choice of clip levels for beam width measurements using knife-edge techniques. IEEE J. Quantum Electron. 27:1098–1104. [Google Scholar]
- 19.Vogel, A., I. Apitz, S. Freidank, and R. Dijkink. 2006. Sensitive high-resolution white-light Schlieren technique with large dynamic range for the investigation of ablation dynamics. Opt. Lett. 31:1812–1814. [DOI] [PubMed] [Google Scholar]
- 20.Landau, L. D., and E. M. Lifschitz. 1987. Fluid Mechanics, 2nd Ed. Pergamon Press, Oxford.
- 21.Jiménez, J. L., G. del Valle, and I. Campos. 2005. A canonical treatment of some systems with friction. Eur. J. Phys. 26:711–725. [Google Scholar]
- 22.Dingus, R. S. 1992. Laser-induced contained vaporization in tissue. Proc. SPIE. 1646:266–274. [Google Scholar]
- 23.Dingus, R. S. 1993. Momentum induced by laser-tissue interaction. Proc. SPIE. 1882:399–411. [Google Scholar]
- 24.Vogel, A., and V. Venugopalan. 2003. Mechanisms of pulsed laser ablation of biological tissues. Chem. Rev. 103:577–644. [DOI] [PubMed] [Google Scholar]
- 25.Litjens, R. A. J., T. I. Quickenden, and C. G. Freeman. 1999. Visible and near-ultraviolet absorption spectrum of liquid water. Appl. Opt. 38:1216–1223. [DOI] [PubMed] [Google Scholar]
- 26.Oraevsky, A. A., S. L. Jacques, G. H. Pettit, I. S. Saidi, F. K. Tittel, and P. D. Henry. 1992. XeCl laser ablation of atherosclerotic aorta: optical properties and energy pathways. Lasers Surg. Med. 12:585–597. [DOI] [PubMed] [Google Scholar]
- 27.Vogel, A., S. Busch, and U. Parlitz. 1996. Shock wave emission and cavitation bubble generation by picosecond and nanosecond optical breakdown in water. J. Acoust. Soc. Am. 100:148–165. [Google Scholar]
- 28.Anderholm, N. C. 1970. Laser-generated stress waves. Appl. Phys. Lett. 16:113–115. [Google Scholar]
- 29.Ashkin, A. 1986. Observation of a single beam gradient force trap for dielectric particles. Opt. Lett. 11:288–290. [DOI] [PubMed] [Google Scholar]
- 30.Schütze, K., and A. Clement-Sengewald. 1994. Catch and move—cut or fuse. Nature. 368:667–668. [DOI] [PubMed] [Google Scholar]
- 31.Greulich, K. O. 1999. Micromanipulation by Light in Biology and Medicine. Birkhäuser, Basel, Boston, Berlin.
- 32.Stolarski, J., J. Hardman, C. G. Bramlette, G. D. Noojin, R. J. Thomas, B. A. Rockwell, and W. P. Roach. 1995. Integrated light spectroscopy of laser-induced breakdown in aqueous media. Proc. SPIE. 2391:100–109. [Google Scholar]
- 33.Apitz, I., and A. Vogel. 2005. Material ejection in nanosecond Er:YAG laser ablation of water, liver, and skin. Appl. Phys. A. 81:329–338. [Google Scholar]
- 34.Tam, A. C., W. P. Leung, W. Zapka, and W. Ziemlich. 1992. Laser-cleaning techniques for removal of surface particulates. J. Appl. Phys. 71:3515–3523. [Google Scholar]
- 35.Luk'yanchuk, B., editor. 2002. Laser Cleaning. World Scientific Publishing, Singapore.
- 36.Arnold, N. 2002. Dry laser cleaning of particles by nanosecond pulses: theory. In Laser Cleaning. B. Luk'yanchuk, editor. World Scientific Publishing, Singapore.
- 37.Vogel, A., P. Schweiger, A. Frieser, M. Asiyo, and R. Birngruber. 1990. Intraocular Nd:YAG laser surgery: light-tissue interaction, damage range, and reduction of collateral effects. IEEE J. Quantum Electr. 26:2240–2260. [Google Scholar]
- 38.Niemz, M. H., E. G. Klancnik, and J. F. Bille. 1991. Plasma-mediated ablation of corneal tissue at 1053 nm using a Nd:YLF oscillator/regenerative amplifier laser. Lasers Surg. Med. 11:426–431. [DOI] [PubMed] [Google Scholar]
- 39.Freund, D. E., R. L. McCally, R. A. Farrell, and D. H. Sliney. 1996. A theoretical comparison of retinal temperature changes resulting from exposure to rectangular and Gaussian beams. Lasers Life Sci. 7:71–89. [Google Scholar]
- 40.Carslaw, H. S., and J. C. Jaeger. 1959. Conduction of Heat in Solids, 2nd Ed. Oxford University Press, Oxford.
- 41.Pearce, J., and S. Thomsen. 1995. Rate process analysis of thermal damage. In Optical-Thermal Response of Laser-Irradiated Tissue. A. J. Welch and M. Van Germert, editors. Plenum Press, New York.
- 42.Huettmann, G., and R. Birngruber. 1999. On the possibility of high-precision photothermal microeffects and the measurement of fast thermal denaturation of proteins. IEEE J. Sel. Topics Quantum Electron. 5:954–962. [Google Scholar]
- 43.Simanowskii, D. M., M. A. Mackanos, A. R. Irani, C. E. O'Connell-Rodwell, C. H. Contag, H. A. Schwettman, and D. V. Palanker. 2005. Cellular tolerance to pulsed hyperthermia. Phys. Rev. E. 74:011915. [DOI] [PubMed] [Google Scholar]
- 44.Nahen, K., and A. Vogel. 1996. Plasma formation in water by picosecond and nanosecond Nd:YAG laser pulses. Part II. Transmission, scattering, and reflection. IEEE J. Sel. Top. Quant. Electron. 2:861–871. [Google Scholar]
- 45.Vogel, A., J. Noack, K. Nahen, D. Theisen, S. Busch, U. Parlitz, D. X. Hammer, G. D. Nojin, B. A. Rockwell, and R. Birngruber. 1999. Energy balance of optical breakdown in water at nanosecond to femtosecond timescales. Appl. Phys. B. 68:271–280. [Google Scholar]
- 46.Coohill, T. P. 2002. Uses and effects of ultraviolet radiation on cells and tissues. In Lasers in Medicine. R. W. Waynant, editor. CRC Press, Boca Raton, London, New York, Washington, DC.
- 47.de With, A., and K. O. Greulich. 1995. Wavelength dependence of laser-induced DNA damage in lymphocytes observed by single-cell gel electrophoresis. J. Photochem. Photobiol. B Biol. 30:71–76. [DOI] [PubMed] [Google Scholar]
- 48.Tyrrell, R. M., and S. M. Keyse. 1990. The interaction of UVA radiation with cultured cells. J. Photochem Photobiol. B Biol. 4:349–361. [DOI] [PubMed] [Google Scholar]
- 49.Bertling, C. D., F. Lin, and A. W. Girotti. 1996. Role of hydrogen peroxide in the cytotoxic effects of UVA/B radiation on mammalian cells. J. Photochem. Photobiol. 64:137–142. [DOI] [PubMed] [Google Scholar]
- 50.Hockberger, P. E., T. A. Skimina, V. E. Centonze, C. Lavin, S. Chu, S. Dadras, J. K. Reddy, and J. G. White. 1999. Activation of flavin-containing oxidases underlies light-induced production of H2O2 in mammalian cells. Proc. Natl. Acad. Sci. USA. 96:6255–6260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mayer, A., M. Stich, D. Brocksch, K. Schütze, and G. Lahr. 2002. Going in vivo with laser microdissection. Methods Enzymol. 356:25–33. [DOI] [PubMed] [Google Scholar]
- 52.Stich, M., S. Thalhammer, R. Burgemeister, G. Friedemann, S. Ehnle, C. Lüthy, and K. Schütze. 2003. Live cell catapulting and recultivation. Pathol. Res. Pract. 199:405–409. [DOI] [PubMed] [Google Scholar]
- 53.Barron, J. A., P. Wu, H. D. Ladouceur, and B. R. Ringeisen. 2004. Biological laser printing: a novel technique for creating heterogeneous three-dimensional cell patterns. Biomed. Microdev. 6:139–147. [DOI] [PubMed] [Google Scholar]
- 54.Lokhandwalla, M., and B. Sturtevant. 2001. a. Mechanical hemolysis in shock wave lithotripsy (SWL): I. Analysis of cell deformation due to SWL flow-fields. Phys. Med. Biol. 46:413–437. [DOI] [PubMed] [Google Scholar]
- 55.Bustin, S. A. 2000. Absolute quantification of mRNA using real-time reverse transcription polymerase chain reaction assays J. Mol. Endocrinol. 25:169–193. [DOI] [PubMed] [Google Scholar]
- 56.Von Smolinski, D., I. Leverkoehne, G. von Samson-Himmelstjerna, and A. D. Gruber. 2005. Impact of formalin-fixation and paraffin-embedding on the ratio between mRNA copy numbers of differently expressed genes. Histochem. Cell Biol. 124:177–188. [DOI] [PubMed] [Google Scholar]
- 57.Von Smolinski, D., M. Blessenohl, C. Neubauer, K. Kalies, and A. Gebert. 2006. Validation of a novel ultra-short immuno-labeling method for high quality mRNA preservation in laser microdissection and real-time RT-PCR. J. Mol. Diagn. 8:246–253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Krafft, A. E., B. W. Duncan, K. E. Bijwaard, J. K. Taubenberger, and J. H. Lichy. 1997. Optimization of the isolation and amplification of RNA from formalin-fixed, paraffin-embedded tissue. The Armed Forces Institute of Pathology Experience and Literature Review. Mol. Diagn. 2:217–230. [DOI] [PubMed] [Google Scholar]
- 59.Stanta, G., and C. Schneider. 1991. RNA extracted from paraffin-embedded human tissues is amenable to analysis by PCR amplification. Biotechniques. 11:304–308. [PubMed] [Google Scholar]
- 60.Lewis, F., N. J. Maughan, V. Smith, K. Hillan, and P. Quirke. 2001. Unlocking the archive–gene expression in paraffin-embedded tissue. J. Pathol. 195:66–71. [DOI] [PubMed] [Google Scholar]
- 61.Abrahamsen, H. N., T. Steiniche, E. Nexo, S. J. Hamilton-Dutoit, and B. S. Sorensen. 2003. Towards quantitative mRNA analysis in paraffin-embedded tissues using real-time reverse transcriptase-polymerase chain reaction: a methodological study on lymph nodes from melanoma patients. J. Mol. Diagn. 5:34–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Vogel, A., K. Nahen, and D. Theisen. 1996. Plasma formation in water by picosecond and nanosecond Nd:YAG laser pulses. Part I. Optical breakdown at threshold and superthreshold irradiance. IEEE J. Sel. Top. Quant. Electron. 2:847–860. [Google Scholar]
- 63.König, K., I. Riemann, P. Fischer, and K. Halbhuber. 1999. Intracellular nanosurgery with near infrared femtosecond laser pulses. Cell. Mol. Biol. 45:195–201. [PubMed] [Google Scholar]
- 64.Yanik, M. F., H. Cinar, H. N. Cinar, A. D. Chisholm, Y. Jin, and A. Ben-Yakar. 2004. Functional regeneration after laser axotomy. Nature. 432:822. [DOI] [PubMed] [Google Scholar]
- 65.Tirlapur, U. K., and K. König. 2002. Targeted transfection by femtosecond laser. Nature. 418:290–291. [DOI] [PubMed] [Google Scholar]
- 66.Colombelli, J., E. G. Reynaud, J. Rietdorf, R. Pepperkork, and E. H. K. Stelzer. 2005. Pulsed UV laser nanosurgery: retrieving the cytoskeleton dynamics in vivo. Traffic. 6:1093–1102. [DOI] [PubMed] [Google Scholar]
- 67.Paltauf, G., and P. Dyer. 2003. Photomechanical processes and effects in ablation. Chem. Rev. 103:487–518. [DOI] [PubMed] [Google Scholar]
- 68.Zergioti, I., A. Karaiskou, D. G. Papazoglou, C. Fotakis, M. Kapsetaki, and D. Kafetzopoulos. 2005. Femtosecond laser microprinting of biomaterials. Appl. Phys. Lett. 86:163902. [Google Scholar]
- 69.Zergioti, I., D. G. Papzoglou, A. Karaiskou, C. Fotakis, E. Gamaly, and A. Rode. 2003. A comparative Schlieren imaging study between ns and sub-ps laser forward transfer of Cr. Appl. Surf. Sci. 208–209:177–180. [Google Scholar]
- 70.Tolbert, W. A., I. Y. S. Lee, M. M. Doxtader, E. W. Ellis, and D. D. Dlott. 1993. High-speed color imaging by laser ablation transfer with a dynamic release layer: fundamental mechanisms. J. Imaging Sci. Technol. 37:411–421. [Google Scholar]
- 71.Bäuerle, D. 2000. Laser Processing and Chemistry. Springer, Berlin, Heidelberg and New York.
- 72.Colina, M., M. Duocastella, J. M. Fernández-Pradas, P. Serra, and J. L. Morenza. 2006. Laser-induced forward transfer of liquids: study of the droplet ejection process. J. Appl. Phys. 99:084909. [Google Scholar]
- 73.Lippert, T., M. Hauer, C. R. Phipps, and A. Wokaun. 2003. Fundamentals and applications of polymers designed for laser ablation. Appl. Phys A. 77:259–264. [Google Scholar]
- 74.Wu, P. K., B. R. Ringeisen, D. B. Krizman, C. G. Frondoza, M. Brooks, D. M. Bubb, R. C. Y. Auyeung, A. Piqué, B. Spargo, R. A. McGill, and D. B. Chrisey. 2003. Laser transfer of biomaterials: matrix-assisted pulsed laser evaporation (MAPLE) and MAPLE Direct Write. Rev. Sci. Instrum. 74:2546–2557. [Google Scholar]
- 75.Chrisey, D. B., A. Piqué, R. A. McGill, J. S. Horwitz, B. R. Ringeisen, D. M. Bubb, and P. K. Wu. 2003. Laser deposition of polymer and biomaterial films. Chem. Rev. 103:553–576. [DOI] [PubMed] [Google Scholar]
- 76.Piqué, A., H. Kim, R. Y. C. Auyeung, and S. A. Mathews. 2006. Use of laser direct write in microelectronics fabrication. In Proc. 4th Int. Congr. Laser Advanced Materials Processing, May 16–19, 2006 Kyoto, Japan (in press).
- 77.Kuchling, H. 2004. Handbook of Physics, 18th Ed. Carl Hanser Verlag, München.
- 78.Neumann, J., and R. Brinkmann. 2005. Boiling nucleation on melanosomes and microbeads transiently heated by nanosecond and microsecond laser pulses. J. Biomed. Opt. 10:024001. [DOI] [PubMed] [Google Scholar]
- 79.Simanowskii, D., M. Sarkar, A. Irani, C. O'Connell-Rodwell, C. Contag, A. Schwettman, and D. Palanker. 2005. Cellular tolerance to pulsed heating. Proc. SPIE. 5695:254–259. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
[Supplement]