Calculation of Free Energy Barriers to the Fusion of Small Vesicles (original) (raw)

Abstract

The fusion of small vesicles, either with a planar bilayer or with one another, is studied using a microscopic model in which the bilayers are composed of hexagonal- and lamellar-forming amphiphiles. The free energy of the system is obtained within the self-consistent field approximation. We find that the free energy barrier to form the initial stalk is hardly affected by the radius of the vesicle, but that the barrier to expand the hemifusion diaphragm and form a fusion pore decreases rapidly as the radius decreases. As a consequence, once the initial barrier to stalk formation is overcome, one which we estimate at 13 k_B_T for biological membranes, fusion involving small vesicles should proceed with little or no further input of energy.

Introduction

Membrane fusion is a critical event in many biological processes such as viral infection, cellular trafficking, and neurotransmitter release. It is widely accepted that fusion proceeds through an intermediate, called a “stalk,” which is formed when hydrophobic tails from two apposing membranes come into contact via a fluctuation and make a hydrophobic bridge between them. In the standard stalk mechanism, first proposed by Kozlov and Markin (1), the stalk expands radially or, equivalently, the two cis leaves of the original bilayers recede. This leaves a hemifusion diaphragm consisting of the two trans leaves of the bilayers. When a hole forms in this diaphragm, a fusion pore is formed and the process is essentially complete. An alternative path that begins with a stalk has also been proposed (2,3) and observed in simulations (2–7) along with the standard one. In this mechanism, the stalk elongates around a hole that had formed in one or both of the bilayers next to it. When the hole is completely surrounded by the elongated stalk, the resulting structure resembles a hemifusion diaphragm, which can rupture to form a fusion pore. In microscopic studies of fusion barriers, the barrier energies of the standard and alternative mechanisms are found to be comparable (8,9).

As membranes are brought in proximity to each other, water is expelled from the space between them and consequently their free energy per unit area increases; that is, they are placed under tension. Fusion, a process that reduces area, is one possible response to this tension. During this process, lipids must necessarily rearrange, and the resulting deformation of the membranes gives rise to a free energy barrier. The capacity of membranes for such deformation depends on such factors as their lipid architecture, membrane composition, and intermembrane distance, among others. Since fusion intermediates such as the stalk and hemifusion diaphragm are curved structures, membranes that consist of hexagonal-forming lipids, such as the phosphatidylethanolamines, are expected to fuse more readily than those containing lamellar-forming lipids, such as the phosphatidylcholines. We have shown that the addition of hexagonal formers, especially in the cis leaflets, greatly reduces the barrier energies of the process (9), thus making the process more likely. This is in agreement with experiment (10–13).

The theoretical works cited above, like most others on the free energy barriers to fusion, consider the fusion of two planar bilayers. This is reasonable given that the region actively undergoing fusion is presumably much smaller than the characteristic size of the vessels to be fused. A significant exception to this is the fusion of a synaptic vesicle with the plasma membrane. While the latter can be modeled as flat, a synaptic vesicle is small, with a radius typically of ∼25 nm, but which can be as small as 14 nm (14,15). This is only a few times larger than the vesicle's bilayer thickness of 3–4 nm. In such a case, one expects that the small radius, _R_v, of the vesicle increases its free energy per unit area, which is to say that it imparts to it an effective surface tension. Indeed, in phenomenological theories, this effective surface tension would be proportional to 1/Rv2 (16). As the free energy barriers to fusion decrease with increasing tension (17,18), one expects these vesicles to fuse more easily the smaller they are. This is indeed observed in experiment. Lentz et al. (19) studied fusion of model membranes of varying diameters and observed that fusion took place only for highly curved, small unilamellar vesicles, while there was no appreciable mixing of contents for large unilamellar vesicles of the same composition. In a more recent experiment by Martens et al. (20), it was found that synaptotagmin-1 promoted SNARE-mediated fusion of synaptic vesicles. It also induced the formation from bilayers of tubes of radius of ∼9 nm. It was postulated that the promotion of this large curvature was the cause of the enhanced fusion.

There are few theoretical studies (21,22) that consider the effect on the barriers to fusion due to the finite radii of one or both of the fusing vesicles. Both employ free energies in which the elastic energy is supplemented by other phenomenological terms representing work done against hydration and other forces. The fusion of such vesicles has been studied in simulation (5,7,18,23–25) but the manner in which the fusion barriers depend upon the radius of the vesicle has not. The purpose of this work is to elucidate this very question utilizing the field-theoretic methods that we have employed previously (8,9,17,26). We consider both the fusion of a vesicle with a planar bilayer and also the fusion of two vesicles with one another. We find that the increased curvature has little effect on the barrier to produce the initial stalk at a given intermembrane separation, but it significantly reduces the second barrier—that between the expansion of the hemifusion diaphragm and the formation of the pore itself. Thus, once the initial stalk is formed, fusion can proceed readily with little additional energy input.

The model

Our basic assumption is that the self-assembly of lipids into bilayer membranes and various fusion intermediates is common to systems of amphiphiles. Therefore, the choice of a specific amphiphilic system to study theoretically is a matter of convenience. Indeed vesicles composed of diblock copolymers have been shown to exhibit behaviors similar to those of biological membranes (27). Energy scales, of course, are specific to the system. We have shown that the scale in our model of diblocks is smaller by a factor of 2.6 than those characterizing lipid membranes in water (26). We adjust accordingly when explicitly comparing energies to relevant biological processes.

As in our previous calculations, we consider two types of AB diblock copolymers as membrane constituents, and A homopolymers as solvent, all contained in a volume V. The statistical segment length of monomers A and B is assumed to be the same. Each diblock of type 1 is characterized by its molecular volume Nv, where v is the segment volume, and its hydrophilic fraction, _f_1, is arbitrarily chosen to be of type A. Diblocks of type 2 are similarly characterized by the molecular volume α˜Nv, where α˜ denotes the ratio of the type 2 diblock length to the type 1 diblock length. The hydrophilic fraction is _f_2. We set _f_1 = 0.4 and _f_2 = 0.294 as these values produce spontaneous curvatures close to those of dioleoylphosphatidylcholine and dioleoylphosphatidylethanolamine (17). In addition, we set (1−f1)Nv=(1−f2)α˜Nv such that hydrophobic tails of type 1 and 2 amphiphiles are of equal length. For _f_1 = 0.4 and _f_2 = 0.294, α˜=0.85. The characteristic energy between hydrophilic and hydrophobic segments is described by a Flory interaction parameter, χ, which is related to the inverse temperature, 1/T. The solvents are represented by A type homopolymers of volume Nv. As the penetration into the bilayer of the homopolymer solvent varies with its volume, this choice is made to ensure that the penetration occurs primarily in the headgroup region, as shown in Fig. 3 of Katsov et al. (17), and falls rapidly as the hydrophobic region is entered as it should. Lastly, the bulk three-dimensional system is assumed to be incompressible. This does not mean that the bilayer itself cannot be stretched or compressed, but only that any volume changes in the bilayer must be compensated by opposite ones in the surrounding solvent. The model is now completely defined.

Figure 3.

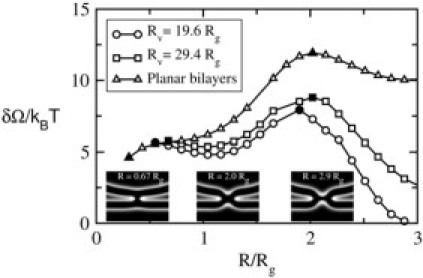
Figure 3

Excess free energy of stalk/hemifusion intermediates for two-component bilayers comprised of lamellar-forming _f_1 = 0.4 and hexagonal-forming _f_2 = 0.294 AB diblocks under zero tension. The upper curve (triangles) is for two planar bilayers, the middle curve (squares) is for a planar bilayer and a vesicle of _R_v = 29.4_R_g, and the bottom (circles) is for a planar bilayer and a vesicle of _R_v = 19.6_R_g. The distance between the two bilayers is H = 1.96_R_g. Solid symbols indicate the first and second barriers for each system. Insets below the curves show density plots of headgroups of a stalk of R = 0.67_R_g at which the first barrier occurs, a hemifusion diaphragm of R = 2.0_R_g at which the second barrier occurs, and a hemifusion diaphragm of the largest radius shown in the plot (R = 2.9_R_g) between a planar bilayer and a vesicle of _R_v = 29.4_R_g.

The free energy of the system of flexible chains with Gaussian chain statistics is easily formulated (28,29) but is too difficult to be evaluated analytically. Hence, we evaluate it within the self-consistent field approximation. Within this formalism the free energy, Ω(T,V,A,ζ1,ζ2,ζs), of the system containing a planar bilayer of area A is given by the minimum of the functional Ω˜,

NvkBTΩ˜=−ζ1Q1−ζ2Q2−ζsQs +∫dr[χNφA(r)φB(r)−wA(r)φA(r) −wB(r)φB(r)−ξ(r)(1−φA(r)−φB(r))], (1)

where _Q_1, _Q_2, and _Q_s are the single chain partition functions of amphiphiles of type 1 and 2 and of solvent molecules, respectively (17). The numbers of these molecules, _n_1, _n_2, and _n_s, is controlled by the activities _ζ_1, _ζ_2, and _ζ_s. Due to the incompressibility condition, only two of them are independent. The local volume fractions _φ_A and _φ_B are the sum of A and B type monomer volume fractions from different types of molecules: _φ_A = _φ_1, A + _φ_2, A + _φ_s, and _φ_B = _φ_1, B + _φ_2, B. The mean fields associated with A and B type monomers which are generated by the approximation are denoted _w_A and _w_B. A Lagrange multiplier ξ(r) enforces the incompressibility constraint at every point in space. These fields, and the Lagrange multiplier ξ(r), are determined by the self-consistent equations which result from minimizing the free energy functional. (See the Appendix.) Insertion of these fields into the free energy functional, Eq. 1, yields the free energy within the self-consistent field approximation,

NvkBTΩ(T,V,A,{ζi})=−ζ1Q1(T,[wA,wB]) −ζ2Q2(T,[wA,wB])−ζsQs(T,[wA]) −∫drχNφA(r)φB(r), (2)

where {_ζ_i} denotes the set of the three activities _ζ_1, _ζ_2, and _ζ_s. The free energy of the system without the bilayer, i.e., a homogeneous solution, is denoted Ω0(T, V, {_ζ_i}). The difference between these two free energies, in the thermodynamic limit of infinite volume, defines the excess free energy of the system:

δΩ(T,A,{ζi})≡limV→∞[Ω(T,V,A,{ζi})−Ω0(T,V,{ζi})]. (3)

With the excess free energy known, the surface free energy per unit area, or equivalently, the surface tension, γ, is obtained from the excess free energy, _δ_Ωbilayer, of a flat bilayer,

γ(T,{ζi})≡limA→∞δΩbilayer(T,A,{ζi})A. (4)

To describe the system containing a planar bilayer and a vesicle in close apposition, we impose additional constraints to specify the location of the hydrophilic/hydrophobic interface of the cis leaflet of the vesicle, r v, and of the planar bilayer, r p, away from their region of contact. These positions are specified as follows. We take the vesicle to be formed by rotating a semicircle about the z axis in a cylindrical coordinate system, and the planar bilayer to be situated perpendicular to the z axis, a distance H from the vesicle, where H is measured between hydrophilic/hydrophobic interfaces of cis leaflets of either bilayer along the z axis. The configuration is depicted in Fig. 1 a. If we choose the midpoint between the vesicle and the planar bilayer to occur at z = 0, ρ = 0, then r p with components (_ρ_p, _θ_p, _z_p) is given by z_p = −_H/2 for all _ρ_p and _θ_p, and the components (_ρ_v, _θ_v, _z_v) of r v are such that rv=ρv2+[Rv−(zv−H/2)]2 for all _θ_v, where _R_v is the distance from the center of the vesicle to the hydrophilic/hydrophobic interface of the outer leaflet of the vesicle. To enforce that the hydrophilic/hydrophobic interface pass through these locations, we employ a Lagrange multiplier λ, so that the free energy functional is now given by

NvΩ˜kBT=−ζ1Q1−ζ2Q2−ζsQs+∫dV[χNφA(r)φB(r)−wA(r)φA(r)−wB(r)φB(r)−ξ(r)(1−φA(r)−φB(r)) −λ[δ(r−rp)+δ(r−rv)](φA(r)−φB(r))]. (5)

To calculate the free energy of fusion intermediates (such as the stalk, hemifusion diaphragm, or fusion pore) as a function of a radius, R, that we stipulate, we must ensure that the hydrophilic/hydrophobic interface pass through this radius. It is defined to be the minimum value of the _ρ_-coordinate of the hydrophilic/hydrophobic interface connecting the cis leaflets of the bilayer and vesicle. Since there is no reflection symmetry about z = 0, the minimum value of ρ does not necessarily occur at z = 0. We found that the z coordinate at which the minimum radius occurs is generally close to _z_m, the midpoint between the unfused vesicle and planar bilayer at fixed ρ = R. Consequently, we use a Lagrange multiplier, ψ, to impose that the hydrophilic/hydrophobic interface pass through the circle defined by ρ = R and z = _z_m (30). It remains only to specify where the hydrophilic/hydrophobic interface in the fusion region is to join up with the locations r p and r v above of the unperturbed planar bilayer and vesicle. We do this by imposing the constraint that the interface pass through r p and r v only in the region ρ ≥ R + _R_c, where _R_c is positive and at least as large as the hydrophilic thickness of the bilayer (see Fig. 1 b). The free energy expression for fusion intermediates is finally given by

NvΩ˜kBT=−ζ1Q1−ζ2Q2−ζsQs+∫dV[χNφA(r)φB(r)−wA(r)φA(r)−wB(r)φB(r)−ξ(r)(1−φA(r)−φB(r))−ψδ(ρ−R)δ(z−zm)(φA(r)−φB(r))−λ[δ(r−rp)+δ(r−rv)]Θ[ρ−(R+Rc)](φA(r)−φB(r))], (6)

where Θ is the Heaviside step function. The requirement that this free energy functional be stationary with respect to variation of the functions _φ_A(r), _φ_B(r), _w_A(r), _w_B(r), and ξ(r) again yields a set of self-consistent equations, Eqs. 10–14 of the Appendix, which are solved in real space to obtain the free energy of the system containing the corresponding intermediate, Ω(T,V,A,{ζi},H,Rv,R). Again, the excess free energy is defined as the difference between this and the free energy of the homogeneous solution

δΩ(T,A,{ζi},H,Rv,R)≡limV→∞[Ω(T,V,A,{ζi},H,Rv,R) −Ω0(T,V,{ζi})]. (7)

To determine the free energy of the intermediate, we calculate the excess free energy of the unperturbed system of bilayer and vesicle of radius _R_v, which are a distance H apart. Denote this excess free energy as δΩunpert(T,A,{ζi},H,Rv). Then the excess free energy of the intermediate of radius R, when the perturbed vesicle of radius _R_v is at the same distance H from the planar bilayer, is given by

δΩint(T,{ζi},H,Rv,R)≡limA→∞[δΩ(T,A,{ζi},H,Rv,R) −δΩunpert(T,A,{ζi},H,Rv)]. (8)

Figure 1.

Figure 1

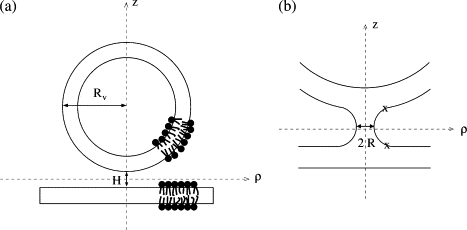
(a) Apposed planar bilayer and vesicle, separated by distance H. The size of the vesicle is measured by the distance, _R_v, from its center to the hydrophilic/hydrophobic interface of the outer leaflet, and H is measured between the hydrophilic/hydrophobic interfaces of cis leaflets at the minimum separation. Only some of the lipids in the bilayers are shown to more easily visualize the location of the hydrophilic/hydrophobic interfaces. (b) Stalk/hemifusion intermediate in the system of planar bilayer and vesicle. The radius R of the intermediate is shown. The X symbols denote the distance R + _R_c beyond which the constraint is imposed that the bilayer and vesicle take their unperturbed locations.

Results and discussion

We first examine the effect of curvature on the barrier energy to membrane fusion for bilayers composed entirely of a lamellar-forming amphiphile with hydrophilic volume fraction f = 0.4. In Fig. 2, we show the characteristic energies of stalk/hemifusion intermediates and fusion pores as a function of R for membrane merger in two systems: one consisting of two planar bilayers, the other consisting of a single planar bilayer and a highly curved vesicle of _R_v = 19.6_R_g. The characteristic size, _R_g, in the polymer system is the radius of gyration of the diblocks of type 1 and of the solvent homopolymers, _R_g = (_Na_2/6)1/2 with a the common statistical segment length of monomers A and B. The bilayers shown here are either under zero applied tension or one of γ = 0.067_γ_0, which corresponds to ∼2.7 mN/m. Such a value is at the lower end of tensions which can cause lysis (31), so that these results span the entire range of relevant applied tensions. Again, _R_v is the distance from the center of the vesicle to the hydrophilic/hydrophobic interface of the outer leaf. If we include the thickness of the hydrophilic headgroups of the outer leaf, measured from the above interface to that at which the headgroup and solvent densities are equal, the radius of the vesicle is ∼20.3_R_g. The thickness of a planar bilayer, measured from the point at which the volume fractions of headgroup and solvent are equal on one side to the other, is 4.3_R_g. Therefore the vesicles with _R_v = 19.6_R_g are characterized by a radius which is approximately five times larger than the planar bilayer thickness. This is reasonable for a highly curved vesicle. The radius of a synaptic vesicle, one of the smallest endocytotic vesicles, can be as small as 14 nm (15), ∼3.5–4.5 times the thickness of the typical membrane thickness of 3–4 nm (32). To highlight the effects of the curvature, we fix the distance between bilayer and vesicle. The value of H chosen is 1.96_R_g, the distance at which a minimum occurs in the free energy between the planar bilayer and the single component vesicle of _R_v = 19.6_R_g. This minimum arises from the attractive depletion force between bilayer and vesicle. We note from the figure that the barrier to make the initial stalk itself is not greatly affected by the curvature of the vesicle. This feature is in agreement with the observations that large membrane curvature does not have a significant effect on the rate of formation of the initial intermediate (19,33), and is one that has not been captured by previous phenomenological calculations (21,22). In contrast, the energy barrier for the stalk to expand and convert to a fusion pore is significantly reduced from the value obtained in the system of two planar bilayers. Assuming that the barrier energy to fusion occurs where the energies of stalk/hemifusion intermediates and of pores are equal, we observe a barrier reduction of ∼5 k_B_T from the fusion of planar membranes to fusion of a planar membrane and a vesicle. This corresponds to 13 k_B_T in a biological system. It should also be noted that there is no metastable stalk in this system. As a consequence, the barrier to fusion is the difference between the free energy at which the pore forms and the free energy of the unperturbed system. Further, fusion along this path would have to occur in a single activated step.

Figure 2.

Figure 2

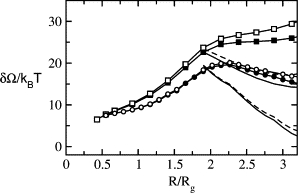
Excess free energy of stalk/hemifusion intermediates and fusion pores for systems comprised of f = 0.4 diblocks. The bilayers here are either under zero tension (open symbols) or an external tension of γ/_γ_0 = 0.067 (solid symbols), with _γ_0 the interfacial tension between coexisting solutions of hydrophobic and hydrophilic homopolymers. The bilayers are separated by H = 1.96_R_g. Squares represent the excess energy of stalk/hemifusion intermediates between two planar bilayers and circles are for stalk/hemifusion intermediates between a planar bilayer and a vesicle of _R_v = 19.6_R_g. The excess energy of fusion pores is represented by either dashed lines (zero tension) or solid lines (γ/_γ_0 = 0.067), of which two upper curves are for pores between two planar bilayers and two lower curves are for pores between a planar bilayer and a vesicle of _R_v = 19.6_R_g.

To model a more realistic membrane composition, we add hexagonal-forming amphiphiles of _f_2 = 0.294 and α˜=0.85 to the bilayers such that the average volume fraction is 0.4. This mimics the approximate composition of lamellar formers and hexagonal formers in the plasma membrane of human red blood cells (34). In Fig. 3, we show the energies of stalk/hemifusion intermediates as a function of their radius R for fusion between two planar bilayers (upper curve), between a planar bilayer and a vesicle of _R_v = 29.4_R_g (middle curve), and _R_v = 19.6_R_g (lower curve). With the size of the headgroup included, these vesicles are of radii which are approximately seven and five times greater than the bilayer thickness, and therefore comparable in size to small synaptic vesicles. The system is under zero applied tension, and the value of H is the same as in Fig. 2. Again, the free energy barrier to create the initial stalk is not greatly affected. The barrier to its formation is ∼6 k_B_T, corresponding to ∼16 k_B_T for a biological system. These barriers are shown by the solid square and circle at R/_R_g ≈ 0.6 for the fusion of the vesicles with _R_v = 29.4_R_g and 19.6_R_g, respectively. However, in the case of fusion of the planar bilayer and this vesicle, the stalk is now a metastable entity, which means that fusion can occur in a two-step process. The increase of free energy as the radius of the stalk decreases from its value at the local minimum is due to the greater crowding of the hydrophobic entities into the increasingly narrow stalk. For very small stalk radii, there are simply no solutions of the self-consistent equations (Eqs. 10–14). Note from the middle and lower curves of the figure, those for the fusion of a vesicle and planar membrane, that the energy to go from the metastable stalk across the maximum to the fusion pore, that is, the second barrier in the process (shown by the solid square and circle at R/_R_g ≈ 2), is now less than the barrier to make the initial stalk itself. Thus, formation of the stalk is now the rate-limiting process. Plots of the headgroup density at the two barriers are shown in the insets together with a similar plot for a well-developed hemifusion diaphragm. Finally one sees that the effect of increasing the curvature of one of the fusing vesicles from zero, that of a planar bilayer, to a value appropriate for a synaptic vesicle, is to reduce markedly the second barrier to fusion, that between the expansion of the hemifusion diaphragm and the formation of the fusion pore. Therefore we expect that fusion between a planar bilayer and a vesicle will take place the more readily the smaller the radius of the vesicle. This is in agreement with experiment (19).

There are several reasons for this behavior. We have already mentioned that a spherical vesicle, even under zero applied tension, will behave as if it were under a tension proportional to 1/Rv2, the square of its curvature. Thus a smaller vesicle, one with larger curvature, behaves as if it were under a larger tension. As we have shown that the second barrier to fusion decreases with increasing tension (17), it is not surprising that this second barrier decreases with increasing curvature. This large effective tension presumably overshadows any actual applied tension, which is why it has so little effect on the results of Fig. 2. The origin of this effective tension is also clear. The system is such that a planar bilayer is a favorable structure. Bending of the bilayer causes the hydrophilic parts of the chains on the inner, concave, leaf to become crowded while those on the outer, convex, leaf become somewhat diluted. Both responses are departures from their preferred configuration (16). One expects that as a result of the curvature, the inverse-hexagonal-forming lipids, component 2, will have a somewhat larger concentration in the concave leaf than when in the planar bilayer. Consequently, the lamellar-forming lipids, component 1, will be slightly concentrated in the outer, convex, leaflet. To verify this, we plot the density profiles of hydrophobic tails of type 1 and 2 amphiphiles in Fig. 4. The one-dimensional density profiles are the result of making a cut parallel to the z axis at different values of ρ, the distance from the axis of symmetry. In the figure they are, from top to bottom, at ρ = 0, 2.45_R_g, and 4.9_R_g. Of the two peaks, that on the right-hand side is for the vesicle and that on the left is for the planar bilayer. For the cut made through ρ = 0, i.e., at the minimum separation distance between the bilayer and the vesicle, we see an elevated density of lamellar formers and reduced density of hexagonal formers at the outer leaflet (cis leaflet) of the vesicle. The local composition of the inner leaflet shows the opposite. Note that these changes in local composition due to the curvature are just the reverse of those which promote fusion (i.e., increased hexagonal formers in the cis leaf). However, the relative change in volume fraction is small as the amphiphiles tend to distribute evenly throughout the membrane to maximize their entropy of mixing. Thus, this change in local composition does not overwhelm the primary effect of the curvature, which is to promote fusion.

Figure 4.

Figure 4

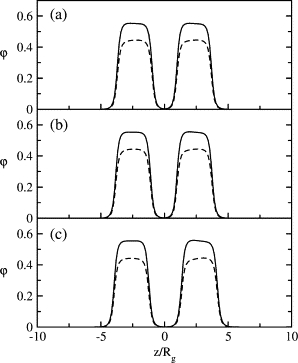
Density profiles of hydrophobic tails of lamellar formers (solid curve) and hexagonal formers (dashed curve) in apposed planar bilayer and vesicle of _R_v = 19.6_R_g along (a) ρ = 0, (b) ρ = 2.45_R_g, and (c) ρ = 4.9_R_g. The planar bilayer is on the left.

A second effect which tends to lower the initial barrier to create a stalk is that the distance at which the minimum free energy occurs in the system of a vesicle and planar bilayer is smaller than the analogous distance between two planar bilayers. This comes about simply because the distance between vesicle and plane increases as one moves away from the point of closest approach and hence the repulsion decreases. In particular, the distance at which the minimum free energy occurs for two planar bilayers of the composition used above is _H_min = 2.2_R_g, while that for a planar bilayer and a vesicle of _R_v = 19.6_R_g of the same composition is _H_min = 1.7_R_g. As the barrier to make the initial stalk increases with its length (26), that between the vesicle and planar bilayer is somewhat less than the barrier to make the initial stalk between planar bilayers.

Lastly, we have examined the fusion between two vesicles of the same radius. The problem is a simpler one because of the reflection symmetry about the z = 0 plane. From the above, we would expect that the second barrier to fusion in this case would be reduced from that in the system of one vesicle fusing with a planar bilayer. That is indeed the case. Whereas the middle curve of Fig. 3 showed the free energies of intermediates in the fusion of a planar bilayer and a vesicle of radius _R_v = 19.6_R_g, the upper curve of Fig. 5 shows the analogous results for the fusion of two such vesicles. Note that the second barrier, that between the metastable stalk and the formation of the fusion pore, is now very small. One would expect that in the fusion of two similar, but even smaller, vesicles, this second barrier would disappear completely. That this is correct is shown in Fig. 5 where we have plotted the free energy of the intermediates in the fusion of vesicles characterized by a distance from their center to the hydrophobic/hydrophilic interface of _R_v equal to 19.6_R_g, 17.2_R_g, 14.8_R_g, and 7.4_R_g. In agreement with the phenomenological calculations of Malinin and Lentz (22), there is a dramatic decrease in the barrier between the initial stalk and the expansion and conversion to a pore with increasing curvature. However, the effect is much larger in our calculation. Indeed the difference between the two barriers vanishes for vesicles of radius 19.6 _R_g measured to the hydrophilic/hydrophobic interface. When the additional thickness of the hydrophilic headgroups is included, the radius of this vesicle is ∼20 _R_g. Given that our bilayers are of thickness 4.3_R_g from headgroup to headgroup, and that typical bilayers are on the order of 4 nm, the radius of this vesicle would correspond to ∼19 nm. The vanishing of the difference between barriers at such a radius is in nice agreement with the observation of Lentz and Lee (35) that the barriers to these two intermediates are equal in the fusion of vesicles of radius of 22.5 nm. As a further note, the absolute value of the barriers as calculated here are smaller than those obtained in the phenomenological calculations of the literature (21,22) by factors ranging from 2 to 10.

Figure 5.

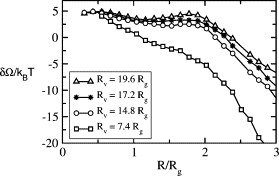
Figure 5

Free energies of fusion intermediates in the fusion of identical vesicles. From top to bottom, the radii are 19.6_R_g, 17.2_R_g, 14.8_R_g, and 7.4_R_g.

The smallest vesicles considered above, those with a distance to the hydrophilic/hydrophobic interface of _R_v = 7.4_R_g, or a radius of ∼8.1 _R_g when the headgroups are included, correspond to vesicles with a diameter of ∼17 nm. This is approximately the diameter of the lipid tubes that were caused to form by synaptotagmin in recent experiments (20). From Fig. 5, one sees that once the barrier to the formation of a stalk between two small vesicles is overcome, a barrier we estimate at ∼13 k_B_T in a biological membrane, hemifusion expansion, and pore formation can occur without further energy input.

Acknowledgments

This work was supported by the National Science Foundation under grant No. DMR-0503752 and by the U.S.-Israel Binational Science Foundation under grant No. 287/02.

Footnotes

Appendix: Model parameters

As noted earlier, our model has been completely specified. It contains several parameters. They are the strength of the repulsive interaction between A and B monomers, χ, the polymerization index, N, the ratio, α˜, of the molecular volumes of diblock 2 to diblock 1, the polymer segment volume, v, and the statistical segment lengths _a_A = _a_B, which have been set equal to one another, a. More generally, they could be taken to differ, but this would simply alter the energies of all quantities (36) and therefore the scaling factor relating the model energies to the biological ones. As the statistical segment lengths are equal, the ratio of the volume fractions and lengths of copolymers 1 and 2 are equal. This leaves us with five parameters to be specified. By measuring all lengths in units of the radius of gyration of polymer 1 and of the homopolymer, _R_g = (_Na_2/6)1/2, we reduce the number of parameters to four. Within the self-consistent field theory, N and χ do not enter the equations independently, but only in the combination χN, so there are only three parameters to specify. We have taken α˜=0.85 so that the tails of the two amphiphiles are of equal length. To compare our results for the polymer system with a previous simulation of such polymers (4), we choose χN = 30. Lastly, the volume of the system is of no interest but rather the free energy per unit volume which depends upon the volume per molecule. Again to make contact with the simulations, we choose V/[(n1+n2+ns)Rg3]=1.54. All parameters are now specified.

The free energy per unit volume depends on the temperature, T, and the number of molecules per unit volume of type 1, _n_1/V, of type 2, _n_2/V, and of solvent, _n_s/V. Equivalently, it depends on the temperature and the three chemical potentials _ζ_1, _ζ_2, and _ζ_3. By measuring all energies in units of k_B_T, we need not specify the temperature. Finally, the condition of bulk incompressibility,

reduces the number of independent chemical potentials to two.

The free energy in the self-consistent field approximation is equal to the minimum of the free energy functional of Eq. 6. This functional is extremized with respect to the five functions _w_A(r), _w_B(r), ζ(r), _φ_A(r), and _φ_B(r), which yields the five equations

wA(r)=χNφB(r)+ξ(r)−ψδ(ρ−R)δ(z−zm) −λ[δ(r−rp)+δ(r−rv)]Θ[ρ−(R+Rc)], (10)
wB(r)=χNφA(r)+ξ(r)+ψδ(ρ−R)δ(z−zm) +λ[δ(r−rp)+δ(r−rv)]Θ[ρ−(R+Rc)], (11)
φA(r)=δQ1[wA,wB]δwA+δQ2[wA,wB]δwA+δQs[wA,wB]δwA, (13)
φB(r)=δQ1[wA,wB]δwB+δQ2[wA,wB]δwB. (14)

The partition functions are obtained from single-chain propagators in the usual way familiar from polymer physics (28,37). For example, the solvent partition function

where the homopolymer single-chain propagator, _q_h(r, s), satisfies the modified diffusion equation

∂qh(r,s)∂s=Rg2∇2qh(r,s)−wA(r)qh(r,s), (16)

and the boundary condition _q_h(r, s = 0) = 1. Methods for solving these equations are discussed by Fredrickson (28) and by Matsen (29).

References