Closed-loop control of cellular functions using combinatory drugs guided by a stochastic search algorithm (original) (raw)
Abstract
A mixture of drugs is often more effective than using a single effector. However, it is extremely challenging to identify potent drug combinations by trial and error because of the large number of possible combinations and the inherent complexity of the underlying biological network. With a closed-loop optimization modality, we experimentally demonstrate effective searching for potent drug combinations for controlling cellular functions through a large parametric space. Only tens of iterations out of one hundred thousand possible trials were needed to determine a potent combination of drugs for inhibiting vesicular stomatitis virus infection of NIH 3T3 fibroblasts. In addition, the drug combination reduced the required dosage by ≈10-fold compared with individual drugs. In another example, a potent mixture was identified in thirty iterations out of a possible million combinations of six cytokines that regulate the activity of nuclear factor kappa B in 293T cells. The closed-loop optimization approach possesses the potential of being an effective approach for manipulating a wide class of biological systems.
Keywords: combinatory drug therapy, drug cocktail, drug resistance, feedback control, viral infection
Diseases arise from altered cellular functions and activities. Modifying cellular activities by a combination of agonists can lead to an effective strategy for disease therapeutics. A mixture of drugs, in many cases, is more effective than using a single stimulus (1–5). However, the combination of various possible concentrations of a set of agonists creates a large testing parametric space. As such, identifying the optimum combination of multiple drugs to control a complex biological system presents a major challenge (6, 7). Here, we experimentally demonstrate that a closed-loop optimization scheme can serve as an alternative approach to trial and error, which needs to test a large number of all of the possible combinations. The approach suggested in this work effectively searches for potent drug combinations that manipulate the cellular network toward a therapeutic goal.
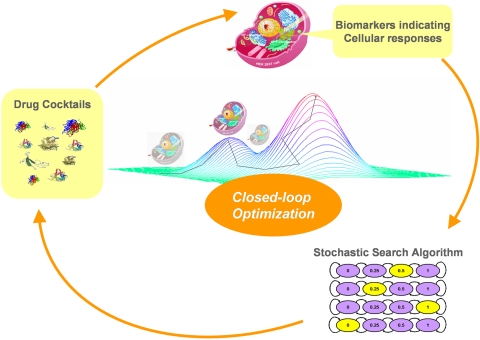
Cellular functions and activities are regulated by complex networks of signaling and regulatory pathways. The current approach aims to circumvent the need for detailed information of biological signaling and regulatory networks. To experimentally implement the closed-loop optimization approach for searching for a potent drug mixture, combinations of cytokines and drugs are applied to stimulate the system of interest. Biomarkers indicating the biological responses of interest, such as viral activity, are then evaluated. Based on the biological responses, a stochastic search algorithm chooses a new drug mixture for the next test. Iteratively, the closed-loop control scheme will drive the systems to desired phenotypic responses (Fig. 1). We have demonstrated that only tens of iterations out of a large number of possible combinations are needed. This effort-saving approach actively manipulates the complex biological systems as a whole, rather than analyzing the processes through individual signaling pathways in a network.
Fig. 1.
Iterative cycle of the closed-loop optimization approach. At each iteration, the cells are stimulated by a drug mixture from a predetermined set of concentrations. The biological activity of interest is then evaluated. The information is then fed into a stochastic search algorithm to determine the drug combination for the next iteration. The cycle repeats iteratively until a potent drug mixture is identified.
The closed-loop control can serve as a generic approach in devising multidrug therapies against wide classes of pathogens and diseases. We have chosen two model systems to explore this closed-loop optimization approach. In the first system, we consider combinations of interferons (IFNs) and antiviral drugs for inhibiting viral activity. Specifically, vesicular stomatitis virus (VSV) infection of NIH 3T3 fibroblasts was used as the model system. Although a combination of cytokines and drugs is known to have a stronger antiviral activity than that from a single agent, the complex interactions among the pathways and the large parametric space constituted by the combinatorial drugs impose a major challenge to identifying potent combinations. In the second system, the activity of nuclear factor kappa B (NF-κB) was chosen as the endpoint. The therapeutic effect of combinatorial cytokines on human embryonic kidney 293T cells was explored by searching for a potent combination of cytokines for maximizing the activity of NF-κB. NF-κB regulates expression of several genes that mediate the inflammatory responses and cell proliferation, and is one of the major therapeutic targets for chronic inflammatory disease and cancer (8, 9).
Results
Stochastic Search Algorithm.
Stochastic search algorithms constitute one of the most effective approaches to solving large-scale combinatorial optimization problems of highly complex systems. Stochastic search algorithms do not require training of data to form a metamodel as in surrogate-based optimization (e.g., neural networks) (10). Therefore, only a small number of experiments is typically required. Simulated annealing (11), genetic algorithms (12), ant colony optimization (13), and Gur Game (14) are some of the well established stochastic search algorithms. These algorithms have been demonstrated in a variety of applications, such as crystal structure predications (11), routing in communication networks (13), and distributed control in robotics (16, 17). These methods have also been applied in computational biology (18) and protein-folding studies (19). A major goal of the current study is to demonstrate the stochastic search approach to find effective drug combinations and to show that fast convergence, that is, a small number of iterations, can be achieved.
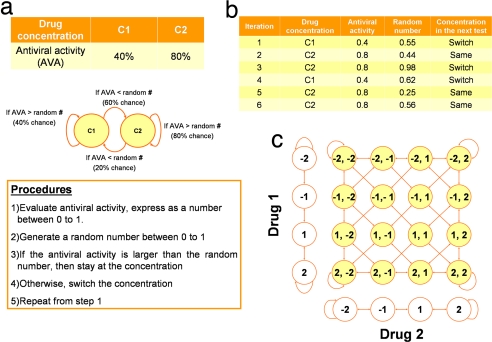
Several stochastic search algorithms can potentially be applied for regulating complex biological systems. In this work, we selected the Gur Game to demonstrate the closed-loop optimization approach. Similar to other stochastic search algorithms, the Gur Game does not require detailed information about the biological system or how the system responds to manipulation of input variables. The property of rapid convergence of the Gur Game is invaluable for experimental manipulation of complex biological systems with a large parametric space. Furthermore, it is robust to random noise and nonlinear changes in the system and the environment, which are commonly observed in a biological system. The Gur Game is based on biased random walks of the input states (drug concentrations) collectively driving the system (a cell) toward higher performance (the biological activity). The principle and implementation of the approach are illustrated by a simplified example of searching antiviral drugs in Fig. 2. More details of the Gur Game are discussed in the supporting information (SI) Appendix.
Fig. 2.
The principle and procedure of the Gur Game are illustrated by searching drugs with potent antiviral activities. The antiviral activity (AVA) refers to the percentage of cells not being infected by the virus. (a) Assume the drug concentrations, C1 and C2, have AVA of 40% and 80%, respectively (Top). The procedure of performing the Gur Game for searching for the best concentration of the antiviral drug is shown in Middle and Bottom. In the experiment, the AVA is first tested and expressed as a number between 0 (0% AVA) and 1 (100% AVA). A random number between 0 and 1 is generated after each test. If the AVA is smaller than the random number, then the concentration will be switched in the next iteration. Otherwise, the drug concentration will stay in the next iteration. In this example, the system has a higher chance to stay at concentration C2 and to switch at concentration C1. This asymmetric decision provides the “bias” of the search that leads the concentration toward high AVA. The random number introduces “randomness” in the decision, because the concentration of the drug may switch even at a high AVA. As a result, the search will not be trapped at a drug concentration of a local maximal biological response. (b) A hypothetical experiment is shown to illustrate the procedure. In this example, it can be proven mathematically that the chance of the system to choose the drug concentration C2 (AVA = 0.8) will be 0.75, whereas the probability of choosing drug concentration C1 (AVA = 0.4) is 0.25 (see SI Appendix). (c) The procedure can be extended to multiple drugs with different concentration levels each. An example of two drugs with four concentrations each is shown. Each drug is assigned with a set of discrete concentrations, represented by −2, −1, 1, and 2. After each experiment, a random number is generated for each drug. If the random number is larger than AVA, the concentration will be switched. Otherwise, the concentration will either stay or be switched in an attempt to further improve the performance (see SI Appendix). The random number introduces randomness in the search and the system collectively “biases” toward drug combinations with potent antiviral effects. Therefore, the procedure implements a “bias random walk” of drug concentrations to search for potent drug cocktails.
Drug Cocktails for the Inhibition of Viral Activity.
We have applied the approach of closed-loop control to search for effective drug combinations for the inhibition of viral activity. VSV infection of NIH 3T3 fibroblasts was used as the model system in this investigation. Several antiviral agents, including IFNα, IFNβ, IFNγ, puromycin, and ribavirin and their combinations, were considered. The virus was genetically engineered with a green fluorescent protein (GFP) reporter for assessing the infection to the host cells (20). Cells were cultured in 96-well plates to 60–80% confluence before the experiment. VSV and drug combinations were applied to the cells at the beginning of each iteration. The percentage of cells expressing GFP were counted and fed into the Gur Game algorithm for determining the drug combination in the next iteration. A new batch of cells was applied for each experiment. In our control experiments, which were performed throughout this investigation, >95% of the cells were infected and expressing GFP when incubated with VSV at a multiplicity of infection of 1 (data not shown). The morphology and doubling rate of the cells were monitored throughout the experiment.
Closed-Loop Optimization of Potent Drug Cocktails.
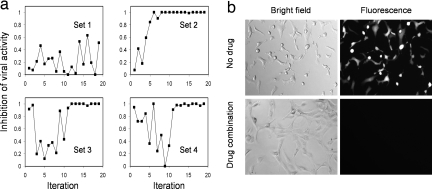
Four sets of experiments were performed in this investigation. All five agents, IFNα, IFNβ, IFNγ, puromycin, and ribavirin, were considered for sets 2 to 4. For set 1, only IFNα, IFNβ, and IFNγ were considered. For set 1 and set 2, six concentrations were assigned for each agent whereas ten concentrations were considered in set 3 and set 4 (see SI Tables 2–5 in SI Appendix). Ten concentrations each of five drugs led to one hundred thousand (105) possible combinations. For set 1 and set 2, initial concentrations were zero for all agents and random initializations were applied for set 3 and set 4. The antiviral activity, which is defined as the percentage of cells not expressing GFP after incubation with VSV for 13 h, was considered as the output biological response for the optimization of the drug mixture. The percentage of cells expressing GFP was counted after incubation with VSV and the drug mixture. According to this information, the Gur Game determined the concentration of each drug for the next iteration (see SI Appendix for details). These processes were repeated during each iteration. In the experiment, set 2 rapidly reached a potent combination that totally inhibited the GFP expression and converged to the solution in less than ten iterations (Fig. 3). This is likely because of the smaller set of concentrations applied in set 2. Similarly, set 3 and set 4 converged to potent combinations that inhibited 100% of viral activity after 12 and 14 iterations, respectively. The results of set 3 are listed in Table 1 to illustrate a typical iteration of the search process. However, set 1 containing only three types of IFN reached a maximum viral inhibition value of ≈0.63, that is, 63% of the cells were not expressing GFP.
Fig. 3.
Optimizing antiviral drug combinations with the Gur Game. Inhibition of viral activity is defined as the percentage of uninfected cells (indicated by GFP expression). (a) Four sets of experiments were performed to determine potent drug cocktails. Set 2 converges in <10 iterations and identifies a potent combination that inhibits the viral activity completely. Set 3 and set 4 converge at the 12th and 14th iteration, respectively. (b) Bright field and fluorescence micrographs of NIH 3T3 cells treated with VSV at 1 multiplicity of infection (moi) with and without the drug combination identified in set 2.
Table 1.
List of drug concentrations and random numbers generated by Gur game in viral inhibition experiment of set 3 test
| Iteration | IFNα, pg/ml | Random no. IFNα | IFNβ, ng/ml | Random no. IFNβ | IFNγ, ng/ml | Random no. IFNγ | Puromycin, μg/ml | Random no. Puromycin | Ribavirin, μg/ml | Random no. Ribavirin | Reward |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 7.8 | 1 | 0.6 | 0.23 | 60 | 0.2 | 1.5 | 0.68 | 6 | 0.28 | 0.92 |
| 2 | 15.6 | 0.06 | 0.3 | 0.5 | 30 | 0.14 | 0.75 | 0.81 | 3 | 0.14 | 0.98 |
| 3 | 32.5 | 0.27 | 0.1 | 0.72 | 10 | 0.26 | 0.25 | 0.13 | 1 | 0.66 | 0.2 |
| 4 | 15.6 | 0.53 | 0.3 | 0.7 | 30 | 0.84 | 0.125 | 0.29 | 3 | 0.33 | 0.4 |
| 5 | 7.8 | 0.15 | 0.6 | 0.86 | 60 | 0.65 | 0 | 0.51 | 1 | 0.13 | 0.12 |
| 6 | 15.6 | 0.96 | 1.2 | 0.72 | 120 | 0.26 | 0.125 | 0.46 | 3 | 0.25 | 0.33 |
| 7 | 7.8 | 0.26 | 0.6 | 0.39 | 250 | 0.55 | 0.25 | 0.88 | 1 | 0 | 0.38 |
| 8 | 3.9 | 0.93 | 1.2 | 0.25 | 120 | 0.71 | 0.75 | 0.28 | 0.5 | 0.59 | 0.21 |
| 9 | 7.8 | 0.04 | 0.6 | 0.11 | 60 | 0.36 | 1.5 | 0.9 | 1 | 0.99 | 0.89 |
| 10 | 3.9 | 0.47 | 0.3 | 0.32 | 30 | 0.55 | 3 | 0.15 | 3 | 0.52 | 0.43 |
| 11 | 7.8 | 0.6 | 0.1 | 0.55 | 60 | 0.57 | 6.25 | 0.65 | 6 | 0.95 | 0.93 |
| 12 | 3.9 | 0.35 | 0.05 | 0.45 | 30 | 0.77 | 12.5 | 0.35 | 12 | 0.59 | 1 |
| 13 | 1.3 | 0.2 | 0 | 0.71 | 10 | 0.24 | 25 | 0.4 | 25 | 0.56 | 1 |
| 14 | 0.65 | 0.79 | 0 | 0.62 | 5 | 0.24 | 50 | 0.16 | 50 | 0.61 | 1 |
| 15 | 0 | 0.53 | 0 | 0.46 | 0 | 0.06 | 50 | 0.28 | 100 | 0.69 | 1 |
| 16 | 0 | 0.76 | 0 | 0.2 | 0 | 0.45 | 50 | 0.51 | 200 | 0.03 | 0.97 |
| 17 | 0 | 0.19 | 0 | 0.24 | 0 | 0.03 | 50 | 0.73 | 200 | 0.4 | 1 |
| 18 | 0 | 0.89 | 0 | 0.21 | 0 | 0.39 | 50 | 0.43 | 200 | 0.19 | 1 |
| 19 | 0 | 0.32 | 0 | 0.36 | 0 | 0.36 | 50 | 0.48 | 200 | 0.49 | 1 |
| 20 | 0 | 0 | 0 | 50 | 200 |
Cytokine Combinations for Activating NF-κB.
To illustrate that the closed-loop control scheme can be applied in different biological systems, we searched for cytokine combinations that regulate NF-κB activity in 293T cells. Six cytokines (TNFα, TNFβ, IL-1α, IL-1β, EGF, and BAFF) were considered for regulating the NF-κB activity. The six stimuli, belonging to three families of cytokines and growth factors, represent various possibilities of pathway interactions: (i) effectors trigger different receptors and mechanisms of a single-pathway component, and/or (ii) parallel pathways are triggered simultaneously, each of which exerts effects on a subsequent phenotype. Tumor necrosis factor (TNF) and interleukin 1 (IL-1) are commonly used for stimulating the NF-κB signal transduction pathway (21). Although TNFα, TNFβ, IL-1α, and IL-1β have similar functions, they are known to have distinct roles in the cellular responses (22). Stimulation with TNFα and IL-1β simultaneously was reported to activate NF-κB (23) and other cellular functions (24) synergistically. The effect of epidermal growth factor (EGF) on NF-κB signaling is cell-type specific. For example, EGF has been reported to up-regulate NF-κB activity in several cell lines that have high levels of EGF receptor expression (25). However, EGF does not enhance NF-κB activity in human microvascular endothelial cells (26) and suppresses oxidant-induced NF-κB activity in intestinal epithelial cells (27). BAFF (B cell-activating factor belonging to the TNF family) has been shown to activate NF-κB by a NF-κB essential modulator (NEMO) (IKKγ) independent pathway in maturing B cells (28). The possible interactions of the six cytokines and the resulting combinatorial effects on NF-κB in 293T cell are not fully understood. In this study, each agonist was assigned 10 discrete concentrations: 0, 0.25, 0.5, 1, 2.5, 5, 10, 25, 50, or 100 ng/ml. The values spanned over three orders of magnitude in concentration. The concentrations were selected to maximize the range to be considered while maintaining acceptable resolution in cytokine concentrations (i.e., the difference between concentrations). The lowest concentration that showed an observable effect was between 0.25 and 1 ng/ml. Concentrations >100 ng/ml resulted in a considerable amount of cytotoxicity and, therefore, were not considered in this study. Ten concentrations each of six cytokines led to one million (106) possible combinations in the search space.
Closed-Loop Optimization of NF-κB Activity.
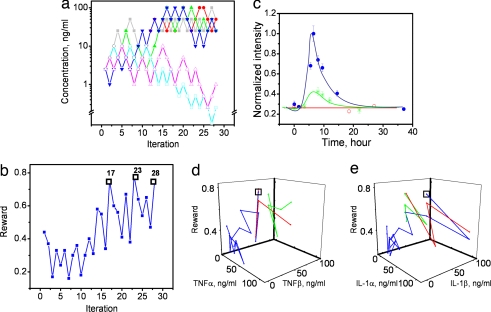
The closed-loop optimization experiment started with choosing a set of cytokine concentrations. Then, the cells cultured inside a microfluidic channel were transiently stimulated with the set of cytokines for one hour. The duration is based on previous reports of the dynamic of NF-κB and selected so that no oscillatory response of the NF-κB will take place (29). The fluorescent light is linearly proportional to the NF-κB expression level (30). The GFP fluorescence intensities of individual cells were recorded seven hours after the stimulation at the peak time point of the fluorescence induction. The average GFP intensity of ≈100 cells was fed to the Gur Game. According to the intensity, the Gur Game determined the concentration of each cytokine for the next iteration. These processes were repeated during each iteration. At the beginning of the experiment, the cytokine concentrations were chosen randomly by the Gur Game to explore cytokine combinations with high NF-κB outputs (Fig. 4 a and b). The system was not trapped by several cytokine combinations with apparently high outputs, e.g., iteration 14. Near iteration 12, the algorithm “detected” a promising trend. Four cytokines (TNFα, TNFβ, IL-1α, and IL-1β) were driven to higher concentrations but the other two (EGF and BAFF) were driven to lower concentrations. At iteration 17, the system determined a potent combination of cytokines for activating the NF-κB. Because of the random walk nature of the Gur Game, the algorithm did not settle with the large performance gains at iteration 17. The most potent cytokine combination was (TNFα = 25 ng/ml, TNFβ = 50 ng/ml, IL-1α = 50 ng/ml, IL-1β = 50 ng/ml, EGF = 2.5 ng/ml, BAFF = 2.5 ng/ml). The random walk nature of the algorithm continually looked for other states with better performance, and the reward function decreased significantly several times during the search. However, the system returned to the similar NF-κB activity at iterations 23 and 28. A comparison between NF-κB activities under stimulation of TNFα and the cytokine combination is shown in Fig. 4c. The searching paths are shown in Fig. 4 d and e.
Fig. 4.
Searching for a cytokine mixture that optimizes NF-κB activity. (a) Concentration of individual cytokines TNFα (gray filled square), TNFβ (red filled circle), IL-1α (green filled triangle), IL-1β (blue inverted triangle), EFG (cyan open square), and BAFF (magenta open triangle) applied at different iterations. The initial concentration of all of the cytokines was 2.5 ng/ml. (b) Normalized GFP intensity at different iterations. Iterations 17, 23, and 28 are labeled with black open squares. (c) Dynamic response of NF-κB activity for cells treated with the cytokine combination (blue filled circle), TNFα 50 ng/ml (green asterisk), and control (red open circle). Data are normalized to the maximum intensity for cells treated with the cytokine combination. Data represent the mean ± SEM from at least 100 cells inside the microfluidic channels. (d) Searching paths for TNFα and TNFβ and (e) searching paths for IL-1α and IL-1β. Black open squares represent cytokine concentrations at iteration 17. Each color represents a particular path.
Discussion
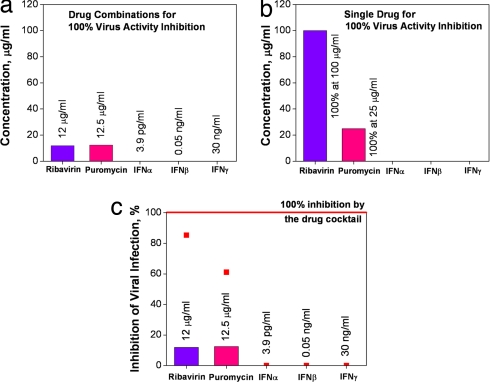
In the viral infection experiment, we have shown that potent drug combinations can be identified rapidly by using a closed-loop optimization approach. With only tens of experiments, potent drug combinations, which can inhibit close to 100% of VSV activity in NIH 3T3 cells, have been identified. The closed-loop optimization scheme not only enhances the antiviral activity of cytokines and drugs, but also minimizes their dosages. To elucidate the effectiveness of drug cocktails, we compared the antiviral activity of a potent drug mixture (IFNα = 3.9 pg/ml; IFNβ = 0.05 ng/ml; IFNγ = 30 ng/ml; puromycin = 12.5 μg/ml; ribavirin = 12 μg/ml) with individual drugs. If a single drug is applied, much higher concentrations are required. Fig. 5a shows the dosages required for completely inhibiting the viral activity by using the potent drug combination. If applied individually, concentrations of 100 μg/ml and 25 μg/ml (Fig. 5b) were required for ribavirin and puromycin, respectively. Interferons were not able to totally inhibit the viral activity in the concentration range tested (up to 10 mg/ml). However, the drug combination identified by the Gur Game reduced the required dosage by 10-fold for individual drug. For example, only 12 μg/ml of ribavirin (Fig. 5a) is needed in combinatory drugs, but 100 μg/ml of rivavirin (Fig. 5b) is needed for single-drug treatment for 100% inhibition of viral infection. Fig. 5c shows the percentage of viral inhibition for applying single drugs at the concentrations in the potent combination. The data indicate the effectiveness of using drug combinations for inhibiting the viral activity. Inhibiting viral activity with low-dosage combinations provides new opportunities in antiviral therapeutics, because high dosage always associates with cytotoxicity and other side effects on biological systems. As shown in Fig. 4c, the activity of NF-κB activated by the drug combination is significantly higher than TNFα, which is a cytokine applied in numerous NF-κB studies. It further indicates that a mixture of drugs is often more effective than using a single stimulus. Furthermore, combinatorial drugs are involved in actions among multiple pathways in the network. The effective closed-loop control scheme may open up a new paradigm for facilitating the study of interactions among the various mechanisms involved.
Fig. 5.
Effectiveness of drug cocktails. (a) Low dosages of combinatory drugs for inhibiting 100% of the virus activity. After optimization, the optimal drug combination contains IFNα and IFNγ with concentrations orders of magnitude smaller than ribavirin and puromycin; therefore, they are not visible in the plot. All of the concentrations are labeled in the plot. (b) When drug is applied individually, a high concentration of ribavirin or puromycin is required to completely inhibit VSV activity. (c) Percentages of inhibition by individual drugs at the concentrations found in the potent drug combination. Red line represents inhibition of viral activity by using the potent drug combination. Red dots present inhibition of viral activity by individual drugs.
In the viral inhibition experiment, set 1 did not converge to a drug combination that can inhibit the viral activity completely. In fact, when the three interferons were used individually, the highest viral inhibition observed in our experimental conditions was ≈15% at 100 ng/ml of IFNβ. The IFN combination identified in iteration 16 of set 1 is (IFNα = 1.3 pg/ml, IFNβ = 1 ng/ml, and IFNγ = 50 ng/ml) and can inhibit >50% of VSV activity. The other three independent tests (set 2, set 3, and set 4) started with very different initial drug combinations, and they all converged to the prevention of the viral infection within 15 iterations. This indicates the rapid convergence of the closed-loop optimization approach for searching for potent drug combinations. This result shows the search scheme can arrive at 100% inhibition with different initial conditions in the viral infection experiment. As reflected by the fast convergence of set 2, fewer concentrations within the range results in fast searching of the space. In general, several parameters should be considered during the experimental design of a Gur Game study. The concentration of the drug and the reward function, that is, the outputs of biomarkers indicating the desired phenotypes, should be adjusted to fine tune the balance between the robustness, converging rate, and the ability to escape from local peaks. In our experiment, we increased the “randomness” with a larger step size to improve the chance for the drug combinations to escape from local optima while maintaining the resolution of the drug concentration. If necessary, multiple experimental investigations can be performed to identify the optimal configuration for the optimization experiment. In the current study, the Gur Game rapidly identifies potent cytokine and drug combinations in the search space in both model systems. In principle, even a larger parametric space, for example, 7, 8, or more cytokines with 107, 108, or more combinations, is expected to achieve a similar rapidly converging rate by using a stochastic search (see also the SI Appendix for further discussion).
The robustness of the approach was also illustrated by the observation that the paths by which the cytokine combinations moved toward the peak were different in the NF-κB experiment (Fig. 4 d and e). The system did not settle with the particular cytokine combination at iteration 17 because of the random walk nature of the Gur Game. The Gur Game continuously searched for other regions in the search space, that is, different combinations of cytokines. The system states moved away and again reached the peak response (iterations 23 and 28) along several different paths, indicating the effectiveness of the search algorithm. Because the Gur Game determines the next states only according to the current states, every iteration can be considered to be an initial search. This resembles the random initialization in other gradient search schemes (15).
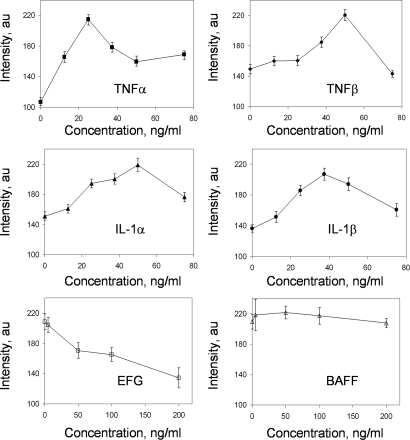
With the potent combination of cytokines efficiently determined by the closed-loop optimization scheme, we then varied the concentration of a specific cytokine while holding others constant to understand the sensitivity of that cytokine and to verify our search result (Fig. 6). TNFα was found to be the most sensitive in the combination in affecting the activity of NF-κB. Elimination of TNFα in the cytokine combination resulted in a ≈50% decrease in fluorescence intensity. Total elimination of any one of TNFβ, IL-1α, or IL-1β resulted in ≈30% decrease in GFP intensity. The effects of IL-1α and IL-1β were not very sensitive to their concentrations in the range of 25–50 ng/ml. When combined with the potent cytokine combination, EGF decreased the NF-κB activity with increasing dose concentration. It should be noted that EGF alone did not show a strong effect on the NF-κB activity in 293T cells (data not shown). For the case of BAFF, it had a minimal effect on NF-κB activity with or without the potent cytokine combination. It was also very interesting to note that the Gur Game suggested lower and lower concentrations of both EGF and BAFF as the iterations proceeded (Fig. 4a). Therefore, the Gur Game algorithm confidently locates the most favorable concentrations for each cytokine, and there is no indication that a more effective combination exists in the entire search space. These data also indicate that the effects of individual cytokines are not additive in the combinatorial tests and the interactions among pathways are nonlinear.
Fig. 6.
Sensitivity analysis of individual cytokines in the potent cytokine combination. Concentrations of TNFα (a), TNFβ (b), IL-1α (c), IL-1β (d), EGF (e), and BAFF (f) were varied while keeping the other cytokine concentrations constant. Data show mean ± SEM of at least 300 cells. Experiments were conducted in 96-well plates. The cells were stimulated with the appropriate concentration of cytokines for one hour and washed with fresh media. Fluorescence measurements were carried out seven hours after stimulations.
With a stochastic search algorithm to use the output information obtained from the biological response, the closed-loop optimization approach can effectively search for a potent drug mixture without the need for detailed information about the effects of each agent on the networks of pathways. We also found that a much lower dosage is required with the drug mixture compared with individual drugs in the viral infection experiment. In addition, new phenomena can be identified for furthering our understanding of the complex nonlinear interactions in a broad class of biological systems with this approach.
Methods
Materials.
Cell culture medium was supplied by Cellgro. Plasmid was purchased from Clontech. Lipofectamine 2000 transfection reagent was purchased from Invitrogen. All other reagents and chemicals were supplied by Sigma unless stated otherwise.
Viral Infection.
GFP-tagged vesicular stomatitis virus (VSV) was prepared by propagation of virus on confluent monolayers of MDCK cells. Supernatant from infected cells were cleared of debris by centrifugation and spun at >100,000 × g through a 25% sucrose cushion by using a Beckman SW28 rotor for 2 h. Virus pellet was gently rinsed and resuspended in PBS. Viral titers were determined by using standard plaque assay procedures on monolayers of MDCK cells. For all experimental infections cells were incubated with viral inoculums at a multiplicity of infection of 1.
Plasmid Construction and Cell Line Establishment.
The expression construct pCEP4-NF-κB-d2EGFP was generated by cutting out the NF-κB-d2EGFP fragment from pNF-κB-d2EGFP vector at BglII and AccI sites and inserting it into pCEP4 vector, which has EBNA-1 and oriP to maintain episomal DNA replication (Invitrogen). pNF-κB-d2EGFP vector has a kappa enhancer element (κB4) located in the promoter region of a d2EGFP reporter gene (a destabilized variant of the enhanced green fluorescent protein with a half-life of 2 h) (30). pCEP4 vector expresses a Hygromycin B drug selection marker. The resulting construct pCEP4-NF-κB-d2EGFP was transfected into human embryonic kidney 293T cells by using Lipofectamine 2000 (Invitrogen) and normal cell culture media supplemented with 200 μg/ml Hygromycin B (Invitrogen) was used to establish the cell line 293T/NF-κB-d2EGFP.
Cell Culture.
293T/NF-κB-d2EGFP cells were grown in DMEM with 10% FBS (Omega), 500 IU/ml Penicillin (Cellgro), 500 μg/ml Streptomycin (Cellgro) supplemented with 200 μg/ml Hygromycin B in 5% CO2 at 37°C. The cells have a doubling time of ≈1 day and we split them every 3–4 days to avoid confluence. For 96-well-plate experiments, cells were cultured in the plate overnight and allowed to reach ≈80% confluence. The cells were stimulated with the appropriate concentration of cytokines for 1 h and washed with fresh media. Fluorescence measurements were performed 7 h after stimulations, when the fluorescence intensity reaches maximum value.
Microfluidics.
A microfluidic platform has been developed to implement the closed-loop optimization approach. Microfluidic channels were fabricated by micromolding of polydimethylsiloxane (PDMS) (Sylgard, 184) on photoresist master. The masters for micromolding were fabricated by photolithography of positive photoresist SJR 5740 (MicroChem, 41001). Three layers of photoresist were spun on the glass substrate to achieve a final thickness of 60 μm. After curing, the PDMS replicas were carefully peeled off from the master. The channels were sealed with a 0.17-mm-thick cover glass. The PDMS replicas and the glass pieces were oxidized for 1 min in a plasma cleaner (Harrick, PDC-001). The two layers were immediately brought into contact to achieve irreversible sealing of the channels.
The microfluidic channel is loaded inside a closed chamber (Instec Inc., HCS60-STC20A) with temperature control, adjusted to 37°C during cell culture experiment. The chamber is supplied with 5% CO2 mixed with air. The diffusivities for O2 and CO2 in PDMS are 4.1 × 10−5 and 2.6 × 10−5 cm2/sec, respectively. More information is available in the SI Appendix.
Supplementary Material
Supporting Information
Acknowledgments.
We thank Dr. Steve Ho for his invaluable suggestions in the implementation of the control algorithm. This work was supported in part by the National Institutes of Health (NIH) through the NIH Roadmap for Nanomedicine (PN2 EY018228) and, in part, by the Institute for Cell Mimetic Space Exploration (CMISE; NCC 2-1364), a National Aeronautics and Space Administration (NASA) University Research, Engineering and Technology Institute (URETI) program.
Footnotes
The authors declare no conflict of interest.
References
- 1.De Francesco R, Migliaccio G. Challenges and successes in developing new therapies for hepatitis C. Nature. 2005;436:953–960. doi: 10.1038/nature04080. [DOI] [PubMed] [Google Scholar]
- 2.Sawyer CL. Mixing cocktails. Nature. 2007;449:993–996. doi: 10.1038/449993a. [DOI] [PubMed] [Google Scholar]
- 3.Izumi Y, Xu L, di Tomaso E, Fukumura D, Jain RK. Tumor biology—Herceptin acts as an anti-angiogenic cocktail. Nature. 2002;416:279–280. doi: 10.1038/416279b. [DOI] [PubMed] [Google Scholar]
- 4.Blakey GE, et al. Pharmacokinetic and pharmacodynamic assessment of a five-probe metabolic cocktail for CYPs 1A2, 3A4, 2C9, 2D6 and 2E1. Br J Clin Pharmacol. 2004;57:162–169. doi: 10.1046/j.1365-2125.2003.01973.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chesney MA, Ickovics J, Hecht FM, Sikipa G, Rabkin J. Adherence: A necessity for successful HIV combination therapy. AIDS. 1999;13:S271–S278. [PubMed] [Google Scholar]
- 6.Dancey JE, Chen HX. Strategies for optimizing combinations of molecularly targeted anticancer agents. Nat Rev Drug Discovery. 2006;5:649–659. doi: 10.1038/nrd2089. [DOI] [PubMed] [Google Scholar]
- 7.Decker S, Sausville EA. Preclinical modeling of combination treatments: Fantasy or requirement? Ann N Y Acad Sci. 2005;1059:61–69. doi: 10.1196/annals.1339.024. [DOI] [PubMed] [Google Scholar]
- 8.Nakanishi C, Toi M. Nuclear factor-kappa B inhibitors as sensitizers to anticancer drugs. Nat Rev Cancer. 2005;5:297–309. doi: 10.1038/nrc1588. [DOI] [PubMed] [Google Scholar]
- 9.Stancovski I, Baltimore D. NF-kappa B activation: The I kappa B kinase revealed? Cell. 1997;91:299–302. doi: 10.1016/s0092-8674(00)80413-4. [DOI] [PubMed] [Google Scholar]
- 10.Queipo NV, et al. Surrogate-based analysis and optimization. Prog Aerospace Sci. 2005;41:1–28. [Google Scholar]
- 11.Pannetier J, Bassasalsina J, Rodriguezcarvajal J, Caignaert V. Prediction of crystal-structures from crystal-chemistry rules by simulated annealing. Nature. 1990;346:343–345. [Google Scholar]
- 12.Forrest S. Genetic algorithms—Principles of natural-selection applied to computation. Science. 1993;261:872–878. doi: 10.1126/science.8346439. [DOI] [PubMed] [Google Scholar]
- 13.Bonabeau E, Dorigo M, Theraulaz G. Inspiration for optimization from social insect behaviour. Nature. 2000;406:39–42. doi: 10.1038/35017500. [DOI] [PubMed] [Google Scholar]
- 14.Tsetlin ML. Finite automata and the modeling of the simplest forms of behavior. Uspekhi Matem Nauk. 1963;8:1–26. [Google Scholar]
- 15.Hartmann AK, Rieger H. Optimization Algorithms in Physics. Berlin: Wiley; 2002. [Google Scholar]
- 16.Tung B. Los Angeles: University of California; 1994. Distributed control using simple automata. PhD dissertation. [Google Scholar]
- 17.Tung B, Kleinrock L. Using finite state automata to produce self-optimization and self-control. IEEE Trans Parallel Distrib Syst. 1996;7:439–448. [Google Scholar]
- 18.Slepchenko BM, Schaff JC, Carson JH, Loew LM. Computational cell biology: Spatiotemporal simulation of cellular events. Annu Rev Biophys Biomol Struct. 2002;31:423–441. doi: 10.1146/annurev.biophys.31.101101.140930. [DOI] [PubMed] [Google Scholar]
- 19.Gillespie B, Plaxco KW. Using protein folding rates to test protein folding theories. Annu Rev Biochem. 2004;73:837–859. doi: 10.1146/annurev.biochem.73.011303.073904. [DOI] [PubMed] [Google Scholar]
- 20.Fernandez M, Porosnicu M, Markovic D, Barber GN. Genetically engineered vesicular stomatitis virus in gene therapy: Application for treatment of malignant disease. J Virol. 2002;76:895–904. doi: 10.1128/JVI.76.2.895-904.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Malinin NL, Boldin MP, Kovalenko AV, Wallach D. MAP3K-related kinase involved in NF-kappa B induction by TNF, CD95 and IL-1. Nature. 1997;385:540–544. doi: 10.1038/385540a0. [DOI] [PubMed] [Google Scholar]
- 22.Siebenlist U, Franzoso G, Brown K. Structure, regulation and function of Nf-Kappa-B. Ann Rev Cell Biol. 1994;10:405–455. doi: 10.1146/annurev.cb.10.110194.002201. [DOI] [PubMed] [Google Scholar]
- 23.Kan H, Xie ZR, Finkel MS. TNF-alpha enhances cardiac myocyte NO production through MAP kinase-mediated NF-kappa B activation. Am J Physiol. 1999;277:H1641–H1646. doi: 10.1152/ajpheart.1999.277.4.H1641. [DOI] [PubMed] [Google Scholar]
- 24.Marcus JS, Karackattu SL, Fleegal MA, Sumners C. Cytokine-stimulated inducible nitric oxide synthase expression in astroglia: Role of Erk mitogen-activated protein kinase and NF-kappa B. Glia. 2003;41:152–160. doi: 10.1002/glia.10168. [DOI] [PubMed] [Google Scholar]
- 25.Biswas DK, Cruz AP, Gansberger E, Pardee AB. Epidermal growth factor-induced nuclear factor kappa B activation: A major pathway of cell-cycle progression in estrogen-receptor negative breast cancer cells. Proc Natl Acad Sci USA. 2000;97:8542–8547. doi: 10.1073/pnas.97.15.8542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Izumi H, et al. Cross-talk of tumor-necrosis-factor-alpha and epidermal growth-factor in human microvascular endothelial-cells. Exp Cell Res. 1994;214:654–662. doi: 10.1006/excr.1994.1303. [DOI] [PubMed] [Google Scholar]
- 27.Banan A, et al. Evidence that nuclear factor-kappa B activation is critical in oxidant-induced disruption of the microtubule cytoskeleton and barrier integrity and that its inactivation is essential in epidermal growth factor-mediated protection of the monolayers of intestinal epithelia. J Pharmacol Exp Ther. 2003;306:13–28. doi: 10.1124/jpet.103.047415. [DOI] [PubMed] [Google Scholar]
- 28.Claudio E, Brown K, Park S, Wang HS, Siebenlist U. BAFF-induced NEMO-independent processing of NF-kappa B2 in maturing B cells. Nat Immunol. 2002;3:958–965. doi: 10.1038/ni842. [DOI] [PubMed] [Google Scholar]
- 29.Hoffmann A, Levchenko A, Scott ML, Baltimore D. The I kappa B-NF-kappa B signaling module: Temporal control and selective gene activation. Science. 2002;298:1241–1245. doi: 10.1126/science.1071914. [DOI] [PubMed] [Google Scholar]
- 30.Li XQ, et al. Generation of destabilized green fluorescent protein transcription reporter. J Biol Chem. 1998;273:34970–34975. doi: 10.1074/jbc.273.52.34970. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information