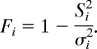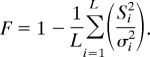Genome-wide assessment of worldwide chicken SNP genetic diversity indicates significant absence of rare alleles in commercial breeds (original) (raw)
Abstract
Breed utilization, genetic improvement, and industry consolidation are predicted to have major impacts on the genetic composition of commercial chickens. Consequently, the question arises as to whether sufficient genetic diversity remains within industry stocks to address future needs. With the chicken genome sequence and more than 2.8 million single-nucleotide polymorphisms (SNPs), it is now possible to address biodiversity using a previously unattainable metric: missing alleles. To achieve this assessment, 2551 informative SNPs were genotyped on 2580 individuals, including 1440 commercial birds. The proportion of alleles lacking in commercial populations was assessed by (1) estimating the global SNP allele frequency distribution from a hypothetical ancestral population as a reference, then determining the portion of the distribution lost, and then (2) determining the relationship between allele loss and the inbreeding coefficient. The results indicate that 50% or more of the genetic diversity in ancestral breeds is absent in commercial pure lines. The missing genetic diversity resulted from the limited number of incorporated breeds. As such, hypothetically combining stocks within a company could recover only preexisting within-breed variability, but not more rare ancestral alleles. We establish that SNP weights act as sentinels of biodiversity and provide an objective assessment of the strains that are most valuable for preserving genetic diversity. This is the first experimental analysis investigating the extant genetic diversity of virtually an entire agricultural commodity. The methods presented are the first to characterize biodiversity in terms of allelic diversity and to objectively link rate of allele loss with the inbreeding coefficient.
Keywords: alleles, biodiversity, poultry
Global production of chickens has experienced massive change and growth over the past 50 years. The commercial broiler and layer markets produce more than 40 billion birds annually to meet current worldwide consumer demands of more than 61 metric tons of meat and more than 55 million metric tons of eggs. In fact, poultry has become the leading meat consumed in the United States and most other countries and is the most dynamic animal commodity in the world; production has increased by 436% since 1970, more than 2.3 times and 7.5 times the corresponding growth in swine and beef, respectively (1). Selection for specific traits by poultry breeders was the key factor in the steep rise in productivity, accounting for up to 90% of the increase (2). For the industry to remain successful, sufficient genetic diversity must exist within companies, because (unlike in crop agriculture) introgression from noncommercial birds is rarely used.
The goal of this research was to determine the extent to which noncommercial and ancestral populations might contain potentially useful germplasm not found in commercial populations. Initially, in North America and Europe, chickens of numerous standard breeds (e.g., Rhode Island Red, Single-Comb White Leghorn) were raised in small backyard flocks primarily for the production of eggs and meat as food, with others developed as game birds for sport and still others developed as fancy breeds for show. Beginning in the 1950s, modern poultry production emerged, with specialized industrial chicken breeds selected intensively for either meat-type (broiler) or egg-type (layer) chickens. All commercial white egg chicken lines are based in the White Leghorn breed, whereas brown egg chicken lines were initially selected from North American dual-purpose breeds (selected for both meat and egg qualities), such as Rhode Island Red and White Plymouth Rock, which originated from crosses between Asian and European breeds. Due to the negative genetic correlation between production (growth) and reproduction (egg number) (3), commercial poultry meat production uses crosses among specialized broiler lines. Lines selected primarily for growth traits are referred to as sire or male lines, because only males are used in the final commercial cross. The lines used for the female side of the cross are selected for both reproductive and growth traits and are referred to as dam or female lines. The male lines are derived from Cornish stock, originating from the British Cornish Indian Game breed, having a thick compact body type with a high proportion of breast muscle. The dam lines originate from many of the same dual-purpose breeds used for brown egg production (e.g., Barred Plymouth Rock, White Plymouth Rock, New Hampshire). Thus, the first tier of genetic diversity reduction was due to limited breed utilization.
The second tier of genetic diversity reduction is ongoing and due to breeding structure and within-line selection. The industry is structured such that the final commercial product is the result of intense within-line selection, followed by a pyramid expansion scheme. This scheme is designed so at the top or pure line level, a limited number of individuals are measured for critical production traits, because the collection of phenotypes is expensive and time-consuming. Genetic improvement based on these traits is performed within a line and is then multiplied by crossing with other selected lines, for same or different traits, for three or four generations. At each generation, the number of offspring from a single bird can exceed 200. As a result, superior genetics of a single primary layer or broiler can be expanded more than a million-fold to produce end products of meat or eggs. Because these pure lines have dramatically different agronomic traits than noncommercial standard breeds, gene flow does not occur between commercial and noncommercial poultry, resulting in essentially closed breeding structures. Thus, inbreeding reduces genetic diversity within the pure lines, although poultry breeders work to avoid inbreeding to the greatest extent possible within closed populations.
Because inbreeding converts within-line genetic variability into between-line variability (4, 5), and because all commercial companies have many pure lines, regardless of the within-line inbreeding, multiple independent lines help preserve alleles within a company. But intense competition within the industry in recent decades has left only a few multinational companies remaining as genetic suppliers of the majority of commercial birds (6). Thus, this final tier limits preservation of alleles between lines.
Because of these multitiered diversity-reducing mechanisms, there is a realistic concern that genetic diversity for future needs may be compromised. Inadequate genetic diversity has had severe negative consequences in both plant and animal species. Oft-cited examples include the 1970 corn leaf blight outbreak due to the widespread use of the Texas male-sterile cytoplasm (7) and the high prevalence of bovine leukocyte adhesion deficiency (BLAD, an autosomal recessive hereditary disease) in Holstein cattle due to the carrier status of several prominent bulls used for artificial insemination (8).
To achieve our objectives, we used the recent chicken genome sequence (9), the identification of more than 2.8 million single-nucleotide polymorphisms (SNPs) (10), and the ability to perform high-throughput genotyping to evaluate the existing genetic diversity in commercial pure lines. Using analytical methods that account for inbreeding and SNP ascertainment bias, we found that commercial poultry breeds have considerably less allelic diversity compared with noncommercial breeds, due primarily to the first tier of narrowing genetic diversity, that is, the limited number of chicken breeds that went into the formation of modern commercial lines. A possible strategy for preserving and accessing more genetic diversity is discussed.
Results
SNP Verification and Genotyping Performance.
All but 14 of the 2580 DNA samples collected from commercial pure lines, experimental chickens, and standard breeds were genotyped successfully (0.54% sample failure rate). Of the 3072 SNPs spaced evenly throughout the chicken genome and examined [see supporting information (SI) Table S1], 2733 provided results, for a success rate (89.0%) that is within the expected 5%–10% loss range because of multiplex amplification issues. The reproducibility rate was 99.996% based on plate and other controls. A comparison of the allele calls with the control DNAs (those used in the actual SNP discovery process) indicated that 2428 of the 2706 SNPs (89.7%) were in full agreement. A minor allele frequency (MAF) of ≥ 2% was observed for 2416 of the 2733 working SNPs (88.4%); 182 SNPs were monomorphic (6.7%), leaving 2551 SNPs segregating in this collection. No significant difference in allele frequency distributions were observed between the tolerant coding nonsynonymous SNP (cnSNPs) and all of the remaining SNPs.
Reconstructing Allele Frequencies for the Hypothetical Ancestral Population (HAP).
Results of the unweighted pair-group method using arithmetic averages (UPGMA) clustering of samples are given in Table S2. The effect of number of clusters on resulting allele frequency distribution is shown in Fig. S1. Level N (Table S2) was our a priori clustering distance based on known relationships of broiler lines. For one level below N and two levels above N, clustering level had little effect on allele frequency distribution; however, at the highest level (Q), the distribution was severely skewed to the right. For a SNP discovery depth of 2, an approximate uniform distribution would be expected (11), thus, level Q clearly is incorrect. For all levels below Q examined, the distribution was approximately uniform, but with a slight skew toward more alleles in the lowest frequency bin.
Distribution of Allele Frequencies and Ascertainment Bias Correction.
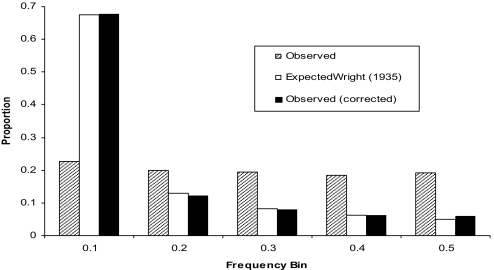
Allele frequency distributions for the observed and after ascertainment bias correction are shown in Fig. 1. Because the ancestral state of the alleles was not known, the distribution was folded based on MAF. When corrected for ascertainment, a folded U-shaped distribution resulted, which, when fit to Wright's distribution (12): φ(q) = _Nvq_4_Nv_− 1, was nearly exact for a parameter estimate of 4Nv = 0.184. A number of tests use estimates of Wright's distribution and variations thereof to infer divergence from the neutral model as a method of detecting positive selection (13–15). This is the first time that an estimate of this parameter was done with a data set of sufficient size to approximate the distribution in economically important chickens. These data tend to support the neutral model even for animals that have been highly selected. Two possible explanations for this are that the proportion of the genome actually under selection may be quite small, or that the SNP loci used were in linkage equilibrium with quantitative trait loci under selection. The possibility that SNP were in linkage equilibrium with quantitative trait loci is supported by results showing linkage disequilibrium in these populations can extend to <0.1 cM, whereas the SNPs in our study were spaced ≈1 cM apart (16, 17).
Fig. 1.
Observed, corrected, and expected allele frequency distributions.
Inbreeding.
Estimation of the allele frequencies for the sampled loci were based on the HAP. For a correct estimate, sufficient diversity must be sampled to be representative of at least two alternative independent lineages. The accuracy of the estimate (bias) is not dependent on the number of lineages sampled, because the expected average allele frequency over independent lineages is the allele frequency in the HAP; however, the precision (variance) of the estimate improves with the number of independent lineages sampled. The estimate is dependent on correctly separating those samples into representative strata (lineages).
Estimation of inbreeding is dependent on several factors, including the formula used, due to potential ascertainment bias. This issue of estimation was resolved by using three approaches for finding FIT: (1) per individual based on the reduction in total heterozygosity across loci, then averaged across individuals; (2) per locus based on the reduction in heterozygosity, then averaged across loci; and (3) per locus based on the reduction in variance. The regression of FIT estimated from methods 2 and 3 (Fig. S2) resulted in good agreement, with an _R_2 of 98% and a slope of 1.04 ± .04, which is not significantly different from 1, as expected. In addition, the regression of FIT estimated from method 1 on method 2 (Fig. S3) resulted in a slope of 1.02 ± .05, which also is not significantly different from 1. Because all three methods are in good agreement, method 1 was used.
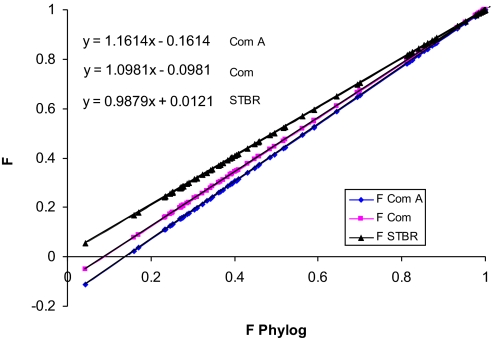
The impact of alternative clustering and known insufficient sampling on estimates of inbreeding was examined by reconstituting the HAP with various subsamples and using an alternative clustering method. The first subsample was based only on the standard breed populations (STBR), the second subsample was based only on industry pure lines (COM), and the third subsample was based on all sampled pure lines within only a single commercial broiler company (COM A). These inbreeding estimates were regressed on lineages defined by UPGMA clustered at level N; the results are shown in Fig. 2. These regressions show that, as expected, bias resulted when sampling was not representative of the HAP. This bias increased as the samples deviated more greatly from a representative sample of the true HAP. The use of just the STBR lines as lineages resulted in nearly identical estimates as those from the UPGMA-reconstituted HAP, with a difference of <2%. When only commercial lines (broiler and layer) were used to define the HAP, then the resulting bias was almost 10%. Finally, when a single company attempted to estimate inbreeding using these methods by combining all lines within the company, then the bias exceeded 16%.
Fig. 2.
Estimation of F with different subpopulations contributing to the HAP.
In all cases, the bias was downward; that is, the amount of inbreeding would have been underestimated. Thus, by extrapolation, we conclude that if our samples are not representative of the true HAP, then our estimates will be biased downward as well, resulting in a conservative estimate of the true level of inbreeding. Our analysis could overestimate the level of inbreeding if our samples have greater genetic variability compared with the HAP; but because genetic sampling (inbreeding) always reduces genetic variability, it is not likely that our samples represent greater variability compared with the HAP.
For comparison, other methods of defining strata were used, including principal component analysis (PCA), as described by Price et al. (18), who showed that PCA can be used to correct for stratification and neighbor-joining clustering (see Figs. S4–S6). Clusters also were confirmed by bootstrapping an UPGMA tree using 5000 replicates (see Fig. S7). Bootstrapping values of 90% were set at as the cutoff. Comparing clusters based on bootstrapping cutoff values and those determined from a priori knowledge shows that they are very similar and suggests that their separation is strongly supported by the data. In addition, regression of inbreeding estimates based on UPGMA and PCA were within 3%. As such, all methods gave very similar results, indicating that the allele frequency estimates in the HAP are somewhat robust to the clustering method and, by extension, the estimated level of inbreeding within subpopulations. Estimates of inbreeding for each line are given in Table S3.
Proportion of Missing Alleles.
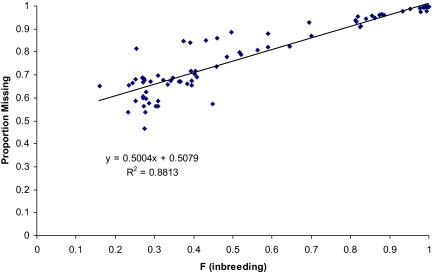
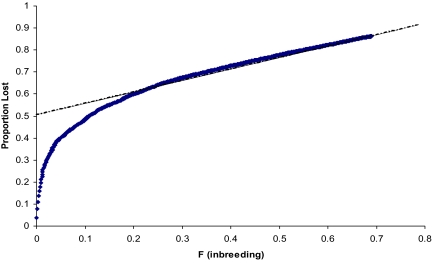
The proportions of alleles missing (Ω) estimated using SNP weights (SNP_WTs; see Table S4) are given in Table S5. These results demonstrate at least 20% inbreeding for each line on average, with a corresponding 60% reduction in allelic diversity. The relationship between Ω and inbreeding is shown in Fig. 3. The regression shows a linear relationship between the proportion of missing alleles and F, with alleles missing at a proportional rate of 50% per unit increase in F, but with an intercept of 50% loss. This was surprising, because when F = 0, then clearly Ω = 0, indicating the existence of an extreme nonlinear relationship between F = 0 and 0.2. This relationship was examined using simulations with an initial distribution of allele frequencies based on Wright's equation (12) with 4Nv = 0.184, as estimated in the Results section on distributions. Results from these simulations (see Fig. 4) clearly show the nonlinearity with low levels of inbreeding. If only data with F > 0.2 were used, then the same relationship was found as with the observed data, that is, an intercept of 0.5 and a slope of 0.5, as indicated by the dotted line. The simulation results lend validity to using the SNP_WT method as a metric to quantify missing allelic diversity in populations. Equally important is the conclusion that major effects on allelic diversity are incurred by relatively minor amounts of inbreeding, followed by a loss that is linear with inbreeding.
Fig. 3.
Empirical relationship between inbreeding and missing alleles (Ω).
Fig. 4.
Simulation results showing lost alleles (Ω) with inbreeding. The dotted line gives the slope and intercept of the linear portion of the curve.
These results make sense when viewed as a departure from equilibrium. The HAP is assumed to be in a dynamic equilibrium, in which the rate of loss of alleles due to inbreeding is balanced by new mutations. This means that the vast majority of allelic diversity in the HAP is rare. Any change in mutation rate or effective population size will alter that equilibrium. If we assume that mutation rates are approximately constant per generation but effective population size fluctuates, and, in particular, if the effective population size is reduced, as is the case for most domestic species, then rare alleles are lost preferentially. This result is verified in Fig. S8, which shows for a representative line that rare alleles are eliminated first. The effect of missing rare alleles as it relates to addressing future commercial poultry needs is unknown; however, rare alleles have been relevant for some production traits in other livestock species (19–22), and reduction of genetic diversity is not favorable for identifying genetic resistance factors to new or emerging infectious diseases.
Assuming that phenotypic variation in traits are due to single base changes in or around functional genes (quantitative trait nucleotide [QTN]), and that the ability to respond to future challenges is reflected by single base changes that have not realized their full evolutionary potential for a given environment, then the rate of frequency reduction of neutral SNPs should be reflective of the rate of frequency reduction of QTN alleles, provided that the QTN alleles are neutral. Thus, the evolutionary potential of a commercial population can be inferred by the absence of random SNPs, provided that their effects on fitness are neutral. Therefore, information on missing random SNPs can be used as an indicator of missing neutral functional alleles in the genome. But alleles that are not neutral may behave much differently, depending on the strength and direction of selection. Besides validating the allelic frequency reduction results, this method has the added functional attribute of being applicable to any poultry population using these SNPs, because the weights are now known.
Recovery of Genetic Diversity.
To explore whether genetic diversity could be reconstituted within existing commercial pure lines, in silico groups were generated by combining all lines within a company, across a breed category, and as a single all-encompassing commercial group. Expected heterozygosity (Hs) of the combined lines was calculated based on average allele frequencies across those lines. This value was then used to compute a biased estimate of the inbreeding coefficient (Fst); that is, targeted genotyping of SNP discovered from a small sample may overestimate the expected heterozygosity (Hs), resulting in an underestimate of (Fst) (23). Therefore, downward-biased estimates of Fst are given in Table S6 for combinations of tested lines within a company and across the industry. This result suggests that combining all lines across all companies would result in a population with a conservative estimate of ≈10% inbreeding coefficient. This equates to missing at least 50% of the alleles present in the HAP (Fig. 4). Combining all commercial lines in silico is the same as creating a HAP based only on the commercial lines. In this case, the commercial-HAP (C-HAP) is a subset of the predomestication HAP and represents the inbreeding that occurred in the first tier of narrowing genetic diversity, that is, the few breeds that contributed to modern poultry breeding programs. These results suggest that among domesticated lines, the larger reservoir of allelic genetic diversity will be found outside breeds contributing to commercial poultry, that is, STBR.
Discussion
The results of the two analyses, which used different approaches, indicate that commercial pure lines of chicken, both broiler (meat) and layer (egg) lines, are missing significant genetic diversity found in noncommercial chickens. We explored possible strategies for companies to restore genetic diversity within lines by crossing multiple pure lines. Crossing combines the diversity preserved among lines, thereby restoring some or all of the within-line variability depending on the number of lines maintained and crossed. In addition, it is possible that industry consolidation will continue, meaning that gene flow could occur across companies in the future. However, as shown in Table S6, such in silico crosses, if done across the entire poultry industry, could reduce the inbreeding coefficient to 10%, but this reduction does not translate into a large recovery of missing alleles. The minimum missing alleles were determined by interpolating the estimated inbreeding coefficients from Table S6 onto the allele loss from Fig. 4. This method provides a conservative estimate of missing alleles, because the in silico estimates of inbreeding are biased downward by the ascertainment bias. As shown in Fig. 4, an inbreeding coefficient as low as 0.10 results in an allele loss of almost 50% from a population experiencing inbreeding. Thus, even in the unlikely and hypothetical situation in which all commercial birds were combined into a single population, a limited increase in allelic diversity would result; that is, a large proportion of genetic diversity would not be present in early lines used for the formation of commercial breeds. An independent assessment of 65 diverse chicken populations showed that commercial birds form their own clusters with very low admixtures with other clusters (24). These findings indicate that the poultry industry, across both the egg and meat pure line stocks, has a narrowed genetic reservoir and possibly a reduced capacity to respond to future industry needs.
Interestingly, the question arises as to whether modern agricultural practices further contribute to this diversity reduction. Although some pure lines are highly inbred, others show very moderate levels. Crosses among lines within a company would result in an inbreeding level between 14% and 15%, as opposed to crossing of all lines across all breeds, which would result in a 10% level of inbreeding. Thus, on average, modern agriculture has contributed less than 5% to the level of inbreeding despite intense levels of selection, closed populations, and industry consolidation. It is worthwhile to note that these findings do not preclude future genetic progress, especially given the results of long-term selection studies in maize, which show continued phenotypic response after 100 generations of intense selection (25). Therefore, new mutations may provide needed genetic variability and contribute to a lack of a perceived “selection wall” for growth and reproduction traits (26). But our findings do raise concerns about traits attributed only to rare alleles, such as resistance to certain infectious diseases, which may be missing in commercial poultry. Under these conditions, there may be no easy way for the industry to access the relevant genetic diversity other than by introgression (slow) or direct genetic manipulation (controversial). Certainly, as a source for rare alleles, our findings reemphasize the need for support and planning for ongoing, new, or novel efforts to maintain genetic diversity using noncommercial and native poultry populations. Future food production challenges are unpredictable and likely will include new diseases or more virulent recurring diseases, environmental changes, changes to animal welfare and consumer preferences, as well as expansion of poultry-related nutritional demands from a global society, necessitating alternatives. Therefore, a healthy genetic reservoir in food-producing animals remains as crucial as ever. Indeed, noncommercial flocks, including those found in many underdeveloped and developing countries, potentially represent the reservoir opportunity for alleles “missing” from commercial pure line stocks.
Materials and Methods
Chickens.
To survey the extant biodiversity of commercial poultry, an extensive collection of DNA from commercial pure lines was assembled. Four major breeding companies (three broiler breeders and one layer breeder), which together account for ≈90% of meat-type and ≈40% of egg-type chickens supplied commercially worldwide, each provided material from 40 selected birds in each of 9 pure lines. Furthermore, to establish a baseline for diversity, additional DNA was collected from a Red Jungle Fowl line (the progenitor of domestic chickens (27)), standard breeds, and experimental lines derived from commercial and standard breeds, which yielded a total of 2580 unique individuals; 1440 commercial birds (representing male and female broilers, white and brown egg layer pure lines), 1136 experimental and standard breed chickens, and 4 controls (UCD 001 #256 Red Jungle Fowl, the sequenced bird; Chinese Silkie, commercial broiler, and experimental White Leghorn, the actual birds used in the SNP discovery process). Table S7 shows how the lines were grouped and coded.
SNP Selection and Genotyping.
To obtain SNPs evenly spaced throughout the chicken genome, the genome sequence (WASHUC1) was divided into 3072 bins, taking into account the recombination rate per chromosome. For each bin, three SNPs from the 2.8 million SNP data set identified previously by Wong et al. (10) were selected (see Table S1). Preference was given to high-confidence SNPs in genes, especially those judged to be tolerant cnSNPs, which accounted for 1124 assays. All SNPs were evaluated for assay suitability, and a single suitable SNP was selected from each bin. In addition, 34 SNPs in genes of interest were evaluated. The DNAs were genotyped at Illumina.
Reconstructing Allele Frequencies for the HAP.
To determine inbreeding, loss of heterozygosity, and proportion of alleles missing, it was first necessary to reconstruct a HAP (28) as a reference. Neutral drift theory posits that if an ancestral population is divided into a number of independent subpopulations, then the average allele frequency across a random sample of such subpopulations will remain unchanged, and it provides an unbiased estimate of allele frequencies in the original base population (12). Because our samples (lines) are not independent, it was important to recombine these samples in a manner consistent with the subdivision structure in which they arose. Because the lineages and relationships between lineages for our samples were relatively unknown, it was necessary to reconstruct this information from the data. This reconstruction was performed using cluster analysis. For clustering of lines (samples) into lineages, genetic distances between samples i and i′ were computed as Dii′ = (Σ_jL_(pij − pi′j)2)1/2, where pij is the allele frequency at the _j_th locus in the _i_th population. The distances were then clustered using the UPGMA clustering method of SAS. Next, it was necessary to determine how many clusters were in the samples. Although a number of methods are available to achieve this goal, all have limitations and restricting assumptions, and none is universally accepted as the best for all situations. Thus, we used an empirical clustering criteria based on prior knowledge of the poultry industry. For example, it is known that all broiler male lines across the industry have a White Cornish ancestry in common, whereas all white egg-type lines have a Single-Comb White Leghorn ancestry in common; therefore, we set a genetic distance between clusters such that all broiler male lines were in the same cluster as our criterion, then used this cluster distance to differentiate all clusters. The effect of clustering criteria on results was examined by comparing outcomes that would have been obtained had the number of clusters been more or less than that set as our criterion. PCA (16), another clustering method, also was conducted for comparison.
Allele frequencies were averaged over samples first within clusters, then across clusters. These averages provided our best estimate of allelic frequencies in the HAP. These estimates are a biased representation of the allele frequency distribution due to ascertainment bias, however.
Ascertainment Bias Correction.
Ascertainment bias is relevant for SNPs because of the way in which SNPs are discovered. In poultry, SNPs were discovered by comparing sequences from essentially only two chromosomes, one from three birds that were sampled sequenced at 1/4X coverage (10) and the other being the Red Jungle Fowl 6.6X whole genome sequence (9). Although a high stringency was applied to the reads, these SNPs are putative as they could be due to sequencing errors. Verification is needed to confirm that the loci are polymorphic, which was one of the goals of this research. Because the results of SNP genotyping are based on polymorphisms observed from a limited number of individuals (two for poultry), these represent conditional probabilities, that is, the probability of observing an SNP in a randomly genotyped individual j given that it was observed in the previously sequenced individuals s and s′. As such, the observed frequencies will tend to overestimate the frequencies of common alleles and underestimate those of rare alleles. Ascertainment bias correction is necessary to obtain the true probability distribution of SNP frequencies in the HAP. The correction was applied to these data using the methods provided by Nielsen and colleagues (11, 29). In essence, this procedure estimates the actual SNP frequency had all of the birds been sequenced rather than genotyped and had all resulting SNP observed been scored.
Proportion of Missing Allele Calculations.
The corrected allele frequency distribution of SNPs in the HAP presents a standard for comparing the effect of inbreeding on that distribution. Let Li be the observed number of loci with frequency i/2N and let N be the total number of individuals sampled. The corrected relative frequencies (Ci) of samples in those bins were found using the Fortran program AS_BIAS given in SI Materials based on the formula of Nielsen and colleagues (11, 29) for a SNP discovery depth of 2. The depth was 2 because SNP were discovered based on only two birds at a time (10). The proportion of the corrected frequency distribution represented by each SNP was SNP_ WTi = (Ci/Li). These SNP_WTs sum to 1 over loci in the HAP; as such, these SNP represent sentinels of biodiversity. If absent in a subpopulation, they represent that proportion of the original distribution missing in that subpopulation. The proportion of missing alleles in any subpopulation is found by first scoring each allele, based on MAF, as present (zi = 1) or absent (zi = 0) in the subpopulation, then weighted using the SNP-WTs from the HAP:
The weighted mean estimates the proportion of alleles missing (Ω) in the subpopulation relative to the HAP.
Inbreeding.
Wright's F statistics (FST, FIS, and FIT) (30) are common measures of population differentiation. Differentiation among populations is directly related to the FST coefficient, which is the expected heterozygosity within subpopulations relative to the total heterozygosity in the HAP. But FIT is the best indicator of loss of genetic diversity (31), because it compares the observed heterozygosity in the sample to that in the HAP. Here, total inbreeding (FIT) was calculated in two ways. First, it was calculated as a reduction in heterozygosity, as was shown by Hartl and Clark (4) for bi-allelic loci. After monomorphic loci were removed, total heterozygosity in the HAP, unadjusted for ascertainment bias, was computed as H_T = 1LΣ_i = 1_L_2_pi_(1 − pi), where L is the number of polymorphic loci observed across the entire sample and pi is the allele frequency at the i_th locus when averaged first within strata and then over strata, as described previously for PCA. The observed average heterozygosity of the k_th individual was computed as HIk = 1LΣ_i = 1_L G _ki_12, where G _ki_12 is 1 or 0 if the _k_th individual was heterozygous or not at the _i_th locus. Estimates of heterozygosity for both the individual and HAP are biased upward due to ascertainment, because loci with intermediate frequency and thus higher heterozygosity are overrepresented. But because inbreeding is based on the ratio of observed to expected heterozygosity, the bias is largely canceled. Inbreeding was calculated as
which estimates Wright's FIT statistic (30) for the _k_th individual.
Second, inbreeding was estimated by within-population reduction in allelic variance, on a per locus bases, then averaged over all loci. The allelic variance at the _i_th locus in the HAP is σ_i_2 = pi (1 − pi). The corresponding allele frequency at _i_th locus in the _s_th subpopulation is pi* with variance _Si_2 = pi*(1 − pi*). Inbreeding is measured as the reduction in variance, that is,
This estimate is free from ascertainment bias, because it is based on the conditional variance in the subpopulation given the _i_th locus, divided by the conditional variance in the HAP, given the same locus; thus, the estimate is independent of distribution. The inbreeding coefficient, when averaged over all loci in the “s” subpopulation, is
This variance reduction method of estimating inbreeding gives approximately the same result as that of Spiess (5), who used the formula
This estimate is based on reduction in heterozygosity but is free from ascertainment bias because it is based on the conditional probability of heterozygosity in the subpopulation, given the i_th locus, divided by the conditional probability of heterozygosity in the HAP, given the i_th locus. Thus, the estimate is independent of distribution. The inbreeding coefficient, averaged over all loci, is F = 1LΣ_i − 1_L Fi.
Relationship between Inbreeding and Missing Alleles.
The relationship between the inbreeding coefficient and proportion of alleles lost was found empirically by regressing the proportion of alleles lost for each subpopulation on the inbreeding coefficient of that subpopulation. This relationship was further examined using simulations. Simulations were needed not only for verification, but also because our data were incomplete, because there were few subpopulations with inbreeding <20%. The simulations were based on the gene level program of Muir (32) using a genetic architecture with 20,000 bi-allelic loci in mutation-drift equilibrium. The mutation-drift distribution of allele frequencies (q) was based on a neutral model (s = 0) in a population of finite size (N) and irreversible mutation rate v, as given in equation (18) of Wright (12): φ(q) = Nvq_4_Nv_− 1. For the simulation, the population was set to 1000 females and 100 males and randomly mated for 1000 generations. The average heterozygosity and loss of alleles were determined at each generation. Inbreeding was based on reduction in heterozygosity. The value of 4_Nv was estimated by trial and error based on the observed rate of loss of alleles with inbreeding; that is, for the proportion of the curve where data were available, the value of 4_Nv_ was adjusted until the observed rate of allele loss matched (using least squares) the simulations. Data from the simulations were then used to infer the relationship between inbreeding and allele loss for the missing portion of the curve, that is, F <0.2.
Supplementary Material
Supporting Information
Acknowledgments.
We thank Laurie Molitor, Tom Goodwill, and Evelyn Young for excellent technical support; Hy-Line International and Aviagen for materials; and Michael Zanus for helpful discussions on clustering methods. This work was supported United States Department of Agriculture National Research Initiative Competitive Grants Program Grant 2004-05434 (to H.H.C., H.Z., M.A.M.G., G.K.S.W., and W.M.M.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Food and Agriculture Organization of the United Nations. [Accessed June 1, 2008];FAOStat. 2008 Available at http://faostat.fao.org.
- 2.Havenstein GB, Ferket PR, Qureshi MA. Growth, livability, and feed conversion of 1957 versus 2001 broilers when fed representative 1957 and 2001 broiler diets. Poultry Sci. 2003;82:1500–1508. doi: 10.1093/ps/82.10.1500. [DOI] [PubMed] [Google Scholar]
- 3.Fairfull RW, Gowe RS. In: Poultry Breeding and Genetics. Crawford RD, editor. New York: Elsevier; 1990. pp. 705–760. [Google Scholar]
- 4.Hartl DL, Clark AG. Principles of Population Genetics. Sunderland, MA: Sinauer Associates; 2007. [Google Scholar]
- 5.Spiess EB. Genes in Population. New York: Wiley; 1989. [Google Scholar]
- 6.Arthur JA, Albers GAA. In: Poultry Genetics, Breeding and Biotechnology. Muir WM, Aggrey SE, editors. Cambridge, MA: CABI Publishing; 2003. pp. 1–12. [Google Scholar]
- 7.Ullstrup AJ. The impacts of the southern corn leaf blight epidemics of 1970–1971. Annu Rev Phytophathol. 1972;10:37–50. [Google Scholar]
- 8.Nagahata H. Bovine leukocyte adhesion deficiency (BLAD): a review. J Vet Med Sci. 2004;66:1475–1482. doi: 10.1292/jvms.66.1475. [DOI] [PubMed] [Google Scholar]
- 9.Hillier LW, et al. Sequence and comparative analysis of the chicken genome provide unique perspectives on vertebrate evolution. Nature. 2004;432:695–716. doi: 10.1038/nature03154. [DOI] [PubMed] [Google Scholar]
- 10.Wong GK, et al. A genetic variation map for chicken with 2.8 million single-nucleotide polymorphisms. Nature. 2004;432:717–722. doi: 10.1038/nature03156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nielsen R, Hubisz MJ, Clark AG. Reconstituting the frequency spectrum of ascertained single-nucleotide polymorphism data. Genetics. 2004;168:2373–2382. doi: 10.1534/genetics.104.031039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wright S. The distribution of gene frequencies under irreversible mutation. Proc Natl Acad Sci U S A. 1938;24:253–259. doi: 10.1073/pnas.24.7.253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fay JC, Wu CI. Hitchhiking under positive Darwinian selection. Genetics. 2000;155:1405–1413. doi: 10.1093/genetics/155.3.1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tajima F. Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics. 1989;123:585–595. doi: 10.1093/genetics/123.3.585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zeng K, Fu YX, Shi S, Wu CI. Statistical tests for detecting positive selection by utilizing high-frequency variants. Genetics. 2006;174:1431–1439. doi: 10.1534/genetics.106.061432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Aerts J, et al. Extent of linkage disequilibrium in chicken. Cytogenet Genome Res. 2007;117:338–345. doi: 10.1159/000103196. [DOI] [PubMed] [Google Scholar]
- 17.Muir WM, et al. Review of the initial validation and characterization of a 3K chicken SNP array. World Poultry Sci J. 2008;64:219–225. [Google Scholar]
- 18.Price AL, et al. Principal components analysis corrects for stratification in genome-wide association studies. Nat Genet. 2006;38:904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
- 19.Freking BA, et al. Identification of the single base change causing the callipyge muscle hypertrophy phenotype, the only known example of polar overdominance in mammals. Genome Res. 2002;12:1496–1506. doi: 10.1101/gr.571002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Grobet L, et al. A deletion in the bovine myostatin gene causes the double-muscled phenotype in cattle. Nat Genet. 1997;17:71–74. doi: 10.1038/ng0997-71. [DOI] [PubMed] [Google Scholar]
- 21.McPherron AC, Lee SJ. Double muscling in cattle due to mutations in the myostatin gene. Proc Natl Acad Sci U S A. 1997;94:12457–12461. doi: 10.1073/pnas.94.23.12457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Smit M, et al. Mosaicism of Solid Gold supports the causality of a noncoding A-to-G transition in the determinism of the callipyge phenotype. Genetics. 2003;163:453–456. doi: 10.1093/genetics/163.1.453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Clark AG, Hubisz MJ, Bustamante CD, Williamson SH, Nielsen R. Ascertainment bias in studies of human genome-wide polymorphism. Genome Res. 2005;15:1496–1502. doi: 10.1101/gr.4107905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hillel J, et al. Molecular markers for the assessment of chicken biodiversity. World Poultry Sci J. 2007;63:33–45. [Google Scholar]
- 25.Dudley JW, Lambert RJ. In: Plant Breeding Reviews, Part 1: Long-Term Selection: Maize. Janick J, editor. vol. 24. New York: Wiley; 2003. pp. 79–110. part 1. [Google Scholar]
- 26.Cahaner A, Smith EJ, Swenson S, Lamont SJ. Associations of individual genomic heterozygosity, estimated by molecular fingerprinting, and of dam major histocompatibility complex with growth and egg production traits in layer chickens. Poultry Sci. 1996;75:1463–1467. doi: 10.3382/ps.0751463. [DOI] [PubMed] [Google Scholar]
- 27.Fumihito A, et al. One subspecies of the red junglefowl (Gallus gallus gallus) suffices as the matriarchic ancestor of all domestic breeds. Proc Natl Acad Sci U S A. 1994;91:12505–12509. doi: 10.1073/pnas.91.26.12505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Pritchard JK, Stephens M, Donnelly P. Inference of population structure using multilocus genotype data. Genetics. 2000;155:945–959. doi: 10.1093/genetics/155.2.945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Nielsen R, Signorovitch J. Correcting for ascertainment biases when analyzing SNP data: Applications to the estimation of linkage disequilibrium. Theor Popul Biol. 2003;63:245–255. doi: 10.1016/s0040-5809(03)00005-4. [DOI] [PubMed] [Google Scholar]
- 30.Wright S. The interpretation of population structure by F-statistics with special regard to systems of mating. Evolution. 1965;19:395–420. [Google Scholar]
- 31.Toro MA, Caballero A. Characterization and conservation of genetic diversity in subdivided populations. Philos Trans R Soc Lond B Biol Sci. 2005;360:1367–1378. doi: 10.1098/rstb.2005.1680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Muir WM. Comparison of genomic and traditional BLUP-estimated breeding value accuracy and selection response under alternative trait and genomic parameters. J Anim Breed Genet. 2007;124:342–355. doi: 10.1111/j.1439-0388.2007.00700.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information