Integrating Computational and Biochemical Studies to Explore Mechanisms in NF-κB Signaling (original) (raw)

Biochemistry involves the quantitative characterization of molecular mechanisms in biology. Contextualizing in vitro molecular studies within cellular or human physiology and disease is an important and often challenging component. Computational models of reaction networks may be useful in this regard, and recent advances in commercially and freely available software are likely to broaden the impact of this approach. This review will highlight the utility and strategy of integrating biochemical and computational techniques by describing how such an approach was taken to analyze the regulation of NF-κB.2

Introduction to Computational Modeling of Cellular Signaling Networks

Signal transduction networks regulate cellular function and respond to changes in intra- and intercellular environments. They control both homeostatic and stimulus-induced responses. However, the role and importance of individual network components in the function of the network are often difficult to discern. This is evident when a genetic deletion or mutation does not show an expected phenotype or when a pharmacological treatment has surprising effects.

Computational simulations with networks reconstructed in silico as mathematical equations enable functional analysis of network behavior and are well suited to complement in vivo and in vitro studies (1–4). The utility of integrating experimental and computational methodologies derives from the iterative application of each approach to inform the other. Experimental analyses provide critical insight to select the components and reactions to include in the computational model and to constrain the simulation parameters. In turn, the computational analyses provide mechanistic insights to drive further experimental analyses.

Studies of the lac operon in Escherichia coli are often cited as original examples of this integrated approach wherein a simple set of mathematical equations was sufficient to account for the transcriptional negative feedback of the lac operon (5). In eukaryotic systems, developmental, cell cycle control, and circadian rhythm processes in several organisms have been examined and validated in silico (6–10). Models of protein kinase cascades have produced important insights such as amplification and temporal fidelity, bistability, and signaling cross-talk (11).

More recently, advances in systems biology have produced increasingly complete cellular parts lists that have enabled statistical modeling to reconstruct large scale molecular networks (12,13). However, the resulting models are largely non-quantitative and do not consider the temporal dimension, although these aspects are essential to biological regulation (4). With top-down network reconstruction efforts identifying functional modules, traditional biochemical bottom-up approaches are critical for providing mechanistic detail. This is where kinetic computational modeling of molecular networks may function as an important bridge for these distinct approaches.

NF-κB Transcription Factor Signaling Network

The members of the NF-κB family of transcription factors are central mediators of cellular responses to inflammatory and developmental cues (14). Misregulation of NF-κB signaling has severe health consequences, and untangling the combinatorial complexity of the NF-κB network is likely to have broad biomedical impact in understanding disease and devising therapeutic strategies (15). For instance, persistent elevated NF-κB activity is associated with chronic inflammatory diseases such as rheumatoid arthritis, asthma, and heart disease and multiple forms of cancer (16–18).

There are five NF-κB monomer subunits that form up to 15 NF-κB transcription factor dimers. In unstimulated cells, these dimers are held in a latent form in the cytoplasm by stoichiometric associations with inhibitor proteins IκBα, IκBβ, and IκBε and the recently identified IκBδ/p100 isoform (19). Activation of NF-κB requires phosphorylation-mediated degradation of the IκB proteins by the IKK complexes. Upon subsequent nuclear translocation of free NF-κB, each dimer activates overlapping but distinct gene expression programs (20) that include the genes for some NF-κB monomers and IκB proteins (14). Thus, NF-κB is regulated via combinatorial complexity that arises from the temporal, stimulus-specific, and cell type-specific expression of dimers, their activation, and their control via both negative and positive feedback mechanisms (14,21).

Constructing a Computational Model of the NF-κB Signaling Network

A computational model was constructed to examine the dynamical control of NF-κB signaling (22) and to ascertain the individual roles of the three canonical IκB proteins (IκBα, IκBβ, and IκBε) in regulating NF-κB activity in response to the inflammatory cytokine TNF. The construction of the computational model required consideration of several questions. 1) What defines the scope of the model? 2) How much molecular detail should the model contain? 3) Which computational modeling technique is best suited? 4) What are the values of the parameters that govern the network reactions?

_Model Scope_—The most basic utility of a model is to predict relationships between a network stimulus or perturbation (input) and the resulting cellular response or network behavior (output). As NF-κB is a pleiotropic transcription factor that responds to numerous intra- and intercellular signaling events, the boundaries of the module were selected to allow for experimentally measurable input and output activities (Fig. 1_A_). With only a few exceptions, the varied upstream activation pathways all converge on IKK, and thus, the activity of IKK was used as the model input. The output of the model is defined as the presence of free NF-κB dimer in the nucleus (_NF-κ_B activity). Although much quantitative data exist for the expression of NF-κB-responsive genes (microarray, qPCR, etc.), the mechanisms that translate NF-κB activity to gene expression are promoter-specific and are not yet well enough understood to be included in a computational model. By limiting the scope of the model to nuclear NF-κB activity, the model is relevant for NF-κB-responsive genes in general. The model, as constructed, is therefore a predictive tool to relate specific stimulus-induced IKK activities to specific NF-κB responses.

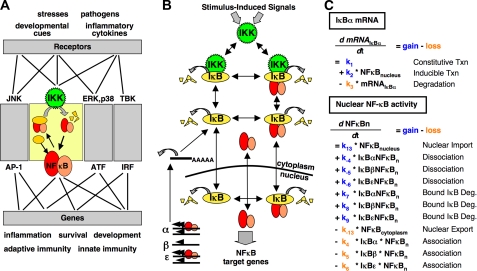
FIGURE 1.

FIGURE 1.

A, the cell responds to external and internal stimuli through complex signal transduction networks that utilize distinct signaling modules to exact specific cellular responses. The NF-κB signaling module is one such key mediator. IKK is activated in response to cellular stimuli and causes accumulation of the NF-κB transcription factor in the nucleus that drives stimulus-specific gene expression programs. Some of the many connections between stimuli and cellular responses are shown and are illustrative of the combinatorial complexity inherent in the cellular signal transduction network. JNK, Janus kinase; ERK, extracellular signal-regulated protein kinase. AP-1, activator protein 1;ATF, activating transcription factor; IRF, interferon regulatory factor. B, schematic diagram of the components and reactions that are described within the NF-κB computational model. Distinct reactions exist for each IκB isoform (IκBα, IκBβ, and IκBε) and are controlled by isoform-specific reaction rate constants. Reactions control synthesis and degradation of the IκB proteins; association and dissociation of IκB proteins, NF-κB, and IKK; and cellular localization. NF-κB is a product or reactant in multiple reactions and, for clarity, is included once in the middle of the diagram. The temporal profile of IKK activity is used as the model input. C, two examples of the 24 ODEs that are contained within the NF-κB model. The flux for each component is calculated via mass action kinetics by subtracting the sum of the reactions that remove the component from the sum of the reactions that produce the component. Shown first is the equation governing IκBα mRNA expression, which contains the reactions of constitutive and NF-κB-inducible transcription (Txn) and mRNA degradation (Deg.). Shown second is the equation governing the amount of free NF-κB protein in the nucleus (NF_κ_Bn), which is controlled by association and dissociation with IκB proteins, protein degradation of NF-κB-bound IκB proteins, and cellular localization reactions.

Model Graininess_—Model graininess defines which reactions and which components are described in the model, with a very detailed model being fine-grained and a simplified model being_coarse-grained. Even small biological networks can lead to insurmountable complexity if too much detail is included, and it is critical to select the minimum level of detail that allows the questions that drive the project to be addressed.

As the IκB proteins are the key mediators of NF-κB nuclear localization, the model describes reactions that govern IκB metabolism, including synthesis, degradation, cellular localization, and association/dissociation with NF-κB (Fig. 1_B_). To reduce complexity, some multistep biochemical events were combined into single-reaction mechanisms based on prior biochemical knowledge. For example, IκB proteins are known to be rapidly degraded via the ubiquitin-dependent proteasome pathway following IKK-mediated phosphorylation. As only IKK-mediated phosphorylation had been found to be rate-limiting, the model employed a single IKK-dependent protein degradation reaction in lieu of multiple explicit reactions governing the ubiquitin-mediated proteasome pathway. Similar reductions were made in removing transport machinery for cellular shuttling events; combining mRNA synthesis, processing, and cytoplasmic localization into a single reaction; and treating protein translation as a single-step process.

_Mathematical Modeling Methodology_—There are several mathematical approaches that have been found to be useful for modeling biochemical reaction networks. Boolean modeling based on the electronics-derived concept of AND and OR gates (and many others) is useful when analyzing how multiple inputs cooperate to produce an output, as for example in the combinatorial transcription factor control of gene expression (23). Flux balance analysis has been used to predict how networks alter their steady-state behavior to achieve a particular physiological objective, as in metabolism controlling bacterial cell growth (24). In cell signaling, however, responses to stimuli are often non-steady-state (e.g. transient) events and therefore necessitate a mathematical approach that can calculate the time-dependent changes in the concentration or activity of network components. ODEs that utilize mass action kinetics and rate constants are often used to describe dynamic cell signaling. Furthermore, in some regulatory networks, when molecule numbers are low, the mathematical model must account for the fact that molecular processes are not graded, but are essentially stochastic. Such molecular noise can play significant roles as exemplified by cell fate decision making and the viral latency/lysis switch noise (25,26).

In modeling NF-κB activity, both homeostatic and stimulated states are of interest. Because the molecule numbers are high (>100,000 NF-κB dimers/cell), a system of ODEs rather than the more computationally demanding stochastic approach was chosen to describe mass action kinetics (22). Examples of the ODEs that represent the rate of change in the IκBα mRNA and the nuclear NF-κB activity are shown inFig. 1_C_. Each ODE represents the flux for one component as a function of time, and the model contains 24 components and ODEs.

These mathematical equations can be written and solved with the help of programs such as Mathematica® (Wolfram Research, Inc.) and MATLAB® (The MathWorks, Inc.) that offer suites of numerical solvers for solving systems of ODEs. Models may also be written using Systems Biology Markup Language (SBML) via one of the many software packages that permit construction and simulation of these models, like MATLAB SimBiology® (The MathWorks, Inc.) and CellDesigner™ (The Systems Biology Institute, Tokyo, Japan). Some of these tools also have graphical interfaces that enable model construction simply by drawing a reaction network and entering rate constants. These applications represent a step toward making modeling as user-friendly as other bioinformatic tools, such as those for nucleotide and peptide alignment (27).

Model Reaction Rate Constants_—The equations of a model constitute the model structure as they define the connectivity between components. The rate constants quantify the connectivity, and_parameterizing a model (defining the values of the rate constants) is the final and often the most difficult step in model construction. Ideally, all values would be measured, but in practice, this is not always feasible, and models contain rates that are measured, experimentally constrained, or estimated/fit. For instance, the rates of protein-protein interactions, cellular localization, and protein half-lives are measurable quantities. Other values are difficult to directly measure or are composite parameters as a result of a coarse-grained model structure. Related experiments can constrain the values of some of these rates. For example, measurements of mRNA and protein abundances can constrain the values of synthesis parameters when coupled to measurements of degradation rates. Finally, the module input/output relationship can be used as a constraint to fit the remaining parameter values such that the model recapitulates this relationship.

A balance must be achieved during the parameterization process to avoid_under-_ or over-constraining the model. If too few values are experimentally determined, there may be several possible parameter sets that recapitulate network behavior, but conversely, when too many experiments are done, the model may be incapable of doing so. In these cases, the data that cannot be accounted for by the model may motivate subsequent studies and in turn result in a revised version of the model.

In the case of the NF-κB signaling module, a rich literature of biochemical rate constants derived from in vitro measurements and quantitative cell biology meant that one-third of the 73 parameters were known with a high degree of confidence, one-third were significantly constrained by literature data, and only the remaining third had to be derived from parameter fitting. To this end, experimental data from three cell lines, each expressing only one of the three IκB proteins (double knockouts), were used as fitting constraints. The supplemental data reported by Hoffmann et al. (22) contain an extensive accounting of the sources for each reaction rate constant.

Utility of Computational Modeling

There have been numerous studies that have expanded upon and/or refined the original NF-κB model (19,22,28–34). In addition, other studies have reduced the complexity of the model to focus only on critical reactions (35–37). In our view, each modification ought to be motivated by specific biological questions. In this context, we consider the utility of computational modeling more generally.

_Sufficiency Test_—In its simplest form, a mathematical model is the summary of our molecular or mechanistic knowledge of a biological process. A model that fails to recapitulate the cellular response (network behavior) indicates that our knowledge of the molecular mechanisms is insufficient. Indeed, further simulations can inform experimental studies to look for missing mechanisms. In this way, the modeling process is integrated with experimental analyses, and iterative tests of sufficiency can be used to increase the scope and detail of both the model and our biochemical understanding.

_Emergent Properties_—A network of molecular reactions has functional characteristics that are not evident from studying a single reaction. These characteristics are called network emergent properties. Network behaviors such as dose responses, dynamic negative feedback regulation, compensation between redundant or overlapping mechanisms, cross-talk between stimuli, and functional memory are examples of emergent properties that can be addressed through mathematical modeling.

_Perturbation Studies_—One of the advantages of having a virtual representation of the biochemical network is that in contrast to biological experiments, virtual experiments can be done systematically, cheaply and fast. One simple strategy is to use simulations of knockouts, in which specific components are removed from the model, to discern the effects (phenotypes) and to reveal emergent properties, including compensation mechanisms. For example, by removing IκBα from the model, its role in post-induction repression of NF-κB was assessed (22).

Similarly, parameter sensitivity analysis involves simulating the model repeatedly with a range of values for one or more rate constants to identify the contribution each reaction makes to the network behavior. Unlike for linear reaction pathways, where the rate-limiting step is the slowest reaction, complex signaling networks may have non-obvious rate-limiting steps. In particular, the rate-limiting step often depends on the homeostatic state of the cell and the stimulus used. The application of parameter sensitivity analyses to biomedical sciences can identify which reactions are sensitive to modulation within the ranges achievable by genetic or pharmacological tools. Furthermore, it may also provide insight into how a drug with a known molecular target within the network will affect the network response. Simulations of the model with the drug-induced perturbation(s) that do not recapitulate observed experimental results may suggest that the drug has unknown targets within the cell.

Insights Derived from Analyses of NF-κB Computational Models

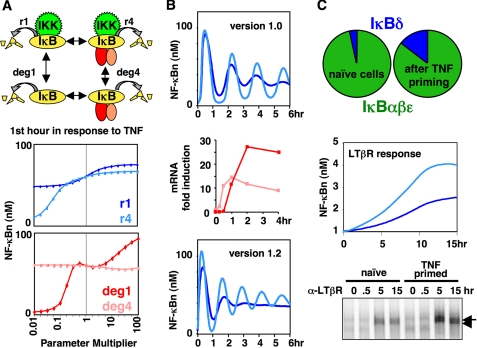
_Parameter Sensitivity Analysis_—In the first of several examples we describe here, parameter sensitivity analysis was used to investigate the relative importance of the four distinct IκB degradation reactions included in the model, of which only the IKK-mediated degradation of NF-κB-bound IκB had been extensively studied (33). TNF signaling was simulated using a range of IκB degradation rates, and the results not only confirmed the critical role of the well studied reaction but also revealed that the IKK-independent degradation of free IκBis also crucial (Fig. 2_A_). These results prompted experimental studies to more accurately measure the IκB degradation rate constants and to characterize the biochemical mechanisms controlling the free IκB degradation pathways. Inclusion of the new degradation rate constants in a revised model resolved a discrepancy in the original that predicted a much greater pool of free IκB protein than evident in experimental studies (33).

FIGURE 2.

FIGURE 2.

A, parameter sensitivity analysis reveals the importance of a second IκB protein degradation mechanism (33). Upper, schematic diagram of the four distinct IκB degradation reactions;lower, “spider charts” showing the sensitivity of the model to perturbations of each of the four degradation reaction rate constants from 0.01× to 100×. Each point represents the average of the first hour of NF-κB activity in model simulations with the parameter multiplier indicated on the x axis. The response of the wild-type system (1× multiplier) is shown in the middle of each plot. Upper plot, IKK-dependent IκB degradation rates_r_1(blue) and _r_4(light blue); lower plot, IKK-independent IκB degradation rates deg1 (red) and deg4 (pink). B, IκB negative feedback regulates oscillations in NF-κB activity (32). Upper, simulation results with chronic TNF stimulation in Model Version 1.0 (22) with (blue) or without (light blue) IκBβ-regulated NF-κB nuclear export; middle, quantitation of IκBα (pink) and IκBε (red) mRNA expression in response to chronic TNF stimulation in wild-type fibroblast cells as measured by RNase protection assay; lower, simulation results in an updated model (Version 1.2), containing an NF-κB-inducible IκBε synthesis reaction, in wild-type (blue) versus IκBε-deficient (light blue) model systems. NF_κ_Bn, free NF-κB protein in the nucleus. C, the IκBδ/p100 IκB isoform mediates cross-talk between inflammatory and developmental signaling pathways (19). Upper, simulation results in Model Version 3.0 show that IκBδ represents a small fraction of the total IκB pool in naïve cells but is increased following priming by transient inflammatory (TNF) stimulation; middle and lower, simulations and cell culture measurements of NF-κB activity by electrophoretic mobility shift assay, respectively, in naïve (light blue) versus TNF-primed (blue) cells in response to developmental (lymphotoxin-β) stimulation. LT_β_R, lymphotoxin-β receptor.

_Sufficiency Test_—In another study, a failed sufficiency test led to the discovery of a novel feedback regulator (32). Negative feedback of NF-κB was initially thought to involve inducible expression of only the IκBα isoform (38), which drives severe oscillations in NF-κB activity when overexpressed or in cells deficient in IκBβ and IκBε (22,28,31). Wild-type cells show dampened oscillations, and the original model attributed the dampening function to IκBβ via a mechanism whereby it stabilizes nuclear localization of active NF-κB (39). This mechanism was later found not to be present in the fibroblast cell type from which the model was derived, but without, it the model was insufficient to dampen oscillations (32). To address this insufficiency, we re-examined IκB mRNA and protein expression profiles in response to TNF and found, unexpectedly, that like IκBα, IκBε is a strongly inducible NF-κB target gene. However, inducible IκBε expression is temporally delayed by 45 min with respect to IκBα, and including this delay in the computational model revealed that IκBε feedback counteracts IκBα-induced NF-κB oscillations (Fig. 2_B_) and suggested that there is dynamic interplay between the two antiphase negative regulators to achieve steadied late phase NF-κB activity in response to inflammatory stimulation.

_Dynamic Model Inputs_—In a third example, dynamic control of NF-κB was investigated by utilizing a library of diverse IKK inputs to probe whether the model can achieve stimulus-specific NF-κB activity (34). Different stimuli activate distinct NF-κB-responsive gene expression programs, and it was hypothesized that stimulus-specific IKK activity might regulate these different responses. An extensive library of theoretical IKK inputs was constructed and used to probe network behavior. These simulations revealed, among other findings, that NF-κB activity is relatively insensitive to the amplitude of early (first phase) IKK activity but very sensitive to small differences in late (second phase) IKK activity. This insight led to the prediction that late activity of IKK is tightly controlled in the cell, prompting experimental studies of negative and positive feedback loops that control late IKK activity in response to the inflammatory stimuli lipopolysaccharide and TNF.

_Analyses of Multiple Negative Feedback Regulators Reveal Signaling Cross-talk_—In a fourth example, the model was expanded to include a newly discovered IκB activity, IκBδ,to account for NF-κB/RelA activation in response to non-canonical signals that play a role in developmental processes such as lymph node development via the lymphotoxin receptor (19). Because experiments showed that IκBδ mRNA expression is inducible by inflammatory stimuli, we used computational simulations to determine whether and under which conditions IκBδ could provide signaling cross-talk between inflammatory and developmental pathways. Resting cells contain only little IκBδ-bound NF-κB and thus respond weakly to developmental cues. However, upon inflammatory stimulation, IκBδ expression is induced, and subsequent developmental stimulation through lymphotoxin (LTαβ) shows hyperactivation of NF-κB (Fig. 2_C_). Experimental studies confirmed the modeling prediction and showed that this effect lasts for some time, effectively constituting a form of cellular memory. Together, they suggested that the two signaling pathways, previously thought to be distinct, engage in cross-talk that has an important physiological and pathological function in cellular contexts where both stimuli are present.

Conclusions

As biochemists interested in molecular mechanisms, we have found that mathematical modeling enriches our experimental studies. At a minimum, model construction makes us more aware of all the molecular mechanisms that may be involved in a physiological process. When a model is functioning for one task but not for another, it motivates further experimental studies to identify novel mechanisms. Computational simulations allow us to explore the functional importance (and at best, physiological relevance) of specific mechanisms and, maybe most strikingly, have provided a tool to address the dynamic or kinetic control of signaling that static wiring diagrams of the network cannot provide. As a result, our understanding of the regulation of NF-κB through multiple IκB proteins is more complete and may inform similar systems biology approaches with upstream, downstream, or parallel network modules that control inflammatory and immune responses.

Supplementary Material

[Author Profile]

Acknowledgments

We thank A. Levchenko (Johns Hopkins University) for critical guidance and P. Loriaux and M. Behar (University of California, San Diego) for reading the manuscript.

*

This work was supported, in whole or in part, by National Institutes of Health Grants R01 GM72024, GM69013, and GM71573. This work was also supported by a predoctoral fellowship award from the American Heart Association. This is the third article of six in the Thematic Minireview Series on Computational Biochemistry: Systems Biology. This minireview will be reprinted in the 2009 Minireview Compendium, which will be available in January, 2010.

Footnotes

2

The abbreviations used are: NF-κB, nuclear factor-κB; IKK, IκB kinase; TNF, tumor necrosis factor; ODE, ordinary differential equation.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Author Profile]