Fast Adaptation in Vestibular Hair Cells Requires Myosin-1c Activity (original) (raw)
. Author manuscript; available in PMC: 2009 May 14.
Summary
In sensory hair cells of the inner ear, mechanical amplification of small stimuli requires fast adaptation, the rapid closing of mechanically activated transduction channels. In frog and mouse vestibular hair cells, we found that the rate of fast adaptation depends on both channel opening and stimulus size and that it is modeled well as a release of a mechanical element in series with the transduction apparatus. To determine whether myosin-1c molecules of the adaptation motor are responsible for the release, we introduced the Y61G mutation into the Myo1c locus and generated mice homozygous for this sensitized allele. Measuring transduction and adaptation in the presence of NMB-ADP, an allele-specific inhibitor, we found that the inhibitor not only blocked slow adaptation, as demonstrated previously in transgenic mice, but also inhibited fast adaptation. These results suggest that mechanical activity of myosin-1c is required for fast adaptation in vestibular hair cells.
Introduction
The inner ear enhances detection of low-amplitude sounds by amplifying them. In the mammalian cochlea, outer hair cells boost small signals with the cochlear amplifier (Davis, 1983). Although outer hair cells require somatic electromotility for amplification (Liberman et al., 2002), a similar signal enhancement in nonmammalian vertebrates is accomplished by the mechanically sensitive hair bundle (Fettiplace and Ricci, 2003). Bundle mechanisms operate in the mammalian cochlea too; when mechanically stimulated, bundles of outer hair cells exert large forces, which may be coupled to cochlear amplification (Kennedy et al., 2005).
The hair bundle performs mechanotransduction in the ear. By stretching elastic gating springs (Corey and Hudspeth, 1983), mechanical displacements of the hair bundle rapidly open cation-selective transduction channels; these channels then close on fast (a few milliseconds or less) and slow (tens of milliseconds) time scales (Holt and Corey, 2000). Slow adaptation occurs when the molecular motor myosin-1c (Myo1c) reduces tension applied to the channels (Holt et al., 2002). When tension is high, a cluster of Myo1c molecules—the adaptation-motor complex—slips down the actin cytoskeleton, reducing tension; by contrast, when tension is low, the Myo1c molecules climb stereocilia actin filaments to restore tension (Gillespie and Cyr, 2004).
Fast adaptation is thought to be the electrical correlate of bundle mechanical amplification (Fettiplace and Ricci, 2003). The prevailing model for fast adaptation suggests that Ca2+, entering through an open transduction channel, binds to or near the channel and causes it to close; this mechanism changes the relationship between gating-spring tension and Po such that channels require more force to open (Howard and Hudspeth, 1988). Negative mechanical movements of the bundle in response to force stimuli support this channel-reclosure model (Benser et al., 1996; Ricci et al., 2000, 2002). However, three unexpected results do not support the model: Ca2+ dependence of the swing of the channel’s gate (Martin et al., 2000), biphasic mechanical response to transepithelial current pulses (Bozovic and Hudspeth, 2003), and polarity of large bundle forces exerted by outer hair cells during fast adaptation (Kennedy et al., 2005). In an alternative model, a component of the transduction apparatus becomes more compliant or releases (Bozovic and Hudspeth, 2003; Martin et al., 2003); the resulting reduction of tension then allows the channels to close rapidly, also explaining the mechanical results. In this release model, the relationship between tension and Po remains constant.
We sought to distinguish between these two models for fast adaptation. We found that, in frog and mouse vestibular hair cells, slow adaptation is proportionally slower for small displacements. In addition, a reciprocal relationship between the extents of fast and slow adaptation suggests that both reduce gating-spring tension. These findings are consistent with the release model but not with the channel-reclosure model.
Moreover, Myo1c seems to play an integral role in fast adaptation. First, the rate of fast adaptation is affected by the Myo1c allele expressed in hair cells. Second, NMB-ADP, an allele-specific inhibitor of a mutant Myo1c, rapidly blocks fast adaptation. These results lead us to conclude that fast adaptation depends upon Myo1c activity and likely arises from a rapid conformational change in the motor that relieves tension and allows transduction channels to close in a Ca2+-dependent manner.
Results
Fast and Slow Positive Adaptation in Frog Hair Cells
The two models for fast adaptation predict different rates of slow adaptation for small displacements. Because the adaptation motor behaves viscously (Howard and Hudspeth, 1987; Assad and Corey, 1992), the rate of slow adaptation should be proportional to the tension applied to the motor. In the channel-reclosure model for fast adaptation, rapid channel closure shortens the mechanical chain connecting the motor to the gating spring, tensing the spring; therefore, elevated tension should increase the rate of positive adaptation in response to small stimuli (Figure 1B). Moreover, the distance the motor moves—the extent of slow adaptation—also should increase, because the motor must slip farther down the stereociliary actin filaments to reduce tension to its steady-state level.
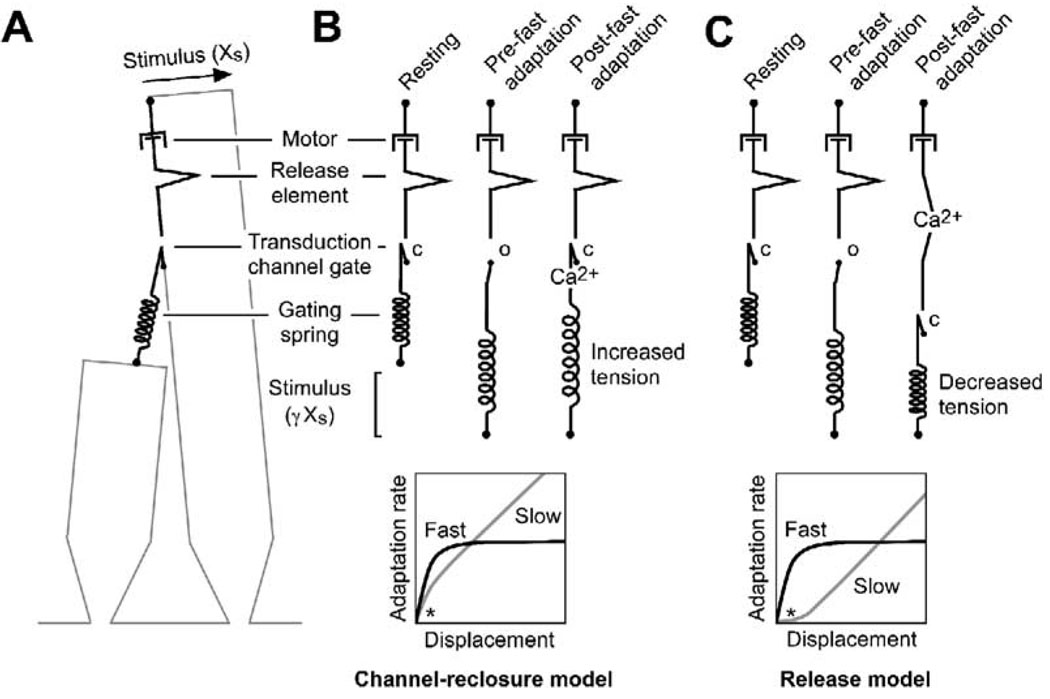
Figure 1. Two Models for Fast Adaptation.
(A) Mechanical model for transduction apparatus. Four mechanical elements are included: an elastic gating spring, a channel with a swinging gate, a release element, and an adaptation motor. Note that, although the gating spring is depicted here to be the tip link, present evidence locates it elsewhere (Gillespie et al., 2005), although still mechanically in series. When the channel is open, the mechanical chain is lengthened; when it is closed, the chain is shortened. The release element lengthens the mechanical chain when unfolded. The motor is modeled as a purely viscous element; force production by the adaptation motor is assumed to be constant and is not depicted. After Howard and Hudspeth (1987).
(B) Channel-reclosure model. A positive mechanical stimulus (Xs) stretches the gating spring to open the channel. Fast adaptation occurs when Ca2+ enters, binds on or near the channel, and forces the channel to close. Increased tension in the gating spring occurring due to channel closing raises the tension felt by the adaptation motor and hence increases the rate of slow adaptation. (Bottom) Hypothetical adaptation rates. Over most of the displacement range, because the adaptation motor exhibits purely viscous behavior, the rate is linear with displacement; over the range where fast adaptation develops, however, the rate of slow adaptation is relatively higher for small displacements because of increased tension (*).
(C) Release model. Ca2+ entering an open channel binds to the release element, lengthening the mechanical chain in series with the channel and gating spring. Reduced tension decreases the channel’s Po. (Bottom) Because the release reduces the force applied to the adaptation motor, for small displacements, the slow adaptation rate is reduced relative to purely viscous behavior (*). Models where Ca2+ changes the stiffness of a mechanical element in series with the channel are formally similar to the release model.
By contrast, in the release model, fast adaptation lengthens the mechanical chain connected to the gating spring; the resulting reduction in tension should then decrease the rate of slow adaptation (Figure 1C). Fast adaptation thus diminishes the extent of slow adaptation; if the lengthening induced by the release is larger than the stimulus amplitude, no slow adaptation will ensue. In both models, slow adaptation approaches linear viscous behavior with larger-sized stimuli.
We tested these models by measuring fast and slow adaptation for a range of mechanical displacements in 15 bullfrog saccule hair cells. We stimulated hair cells with stiff glass probes, which allowed us to avoid the complications of cooperative transduction-channel gating and time-dependent bundle movements. For each cell, we first measured the current-displacement curve, which describes the activation of transduction channels in response to a stimulus. We follow previous convention (Eatock et al., 1987) by defining adaptation as the time-dependent shift of the current-displacement curve along the displacement axis, not channel closing per se; for example, for very large bundle displacements, when channels are mostly open, a substantial shift of the current-displacement curve can occur with very little change in open probability.
To measure the progress of adaptation, we used the inferred-shift method (Shepherd and Corey, 1994). In this method, the transduction current at every point during an adapting stimulus is mapped back onto the current-displacement curve to determine Xe(t), the adaptive shift or extent of adaptation. The validity of the method rests on the assumption that, during adaptation, neither the size nor shape of the current-displacement curve changes (Shepherd and Corey, 1994). Similar to previous results in hair cells of the frog (Shepherd and Corey, 1994; Cheung and Corey, 2005) and mouse (Holt et al., 1997, 2002; Vollrath and Eatock, 2003), we found that this assumption holds in our experiments (see Figures S1A and S1B in the Supplemental Data available online). The inferred-shift method is described in detail in Figure S1C.
We separated fast and slow adaptation by fitting the Xe(t) data with double-exponential functions (Figure 2B), allowing us to calculate independent fast and slow time constants for each stimulus (see Figure S2 for validation of the fitting routine). The adaptive shift in response to each stimulus size was therefore described by individual values of time constants, τfast and τslow, as well as final amplitudes (adaptation extent) Xe(fast) and Xe(slow). Note that the inferred-shift method gives us the temporal resolution necessary to accurately separate fast and slow adaptation.
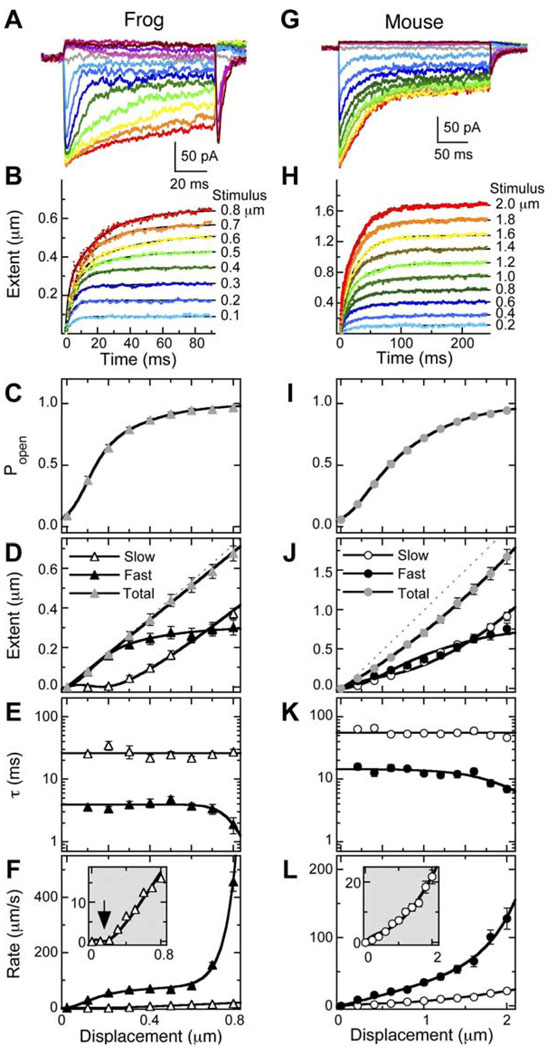
Figure 2. Separation of Fast and Slow Adaptation in Frog and Mouse Hair Cells.
(A and G) Examples of transduction currents in frog saccule hair cells (A) and mouse utricle hair cells (G) in response to mechanical displacements of 150 ms (frog) or 250 ms (mouse). Color scheme of currents is same as in (B) and (H).
(B and H) Extent of adaptation as a function of time [Xe(t)] from currents in (A) and (G) using the inferred-shift method. Data were fit with double-exponential functions.
(C–F) Analysis of averaged data from 15 frog saccule hair cells.
(I–L) Analysis of averaged data from 31 pooled CD-1 and C57BL/6 mouse utricle hair cells.
(C and I) Average instantaneous current-displacement curves derived by converting the peak transduction current into Po. Data were fit with Equation S9 (Supplemental Data), a three-state Boltzmann function. Displacements were −0.4 to +0.8 µm ([C], frog) or −1 to +2 µm ([I], mouse); only Po values from positive displacements are displayed. Frog parameter values: Z01 = 67 fN, X01 = 0.13 µm, Z02 = 20 fN, X02 = 0.019 µm. Mouse parameter values: Z01 = 22 fN, X01 = 0.28 µm, Z02 = 8.0 fN, X02 = 0.51 µm.
(D and J) Average final extent of adaptation. Total extent was fit with a straight line ([D], frog; slope = 0.85) or a second-order polynomial ([J], mouse). For (D), fast extent was fit with Equation S5 (Supplemental Data); Xe(fast) ∞ was the only free parameter and was 0.29 µm. For (J), fast extent was fit with Equation S5, yielding an Xe(fast) ∞ of 0.76 µm. Lines describing slow adaptation in (D) and (J) are not fits, but instead are the total extent fit minus fast extent fit. (E and K) Average time constants for adaptation. Slow adaptation time constants were fit with a flat line (for frog, τslow = 26 ms; for mouse, τslow = 56 ms). Fast adaptation time constants were fit with Equation S6 (Supplemental Data).
(F and L) Average initial rate of adaptation (Xe/τ). Fast adaptation data were fit with an equation of the form rate = kfast × Xe(fast), where kfast is the rate constant for fast adaptation and depends on displacement (E and K). Slow adaptation data were fit with Equation S8. For (F), kslow was 42 s−1. For (L), kslow was 22 s−1.
Fast and slow adaptation were prominent in all cells examined and, as previously noted (Hirono et al., 2004), their properties were relatively stable over dialysis of 5 min or more. As described previously (Shepherd and Corey, 1994), the total extent of adaptation—the shifts of the current-displacement curves on fast and slow time scales in response to an adapting stimulus—was linear between 0 and 0.8 µm (Figure 2D); the slope of the displacement-extent curve (X′e(total)) was 0.85.
By contrast, the extent of fast adaptation saturated. This result is predicted by both models; in the channel-reclosure model, the extent depends on the relative free energies of Ca2+-free and Ca2+-bound channels, while in the release model, the extent depends on the length of the release element. Notably, the dependence of fast extent on stimulus size resembled that of the current-displacement curve (Figure 2C). We fit fast-adaptation extent data with a product of Xe(fast) ∞, the maximum amplitude of the fast shift, and Po (see Equation S5 in the Supplemental Data); the data were fit well and gave Xe(fast) ∞ of 0.29 µm. This value is reported in tip coordinates; conversion to the movement at the level of the adaptation motor requires multiplication by the geometrical gain γ (0.12–0.14 in frog; Jacobs and Hudspeth, 1990). We interpret the observed dependence on Po as a reflection of fast adaptation’s requirement for Ca2+ entry during transduction (Fettiplace and Ricci, 2003).
At the largest stimulus amplitudes, τfast decreased (Figure 2E). We fit the time constants as a function of displacement with Equation S6 (see the Supplemental Data), assuming that fast adaptation proceeds with two rates: one independent of stimulus size (and hence independent of force) and the other force dependent. Despite the faster rate for large stimuli, the extent of fast adaptation remained the same; this result suggested that the dependence of extent on Po and of τfast on force were different manifestations of a single process that can be triggered by either Ca2+ or force. The decrease in τfast is consistent with the release model, as force could directly cause the conformational shift producing the release, but is inconsistent with the channel-reclosure model, as larger forces in the gating spring would be unlikely to speed channel closing. The distinct behavior of Xe(fast) and τfast produces a displacement dependence for the initial rate of fast adaptation, Xe(fast)/τfast (Figure 2F), that is more complex than that diagrammed in Figure 1.
The response of slow adaptation to displacements was markedly different. There was essentially no slow shift of the current-displacement curve (i.e., near-zero extent of slow adaptation) for small Xs, and with larger Xs, the extent of slow adaptation became linear with Xs (Figure 2D). In addition, τslow did not depend on stimulus size (Figure 2E).
The upward-curving slow-adaptation rate curve, in which the rate of slow adaptation is near zero for small displacements (Figure 2F, arrow in inset), is consistent with the release model for fast adaptation (Figure 1C). The slow rate was fit by assuming that the adaptation motor was a linearly viscous element that responds to the difference between total and fast extent (Equation S8 in the Supplemental Data). We interpret this relationship as indicating that fast and slow adaptation combine linearly to produce the final extent of adaptation: because a release decreases tension, fast adaptation reduces the force that drives slow adaptation. Equation S8 (Supplemental Data) allowed an excellent fit of the data with a single free parameter, the rate constant for slow adaptation, which was 42 s−1.
Fast and Slow Positive Adaptation in Mouse Hair Cells
To determine the generality of these conclusions, we turned to hair cells of the mouse utricle (Figures 2G–2L). Although we initially analyzed data separately from the outbred strain CD-1 and the inbred strain C57BL/6, we found that transduction and adaptation properties were sufficiently similar to pool the two datasets. The rate of fast positive adaptation was significantly lower in mouse than in frog vestibular hair cells (Vollrath and Eatock, 2003), both because of intrinsic differences between the two species and because mouse data were acquired at a lower extracellular Ca2+ concentration (1.3 mM, versus 4 mM in frog hair cells). All of the features of fast and slow adaptation that we identified in frog hair cells with the inferred-shift analysis were also present in the mouse (Figures 2I–2L), although less prominent; for example, τfast decreased (from ~12 ms to <8 ms) with our largest stimuli (Figures 2K and 2L). Moreover, the extent of fast adaptation was proportional to Po, yielding an Xe(fast) ∞ of 0.76 µm; that this value is larger than that of frog is not surprising, given the smaller value of γ in mouse (0.05). These results show that fast positive adaptation in mouse vestibular hair cells is mechanistically similar to that in frog saccule hair cells, as shown previously (Vollrath and Eatock, 2003).
Moreover, the properties of slow positive adaptation in mouse vestibular hair cells were similar to those in frog vestibular cells. The relation between displacement and slow-adaptation rate in mouse was curved upward and was well fit with Equation S8, the model used for frog adaptation (Figure 2I, inset); the rate constant for slow adaptation was 22 s−1. Again, this result is most consistent with the release model for slow adaptation.
As reported previously (Vollrath and Eatock, 2003), the relationship between the total extent of adaptation and displacement in mouse hair cells was not linear (Figure 2J). Our data were fit well with a second-order polynomial with positive parameter values and were consistent with an extent spring that decreases in stiffness with increasing displacement.
Total Extent Is Constant in Frog and Mouse Hair Cells
Rates and extents of fast and slow adaptation varied substantially from cell to cell, particularly in the mouse utricle. We found no correlation between the rates of fast and slow adaptation in individual frog or mouse hair cells (Figure 3A). By contrast, when we compared slopes of linear fits to displacement-extent plots, we found a strong inverse correlation (R = 0.90 for all mouse cells) between the slopes of the fast and slow adaptation plots in individual vestibular hair cells, even in cells of different genotypes; a cell with a higher extent of fast adaptation had little slow adaptation and vice versa (Figure 3B).
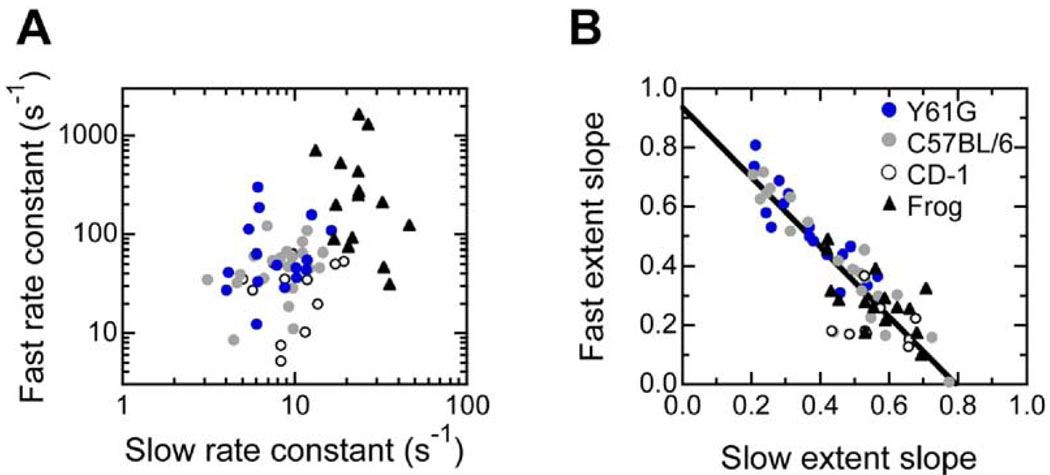
Figure 3. Comparison of the Rate and Extent of Fast and Slow Adaptation.
(A) No correlation between fast and slow adaptation rates measured in individual cells.
(B) Inverse correlation between fast and slow adaptation extent slopes in individual cells. For each cell, fast and slow extents were determined over a range of displacements; the slopes (dimensionless) of the resulting fast and slow displacement-extent relations were plotted for each cell. A linear fit to mouse data (all genotypes: Y61G, C57BL/6, and CD-1) is shown: slope, −1.18; y-intercept, 0.94; R = 0.90. Legend applies to (A) and (B).
Because the slow and fast extents need not add to a constant value, the presence of the inverse correlation is an important consideration. The release model predicts this relationship because progression of fast adaptation reduces the force that drives slow adaptation, and the adaptation motor need not slip as far to reduce tension. The channel-reclosure model predicts the opposite: the extent of slow adaptation will increase with more fast adaptation. Another explanation for the plateau in slow adaptation rate for small displacements (Figures 2D and 2J) is that the adaptation motor is deprived of Ca2+ because fast adaptation closes channels. However, this explanation cannot explain the data of Figure 3B, since the adaptation extents were derived from data spanning the entire displacement range, not just over the narrow range in which channel closure might affect Ca2+ levels.
Fast Phase of Negative Adaptation in Frog and Mouse Hair Cells
When bundles are moved in the negative direction, adaptation responds to the reduced gating-spring tension by generating force, thereby restoring sensitivity. We assessed negative adaptation by moving hair bundles sufficiently far in the negative direction that channels stayed closed, despite adaptation; upon return of the bundle to rest, an overshoot current developed whose amplitude reflected the extent of adaptation during the stimulus (Figure 4A). As reported previously (Hirono et al., 2004), negative adaptation in frog hair cells occurred in two phases, one fast and exponential and the second slower and linear (Figure 4B). In 12 frog cells, the time constant for the fast phase was 10 ± 2 ms, and its amplitude (in tip coordinates) was 0.12 ± 0.02 µm (initial rate of 12 µm/s), while the rate of the slow linear phase was 0.97 ± 0.15 µm/s. We conclude that the fast phase corresponds to reversal of the fast adaptation release (as Ca2+ entry is blocked), and the slow phase results from adaptation-motor myosins cyclically climbing the stereocilia actin cores.
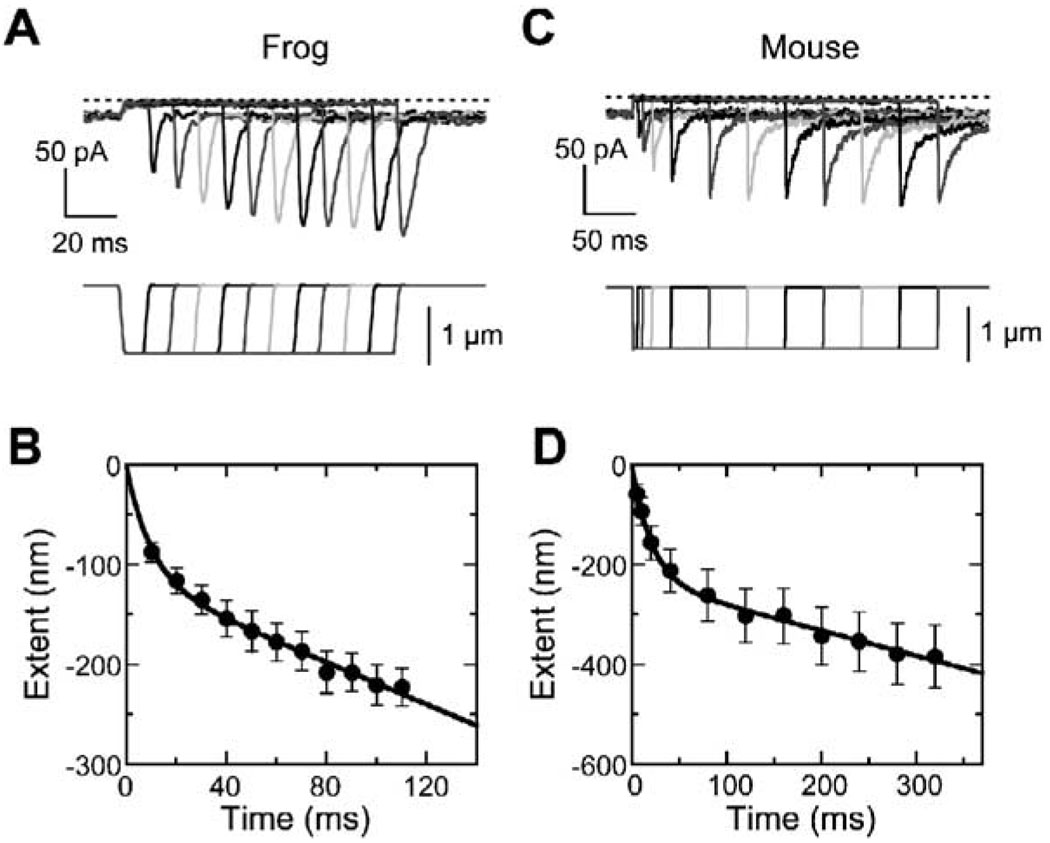
Figure 4. Negative Adaptation in Frog and Mouse Hair Cells.
(A) Negative adaptation in a representative frog hair cell, assessed with negative steps of −0.8 µm for 10–110 ms in 10 ms increments (indicated below). Channels closed completely (dotted line) during the negative steps; upon return of the bundle to rest, a large rebound current developed that was proportional to the extent of negative adaptation that occurred during the stimulus.
(B) Frog negative adaptation (average of 12 cells). Overshoot currents were converted to adaptation extent by comparison with the current-displacement curve. Data points were fit with sum of exponential and linear functions.
(C) Representative mouse (C57BL/6) hair cell subjected to increasing-duration protocol (−1 µm step).
(D) Mouse (C57BL/6) negative adaptation (average of 12 cells). Overshoots were converted to extent and fit as in (B).
Adaptation to negative steps in mouse vestibular hair cells also showed fast exponential and slow linear phases (Figures 4C and 4D). In 12 C57BL/6 control cells, the time constant for the fast phase was 34 ± 13 ms, and its amplitude was 0.27 ± 0.04 µm; averaging rates from individual cells, the initial rate was 18 ± 5 µm/s. The rate of the slow linear phase was 0.38 ± 0.10 µm/s.
Y61G Knockin
We used a chemical-genetic strategy (Holt et al., 2002) to investigate the mechanism and molecule responsible for fast adaptation. The release model could be satisfied if Myo1c itself dissociates from actin or changes configuration rapidly in response to force and Ca2+ (Hudspeth and Gillespie, 1994; Bozovic and Hudspeth, 2003; Batters et al., 2004b). To allow us to specifically and selectively arrest all Myo1c in stereocilia and prevent its mechanical movements, we generated mice with a targeted gene replacement that introduced the Y61G mutation into both Myo1c alleles. This mutation sensitizes Myo1c to N6-modified ADP analogs; for example, N6(2-methyl butyl) ADP (NMB-ADP) blocked Y61G-Myo1c activity while having little effect on wild-type Myo1c (Gillespie et al., 1999). Although we previously generated a transgenic mouse expressing Y61G-Myo1c (Holt et al., 2002), relatively poor expression of the transgene ensured that wild-type Myo1c was the majority of the myosin-1c protein in those mice. In our studies of slow adaptation, the presence of a minority of mutant Myo1c tightly bound to actin was sufficient to arrest the movement of a plaque of Myo1c.
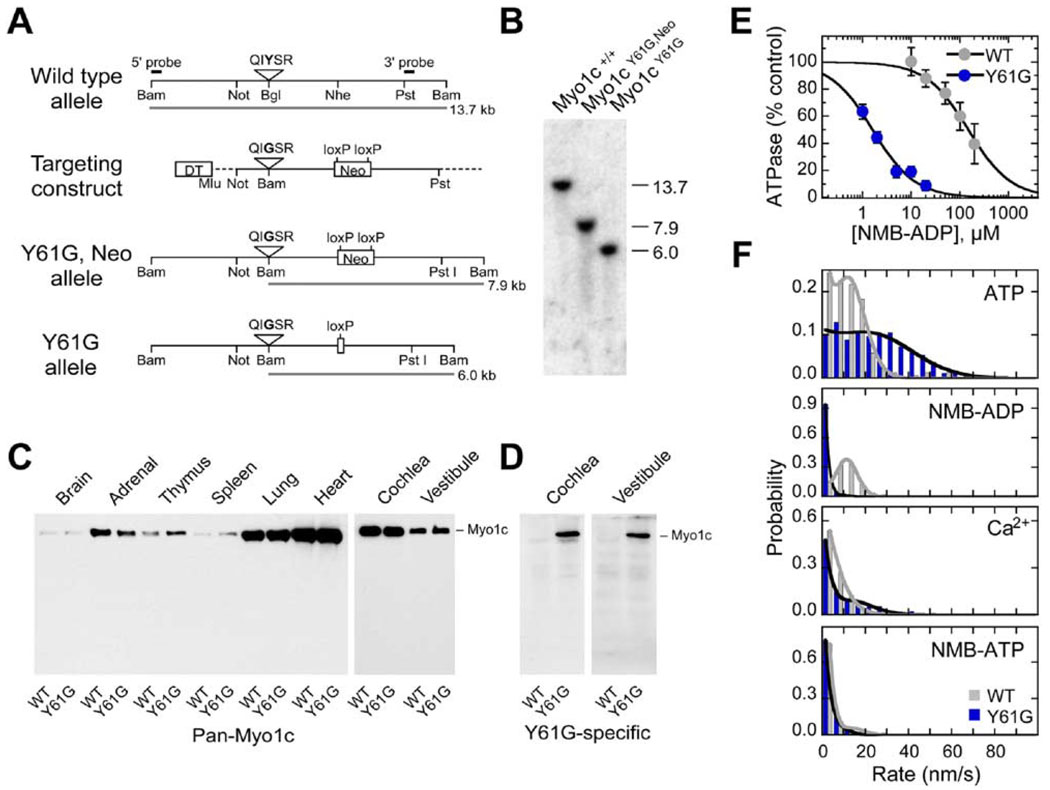
We introduced the Y61G mutation and a loxP-flanked neomycin resistance cassette into a targeting construct (Figure 5A), electroporated the construct into mouse embryonic stem cells, and injected targeted ES cells into blastocysts. We generated one chimeric mouse that transmitted the Y61G mutation to subsequent generations. Mice positive for Y61G were crossed with mice expressing Cre recombinase to remove the neomycin cassette (Figure 5B) and backcrossed to C57BL/6 mice.
Figure 5. Generation and Characterization of _Myo1c_Y61G Knockin Mice.
(A) Targeting strategy. Sequence coding for the Y-to-G mutation at amino acid residue 61 was inserted, resulting in conversion of a Bgl II restriction site to BamH I. The loxP-flanked neomycin-resistance cassette was introduced into a large intron between exons 4 and 5.
(B) Southern blot demonstrating successful targeting and Neo removal. DNA from homozygous wild-type, Y61G/Neo, or Y61G mice was digested with BamH I and detected with a 3′ probe (indicated in [A]).
(C) Immunoblot analysis of Myo1c expression in tissues of wild-type and Y61G mice. Equal amounts of total protein from wild-type or homozygous Y61G mice from the indicated tissues were loaded. Myo1c position (~120 kDa) indicated.
(D) Immunoblot analysis with anti-Y61G-Myo1c, selective for the mutant sequence. Equal amounts of total protein from wild-type or homozygous Y61G mice were loaded on the same gel. Cochlea lanes were exposed to film for 20 s and vestibule lanes for 120 s.
(E) Inhibition of ATPase activity by NMB-ADP. Wild-type and Y61G Myo1c were expressed with baculovirus and purified on Ni2+-NTA agarose; ATPase assays were carried out with 10 µM ATP.
(F) In vitro motility of Myo1c. Wild-type and Y61G Myo1c were expressed with baculovirus, then purified with Ni2+-NTA agarose and actin cycling. Motility assays were carried out using the following solutions: ATP, 2 mM ATP, 1 mM EGTA; NMB-ADP, 2 mM ATP, 250 µM NMB-ADP, 1 mM EGTA; Ca2+, 2 mM ATP, 0.1 mM CaCl2; NMB-ATP, 2 mM NMB-ATP, 1 mM EGTA. Other components of motility solution were as described previously (Gillespie et al., 1999). Filament rates were quantified and binned. Data were fit assuming one population of immobile filaments and another population of moving filaments, with Gaussian-distributed velocities.
Myo1c levels in wild-type and homozygous Y61G mice were nearly identical in all tissues examined (Figure 5C). Moreover, immunoblotting with an antibody that specifically recognizes the Y61G mutant demonstrated directly that Y61G-Myo1c was expressed in the auditory and vestibular systems of Y61G mice (Figure 5D).
Mouse Y61G-Myo1c Is Inhibited by NMB-ADP
We previously used rat Myo1c to characterize the Y61G mutation (Gillespie et al., 1999). Because mouse Myo1c differs from rat Myo1c at several amino acid residues, including residue 62 (Thr in rat, Ser in mouse), we reinvestigated the inhibition of Myo1c activity by NMB-ADP. After expressing full-length wild-type and Y61G mouse Myo1c using baculoviruses, we purified these proteins and measured their ATPase activities. Y61G-Myo1c hydrolyzed ATP with a slightly lower Km (9 ± 2 µM; n = 4) than did WT-Myo1c (17 ± 5 µM; n = 4).
NMB-ADP was a potent inhibitor of Y61G-Myo1c ATPase activity. Inhibition of WT-Myo1c required more than 150-fold more NMB-ADP (Ki = 119 ± 10 µM; n = 4) than was required for inhibition of Y61G-Myo1c (0.75 ± 0.10 µM; n = 4) (Figure 5E), indicating that this mutant-inhibitor combination is suitable for examination of the function of mouse Myo1c.
The effect of NMB-ADP on mutant and wild-type Myo1c also was assessed using an in vitro motility assay (Figure 5F). In the presence of 1 mM EGTA, wild-type mouse Myo1c moved actin filaments at 12.4 ± 0.8 nm/s (mean ± SE; n = 323 filaments). As with the rat mutant, mouse Y61G-Myo1c (25.0 ± 0.9 nm/s; n = 317) moved actin filaments faster than wt. In the presence of 2 mM ATP, NMB-ADP (250 µM) had little effect on WT-Myo1c motility (11.0 ± 0.3 nm/s; n = 363) but nearly completely inhibited motility with Y61G-Myo1c (2.7 ± 0.1 nm/s; n = 494).
Ca2+ slowed both wt (6.2 ± 0.3 nm/s; n = 329) and Y61G (12.4 ±1.1 nm/s; n = 243) Myo1c. The relative fraction of immobile filaments was larger in each case; we suggest that motors generate less force in the presence of elevated Ca2+ and cannot overcome the load imparted by ATP-insensitive myosin molecules (“deadheads”) distributed on the surface. Substituting NMB-ATP for ATP also slowed translocation for wt (5.6 ± 0.3 nm/s; n = 394) and Y61G (4.2 ± 0.6 nm/s; n = 87) Myo1c (Figure 5F), perhaps because Myo1c generates less force when NMB-ADP (the hydrolysis product) is bound.
Transduction and Adaptation in Y61G Hair Cells
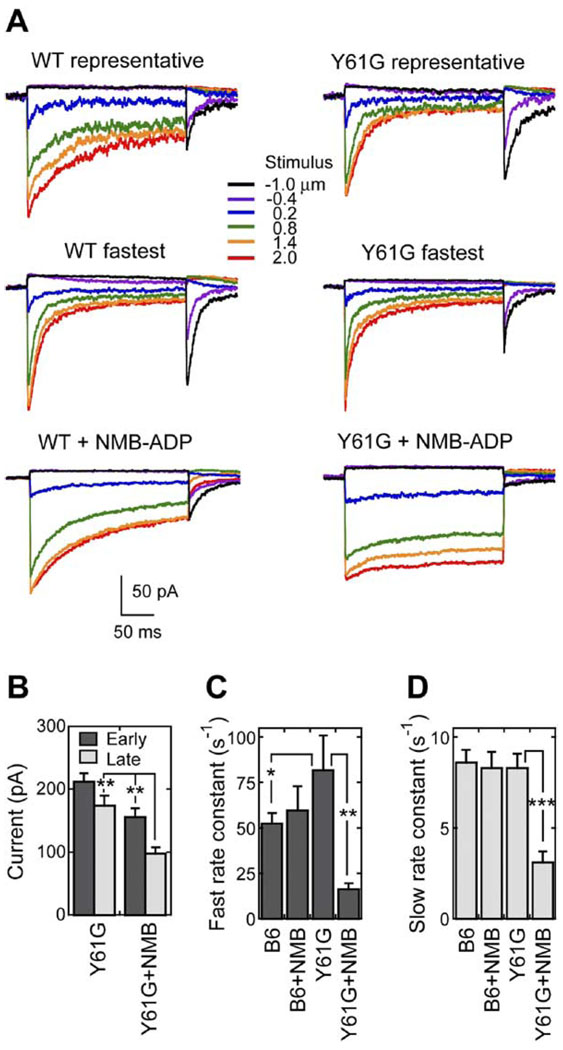
To determine the role of Myo1c in fast adaptation, we recorded transduction currents from Y61G hair cells (and C57BL/6 cells as a control) with or without 250 µM NMB-ADP in the whole-cell recording pipette. When the pipette contained a control solution, transduction-current amplitudes in Y61G hair cells were similar to those in wild-type cells and were relatively stable during dialysis (Figures 6A and 6B).
Figure 6. Adaptation Is Slowed by NMB-ADP in Y61G but Not Wild-Type Hair Cells.
(A) Examples of transduction currents in wt and Y61G hair cells. In both cases, a representative example (top) and the fastest cell in the dataset (middle) are shown for cells filled with control dialysis solutions. In the bottom row, representative cells dialyzed with 250 µM NMB-ADP are shown.
(B) Total transduction currents for Y61G hair cells early (1–3 min) and late (>3 min) during dialysis, with or without NMB-ADP. **p < 0.005.
(C) Rate constants for fast positive adaptation using linear displacement-rate fits. B6 = C57BL/6. *p = 0.11; **p < 0.001.
(D) Rate constants for slow positive adaptation using linear displacement-rate fits. ***p < 0.0001.
Adaptation in the fastest Y61G hair cells was substantially faster than that in the fastest CD-1 or C57BL/6 control hair cells (Figure 6A). We fit rate-displacement data from individual cells with a linear regression and compared the slopes, which correspond to the rate constants (Figure 6C). We found that fast positive adaptation in Y61G hair cells was nearly twice as fast (16 cells; rate constant of 82 ± 19 s−1) than the pooled wild-type hair cells (31 cells; 46 ± 8 s−1) or the geno-typed-matched C57BL/6 hair cells (22 cells; 53 ± 6 s−1). Although this difference reached statistical significance (p < 0.05) for the first comparison, it did not for the second, presumably because of the relatively small Y61G sample size and wide range of adaptation rates. By contrast, the rate constant for slow positive adaptation in Y61G hair cells (8.3 ± 0.8 s−1) was similar to that in all wild-type cells (9.3 ± 1.2 s−1) or in C57BL/6 cells (8.6 ± 0.7 s−1), as shown in Figure 6D. Because they were determined with simple linear fits, these values were smaller than those determined in Figure 2L.
NMB-ADP Reduces Fast and Slow Adaptation Rates in Y61G Hair Cells
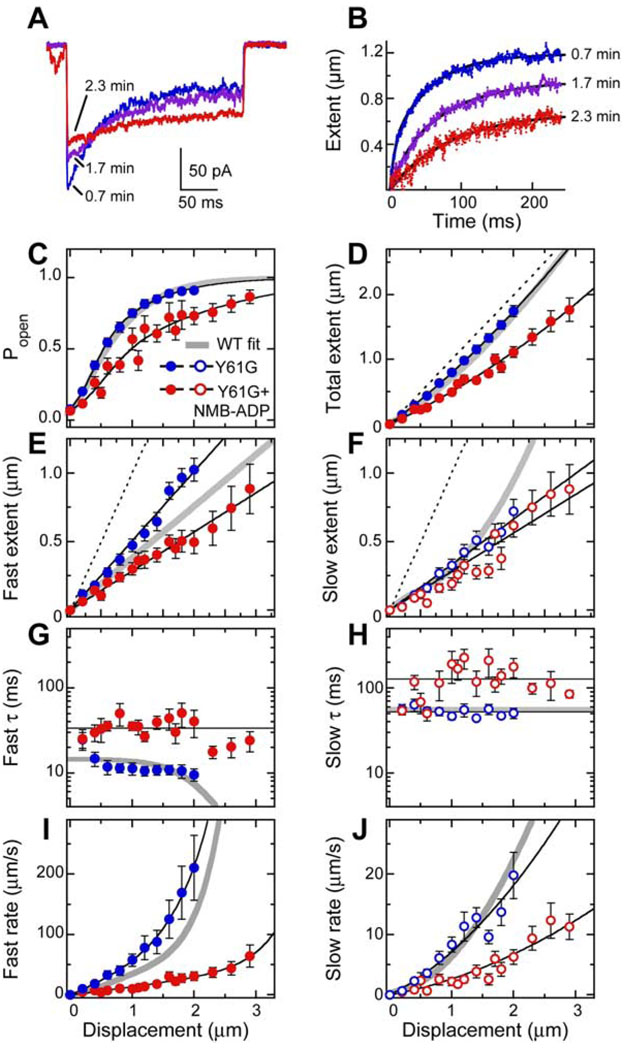
The progressive block of adaptation by NMB-ADP in Y61G hair cells was apparent in Xe(t) plots generated by inferred-shift analysis (Figures 7A and 7B). To dissect the effects of NMB-ADP on Y61G hair cells, we averaged the Po, extent, τ, and rate data from 20 cells for each displacement amplitude to generate average responses (Figures 7C–7J). In Y61G hair cells, NMB-ADP both broadened the current-displacement relation (Figure 7C) and reduced the total extent of adaptation (Figure 7D). By fitting individual current-displacement data with a two-state Boltzmann model, we found that broadening of the average curve was due to a large variability in the midpoint (X0) of the individual curves, rather than a significant change in their slopes (Z) (data not shown). In addition, as noted previously (Holt et al., 2002), maximum transduction current amplitudes decreased somewhat in Y61G hair cells (but not in C57BL/6 controls; data not shown) when NMB-ADP was included in the pipette (Figure 6B). NMB-ADP had no significant effects on transduction or adaptation in C57BL/6 control hair cells.
Figure 7. Fast and Slow Positive Adaptation Are Slowed by NMB-ADP in Y61G Hair Cells.
(A and B) Progression of inhibition of adaptation in a Y61G hair cell dialyzed with 250 µM NMB-ADP. Responses to 1.8 µm stimuli.
(A) Transduction currents. Note slowing of adaptation. Times indicate minutes after establishment of the whole-cell configuration.
(B) Extent of adaptation determined from data in (A) using inferred-shift analysis. Double-exponential fits. Initial rates of fast adaptation: 60 µm/s (0.7 min), 9.4 µm/s (1.7 min), and 4.3 µm/s (2.3 min). Initial rates of slow adaptation: 15 µm/s, 8.6 µm/s, and 3.8 µm/s.
(C–J) Averaged data from 16 Y61G cells filled with a control solution (blue symbols) and 20 Y61G cells filled with 250 µM NMB-ADP. Thick gray lines in (A)–(H) correspond to mouse control fits from Figure 2.
(C) Current-displacement curves. Fits used Equation S9.
(D) Total extent of adaptation. Fits used second-order polynomial functions.
(E) Fast adaptation extent. Linear fits for Y61G (slope, 0.51; R = 0.99) and Y61G + NMB-ADP (slope, 0.29; R = 0.99).
(F) Slow adaptation extent. Lines correspond to total extent minus fast extent. Open symbols correspond to slow adaptation parameters (same color scheme as in [A]).
(G) Fast adaptation time constant. Data for Y61G cells without NMB-ADP were fit with a flat line (data not shown), giving a displacement-independent time constant of 13 ms; data with NMB-ADP were fit with a flat line (τfast = 34 ms). Data from the smallest stimulus (0.2 µm) were excluded due to uncertainty in assignment to fast or slow adaptation.
(H) Slow adaptation time constant. Data (except those from 0.2 µm stimulus) were fit with flat lines: for Y61G, τslow = 53 ms; for Y61G + NMB-ADP, τslow = 129 ms.
(I) Fast adaptation rate. Data were fit with an equation of the form rate = kfast × Xe(fast). The decrease in τ for large displacements means that the fast rate cannot be described by a single parameter.
(J) Slow adaptation rate. As in Figure 2L, data were fit with Equation S8. In Y61G hair cells, kslow (rate constant for slow adaptation) was 25 s−1. For Y61G hair cells filled with NMB-ADP, kslow was 11 s−1.
The rate constant for fast positive adaptation in Y61G hair cells was greatly reduced by 250 µM NMB-ADP (Figure 6C and Figure 7I). Averaging linear rate-displacement fits, we found a rate constant for fast positive adaptation of 16 ± 3 s−1, or one-fifth that of the same cells in the absence of the nucleotide. Fast-adaptation rates were significantly different when NMB-ADP was present (p < 0.01) for the three largest displacement steps (0.8, 1.4, and 2.0 µm). The effect of NMB-ADP on fast positive adaptation arose both from a 50% decrease in final extent of fast adaptation (Figure 7E) and a 3-fold increase in τfast (Figure 7G). Consistent with our previous result (Holt et al., 2002), NMB-ADP reduced the rate constant for slow positive adaptation (to 3.1 ± 0.5 s−1; Figure 6D and Figure 7J). NMB-ADP thus blocks both fast and slow positive adaptation in Y61G hair cells, suggesting that Myo1c underlies both processes.
NMB-ADP Slows Negative Adaptation
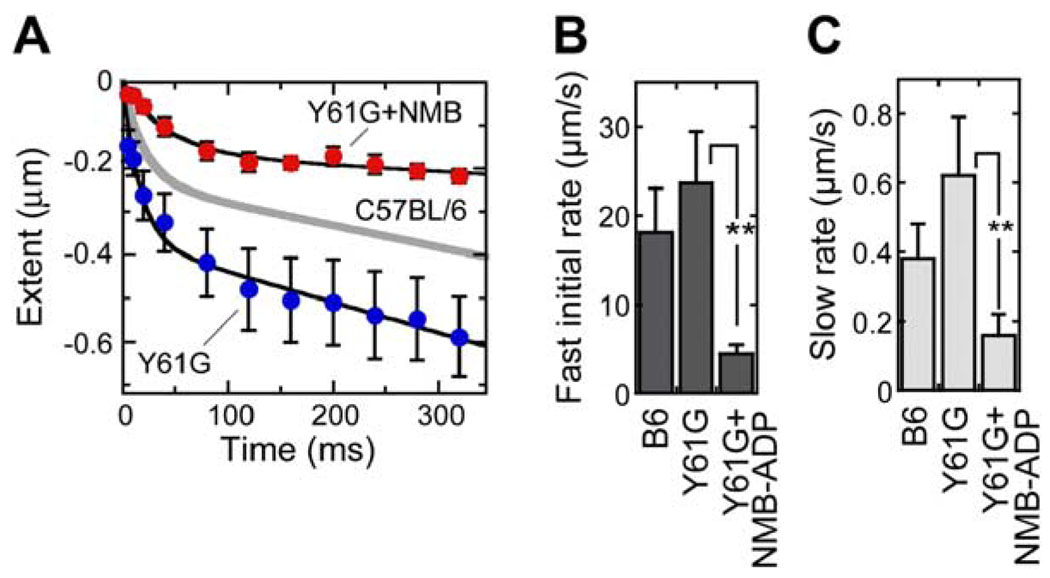
As shown in Figures 8A and 8B, fast negative adaptation in the nine Y61G hair cells we analyzed was about one-third faster than in C57BL/6 controls (τ of 18 ± 3 ms and extent of 373 ± 81 nm in Y61G). Averaging results from individual cells, the initial rate of fast negative adaptation was 24 ± 6 µm/s in Y61G hair cells. As expected given the faster motility of Y61G-Myo1c (Figure 5F), slow negative adaptation was almost twice as fast in Y61G hair cells (0.62 ± 0.17 µm/s) as in wt (Figure 8C).
Figure 8. Fast and Slow Negative Adaptation Are Slowed by NMB-ADP in Y61G Hair Cells.
(A) Negative adaptation from nine Y61G hair cells dialyzed with a control solution and seven Y61G hair cells dialyzed with 250 µM NMB-ADP. Overshoots were converted to extent and fit with summed exponential and linear components as in Figure 4. Gray line is C57BL6 control data from Figure 4.
(B) Fast (exponential) negative adaptation initial rates. **p < 0.05.
(C) Slow (linear) negative adaptation rates. Y61G, 0.62 ± 0.17 µm/s (n = 9); Y61G+NMB-ADP, 0.12 ± 0.07 µm/s (n = 7).
In seven cells analyzed, NMB-ADP slowed both the fast exponential phase and the slow linear phase of adaptation to negative displacements (Figure 8). The effect of NMB-ADP on fast negative adaptation was due to slowing of τ (to 68 ± 28 ms) and a decrease in extent (to 164 ± 42 nm); averaging results from individual cells, NMB-ADP reduced the initial rate to one-sixth its control value, or 4 ± 2 µm/s (Figure 8B). At 0.12 ± 0.07 µm/s, slow negative adaptation was reduced by NMB-ADP dialysis to one-fifth its control value (Figure 8C). Both fast and slow negative adaptation are thus inhibited by NMB-ADP in Y61G hair cells, indicating that Myo1c activity is required for both.
Discussion
Two sets of experiments lead us to propose that fast adaptation in vestibular hair cells arises from the Ca2+-and tension-dependent release of a mechanical element in series with the transduction channel. First, over the narrow displacement range in which fast adaptation produces near-complete adaptation, the drive for slow adaptation was greatly reduced; this result is consistent with fast and slow adaptation each decreasing gating-spring tension. Second, the extent of slow positive adaptation is inversely proportional to that of fast adaptation (Figure 3B); the channel-reclosure model instead predicts a nonlinear, positive correlation between fast and slow extents.
Moreover, a second set of experiments suggests that the molecule responsible for the fast release is Myo1c. Fast adaptation is faster in hair cells of homozygous Y61G knockin mice under control conditions, suggesting that the biochemical properties of Myo1c directly influence the rate of fast adaptation. In addition, fast adaptation in Y61G mice slows to less than 20% of control in the presence of the selective inhibitor NMB-ADP. These observations suggest that the identity of the nucleotide bound to the myosin influences the rates and amplitudes of mechanical transitions underlying fast adaptation. We suggest that NMB-ADP induces Y61G-Myo1c to adopt a conformation in which Ca2+ cannot trigger fast adaptation (Figure 9). Taken together, these results suggest that Myo1c mechanical activity is intimately associated with fast adaptation.
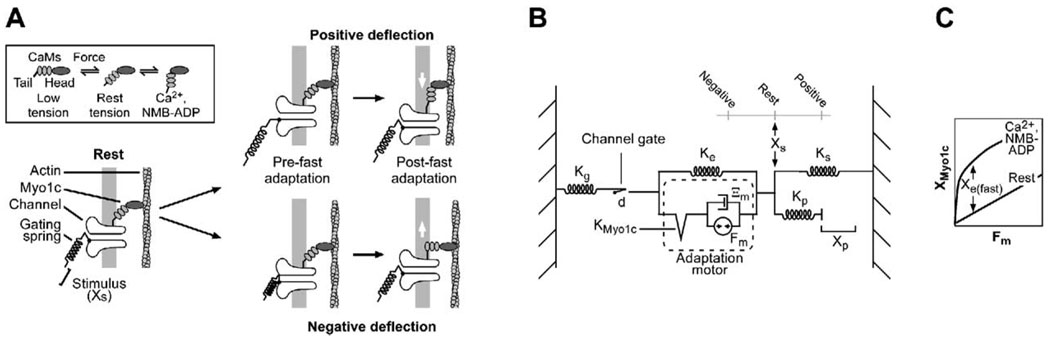
Figure 9. Model for Fast Adaptation in Response to Positive and Negative Stimuli.
(A) Cartoon model. (Inset) Force (downward in diagram) rotates the lever arm (extended IQ domains that bind calmodulin molecules [CaMs]). By reducing crossbridge stiffness, Ca2+ or NMB-ADP produces further rotation of lever arm under tension. During a positive deflection, tension in the gating spring increases; entering Ca2+ triggers lever arm movement. Tension decreases, allowing channels to close. Slow positive adaptation occurs as Myo1c molecules detach and reattach cyclically to further reduce tension (data not shown). During a negative deflection, reduced gating spring tension (and reduction in intracellular Ca2+) allows the lever arm to rotate to the zero-force state, producing fast negative adaptation. Tension increases modestly in the gating spring, but is not enough to reopen channels. Slow negative adaptation occurs as Myo1c molecules detach and reattach cyclically to further increase tension (data not shown).
(B) Mechanical model. After Shepherd and Corey (1994). Kg, gating spring stiffness; Ke, extent spring stiffness; KMyo1c, myosin-actin cross-bridge stiffness (diagrammed as release element); Ξm, adaptation-motor viscous element; Fm, adaptation-motor force generator; Xs, bundle position; Ks, stereocilia spring stiffness; Kp, probe stiffness; Xp, probe displacement. Fm increases tension both on the gating spring and the stereociliary springs when active, moving the bundle (Xs) to the rest point. Release of KMyo1c decreases tension in Kg, allowing channels to close.
(C) Predicted effect of Ca2+ or NMB-ADP on force-displacement relationship for KMyo1c. We hypothesize that the spring becomes very compliant for small displacements, but larger displacements re-engage the stiff spring. This behavior will resemble a pure release. The offset between the two curves corresponds to Xe(fast), the release distance.
Using similar experiments with a transgenic mouse line, we originally drew a different conclusion (Holt et al., 2002). Although fast adaptation in hair cells expressing Y61G-Myo1c from a transgene occasionally persisted in the presence of NMB-ADP (Holt et al., 2002), the mutant myosin was present at a level substantially lower than that of wild-type Myo1c in those cells. While the presence of a few Y61G Myo1c molecules were sufficient to arrest the adaptation motor and inhibit slow adaptation, a significant number of wild-type Myo1c molecules were still available to undergo the rapid conformational changes that underlie fast adaptation. By contrast, the present experiments differ in that no wild-type Myo1c molecules—which might have carried out fast adaptation—were present in the homozygous Y61G knockin mice used.
Are the properties of fast adaptation described here similar to those of other preparations? Our data required division into fast and slow components for accurate fitting, and fast adaptation in mouse utricle hair cells is qualitatively similar in its features to that in frog saccule hair cells. Others have also shown that fast adaptation is similar in mouse and frog vestibular hair cells (Vollrath and Eatock, 2003). Although the mechanical behavior of mouse vestibular hair cells has yet to be studied, fast adaptation in frog vestibular hair cells is mechanically similar to that in the best-characterized auditory preparation, hair cells of the turtle cochlea, with speed being the main difference between preparations (Fettiplace and Ricci, 2003). We therefore believe that fast adaptation in mouse vestibular hair cells is mechanistically similar to that in other hair cells, just slower.
Slower fast adaptation in vestibular hair cells makes physiological sense. The rate of fast adaptation correlates well with the natural stimulus frequency encoded by a given hair cell (Fettiplace and Ricci, 2003). Vestibular hair cells are sensitive to low frequencies, consistent with their slow rates of adaptation; moreover, the wide differences in adaptation rates between individual mouse utricle hair cells likely reflects the broad range of stimulus frequencies thought to be encoded by this organ (Goldberg et al., 1990). Thus, even though fast adaptation in vestibular hair cells is about two orders of magnitude slower than that in cochlear outer hair cells (Kennedy et al., 2003), this difference is not unexpected.
Model for Fast Adaptation
Bozovic and Hudspeth (2003) suggested that when a hair bundle is subjected to an impulse transepithelial electrical stimulus, driving a transient burst of Ca2+ into a hair cell, Ca2+ lengthens a mechanical element in series with the gating spring, causing an immediate drop in tension and producing bundle movement in the positive direction. The resulting reduction in tension allows transduction channels to close, restoring some tension in the gating springs and inducing a negative bundle movement. This rebound movement would be augmented when the release element shortens to its resting state when [Ca2+] falls. Although the Bozovic and Hudspeth (2003) data are not definitive, the release mechanism allows successful modeling of the spontaneous mechanical activity of hair bundles (Martin et al., 2003). Specifically, Hudspeth and colleagues suggested that Ca2+ could reduce the stiffness of Myo1c molecules tightly bound to actin (“crossbridges”), denoted in our model by KMyo1c (Figure 9B), to the point where they become a significant compliance of the transduction apparatus (Bozovic and Hudspeth, 2003; Martin et al., 2003). A decrease in (linear) crossbridge stiffness is less likely than a release, as the slope of the current-displacement curve would decrease as fast adaptation proceeds, which is not seen.
We instead propose a model combining these ideas: fast adaptation occurs when Ca2+ changes the motor’s stiffness nonlinearly, effectively producing a release. How would changes in the stiffness of Myo1c cross-bridges close channels? In models without significant myosin-actin crossbridge compliance, the slope of the current-displacement curve (Z) is proportional to the gating-spring stiffness Kg (Hudspeth, 1992; Shepherd and Corey, 1994). By contrast, in the mechanical model shown in Figure 9B, the size of the stimulus felt by the gating spring is reduced by the parallel combination of Ke (the extent-spring) and KMyo1c, which in turn is in series with the gating spring. Z is therefore proportional to the effective gating-spring stiffness (Keff):
| Keff=Kg(Ke+KMyo1c)Kg+Ke+KMyo1c | (1) |
|---|
As KMyo1c decreases, so does Keff. In hypothetical data plotted in Figure 9C, in the absence of Ca2+, KMyo1c (1/slope) is constant. As Ca2+ binds to calmodulin light chains on Myo1c, the force-extension curve becomes nonlinear; with a constant force, the motor switches from the rest curve to the Ca2+-bound curve and lengthens. Because the Ca2+-bound curve has the same limiting slope for large displacements as the rest curve, the current-displacement curve should not change shape in response to larger stimuli. This model functionally predicts a release.
One of the attractive features of the release model is that it predicts positive cooperativity when a bundle is displaced by a force stimulus. Within a single motor complex, as each Myo1c molecule releases, the stimulus force previously stretching the myosin spring should redistribute to the remaining Myo1c molecules, making them more likely to release. Then, as a substantial fraction of the myosin molecules within the single motor complex cooperatively release, the force in the connected gating spring would drop; that force would then be redirected to other transduction channel complexes. As a consequence, channels would open with smaller forces than would be required for a noncooperative mechanism. Note that the channel-reclosure model makes the opposite prediction; as channels close, exerting force on the bundle, tension in the remaining gating springs will decline, reducing the likelihood that remaining channels will open.
The release model for fast adaptation is consistent with data from rat cochlear outer hair cells from Kennedy et al. (2005), showing that fast adaptation coincided with a large forward movement of a hair bundle. Specifically, we suggest that the large forces they measured following fast adaptation occurred when the release allowed stored tension in the stereociliary spring Ks to move the bundle in the positive direction. Kennedy et al. noted that their data can be explained by a model where a molecule in series with the gating spring rocks to rapidly reduce tension. Although they suggested that a myosin is not fast enough to carry out such a mechanism, that concern is relevant only if the myosin must traverse through the remainder of its ATPase cycle to reprime itself for another mechanical event. In our model, the conformational changes reflecting fast adaptation are reversible and do not correspond to irreversible state changes in the myosin-actin ATPase cycle; the speed of this mechanism is dictated by Ca2+ binding and unbinding kinetics, as well as force felt by the myosin.
By contrast, our interpretation conflicts with those derived from mechanical measurements in turtle auditory hair cells (Ricci et al., 2000, 2002) and frog vestibular hair cells (Cheung and Corey, 2005). Both groups favor the channel-reclosure model, arguing that Ca2+ entry makes the transduction channel more difficult to open. Both Ricci et al. (2000, 2002) and Cheung and Corey (2005) point to the correlation of negative bundle movement with channel reclosure to support this model. The release model also predicts this movement, due to the restoration of tension by closing transduction channels, but only if the size of the release is not too large. Moreover, close examination of mechanical records from hair cells under low-Ca2+ conditions reveals a biphasic positive movement of the bundle prior to the negative “twitch” or “recoil” (Ricci et al., 2000; Benser et al., 1996; Cheung and Corey, 2005), supporting the release model.
Also in apparent conflict with our data, Cheung and Corey (2005) demonstrated a force dependence of fast bundle movements elicited by a depolarization-hyper-polarization protocol that cannot be explained quantitatively by a release model; their data are instead well described by transduction channels requiring ~3 pN more force to open them when Ca2+ binds. In their experiment, Ca2+ entry was driven by large changes in membrane potential, rather than by channel gating, possibly accounting for the apparent conflict. Our results could be reconciled with theirs, however, if the two mechanisms coexisted in the same hair cell. Because the mechanical consequences of the two mechanisms oppose each other, differential timing of Ca2+-induced release and channel reclosure might allow force production in the proper direction at different points of an oscillatory stimulus.
Another complication to our model arises from data suggesting that Ca2+ binding sites regulating fast and slow adaptation are >50 nm from each other (Wu et al., 1999). If Myo1c is responsible for both fast and slow adaptation, the two processes could result from different Ca2+-occupancy states of the Myo1c-calmodulin complex (Gillespie and Cyr, 2004). Alternatively, membrane lipids interacting with Myo1c could produce two or more pools of Myo1c with different Ca2+ sensitivity (Hirono et al., 2004).
Inhibition of Fast Adaptation by NMB-ADP
NMB-ADP blocks fast adaptation, suggesting either that the nucleotide prevents the movement that causes fast adaptation or that it allows the movement to take place prior to the stimulus. We suggest the latter: bound NMB-ADP causes Y61G-Myo1c to adopt a mechanical state resembling the Ca2+-bound one (Figure 9A). If Myo1c crossbridges with bound NMB-ADP are in a relaxed state prior to a stimulus, crossbridges might be preadapted by resting tension, diminishing the amplitude of Xe(fast) during a stimulus. Moreover, relaxed crossbridges would be unable to sustain as much force as stiff ones, explaining why the resting Po did not increase in Y61G hair cells dialyzed with NMB-ADP, in contrast with earlier experiments involving dialysis of ADP or ADPβS (Gillespie and Hudspeth, 1993). Slowing of Y61G-mediated actin-filament translocation with NMB-ATP relative to ATP is consistent with this model; compliant crossbridges, those with the hydrolysis product NMB-ADP bound, would generate less force than stiff ones, slowing movement of filaments in this assay.
Inhibition of Slow Adaptation by NMB-ADP
NMB-ADP reduces the rate of slow adaptation in Y61G hair cells to ~50% of control, a surprising result given our previous analysis of transgenic mice (Holt et al., 2002). Three factors may contribute to the smaller effect observed with the homozygous knockin mutants, however. First, the inferred-shift analysis used here may provide a more quantitative separation of fast and slow adaptation than the transduction-current fitting used in the previous work. Second, because fast adaptation slows substantially with NMB-ADP, tension will remain high for a longer time, driving the slow mechanism more forcefully. Third, and most importantly, if fast and slow adaptation are not mechanistically independent processes, but instead are two phases of Myo1c mechanochemical activity, our separation of them may be artificial.
We see no evidence for the participation of other myosin isoforms in slow (or fast) adaptation. The rates of slow linear negative adaptation (“climbing adaptation”) are consistent with this conclusion; after correction for the mechanical gain γ, adaptation rates were 19 and 31 nm/s for wt and Y61G adaptation, very close to the values obtained in the in vitro motility assay (12 and 25 nm/s). These values are not in conflict with the higher values determined previously (Holt et al., 2002); that analysis did not distinguish between fast and slow phases of negative adaptation, so the rates determined there were dominated by the fast phase.
Mechanism of Myo1c Fast Conformational Change
As pointed out by Batters et al. (2004b), the Myo1c fast-adaptation behavior is reminiscent of that of muscle subjected to rapid release and stretch (Huxley and Simmons, 1971). In muscle, force redevelops rapidly in response to transient tension changes because myosin carries its working stroke forward to release or reverses the working stroke to stretch. Fast positive adaptation thus could correspond to reversal of the Myo1c power stroke as the myosin rocks backward while still attached to actin. Nevertheless, fast adaptation is significantly different from Huxley-Simmons behavior; the mechanism in hair cells depends on Ca2+ and is substantially slower—at least in the vestibular hair cells studied here—than that of muscle (τ = ~1 ms). The response of hair cells to negative deflections may be identical to the Huxley-Simmons response to rapid muscle shortening, however. We similarly interpret the fast phase as resulting from myosin-actin crossbridges reorienting rapidly prior to detachment, and the slow phase as cyclic movement of myosin along actin filaments.
Size of the Fast-Adaptation Release
After scaling the amplitudes of positive and negative extent by γ, the geometric gain, the fast positive release in both frog and mouse corresponds to ~40 nm and the fast negative movement to ~15 nm. These values are much larger than the movements of single Myo1c molecules in vitro (maximum ~7 nm; Batters et al., 2004a). There are several reasons why these values might appear to be inconsistent. First, an extended tail domain or interacting protein could increase the effective length of the lever arm, amplifying myosin movements. Second, our assumption that Myo1c molecules are arranged in parallel could be inaccurate; a series arrangement of Myo1c molecules would also increase the movement. Third, if a fraction of the myosin molecules detached from actin, extent would increase; this distance could be larger than movements within a single myosin molecule.
Finally, in vitro measurements of Myo1c movements are done under low tension, unlike the situation in the adaptation motor. If Myo1c has a linear stiffness of 0.5 mN/m (Batters et al., 2004a), ten attached Myo1c molecules (Gillespie and Cyr, 2004) would each be extended by ~4 nm following a 400 nm stimulus (20 pN imparted through a gating-spring stiffness of 1 mN/m, after correcting for geometrical gain). If Ca2+ binding reduces Myo1c stiffness by a factor of 5 and the Myo1c spring is linearly elastic over that range, the extension could increase to ~20 nm. Because our data are more consistent with a release than a change in linear stiffness, we suggest a different mechanism: in the absence of Ca2+, the neck-head junction is stiff; Ca2+ binding to calmodulin attached to IQ1 causes a conformational change that renders the neck-head junction flaccid (Gillespie and Cyr, 2004), effectively causing a release (Figure 9A). Consistent with this hypothesis, structural studies show that this region of myosin is particularly flexible (Gourinath et al., 2003).
Conclusions
Our experiments thus suggest that fast adaptation in vestibular hair cells occurs when a mechanical element, which we propose is Myo1c, rapidly releases. As the hair bundle is strung like a bow, with the stereociliary pivot spring extended (Hudspeth, 1992), release of the gating spring allows relatively large forces to be generated at the tip of the hair bundle. If this release mechanism involving Myo1c holds for fast adaptation in cochlear hair cells, Myo1c may also play a critical role in cochlear amplification; the speed of this mechanism is only limited by how fast Ca2+ increases and decreases in the stereocilium, as well as intrinsic binding kinetics of the ion for the release site.
Experimental Procedures
Electrophysiology
Whole-cell recording and mechanical stimulation for isolated frog saccule hair cells were carried out exactly as described previously (Hirono et al., 2004). Recording and stimulation of mouse utricle hair cells in intact epithelia were carried out using methods similar to those previously described (Holt et al., 2002). Sensory epithelia were excised from P0–P7 mice in MEM (Invitrogen, Carlsbad, CA) supplemented with 10 mM HEPES, pH 7.4 (Sigma, St. Louis, MO). To remove the otolithic membrane, the tissue was bathed for 20 min in 0.1 mg/ml protease XXIV (Sigma) dissolved in MEM plus 10 mM HEPES (pH 7.4). The tissue was mounted onto a glass cover-slip and held flat by two glass fibers; the coverslip was mounted in an experimental chamber on a fixed-stage upright microscope (Axioskop FS; Zeiss, Oberkochen, Germany) and viewed with a 63×water-immersion objective with differential interference contrast optics.
Electrophysiological recordings were performed in an artificial perilymph solution that contained (in mM): 137 NaCl, 5.8 KCl, 10 HEPES, 0.7 NaH2PO4, 1.3 CaCl2, 0.9 MgCl2, and 5.6 D-glucose, vitamins and amino acids as in MEM (Invitrogen), pH 7.4 and 311 mOsm/kg. Recording electrodes (from R-6 soda lime glass, Garner Glass, Claremont, CA; 3–5 MΩ) were filled with (in mM): 135 KCl, 5 EGTA-KOH, 5 HEPES, 2.5 Na2ATP, 2.5 MgCl2, and 0.1 CaCl2; this solution was pH 7.4 and 284 mOsm/kg. NMB-ADP was synthesized as described (Gillespie et al., 1999) and added to the internal solution to a final concentration of 250 µM.
Hair cells were stimulated by drawing the kinocilium into a pipette filled with extracellular solution (Holt et al., 2002), holding the kinocilium fixed using a constant pressure applied with a pressure-clamp device (ALA Scientific Instruments HSPC-1). To reduce mechanical biases introduced by positioning the stimulus pipette, we adjusted the resting open probability to ~0.05. Movement of the stimulus pipette was driven by a piezoelectric device that had a 10%–90% rise time of 0.6 ms. During experiments, stimulation was monitored by video microscopy using a CCD camera (Hamma-matsu, Japan), and data were excluded if there was any indication of probe slippage, which was also apparent from transduction records.
We recorded from hair cells using the whole-cell, tight-seal technique using an Axopatch 700A Multiclamp amplifier (Axon Instruments, Foster City, CA). Cells were held at −64 mV; transduction currents were filtered at 1 kHz with a low-pass Bessel filter, digitized at ≥5 kHz with a 12 bit acquisition board (Digidata 1322A), and collected using pClamp 8.2 software (Axon Instruments). The clamp time constant in mouse was 0.15 ± 0.05 ms (n = 28) and in frog was 0.16 ± 0.01 ms (n = 12); series resistance compensation was not used.
All data are reported as mean ± SEM and are in tip coordinates unless otherwise noted. Statistical tests used the two-tailed Student’s t test assuming equal variance. Data analysis is described in Supplemental Data.
Generation of Y61G Knockin Mice
We generated the targeting construct using a 6.5 kbp Not I–Pst I fragment of the BamH I genomic clone described previously (Holt et al., 2002). Tyrosine 61 was converted to glycine by changing the codon to GGA; to permit efficient screening, we added additional silent mutations ~30 bp from the Y61G mutation. The neomycin-resistance positive selection cassette, flanked with loxP sites, was inserted into a Nhe I site located in the large intron between exons 4 and 5 (see diagram in Holt et al., 2002). The short homology arm was thus ~0.5 kb and the long arm ~3 kb. We also added a negative selection cassette containing the diphtheria toxin gene, outside the region of homology. ES cells (129S4 clone) were electro-porated with the targeting construct, and two positive clones were identified by PCR and Southern blot screening. Clones were injected into blastocysts, and one chimeric mouse was identified that transmitted the mutation to subsequent generations.
Animals heterozygous for the floxed allele were bred to the Cre deleter mouse, which expresses Cre recombinase ubiquitously from the two-cell stage using the human cytomegalovirus promoter (Schwenk et al., 1995). Experiments described here used homozygous Y61G mice with or without the loxP-Neo cassette present. Although Neo can act in cis to suppress expression of nearby genes (Pham et al., 1996), we found no evidence of that effect in our experiments.
The Y61G mice were backcrossed to C57BL/6J (>10 generations). Although C57BL/6 mice suffer age-related hearing loss due to the ahl1 mutation of cadherin 23, our experiments exclusively used early postnatal mouse pups with no hearing loss (Keithley et al., 2004). We confirmed that Y61G and C57BL/6 control mice had normal auditory brainstem responses (ABRs) at >21 days (data not shown).
Myo1c Biochemistry
We generated recombinant wt and Y61G baculoviruses using the BaculoDirect system (Invitrogen) and coinfected Sf9 cells with Myo1c and calmodulin viruses at a multiplicity of infection of 4:2 (Gillespie et al., 1999). Myo1c was purified by Ni2+-NTA chromatography and, for in vitro motility, by actin cycling (Gillespie et al., 1999). ATPase activity was measured using [γ-32P]ATP (Pollard, 1982). In vitro motility activity was measured as previously described (Gillespie et al., 1999) except that images were captured using a Photometrics CoolSnap CCD camera on a Nikon 800 upright microscope using a 100×, 1.40 NA lens; MetaMorph (version 6.1r4; Molecular Devices, Sunnyvale, CA) was used to control the camera and analyze filament movement (using the Track Objects module).
Supplementary Material
Acknowledgments
Supported by NIH grants R01 DC003279 (J.A.M., P.G.G., and J.R.H), R01 DC005439 (J.R.H.), R01 DC002368 (P.G.G.), and P30 DC005983 (P.G.G.).
References
- Assad JA, Corey DP. An active motor model for adaptation by vertebrate hair cells. J. Neurosci. 1992;12:3291–3309. doi: 10.1523/JNEUROSCI.12-09-03291.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batters C, Arthur CP, Lin A, Porter J, Geeves MA, Milligan RA, Molloy JE, Coluccio LM. Myo1c is designed for the adaptation response in the inner ear. EMBO J. 2004a;23:1433–1440. doi: 10.1038/sj.emboj.7600169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Batters C, Wallace MI, Coluccio LM, Molloy JE. A model of stereocilia adaptation based on single molecule mechanical studies of myosin I. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2004b;359:1895–1905. doi: 10.1098/rstb.2004.1559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benser ME, Marquis RE, Hudspeth AJ. Rapid, active hair bundle movements in hair cells from the bullfrog’s sacculus. J. Neurosci. 1996;16:5629–5643. doi: 10.1523/JNEUROSCI.16-18-05629.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bozovic D, Hudspeth AJ. Hair-bundle movements elicited by transepithelial electrical stimulation of hair cells in the sacculus of the bullfrog. Proc. Natl. Acad. Sci. USA. 2003;100:958–963. doi: 10.1073/pnas.0337433100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung EL, Corey DP. Ca2+ changes the force sensitivity of the hair-cell transduction channel. Biophys. J. 2005 doi: 10.1529/biophysj.105.061226. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corey DP, Hudspeth AJ. Kinetics of the receptor current in bullfrog saccular hair cells. J. Neurosci. 1983;3:962–976. doi: 10.1523/JNEUROSCI.03-05-00962.1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis H. An active process in cochlear mechanics. Hear. Res. 1983;9:79–90. doi: 10.1016/0378-5955(83)90136-3. [DOI] [PubMed] [Google Scholar]
- Eatock RA, Corey DP, Hudspeth AJ. Adaptation of mechanoelectrical transduction in hair cells of the bullfrog’s sacculus. J. Neurosci. 1987;7:2821–2836. doi: 10.1523/JNEUROSCI.07-09-02821.1987. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fettiplace R, Ricci AJ. Adaptation in auditory hair cells. Curr. Opin. Neurobiol. 2003;13:446–451. doi: 10.1016/s0959-4388(03)00094-1. [DOI] [PubMed] [Google Scholar]
- Gillespie PG, Cyr JL. Myosin-1c, the hair cell’s adaptation motor. Annu. Rev. Physiol. 2004;66:521–545. doi: 10.1146/annurev.physiol.66.032102.112842. [DOI] [PubMed] [Google Scholar]
- Gillespie PG, Hudspeth AJ. Adenine nucleoside diphosphates block adaptation of mechanoelectrical transduction in hair cells. Proc. Natl. Acad. Sci. USA. 1993;90:2710–2714. doi: 10.1073/pnas.90.7.2710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillespie PG, Gillespie SK, Mercer JA, Shah K, Shokat KM. Engineering of the myosin-Iβ nucleotide-binding pocket to create selective sensitivity to N6-modified ADP analogs. J. Biol. Chem. 1999;274:31373–31381. doi: 10.1074/jbc.274.44.31373. [DOI] [PubMed] [Google Scholar]
- Gillespie PG, Dumont RA, Kachar B. Have we found the tip link, transduction channel, and gating spring of the hair cell? Curr. Opin. Neurobiol. 2005;15 doi: 10.1016/j.conb.2005.06.007. in press. [DOI] [PubMed] [Google Scholar]
- Goldberg JM, Desmadryl G, Baird RA, Fernandez C. The vestibular nerve of the chinchilla. IV. Discharge properties of utricular afferents. J. Neurophysiol. 1990;63:781–790. doi: 10.1152/jn.1990.63.4.781. [DOI] [PubMed] [Google Scholar]
- Gourinath S, Himmel DM, Brown JH, Reshetnikova L, Szent-Gyorgyi AG, Cohen C. Crystal structure of scallop myosin S1 in the pre-power stroke state to 2.6 Å resolution: flexibility and function in the head. Structure (Camb.) 2003;11:1621–1627. doi: 10.1016/j.str.2003.10.013. [DOI] [PubMed] [Google Scholar]
- Hirono M, Denis CS, Richardson GP, Gillespie PG. Hair cells require phosphatidylinositol 4,5-bisphosphate for mechanical transduction and adaptation. Neuron. 2004;44:309–320. doi: 10.1016/j.neuron.2004.09.020. [DOI] [PubMed] [Google Scholar]
- Holt JR, Corey DP. Two mechanisms for transducer adaptation in vertebrate hair cells. Proc. Natl. Acad. Sci. USA. 2000;97:11730–11735. doi: 10.1073/pnas.97.22.11730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holt JR, Corey DP, Eatock RA. Mechanoelectrical transduction and adaptation in hair cells of the mouse utricle, a low-frequency vestibular organ. J. Neurosci. 1997;17:8739–8748. doi: 10.1523/JNEUROSCI.17-22-08739.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holt JR, Gillespie SK, Provance DW, Shah K, Shokat KM, Corey DP, Mercer JA, Gillespie PG. A chemical-genetic strategy implicates myosin-1c in adaptation by hair cells. Cell. 2002;108:371–381. doi: 10.1016/s0092-8674(02)00629-3. [DOI] [PubMed] [Google Scholar]
- Howard J, Hudspeth AJ. Mechanical relaxation of the hair bundle mediates adaptation in mechanoelectrical transduction by the bullfrog’s saccular hair cell. Proc. Natl. Acad. Sci. USA. 1987;84:3064–3068. doi: 10.1073/pnas.84.9.3064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard J, Hudspeth AJ. Compliance of the hair bundle associated with gating of mechanoelectrical transduction channels in the bullfrog’s saccular hair cell. Neuron. 1988;1:189–199. doi: 10.1016/0896-6273(88)90139-0. [DOI] [PubMed] [Google Scholar]
- Hudspeth AJ. Hair-bundle mechanics and a model for mechanoelectrical transduction by hair cells. Soc. Gen. Physiol. Ser. 1992;47:357–370. [PubMed] [Google Scholar]
- Hudspeth AJ, Gillespie PG. Pulling springs to tune transduction: adaptation by hair cells. Neuron. 1994;12:1–9. doi: 10.1016/0896-6273(94)90147-3. [DOI] [PubMed] [Google Scholar]
- Huxley AF, Simmons RM. Proposed mechanism of force generation in striated muscle. Nature. 1971;233:533–538. doi: 10.1038/233533a0. [DOI] [PubMed] [Google Scholar]
- Jacobs RA, Hudspeth AJ. Ultrastructural correlates of mechanoelectrical transduction in hair cells of the bullfrog’s internal ear. Cold Spring Harb. Symp. Quant. Biol. 1990;55:547–561. doi: 10.1101/sqb.1990.055.01.053. [DOI] [PubMed] [Google Scholar]
- Keithley EM, Canto C, Zheng QY, Fischel-Ghodsian N, Johnson KR. Age-related hearing loss and the ahl locus in mice. Hear. Res. 2004;188:21–28. doi: 10.1016/S0378-5955(03)00365-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kennedy HJ, Evans MG, Crawford AC, Fettiplace R. Fast adaptation of mechanoelectrical transducer channels in mammalian cochlear hair cells. Nat. Neurosci. 2003;6:832–836. doi: 10.1038/nn1089. [DOI] [PubMed] [Google Scholar]
- Kennedy HJ, Crawford AC, Fettiplace R. Force generation by mammalian hair bundles supports a role in cochlear amplification. Nature. 2005;433:880–883. doi: 10.1038/nature03367. [DOI] [PubMed] [Google Scholar]
- Liberman MC, Gao J, He DZ, Wu X, Jia S, Zuo J. Prestin is required for electromotility of the outer hair cell and for the cochlear amplifier. Nature. 2002;419:300–304. doi: 10.1038/nature01059. [DOI] [PubMed] [Google Scholar]
- Martin P, Mehta AD, Hudspeth AJ. Negative hair-bundle stiffness betrays a mechanism for mechanical amplification by the hair cell. Proc. Natl. Acad. Sci. USA. 2000;97:12026–12031. doi: 10.1073/pnas.210389497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin P, Bozovic D, Choe Y, Hudspeth AJ. Spontaneous oscillation by hair bundles of the bullfrog’s sacculus. J. Neurosci. 2003;23:4533–4548. doi: 10.1523/JNEUROSCI.23-11-04533.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pham CT, MacIvor DM, Hug BA, Heusel JW, Ley TJ. Long-range disruption of gene expression by a selectable marker cassette. Proc. Natl. Acad. Sci. USA. 1996;93:13090–13095. doi: 10.1073/pnas.93.23.13090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollard TD. Assays for myosin. Methods Enzymol. 1982;85:123–130. doi: 10.1016/0076-6879(82)85015-5. [DOI] [PubMed] [Google Scholar]
- Ricci AJ, Crawford AC, Fettiplace R. Active hair bundle motion linked to fast transducer adaptation in auditory hair cells. J. Neurosci. 2000;20:7131–7142. doi: 10.1523/JNEUROSCI.20-19-07131.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ricci AJ, Crawford AC, Fettiplace R. Mechanisms of active hair bundle motion in auditory hair cells. J. Neurosci. 2002;22:44–52. doi: 10.1523/JNEUROSCI.22-01-00044.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwenk F, Baron U, Rajewsky K. A cretransgenic mouse strain for the ubiquitous deletion of loxP-flanked gene segments including deletion in germ cells. Nucleic Acids Res. 1995;23:5080–5081. doi: 10.1093/nar/23.24.5080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shepherd GMG, Corey DP. The extent of adaptation in bullfrog saccular hair cells. J. Neurosci. 1994;14:6217–6229. doi: 10.1523/JNEUROSCI.14-10-06217.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vollrath MA, Eatock RA. Time course and extent of mechanotransducer adaptation in mouse utricular hair cells: comparison with frog saccular hair cells. J. Neurophysiol. 2003;90:2676–2689. doi: 10.1152/jn.00893.2002. [DOI] [PubMed] [Google Scholar]
- Wu YC, Ricci AJ, Fettiplace R. Two components of transducer adaptation in auditory hair cells. J. Neurophysiol. 1999;82:2171–2181. doi: 10.1152/jn.1999.82.5.2171. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.