Identifying novel constrained elements by exploiting biased substitution patterns (original) (raw)
Abstract
Motivation: Comparing the genomes from closely related species provides a powerful tool to identify functional elements in a reference genome. Many methods have been developed to identify conserved sequences across species; however, existing methods only model conservation as a decrease in the rate of mutation and have ignored selection acting on the pattern of mutations.
Results: We present a new approach that takes advantage of deeply sequenced clades to identify evolutionary selection by uncovering not only signatures of rate-based conservation but also substitution patterns characteristic of sequence undergoing natural selection. We describe a new statistical method for modeling biased nucleotide substitutions, a learning algorithm for inferring site-specific substitution biases directly from sequence alignments and a hidden Markov model for detecting constrained elements characterized by biased substitutions. We show that the new approach can identify significantly more degenerate constrained sequences than rate-based methods. Applying it to the ENCODE regions, we identify as much as 10.2% of these regions are under selection.
Availability: The algorithms are implemented in a Java software package, called SiPhy, freely available at http://www.broadinstitute.org/science/software/.
Contact: xhx@ics.uci.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Evolution constantly tinkers with genome sequences and tests the results by natural selection. A great deal of information on the functionality of a sequence can be learned by studying how the sequence changed throughout evolution. Recently, many genomes have been sequenced primarily for their comparative analytic value (Green, 2007; Margulies and Birney, 2008; Margulies et al., 2005; Stark et al., 2007). For example, in the clade of placental mammals over 24 genomes have been sequenced and many more promise to come in the future (Margulies et al., 2005; Miller et al., 2007). These data provide a great opportunity to detect and interpret functional elements encoded in these genomes, and to study their evolution. Currently, a major challenge is to develop efficient and sensitive methods that can maximally extract evolutionary and functional information from these data.
Several methods to detect conservation exist. These methods include the widely used PhastCons program, which aims to identify regions that show slower rates of mutation than neutrally evolving sequences (Siepel et al., 2005). PhastCons models this evolutionary constraint as a shortened phylogenetic tree connecting the species being compared. The GERP program uses the concept of rejected substitutions to discover sequences that harbor fewer mutations than would be expected for neutral sequences (Cooper et al., 2005). BinCons and SCONE use parsimony-based methods to infer the ancestral sequences and to identify sequences containing fewer inferred mutational events than neutral sequence (Asthana et al., 2007; Margulies et al., 2003). Although differing on the specific algorithms to infer ancestral states, these methods all attempt to single out conserved bases or regions that exhibit a reduced mutation rate when compared to neutrally evolving sequence. We will refer to such methods collectively as rate-based methods.
Although widely used and successful in revealing constrained sequences, the rate-based methods have two main disadvantages. First, they do not capture all aspects of the evolution of functional sequences. Functional constraint need not act simply as a decreased rate of mutation but can also act as a biased substitution pattern. For example, consider amino acid codon redundancy. Many bases can freely change so long as they do not disrupt the protein sequence. For instance, lysine is encoded by two codons, AAA and AAG; the third nucleotide is allowed to freely mutate between A and G. Thus, many mutations between A and G may occur during the course of evolution; rate-based methods may misidentify the site as unconstrained. Such limitation is not confined only to protein-coding genes, but is also likely to impact regulatory sequences, which are known to tolerate degeneracy without affecting binding affinity. Second, rate-based methods only report whether a sequence is conserved or not, but do not provide information regarding the specific constraint on each individual base. In the lysine example described above, it is much more informative to tell not only just that the third position is constrained, but also that the base can only be a purine. The availability of such sitewise nucleotide-specific constraint information can provide important clues to the underlying function of the constrained sequence.
Here, we propose a fundamentally different approach to identifying sequences under functional constraint. Rather than modeling the rate of substitutions, our approach focuses on examining the substitution pattern at every site and singling out those that are biased. Our algorithm infers the underlying nucleotide substitution pattern at each base directly from a multiple sequence alignment. We identify sites under constraint as those with a nucleotide substitution pattern significantly deviating from the neutral pattern. In the case of a 2-fold degenerate (2D) codon above, the substitution pattern corresponding to the third codon position will be highly weighted toward A ↔ G substitutions since all other substitutions change the encoded amino acid. This is in contrast to the neutral model where all substitutions, albeit at different frequencies, are expected.
In the following, we first describe the probabilistic model underlying our method (more fully explained in Section 2) and an efficient algorithm for inferring the parameters of the model from sequence alignments. Then we explore the power of the method using both simulation studies and real biological data [genomic sequences in the ENCODE regions (Birney _et al._, 2007)]. In the end, we incorporate our method into a hidden Markov model (HMM) framework to automatically segment a genome into constrained and non-constrained regions. The algorithms described in the article are implemented in a Java software package, called SiPhy (SIte-specific PHYlogenetic analysis), freely available over the web.
2 METHODS
2.1 Inference algorithm in SiPhy
Likelihood function: consider the aligned bases at a position from M species, denoted by (_x_1,…, x M). The likelihood of observing the alignment under the evolutionary model with tree 𝒯 and rate matrix Q is
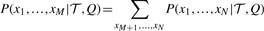 |
(1) |
|---|
where the summation is over all variables in the ancestral nodes of the tree. P(_x_1,…, x N|𝒯, Q) is the complete likelihood, and can be expressed as a product form
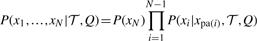 |
(2) |
|---|
where P(x N) represents the prior distribution in the root node. P(x i|_x_pa(i), 𝒯, Q) is the conditional probability of observing x i at node i conditioned on its parent node pa(i), as in Equation (9). The summation in the likelihood function Equation (1) can be efficiently calculated using Felsenstein's pruning algorithm (Felsenstein, 2003).
Learning parameters: parameters in the rate matrix Q are inferred from observed sequence alignments by maximizing the likelihood function in Equation (1)
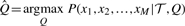 |
(3) |
|---|
We implement an EM-algorithm to solve the problem (Dempster et al., 1977). The algorithm iterates in two steps: E-step, infer the posterior distribution of the variables at the internal nodes; M-step, update Q based on the inferred posterior distribution. Because of the tree structure, the E-step can be solved efficiently using Felsenstein's pruning and peeling algorithm (Felsenstein, 2003). Next we focus on the M-step: find a new Q that maximizes the averaged log likelihood function
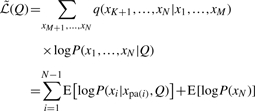 |
(4) |
|---|
where q(·) is the posterior distribution of the variables at the internal nodes conditioned on observed data and the previously estimated parameters. E[_z_] denotes the expectation of z over the posterior distribution q.
The gradient of 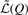 with respect to Q is in general not easy to calculate because Equation (9) involves an exponential matrix term. However, the gradient of
with respect to Q is in general not easy to calculate because Equation (9) involves an exponential matrix term. However, the gradient of 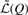 can be greatly simplified by using the sufficient statistics to summarize the continuous time Markov process (CTMP) at each branch (Holmes and Rubin, 2002). Consider a CTMP starting from state a and ending at state b. If all the internal transitional events (denoted as Z) of the Markov process are known, then the transitional probability from a to b conditioned on the internal states can be expressed as
can be greatly simplified by using the sufficient statistics to summarize the continuous time Markov process (CTMP) at each branch (Holmes and Rubin, 2002). Consider a CTMP starting from state a and ending at state b. If all the internal transitional events (denoted as Z) of the Markov process are known, then the transitional probability from a to b conditioned on the internal states can be expressed as
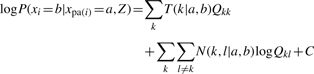 |
(5) |
|---|
where T(k|a, b) summarizes the duration of state k, N(k, l|a, b) is the number of transitions from state k to l, for all k, _l_=1,…, 4 and C denotes variables independent of Q. In general, both T(k|a, b) and N(k, l|a, b) depend on Q. However, we can treat them as latent variables and infer their posterior distributions at the E-step of the EM-algorithm. Details of the derivation are given in the Supplementary Material. In the end, the averaged log likelihood function in Equation (1) can be written as
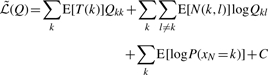 |
(6) |
|---|
where E[T(k)] is the expected duration of state k summed over all branches of the tree, and similarly _E_[N(k, l)] is the expected total number of transitions from k to l. Both of the expectations can be calculated efficiently (see Supplementary Material).
Our goal is to learn ω and π in the Q matrix. The optimal values for both π and ω can be found explicitly by taking the derivative of 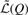 in Equation (6) with respect to π and ω to be 0, leading to the following update rule
in Equation (6) with respect to π and ω to be 0, leading to the following update rule
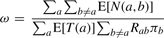 |
(7) |
|---|
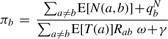 |
(8) |
|---|
for all _b_=1,…, 4. q N b is the posterior distribution of base b at the root node. γ is a Lagrange multiplier and can be found by solving the normalization constraint ∑_b_π_b_=1.
This completes one iteration of the M-step. Note that both ω and π can be found at one step without resorting to gradient-based methods. This implementation significantly improves the speed of the algorithm.
2.2 Sequence data and parameters
Sequence alignments: the Thread Blockset Aligner [TBA, see (Blanchette _et al._, 2004)] of ENCODE regions (September 2005 ENCODE MSA freeze) were downloaded from the UCSC genome browser (Kent et al., 2002). Ancestral repeat (AR) alignments were built from the region alignments by extracting all columns that overlapped ARs>22% diverged from consensus as determined by RepeatMasker. A bootstrapped alignment was obtained by sampling with replacement 250 000 columns from the prior alignment. Both alignment and sequence gaps are treated as missing data in the same way as described in Siepel et al. 2005). For constrained sequence identification, we limited our analysis to columns where the total (neutral) branch length of the species that had an aligned (ungapped) base was larger than 0.5.
SiPhy-HMM parameters: in this work, the two parameters in SiPhy-HMM, α and β, are chosen according to the expected coverage the smoothness of the constrained elements (Siepel et al., 2005). Briefly, coverage can be understood as the prior expected proportion (=α/(α+β)) of conserved bases in the regions being analyzed, and smoothness as prior expectation of the minimum conserved element length (=1/β). These two parameters can be specified in a problem-dependent way. In our analysis of the ENCODE regions, we choose a prior expectation of 8% of constrained sequences and the expected constrained element size of 12 bp which limit the bases called on bootstrapped AR alignments to<0.5%.
3 RESULTS
3.1 The SiPhy model
Suppose we are provided with a set of aligned sequences from M species, whose evolutionary relationship is described by a phylogenetic tree 𝒯=(𝒩, ℰ), specified by a collection of nodes 𝒩 and edges ℰ. Assume 𝒯 is a rooted binary tree, in which case the tree contains _N_=2_M_−1 nodes with _M_−1 being internal (corresponding to ancestral species) and not directly observable. For simplicity, we index the leaf nodes from 1 to M and the ancestral nodes from M+1 to N, always using N for the root node. Denote the variable at node i by S i, which consists of a string of characters drawn from Σ={A, C, G, T}, and represents the orthologous sequence from species i.
We use a probabilistic framework to describe molecular evolution, and model the evolution of sequences along each edge (also referred as branch) of the tree as a CTMP (Durbin et al., 1998; Felsenstein, 2003). Denote the parent of node i by pa(i) and the branch length connecting the two nodes by t i. Assuming that sites evolve independently, the probability of observing base l b at site j in node i conditioned on its parent node having base l a at the same site is
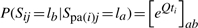 |
(9) |
|---|
for all l a, l _b_∈Σ. Here Q is the instantaneous rate matrix of the CTMP; a and b are indices of base l a and l b in Σ.
Modeling evolutionary constraints: the instantaneous rate matrix Q describes the substitution pattern among the four nucleotides. In this work we decompose Q into three factors: (i) the rate of substitution; (ii) the neutral pattern of substitution; and (iii) the site-specific pattern of substitution. We model these dependencies by parametrizing Q as a product of these three factors:
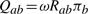 |
(10) |
|---|
for the overall substitution rate of base l a_→_l b.
The three components represent the contributions from three different aspects of molecular evolution. The scalar ω models the overall mutation rate and does not depend on either the original base or the base being substituted to. The matrix R, estimated from neutral sequence prior to running SiPhy (see Section 2), models the substitution pattern between the four nucleotides when they are evolving under no selective pressure, and captures neutral substitution biases, such as transition versus transversion. The vector π=(π1, π2, π3, π4), on the other hand, captures the substitution biases that are site-specific and dependent on the underlying evolutionary constraint acting on the site. For example, the vector π=(1, 0, 0, 0) models a strong selective pressure of preserving nucleotide A at the site, whereas the vector π=(0.5, 0.5, 0,0) captures the evolutionary constraint of a 2D site (A or C), which tolerates mutations between A and C, but not others. Hence, we interpret π_b_ as the selective bias operating on the site: a high value of π_b_ indicates that the site has a preference, due to selective pressure, to be nucleotide l b.
In this work we assume that the substitution matrix R is symmetric (which is equivalent to the assumption that the model is time-reversible). R being symmetric implies that π is the equilibrium distribution of the CTMP with rate matrix Q. Thus, π represents the preferred distribution patterns among the four nucleotides, as constrained by the underlying molecular evolution. A significant deviation of π from the one corresponding to neutral sequences would suggest strong functional constraints acting upon the site. From now on, we will refer to π as the constraint vector at the site.
Note that the previous rate-based methods for constraint detection mainly focus on inferring ω in the above model while ignoring the π factor. In other words, the evolutionary model used by these methods is independent of the specific nucleotide at each site.
Inferring constraints from sequence alignments: the constraint vector π is estimated directly from a multiple sequence alignment (see Section 2). We use the maximum likelihood (ML) method to infer π at each site, that is, to find 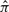 that maximizes the likelihood function, P(_x_1,…, x M|ω, R, π), of observing aligned bases _x_1,…, x M from each of the M aligned species given the constraint vector π, that is
that maximizes the likelihood function, P(_x_1,…, x M|ω, R, π), of observing aligned bases _x_1,…, x M from each of the M aligned species given the constraint vector π, that is
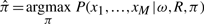 |
(11) |
|---|
In Section 2, we describe a fast and efficient EM-algorithm for solving the ML estimation problem (Dempster et al., 1977). The algorithm treats the sequences at the ancestral nodes and mutational events along each branch of the tree as latent variables and iterates in two steps: (i) E-step, inferring the values of the latent variables conditioned on the current estimation of π. This can be done efficiently using Felsenstein's pruning and peeling algorithm (Felsenstein, 2003); (ii) M-step, deriving a new estimate of π conditioned on the inferred latent variables. In Section 2, we derive a closed analytic expression for the update of π. The scaling factor ω and neutral substitution matrix R can also be inferred from sequence alignments using similar methods (see Section 2).
Measuring significance and identifying constrained elements: once 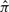 is learned for a given site, we use the log-odds (LO) score to measure the fitness of
is learned for a given site, we use the log-odds (LO) score to measure the fitness of 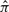 to the observed data,
to the observed data,
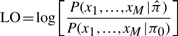 |
(12) |
|---|
where π0 is the neutral nucleotide distribution. High LO scores correspond to sites whose substitution patterns are unexpected under the neutral model and thus are likely under evolutionary constraint. The _P_-value of each LO score is computed based on the distribution of LO scores estimated on neutral sequences (we use ancestral repeats as a surrogate for neutrally evolving sequence in this work, see Section 2). The _P_-value measures the significance of the substitution bias at the position.
In real biological systems, the constrained sites rarely act in isolation; they tend to cluster together, forming larger functional units (e.g. transcription factor-binding sites). Thus, we can pool information from nearby nucleotides to increase the statistical power for detecting constrained sequences. SiPhy achieves this with a moving window-based approach in which we add the individual LO scores within a window of fixed size. Specifically, given the sitewise estimations of the constrained vectors  on a window W of size k, we score the window with
on a window W of size k, we score the window with
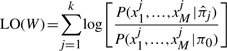 |
(13) |
|---|
where (x_1_j,…, x j M) represents the _j_-th column of aligned bases in W. We also apply the same procedure to neutral sequences to obtain a null distribution of the combined LO scores. We then use this null model to calculate a _P_-value for each LO(W) score. Note that in the window-based approach, the constraint vector is estimated separately for each site and only the scalar LO scores are summed. The actual constraint vector can vary across the window, although power will be reduced if only some sites are under constraint.
3.2 Power estimation
The ML method for estimating π is unbiased and guaranteed to approach the true values when the number of aligned species is sufficiently large. However, in reality, the number and completeness of available genomes limit the types of constrained vectors that are identifiable over those arising by chance. In this section, we use simulated data to investigate how the performance of the ML π estimator depends on both the number of available genomes and the type of substitution bias acting upon each site.
For simplicity we use a star-shaped phylogeny where all aligned species share the same ancestor with equal branch length (d), which is chosen to be _d_=0.47, the number of neutral substitutions per site between human and mouse (Waterston et al., 2002). The star-shaped phylogeny is a simplified, but a good approximation to the phylogeny of the available mammalian genomes (Eddy, 2005; Margulies et al., 2005; Miller et al., 2007), where the non-primates are well separated.
We use information content (IC =2+∑i_=14π_i_log2π_i) to measure how permissive the selection pressure is on each constraint vector π. We randomly generated 200 π vectors with IC evenly distributed between 0 and 2. For each π and a given number of species, we first generated a 200-column alignment by sampling sequences in the leaf nodes using the CTMP model with the rate matrix Q parameterized by π [as in Equation (10)]. We then applied SiPhy to infer π at each aligned column, and computed a LO score for each estimated  . As a comparison, we generated a control alignment using the model with the constraint vector specified by π0=[0.25, 0.25, 0.25, 0.25]. The control alignment corresponds to sequences evolving under no evolutionary pressure. We applied SiPhy to the control alignment to obtain a null distribution of LO scores for calculating _P_-values.
. As a comparison, we generated a control alignment using the model with the constraint vector specified by π0=[0.25, 0.25, 0.25, 0.25]. The control alignment corresponds to sequences evolving under no evolutionary pressure. We applied SiPhy to the control alignment to obtain a null distribution of LO scores for calculating _P_-values.
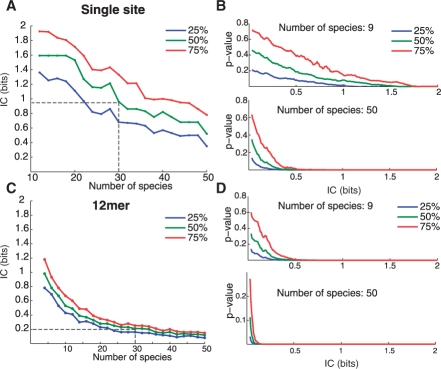
We varied the number of available genomes (M) from 6 to 50. For each M, we identified all π vectors, if any, with at least half of the columns in the corresponding sampled alignment scoring a P <0.001. We picked the one with the lowest IC and used it as a measure of the minimum IC identifiable by SiPhy with the given number of genomes. We found that with _M_=30 SiPhy can reliably identify the constraints with IC as low as 0.95. When M increases to 50, SiPhy can further reduce the minimum IC to 0.5, which roughly amounts to a 3-fold degenerate site (Fig. 1A).
Fig. 1.
Estimating the power of SiPhy for evolutionary constraint detection. The dependence of SiPhy on three factors—the number of available species (M), the IC of each site, and the size of k-mers (1 or 12), is evaluated through a simulation study using a star phylogeny. An element is said to be 50% identifiable by SiPhy if>50% of its instances can be identified by SiPhy with P<0.001, and similarly for 25% and 75% identifiable. (A) The lowest IC of a single site that is 25% (blue), 50% (green) or 75% (red) identifiable is shown as a function of M. (B) The 25%, 50% and 75% percentile _P_- values are shown as the function of the IC of a single site, with the number of species fixed at _M_=9 (top) and _M_=50 (bottom). (C) and (D) show similar plots for 12mers. Plot the number of bases recovered at P<0.001 for a given IC. The blue line corresponds to 25% of bases recovered, green corresponds to 50% of bases recovered and red corresponds to 75% of bases covered.
These simulations demonstrate the power of using SiPhy to identify even weak site-specific constraints when the number of aligned species is sufficiently large. However, it also illustrates the limitation of the method when applied to small datasets. Current datasets have at best a total branch length of 4 substitutions per site, which is roughly equivalent to the star-shaped phylogeny composed of nine species. With only nine species, SiPhy can only reliably identify π vectors with IC >1.65 (Fig. 1B).
To overcome the limitation posed by the small number of available genomes, we used a sliding 12mer window as described above. We picked a 12mer because it is small enough to represent a large regulatory motif, and of sufficient size to provide enough power. A _P_-value was calculated for each 12mer using the same null model described above. Figure 1C plots the minimum IC (averaged over columns within the window) that can be identified by SiPhy as a function of M (again using the same criteria that at least half of the total windows score a P <0.001). With nine aligned species, SiPhy can now reliably identify 12mers with the average IC < 0.6. In other words, the availability of the current genomes should enable SiPhy to detect 12mers whose sites are on average close to 3-fold degenerate (Fig. 1D).
3.3 Application I: detecting degenerate functional sites
As discussed in the Section 1, many third nucleotides in codons are 2D sites, which can alternate between two bases without affecting the encoded amino acid. Assuming no strong codon bias, these sites provide an excellent biological dataset to benchmark the performance of SiPhy to detect functional sites that are degenerate.
We created a test dataset by concatenating the aligned columns at the 2D sites of the genes in the ENCODE regions (Birney et al., 2007). As a comparison, we also created a control dataset by extracting and concatenating columns at the 4-fold degenerate (4D) codon positions, that is, the positions at which nucleotides can freely change without affecting the encoded amino acids.
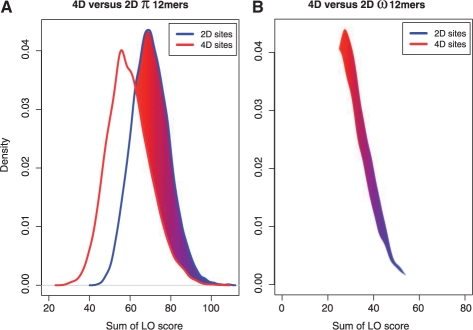
We applied SiPhy to infer π and calculate the corresponding LO score at each site, and then integrated the LO scores over a 12mer window as described in the previous section. Figure 2A plots the distributions of 12mer LO scores for both the 2D and the 4D datasets. It shows that the distributions of π LO scores for the two functionally distinct datasets are clearly well separated, with a median of 70.1 versus 59.5 for 2D and 4D sites, respectively. If we use the 4D dataset as a control, 42.9% of the 12mers in the 2D dataset can be identified as constrained by SiPhy.
Fig. 2.
SiPhy shows greater power for detecting degenerate sites. The figure shows the distributions of LO scores for separating constrained 12mers from neutral ones within two datasets: the 2D and the 4D degenerate sites in the third codon positions. The LO scores are calculated using either π-based method (A) or a rate-based method (B). The shaded regions represent the portion of the sites that show excess constraint in the 2D dataset if the 4D dataset is used as a control.
We also implemented a procedure to estimate the rate parameter ω only, as a representative of the rate-based methods [see Equation (10) and the section on the SiPhy model]. Specifically, we fix π=π0, the neutral background distribution, then infer ω, compute a LO score at every site and integrate it over a 12mer window, similar to the π-based method. The ω LO score distributions for the 2D and 4D datasets are shown in Figure 2B; clearly the two distributions are much closer than the corresponding π LO score distributions, with medians of 28.9 and 25.6 for 2D and 4D sites, respectively. In particular, using the 4D sites as a control, only 16.1% of all 12mers in the 2D dataset can be identified as constrained, almost a 3-fold decrease in predictive power compared to the 42.9% called by the π-based method. This suggests that the π method has increased power to detect degenerate constraint.
3.4 Application II: 1% of the human genome
We next applied our approach to the ENCODE regions. These regions represents 1% of the human genome and have been deeply sequenced across 21 placental mammals corresponding to a total branch length of approximately 3.0 substitutions per site (Birney et al., 2007) (see Supplementary Fig. 1). However, due to missing sequences and alignment gaps, the effective branch length available at each site is typically much smaller: 75% of the sites have total branch length less than 2.2, roughly equivalent to having _M_=4.7 genomes in the our simulation study above. Analysis of this dataset therefore requires a window-based approach to gain enough power. In the simulation study, we show that with _M_=4.7 SiPhy is able to detect constraints with an average IC=1 bit (or 2D) using a 12mer window (Fig. 1C). Although using a longer window can alleviate the IC limitation, it decreases the power for detecting short functional elements. Thus, we focus our analysis here using a 12mer window; in a later section we will introduce a method to overcome the need of fixing a window size.
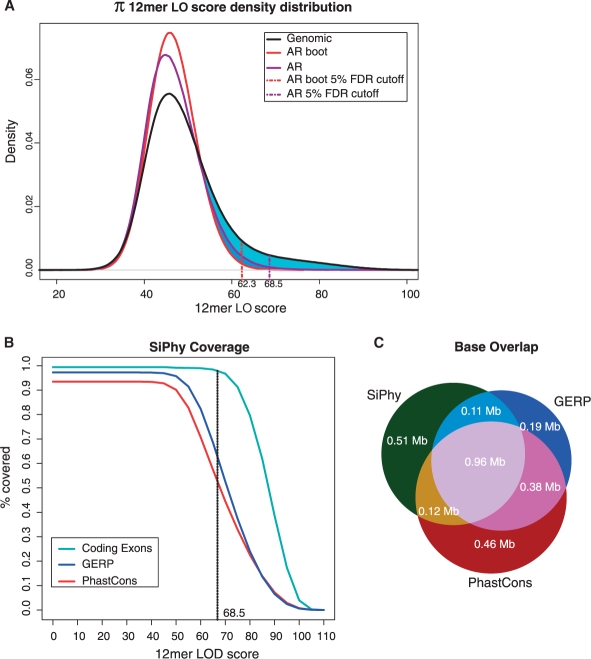
How much is under constraint? The distribution of the combined LO scores calculated by SiPhy over all 12mer windows in the ENCODE regions is plotted in Figure 3A, which shows a clear enrichment of high scoring 12mers. To estimate the portion of the 12mers that are truly under evolutionary constraint, we also calculated the distribution of 12mer LO scores using two control datasets from the same regions. One dataset consists of aligned sequences that have been annotated as ARs (see Section 2). ARs typically originate from transposable elements or remnants of inactive transposons. Although ARs have been commonly used as a surrogate for neutral sequences, recent studies suggest that a small subset of the AR sequences might be functional (Bejerano et al., 2006; Kamal et al., 2006; Xie et al., 2006). To account for this effect, we also curated a second control dataset via bootstrapping by randomly sampling aligned columns from the AR alignments as described in (Cooper et al., 2005). The bootstrapped dataset destroys local dependency between the aligned columns, and therefore dilutes the effect of potential functional sequences.
Fig. 3.
Estimating constraint in the ENCODE regions. (A) Comparison of constraints in neutral sequences versus genomic (ENCODE) regions. The 12mer LO scores are computed by SiPhy for ARs, bootstrapped ancestral repeats (AR boot) and genomic regions (black). Excess constraint in the genomic regions is highlighted by the shaded region in light blue when compared to AR, and in both light blue and dark blue when compared to AR boot. (B) Overlap between SiPhy elements and three other types of elements: coding exons (green), GERP (blue) and PhastCons (red). Each curve shows the percentage of the elements overlapped by SiPhy 12mers for a given LO score cutoff. (C) A Venn diagram of SiPhy, PhastCons and GERP elements in the ENCODE regions.
The three distributions of π LO scores are plotted together in Figure 3A. Compared to the control datasets, the distribution of LO scores in the ENCODE regions shows a clear enrichment of high scores. Using the AR dataset as a control, we estimate that 7.4% of the 12mers in the ENCODE regions show an excess of high LO scores, and therefore likely evolve under constraint. With the bootstrapped AR as a control, 9.4% of the 12mers are estimated to evolve under constraint. Since the AR control dataset potentially contains functional sequences while the bootstrapped AR control dataset ignoring local dependencies, these estimates give lower and upper bounds for the true percentage of the 12mers evolving under selection. Note that these numbers are not the same as the actual fraction of bases under selection since overlapping windows are used.
Comparison to the constrained elements identified by other methods: to generate a high confidence list of 12mers that are likely under evolutionary constraint, we used a LO score threshold that controls the false discovery rate (FDR) at 5%. The FDR at a given LO score threshold (s) is estimated to be the ratio between the number of the 12mers with LO scores ≥s in a control dataset and the number in the entire ENCODE regions, normalized by the total sizes of the two datasets.
Using the AR dataset as a control results in a LO score threshold of _s_=68.5. After merging all overlapping 12mers with scores above the threshold, we obtained 45 229 elements spanning 1.7 M bases, corresponding to 5.8% of the ENCODE regions. If we use instead the bootstrapped AR dataset as a control, controlling FDR at 5% results in a lower LO score threshold of _s_=62.3, from which we identified 3.1M constrained bases, corresponding to 10.2% of the entire ENCODE regions. We therefore estimate that the true percentage of the constrained bases, after controlling FDR at 5%, should be in the range of 5.8–10.2%. Next we compare the constrained elements identified by SiPhy to those discovered by two previous methods—PhastCons (Siepel et al., 2005) and GERP (Cooper et al., 2005).
First, we note that SiPhy identified significantly more sequences as constrained than both PhastCons and GERP. Using bootstrapped sequences as a control and controlling FDR at 5%, PhastCons identified 6.5% of the bases as constrained, whereas GERP called 5.6% as constrained, both of which are lower than the 10.2% identified by SiPhy.
Second, although SiPhy identified most of the constrained elements discovered by PhastCons and GERP, a significant number of SiPhy elements do not overlap with either PhastCons or GERP elements and vise versa (Fig. 4B and C). In particular, only 56% of the elements are shared by all three methods, suggesting that the three methods are likely complementary to each other, capturing different aspects of molecular evolution. We note that the sequences uniquely identified by SiPhy tend to have lower IC than those shared by SiPhy and one of the other methods, suggesting that SiPhy picks up more degenerate sequences than PhastCons or GERP.
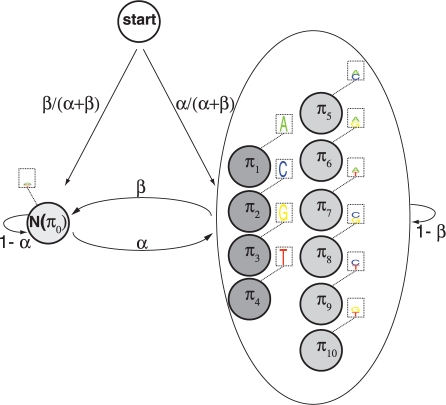
Fig. 4.
SiPhy-HMM state diagram. A schematic representation of the HMM used to identify SiPhy constrained elements. N(π0) represents the neutral state. The constrained state is represented by a mixture of 10 constraint vectors, of which four are non-degenerate (π1–π4) and six are 2D (π6–π10).
Finally, we examined the distribution of the SiPhy elements in the genome and found that they are more enriched in known functional regions such as UTRs and promoters than the PhastCons or GERP elements (Supplementary Table 1). In particular, the SiPhy elements showed a approximately a 3-fold enrichment in uniquely called exonic and promoter bases when compared to the PhastCons or GERP elements, consistent with the notion that these regions are enriched with degenerate regulatory motifs. To explore this further, we focused on the top 207 elements uniquely identified by SiPhy that scored higher than any bootstrapped AR elements, and examined their genomic locations in more detail. Of those 207 unique elements, 58 are exonic, 19 fall in UTRs and 37 are in promoter regions; all together, the elements located in known functional regions account for 55% of the total elements. In contrast, if these elements were distributed randomly across the genome, only 10% are expected to be in these regions.
3.5 Incorporating SiPhy into a HMM
So far we have been using combined LO scores within a window to discover constrained elements. A main disadvantage of the window-based approach is that it uses a fixed window size, while in reality the constrained elements may be of different sizes. To address this limitation, we incorporated SiPhy into a HMM to automatically segment a sequence into constrained and non-constrained regions. We refer to the combined SiPhy and HMM framework as SiPhy-HMM (Fig. 4).
We used a two-state HMM model to model sequence alignments. In this model, each base is either constrained or evolving neutrally, denoted as z _i_=1 or 0, respectively for the base at position i. The probability of observing the aligned bases S _i_=(S_1_i,…, S Mi) at position i is then described by two conditional probabilities P(S i|z _i_=1) and P(S i|z _i_=0), depending upon whether the underlying state is constrained or not.
We use P(S i|z _i_=0)=P(S i|π0), where π0 is the background nucleotide distribution, to model the conditional probability of the state being unconstrained. For constrained states, since we do not know the exact form of constraint at each position, we opted to use a mixture model and assume that the conditional probability P(S i|z _i_=1) is described by a mixture of K constrained evolutionary models:
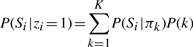 |
(14) |
|---|
where π_k_ represents the constraint vector associated with model k, and P(k) is its prior distribution. In the present work we use _K_=10 constrained π vectors: four non-degenerate vectors and six 2D vector (Fig. 4). The 10 constrained vectors can be viewed as a discretization of the 3-dimensional constraint vector simplex, and we assume a uniform prior on their distribution. We have also added a small pseudo-count to each entry of the vectors to make sure that every entry is non-zero.
The transition between states is described by: α=P(z i+1=1|z _i_=0), which species the transition probability from the neutral state to the constrained state, and β=P(z i+1=0|z _i_=1), which specifies the transition probability from the constrained state to the neutral state. Both α and β can be learned directly from data, or be chosen according to the expected coverage and smoothness of the constrained elements (see Section 2).
Applying SiPhy-HMM to the ENCODE regions: we applied SiPhy-HMM to the ENCODE data and used the Viterbi algorithm to infer the state of each base when given an aligned sequence data (Durbin et al., 1998). Overall, we obtained 31 292 constrained elements, covering a total number of 1.8M bp. There is good agreement with the elements found by the k-mer-based method described in the previous section (77% of bases found there were identified by both methods). On the difference side, the SiPhy-HMM elements are typically larger (with a mean element size of 57 bp versus 37 bp as in the k-mer-based method), and with lower IC. It appears that the k-mer-based method is more suited to find small elements such as transcription factor-binding sites, whereas the HMM approach is preferable to discover larger regions under weaker, or more degenerate, constraint.
The SiPhy-HMM elements overlap most of the PhastCons elements (60%) reported by the ENCODE project (Birney et al., 2007; Margulies et al., 2007). However, there are also significant differences between the two: 11 877 elements spanning 234 Kb are identified by SiPhy-HMM only, and 14 926 elements spanning 437 Kb are identified by PhastCons only. Moreover, the sets of elements unique to each method are markedly different with respect to their distributions in the genome (Table 1). The SiPhy-HMM unique elements are significantly more enriched in UTRs and promoters than the PhastCons unique elements, consistent with the observation made about the SiPhy elements identified in the previous section. In particular, 10.7% of the SiPhy-HMM unique elements are located in the upstream regions of genes (5′ UTRs or promoters), compared to the 2.9% (3.7-fold enrichment) of the PhastCons elements located in these regions. The upstream regions are known to be enriched with transcription factor-binding sites or other types of regulatory motifs. Many of these elements contain degenerate sites, which may explain why SiPhy-HMM picks up more sequences in these regions.
Table 1.
Genomic locations of the elements uniquely identified by SiPhy-HMM
| Region | SiPhy-HMM | PhastCons | SiPhy-HMM | GERP |
|---|---|---|---|---|
| Coding exons | 15 969 (6.8%) | 6441 (2.8%) | 16 395 (7.2%) | 9236 (3.2%) |
| Intronic | 108 564 (46.4%) | 214 488 (49.1%) | 105 919 (46.3%) | 146 287 (49.9%) |
| 5′ UTR | 3839 (1.6%) | 59 (0.0%) | 2934 (1.3%) | 404 (0.1%) |
| 3′ UTR | 9367 (4.0%) | 9656 (2.2%) | 6455 (2.8%) | 11 956 (4.1%) |
| 5 kb from TSS | 21 187 (9.1%) | 12 851 (2.9%) | 18 087 (7.9%) | 9509 (3.2%) |
| 5 kb downstream | 8383 (3.6%) | 12 274 (2.8%) | 8391 (3.6%) | 7033 (2.4%) |
| Intergenic | 66 653 (28.5%) | 179 701 (41.1%) | 70 385 (30.8%) | 108 659 (37.1%) |
| Total | 233 962 | 437 255 | 228 566 | 293 084 |
4 DISCUSSION
In this work, we described a new statistical method for modeling the evolution of sequence under selective constraint. The method works by examining the pattern of base substitutions at each site, rather than the rate of substitutions as all previous methods do. We also presented an efficient learning algorithm and a publicly available software package for inferring sitewise constraints directly from a sequence alignment. We proposed two methods to identify constrained elements—a moving window-based approach and a HMM-based approach. Benchmarking of the new method on sequences consisting of degenerate functional sites demonstrates that the method outperforms the traditional rate-based methods for detecting weakly constrained functional sequences. Application of the method to the ENCODE regions predicts that as much as 10.2% of the sequences in the regions are evolutionarily constrained.
The computational method described here is only a first attempt at using site-specific nucleotide substitution patterns for comparative genome analysis. As such, we have focused on specific evolutionary models and statistical methods, both of which can be further improved. First, in the evolutionary model described by Equation (10) the transition rate from base a to base b only depends only on the constraint at the ending state (π_b_), but not at the starting state (π_a_). The transition rate might be better modeled by the relative constraints between the two, using, for instance, the Halperin–Bruno model (Halpern and Bruno, 1998). Second, our current method treats the alignment gaps as missing sequence. It would be more desirable to model the evolution of indels directly and incorporate the indel model into the nucleotide substitution model (Diallo et al., 2007; Rivas and Eddy, 2008; Snir and Pachter, 2006). Our model assumes that the constraint is shared by all species in the phylogenetic tree, which can be improved by considering lineage-specific changes. Third, at the inference side, we used the ML method to infer the constraint vector π. An alternative strategy is to adopt a Bayesian approach by integrating all potential π vectors weighted by their posterior probabilities. The Bayesian approach will likely be more robust when the number of available genomes is small. Fourth, SiPhy, like other existing methods, heavily depends on the underlying alignment. Alignment errors may influence both false negative and positive discovery rates. Finally, our model assumes that each site evolves independently and thus cannot capture the evolution of sites (e.g. CpG dinucleotide) that is context-dependent. We should also mention that not all biased mutations are the results of selection; a notable exception is the mutation caused by biased gene conversion. To improve our approach, we will need to filter out the sites caused by these neutral biased mutations.
An important feature of our method is that it cannot only detect constrained elements, but it also provides information about the potential functional constraints associated with each base of the constrained sequences. The constraint is described as a weight vector among the four bases, representing the preference of different bases at each position. This type of representation has been widely used in describing the binding properties of transcription factors. Indeed, one immediate usage of the inferred constraint vectors is for de novo motif discovery by clustering the identified constrained elements. Previous comparative genomics methods for genome-wide motif discovery often adopt a reference genome centric view by first searching for a motif site in the reference genome and then checking whether the sites are conserved in other species (Stark et al., 2007; Xie et al., 2005. Motif discovery via clustering constraint vectors does not have such limitation, and can account for sequence variation and phylogeny of all species being compared. Another application of our method is to detect compensatory mutations characteristic of many non-coding RNAs and to characterize sequences with unknown functions such as large ncRNAs (Guttman et al., 2009). As the field begins to transit from identification of conserved elements to characterization of these elements, our method can aid this transition by providing information on specific evolutionary signatures underlying these conserved elements.
ACKNOWLEDGEMENTS
We thank M. Kamal, T. Mikkelsen and Or Zuk for insightful comments on the article; M. Kellis, P. Kheradpour, E. Lander, M. Lin, K. Lindblad-Toh, M. Rasmussen and A. Stark for helpful discussions.
Funding: UCI (to XX); NHGRI (to MG, MC and MZ); Israel Science Foundation (to NF).
Conflict of interest: none declared.
REFERENCES
- Asthana S, et al. Analysis of sequence conservation at nucleotide resolution. PLOS Comput. Biol. 2007;3:e254. doi: 10.1371/journal.pcbi.0030254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bejerano G, et al. A distal enhancer and an ultraconserved exon are derived from a novel retroposon. Nature. 2006;441:87–90. doi: 10.1038/nature04696. [DOI] [PubMed] [Google Scholar]
- Birney E, et al. Identification and analysis of functional elements in 1% of the human genome by the encode pilot project. Nature. 2007;447:799–816. doi: 10.1038/nature05874. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanchette M, et al. Aligning multiple genomic sequences with the threaded blockset Aligner. Genome Res. 2004;14:708–715. doi: 10.1101/gr.1933104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper GM, et al. Distribution and intensity of constraint in mammalian genomic sequence. Genome Res. 2005;15:901–913. doi: 10.1101/gr.3577405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempster A, et al. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. 1997;39:1–38. [Google Scholar]
- Diallo AB, et al. Exact and heuristic algorithms for the indel maximum likelihood problem. J. Comput. Biol. 2007;14:446–461. doi: 10.1089/cmb.2007.A006. [DOI] [PubMed] [Google Scholar]
- Durbin R, et al. Biological Sequence Analysis. New York: Cambridge University Press; 1998. [Google Scholar]
- Eddy SR. A model of the statistical power of comparative genome sequence analysis. PLoS Biol. 2005;3:e10. doi: 10.1371/journal.pbio.0030010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. Inferring Phylogenies. MA., USA: Sinauer Associates Sunderland; 2003. [Google Scholar]
- Green P. 2x genomes Does depth matter? Genome Res. 2007;17:1547–1549. doi: 10.1101/gr.7050807. [DOI] [PubMed] [Google Scholar]
- Guttman M, et al. Chromatin signature reveals over a thousand highly conserved large non-coding rnas in mammals. Nature. 2009;458:223–227. doi: 10.1038/nature07672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halpern A, Bruno W. Evolutionary distances for protein-coding sequences: modeling site-specific residue frequencies. Mol. Biol. Evol. 1998;15:910–917. doi: 10.1093/oxfordjournals.molbev.a025995. [DOI] [PubMed] [Google Scholar]
- Holmes I, Rubin GM. An expectation maximization algorithm for training hidden substitution models. J. Mol. Biol. 2002;317:753–764. doi: 10.1006/jmbi.2002.5405. [DOI] [PubMed] [Google Scholar]
- Kamal M, et al. A large family of ancient repeat elements in the human genome is under strong selection. Proc. Nat. Acad. Sci. 2006;103:2740–2745. doi: 10.1073/pnas.0511238103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent WJ, et al. The Human Genome Browser at UCSC. Genome Res. 2002;12:996–1006. doi: 10.1101/gr.229102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margulies E, Birney E. Approaches to comparative sequence analysis: towards a functional view of vertebrate genomes. Nat. Rev. Genet. 2008;9:303. doi: 10.1038/nrg2185. [DOI] [PubMed] [Google Scholar]
- Margulies E, et al. An initial strategy for the systematic identification of functional elements in the human genome by low-redundancy comparative sequencing. Proc. Natl Acad. Sci. USA. 2005;102:4795–4800. doi: 10.1073/pnas.0409882102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margulies EH, et al. Identification and characterization of multi-species conserved sequences. Genome Res. 2003;13:2507–2518. doi: 10.1101/gr.1602203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margulies EH, et al. Analyses of deep mammalian sequence alignments and constraint predictions for 1% of the human genome. Genome Res. 2007;17:760–774. doi: 10.1101/gr.6034307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller W, et al. 28-Way vertebrate alignment and conservation track in the UCSC Genome Browser. Genome Res. 2007;17:1797. doi: 10.1101/gr.6761107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruitt KD, et al. NCBI Reference Sequence (RefSeq): a curated non-redundant sequence database of genomes, transcripts and proteins. Nucleic Acids Res. 2005;33:D501–D504. doi: 10.1093/nar/gki025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivas E, Eddy SR. Probabilistic phylogenetic inference with insertions and deletions. PLoS Comput. Biol. 2008;4:e1000172. doi: 10.1371/journal.pcbi.1000172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siepel A, et al. Evolutionarily conserved elements in vertebrate, insect, worm, and yeast genomes. Genome Res. 2005;15:1034–1050. doi: 10.1101/gr.3715005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snir S, Pachter L. Phylogenetic profiling of insertions and deletions in vertebrate genomes. In: Apostolico A, et al., editors. Lecture Notes in Computer Science. Vol. 3909. New York: Springer; 2006. pp. 265–275. RECOMB. [Google Scholar]
- Stark A, et al. Discovery of functional elements in 12 drosophila genomes using evolutionary signatures. Nature. 2007;450:219–232. doi: 10.1038/nature06340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waterston RH, et al. Initial sequencing and comparative analysis of the mouse genome. Nature. 2002;420:520–562. doi: 10.1038/nature01262. [DOI] [PubMed] [Google Scholar]
- Xie X, et al. Systematic discovery of regulatory motifs in human promoters and 3′UTRs by comparison of several mammals. Nature. 2005;434:338–345. doi: 10.1038/nature03441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie X, et al. A family of conserved noncoding elements derived from an ancient transposable element. Proc. Nat. Acad. Sci. 2006;103:11659. doi: 10.1073/pnas.0604768103. [DOI] [PMC free article] [PubMed] [Google Scholar]