Explaining worldwide patterns of human genetic variation using a coalescent-based serial founder model of migration outward from Africa (original) (raw)

Abstract

Studies of worldwide human variation have discovered three trends in summary statistics as a function of increasing geographic distance from East Africa: a decrease in heterozygosity, an increase in linkage disequilibrium (LD), and a decrease in the slope of the ancestral allele frequency spectrum. Forward simulations of unlinked loci have shown that the decline in heterozygosity can be described by a serial founder model, in which populations migrate outward from Africa through a process where each of a series of populations is formed from a subset of the previous population in the outward expansion. Here, we extend this approach by developing a retrospective coalescent-based serial founder model that incorporates linked loci. Our model both recovers the observed decline in heterozygosity with increasing distance from Africa and produces the patterns observed in LD and the ancestral allele frequency spectrum. Surprisingly, although migration between neighboring populations and limited admixture between modern and archaic humans can be accommodated in the model while continuing to explain the three trends, a competing model in which a wave of outward modern human migration expands into a series of preexisting archaic populations produces nearly opposite patterns to those observed in the data. We conclude by developing a simpler model to illustrate that the feature that permits the serial founder model but not the archaic persistence model to explain the three trends observed with increasing distance from Africa is its incorporation of a cumulative effect of genetic drift as humans colonized the world.

Keywords: admixture, heterozygosity, linkage disequilibrium, population divergence

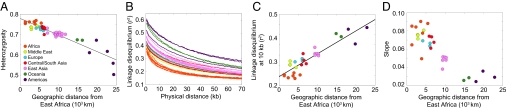
The nature of the origin and geographic spread of anatomically modern humans has been the focus of much recent interest in anthropology and genetics (1–6), with considerable effort having been centered on the potential contribution of archaic hominids to the modern human gene pool (7–12). Within this context, population-genetic studies have examined a variety of aspects of worldwide human variation, identifying several striking geographical patterns in statistics that describe human genetic diversity (Fig. 1). First, the level of genetic variation, as measured by heterozygosity, exhibits a linear decline as a function of geographic distance from Africa (13–15). Second, LD increases linearly as a function of geographic distance from Africa (16). Third, the ancestral allele frequency spectrum “flattens” with increasing geographic distance from Africa, indicating that derived alleles tend to be more frequent in populations at a greater distance away from Africa (15).

Fig. 1.

Fig. 1.

Patterns of heterozygosity, LD, and the ancestral allele frequency spectrum observed in human population-genetic data. (A) Heterozygosity as a function of distance from East Africa (redrawn from ref. 14 as in figure 7C of ref. 32). (B) LD measured by _r_2 as a function of physical distance in kb (redrawn from supplemental figure 4 of ref. 16). (C) LD at 10 kb measured by _r_2 as a function of distance from East Africa (based on data in supplemental figure 4 of ref. 16). (D) Slope of the ancestral allele frequency spectrum in the range of 20% to 80% ancestral allele frequency as a function of distance from East Africa (modified from figure 4B of ref. 15 using a resampling technique and the allele frequencies in Fig. S4).

These three patterns point to an important role for Africa in the history of human genetic variation. Thus, many models involving migrations outward from Africa have been proposed for providing simulation-based explanations of geographical patterns in human genetic data. This collection of models includes coalescent-based migration models that proceed retrospectively in time and that are easily simulated, but that involve relatively few populations, each of which typically represents a large geographic region (11, 17–19). It also includes models that permit complex phenomena and multiple populations per continent through a prospective approach, but that are often limited in terms of computation time and applicability to statistical inference (14, 20–22).

One model that has performed well in explaining the decline of heterozygosity with increasing distance from Africa is a model of serial founder events beginning from an African origin (14, 22, 23). In this model, starting with a single source population, a new population is formed from a subset of the individuals in the founding population. The new population experiences a bottleneck, in that it is founded by a small group. It grows to a larger size, after which a subset of the population becomes the founding group for a third population. The founding process is then iterated (Fig. 2A). Simulations of the serial founder model in a prospective framework produce a decrease of heterozygosity in each subsequent group, so that heterozygosity appears to decline linearly with the number of colonization steps from the source population. Intuitively, when a new colony is founded, it carries only a subset of the diversity from the previous colony, and therefore, a heterozygosity decrease occurs. Thus, it has been shown that, if the source is placed in Africa, then the prediction of serial founder models matches the observed pattern of heterozygosity (14, 22, 23). It has also been suggested that the serial founder model can explain worldwide patterns in LD and the ancestral allele frequency spectrum (15, 16), although these claims have not yet been verified in simulations of the model.

Fig. 2.

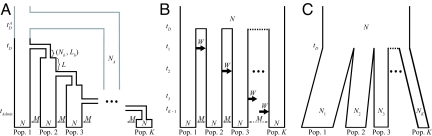
Fig. 2.

Models. (A) Serial founder model with population size N diploid individuals in each of K populations, time _t_D of the first divergence from the founding population, bottleneck size _N_b, bottleneck length _L_b, time interval L between successive bottlenecks, and symmetric migration rate M between neighboring populations. An extension of the model that allows admixture with archaic humans has additional parameters for the population size for archaic humans (_N_A), divergence time between modern and archaic humans (t_D_A), and time of admixture between a specific modern population and the archaic population (_t_Admix). (B) Archaic persistence model with population size N diploid individuals in each of K populations, time _t_D of the divergence of archaic populations, symmetric migration rate M between neighboring populations, and migration rate W for the migration wave from population k to population k + 1 at time _t_k. (C) Instantaneous divergence model with population sizes _N_k for populations k = 1, 2, …, K, population size N for the ancestral population, and divergence time _t_D.

Here, we develop a retrospective coalescent approach that enables a generalization of the serial founder model. Because few models of human range expansions have considered linked loci (24), our approach makes it possible to examine a broader variety of patterns than have been studied in most out-of-Africa models. Rather than performing formal statistical inference under our new general model, we aim to determine whether the model qualitatively accords with worldwide trends in human genetic variation. We indeed find that the new model provides explanations not only of geographic patterns of heterozygosity, but also of patterns of LD and the ancestral allele frequency spectrum. The model accommodates migration between neighboring colonies and admixture between modern and archaic populations; through the introduction of two additional models, an archaic persistence model and an instantaneous divergence model, we discuss the extent to which these phenomena are compatible with worldwide variation patterns.

Results

Overview of Models.

Our serial founder model is a special case of a more general model (Fig. 2A). In our serial founder model, each of K populations, numbered with increasing distance from a founding group (population 1), has present population size N diploid individuals. The divergence time of populations 1 and 2, _t_D generations ago, represents the time of formation of a second modern human population. The model proceeds as a series of founding events in which a group of individuals migrates from the most recently founded colony to form a new colony. Because each founding group is small compared with its source, when a new colony k is founded, it undergoes a bottleneck of size _N_b < N individuals lasting _L_b generations. It then immediately expands to size N. After L generations, a group of individuals migrates from colony k to found population k + 1. Population divergence times are arranged such that founding events occur at intervals of _t_D/(K − 1) generations. Thus, L + _L_b = _t_D/(K − 1).

To include migration between neighboring populations, as in Deshpande et al. (22), we add symmetric migration between neighbors at rate M = 4_Nm_, where m is the per-generation fraction of a population consisting of new migrants. Backward in time, population k sends migrants to populations k − 1 and k + 1, each with rate M, and populations k − 1 and k + 1 send migrants to population k, each with rate M. Migration only involves populations that have already been founded, so that during the stage when population k is the newest population, it only experiences migration with one colony instead of two. Populations 1 and K never experience migration with two populations during the entire time of their existence.

In our general model, an archaic population diverges at time t_D_A generations (t_D_A > _t_D) to form a population of constant diploid size _N_A individuals. After a period of isolation, the archaic population admixes with a single modern population k* at rate γ so that at time _t_Admix generations, the probability that a lineage from population k* enters the archaic population is γ going back in time. Admixture occurs L/2 generations after population k* expands to size N.

Simulations.

Sets of K populations under the basic serial founder model, the migration model, and the archaic admixture model were simulated using the coalescent simulator MS (25). For each model, parameter values that produced representative phenomena were selected within plausible ranges. Each population sample consisted of n 100 kb chromosomes, randomly paired to create n/2 diploid individuals. We used a 25-year generation time, a sequence length _S_L = 105 bases, a per-base mutation rate μs = 2.5 × 10−9, a per-base recombination rate _r_s = 2.50025 × 10−9, and a population size N = 10,000. These values produce a population mutation rate θ = 4_N_μ = 10, where μ = _S_Lμs, and a population recombination rate ρ = 4_N_r = 10, where r = (_S_L − 1)_r_s. For each model, we simulated 5,000 datasets of K = 100 populations, each with a sample of size n = 50. Heterozygosity, LD, and the slope of the ancestral allele frequency spectrum were calculated for each dataset, and weighted averages were taken over replicate simulations to produce final values of the statistics (see Materials and Methods). MS commands appear in SI Appendix.

Basic Model.

We first examined a basic serial founder model with _t_D = 2,079 (51.975 kya), with no migration between neighbors and no archaic admixture. We used a bottleneck size of _N_b = 250, a bottleneck length of _L_b = 2, and a time length between a population expansion and the founding of a new colony of L = 19. These choices were largely designed to mimic values used in past simulations (14, 21).

Under this model, Fig. 3A displays a linear decline in heterozygosity with increasing colony number. The heterozygosities are small, because they are means over all segregating sites, and many sites are monomorphic within a given population sample. However, the qualitative pattern matches that seen in data (Fig. 1A) and in forward simulations (14, 21, 22). The LD decay with increasing distance along a chromosome has a pattern in which populations far from the parental colony have the highest LD (Fig. 3B). Focusing on LD at 10 kb, a linear LD increase with increasing colony number is apparent (Fig. 3C). We can also observe a flattening of the ancestral allele frequency spectrum with increasing colony number, as reflected in a decline in the regression slope of this spectrum on ancestral allele frequency (Fig. 3D). Thus, the serial founder model produces LD patterns and ancestral allele frequency spectra that match those observed in data (Fig. 1).

Fig. 3.

Fig. 3.

Patterns of heterozygosity, LD, and the ancestral allele frequency spectrum in simulations of the basic serial founder model. (A) Heterozygosity as a function of colony number. (B) LD measured by _r_2 as a function of physical distance in kilobases. (C) LD at 10 kb measured by _r_2 as a function of colony number. (D) Slope of the ancestral allele frequency spectrum in the range of 20% to 80% ancestral allele frequency as a function of colony number.

Migration.

We next added symmetric migration to our basic model, with rate M = 4_Nm_ between neighboring colonies, holding all other parameters the same. To represent higher and lower migration rates, we considered M = 40 and M = 1.

Fig. 4 and Fig. S1 show, as was observed in the case of no migration, that as colony number increases there is a decline in heterozygosity, an increase in LD, and a decline in the slope of the ancestral allele frequency spectrum. These results suggest that the migration parameter does not have a major effect on the qualitative patterns, and that inclusion of migration only slightly alters the patterns observed with bottlenecks alone.

Fig. 4.

Fig. 4.

Patterns of heterozygosity, LD, and the ancestral allele frequency spectrum in simulations of the serial founder model with symmetric migration at rate M = 40 between neighboring populations. All other parameters are the same as in Fig. 3.

One possible reason for a stronger influence of bottlenecks compared with migration is that in the time scale of the model—with recent bottlenecks followed by short periods of migration—migration between neighbors might not move ancestral lineages very far from their original locations. Instead of being located during the bottleneck at the founding of the population from which two lineages are sampled, the common ancestor for a pair of lineages might be located during a bottleneck only a few steps earlier in the serial expansion. Although migration increases the coalescence time of a random pair of lineages from a population relative to the corresponding time in the model without migration, the extra time to coalescence caused by migration might typically be quite small.

A heterozygosity peak visible in the first few populations (Fig. 4) is likely to result from edge effects. Central populations receive more diverse migrants than edge populations, because migration brings in distant lineages from both sides. In a similar model in which a linearly-arrayed population has persisted for a long time (26), diversity is greatest at the center, because the ancestors of lineages in the center typically wander over a greater range before coalescing. In our model, the fact that central populations originate more recently than populations near the source lessens this effect, because lineages from groups near the source have been through fewer bottlenecks than lineages in the middle and might therefore have deeper coalescence times. As a result of the competing effects of bottlenecks and migration, the highest diversity occurs in populations located between the source and the center.

Archaic Admixture.

We next added archaic admixture to the basic model, using _N_A = 1,000 for the size of the archaic population, t_D_A = 16,000 (400 kya) for the splitting time of the modern and archaic populations, and _t_Admix = 1584.5 (39.6125 kya) for the time of admixture. Archaic admixture occurred in modern population k* = 25, with fraction γ of this population instantaneously taken from the archaic population at time _t_Admix. The parameter choices reflect a model of admixture of a European modern population and Neanderthals, with admixture occurring halfway between the end of one founding event and the beginning of the next founding event. The time and extent of admixture were chosen to have similar values to those used in previous models (10, 11).

In Fig. 5, admixture with γ = 0.05 leads to patterns in heterozygosity, LD, and the slope of the ancestral allele frequency spectrum similar to those observed in the basic serial founder model. However, archaic admixture causes an increase in heterozygosity and a decrease in LD that occur at population 25 and that are carried into subsequent populations. Heterozygosity increases at population 25 because admixture brings in archaic lineages distinct from the modern lineages in that population. The LD decrease at population 25 results from the way in which bottlenecks and admixture interact in our model. Bottlenecks increase the genetic drift experienced by a population, and genetic drift increases short-range LD (27). Admixture can also inflate LD, particularly long-range LD (11), because allelic correlations at distant loci can arise from the separate sets of haplotypes contained in the distinct groups ancestral to a population. If the effect of bottlenecks in producing LD is stronger than the effect of admixture, then including admixture in the model causes short-range LD to be smaller in the first population that experiences the admixture than in the previous population in the series.

Fig. 5.

Fig. 5.

Patterns of heterozygosity, LD, and the ancestral allele frequency spectrum in simulations of the serial founder model with archaic admixture. The model incorporates archaic admixture with an admixture fraction γ = 0.05 of population 25 deriving from the archaic population. All other parameters are the same as in Fig. 3.

Increasing the admixture fraction to γ = 0.1 further increases heterozygosity and decreases short-range LD at population 25 (Fig. S2). The slope of the ancestral allele frequency spectrum increases at population 25, causing a discontinuity that was less visible at population 25 in the case of γ = 0.05. This jump occurs because population 25 receives an influx of ancestral haplotypes from the archaic population, thereby increasing both the frequencies of ancestral alleles and the slope of the ancestral allele frequency spectrum. With larger γ, the amount of LD in population 25 at long physical distances is larger (Fig. S3), compatible with the greater effect of admixture on long-range LD compared with that of bottlenecks.

Archaic Persistence Model.

To examine if an admixture model with substantially greater contributions from archaic populations can explain patterns in heterozygosity, LD, and the ancestral allele frequency spectrum, we developed an “archaic persistence model” to reflect a scenario in which modern humans originate from one archaic population and then expand into a collection of preexisting archaic populations.

In this model (Fig. 2B), K populations, each with size N diploid individuals, diverge _t_D generations ago, and each experiences subsequent migration with its immediate neighbors at rate M in each direction. At _t_1 generations in the past, looking forward in time, population 1 sends a large wave of migrants to population 2 over a series of L_w generations. Backward in time, this wave corresponds to a change from M to W in the backward migration rate from population 2 to population 1, so that a fraction W/(4_N) of population 2 is drawn from population 1 in each of the _L_w generations. For each k, population k sends a similar (forward) wave to population k + 1 at _t_k generations in the past.

Using MS, we simulated 5,000 datasets with K = 100, N = 1,000, n = 50, M = 0.1, _t_D = 40,000, and _t_k = 2,079 − 21(k − 1). The value for _t_k matches the founding time for population k + 1 in our basic serial founder simulations. Each wave lasts _L_w = 2 generations, matching our serial founder bottleneck length, and sends 250 migrants per generation (W = 1,000). The parameter choices reflect a scenario in which archaic humans spread approximately 1 million years ago and modern humans arose via admixture of archaic populations with descendants of a recent expansion out of Africa.

In contrast to the basic serial founder model, the archaic persistence model produces patterns opposite to those observed in human data (Fig. 6). Heterozygosity increases, LD decreases, and the ancestral allele frequency spectrum slope increases with increasing colony number. These results can be understood from the fact that in the long time since the initial divergence, the K archaic populations have enough time to develop distinctive localized variants. As the migration wave travels through them, it accumulates diversity, gathering new variants from each population through which it passes. Thus, heterozygosity increases with increasing colony number in the same way that it increases in the archaic admixture model at the population in which admixture occurs. The difference between models lies in the fact that in the archaic persistence model, archaic admixture occurs in every population, so that heterozygosity increases at each step rather than at a single location. This occurrence of archaic admixture at each step also explains the decrease in LD and increase in the slope of the ancestral allele frequency spectrum that occur at each step. Deviations in the initial and final colonies from the general patterns are likely due to edge effects; the linear arrangement of populations prevents edge populations from accumulating the same level of diversity before the migration wave as that accumulated in central populations.

Fig. 6.

Fig. 6.

Patterns of heterozygosity, LD, and the ancestral allele frequency spectrum in simulations of the archaic persistence model. (A) Heterozygosity as a function of colony number. (B) LD measured by _r_2 as a function of physical distance in kilobases. (C) LD at 10 kb measured by _r_2 as a function of colony number. (D) Slope of the ancestral allele frequency spectrum in the range of 20% to 80% ancestral allele frequency as a function of colony number.

Instantaneous Divergence Model.

A key feature of the serial founder model is that compared with an earlier colony in the series, a subsequent colony has fewer ancestors over a longer period in its history. Thus, to assess if a decline in effective size can explain patterns in heterozygosity, LD, and the ancestral allele frequency spectrum, we devised an instantaneous divergence model that captures this effective size reduction without explicitly modeling bottlenecks. This model, which itself is implausible as a description of human migrations, can help illuminate the features of the serial founder model that allow it to explain observed patterns.

Our instantaneous divergence model (Fig. 2C) has K populations each with a different constant size, chosen so that the total elapsed coalescent time for population k since the divergence equals that elapsed for population k since initial divergence in the basic serial founder model. The cumulative coalescent intensity from the present back t_D generations of a variable-sized population whose size was N(s) at s generations in the past is ∫0_tD 1/N(s)ds (28). The corresponding cumulative intensity from the present back _t_D generations of a population of constant size N_k is ∫0_tD 1/N_k_ds = _t_D/_N_k. Setting the intensities of the variable-sized and constant-sized populations equal, a population of constant size _N_k = _t_D/∫0_tD_1/N(s)ds experiences the same length in coalescent time as a variable-sized population with size function N(s). In our basic serial founder model, bottlenecks last _L_b generations, and during a bottleneck, a population has constant size _N_b. Therefore, for each bottleneck, the elapsed coalescent time is _L_b/_N_b. Because population k experiences k − 1 bottlenecks, the cumulative coalescent time elapsed during bottlenecks is (k − 1)_L_b/_N_b. Similarly, the cumulative coalescent time outside of bottlenecks is [_t_D − (k − 1)_L_b]/N. Thus, we assign population k in the instantaneous divergence model size

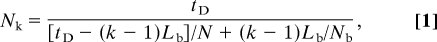
graphic file with name zpq03809-9283-m01.jpg

where N, _N_b, and _L_b are as in the serial founder model.

For this model, using MS, we simulated 5,000 datasets with K = 100 and n = 50. The divergence between the K populations occurred at _t_D = 2,079 (51.975 kya). The ancestral population had size N = 10,000 diploid individuals, and for each k, population k had size _N_k (eq. 1).

Comparing Figs. 3 and 7, the serial founder and instantaneous divergence models display nearly identical patterns and ranges of values for heterozygosity, LD, and the slope of the ancestral allele frequency spectrum. This concordance has the interpretation that the worldwide genetic patterns observed in human populations can be explained by a decrease in the cumulative number of ancestors of a population—that is, an increase in genetic drift and in total elapsed coalescent time—with increasing distance from the source. Thus, the utility of this instantaneous divergence model is that it provides an explanation for the success of the more realistic serial founder model in describing worldwide patterns of variation.

Fig. 7.

Fig. 7.

Patterns of heterozygosity, LD, and the ancestral allele frequency spectrum in simulations of the instantaneous divergence model. (A) Heterozygosity as a function of colony number. (B) LD measured by _r_2 as a function of physical distance in kilobases. (C) LD at 10 kb measured by _r_2 as a function of colony number. (D) Slope of the ancestral allele frequency spectrum in the range of 20% to 80% ancestral allele frequency as a function of colony number.

Discussion

In this article, we developed a general coalescent-based serial founder model that incorporates linked loci, providing a versatile tool for generating and testing hypotheses about features of human population-genetic data. Using several cases of the model, we examined heterozygosity, LD, and the ancestral allele frequency spectrum, mimicking computations performed in past data analyses. If the source population is placed in Africa, then the serial founder model explains three patterns observed in data: a decrease in heterozygosity, increase in LD, and decrease in the slope of the ancestral allele frequency spectrum with increasing distance from Africa. Our use of an instantaneous divergence model suggests that the patterns observed in the data—and the success of the serial founder model—are due to an increase in genetic drift and a corresponding increase in elapsed coalescence time with increasing distance from Africa. Unlike the serial founder model, an archaic persistence model, in which a migration wave of modern humans into preexisting archaic populations has the effect of increasing the diversity of the ancestors for populations at a greater distance from Africa, does not produce increasing drift with increasing distance from Africa, and does not explain observed patterns.

We considered a variant of the basic serial founder model that included migration between neighboring populations, finding that migration did not have a large impact on the decrease in heterozygosity, increase in LD, and decrease in the slope of the ancestral allele frequency spectrum that were observed from the basic model. However, an increased migration rate caused a peak in the level of heterozygosity to appear in populations near the founding colony rather than in the founding colony itself. This result suggests that when using patterns of diversity to pinpoint the origin of an expansion in a serial founder framework (14, 29), the site of origin might reside in a neighboring population to the highest-diversity population, rather than in the highest-diversity population itself.

We examined the effect of limited archaic admixture on the serial founder model and found that it increased heterozygosity, decreased short-range LD, and increased the slope of the ancestral allele frequency spectrum, starting at the admixed population. The LD decrease contrasts with the results of Plagnol and Wall (11), who found that archaic admixture was needed to inflate the level of LD to match that observed in Europeans at intermediate physical distances. Note, however, that whereas we considered the standard _r_2 LD statistic using all loci with minor allele frequency ≥0.05, Plagnol and Wall focused on a statistic specifically designed to be sensitive to archaic admixture, and applied it to a different restricted class of SNPs. Differences in results might also have arisen from modeling differences, such as in the values used for the time of admixture, population size, and bottleneck size. Because the effect we observed for archaic admixture on LD was relatively weak, our LD summaries might not be informative enough to empirically detect archaic admixture.

More generally, the relative similarity of predictions of the basic serial founder, migration, archaic admixture, and instantaneous divergence models suggests that it is difficult to distinguish these models solely using the summary statistics that we have considered. Thus, although a serial founder model is supported by the analysis, many alternatives cannot be excluded. However, the archaic persistence model, whose predictions disagree with the patterns in the data, is not in this collection. Because a migration wave of modern humans in this model carries an increasing diversity of archaic contributions into subsequent populations, this model does not possess the essential feature that permits other models to explain observed patterns, namely an increase in genetic drift with distance from the source. Use of unequal sizes for persisting archaic populations, however, might have produced patterns with greater similarity to those produced by a serial founder model (6, 30). If archaic population sizes had instead decreased with increasing colony number, via an archaic serial founder process, then the production by archaic persistence of patterns opposite to those in the data might have been offset by an archaic serial founder increase in genetic drift with increasing distance from a founding archaic colony.

Such a scenario is likely implausible, because an archaic serial founder process is not expected to have similar behavior to the modern analog that we have analyzed. Let _t_D grow in a serial founder model with migration while holding _L_b and L constant. We expect lineages from each population to find common ancestors before any population split or bottleneck is reached. The model would then approximate the finite linear population model of Wilkins and Wakeley (26), for which predictions differ substantially from those of the serial founder model with migration. The finite linear model predicts that the center of the range receives diverse migrants and therefore has the highest diversity, whereas in the serial founder model with migration, populations near the founding colony have the highest diversity. Thus, although some flexibility exists in the parameters that allow the serial founder model to match observed data, and although we have only explored a small part of the parameter space, consideration of archaic persistence suggests that the model cannot be made too different and still explain the patterns in the data.

Materials and Methods

Heterozygosity.

For the heterozygosity of a population in one simulation we used the standard unbiased estimator (31), averaged over all loci polymorphic in the set of K populations. We then calculated a weighted average across simulations of the mean heterozygosity across loci. We used proportions of segregating sites in a simulated dataset (segregating in the whole simulated set of K populations) relative to the total number of segregating sites from all 5,000 simulated datasets as weights.

Linkage Disequilibrium.

For each population we calculated the _r_2 LD statistic (27) between all distinct pairs of sites with minor allele frequency ≥5% in that population. For each simulation, using the distance between the two sites in a pair, we placed _r_2 values into 1 kb bins representing physical distances in the ranges [0 kb, 1 kb),…, [99 kb, 100 kb). In each population we obtained an average of all _r_2 values in each bin. We then computed an average _r_2 across simulations, weighting the results of a simulation by the proportion of _r_2 comparisons performed for that simulated dataset in that population relative to the total number of _r_2 comparisons in that population from all 5,000 simulations. The [9 kb, 10 kb) bin was used to indicate LD at 10 kb.

Ancestral Allele Frequency Spectrum.

In computing the slope of the ancestral allele frequency spectrum as a function of allele frequency, we modified the method of Li et al. (15) using resampling to evade a discreteness effect in which some frequency bins contain more markers than others due to more discrete frequencies being assigned to those specific bins. We used ancestral and derived allele assignments from Li et al. (15) for 407,001 autosomal markers in the data of Jakobsson et al. (16). For each population, for each locus, we computed ancestral allele frequency using 1000 random draws from the empirical allele frequency distribution. Loci were binned by ancestral frequency into 20 bins, representing [0/20,1/20), [1/20,2/20),…, [19/20,20/20]. For each population, bin counts were normalized by the total number of loci. The slope of the linear regression of the normalized frequency spectrum on ancestral allele frequency was then computed using bins centered at 9/40 to 31/40 (similarly to the use by Li et al. (15) of frequencies 1/5 to 4/5).

For the corresponding computation from our simulations, we used n + 1 bins, so that if a locus had the ancestral allele occurring i times, then the count for bin i/n was incremented. For a given simulation, for each population, counts were normalized by the number of segregating sites in that simulation. For each population, the slope of the linear regression of normalized frequency spectrum on ancestral allele frequency was computed using bins 10/50 through 40/50. In each population, we calculated an average slope across simulations, weighting the value for a simulation by the proportion of segregating sites observed in that simulated dataset relative to the total number of segregating sites from all simulated datasets.

Supplementary Material

Supporting Information

Acknowledgments.

We thank J. Li for ancestral allele frequency details from ref. 15 and three reviewers for helpful comments. This work was supported by National Institutes of Health Grants T32 GM070449 and R01 GM081441 and by grants from the Burroughs Welcome Fund, the Alfred P. Sloan Foundation, and the Swedish Research Council Formas.

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information