A New Equation to Estimate Glomerular Filtration Rate (original) (raw)
. Author manuscript; available in PMC: 2009 Oct 19.
Abstract
Background
Equations to estimate glomerular filtration rate (GFR) are routinely used to assess kidney function. Current equations have limited precision and systematically underestimate measured GFR at higher levels.
Objective
To develop a new estimating equation (CKD-EPI creatinine equation).
Design
Cross-sectional analysis. Separate pooled databases for equation development and validation. Representative U.S. population for prevalence estimates.
Setting
Research studies and clinical populations (“studies”) with measured GFR. National Health and Nutrition Examination Survey (NHANES) 1999-2006.
Patients
Equation development in 10 studies (8254 people) and validation in 16 studies (3896 people). Prevalence estimates based on 16,032 people.
Measurements
GFR measured as the clearance of exogenous filtration markers (iothalamate in the development dataset; iothalamate and other markers in the validation dataset). Linear regression to estimate the logarithm of measured GFR from standardized creatinine, sex, race and age.
Results
In the validation dataset, the CKD-EPI performed better than the MDRD Study equation (p<0.001 for all subsequent comparisons), especially at higher GFR: lesser bias (median difference between measured and estimated GFR of 2.5 vs. 5.5 mL/min/1.73 m2, respectively); improved precision (interquartile range of the differences of 16.6 vs. 18.3 mL/min/1.73 m2, respectively); and greater accuracy (percent of estimated GFR within 30% of measured GFR of 84.1 vs. 80.6%, respectively. In NHANES, median (interquartile range) estimated GFR was 94.5 (79.7 – 108.1) vs. 85.0 (72.9 – 98.5) mL/min/1.73 m2, and the prevalence (95% confidence interval) of CKD was 11.5 (10.6, 12.4) % vs. 13.1 (12.1, 14.0) %, respectively.
Limitations
Limited number of elderly people and racial and ethnic minorities with measured GFR.
Conclusions
The CKD-EPI creatinine equation is more accurate than the MDRD Study equation and could replace it for routine clinical use.
Introduction
Clinical assessment of kidney function is part of routine medical practice for adults, essential for assessing overall health, interpreting signs and symptoms, dosing drugs that are excreted by the kidneys, preparing for invasive diagnostic or therapeutic procedures, and detecting, evaluating and monitoring acute and chronic kidney diseases. The glomerular filtration rate (GFR) is considered the best overall index of kidney function in health and disease. GFR cannot be measured easily in clinical practice. Instead, GFR is estimated from equations using serum creatinine, age, race, sex and body size (1, 2). One such equation, the Modification of Diet in Renal Disease (MDRD) Study equation, has gained widespread acceptance (3, 4), and estimated GFR using this equation is reported by most clinical laboratories when measurement of serum creatinine is ordered (5). The MDRD Study equation is also used to assess the burden of chronic kidney disease in epidemiologic studies and public health (6). Prevalence of CKD in the U.S. has increased from approximately 10% in 1988-1994 to 13% in 1999-2004, corresponding to approximately 26.3 million people in 2000 (6, 7).
The MDRD Study equation was developed in people with CKD, and as such its major limitations are imprecision and systematic underestimation of measured GFR (bias) at higher levels (8). Our objectives were to develop and validate a new estimating equation based on serum creatinine that would be as accurate as the MDRD Study equation at GFR less than 60 ml/min/1.73 m2 and more accurate at higher GFR. We report development and validation of a new equation and compare it to the MDRD Study equation for estimating measured GFR and US prevalence of chronic kidney disease.
Methods
The Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) is a research group established by the National Institutes of Diabetes, Digestive and Kidney Disease. The institutional review boards of all participating institutions approved the study.
Equation Development and Validation
Details about study selection and analytical methods are provided in the Appendix.
Data sources
CKD-EPI collaborators provided data from research studies and clinical populations (hereafter referred to as “studies”). Briefly, we identified studies from the Medline database and through investigators' and collaborators' contacts (Appendix Figure 1). Key inclusion criteria were measurement of GFR using exogenous filtration markers and ability to calibrate serum creatinine assay. Studies for development and internal validation of equations were restricted to those using urinary clearance of iothalamate. Studies for external validation included iothalamate and other filtration markers. Ten studies (6 research studies and 4 clinical populations) with a total of 8,254 participants were divided randomly into separate datasets for development (n=5,504) and internal validation (n=2,750) (Appendix Table 1) (3, 9-15). Sixteen other studies (6 research studies and 10 clinical populations) with a total of 3,896 participants were used for external validation (Appendix Table 2).(13, 16-28)
Laboratory methods
For all studies, we recalibrated serum creatinine values to the standardized creatinine measurements using the Roche enzymatic method (Roche-Hitachi P-Module instrument with Roche Creatininase Plus assay, Hoffman-La Roche, Ltd., Basel, Switzerland) at the Cleveland Clinic Research Laboratory (Cleveland, OH) as previously described (29, 30). We compared new equations to the MDRD Study equation, given by: estimated GFR = 175 × standardized Scr −1.154 × age−0.203 × 1.212 [if black] × 0.742 [if female], where GFR is expressed as mL/min/1.73 m2 of body surface area41 and Scr is expressed in mg/dL(4).
Analyses in the development dataset
We pre-specified a process for developing equations using transformations of continuous variables and inclusion of additional variables and interactions to develop a large number of candidate equations. We used least squares linear regression to relate measured GFR to serum creatinine and clinical characteristics available in all databases. Predictor variables included serum creatinine, age, race (black vs. white and other), and sex in all models, as in the MDRD Study equation, and additional variables [diabetes (yes/no), prior organ transplant (yes/no), and weight, as assigned by the individual studies] in some models. Regression models were fit to all patients in the pooled development dataset, without accounting for study in the models. GFR and serum creatinine were transformed to natural logarithms to reflect their multiplicative (inverse) relationship and to stabilize variance across the range of GFR.
Appropriate transformations of log serum creatinine and age were determined by first fitting non-parametric smoothing splines to characterize the shape of the relationship of these factors with mean log measured GFR and then creating piecewise linear splines to correspond to observed non-linearity (Appendix Table 3) (31). Additional variables and pair-wise interactions between them were included if they were significant (p <0.01 for additional variables and <0.001 for interactions) and improved model performance [relative reduction in root mean square error (RMSE) by 2% or more] (Appendix Table 4).
Analyses in the internal validation dataset
We verified statistical significance of predictor variables and interactions for all models and relative ranking of performance among models. Development and internal validation datasets were combined to derive final coefficients for each model.
Analyses in the external validation dataset
We compared performance of the multiple models developed in the development dataset to each other as well as to the MDRD Study equation using a pre-specified process. Comparisons were performed in the overall dataset and in subgroups defined by estimated GFR, clinical characteristics, and type of filtration marker (iothalamate vs. non-iothalamate). Equations were ranked on performance and ease of application. For all steps, sensitivity analyses were performed to evaluate robustness of results across studies. A single model was selected as the best equation for general use and is referred to here as the “CKD-EPI equation”.
Metrics for equation performance
Measured and estimated GFR were compared for each patient graphically by plotting measured GFR and the difference (measured GFR-estimated GFR) against estimated GFR. Bias was assessed as the median difference, with positive values indicating an under-estimation of measured GFR. Precision was assessed as inter-quartile range (IQR) for the differences. Accuracy was assessed as root mean square error relative to measured GFR and the percent of estimates within 30% of the measured GFR (P30), which takes into account higher errors at higher values and absolute values of the difference between measured and estimated GFR. Confidence intervals were calculated by bootstrap methods (32) (2000 bootstraps) for median difference and IQR of the differences and by the binomial method for P30. Receiver-operating characteristics (ROC) curves were computed for measured GFR <90, <75, <60, <45, <30 and <15 ml/min/1.73 m2. GFR stages were defined as >90, 60-89, 30-59, 15-29, and <15 ml/min/1.73 m2 (1). Sensitivity and specificity and concordance between estimated and measured GFR between equations were compared using the McNemar test. Concordance of estimated GFR stages between equations was compared using the sign test.
Analyses were computed using R (Version 2, Free Software Foundation, Inc., Boston, MA) and SAS software (Version 9.1, Cary, NC).
Estimation of U.S. prevalence
The National Health and Nutrition Examination Survey (NHANES) is a cross-sectional, multistage, stratified, clustered probability samples of the civilian, non-institutionalized population of the U.S. conducted by the National Center of Health Statistics and appropriate for estimates of prevalence of chronic conditions in the U.S. Data were analyzed from 1999-2000, 2001-2002, 2003-2004, and 2005-2006 surveys. The study population for this analysis was limited to 16,032 participants (3,754 in 1999-2000, 4,297 in 2001-2002, 4,017 in 2003-2004, and 3,964 in 2005-2006), who were 20 years and older, had completed the examination in the mobile examination center, were not pregnant or menstruating, and were not missing serum creatinine measurements and did not have an estimated GFR below 15 ml/min/1.73 m2. Methods are similar to previous reports and are summarized briefly here (7).
GFR was not measured in NHANES. Serum creatinine was measured using a kinetic rate Jaffe method and re-calibrated to standardized creatinine measurements obtained in at the Cleveland Clinic Research Laboratory (Cleveland, OH) (33). GFR was estimated using the MDRD Study and the newly developed CKD-EPI equation. Estimates that exceeded 200 mL/min/1.73 m2 were truncated at that level. Methods for collection, analysis, and reporting for albuminuria have been described (7, 34). Albuminuria was defined as albumin-to-creatinine ratio ≥30 mg/g. Repeated measurements, obtained in a subset of 1,241 NHANES 1988-1994 participants approximately 2 weeks after the original examination were used to estimate the persistence of albuminuria (34). NHANES does not have accurate diagnoses of causes of kidney disease. CKD was defined as persistent albuminuria or estimated GFR <60 ml/min/1.73 m2 (1). CKD was classified according to estimated GFR stages as defined above. Distributions of estimated GFR, estimated GFR stages and prevalence of CKD were compared for both equations.
Analyses were performed incorporating the sampling weights to obtain unbiased estimates from the complex NHANES sampling design using Stata (Version 10.0, StataCorp, College Station, TX). Standard errors for all estimates were obtained using the Taylor series (linearization) method following NHANES recommended procedures and weights (35-37). Confidence intervals for prevalence estimates for CKD stages incorporating persistence data on of albuminuria were made using bootstrap methods implemented in Stata. Prevalence estimates were applied to the 2000 U.S. Census to obtain estimates of the number of individuals with CKD in the U.S.
Role of the Sponsor
The study was funded by a cooperative agreement with the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK), which allows the NIDDK substantial involvement in the design of the study and in the collection, analysis, and interpretation of the data. The NIDDK was not required to approve publication of the finished manuscript.
Results
Selection of Studies and Clinical Characteristics
Clinical characteristics of the participants in each dataset are shown in Table 1. In the development dataset, mean (standard deviation) measured GFR was 68 (40) mL/min/1.73 m2 and ranged between 2 and 190 mL/min/1.73 m2. In the external validation dataset, mean measured GFR, sex, and proportion of diabetes was similar to the development and internal validation datasets, but there were differences in age, body size, and the proportion of ethnic and racial minorities, kidney donors and organ transplant recipients.
Table 1.
Subject Characteristics by Dataset
| Development(n=5,504) | Internal validation(n=2,750) | External validation(n=3,896) | P values* | |
|---|---|---|---|---|
| Mean age (SD), y | 47 (15) | 47 (15) | 50 (15) | p<0.001 |
| Age, n (%) | p<0.001 | |||
| <40 y | 2058 (37) | 1018 (37) | 1136 (29) | |
| 41-65 y | 2751 (50) | 1403 (51) | 2192 (56) | |
| >65 y | 695 (13) | 329 (12) | 568 (15) | |
| 66-70 y | 476 (9) | 220 (8) | 254 (7) | |
| 71-75 y | 150 (3) | 66 (2) | 185 (5) | |
| 76-80 y | 41 (0) | 30 (1) | 92 (2) | |
| >80 y | 28 (0) | 13 (0) | 37 (0) | |
| Women, n (%) | 2391 (43) | 1215 (44) | 1767 (45) | p=0.084 |
| Race, n (%) | p<0.001 | |||
| Black | 1728 (32) | 857 (31) | 384 (10) | |
| Hispanic | 247 (5) | 106 (4) | 67 (2) | |
| Asian | 62 (1) | 38 (1) | 67 (2) | |
| White and other | 3467 (63) | 1749 (64) | 3378 (87) | |
| Kidney donor, n (%) | 694 (13) | 336 (12) | 608 (16) | p<0.001 |
| Transplant recipient, n (%) | 241 (4) | 119 (4) | 1134 (29) | p<0.001 |
| Diabetes, n (%) | 1581 (29) | 825 (30) | 1089 (28) | p=0.173 |
| Mean height (SD), cm | 170 (10) | 170 (10) | 170 (10) † | p=0.90 |
| Mean weight (SD), kg | 82(20) | 82 (20) | 79 (18) | p<0.001 |
| Mean body mass index (SD), kg/m2 | 28 (6) | 28 (6) | 27 (6) † | p<0.001 |
| Mean body surface area (SD), m2 | 1.93 (0.20) | 1.93 (0.20) | 1.90 (0.23) † | p<0.001 |
| Mean GFR (SD), _mL/min per 1.73 m_2‡ | 68 (40) | 67 (40) | 68 (36) | p=0.70 |
| Mean serum creatinine level (SD) | p<0.001 | |||
| μmol/L | 146 (106) | 148 (106) | 134 (88) | |
| mg/dL | 1.65 (1.20) | 1.67 (1.20) | 1.52 (1.00) |
Description of CKD-EPI Creatinine Equation
Variables included in the CKD-EPI equation for estimating log GFR are log serum creatinine [modeled as a two-slope linear spline with sex-specific knots at 62 μmol/L (0.7 mg/dL) in women and 80 μmol/L (0.9 mg/dL) in men], sex, race and age on the natural scale, compared to log serum creatinine without a spline, sex, race and age on the log scale in the MDRD Study equation (Appendix Table 5). In the CKD-EPI equation, the spline for log serum creatinine allows for steeper and identical slopes of GFR vs. serum creatinine for men and women for creatinine levels above the knots and less steep and different slopes for men and women for creatinine levels below the knots, leading to higher estimated GFR at lower creatinine values. The slope above the knots is similar to the MDRD Study equation. In both equations, the coefficient for Blacks is greater than 1.0, leading to a higher estimated GFR for Blacks than Whites at all levels of serum creatinine, but lower than in the MDRD Study equation. In the CKD-EPI equation, the relationship between GFR and sex varies according to the level of serum creatinine. For example, the predicted female-to-male ratio for estimated GFR varies from 0.83 to 0.92 when serum creatinine is between 44 to 71 μmol/L (0.5 and 0.8 mg/dL), and is 0.75 when serum creatinine is ≥80 μmol/L (≥0.9 mg/dL), whereas it is constant for the MDRD Study equation at 0.74 at all values for serum creatinine. There is an inverse relationship between estimated GFR and age for both equations, but at older age, the age term on the natural scale in the CKD-EPI equation leads to lower estimated GFR for the same level of creatinine than does the log age term in the MDRD Study equation. In the external validation dataset, models with additional variables for diabetes, organ transplant, and weight, or interactions among variables did not lead to substantially improved performance compared to the simpler models. Table 2 shows the CKD-EPI equation in a form that could be implemented in clinical laboratories.
Table 2. The CKD-EPI Equation for Estimating GFR on the Natural Scale*.
| Race and Sex | Serum Creatinine μmol/L (mg/dL) | Equation |
|---|---|---|
| Black | ||
| Female | ≤62 (≤0.7) | GFR = 166 × (Scr/0.7)-0.329 × (0.993)Age |
| >62 (>0.7) | GFR = 166 × (Scr/0.7)-1.209 × (0.993)Age | |
| Male | ≤80 (≤0.9) | GFR = 163 × (Scr/0.9)-0.411 × (0.993)Age |
| >80 (>0.9) | GFR = 163 × (Scr/0.9)-1.209 × (0.993)Age | |
| White or other | ||
| Female | ≤62 (≤0.7) | GFR = 144 × (Scr/0.7)-0.329 × (0.993)Age |
| >62 (>0.7) | GFR = 144 × (Scr/0.7)-1.209 × (0.993)Age | |
| Male | ≤80 (≤0.9) | GFR = 141 × (Scr/0.9)-0.411 × (0.993)Age |
| >80 (>0.9) | GFR = 141 × (Scr/0.9)-1.209 × (0.993)Age |
Comparison of Performance of MDRD Study and CKD-EPI Equations
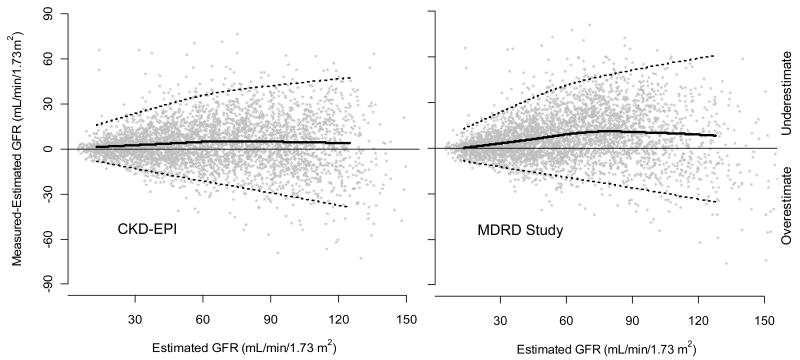
Figure 1 and Table 3 shows the performance of both equations in the validation dataset. (Appendix Table 6 also shows performance in the development and internal validation datasets.) Median difference (bias), IQR, P30 and root mean square error, were all improved with the CKD-EPI equation (p<0.001 for all). The CKD-EPI equation was as accurate as the MDRD Study equation in the subgroup with estimated GFR less than 60 ml/min/1.73 m2 and substantially more accurate in the subgroup with estimated GFR greater than 60 ml/min/1.73 m2. Results were consistent across studies and subgroups defined by age, sex, race, diabetes, transplant status, and body mass index (BMI) (data not shown).
Figure 1. Comparison of performance of Modification of Diet in Renal Disease (MDRD) Study and Chronic Kidney Disease Epidemiology Collaboration (CKD-EPI) equations by estimated GFR in the external validation dataset.
Panel 1. Measured vs. estimated GFR. Panel 2. Difference between measured and estimated vs. estimated GFR. Shown are smoothed regression line and 95% CI (computed using the lowess smoothing function in R), using quantile regression, excluding lowest and highest 2.5% of estimated GFR values. To convert GFR from mL/min/1.73 m2 to mL/s/m2, multiply by 0.0167.
Table 3. Comparison of Performance of CKD-EPI and MDRD Study Equations in the Validation Dataset.
| Variable and Equation | All Patients | Patients with estimated GFR <60 ml/min/1.73 m2 | Patients with estimated GFR ≥60 ml/min/1.73 m2 |
|---|---|---|---|
| Median difference (95% CI), mL/min per 1.73 m2† | |||
| CKD-EPI | 2.5 (2.1 - 2.9) | 2.1 (1.7 - 2.4) | 3.5 (2.6 - 4.5) |
| MDRD Study | 5.5 (5.0 - 5.9) | 3.4 (2.9 - 4.0) | 10.6 (9.8 - 11.3) |
| Interquartile range for differences (95% CI) - mL/min per 1.73 m2‡ | |||
| CKD-EPI | 16.6 (15.9 - 17.3) | 11.3 (10.7 - 12.1) | 24.2 (22.8 - 25.3) |
| MDRD Study | 18.3 (17.4 - 19.3) | 12.9 (12.0 - 13.6) | 25.7 (24.4 - 27.1) |
| P30 (95% CI) - %§ | |||
| CKD-EPI | 84.1 (83.0 - 85.3) | 79.9 (78.1 - 81.7) | 88.3 (86.9 - 89.7) |
| MDRD Study | 80.6 (79.5 - 82.0) | 77.2 (75.5 - 79.0) | 84.7 (83.0 - 86.3) |
| Root mean square error (95% CI) | |||
| CKD-EPI | 0.250 (0.241 - 0.259) | 0.284 (0.270 - 0.298) | 0.213 (0.203 - 0.223) |
| MDRD Study | 0.274 (0.265 - 0.283) | 0.294 (0.280 - 0.308) | 0.248 (0.238 - 0.258) |
There was no difference between the CKD-EPI and MDRD Study equations in ROC curves to detect GFR <90, <75, <60, <45, <30 and <15 ml/min/1.73 m2. Areas under ROC curves were 0.95, 0.96, 0.96, 0.97, 0.97, and 0.98, respectively, for both equations. For detection of measured GFR <60 ml/min/1.73 m2, the estimated GFR value with highest combination of sensitivity and specificity was 59 ml/min/1.73 m2 for the CKD-EPI equation and 55 ml/min/1.73 m2 for the MDRD Study equation. The sensitivity and specificity of estimated GFR <60 ml/min/1.73 m2 were 91% and 87%, respectively, using the CKD-EPI equation and 95% and 82%, respectively, using the MDRD Study equation (p<0.001 for both comparisons). Concordance of estimated and measured GFR stages was 69% for the CKD-EPI equation vs. 64% for the MDRD Study equation (p<0.001). Table 4 shows classification of GFR stages estimated by the CKD-EPI and MDRD Study equations, with significant (p<0.001) reclassification to higher values by the CKD-EPI equation at values of 30-59 ml/min/1.73 m2 and higher. Of those classified differently by the two equations, classification by the CKD-EPI equation was correct more often than classification by the MDRD Study equation (63% vs. 34%, p<0.001). Overall, these results indicate better classification by estimated GFR using the CKD-EPI equation, primarily due to reduction in bias.
Table 4. Comparison of the CKD-EPI and MDRD Study Equations in Estimating GFR Stage and Comparison With Measured GFR in the Validation Data Set*.
| CKD-EPI-Estimated GFR and Measured GFR | MDRD Study–Estimated GFR, n (%) | Total Patients, n (%) | ||||
|---|---|---|---|---|---|---|
| >90 mL/min per 1.73 m2 | 60–89 mL/min per 1.73 m2 | 30–59 mL/min per 1.73 m2 | 15–29 mL/min per 1.73 m2 | <15 mL/min per 1.73 m2 | ||
| Estimated GFR >90 mL/minper 1.73 m2 | 670 (17.2) | 319 (8.2) | 0 | 0 | 0 | 989 (25.4) |
| Measured GFR | ||||||
| >90 mL/min per 1.73 m2 | 586 (15.0) | 221 (5.7) 93 (2.4) | ||||
| 60-89 mL/min per 1.73 m2 | 75 (1.9) | 4 (0.1) | ||||
| 30-59 mL/min per 1.73 m2 | 9 (0.3) | 1 (0.0) | ||||
| 15-29 mL/min per 1.73 m2 | 0 | 0 | ||||
| <15 mL/min per 1.73 m2 | 0 | |||||
| Estimated GFR 60-89 mL/min per 1.73 m2 | 2 (0.0) | 803 (20.6) | 190 (4.9) | 0 | 0 | 995 (25.5) |
| Measured GFR | ||||||
| >90 mL/min per 1.73 m2 | 0 | 263 (6.8) | 11(0.3) | |||
| 60-89 mL/min per 1.73 m2 | 1 (0.01) | 459 (11.8) | 110 (2.8) | |||
| 30-59 mL/min per 1.73 m2 | 1 (0.0) | 77 (2.0) | 69 (1.8) | |||
| 15-29 mL/min per 1.73 m2 | 0 | 4 (0.1) | 0 | |||
| <15 mL/min per 1.73 m2<15 | 0 | 0 | 0 | |||
| Estimated GFR 30-59 mL/min per 1.73 m2 | 2 (0.0) | 1251 (32.1) | 42 (1.1) | 0 | 1295 (33.2) | |
| Measured GFR | ||||||
| >90 mL/min per 1.73 m2 | 0 | 118 (3.0) | 0 | |||
| 60-89 mL/min per 1.73 m2 | 2 (0.0) | 221 (5.7) | 0 | |||
| 30-59 mL/min per 1.73 m2 | 0 | 903 (23.7) | 20 (0.5) | |||
| 15-29 mL/min per 1.73 m2 | 0 | 105 (2.7) | 21 (0.5) | |||
| <15 mL/min per 1.73 m2 | 0 | 4 (0.1) | 0 | |||
| Estimated GFR 15-29 mL/min per 1.73 m2 | 0 | 0 | 9 (0.2) | 462 (11.9) | 2 (0.0) | 473 (12.1) |
| Measured GFR | ||||||
| >90 mL/min per 1.73 m2 | 0 | 0 | 0 | |||
| 60-89 mL/min per 1.73 m2 | 0 | 0 | 0 | |||
| 30-59 mL/min per 1.73 m2 | 5 (0.1) | 109 (2.8) | 1 (0.0) | |||
| 15-29 mL/min per 1.73 m2 | 4 (0.1) | 302 (7.8) | 1 (0.0) | |||
| <15 mL/min per 1.73 m2 | 0 | 51 (1.3) | 0 | |||
| Estimated GFR <15 mL/min per 1.73 m2 | 0 | 0 | 0 | 5 (0.1) | 139 (3.6) | 144 (3.7) |
| Measured GFR | ||||||
| >90 mL/min per 1.73 m2 | 0 | 0 | ||||
| 60-89 mL/min per 1.73 m2 | 0 | 2 (0.0) | ||||
| 30-59 mL/min per 1.73 m2 | 0 | 0 | ||||
| 15-29 mL/min per 1.73 m2 | 2 (0.0) | 32 (0.8) | ||||
| <15 mL/min per 1.73 m2 | 3 (0.1) | 105 (2.7) | ||||
| Total | 672 (17.3) | 1124 (28.9) | 1450 (37.2) | 509 (13.1) | 141 (3.6) | 3896 (100) |
Comparison of estimated GFR and Prevalence of CKD in NHANES using MDRD Study and CKD-EPI Equations
The transformations and coefficients for variables in the CKD-EPI equation translate into differences in the distribution of estimated GFR and prevalence of CKD in NHANES 1999-2006 compared to the MDRD Study equation. Both equations show a similar distribution at estimated GFR <45 mL/min/1.73 m2 but the CKD-EPI equation leads to a shift to the right at higher levels of estimated GFR (Figure 2A). The mean (SE) estimated GFR was 93.2 (0.39) vs. 86.3 (0.40) mL/min/1.73 m2, respectively; median (IQR) was 94.5 (79.7 – 108.1) vs. 85.0 (72.9 – 98.5) mL/min/1.73 m2, respectively. Comparison of classification of stages of estimated GFR showed reclassification to higher values using the CKD-EPI equation at values of 30-59 ml/min/1.73 m2 and higher (Appendix Table 7). Similar reclassification in distribution of estimated GFR was observed among patients with and without albuminuria (Appendix Table 8).
The CKD-EPI equation leads to a lower estimated prevalence (95% CI) of CKD compared to the MDRD Study equation [11.5 (10.6, 12.4) vs. 13.1 (12.1, 14.0) %, respectively], primarily due to a lower prevalence of Stage 3 [6.3 (5.8, 6.9) vs. 7.8 (7.2, 8.5) %, respectively] (Figure 2B). Reclassification to higher estimated GFR stages leads to a higher prevalence of CKD stage 1 and lower prevalence of CKD stage 2. The CKD-EPI equation leads to a lower prevalence in women and Whites, such that the prevalence of CKD stages 3-4 is not significantly higher in women vs. men and in Whites vs. Blacks as it is in the MDRD Study (data not shown). Using both equations, the prevalence of CKD rises with age, but among subjects older than 70 years the CKD-EPI equation leads to a similar rather than lower estimated prevalence of CKD. Based on the 2000 U.S. population of 201 million people greater than 20 years of age, the prevalence (95% CI) of CKD using the CKD-EPI equation is 23.2 (21.3, 25.0) million, approximately 3 million fewer people than using the MDRD Study equation (Appendix Table 9).
Discussion
We developed a new equation, the CKD-EPI equation, to estimate GFR in adults from serum creatinine using a large database pooled from 10 studies. Using data pooled from 16 additional studies, we validated the CKD-EPI equation and showed that it is more accurate than the widely-used MDRD Study equation. The CKD-EPI equation has lower bias, especially at estimated GFR greater than 60 mL/min/1.73 m2; however, precision remains limited. The improved accuracy of the CKD-EPI equation overcomes some of the limitations of the MDRD Study equation and has important implications for public health and clinical practice.
Lower bias at higher estimated GFR reflects use of a spline term for serum creatinine. The spline accounts for a weaker relationship between creatinine and GFR at lower vs. higher creatinine levels, consistent with reports from studies comprised primarily of subjects with higher measured GFR, such as kidney donors and young people with Type 1 diabetes without microalbuminuria (10, 15, 38). Like the MDRD Study equation, the CKD-EPI equation includes age, race and sex as surrogates for non-GFR determinants of serum creatinine. These variables are associated with muscle mass, the main determinant of creatinine generation (39). Imprecision of GFR estimates suggests that age, race and sex do not account for all variation in non-GFR determinants of serum creatinine.
The CKD-EPI equation should lead to more accurate estimates of the distribution of estimated GFR and the burden of CKD in the US population. Median estimated GFR was 9.5 ml/min/1.73 m2 higher, leading to a 1.6% lower prevalence estimate for CKD (11.5% compared to 13.1% using the MDRD Study equation). Concerns have been raised about the use of the MDRD Study equation because of the high prevalence estimates in the elderly, women and Whites, compared to the low incidence rates of treated kidney failure in these groups (7, 40, 41). Using the CKD-EPI equation, the prevalence is reduced in women and Whites, but remains high in the elderly. Possible explanations for the remaining disparities between prevalence and incidence include competing risk from fatal cardiovascular disease in the elderly and faster progression of kidney disease in men and Blacks (42, 43).
Greater accuracy of the CKD-EPI equation should improve clinical decision making in patients with decreased kidney function. In particular, lower bias should reduce the rate of false-positive diagnoses of CKD stage 3 (estimated GFR <60 ml/min/1.73 m2) in patients without CKD (measured GFR above 60 ml/min/1.73 m2 and absence of markers of kidney damage). Patients with CKD are at higher risk for a variety of complications (44-50), and guidelines and recommendations call for reduction in dosage of drugs excreted by the kidney, avoidance of contrast media for imaging procedures, avoidance of phosphate-based enemas in preparation for colonoscopy, and lower targets for cardiovascular risk factors in patients with decreased GFR. Importantly, falsely low levels of estimated GFR could lead to insufficient drug dosing, withholding important diagnostic tests, and over-aggressive cardiovascular risk factor reduction in patients without CKD. The impact of more accurate estimates at higher levels of GFR on clinical decision making should be evaluated.
Strengths of this study include its design, with separate large databases for development and validation of the new equation, and a pre-specified rigorous statistical analytical plan for introduction and testing of all variables in the development dataset. The pooled development and validation databases include participants with diverse clinical characteristics, with and without kidney disease, and across a wide range of measured GFR, allowing more general applicability than the MDRD Study equation. Comparison of equations in a separate validation dataset overcomes limitations of differences among studies in patient characteristics and methods for measurement of GFR and serum creatinine.
There are weaknesses of this study. First, it is unlikely that a single equation will work equally well in all populations. Second, we have pooled studies of different populations to develop and validate the CKD-EPI equation. We performed extensive analyses to examine possible study-effects, but cannot rule out that some of the findings may reflect the specific studies included in our database. Third, the study population with higher levels of GFR is not representative of the general population, and there were relatively few participants older than 70 years of age or racial minorities other than Black who are at increased risk for CKD. Fourth, we had incomplete data on diabetes type, immunosuppressive agents for transplantation, measures of muscle mass, and other clinical conditions and medications that might affect serum creatinine independently from GFR; however, the variables that we evaluated are the most readily available and easy to ascertain for widespread clinical application. Fifth, the CKD-EPI equation is more complex than the MDRD Study equation, but can readily be implemented into clinical laboratory information systems using the same input variables as required for use of the MDRD Study equation. Finally, the new equation does not overcome limitations of serum creatinine as an endogenous filtration marker. All creatinine-based equations should be used with caution in people with abnormally high or low levels of muscle mass. Nevertheless, serum creatinine is central for clinical assessment of kidney function at the present time, and GFR estimates based on serum creatinine will continue to be used in clinical practice for the foreseeable future.
Further research is necessary to improve GFR estimation. Imprecision in GFR estimates may be secondary to non-GFR determinants of creatinine. Measures of imprecision may also be inflated by measurement error in GFR. Research should be directed towards improving GFR measurement and evaluation of cystatin C and novel filtration markers for GFR estimation, either alone or in combination with serum creatinine (51). Studies in representative populations are necessary, especially in the elderly and racial and ethnic minorities.
In summary, the CKD-EPI creatinine equation is more accurate than the MDRD Study equation across a wide variety of populations and clinical conditions. Bias is improved, especially at higher levels of estimated GFR, although precision remains suboptimal. Improved accuracy of the CKD-EPI equation could have important implications for public health and clinical practice. We suggest that the CKD-EPI equation could replace the MDRD Study equation for estimated GFR reporting for general clinical use.
Supplementary Material
Appendix
Appendix Figure 1
Appendix Figure 2
Appendix Tables
Acknowledgments
Funding Source: National Institutes of Health UO1 DK 053869, UO1 DK 067651, and UO1 DK 35073
Sources of funding/support: This research was supported by the following grants: UO1 DK 053869, UO1 DK 067651, and UO1 DK 35073. CKD-EPI is funded as part of a cooperative agreement in which the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK) has substantial involvement in the design of the study and the collection, analysis, and interpretation of the data. The NIDDK was not required to approve publication of the finished manuscript.
Footnotes
For a list of CKD-EPI collaborators, see the Appendix. Aghogho Okparavero, MBBS, MPH provided assistance in communications and manuscript preparation.
Statement of individual authors' contributions: We have received confirmation from Drs. Levey, Stevens, Schmid, Feldman, Kusek, Eggers, Greene, Coresh and Ms. Zhang that they have returned completed authors' forms to Annals. We are awaiting confirmation from Dr. Van Lente and Mr. Castro.
Disclosure of conflicts of interest: We have received confirmation from Drs. Levey, Stevens, Schmid, Feldman, Kusek, Eggers, Greene, Coresh and Ms. Zhang that they have returned completed conflicts of interest forms to Annals. We are awaiting confirmation from Dr. Van Lente and Mr. Castro.
Data access and responsibility: Dr. Lesley Stevens had full access to all the data in the study and takes responsibility for the integrity of the data and the accuracy of the data analysis for the CKD-EPI database. Dr. Josef Coresh had full access to all the data in the study and takes responsibility for the integrity of the data and the accuracy of the data analysis for the NHANES database.
Availability of Research Materials
Protocol: Available to interested readers by contacting Dr. Levey Statistical Code: Not available
Data: Not available
References
- 1.National Kidney Foundation. K/DOQI clinical practice guidelines for chronic kidney disease: Evaluation, classification, and stratification. Am J Kidney Dis. 2002;39(2):S1–266. [PubMed] [Google Scholar]
- 2.Stevens LA, Coresh J, Greene T, Levey AS. Assessing kidney function - measured and estimated glomerular filtration rate. N Engl J Med. 2006;354:2473–83. doi: 10.1056/NEJMra054415. [DOI] [PubMed] [Google Scholar]
- 3.Levey AS, Bosch JP, Lewis JB, Greene T, Rogers N, Roth D. A more accurate method to estimate glomerular filtration rate from serum creatinine: A new prediction equation. Modification of Diet in Renal Disease Study Group. Ann Intern Med. 1999;130(6):461–470. doi: 10.7326/0003-4819-130-6-199903160-00002. [DOI] [PubMed] [Google Scholar]
- 4.Levey AS, Coresh J, Greene T, Stevens LA, Zhang YL, Hendriksen S, et al. Using standardized serum creatinine values in the modification of diet in renal disease study equation for estimating glomerular filtration rate. Ann Intern Med. 2006;145(4):247–54. doi: 10.7326/0003-4819-145-4-200608150-00004. [DOI] [PubMed] [Google Scholar]
- 5.Miller WG. Reporting estimated GFR: a laboratory perspective. Am J Kidney Dis. 2008;52(4):645–8. doi: 10.1053/j.ajkd.2008.07.032. [DOI] [PubMed] [Google Scholar]
- 6.Levey AS, Andreoli SP, DuBose T, Provenzano R, Collins AJ. Chronic kidney disease: common, harmful, and treatable--World Kidney Day 2007. Am J Kidney Dis. 2007;49:175–79. doi: 10.1053/j.ajkd.2006.12.013. [DOI] [PubMed] [Google Scholar]
- 7.Coresh J, Selvin E, Stevens LA, Manzi J, Kusek J, Eggers PW, et al. Prevalence of chronic kidney disease in the United States. JAMA. 2007;298(17):2038–47. doi: 10.1001/jama.298.17.2038. [DOI] [PubMed] [Google Scholar]
- 8.Stevens LA, Coresh J, Deysher AE, Feldman HI, Lash JP, Nelson R, et al. Evaluation of the MDRD Study equation in a large diverse population. J Am Soc Nephrol. 2007;18(10):2749–57. doi: 10.1681/ASN.2007020199. [DOI] [PubMed] [Google Scholar]
- 9.Lewis JB, Agodoa L, Cheek D, Greene T, Middleton J, O'Connor D, et al. Comparison of cross-sectional renal function measurements in African-Americans with hypertensive nephrosclerosis and of primary formulas to estimate glomerular filtration rate. Am J Kidney Dis. 2001;38(4):744–753. doi: 10.1053/ajkd.2001.27691. [DOI] [PubMed] [Google Scholar]
- 10.Ibrahim H, Mondress M, Tello A, Fan Y, Koopmeiners J, Thomas W. An alternative formula to the Cockcroft-Gault and the Modification of Diet in Renal Diseases formulas in predicting GFR in individuals with type 1 diabetes. J Am Soc Nephrol. 2005;16(4):1051–60. doi: 10.1681/ASN.2004080692. [DOI] [PubMed] [Google Scholar]
- 11.Nelson R, Bennett P, Beck G, Tan M, Knowler W, Mitch W, et al. Development and progression of renal disease in Pima Indians with non-insulin-dependent diabetes mellitus. Diabetic Renal Disease Study Group. N Engl J Med. 1996;335(22):1636–42. doi: 10.1056/NEJM199611283352203. [DOI] [PubMed] [Google Scholar]
- 12.Lewis EJ, Kunsicker LG, Bain RP, Rohde RD, Collaborative Study Group The effect of angiotensin-converting enzyme inhibition on diabetic nephropathy. N Engl J Med. 1993;329(20):1456–1462. doi: 10.1056/NEJM199311113292004. [DOI] [PubMed] [Google Scholar]
- 13.Feldman HI, Appel LJ, Chertow GM, Cifelli D, Cizman B, Daugirdas J, et al. The Chronic Renal Insufficiency Cohort (CRIC) Study: Design and methods. J Am Soc Nephrol. 2003;14(7):S148–53. doi: 10.1097/01.asn.0000070149.78399.ce. [DOI] [PubMed] [Google Scholar]
- 14.Poggio ED, Wang X, Greene T, Van Lente F, Hall PM. Performance of the modification of diet in renal disease and Cockcroft-Gault equations in the estimation of GFR in health and in chronic kidney disease. J Am Soc Nephrol. 2005;16(2):459–66. doi: 10.1681/ASN.2004060447. [DOI] [PubMed] [Google Scholar]
- 15.Rule AD, Larson TS, Bergstralh EJ, Slezak JM, Jacobsen SJ, Cosio FG. Using serum creatinine to estimate glomerular filtration rate: Accuracy in good health and in chronic kidney disease. Ann Intern Med. 2004;141(12):929–937. doi: 10.7326/0003-4819-141-12-200412210-00009. [DOI] [PubMed] [Google Scholar]
- 16.Gonwa TA, Jennings L, Mai ML, Stark PC, Levey AS, Klintmalm GB. Estimation of glomerular filtration rates before and after orthotopic liver transplantation: evaluation of current equations. Liver Transpl. 2004;10(2):301–9. doi: 10.1002/lt.20017. [DOI] [PubMed] [Google Scholar]
- 17.Chapman AB, Guay-Woodford LM, Grantham JJ, Torres VE, Bae KT, Baumgarten DA, et al. Renal structure in early autosomal-dominant polycystic kidney disease (ADPKD): The Consortium for Radiologic Imaging Studies of Polycystic Kidney Disease (CRISP) cohort. Kidney Int. 2003;64(3):1035–45. doi: 10.1046/j.1523-1755.2003.00185.x. [DOI] [PubMed] [Google Scholar]
- 18.Bosma R, Doorenbos C, Stegeman C, van der Heide J, Navis G. Predictive performance of renal function equations in renal transplant recipients: An analysis of patient factors in bias. Am J Trans. 2005;5:2193–2203. doi: 10.1111/j.1600-6143.2005.00982.x. [DOI] [PubMed] [Google Scholar]
- 19.Rook M, Hofker HS, van Son WJ, van der Heide J, Ploeg R, Navis G. Predictive capacity of pre-donation GFR and renal reserve capacity for donor renal function after living kidney donation. Am J Trans. 2006;6:1653–9. doi: 10.1111/j.1600-6143.2006.01359.x. [DOI] [PubMed] [Google Scholar]
- 20.Grubb A, Nyman U, Bjork J, Lindstrom V, Rippe B, Sterner G, et al. Simple cystatin C-based prediction equations for glomerular filtration rate compared with the Modification of Diet in Renal Disease Prediction Equation for adults and the Schwartz and the Counahan-Barratt Prediction Equations for children. Clin Chem. 2005;51(8):1420–1431. doi: 10.1373/clinchem.2005.051557. [DOI] [PubMed] [Google Scholar]
- 21.Mauer M, Drummond K. The early natural history of nephropathy in type 1 diabetes: I. Study design and baseline characteristics of the study participants. Diabetes. 2002;51(5):1572–9. doi: 10.2337/diabetes.51.5.1572. [DOI] [PubMed] [Google Scholar]
- 22.Froissart M, Rossert J, Jacquot C, Paillard M, Houillier P. Predictive performance of the modification of diet in renal disease and Cockcroft-Gault equations for estimating renal function. J Am Soc Nephrol. 2005;16(3):763–73. doi: 10.1681/ASN.2004070549. [DOI] [PubMed] [Google Scholar]
- 23.Mauer M, Zinman B, Gardiner R, Drummond KN, Suissa S, Donnelly SM, et al. ACE-I and ARBs in early diabetic nephropathy. J Renin Angiotensin Aldosterone Syst. 2002;3(4):262–9. doi: 10.3317/jraas.2002.048. [DOI] [PubMed] [Google Scholar]
- 24.Hansen HP, Tauber-Lassen E, Jensen BR, Parving HH. Effect of dietary protein restriction on prognosis in patients with diabetic nephropathy. Kidney Int. 2002;62(1):220–8. doi: 10.1046/j.1523-1755.2002.00421.x. [DOI] [PubMed] [Google Scholar]
- 25.Jacobsen P, Andersen S, Rossing K, Hansen BV, Parving HH. Dual blockade of the renin-angiotensin system in type 1 patients with diabetic nephropathy. Nephrol Dial Transplant. 2002;17(6):1019–24. doi: 10.1093/ndt/17.6.1019. [DOI] [PubMed] [Google Scholar]
- 26.Jacobsen P, Andersen S, Rossing K, Jensen BR, Parving HH. Dual blockade of the renin-angiotensin system versus maximal recommended dose of ACE inhibition in diabetic nephropathy. Kidney Int. 2003;63(5):1874–80. doi: 10.1046/j.1523-1755.2003.00940.x. [DOI] [PubMed] [Google Scholar]
- 27.Mathiesen ER, Hommel E, Giese J, Parving HH. Efficacy of captopril in postponing nephropathy in normotensive insulin dependent diabetic patients with microalbuminuria. Brit Med J. 1991;303(6794):81–7. doi: 10.1136/bmj.303.6794.81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tarnow L, Rossing P, Jensen C, Hansen BV, Parving HH. Long-term renoprotective effect of nisoldipine and lisinopril in type 1 diabetic patients with diabetic nephropathy. Diabetes Care. 2000;23(12):1725–30. doi: 10.2337/diacare.23.12.1725. [DOI] [PubMed] [Google Scholar]
- 29.Levey AS, Coresh J, Greene T, Marsh J, Stevens LA, Kusek J, et al. Expressing the MDRD study equation for estimating GFR with standardized serum creatinine values. Clin Chem. 2007;53(4):766–72. doi: 10.1373/clinchem.2006.077180. [DOI] [PubMed] [Google Scholar]
- 30.Stevens LA, Manzi J, Levey AS, Chen JL, Deysher AE, Ojo A, et al. Impact of creatinine calibration on performance of GFR estimating equations in a pooled individual patient database. Am J Kidney Dis. 2007;50(1):21–35. doi: 10.1053/j.ajkd.2007.04.004. [DOI] [PubMed] [Google Scholar]
- 31.Chambers J, Hastie T, editors. Statistical Methods in S. London: Chapman and Hall; 1993. Generalized Additive Models; pp. 104–154. [Google Scholar]
- 32.Efron B, Tibshirani RJ. An Introduction to the Bootstrap. New York: Chapman and Hall; 1993. [Google Scholar]
- 33.Selvin E, Manzi J, Stevens LA, Van Lente F, Lacher DA, Levey AS, et al. Calibration of serum creatinine in the National Health and Nutrition Examination Surveys (NHANES) 1988-1994, 1999-2004. Am J Kidney Dis. 2007;50(6):918–26. doi: 10.1053/j.ajkd.2007.08.020. [DOI] [PubMed] [Google Scholar]
- 34.Coresh J, Astor B, Greene T, Eknoyan G, Levey A. Prevalence of chronic kidney disease and decreased kidney function in the adult US population: Third National Health and Nutrition Examination Survey. Am J Kidney Dis. 2003;41(1):1–12. doi: 10.1053/ajkd.2003.50007. [DOI] [PubMed] [Google Scholar]
- 35.Centers for Disease Control and Prevention. National Health and Nutrition Examination Survey (NHANES) US Department of Health and Human Services; 2007. Vol. [Google Scholar]
- 36.National Center for Health Statistics. National Health and Nutrition Examination Survey (NHANES)-Analytic Guidelines. US Department of Health and Human Services; 2007. Vol. [Google Scholar]
- 37.Analytic and reporting guidelines: the Third National Health and Nutrition Examination Survey, NHANES III (1988-94) National Center for Health Statistics: Centers for Disease Control and Prevention; 2007. Vol. [Google Scholar]
- 38.Poggio ED, Wang X, Greene T, Van Lente F, Hall P. Performance of the MDRD and Cockcroft-Gault equations in the estimation of glomerular filtration rate in health and in chronic kidney disease. J Am Soc Nephrol. 2005;16(2):459–66. doi: 10.1681/ASN.2004060447. [DOI] [PubMed] [Google Scholar]
- 39.Perrone RD, Madias NE, Levey AS. Serum creatinine as an index of renal function: new insights into old concepts. Clin Chem. 1992;38(10):1933–53. [PubMed] [Google Scholar]
- 40.Glassock RJ, Winearls C. An epidemic of chronic kidney disease: fact or fiction? Nephrol Dial Transplant. 2008;23(4):1117–21. doi: 10.1093/ndt/gfn086. [DOI] [PubMed] [Google Scholar]
- 41.U.S Renal Data System. Bethesda, MD: National Institutes of Health, National Institute of Diabetes and Digestive and Kidney Diseases; 2008. [11 December 2008]. USRDS 2008 Annual Data Report: Atlas of Chronic Kidney Disease and End-Stage Renal Disease in the United States. Accessed at http://www.usrds.org/adr.htm. [Google Scholar]
- 42.Coresh J, Stevens LA, Levey AS. Chronic kidney disease is common: what do we do next? Nephrol Dial Transplant. 2008;23(4):1122–5. doi: 10.1093/ndt/gfn117. [DOI] [PubMed] [Google Scholar]
- 43.Hallan SI, Coresh J, Astor BC, Asberg A, Powe NR, Romundstad S, et al. International comparison of the relationship of chronic kidney disease prevalence and ESRD risk. J Am Soc Nephrol. 2006;17(8):2275–84. doi: 10.1681/ASN.2005121273. [DOI] [PubMed] [Google Scholar]
- 44.Aronoff GR, Berns JS, Brier ME, Golper TA, Morrison G, Singer I, et al. Dosing Guidelines for Adults. 4. Philadelphia, PA: American College of Physicians; 1999. Drug Prescribing in Renal Failure. [Google Scholar]
- 45.Seliger SL, Zhan M, Hsu VD, Walker LD, Fink JC. Chronic kidney disease adversely influences patient safety. J Am Soc Nephrol. 2008;19(12):2414–9. doi: 10.1681/ASN.2008010022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Benko A, Fraser-Hill M, Magner P, Capusten B, Barrett B, Myers A, et al. Canadian Association of Radiologists: consensus guidelines for the prevention of contrast-induced nephropathy. Can Assoc Radiol J. 2007;58(2):79–87. [PubMed] [Google Scholar]
- 47.Food and Drug Administration. Information for Healthcare Professionals Gadolinium-Based Contrast Agents for Magnetic Resonance Imaging (marketed as Magnevist, MultiHance, Omniscan, OptiMARK, ProHance) 2008 June 4; [Google Scholar]
- 48.Khurana A, McLean L, Atkinson S, Foulks CJ. The effect of oral sodium phosphate drug products on renal function in adults undergoing bowel endoscopy. Arch Intern Med. 2008;168(6):593–7. doi: 10.1001/archinte.168.6.593. [DOI] [PubMed] [Google Scholar]
- 49.Hsu CY, Ordonez JD, Chertow GM, Fan D, McCulloch CE, Go AS. The risk of acute renal failure in patients with chronic kidney disease. Kidney Int. 2008;74(1):101–7. doi: 10.1038/ki.2008.107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Sarnak MJ, Levey AS, Schoolwerth AC, Coresh J, Culleton B, Hamm LL, et al. Kidney disease as a risk factor for development of cardiovascular disease: a statement from the American Heart Association Councils on Kidney in Cardiovascular Disease, High Blood Pressure Research, Clinical Cardiology, and Epidemiology and Prevention. Circulation. 2003;108(17):2154–69. doi: 10.1161/01.CIR.0000095676.90936.80. [DOI] [PubMed] [Google Scholar]
- 51.Stevens LA, Coresh J, Schmid CH, Feldman HI, Froissart M, Kusek J, et al. Estimating GFR using serum cystatin C alone and in combination with serum creatinine: a pooled analysis of 3,418 individuals with CKD. Am J Kidney Dis. 2008;51(3):395–406. doi: 10.1053/j.ajkd.2007.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix
Appendix Figure 1
Appendix Figure 2
Appendix Tables