Heterogeneity in chronic myeloid leukaemia dynamics during imatinib treatment: role of immune responses (original) (raw)
Abstract
Previous studies have shown that during imatinib therapy, the decline of chronic myeloid leukaemia BCR-ABL transcript numbers involves a fast phase followed by a slow phase in averaged datasets. Drug resistance leads to regrowth. In this paper, variation of treatment responses between patients is examined. A significant positive correlation is found between slopes of the fast and the slow phase of decline. A significant negative correlation is found between slopes of the slow phase of decline and the regrowth phase. No correlation is found between slopes of the fast phase of decline and the regrowth phase. A mathematical model that is successfully fitted to diverse clinical profiles explains these correlations by invoking the immune response as a key determinant of tumour decline during treatment. Boosting immunity during drug therapy could enhance the response to treatment in patients.
Keywords: mathematical models, population dynamics, immune system, dynamics, cancer treatment dynamics
1. Introduction
Chronic myeloid leukaemia (CML; Shet et al. 2002; Calabretta & Perrotti 2004; Yoshida & Melo 2004) is a cancer of the haematopoietic system and progresses in three stages: the chronic phase, the accelerated phase and blast crisis. During the chronic phase, the tumour grows slowly and most cells show a high degree of differentiation. During the accelerated phase, and especially during blast crisis, cancer growth explodes and the fraction of immature blast cells increases sharply. The targeted drug imatinib (inhibiting the product of the BCR-ABL fusion gene that is thought to maintain the cancer) has been successful in suppressing the disease, especially when treatment is applied during the chronic phase (Gorre et al. 2001; Deininger & Druker 2003; Shah et al. 2004; Yoshida & Melo 2004). Alternative targeted drugs have since become available, most notably dasatinib and nilotinib (Bradeen et al. 2006; Talpaz et al. 2006; Deininger 2007; Weisberg et al. 2007). Datasets have been collected that document the dynamics of BCR-ABL transcript numbers (which are not equal to but reflect the dynamics of the cancer cells) during imatinib treatment (Michor et al. 2005; Roeder et al. 2006). On average, a bi-phasic decline of BCR-ABL transcript numbers is observed (figure 1), with an initial fast phase of decline followed by a second slower phase. In the case of treatment failure, BCR-ABL transcript numbers subsequently rise again. The reason for this bi-phasic decline is unclear; intrinsic cancer stem cell resistance and cellular quiescence have been suggested as possible causes (Michor et al. 2005; Roeder et al. 2006; Komarova & Wodarz 2007). This paper examines the heterogeneity among treatment responses in individual patients. Based on data analysis and computational methods, it is found that transient immune responses during imatinib therapy could be key to explaining the observed dynamics.
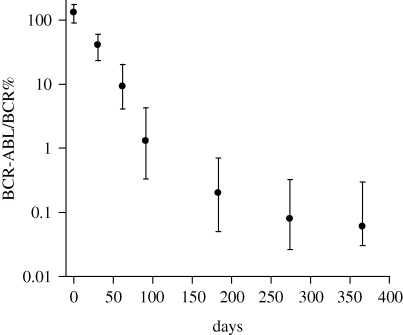
Figure 1.
Average dynamics of CML during imatinib treatment, taken from Michor et al. (2005). The BCR-ABL/BCR ratios are plotted over time, averaged over many patients. Patients who relapsed during therapy were excluded. See Michor et al. (2005) for more details. A bi-phasic decline is observed, where an initial fast-decline phase is followed by a slower-decline phase. This was the first study that published such averaged time series, and similarly averaged dynamics were found in patients from the German cohort of the IRIS study (Roeder et al. 2006), not shown here.
2. Material and methods
Standard statistical methods were used to quantify the slopes of the various treatment dynamics taken from published data, and to determine correlations between the individual slopes. The mathematical model explored in the paper is given by a set of ordinary differential equations, which were analysed by standard methods. The mathematical model was fitted to the clinical data using nonlinear least-squares regression. Details regarding the patient data, the methods of analysis, the properties of the mathematical model and the model fitting are found in the electronic supplementary material.
3. Results
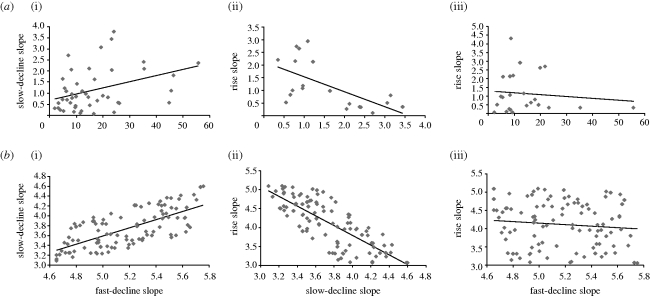
Rather than looking at averages, individual treatment dynamics and the heterogeneity between patients are studied in this paper using data from the German cohort of the IRIS study published by Roeder et al. (2006). In many patients, the dynamics appear to begin with a shoulder phase upon start of treatment, during which BCR-ABL transcript numbers fall slowly, if at all. If present, this is followed by a relatively fast phase of exponential decline; otherwise, the treatment response begins with this fast phase of decline. In some patients, this decline continues for the duration of the study. In most patients, however, this fast phase of decline is followed by a slower phase of exponential decline, as documented in the averages (Michor et al. 2005; Roeder et al. 2006). In many patients, BCR-ABL transcript numbers resurge subsequently. Therefore, in most patients, there are three important slopes if the dynamics of BCR-ABL numbers are documented on a log-scale: the slope of the fast decline phase, the slope of the slower decline phase and the slope of the eventual rise. The values of these slopes were quantified by fitting a three-phase exponential growth/decline model (see electronic supplementary material) to the data, using nonlinear least-squares regression and ignoring the initial shoulder phase of the dynamics (figure 2a). A significant positive correlation was found between the slopes of the fast and the slow phases of decline. A significant negative correlation was found between the slopes of the slow phase of decline and the regrowth. Finally, no significant correlation was found between the slope of the fast phase of decline and the regrowth.
Figure 2.
Correlations between the slopes of the fast decline, slow decline and the regrowth of BCR-ABL transcript numbers. (a) Correlations found in the clinical data from the German cohort of the IRIS study (Roeder et al. 2006). Only patients who were characterized by the presence of the relevant two slopes were included. Two significantly outlying data points were excluded. For (i) and (ii), the correlation is significant (p = 0.009 and p = 0.003, respectively). For (iii), there is no significant correlation (p = 0.59). (b) Correlations between the slopes of the fast decline, the slow decline and the regrowth, as predicted by computer simulations of the mathematical model. Simulations were run 100 times, randomly varying both the rate of specific immune proliferation, c, and the growth rate of the resistant cancer cells, r. For (i) and (ii), the correlations are significant (p < 0.0001 in each case), while for (iii) the correlation is not significant (p = 0.32). The remaining parameters of the model (chosen for illustrative purposes) were: d = 1; p = 3; b = 0.5; q = 0.01; ε = 1; η = 1 (units are yr−1). _x_0 = 100; _y_0 = 0.001; _z_0 = 0.5.
The negative correlation between the slopes of the slow phase of decline and the rise implies that both could be influenced by the presence of drug-resistant mutants (Gorre et al. 2001; Deininger & Druker 2003; Druker 2003, 2004; Gambacorti-Passerini et al. 2003; Nardi et al. 2004; Shah et al. 2004). The rise of drug-resistant mutants can slow down the decline of BCR-ABL transcript numbers and is responsible for the eventual rise of BCR-ABL transcripts. The fact that the slopes of the slow and fast decline phases are positively correlated means that these two phases share a common mechanism of cell death that varies over time in strength. One such factor could be the immune system, which has been suggested to play a role in CML therapy before (Wang et al. 2005; Chen et al. 2008; Kim et al. 2008). In particular, T cell responses (both CD4+ and CD8+) have been implicated. Data indicate that the level of immune responses against CML is low before treatment, rises as treatment is administered and declines again as the BCR-ABL transcript numbers fall to low levels. These are similar immune response dynamics to those observed in patients infected with human immunodeficiency virus (HIV) and hepatitis C virus (HCV) who receive anti-viral drug therapy (Kalams et al. 1999; Ogg et al. 1999; Barnes et al. 2002), and can be explained in the same way. While the cancer cells impair immunity, treatment reduces the amount of impairment, leading to a rise of immunity. As the number of cancer cells declines, withdrawal of antigenic stimulation causes a drop in immune responses. Such impairment dynamics have been explored extensively with mathematical models in the context of viral infections (Wodarz & Nowak 1999; Wodarz 2001; Komarova et al. 2003), and more recently also in the context of CML (Kim et al. 2008). The following will use a basic mathematical model that captures these assumptions. Model fitting to individual patient data demonstrates consistency with clinical observations, and the model further predicts the correlations found in the data.
A mathematical model is adapted that was previously published in the context of viral infections (Komarova et al. 2003) and that captures the necessary assumptions. It includes a population of cells that grow over time and that have the ability to impair immunity, as well as an immune response that reacts to this cell population and removes it. The mathematical model is part of a general class of models that share common properties (Komarova et al. 2003). Results obtained from the model are therefore not dependent on the particular mathematical formulation used, but are robust. The equations that describe the immune response make the very basic assumptions that cancer cells can both stimulate the specific immune cells to proliferate and impair the response. Because of the general nature of the model, this can be applied to any branch of the adaptive immune system, including the T cell responses that are thought to play a role during CML therapy (Wang et al. 2005; Chen et al. 2008; Kim et al. 2008). Further discussion of the biological assumptions, aspects of robustness and mathematical methods is given in the electronic supplementary material. The basic model is characterized by the following outcomes, assuming that the degree of stimulation of immune cells is strong enough to drive immune expansion: (i) an immune response is successfully established and the system converges to a stable equilibrium in which cancer is controlled at relatively low levels; (ii) the immune response goes extinct and the cancer cell population converges to an equilibrium characterized by a large number of tumour cells. If the degree of immune impairment is relatively low, only the cancer control outcome is stable. If the degree of immune impairment lies above a threshold, both outcomes are stable. To which outcome the system converges depends on the initial conditions, with a high initial number of immune cells and a low initial number of tumour cells promoting the cancer control outcome. For the current purposes, this general model was modified to include two sub-populations of cancer cells: drug-sensitive and drug-resistant cells. Since the analysis focuses on the treatment phase only, it is assumed that drug-sensitive cells simply decline exponentially, and that this is brought about by a combination of the cells' natural death rate and immune-induced death. On the other hand, it is assumed that drug-resistant cells expand exponentially during treatment. This expansion can, however, be countered by the immune response. Further details of this overview are given in the electronic supplementary material.
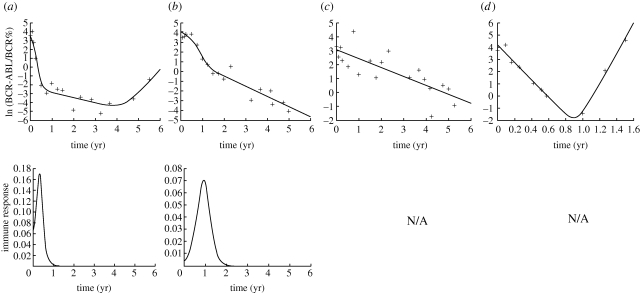
The model can give rise to treatment dynamics that can describe diverse clinical data well, shown by nonlinear least-squares fits of the model to selected patient data (figure 3). Figure 3a shows a response that involves an initial shoulder phase, followed by a faster and a slower phase of decline, eventually leading to a resurgence of the cancer. Immunity is low at the beginning, accounting for a relatively slow initial decline of cells during the shoulder phase. Immunity rises as the number of CML cells starts to decline because of reduced immune impairment. This accounts for the fast phase of CML decline. Immunity subsequently falls owing to lack of antigenic stimulation. This, together with the rise of a resistant mutant, accounts for the slower phase of decline. The rise of the resistant mutant eventually leads to resurgence of cancer. Figure 3b shows the same kind of profile without eventual resurgence of the cancer. In this case, a resistant mutant is not present. Figure 3c shows a single-phase exponential decline of CML cells, while figure 3d shows an exponential decline followed by re-growth of the cancer. In these cases, immunity does not expand during the treatment dynamics according to the model, correlating with a significantly slower decline rate of the cancer. In figure 3c, no resistant mutant exists, while in figure 3d, a resistant mutant grows during therapy.
Figure 3.
Examples of individual treatment response data from the German cohort of the IRIS study, taken from Roeder et al. (2006). The dots are the actual clinical data. The line is the model fitted to the data, obtained by nonlinear least-squares regression. In (a,b), immune responses rise temporarily during therapy, contributing to the overall treatment dynamics. In (c,d), the model predicts that immune responses did not rise during therapy. Drug-resistant mutants play a role in (a) and (d), but not in (b) and (c). For further discussion, see text. Model parameter values are as follows (see electronic supplementary material for discussion of parameter values). (a) r = 2.69; c = 17.04; d = 0.58; p = 80.3; b = 8.84; q = 0.10; ε = 1; η = 1; _x_0 = 35.53; _y_0 = 2.73 × 10−5; _z_0 = 0.06. (b) r = 0; c = 14.00; d = 1.04; p = 43.60; b = 8.97; q = 4.88 × 10−4; ε = 2.85; η = 1; _x_0 = 60.76; _y_0 = 0; _z_0 = 0.0044. (c) r = 0; c = 0; d = 0.65; p = 0; b = 0; q = 0; ε = 0; η = 0; _x_0 = 21.17; _y_0 = 0; _z_0 = 0. (d) r = 12.4; c = 0; d = 7.23; p = 0; b = 0; q = 0; ε = 0; η = 0; _x_0 = 65.92; _y_0 = 9.61 × 10−7; _z_0 = 0. Units are yr−1 for all models.
To examine predicted correlations between the slopes, the simulation was run many times, randomly varying the growth rate of drug-resistant CML cells and the rate of immune expansion against CML. Consistent with the experimental data, the model predicts a significant positive correlation between the slopes of the fast and slow phase of decline, a significant negative correlation between the slopes of the slow phase of decline and the regrowth, and a lack of a significant correlation between the slopes of the fast phase of decline and the regrowth (figure 2b). The reason is as follows. The immune response largely drives the fast phase of decline. Part of the reason for the slower decline is a fall of immune responses as the number of CML cells drops to low levels. However, the strength of the declining immunity is still proportional to the strength of immunity at its peak, hence the positive correlation. Another reason for the slowing decline is the rise of drug-resistant mutants. In addition, growth of resistant mutants completely determines the eventual rise of CML cells, hence the negative correlation. Since the fast phase of decline is mostly determined by immunity while the initial rise of resistant mutants is mostly determined by their replication rate, there is no correlation between these slopes. Apart from these correlations, the model can give rise to alternative outcomes if the variation in one parameter is significantly more pronounced than variation in the second parameter, which is discussed further in the electronic supplementary material.
4. Discussion
The correlations found between the various slopes in the clinical data are fully consistent with the hypothesis that a transient immune response during the initial stages of drug treatment is a major factor in shaping the dynamics of CML decline during therapy. Reduction of immune impairment after initiation of treatment induces a rise of immunity, which subsequently falls as the amount of antigenic stimulation diminishes. Such immune response dynamics have in fact been demonstrated in clinical data from imatinib-treated patients (Wang et al. 2005; Chen et al. 2008). This type of CML-immune dynamics has also been modelled previously in a different context (Kim et al. 2008), which in turn is similar to data and modelling results from other immunity-impairing diseases, such as HIV or HCV infections (Kalams et al. 1999; Ogg et al. 1999; Wodarz & Nowak 1999; Wodarz 2001; Barnes et al. 2002; Komarova et al. 2003). In addition, the analysis suggests that drug-resistant mutants contribute to the slowing down of the decline of CML cells, and to the possible regrowth of the cancer. The extent to which drug-resistant mutants slow down the decline depends on the growth rate of the mutants during therapy, which can vary between different mutants.
These notions give rise to the following implications: in the absence of the transient immune response during treatment, the CML decline occurs with a significantly slower rate (i.e. the fast initial phase of decline is absent). Conversely, if specific immune responses could be boosted during therapy, the rate of CML decline could be significantly accelerated. Variations in immune response dynamics during treatment are likely to significantly account for variations in the observed treatment dynamics.
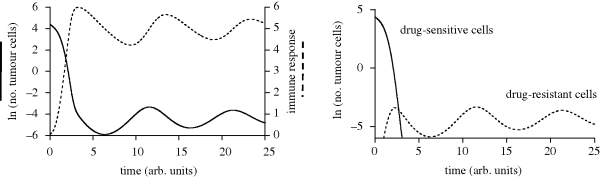
If immune responses that arise during treatment are sustained, they could in principle suppress the population of drug-resistant cancer cells. In some patients, discontinuation of therapy after 2 years did not result in the relapse of the cancer (Rousselot et al. 2006). It can be hypothesized that in these cases, immunity became fully established during therapy rather than rising only temporarily. This possibility is demonstrated by computer simulation in figure 4. Establishment of sustained immune responses during therapy of immunosuppressive diseases has been found to occur in some experimental HCV and simian immunodeficiency virus (SIV) therapy regimes (Lifson et al. 2000; Barnes et al. 2002).
Figure 4.
Computer simulation of the mathematical model, which shows the possibility that during therapy, the immune response is maintained at higher levels rather than dropping to insignificant levels. In this simulation, therapy is started at time zero. As a result of maintained immunity, the initial regrowth of cancer, brought about by drug-resistant mutants, is blunted, and the number of CML cells is kept at low levels in the long term. The right panel shows the CML dynamics separately for the populations of drug-sensitive and drug-resistant cells. Parameters were chosen for illustrative purposes as follows: r = 5; c = 5; d = 0.5; p = 1; b = 0.1; q = 0.01; ε = 0.1; η = 1; _x_0 = 80; _y_0 = 2.7 × 10−5; _z_0 = 0.06. The units of the axes are arbitrary, as the parameter set was chosen for illustrative purposes and is not based on measured parameters, which are currently unknown.
To summarize, the analysis of the clinical data performed here strongly supports an important role of immune responses in the dynamics of CML during therapy. Exploring this notion further could open doors to new therapy options that could improve the outcome of targeted drug treatment of CML. An important next step would be to address experimentally in detail the differences between the dynamics explored here and those described in previous work, which proposed alternative mechanisms (Michor et al. 2005; Roeder et al. 2006; Komarova & Wodarz 2007).
Acknowledgements
This work was funded in part by NIH 1R01CA129286.
References
- Barnes E., Harcourt G., Brown D., Lucas M., Phillips R., Dusheiko G., Klenerman P.2002The dynamics of T-lymphocyte responses during combination therapy for chronic hepatitis C virus infection. Hepatology 36, 743–754 (doi:10.1053/jhep.2002.35344) [DOI] [PubMed] [Google Scholar]
- Bradeen H. A., Eide C. A., O'Hare T., Johnson K. J., Willis S. G., Lee F. Y., Druker B. J., Deininger M. W.2006Comparison of imatinib mesylate, dasatinib (BMS-354825), and nilotinib (AMN107) in an _N_-ethyl-_N_-nitrosourea (ENU)-based mutagenesis screen: high efficacy of drug combinations. Blood 108, 2332–2338 (doi:10.1182/blood-2006-02-004580) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calabretta B., Perrotti D.2004The biology of CML blast crisis. Blood 103, 4010–4022 (doi:10.1182/blood-2003-12-4111) [DOI] [PubMed] [Google Scholar]
- Chen C. I., Maecker H. T., Lee P. P.2008Development and dynamics of robust T-cell responses to CML under imatinib treatment. Blood 111, 5342–5349 (doi:10.1182/blood-2007-12-128397) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deininger M. W.2007Optimizing therapy of chronic myeloid leukemia. Exp. Hematol. 35, 144–154 (doi:10.1016/j.exphem.2007.01.023) [DOI] [PubMed] [Google Scholar]
- Deininger M. W., Druker B. J.2003Specific targeted therapy of chronic myelogenous leukemia with imatinib. Pharmacol. Rev. 55, 401–423 (doi:10.1124/pr.55.3.4) [DOI] [PubMed] [Google Scholar]
- Druker B. J.2003Overcoming resistance to imatinib by combining targeted agents. Mol. Cancer Ther. 2, 225–226 [PubMed] [Google Scholar]
- Druker B. J.2004Imatinib as a paradigm of targeted therapies. Adv. Cancer Res. 91, 1–30 (doi:10.1016/S0065-230X(04)91001-9) [DOI] [PubMed] [Google Scholar]
- Gambacorti-Passerini C. B., Gunby R. H., Piazza R., Galietta A., Rostagno R., Scapozza L.2003Molecular mechanisms of resistance to imatinib in Philadelphia-chromosome-positive leukaemias. Lancet Oncol. 4, 75–85 (doi:10.1016/S1470-2045(03)00979-3) [DOI] [PubMed] [Google Scholar]
- Gorre M. E., Mohammed M., Ellwood K., Hsu N., Paquette R., Rao P. N., Sawyers C. L.2001Clinical resistance to STI-571 cancer therapy caused by BCR-ABL gene mutation or amplification. Science 293, 876–880 (doi:10.1126/science.1062538) [DOI] [PubMed] [Google Scholar]
- Kalams S. A., Goulder P. J., Shea A. K., Jones N. G., Trocha A. K., Ogg G. S., Walker B. D.1999Levels of human immunodeficiency virus type 1-specific cytotoxic T-lymphocyte effector and memory responses decline after suppression of viremia with highly active antiretroviral therapy. J. Virol. 73, 6721–6728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim P. S., Lee P. P., Levy D.2008Dynamics and potential impact of the immune response to chronic myelogenous leukemia. PLoS Comput. Biol. 4, e1000095 (doi:10.1371/journal.pcbi.1000095) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komarova N. L., Wodarz D.2007Effect of cellular quiescence on the success of targeted CML therapy. PLoS ONE 2, e990 (doi:10.1371/journal.pone.0000990) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Komarova N. L., Barnes E., Klenerman P., Wodarz D.2003Boosting immunity by antiviral drug therapy: a simple relationship among timing, efficacy, and success. Proc. Natl Acad. Sci. USA 100, 1855–1860 (doi:10.1073/pnas.0337483100) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lifson J. D., et al. 2000Containment of simian immunodeficiency virus infection: cellular immune responses and protection from rechallenge following transient post-inoculation antiretroviral treatment. J. Virol. 74, 2584–2593 (doi:10.1128/JVI.74.6.2584-2593.2000) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michor F., Hughes T. P., Iwasa Y., Branford S., Shah N. P., Sawyers C. L., Nowak M. A.2005Dynamics of chronic myeloid leukaemia. Nature 435, 1267–1270 (doi:10.1038/nature03669) [DOI] [PubMed] [Google Scholar]
- Nardi V., Azam M., Daley G. Q.2004Mechanisms and implications of imatinib resistance mutations in BCR-ABL. Curr. Opin. Hematol. 11, 35–43 (doi:10.1097/00062752-200401000-00006) [DOI] [PubMed] [Google Scholar]
- Ogg G. S., et al. 1999Decay kinetics of human immunodeficiency virus-specific effector cytotoxic T lymphocytes after combination antiretroviral therapy. J. Virol. 73, 797–800 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roeder I., Horn M., Glauche I., Hochhaus A., Mueller M. C., Loeffler M.2006Dynamic modeling of imatinib-treated chronic myeloid leukemia: functional insights and clinical implications. Nat. Med. 12, 1181–1184 (doi:10.1038/nm1487) [DOI] [PubMed] [Google Scholar]
- Rousselot P., et al. 2006Imatinib mesylate discontinuation in patients with chronic myelogenous leukemia in complete molecular remission for more than two years. Blood 109, 58–60 (doi:10.1182/blood-2006-03-011239) [DOI] [PubMed] [Google Scholar]
- Shah N. P., Tran C., Lee F. Y., Chen P., Norris D., Sawyers C. L.2004Overriding imatinib resistance with a novel ABL kinase inhibitor. Science 305, 399–401 (doi:10.1126/science.1099480) [DOI] [PubMed] [Google Scholar]
- Shet A. S., Jahagirdar B. N., Verfaillie C. M.2002Chronic myelogenous leukemia: mechanisms underlying disease progression. Leukemia 16, 1402–1411 (doi:10.1038/sj.leu.2402577) [DOI] [PubMed] [Google Scholar]
- Talpaz M., et al. 2006Dasatinib in imatinib-resistant Philadelphia chromosome-positive leukemias. N. Engl. J. Med. 354, 2531–2541 (doi:10.1056/NEJMoa055229) [DOI] [PubMed] [Google Scholar]
- Wang H., Cheng F., Cuenca A., Horna P., Zheng Z., Bhalla K., Sotomayor E. M.2005Imatinib mesylate (STI-571) enhances antigen-presenting cell function and overcomes tumor-induced CD4+ T-cell tolerance. Blood 105, 1135–1143 (doi:10.1182/blood-2004-01-0027) [DOI] [PubMed] [Google Scholar]
- Weisberg E., Manley P. W., Cowan-Jacob S. W., Hochhaus A., Griffin J. D.2007Second generation inhibitors of BCR-ABL for the treatment of imatinib-resistant chronic myeloid leukaemia. Nat. Rev. Cancer 7, 345–356 (doi:10.1038/nrc2126) [DOI] [PubMed] [Google Scholar]
- Wodarz D.2001Helper-dependent vs. helper-independent CTL responses in HIV infection: implications for drug therapy and resistance. J. Theor. Biol. 213, 447–459 (doi:10.1006/jtbi.2001.2426) [DOI] [PubMed] [Google Scholar]
- Wodarz D., Nowak M. A.1999Specific therapy regimes could lead to long-term control of HIV. Proc. Natl Acad. Sci. USA 96, 14 464–14 469 (doi:10.1073/pnas.96.25.14464) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoshida C., Melo J. V.2004Biology of chronic myeloid leukemia and possible therapeutic approaches to imatinib-resistant disease. Int. J. Hematol. 79, 420–433 (doi:10.1532/IJH97.04032) [DOI] [PubMed] [Google Scholar]