Organismal complexity, protein complexity, and gene duplicability (original) (raw)
Abstract
Although the evolutionary significance of gene duplication has long been recognized, it remains unclear what determines gene duplicability. We find protein complexity to be an important determinant because the proportion of unduplicated genes (P) increases with the number of subunits in a protein. However, P is high (≥65%) for both monomers and multimers in yeast, but ≤30% in human except for subunits of large multimers, implying that organismal complexity is a stronger determinant of gene duplicability than protein complexity. The same conclusion is reached from a comparison of family sizes in yeast and human.
Despite >30 years of effort (1), it remains unclear what determines gene duplicability. Protein complexity, defined as the number of subunits in a protein (n), might be an important factor because duplication of a protein subunit may cause dosage imbalance among the subunits of the protein (2, 3) and the chance of imbalance might increase with the number of subunits in a protein. By using yeast data, Papp et al. (3) found that 33% of the single-copy genes (singletons) participate in protein complexes (multimers), whereas this frequency drops to ≈21% for genes with three or more paralogues. They therefore concluded that duplication of a subunit of a protein complex is less likely to be successful than duplication of a monomer. However, no monomers were included in their analysis, so the magnitude of difference in survivability between duplication of a monomer and duplication of a protein complex subunit is not known. It is worth emphasizing that duplication of a monomer may also cause dosage imbalance. This may be particularly true for transcription factors, each of which may control many downstream genes. For example, Drosophila embryos produced by mothers with four dosages of bicoid, a maternal morphogen, tend to develop a larger head, and only ≈30% of the embryos produced by mothers with six dosages of bicoid are viable (4). Thus, it is important to include monomers. Indeed, we study the relationship between the survivability of a gene duplication and n by classifying proteins into monomers (n = 1), dimers (n = 2), midsize complexes (3 ≤ n ≤ 10), and large complexes (n > 10). Another factor that may affect the survivability of duplicate genes is organismal complexity. It was suggested that, for transcription factors, dosage imbalance occurs more frequently in a complex organism than in yeast because of the long regulatory cascades during multicellular development (3). However, a complex organism may actually be more robust against dosage increase than a simple organism (see below). Thus, we also examine this factor by contrasting human with yeast. Here, organismal complexity is loosely defined as the number of different types of cells.
Previously we talked about survivability, which may be defined as the probability for a duplicate gene to survive, but adaptive evolution of duplicate genes may also be important. Because, in the end, we see only whether a gene has been duplicated or not, we will use gene duplicability more often than survivability of duplicate genes. Here, gene duplicability is loosely defined as the chance for a gene to be duplicated or, more precisely, the proportion of genes in a genome that have one or more paralogs. Note that here we are mainly concerned with small-scale duplications, but not large duplications such as chromosome or genome duplications, which are known to be deleterious in most cases in higher vertebrates.
Materials and Methods
Identification of Duplicate Genes. Duplicate genes were identified by the tribe-mcl method of Enright et al. (7); tribe-mcl is based on the Markov cluster (MCL) algorithm, previously developed for graph clustering by using flow simulation. The presence of proteins having multiple domains has confounded many previous methods for protein clustering, but this new method, which relies on the MCL method, is able to handle this problem well. Compared with the traditional pairwise grouping method, this method uses graph theory, which clusters proteins into families by using a global treatment that considers all relationships in the similarity space at the same time. This grouping method has been applied to many data sets and Ensemble has used it to obtain gene family annotation for the human genome. For Homo sapiens, we use the version of Ensemble_family_13_1 from the Sanger database [created according to Enright _et al._ (7)], which corresponds to the assembly of NCBI 31. For Saccharomyces cerevisiae, the family classification data were kindly sent to us by A. Enright (Memorial Sloan–Kettering Cancer Center, New York). The gene family sizes were all computed by using the tribe-mcl method. We also followed Papp et al. (3) to use blast with E = 10–10 and the method of Gu et al. (8) to cluster proteins into families from the protein database. The method of Gu et al. is more stringent, whereas the simple blast with E = 10–10 is more relaxed, than the tribe-mcl method. The numbers of duplicate genes detected by the three methods were 1,687, 2,334, and 2,696, respectively. Thus, the estimate by tribe-mcl was intermediate and was used in our analysis. However, our conclusions were essentially the same for the three methods.
Identification of Protein Complexes. We searched through Swiss-Prot/TrEMBL manually to collect the protein complex information, taking advantage of the high quality of this database. For H. sapiens, we found a total of 3,923 entries with subunit information. After a detailed examination of the annotation on each subunit, we only kept those entries that had unambiguous subunit descriptions (n = 2,647). We exclude from our analyses those entries that have more than one possible complex, e.g., those that can form both a dimer and a trimer. For monomer identification, we used only those that have been clearly stated as monomers. We excluded from our analysis each polypeptide that lacked information on whether it was a complex subunit.
For yeast, we used not only the Munich Information Center for Protein Sequences (MIPS) data (5), as did Papp et al. (3), but also the Swiss-Prot/TrEMBL data (6), which provide better information on subunit structure than the MIPS data. First, a set of annotated protein complexes was assembled from the MIPS comprehensive yeast genome database (CYGD) catalog on known protein complexes (http://mips.gsf.de/proj/yeast/catalogues/complexes/index.html). Where complex annotations were hierarchical, we stayed at the lowest level, and we finally obtained 1,136 proteins that were verified complexes. We used only protein complexes that are stable and clearly defined. As pointed out by Papp et al. (3), the balance theory may not be applied to transient interaction and unstable complexes. Therefore, we did not use any high throughput data to identify protein complexes because they may include transient interactions and have high false positive and negative rates (9–11). Second, from Swiss-Prot/TrEMBL we found a total of 874 entries with a record of complex information for S. cerevisiae. For the same reason as for the human data, we kept only 645 entries for further analysis. We further classified them into dimers, midsize complexes (3 ≤ n ≤ 10), and large complexes (n > 10). For monomers, however, we could find only 36 known cases from Swiss-Prot/TrEMBL. Therefore, we used the data obtained as follows. We first gathered all of the recorded protein–protein interactions from both large-scale (high-throughput) and traditional approaches as summarized by von Mering et al. (9). We used the 5,714 ORFs from the Kellis et al. (12) genome revision as our genomic data for yeast. We then excluded all those proteins (ORFs) with putative interactions detected by at least one of the methods as described in Mering et al. (9), and obtained 754 ORFs with no recorded protein interactions. We assumed that these latter polypeptides do not form complexes; that is, they are monomers. This assumption seems reliable, because it is unlikely that a stable protein interaction would have been missed by all methods used to search for protein–protein interactions in yeast. To avoid including pseudogenes and erroneously predicted genes, in some analyses we also excluded unnamed or unclassified genes (genes with the same gene name and ORF name in the Saccharomyces Genome Database); after this exclusion, our final collection of monomers was 341.
Results
We consider three measures of gene duplicability. The first one is the proportion of polypeptides encoded by single-copy genes (Q); it is denoted by _Q_M for known monomers and by _Q_C for known subunits of protein complexes. Obviously, a higher proportion implies lower gene duplicability. For yeast, _Q_M = 0.629 is actually slightly higher than _Q_C = 0.614 (Table 1). In this analysis, the monomers included many unclassified proteins, which may be biased toward singletons (3). When the unclassified proteins are excluded, _Q_M = 0.563, which is similar to the value (0.556) obtained from the 36 known monomers we found in Swiss-Prot/TrEMBL. The true value is probably in between the above two estimates and probably somewhat smaller than _Q_C. For human, _Q_M = 0.167 and _Q_C = 0.153 are similar to each other. Thus, in terms of Q, there is little difference between monomers and complex subunits. What is interesting is that the _Q_M and _Q_C for human are much lower than the corresponding values for yeast, indicating much higher gene duplicability in human than in yeast.
Table 1. Proportion of polypeptides encoded by single-copy genes (singletons).
| Protein structure (n = subunit no.) | Total no. of polypeptides studied | No. of singletons | Proportion of singletons, Q | Total no. of gene families | Proportion of singleton families, P |
|---|---|---|---|---|---|
| Yeast | |||||
| Monomers* | 754 | 474 | 0.629 | 669 | 0.709 |
| Monomers† | 341 | 192 | 0.563 | 306 | 0.627 |
| Protein complex subunits‡ | 1,136 | 697 | 0.614 | 902 | 0.773 |
| Dimer subunits (n = 2)‡ | 171 | 96 | 0.561 | 135 | 0.711 |
| Hetero | 75 | 43 | 0.573 | 62 | 0.694 |
| Homo | 96 | 53 | 0.552 | 73 | 0.726 |
| Midsize complex subunits (3 ≤ n ≤ 10)‡ | 278 | 177 | 0.637 | 231 | 0.766 |
| Hetero | 216 | 150 | 0.694 | 183 | 0.820 |
| Homo | 62 | 27 | 0.435 | 48 | 0.563 |
| Large complex subunits (n > 10) | 196 | 160 | 0.816 | 183 | 0.874 |
| Human | |||||
| Monomers (n = 1) | 198 | 33 | 0.167 | 161 | 0.205 |
| Dimer subunits (n = 2)‡ | 1,492 | 141 | 0.095 | 555 | 0.254 |
| Hetero | 916 | 52 | 0.057 | 208 | 0.250 |
| Hetero§ | 358 | 52 | 0.145 | 205 | 0.254 |
| Homo | 372 | 69 | 0.185 | 258 | 0.267 |
| Midsize complex subunits (3 ≤ n ≤ 10)‡ | 958 | 156 | 0.163 | 521 | 0.299 |
| Hetero* | 538 | 97 | 0.180 | 313 | 0.310 |
| Homo | 233 | 40 | 0.171 | 153 | 0.261 |
| Large complex subunits (n > 10)‡ | 377 | 128 | 0.340 | 295 | 0.434 |
| All protein complex subunits‡ | 2,963 | 453 | 0.153 | 1,399 | 0.324 |
The second measure is the proportion of single-gene (singleton) families among the gene families that encode the studied monomers (_P_M) and that among the families that encode the studied protein complex subunits (_P_C). Here, a single-gene family is a family that consists of only one gene, and therefore _P_M is the proportion of monomers that have no paralogue in the genome; _P_C is similarly defined. For yeast, _P_M is somewhere between 0.709 and 0.627 (Table 1) and so is probably significantly lower than _P_C = 0.773. However, _P_M may not be significantly smaller than _P_C = 0.711 for dimers. _P_C becomes slightly larger (0.766) for midsize complexes and increases to 0.874 for large complexes (Table 1). For human, _P_M (0.205) is only somewhat smaller than _P_C (0.254) for dimers, considerably smaller than that (0.299) for midsize protein complexes, and only half of that (0.434) for large complexes. Again, all these numbers are much smaller than the corresponding values for yeast.
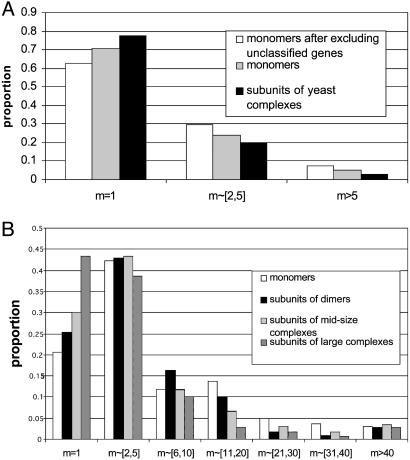
The third measure is the distribution of family sizes (Fig. 1). For the human data we consider dimers, midsize complexes, and large complexes separately, whereas for the yeast data we consider all protein complexes together because of sample size limitation. Clearly, the majority of yeast polypeptides (>60%) are singletons, regardless of whether they are monomers or complex subunits, and only a small proportion of them (<10%) have a family size >5 (Fig. 1_A_). In contrast, the majority of human polypeptides (>55%) have paralogues, and >30% of the polypeptide families, except for subunits of large complexes, have a family size >5 (Fig. 1_B_). Thus, in yeast there are very few large gene families, even for monomers, whereas in human, >5% of the polypeptide families studied have a family size >40, even for subunits of large complexes. In yeast, the mean family size for monomers is between 1.98 and 2.40, depending on whether or not unclassified proteins are included (Table 2). If, for simplicity, we take the simple average, i.e., 2.19, then the mean family size for protein complexes (1.57) represents a 28% reduction (i.e., 1.57/2.19 = 0.72). In contrast, in human the mean family size for protein complex subunits (7.06) represents only a 17% reduction compared with the mean family size for monomers (8.52). Actually, this reduction is almost completely caused by subunits of large protein complexes because the mean family size for dimers (10.54) is actually significantly larger than that for monomers and the mean family size for midsize complexes (8.13) is comparable to that for monomers (Table 2). The mean family size for large complexes is 4.91, which is considerably smaller than that for human monomers. It is worth noting that all mean family sizes in human are much larger than even that for yeast monomers (2.19). This again suggests much higher duplicability of human genes.
Fig. 1.
(A) Distributions of family sizes (m) for yeast monomers and subunits of protein complexes. The distribution for monomers significantly differs from that for complex subunits (P = 0.033) by the two-sample Kolmogorov–Smirnov (K–S) test. After excluding the unnamed genes, P = 0.0001. (B) Distributions of family sizes for human monomers, subunits of dimers, subunits of midsize protein complexes, and subunits of large protein complexes. The K–S test gives P = 0.076 for the difference between the distributions for monomers and dimers and P = 0.058 after excluding the three supergene families of dimers related to the immune system. The K–S test gives P = 0.014 for the difference between the distributions for monomers and midsize complex subunits and P = 3.6 × 10–5 for the difference between the distributions for monomers and large-complex subunits.
Table 2. Mean family sizes of different types of polypepetides.
| Polypeptide type | Mean ± SE |
|---|---|
| Yeast* | |
| Monomers | 1.98 ± 0.12 |
| Monomers after excluding unclassified proteins | 2.40 ± 0.21 |
| Complex subunits (MIPS) | 1.57 ± 0.07 |
| Human† | |
| Monomers | 8.52 ± 0.95 |
| Dimer subunits | 10.54 ± 2.60 |
| Dimer subunits excluding supergene families | 6.45 ± 0.51 |
| Midsize complex subunits | 8.13 ± 1.54 |
| Large complex subunits | 4.91 ± 0.60 |
| All protein complex subunits | 7.06 ± 1.05 |
The above three measures reflect different aspects of polypeptide duplicability. The first one, the proportion of singletons (Q), refers to the proportion of the studied polypeptides that are encoded by single-copy genes. A large Q value means that a small proportion of the polypeptides studied are encoded by duplicate genes, whereas a small Q value means the opposite. Because Q can be strongly affected by the presence of large gene families, it is less desirable than P, the proportion of polypeptide families that consist of a single member. P refers to the proportion of polypeptide types that have no duplicate copy in the genome and is not affected by the presence of large gene families (Table 1). However, although (1 – P) means the proportion of polypeptides that have been duplicated, it does not tell us how many times a polypeptide has been duplicated. This is achieved by using the third quantity, the family size distribution. From this quantity one can see whether there are large gene families for monomers and for protein complex subunits. Although the mean of this distribution is strongly affected by the presence of large gene families, it tells us on average how often a polypeptide type has been duplicated.
Discussion
One caveat in the present study is that the yeast and human data on protein structure are incomplete, so the estimates may be biased to some extent and will need to be revised when better gene and protein annotation data become available. Also, we have not considered the possibility of genome duplication. There appears to have been no genome duplication in the human lineage since the common ancestor of higher vertebrates, although there is the possibility of one or two rounds of genome duplication during early vertebrate evolution, i.e., >400 million years ago (13, 14). On the other hand, the yeast genome has been suggested to have gone through a genome duplication ≈100 million years ago (15). Thus, there is no evidence that genome duplication has contributed more to human than to yeast in terms of the three quantities considered above. Furthermore, in human, even if we include only duplicate pairs with the number of synonymous substitutions per synonymous site (_K_S) < 1.5, the mean family sizes for monomers, dimers, midsize protein complexes, and large protein complexes remain ≈6.7, 3.6, 4.8, and 3.8, respectively, which are still much larger than the corresponding values in yeast. With the assumption of an average synonymous rate of 2.5 × 10–9 per site per year for mammals (16, 17), _K_S = 1.5 corresponds to 1.5/(2 × 2.5 × 10–9) = 300 million years, which is around the fossil date for the divergence between the mammalian and avian lineages and is much younger than the putative genome duplications in early vertebrate evolution.
These caveats notwithstanding, our results clearly support the dosage balance hypothesis. First, the results in Table 1 support the prediction that dosage sensitivity increases with the number (n) of subunits in a protein. Second, the hypothesis should predict weaker dosage sensitivity for homomers than for heteromers because gene duplication for a homomer would not produce free excess of subunits, and our data indeed suggests a slightly higher gene duplicability for homomer subunits than for heteromer subunits when n > 3; for both yeast and human, P is smaller for homomers than heteromers for subunits of midsize protein complexes (Table 1).
However, the rate of increase in dosage sensitivity with n appears to be fairly slow (Table 1). For example, for the human data the proportion of singleton families (P) changes from 0.205 for monomers to 0.254 for dimers, representing a change of only 0.049 in P value for an increase of 1 in n. The change in P is even slower from dimers to midsize complexes (i.e., a change of only 0.045 for a mean increase of 4.5 in n) and from midsize complexes to large complexes (i.e., a change of only 0.135 for an increase of at least 4 in n). Interestingly, a similar rate of increase in P with n holds for the yeast data if we assume that the P value for yeast monomers is the average of the two estimates in Table 1, i.e., P = 0.668. We emphasize that if the proportion of singletons (Q) or the mean family size is used instead of P, the rate of change with n is even slower except when n is large. For example, for the human data the mean family sizes are 8.52, 10.54, 8.13, and 4.91 for n = 1, n = 2, 3≤ n ≤ 10, and n > 10, respectively.
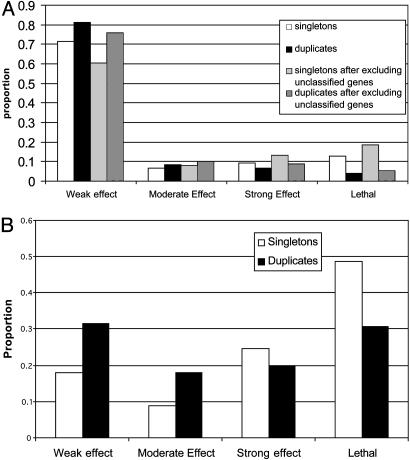
In yeast, the dosage sensitivity issue can be further examined by using gene deletion data (18). Following Gu et al. (8), we classify the fitness effect into four classes: (i) if f > 0.95 for all of the five growth media tested, the deletion has a weak or no fitness effect, (ii) if 0.8 ≤ _f_min < 0.95, where _f_min is the smallest f value for all of the five growth conditions tested, the deletion has a moderate effect, (iii) if 0 < _f_min < 0.8, the deletion has a strong effect, or (iv) the deletion is lethal, i.e., f = 0. For singletons, the proportion of gene deletions with a weak or no fitness effect (ΦW) is ≈60% or 70% for monomers, depending on whether unnamed genes are included or excluded (Fig. 2_A_), whereas ΦW is only ≈17.9% for multimers (Fig. 2_B_). This observation is in agreement with the finding that proteins with many interactions are more likely to be essential in yeast (19). It is also in agreement with that of Papp et al. (3), which they took as evidence for a strong dosage effect for multimers. However, this observation is based on the total absence of a gene product and may reflect differences in functional requirement rather than differences in dosage sensitivity. For example, a multimer might tend to be involved in more functions than a monomer, so that its absence, on average, causes a stronger fitness reduction than does the absence of a monomer. Actually, what is at issue here is the survivability of a gene duplicate, that is, whether an additional copy is good or bad for the fitness of the carriers of the duplicate genes. Thus, it is more pertinent to see the fitness effect of the deletion of a duplicate gene than that of the deletion of a single-copy gene. Fig. 2 shows that the ΦW value for duplicate genes is ≈12% higher than that for singletons, regardless of whether the gene product is a monomer or a subunit of a multimer. Therefore, the data reveal no difference in dosage effect between duplication of a monomer and duplication of a multimer subunit. Note, however, that the data refer to the subset of cases where the gene duplication apparently did not cause any substantial deleterious effect; otherwise, it should have been eliminated from the population. For this reason, the data are likely to give a biased estimate of the dosage effect of gene duplication.
Fig. 2.
(A) Fitness distribution of singletons vs. duplicates for monomers in yeast. (B) Fitness distribution of singletons vs. duplicates for multimers in yeast.
What is most interesting from Fig. 2 is that, for duplicate genes, 1 – ΦW, i.e., the proportion of cases with a moderate or stronger fitness effect of gene deletion (including lethal), is –70% for multimer subunits but only ≈20–25% for monomers. A deletion of a duplicate copy with a moderate or stronger fitness effect may imply that the functions of the two duplicate genes have already diverged to some extent, so that they can no longer completely compensate each other for null mutations. Therefore, we may conclude that for those duplicate genes that have survived the chance for functional divergence seems to be higher for the case of a multimer subunit than for a monomer.
Our results clearly indicate that human genes have a much lower probability to be singletons (unduplicated) and have on average a much larger mean family size than yeast genes, regardless of whether they encode for monomers or complex subunits. This observation suggests that single-gene duplication is less likely to be deleterious in human than in yeast, contrary to the conjecture of stronger dosage sensitivity in complex organisms than in yeast. There are several possible reasons for higher gene duplicability in human than in yeast. First, human may be genetically robust against dosage increase. It has been suggested that large developmental systems are robust against variation in many of their components, although they are also likely to be sensitive to variation in a small subset of their component processes (20). In Drosophila, the expression level of regulatory genes, which are in general subject to tighter regulation than other genes, changes 2- to 10-fold in the process of regulation (20). An interesting example is that the spatial gradient of bicoid displays a high embryo-to-embryo variability, and this variation is strongly decreased at the expression level of the downstream gene hunchback (21). Indeed, the embryos of mothers with four dosages of bicoid are as viable as those of mothers with two dosages (i.e., wild-type mothers) (4). In human, a study using cultured cells showed that >60% of promoter polymorphisms caused >2-fold differences in gene expression level (22). Thus, in complex organisms, a dosage increase caused by gene duplication may often not have a significant consequence in development or physiology. It is interesting to note that large variations in rRNA gene copy number have been observed in Drosophila populations (23), suggesting that Drosophila is not sensitive to dosage variation in rRNAs, which interact with ribosomal proteins. Second, human may have a better feedback system to adjust gene expression levels than yeast, so that gene duplication may not necessarily double the expression level. Third, human may have more efficient systems (e.g., chaperons, ubiquitins, proteases) to protect the cell from or to rid it of free excess subunits of protein complexes. Fourth, overproduction of certain mRNAs or polypeptides may not represent a large physiological burden to human. For example, a human expresses many transposable genes and a large amount of noncoding DNA, a substantial portion of which may not be functional (24). Fifth, and importantly, human may have a higher chance for a gene duplication to be advantageous (adaptive) than yeast. For example, human may require large dosages for certain functions and gene duplication for any of these functions may be advantageous. Furthermore, human has many more cell types than yeast and thus may have a higher chance for duplicate genes to become diversified in function. This is particularly true for defense systems; e.g., if we exclude the three large gene families related to the immune system, the mean family size for dimers decreases from 10.54 to 6.45 (Table 2). Adaptive evolution may be the major factor for the existence of many large gene families in human. This argument is in line with the view that metazoans have a higher evolvability than single-cell organisms and that gene duplication increases evolvability (25). Besides the above reasons, the effect population size of vertebrates would in general be considerably smaller than that of yeast, and this may increase the chance for a slightly deleterious duplication to become fixed in vertebrates compared with that in yeast. However, this factor is unlikely to be responsible for a large gene family size.
In conclusion, the contrast between yeast and human data provides much insight into gene duplicability. It suggests that organismal complexity is a better indicator for gene duplicability than protein complexity. There are two possible reasons. First, complex organisms may tend to be more robust against dosage increase than simple organisms. This robustness might be the major factor that determines whether a gene can be duplicated or not and it may explain why compared with yeast human has a much lower proportion of unduplicated polypeptides. Second, complex organisms may need large dosages for certain functions and may have a higher chance for duplicate genes to diversify in function than simple organisms. That is, there might be a higher chance for adaptive evolution of duplicate genes to occur in complex organisms than in simple ones. This may explain the existence of many large gene families and much larger mean family sizes in human than in yeast. In addition, the classification of proteins into monomers, dimers, midsize protein complexes, and large protein complexes revealed that protein complexity is indeed an important factor for determining gene duplicability. However, the rate of decrease in gene duplicability with subunit number seems to be fairly slow. It will be interesting to see whether these conclusions hold in general when more genomes become available for such analyses.
Acknowledgments
We thank A. Enright for providing the yeast gene family data, and J. Byrnes, J. J. Emerson, Z. Gu, H. Lu, A. Meyer, G. Morris, Fred Nihjout, B. Papp, and K. Weiss for suggestions and help. This work was supported by National Institutes of Health grants.
Abbreviations: MCL, Markov cluster; MIPS, Munich Information Center for Protein Sequences.
References
- 1.Ohno, S. (1970) Evolution by Gene Duplication (Springer, New York).
- 2.Veitia, R. A. (2002) BioEssays 24**,** 175–184. [DOI] [PubMed] [Google Scholar]
- 3.Papp, B., Pal, C. & Hurst, L. D. (2003) Nature 424**,** 194–197. [DOI] [PubMed] [Google Scholar]
- 4.Namba, R., Pazdera, T. M., Cerrone, R. L. & Minden, J. S. (1997) Development (Cambridge, U.K.) 124**,** 1393–1403. [DOI] [PubMed] [Google Scholar]
- 5.Mewes, H. W., Frishman, D., Guldener, U., Mannhaupt, G., Mayer, K., Mokrejs, M., Morgenstern, B., Munsterkotter, M., Rudd, S. & Weil, B. (2002) Nucleic Acids Res. 30**,** 31–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Boeckmann, B., Bairoch, A., Apweiler, R., Blatter, M. C., Estreicher, A., Gasteiger, E., Martin, M. J., Michoud, K., O'Donovan, C., Phan, I., et al. (2003) Nucleic Acids Res. 31**,** 365–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Enright, A. J., van Dongen, S. & Ouzounis, C. A. (2002) Nucleic Acids Res. 30**,** 1575–1584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Gu, Z., Steinmetz, L. M., Gu, X., Scharfe, C., Davis, R. W. & Li, W.-H. (2003) Nature 421**,** 63–66. [DOI] [PubMed] [Google Scholar]
- 9.von Mering, C., Krause, R., Snel, B., Cornell, M., Oliver, S. G., Fields, S. & Bork, P. (2002) Nature 417**,** 399–403. [DOI] [PubMed] [Google Scholar]
- 10.Gavin, A. C., Bosche, M., Krause, R., Grandi, P., Marzioch, M., Bauer, A., Schultz, J., Rick, J. M., Michon, A. M., Cruciat, C. M., et al. (2002) Nature 415**,** 141–147. [DOI] [PubMed] [Google Scholar]
- 11.Ho, Y., Gruhler, A., Heilbut, A., Bader, G. D., Moore, L., Adams, S. L., Millar, A., Taylor, P., Bennett, K., Boutilier, K., et al. (2002) Nature 415**,** 180–183. [DOI] [PubMed] [Google Scholar]
- 12.Kellis, M., Patterson, N., Endrizzi, M., Birren, B. & Lander, E. S. (2003) Nature 423**,** 241–254. [DOI] [PubMed] [Google Scholar]
- 13.Gu, X., Wang, Y. & Gu, J. (2002) Nat. Genet. 31**,** 205–209. [DOI] [PubMed] [Google Scholar]
- 14.McLysaght, A., Hokamp, K. & Wolfe, K. H. (2002) Nat. Genet. 31**,** 200–204. [DOI] [PubMed] [Google Scholar]
- 15.Wolfe, K. H. & Shields, D. C. (1997) Nature 387**,** 708–713.9192896 [Google Scholar]
- 16.Li, W.-H. (1997) Molecular Evolution (Sinauer, Sunderland, MA).
- 17.Kumar, S. & Subramanian, S. (2002) Proc. Natl. Acad. Sci. USA 99**,** 803–808. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Steinmetz, L. M., Scharfe, C., Deutschbauer, A. M., Mokranjac, D., Herman, Z. S., Jones, T., Chu, A. M., Giaever, G., Prokisch, H., Oefner, P. J., et al. (2002) Nat. Genet. 31**,** 400–404. [DOI] [PubMed] [Google Scholar]
- 19.Jeong, H., Mason, S. P., Barabasi, A. L. & Oltvai, Z. N. (2001) Nature 411**,** 41–42. [DOI] [PubMed] [Google Scholar]
- 20.Nijhout, H. F. (2002) BioEssays 24**,** 553–563. [DOI] [PubMed] [Google Scholar]
- 21.Houchmandzadeh, B., Wieschaus, E. & Leibler, S. (2002) Nature 415**,** 798–802. [DOI] [PubMed] [Google Scholar]
- 22.Rockman, M. V. & Wray, G. A. (2002) Mol. Biol. Evol. 19**,** 1991–2004. [DOI] [PubMed] [Google Scholar]
- 23.Ritossa, F. M. & Scala, G. (1969) Genetics 61**,** S305–S317. [PubMed] [Google Scholar]
- 24.Kapranov, P., Cawley, S. E., Drenkow, J., Bekiranov, S., Strausberg, R. L., Fodor, S. P. & Gingeras, T. R. (2002) Science 296**,** 916–919. [DOI] [PubMed] [Google Scholar]
- 25.Kirschner, M. & Gerhart, J. (1998) Proc. Natl. Acad. Sci. USA 95**,** 8420–8427. [DOI] [PMC free article] [PubMed] [Google Scholar]