A Quantitative Evaluation of SAGE (original) (raw)
Abstract
Serial Analysis of Gene Expression (SAGE) is an innovative technique that offers the potential of cataloging both the identity and relative frequencies of mRNA transcripts in a given poly(A+) RNA preparation. Although it is a very effective approach for determining the expression of mRNA populations, there are significant biases in the observed results that are inherent in the experimental process. These are caused by sampling error, sequencing error, nonuniqueness, and nonrandomness of tag sequences. The quantitative information desired from SAGE experiments consists of estimates of the number of genes and the frequency distribution of transcript copy numbers. Of additional concern is the extent to which a given tag sequence can be assumed to be unique to its gene. The present study takes these mathematical biases into account and presents a basis for maximum likelihood estimation of gene number and transcript copy frequencies given a set of experimental results. These estimates of the true state of genomic expression are markedly different from those based directly on the observations from the underlying experiments. It also is shown that while in many cases it is probable that a given tag sequence is unique within the genome, in larger genomes this cannot be safely assumed.
It is well known that the pathobiology of heritable and acquired disease is associated with the altered expression of at least one, but usually many different genes (Dietz and Pyeritz 1995; Fisher et al. 1996). Until recently, traditional approaches to understanding the causal relationship between altered gene expression and a clinical phenotype have included the identification and characterization of mutations affecting individual genes and a detailed study of how these mutations influence their expression (Kadler 1993; Cleary and Gibson 1996). While this approach has yielded critical information regarding the pathogenetics of a wide variety of diseases, it is clear that the overall influence of single gene mutations is far more complex and involves more than the altered expression of a mutant allele or a limited number of mutant alleles. Moreover, in acquired disorders that do not involve heritable or somatic mutations as the initiating events that lead to a phenotype, studies of the functional relationship between altered gene expression and tissue dysfunction are limited (Fisher et al. 1996). Essentially, most of these studies involve the selection of candidate genes and an analysis of the altered expression of these genes associated with the development of a phenotype. Recently, however, functional genomic approaches have permitted the analysis of the altered expression of hundreds, and in some cases thousands, of genes simultaneously. These novel approaches, which include the use of DNA microarrays (Schena et al. 1995, 1996, 1998; Heller et al. 1997) and Serial Analysis of Gene Expression (SAGE) (Velculescu et al. 1995, 1997; Madden et al. 1997; Zhang et al. 1997), have permitted, for the first time, the analysis of entire mRNA populations in cells or tissues as indicators of global transcription profiles.
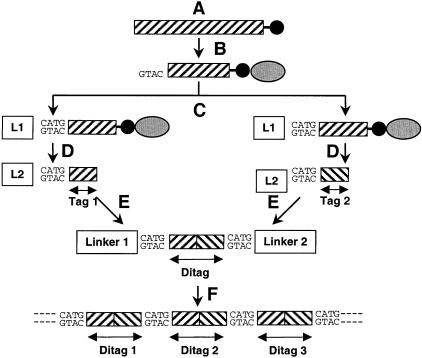
SAGE is based on the generation of short (9–10 bp) nucleotide sequences (tags) from a unique position within each species of mRNA. To obtain the tags, poly(A+)RNA is extracted and transcribed into double-stranded cDNA (Fig. 1A) , using biotinylated oligo(dT) as a primer. Digestion with a type II restriction enzyme (Anchoring Enzyme) results in cDNA fragments with an average length of 256 bp. The biotinylated 3′-most fragments then are isolated using paramagnetic streptavidin beads (Fig. 1B). The isolation step provides tags from a defined position within each cDNA, which is important for the ultimate identification of the corresponding genes.
Figure 1.
Schematic illustration of the SAGE process. (A) Poly(A +)RNA is extracted and transcribed into double-stranded cDNA, primed by biotinylated oligo (dT) (black circles), and digested with the Anchoring Enzyme. (B) The 3′-most fragments are isolated by binding them to streptavidin beads (gray ellipses). (C) The fragments are divided and ligated to different linkers (L1, L2). (D) The isolated linker-tags are blunt-ended. (E) The linker-tags are ligated to linker-ditag-linker constructs and amplified by PCR (E). (F) The ditags are isolated, ligated to concatamers, cloned, and sequenced. This figure is an adaptation of Figure 1 from Velculescu, V.E. et al. (1995).
The fragments subsequently are divided in half and ligated to two different linkers (Fig. 1C). Each linker contains a restriction site for the Tagging Enzyme (a type IIS restriction endonuclease), the Anchoring Enzyme overhang and a priming site for polymerase chain reaction (PCR) amplification. By digesting these bound linker-cDNA sequences with the Tagging Enzyme, fragments consisting of linker and an adhering short cDNA sequence (tag) are released from the streptavidin beads. The isolated linker tags are blunt-ended with the Klenow fragment of DNA polymerase I (Fig. 1D). The two sets of linker tags then are ligated to linker-ditag-linker constructs and amplified by PCR using primers specific to the linkers (Fig. 1E). Digesting these constructs with the Anchoring Enzyme finally releases the ditags, which are isolated, ligated to concatamers (Fig. 1F), cloned, and sequenced. The sequences obtained are compared to different genome databases in order to identify the tags.
Ditag sequence analysis using SAGE provides the potential to identify all the unique mRNAs in any particular poly(A+) RNA preparation — and therefore the active genes — as well as the copy numbers of these mRNAs. The approach is elegant and already has been widely used, both to characterize transcriptomes (Velculescu et al. 1995, 1997) and to study the differences between them (Madden et al. 1997; Zhang et al. 1997; Chen et al. 1998). However, there exist several subtleties in the interpretation of SAGE results that bias the observations in ways that have not been explored previously. In this manuscript, we address these issues and provide a maximum likelihood approach to the estimation of the number of unique transcripts and their frequency distribution. We also provide cautionary estimates of the probability that a given tag sequence is unique to one gene.
RESULTS
Simulations of the SAGE Process
The results of the simulation processes outlined above are summarized in Table 1. Tables 1A and 1B show the results of the simulations described above for a genome of size 15,720, sampled with 62,168 tags. These numbers were chosen to correspond to those published in a study of colonic epithelial cells (Zhang et al. 1997). Table 1A represents the outcomes for 9-base tags, and is presented only for comparison purposes. Table 1B (10-base tags) corresponds more completely to the cited study. Table 1C presents the same basic assumptions as in Table 1B except that both the assumed number of genes and the number of tag sequences generated to sample them have been scaled up by a factor of five. This is presented to correspond to a larger experiment encompassing multiple cell types, and to convey a sense of how interpretation problems change with the experimental scale.
Table 1.
Simulated Results Assuming the Genome Given by Observations
| Model -> | Assumed | Unique, no errors | Unique | Random | Non-random |
|---|---|---|---|---|---|
| A. 9 Base sequences | |||||
| Unique tags | 15,720 | 7994 ± 5 | 11,029 ± 6 | 10,930 ± 6 | 10,427 ± 5 |
| % 1–5 | 64.16 | 38.86 ± 0.02 | 53.63 ± 0.02 | 53.33 ± 0.02 | 51.26 ± 0.02 |
| % 5–50 | 31.0373 | 52.21 ± 0.02 | 40.67 ± 0.02 | 40.26 ± 0.02 | 41.88 ± 0.02 |
| % 50–500 | 4.3815 | 8.17 ± 0.01 | 5.77 ± 0.007 | 5.87 ± 0.007 | 6.28 ± 0.007 |
| % 500–5000 | 0.4212 | 0.76 ± 0.003 | 0.54 ± 0.002 | 0.54 ± 0.002 | 0.57 ± 0.002 |
| % Errors novel | – | – | 94.0 ± 0.01 | 94.2 ± 0.01 | 84.6 ± 0.3 |
| % Unique genes | – | 100 ± 0 | 100 ± 0 | 94.2 ± 0.01 | 81.6 ± 0.01 |
| B. 10 Base sequences | |||||
| Unique tags | 15,720 | 8,003 ± 5 | 11,460 ± 6 | 11,428 ± 6 | 11,268 ± 5 |
| % 1–5 | 64.16 | 38.86 ± 0.02 | 55.44 ± 0.02 | 55.43 ± 0.02 | 54.65 ± 0.02 |
| % 5–50 | 31.0373 | 52.23 ± 0.02 | 38.51 ± 0.02 | 38.50 ± 0.02 | 39.15 ± 0.02 |
| % 50–500 | 4.3815 | 8.16 ± 0.01 | 5.53 ± 0.006 | 5.54 ± 0.006 | 5.68 ± 0.006 |
| % 500–5000 | 0.4212 | 0.75 ± 0.003 | 0.52 ± 0.002 | 0.52 ± 0.002 | 0.52 ± 0.002 |
| % Errors novel | – | – | 98.5 ± 0.007 | 98.5 ± 0.007 | 95.0 ± 0.01 |
| % Unique genes | – | 100 ± 0 | 100 ± 0 | 98.5 ± 0.004 | 94.0 ± 0.008 |
| C. 10 Base sequences (five times larger genome) | |||||
| Unique tags | 78,600 | 47,086 ± 10 | 64,364 ± 10 | 63,407 ± 10 | 58,573 ± 8 |
| % 1–5 | 64.16 | 43.35 ± 0.01 | 58.24 ± 0.009 | 57.77 ± 0.009 | 53.94 ± 0.009 |
| % 6–50 | 31.0373 | 48.71 ± 0.01 | 36.07 ± 0.01 | 36.46 ± 0.01 | 39.77 ± 0.01 |
| % 51–500 | 4.3815 | 7.23 ± 0.004 | 5.26 ± 0.003 | 5.34 ± 0.003 | 5.80 ± 0.003 |
| % 501–5000 | 0.4212 | 0.71 ± 0.001 | 0.43 ± 0.0009 | 0.44 ± 0.0009 | 0.48 ± 0.001 |
| % Errors novel | – | – | 92.5 ± 0.007 | 92.8 ± 0.006 | 79.4 ± 0.01 |
| % Unique genes | – | 100 ± 0 | 100 ± 0 | 92.8 ± 0.004 | 75.4 ± 0.006 |
In each case the presumed number and copy distribution of unique transcripts is given (assumed). The subsequent columns predict the observations to be expected given the four sets of assumptions outlined in Methods. We follow previous convention (Zhang et al. 1997) in presenting the data in terms of estimated transcript copy number per cell, and also have tabulated the percentage of erroneously sequenced tags that are novel, i.e., not present (elsewhere) in the active genome. Finally, we have listed the percentage of genes with unique tag sequences.
In general, the results show that two processes within the SAGE experiments are in opposition, fortuitously reducing some of the bias in observations. First and most significantly, the sampling error leads to a large under-estimate of the number of genes and the percentage of low copy numbers (Table 1, Assumed vs. Unique, No Err). These values are in very good agreement with those predicted from equation 2, which serves as a verification of the technical soundness of the simulation approach. When sequencing error is taken into account, a significant number of novel tag sequences are generated which increase both the number of unique sequences found and the percentage of low copy numbers (Table 1, Unique, No Err vs. Unique). In moving to the Random condition, we see a small decrease in the observed number of genes and the percentage of low copy numbers in the 9-base scenario (Table 1A). This is because of the overlap or nonuniqueness of gene tag sequences. This effect is greatly reduced in Tables 1B and 1C, which involve 10-base tags. The Non-Random condition, however, enhances the trend to decreased gene number and fraction of low copy transcripts in all cases (Table 1, Random vs. Non-Random). This is because the effective population of tag sequences is reduced in this most realistic case, leading to a smaller percentage of erroneous tags being novel (i.e., not present in the genome).
The Extent of Tag Sequence Uniqueness
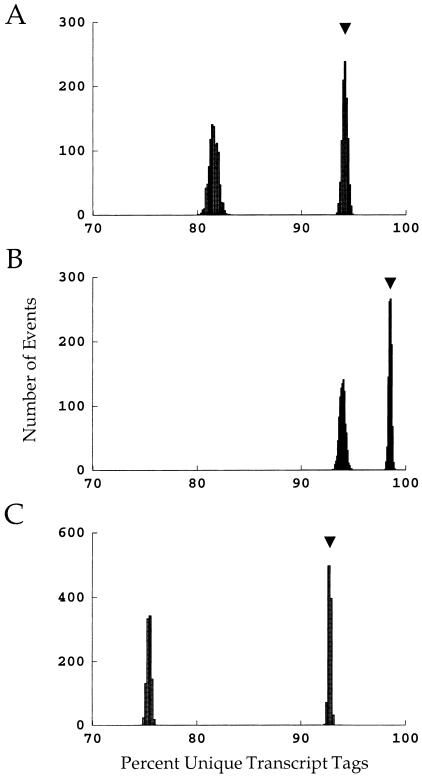
The expected fraction of unique tag sequences, and the expected variability, are shown more clearly in Figure 2. This shows the distribution of the fraction of unique tag sequences for both random (rightmost) and nonrandom (leftmost) DNA sequences (A, 9base tags from 15,720 genes; B, 10-base tags from 15,720 genes; C, 10-base tags from 78,600 genes). The arrows in each panel indicate the expected value for random sequences as predicted by equation 4. Not surprisingly, a 10-base tag protocol gives significantly more uniqueness than a 9-base protocol (Fig. 2B vs. Fig. 2A). However, even with 10-base tags, a significant fraction of the tag sequences found are not unique, particularly when the nonrandom nature of DNA sequences is partially accounted for (Fig. 2B, left-most distribution). In fact, even the limited nonrandom ness incorporated into this model renders 10-base tags ∼ as nonunique as 9-base tags under the assumption of randomness (Fig. 2A, right vs. Fig. 2B, left). Finally, the problem of nonuniqueness is exacerbated further by a large genome (Fig. 2C). These results indicate that caution must be exercised before assuming that a particular SAGE tag sequence is unique to its gene. It also is useful to notice the relatively small variation shown in these distributions — this renders it quite unlikely that statistical coincidence could lead to significantly worse outcomes than those presented here.
Figure 2.
The probabilities that a given gene will have a unique tag sequence under various conditions. In each plot, the right-most distribution arises from random DNA sequences, and the arrows indicate the expected outcome. The left-most distribution in each plot is the probability given nonrandom DNA sequences. (A) 9-base tags and 15,720 genes (the assumptions of Table 1A). (B) 10-base tags and 15,720 genes (the assumptions of Table 1B). (C) 10-base tags and 78,600 genes (the assumptions of Table 1C).
Quantitative Evaluation of SAGE Results
We have seen that sampling error, sequencing error, nonunique tag sequences, and nonrandom DNA sequences all contribute to biases in the observations arising from SAGE experiments. The most direct solution to this problem would be to use the simulations to find the actual parameters (the number of genes and the distribution of transcript copy numbers) that would result in the observations made in the laboratory. Although technically complex, this can in fact be achieved by treating the simulation as a function, the observations as data to be matched, and the true parameters as variables with which to fit function to data (see Methods). A maximum likelihood approach based on the Levenberg-Marquardt method has been used for this purpose in application to the published observations we have cited (Zhang et al. 1997); the results are shown in Table 2.
Table 2.
Interpretation of Genome from Observations
| Model-> | Observed data | Inferred parameters | Predicted data |
|---|---|---|---|
| Unique tags | 15,720 | 25,336 | 15,651 ± 58 |
| % 1–5 | 64.16 | 80.56 | 63.64 ± 0.31 |
| % 6–50 | 31.0373 | 16.51 | 31.74 ± 0.40 |
| % 51–500 | 4.3815 | 2.72 | 4.33 ± 0.098 |
| % 501–5000 | 0.4212 | 0.215 | 0.29 ± 0.01 |
The parameters inferred from a numerical analysis of the data are quite different from the data themselves (compare Observed Data to Inferred Parameters). In general, it is seen that the actual number of genespresent must be substantially larger than the number found (see Discussion), and that the actual frequency distribution favors more transcripts present at low copy numbers than those observed from the data. These inferred parameters can be checked by use as the starting point for the simulations presented previously (assuming nonrandom tag sequences with sequencing error). This provides an estimate of what would have been observed given that these inferred parameters accurately reflect the experimental transcriptome. The close similarity of these predicted data to the observed data gives credence to the inferred parameters.
DISCUSSION
Recent advances have led to dramatic increases in the amount of DNA sequence information available for several genomes. The sequencing efforts of the Human Genome Project have resulted in sequence database entries for thousands of genes and expressed sequence tags (Aaronson et al. 1996; Hillier et al. 1996). In the very near future, the Human Genome Organization (HUGO) will have achieved the goal of a complete sequence of the entire human genome. Current estimates are that the human genome contains some 50,000–80,000 genes, with many of the genes thus far sequenced assigned to a functional class, but fewer than 7000 having a known or putative function (Fields 1997). With so little current knowledge about the functions of these genes, it is important to sort out the developmental, temporal, topographical, histological, and physiological patterns in which genes are expressed. Thus the assessment of expression profiles for hundreds, if not thousands, of genes by quick and reliable means is crucial to provide the information essential to functional genomics. Only with this knowledge will it be possible to elucidate the cause for diseases at the level of gene expression and to find new methods for treatment.
In the past, several approaches have been used to compare levels of gene expression, e.g., reverse transcription-polymerase chain reaction and northern-blot analysis. These approaches are limited to analysis of one gene at a time, whereas other methods like subtractive hybridization or variations of the differential display technique (Liang and Pardee 1992) can determine multiple expression patterns of predetermined sequences (Fischer et al. 1995), with the latter technique being very sensitive but not quantitative. Large numbers of expressed genes also can be investigated using nucleic acid microarrays. These arrays make use of the fact that DNA strands hybridize to their complementary sequences, which can be applied to inert surfaces (Schena et al. 1995). Thousands of short nucleotide sequences can be affixed to those membranes, and thus the expression of hundreds of different genes can be assessed. Recently developed DNA chips can contain up to 100,000 different DNA sequences, 20 nucleotides in length, “printed” on their glass surface, enabling rapid and accurate scanning (Hacia et al. 1996). While quite powerful, all of these techniques have the relative disadvantage of being suitable only for analysis of a fixed number of predetermined gene sequences.
Presently, SAGE is the only technique that promises a quantitative characterization of the complete transcriptome for a cell type or tissue (Velculescu et al. 1997). It is because of the quantitative potential of the approach that it is imperative to consider aspects of SAGE experiments that bias the observed outcomes. Four of these have been considered in the present work: (1) sampling errors in tag selection; (2) sequencing errors; (3) nonuniqueness of tag sequences; and (4) nonrandomness of DNA sequences. Taken together, they lead to a significant under-estimation of the number of active genes in a preparation and in the fraction of genes expressed at low copy numbers. This biasing can be overcome to arrive at maximum likelihood estimates for gene number and transcript copy number distribution if certain assumptions are made. Among these are several that merit more discussion.
The form of the distribution of copy numbers is one assumption that must be made to analyze the experiments quantitatively. Note that the relative frequencies of copy number classes are not assumed. Rather, the assumption deals with whether or not the distribution is continuous or a step function, and whether the mode of the distribution is at one copy per cell or some other number. The latter question appears to have very little impact on the outcome; constructing a distribution with the mode at three copies per cell, for example, produces results almost identical to those presented here.
The choice of a continuous function was based on two unrealistic aspects of the step function. First, it makes for abrupt discontinuities, so that, for example, the likelihood of finding a copy number of 501 could be 10 times less than that of finding 500 copies per cell. There may or may not be true “abundance classes” in the transcriptome (Quinlan et al. 1978), but clearly it is unrealistic to impose that sharp a boundary. The second problem is that the use of a step function forces one to assume that all probabilities within a range are equal, i.e., that copy numbers of 5000 are equally probable as 501. For these reasons, a continuous approximation to the step function was assumed; the choice of the double exponential function was a matter of convenience and should not be taken as a claim that this is the true form of the distribution. Although the major points of this study are borne out even when the step function is used, the best estimates of actual gene number and copy number distribution are changed to some extent. Thus it will be important in future work to assess the shape of the distribution to more accurately apply the analysis presented here.
A second assumption is inherent in the imposition of dinucleotide mutation. As noted in Methods, this cannot be expected to fully capture the extent of nonrandomness within DNA sequences. It is therefore to be expected that the extent of the changes seen between random and nonrandom simulations are underestimated. In particular, this means that the probability that a given tag sequence is unique to its gene is probably overstated in the present work. However, it is important to note that various additional sources of nonrandomness (dinucleotide mutation, selective pressure, evolution of genes from a common ancestor, repetitive sequences, etc.) will not, in general, add in an algebraic sense. For example, a coding region tag sequence may be constrained from dinucleotide mutation owing to selective pressure. Statistical analysis of full mRNA tag sequences following terminal restriction enzyme sites may permit a better estimate of nonrandomness. Another approach, requiring that both total (active) gene number and copy number distribution are well characterized, would be to compare predicted rates at which new tags are generated as tag number increases with the observed rates (Madden et al. 1997; Velculescu et al. 1999).
In addition to sequence nonrandomness, there are other aspects of actual SAGE experiments that are not accounted for in this analysis. These include, but are not limited to, sample contamination, differential RNA splicing, DNA polymorphism, and failure to map tags to correct genes because of incomplete sequence data. While these are beyond the scope of the present analysis, which is focused on inherently mathematical aspects of SAGE, most of them could be incorporated into the SAGE model if (1) the probability of occurrence is well known, and (2) that probability is high enough to be of concern.
The most significant aspect of the nonuniqueness of gene tags is the identification of these tags using genetic databases. As shown in Figure 2C, under realistic assumptions for a complete genome the probability that a given tag sequence is found on only one gene is ∼76% — even for 10-base tag sequences. If the entire genome is represented in the databases, it is straightforward to check whether the tag is found on multiple genes; if not, caution must be exercised in the identification of a tag sequence with a particular gene. This potential nonuniqueness of tags has important implications for the design of SAGE experiments. As shown by the simulations, a smaller genome size will significantly reduce the frequency of nonunique tags. In this vein, it should be noted that the actual genome size is significantly larger than that estimated directly from SAGE results — this, along with limitations in the capture of sequence nonrandomness (above), exacerbates the problem. Thus, applications of SAGE directed at specific cell types, or of tissues with limited cell diversity, clearly will have significant advantages over studies of complex tissues or whole organisms.
While the nonuniqueness of tags raises substantial problems in the identification of genes with tags, it is the sampling error that most profoundly affects the transcript frequency distribution and the number of unique transcripts. The results reported here with respect to the latter are in agreement with experimental findings in which the number of unique transcripts found was still increasing past 15,000 as the tags increased to 60,000 (Madden et al. 1997). Recently, an extensive study was released in which it was found that ∼650,000 tags were needed to adequately sample a transcriptome of ∼56,000 (detection was estimated at 83% for single copy transcripts: Velculescu et al. 1999). Clearly, the sampling of tag sequences will have to be increased if the SAGE approach is to adequately characterize the entire set of cellular transcripts. In the absence of such comprehensive sampling, the quantitative approach reported here represents the best way to find unbiased estimates of the size and frequency distribution of the transcriptome, and to determine sampling adequacy in differential studies.
METHODS
The goal of this work is to present quantitative methods by which data from SAGE experiments can be interpreted. Specifically, one would like to have maximum likelihood estimates for (1) the probability that a given tag sequence is unique to one gene; (2) the number of unique genes in the experimental system; and (3) the distribution of transcript copy numbers. There are four aspects of SAGE experiments that render the best estimates of these parameters considerably different from the values actually detected in the experiments. These are (1) sampling errors in tag selection; (2) sequencing errors; (3) nonuniqueness of tag sequences; and (4) nonrandomness of DNA sequences. These complications will be taken up in order, as they represent a sequential layering of complexity in the quantitative evaluation of SAGE data.
Sampling Errors in Tag Selection
We start with the unrealistic assumptions that the tag sequence of each gene is unique and that there are no sequencing errors (these assumptions will be relaxed below). In this case, the only complication that separates SAGE observations from the actual situation is sampling error — most significantly, the under counting of transcripts present in low copy number. This potential problem has been addressed via stochastic simulation (Zhang et al. 1997), but under the present simplifying assumptions it has an analytical solution. Consider the case where there are “t” transcripts (in total — not unique transcript species) in a preparation, “c ” copies of a particular transcript, and “s” tags sampled. In general, “t” is very large compared to “s” (e.g., 5 μg or ∼1018 transcripts), so the selection of tag sequences can be well approximated as sampling with replacement. The probability that “r” copies of the particular transcript will be found within the set of “s” tags is then the binomial distribution, where the more familiar “p” (the probability of detection) is here represented as c/t (the fraction of total transcripts represented by the given species). Following this notation, the probability that a transcript will be detected in copy numbers between r1 and r2 (inclusive) is:
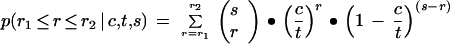 |
1 |
|---|
The binomial distribution of tag sampling provides a simple assessment of the significance of the difference detected in SAGE experiments directed at differential gene expression. When the number of detected tags is five or more, the normal approximation is valid with the mean equal to s. c/t and variance s. c/t. (1-c/t) (Harshbarger 1971). If fewer tags are detected, approximate confidence intervals can be obtained by a test for proportions (Winkler and Hays 1975).
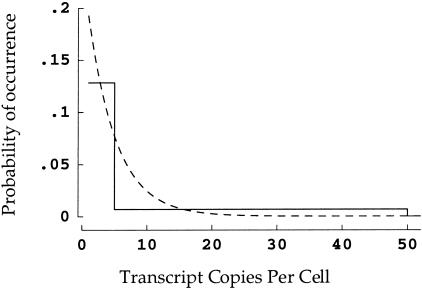
To make use of this equation and to carry out the simulations discussed below, a frequency distribution of transcript copy numbers must be assumed. In much of this study published data (Zhang et al. 1997) for colonic epithelial cells will be used, in which the frequency ranges for transcript copy numbers per cell were 1 to 5, 64.16%; 6 to 50, 31.04%; 51 to 500, 4.38%; and >501, 0.42%. For quantitative purposes, the final range must have an ending point, for which 5000 seems a reasonable choice. It remains to specify the actual form of this distribution, for which the simplest choice is a step function over the four ranges (Fig. 3). For reasons discussed later, we chose instead a double exponential function selected to match the numerical integrals for the corresponding step function over the four ranges (Fig. 3). Preliminary analysis using the step function shown in Figure 3 reveals some differences in relative frequencies observed, but the main points of this study are borne out using either the step or the continuous distribution.
Figure 3.
Two possible forms of copy number distribution. The simplest construction is a step function (solid line). Thus, for example, if there is a 64% chance that a gene is expressed in 1 to 5 transcripts per cell, the first step extends from 1 to 5 at a height of 12.8 (64/5)%. A more plausible assumption is that the distribution is continuous. This has been implemented here by finding a double exponential function with the same integral over each copy number range (dashed line). The graph is truncated at 50 + copies per cell for visual clarity — in fact, both distributions extend out to 5000 (see Methods).
Sequencing Errors
The second complication in the assessment of SAGE experiments is the presence of sequencing errors. As noted in previous work (Zhang et al. 1997), the number of sequencing errors can be calculated readily from the estimated error rate of ∼ 0.7%/base. However, the impact of these errors on data interpretation is less clear: some of these errors will introduce novel tags not represented in the genome, while some will artificially increase the copy numbers of tag sequences that are in fact in the genome. Sequencing error presents somewhat of a dilemma for the experimenter: the probability that a tag sequence is unique to a particular gene increases with tag length, but sequencing errors also are increased.
Nonuniqueness of Tag Sequences
Clearly the 49 or 410 possible tag sequences exceeds the number of genes typically probed, but this is no guarantee that each tag sequence will be present on only one gene.* The simplest assumption is that tag sequences are random in the sense that all 4x possible tag sequences are equally probable (where x is the number of variable bases within the tag sequence). One way of posing the question is to ask for the probability that the entire set of tag sequences for (g) genes are unique. This can be found in the product sequence
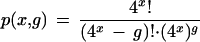 |
2 |
|---|
This expression evaluates to vanishingly small numbers for a significant number of genes: 1.26 x 10–84 (x = 9, g = 10,000) and 1.69 x 10–21 (x = 10, g = 10,000). Clearly there will be duplicated tag sequences in most genomes of interest.
It is perhaps more useful to pose the following question: given a particular tag of interest, what is the probability that its sequence is unique to one gene? If it is again assumed that tag sequences are random, the expression for the stated problem is
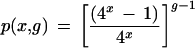 |
3 |
|---|
For a g of 15,720 (from published results [Zhang et al. 1997]; see below) this yields 94.2% and 98.5% for 9– and 10-base sequences, respectively. In other words, there is a ∼ 5.8% chance (g =15,720, x = 9) that the tag of interest is not unique — that the same tag sequence is found on one or more other genes. For a genome 5 times that size, the probabilities fall to 74.1% and 92.8%. Because of the presumed independence and uniform randomness of tag sequences, the above expression also represents the expected value for the fraction of tag sequences that will be unique. That is, it is expected that on average 94.2% of the genes will have unique tag sequences (g = 15,720, x = 9).
A more complete formulation of the situation can be formed from equation 4, which gives the probability that a tag sequence in the genome is present exactly once in the genome. Equation 5 expresses the probability that the tag sequence will be present r times:
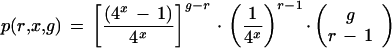 |
4 |
|---|
Evaluation of this shows that as one would expect, the number of tag sequences found on r different genes drops drastically as r increases (e.g., p[r = 2] = 5.65%, p[r = 3] = 0.169%; g = 15,720, x = 9).
In summary, these equations show the possibility that a tag sequence represents multiple genes is a significant potential problem in the interpretation of SAGE results, although less so in the more recent applications (Velculescu et al. 1997; Zhang et al. 1997), which have made use of 10-base tags instead of the 9-base tags used in the original study (Velculescu et al. 1995). As will be seen, the nonrandomness of DNA sequences further exacerbates this problem.
Nonrandomness of DNA Sequences
DNA sequences are in fact known to be nonrandom. Because some sequences will therefore be more probable, a smaller fraction of genes with unique tag sequences is to be expected. To take a simple approximation that captures some of the deviation from random sequences, we assume nucleotide pair ratios based on differential mutation rates as found in pseudogenes (Bulmer 1986). As these are presumably not subject to selective forces, while an individual tag sequence may or may not be, this should represent a conservative estimate of the actual nonrandomness involved. To incorporate this and other complications discussed above requires stochastic or Monte Carlo simulations of the SAGE process.
Mapping Experiment to Simulation
To take all of these factors into account, we have constructed a stochastic model of the SAGE process. The model begins with the assumption that the experimental results — unique tag sequences found, and their relative abundances — represent an estimate of the true number of unique transcripts and their abundances. Taking the results as a starting place, the SAGE process is simulated to produce an outcome that would be observed if the assumption were true. In general, this will produce a set of simulated results that are substantially different from the experimental results. The nature of this difference then can be used to find the actual number of unique transcripts and their abundances, which would in fact have led to the experimental observations.
Four sets of simulations†, incorporating the progression of assumptions outlined above, were undertaken. Common to all are the following steps. (1) Tag sequences are generated for the assumed number of genes using uniform random deviates (1 ≤ n ≤ 4x)‡. (2) Random deviates from the assumed distribution of copy numbers are used to assign each gene a copy number. (3) A list of transcripts is assembled reflecting the various copy numbers. (4) The list is sampled randomly (with replacement) and “sequenced” to produce the equivalent of an experimental result.
To match the first assumptions introduced, the algorithm ensures tag uniqueness and a lack of sequencing errors. Under the second and subsequent sets of assumptions, the estimated sequencing error is introduced (0.7% per nucleotide). In the third set of simulations, the tag sequences are truly random — not forced to be unique. In the fourth and final approach, the tag sequences are subjected to neighbor-based substitutions until the sequences are at equilibrium (Bulmer 1986, 1987), in order to reflect at least some of the nonrandomness found in DNA sequences.
In the final part of the analysis, the fourth simulation algorithm (nonrandom sequences with sequencing error) is treated as a function in order to calculate back to the conditions that must have existed in the mRNA preparation. This is accomplished by inputting the observed number and frequencies of mRNAs (Table 2, Observed Data) and using a fitting approach to find the inferred number and frequencies under which the observations are most likely (Table 2, Inferred Parameters). As a check on the fitting algorithm, these inferred parameters then are fed into the original simulation to confirm a good match between these predicted data (Table 2) and the originally observed data.
Acknowledgments
This work was supported by NSF #IBN97–24035, the American Heart Association, Hawai'i Affiliate HIGS-07–98, a Research Center in Minority Institutions NCRR grant RR03061, and the financial assistance of Unilever Research, Inc.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Footnotes
E-MAIL jesse@pbrc.hawaii.edu; FAX (808) 956–6984.
*
Note that the four-base restriction enzyme sequence by which tags are manipulated does not enter into this calculation. As the sequence is by experimental design unvarying, it does not contribute to the number of possible tag sequences or to the simulations presented below.
†
The program performing these simulations is available free of charge for noncommercial use. Contact the corresponding author for information regarding this software.
‡
Note that many standard language random number generators are inadequate for this large a task, and care should be taken in the algorithm used. (Press et al. 1998)
REFERENCES
- Aaronson J, Eckman B, Blevins R, Borkowski J, Myerson J, Imran S, Elliston K. Toward the development of a gene index to the human genome: an assessment of the nature of high-throughput EST sequence data. Genome Res. 1996;6:829–845. doi: 10.1101/gr.6.9.829. [DOI] [PubMed] [Google Scholar]
- Bulmer M. Neighboring base effects on substitution rates in pseudogenes. Mol Biol Evol. 1986;3:322–329. doi: 10.1093/oxfordjournals.molbev.a040401. [DOI] [PubMed] [Google Scholar]
- Bulmer M. A statistical analysis of nucleotide sequences of introns and exons in human genes. Mol Biol Evol. 1987;4:395–405. doi: 10.1093/oxfordjournals.molbev.a040453. [DOI] [PubMed] [Google Scholar]
- Chen H, Centola M, Altschul SF, Metzger H. Characterization of gene expression in resting and activated mast cells (published erratum appears in J. Exp. Med. 188[12]: 2387) J Exp Med. 1998;188:1657–1668. doi: 10.1084/jem.188.9.1657. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cleary EG, Gibson MA, editors. Elastic tissue, elastin and elastin associated microfibrils. Extracellular Matrix. Australia, Canada, China: Harwood Publishers; 1996. [Google Scholar]
- Dietz H, Pyeritz R. Mutations in the human gene for fibrillin-1 (FBN1) in the Marfan syndrome and related disorders. Hum Mol Genet. 1995;4 Spec No:1799–809. doi: 10.1093/hmg/4.suppl_1.1799. [DOI] [PubMed] [Google Scholar]
- Fields S. The future is function [news] Nat Genet. 1997;15:325–327. doi: 10.1038/ng0497-325. [DOI] [PubMed] [Google Scholar]
- Fischer A, Saedler H, Theissen G. Restriction fragment length polymorphism-coupled domain-directed differential display: a highly efficient technique for expression analysis of multigene families. Proc Natl Acad Sci U S A. 1995;92:5331–5335. doi: 10.1073/pnas.92.12.5331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fisher G, Datta S, Talwar H, Wang Z, Varani J, Kang S, Voorhees J. Molecular basis of sun-induced premature skin ageing and retinoid antagonism. Nature. 1996;379:335–339. doi: 10.1038/379335a0. [DOI] [PubMed] [Google Scholar]
- Hacia J, Brody L, Chee M, Fodor S, Collins F. Detection of heterozygous mutations in BRCA1 using high density oligonucleotide arrays and two-colour fluorescence analysis. Nat Genet. 1996;14:441–447. doi: 10.1038/ng1296-441. [DOI] [PubMed] [Google Scholar]
- Harshbarger TR. Introductory Statistics, Chapter 8.8. New York: The Macmillan Company; 1971. [Google Scholar]
- Heller R, Schena M, Chai A, Shalon D, Bedilion T, Gilmore J, Woolley D, Davis R. Discovery and analysis of inflammatory disease-related genes using cDNA microarrays. Proc Natl Acad Sci U S A. 1997;94:2150–2155. doi: 10.1073/pnas.94.6.2150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillier L, Lennon G, Becker M, Bonaldo M, Chiapelli B, Chissoe S, Dietrich N, DuBuque T, Favello A, Gish W, et al. Generation and analysis of 280,000 human expressed sequence tags. Genome Res. 1996;6:807–828. doi: 10.1101/gr.6.9.807. [DOI] [PubMed] [Google Scholar]
- Kadler K. Learning how mutations in type I collagen genes cause connective tissue disease. Int J Exp Pathol. 1993;74:319–323. [PMC free article] [PubMed] [Google Scholar]
- Liang P, Pardee A. Differential display of eukaryotic messenger RNA by means of the polymerase chain reaction [see comments] Science. 1992;257:967–971. doi: 10.1126/science.1354393. [DOI] [PubMed] [Google Scholar]
- Madden S, Galella E, Zhu J, Bertelsen A, Beaudry G. SAGE transcript profiles for p53-dependent growth regulation. Oncogene. 1997;15:1079–1085. doi: 10.1038/sj.onc.1201091. [DOI] [PubMed] [Google Scholar]
- Press WH, Flannery BP, Teukolsky SA, Vetterling WT. Numerical Recipes in C. New York: Cambridge University Press; 1988. [Google Scholar]
- Quinlan T, Beeler GJ, Cox R, Elder P, Moses H, Getz M. The concept of mRNA abundance classes: a critical reevaluation. Nucleic Acids Res. 1978;5:1611–1625. doi: 10.1093/nar/5.5.1611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schena M, Heller R, Theriault T, Konrad K, Lachenmeier E, Davis R. Microarrays: biotechnology's discovery platform for functional genomics. Trends Biotechnol. 1998;16:301–306. doi: 10.1016/s0167-7799(98)01219-0. [DOI] [PubMed] [Google Scholar]
- Schena M, Shalon D, Davis R, Brown P. Quantitative monitoring of gene expression patterns with a complementary DNA microarray [see comments] Science. 1995;270:467–470. doi: 10.1126/science.270.5235.467. [DOI] [PubMed] [Google Scholar]
- Schena M, Shalon D, Heller R, Chai A, Brown P, Davis R. Parallel human genome analysis: microarray-based expression monitoring of 1000 genes. Proc Natl Acad Sci U S A. 1996;93:10614–10619. doi: 10.1073/pnas.93.20.10614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Velculescu V, Zhang L, Vogelstein B, Kinzler K. Serial analysis of gene expression. Science. 1995;270:484–487. doi: 10.1126/science.270.5235.484. [DOI] [PubMed] [Google Scholar]
- Velculescu V, Zhang L, Zhou W, Vogelstein J, Basrai M, Bassett DJ, Hieter P, Vogelstein B, Kinzler K. Characterization of the yeast transcriptome. Cell. 1997;88:243–251. doi: 10.1016/s0092-8674(00)81845-0. [DOI] [PubMed] [Google Scholar]
- Velculescu VE, Madden SL, Zhang L, Lash AE, Yu J, Rago C, Lal A, Wang CJ, Beaudry GA, Ciriello KM, et al. Analysis of human transcriptomes [letter] Nat Genet. 1999;23:387–388. doi: 10.1038/70487. [DOI] [PubMed] [Google Scholar]
- Winkler RL, Hays WL. Statistics: Probability, Inference, and Decision, Chapter 6.17. New York: Holt, Rinehart and Winston; 1975. [Google Scholar]
- Zhang L, Zhou W, Velculescu V, Kern S, Hruban R, Hamilton S, Vogelstein B, Kinzler K. Gene expression profiles in normal and cancer cells. Science. 1997;276:1268–1272. doi: 10.1126/science.276.5316.1268. [DOI] [PubMed] [Google Scholar]