Processing incommensurately modulated protein diffraction data with Eval15 (original) (raw)
Data processing of an incommensurately modulated profilin–actin crystal is described.
Keywords: modulation, incommensurate, _Eval_15, profilin–actin
Abstract
Recent challenges in biological X-ray crystallography include the processing of modulated diffraction data. A modulated crystal has lost its three-dimensional translational symmetry but retains long-range order that can be restored by refining a periodic modulation function. The presence of a crystal modulation is indicated by an X-ray diffraction pattern with periodic main reflections flanked by off-lattice satellite reflections. While the periodic main reflections can easily be indexed using three reciprocal-lattice vectors a*, b*, c*, the satellite reflections have a non-integral relationship to the main lattice and require a q vector for indexing. While methods for the processing of diffraction intensities from modulated small-molecule crystals are well developed, they have not been applied in protein crystallography. A recipe is presented here for processing incommensurately modulated data from a macromolecular crystal using the Eval program suite. The diffraction data are from an incommensurately modulated crystal of profilin–actin with single-order satellites parallel to b*. The steps taken in this report can be used as a guide for protein crystallographers when encountering crystal modulations. To our knowledge, this is the first report of the processing of data from an incommensurately modulated macromolecular crystal.
1. Introduction
The crystalline state of matter is generally defined by its three-dimensional translational symmetry. This means that the crystal is composed of identical unit cells, with the contents of the asymmetric unit being perfectly replicated by the lattice symmetry operators. In the modulated case, short-range translational symmetry is lost, so that the atomic structure can no longer be defined by the contents of a single unit cell. These modulations can be caused by several phenomena, such as displacement of atomic positions and occupational modulations. Although such modulations destroy short-range symmetry, they themselves possess long-range order that can be used to restore periodicity. One can think of an atomic modulation as a systematic or smoothly varying disorder (van Smaalen, 2007 ▶), which distinguishes it from randomly disordered structures. This smoothly varying disorder is what defines the atomic modulation function (AMF). The AMF is a mathematical description of the modulation and can be a continuous harmonic function represented as a sine/cosine wave or a discontinuous function; it can be represented by, for example, either a saw-tooth or crenel function (Petříček et al., 1995 ▶). For a modulation resulting from a displacement of atomic positions, it is the AMF that describes the movement of the atoms from their average positions in the basic structure. An excellent nonmathematical description of how to solve incommensurately modulated crystals has recently been published (Wagner & Schönleber, 2009 ▶).
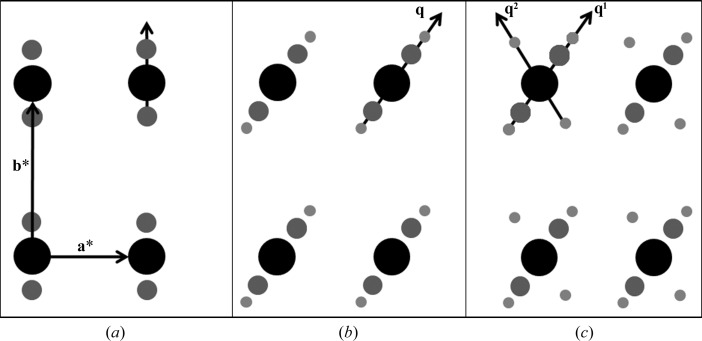
In the periodic state, all reflections can be indexed by the three integer indices, such that

where the main reflections are spanned by linear combinations of a*, b* and c*, and h, k and l are integer indices. Note that vectors are denoted in bold font. The three reciprocal basis vectors shown above describe the basic reciprocal cell of an incommensurately modulated crystal and are used to index the main reflections. The basic unit cell therefore has three-dimensional translational symmetry that is perturbed by the modulation wave. Addition of the terms describing the order and positions of the satellite reflections associated with each main reflection gives
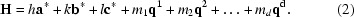
Here, d is the number of satellite directions, the q vectors (q 1, q 2, … q d) describe the direction and magnitude of the satellite reflections relative to the main reflections and m 1, m 2, … m d represent the order of the satellite reflection. For a main reflection, m i = 0. Note that scalar coefficients are denoted in italics. Satellite reflections are then indexed with this q vector. It can then be seen from (2) that the three-dimensional basic lattice can be extended into higher dimensions based on the number of modulations (or q vectors). In the simplest case of an incommensurate crystal, the modulation is in only one direction and is called a (3 + 1)-dimensionally modulated crystal. In this case, there will exist only a single q vector, such that
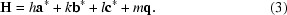
The positions of the satellite reflections are therefore defined by the q vector

For the example in Fig. 1 ▶(a), there is a single modulation vector with single-order satellites that are parallel to b* with values of m = (±1, 0). In this case, (4) then reduces to

Of course, a modulation wave does not have to be parallel to one of the reciprocal basis vectors. Instead, in more complicated cases two or three of the scalar q coefficients in (5) can be nonzero. Furthermore, if the change in structure owing to the modulation is large, multiple-order satellites can exist. In such cases, to index the multiple-order satellites, the q vector representing the elementary displacement from a main reflection would be multiplied by integer values of m ranging beyond −1 to 1. Fig. 1 ▶(b) illustrates a case in which m ranges from −2 to 2 and the single q vector has the form
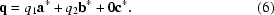
Finally, modulated crystals can have satellite reflections in more than one direction, requiring multiple q vectors. In the example illustrated in Fig. 1 ▶(c), q1 and q2 differ in direction as well as spacing between the satellites and mains and can be expressed by
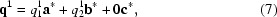
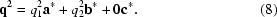
Here, the values of the components for each q vector are determined independently and refined separately to describe the direction and spacing of the two modulation waves. The two q vectors in this example describe two modulation waves that change the atomic position relative to the basic structure. This example represents a (3 + 2)-dimensionally modulated crystal, which would be more difficult to solve.
Figure 1.
(3 + d)-dimensional diffraction scenarios. (a) (3 + 1)-dimensional modulation with a single q vector parallel to b* and first-order satellites (m = ±1). (b) (3 + 1)-dimensional modulation with second-order satellites (m = ±2) and a single q vector in the ab plane. (c) (3 + 2)-dimensional modulated diffraction with two q vectors.
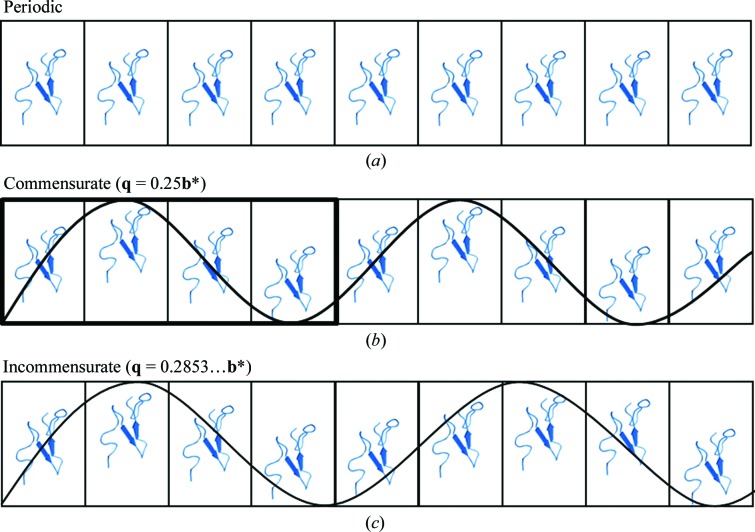
Crystal periodicities can be categorized into three types (Fig. 2 ▶). The first type of crystal is that most commonly solved by macromolecular crystallographers. The crystal is periodic and the unit-cell contents are replicated exactly by the lattice translations (Fig. 2 ▶ a). The second type is the case of a commensurate modulation. Here, the spacing of the satellites relative to the main reflections is a rational value. The diffraction pattern can be indexed and integrated with three integer indices as a supercell. In Fig. 2 ▶(b) the q vector has a rational value of 0.25 (or 1/4) and the modulation of the structure repeats every four unit cells. This means that the lattice parameters for indexing the satellite reflections are integer multiples (1, 2, …, n) and the crystal structure can be described by a supercell (Wagner & Schönleber, 2009 ▶). The third type of crystal is the case of an incommensurately modulated crystal. Here, at least one component of the q vector is irrational and cannot be calculated with a simple fraction (Fig. 2 ▶ c). An accurate description of an incommensurately modulated crystal can only be obtained by describing the diffraction pattern with q vectors. Most of the data-processing packages used in protein crystallography lack modules for calculating q vectors and therefore the satellite intensities cannot be indexed let alone integrated for subsequent structure determination. However, the Eval program suite (http://www.crystal.chem.uu.nl/distr/eval) can handle incommensurately modulated diffraction data from macromolecular crystals. It should be noted that these structures cannot be solved following the ‘lattice-translocation defects’ method (Wang et al., 2005 ▶), nor are the crystals plagued by any form of twinning (Yeates, 1997 ▶).
Figure 2.
Three categories of crystals. (a) Periodic case with identical unit cells. (b) Commensurate modulation. (c) Incommensurate modulation with harmonic modulation wave. Protein structure from PDB entry 2rro.
Although observed in practice, formal reports of incommensurately modulated macromolecular crystals are rare (Aschaffenburg et al., 1972 ▶; Schutt et al., 1989 ▶) and these types of structural modulations in the context of a macromolecular crystal are poorly understood. In 2008, the first q vector from a modulated protein crystal was measured from a single diffraction image from a room-temperature protein crystal (Lovelace et al., 2008 ▶). Research progress was stymied by the reversibility of the modulation at room temperature, which prevented the collection of a full set of diffraction data. Also, the available data-reduction software TwinSolve was unable to successfully integrate the protein diffraction data. In 2010, a possible physical model for a modulated protein crystal was published together with a simulation of the corresponding diffraction pattern containing satellite reflections (Lovelace et al., 2010 ▶). The effect of the size of the structural modulation on the main and satellite reflections was also explored using computer simulations. Separately, in 2010 the _Eval_15 integration method, which is based on ab initio calculations of three-dimensional (x, y, ω) reflection profiles from physical crystal and instrument parameters, was published. The present paper is the next logical step for both research paths. Here, the _Eval_15 data-reduction approach is applied to a difficult protein crystal that is incommensurately modulated.
1.1. Overview of processing incommensurate diffraction data
In the q-vector approach a clear distinction is made between main and satellite reflections. The main reflections are usually (but not always) stronger than the satellites. Thus, the mains can be distinguished from the satellites based on intensity and some software programs use this to decide which reflections are mains (Svensson, 2003 ▶). The basic cell in three dimensions (1) is established by indexing the main reflections. Satellite reflections are then assigned to their respective mains by use of the knowledge that the satellites are not only equidistant from each other but also to the mains and cannot be indexed by the main cell. The distances between mains and satellites (and their direction relative to the main cell) are then used to assign (and refine) the modulation q vector as in (4). Satellite reflections are then given an index m = (±1, ±2, ±3…) based on their diffraction order relative to the main reflections. Once all of the reflections have been properly indexed and predicted, they are integrated. Since satellite reflections are generally weak (I/σ < 2), profile fitting is essential. Profile fitting is used in the well known integration software programs DENZO, MOSFLM and XDS (Leslie, 1999 ▶; Otwinowski & Minor, 1997 ▶; Kabsch, 2010 ▶). The model profiles used to integrate a reflection are learned from strong reflections in the same region of reciprocal space. If reflections are tightly spaced, which can be the case with satellite reflections, many data-processing suites have difficulty modelling them. Establishing accurate reflection profiles and deconvoluting closely spaced reflections is a strength of the _Eval_15 software.
1.1.1. Indexing and calculating reflection profiles
For indexing and integrating our incommensurately modulated profilin–actin (PA) data, the programs DirAx (Duisenberg, 1992 ▶) and _Eval_15 (Schreurs et al., 2010 ▶) were used. The indexing program DirAx was initially developed for solving difficult cases resulting from twin lattices, incommensurate data and long unit-cell axes. DirAx determines direct-lattice vectors by the calculation of reflection ‘triplets’. Here, the endpoints of the three reflection vectors form the corners of a triangle. If the three reflections belong to the same reciprocal lattice, the normal to the plane of the triangle defines the direction of a direct-lattice vector. From the projection of reflection-vector endpoints on this direct-lattice vector a one-dimensional spacing will emerge. This procedure is repeated for many triplets. The three shortest independent direct-lattice vectors determine the primitive direct unit cell, which is subsequently reduced. Nonfitting or ‘alien’ reflections will not fit the direct unit-cell spacings and are therefore easily identified. For a modulated crystal, this is how DirAx separates mains from satellites. Once the reflections have been categorized, the alien reflections are then used to test for possible q vectors. After a q vector has been selected, the final step is to set the order of the modulation (m) and to write the R-matrix file that describes the laboratory-space coordinates of the reciprocal-lattice vectors a*, b* and c*.
For accurate integration of reflection intensities, profiles are needed for all predicted reflections, including both mains and satellites. The _Eval_15 data-integration technique is based on the concept of ‘general impacts’, which was first introduced in the package _Eval_14 (Duisenberg et al., 2003 ▶). It is assumed that a diffracted beam is caused by multiple scattering events according to kinematic diffraction theory. The _Eval_15 integration method was developed out of a need to model profiles from difficult diffraction data resulting from weak scattering, anisotropic mosaicity, _K_α1/_K_α2 splitting and interference from close neighbors and/or satellite reflections. In the program, general impacts on the detector are calculated by ray-tracing photons with a given wavelength λ sampled from a wavelength spectrum and originating from a sampled distribution F of focus points. The photons are diffracted in the crystal, which is sampled by a three-dimensional distribution of grid points K, and the mosaic orientation of the reciprocal lattice at this grid point is sampled from a mosaic distribution Sm (Gaussian, Lorentzian or block-like). The probability distributions are modelled either as homogeneous, Gaussian or Lorentzian. The wavelength spectrum consists of Gaussian or Lorentzian distributions centered around the main spectral lines (monochromatic or _K_α1 and _K_α2). Generally, one has prior knowledge of most parameters, e.g. a face-indexed description of the crystal, the wavelength spectrum, the focus properties and the point-spread function of the detector. Procedures are implemented to find an optimal set of the remaining parameters, notably the mosaic spread, from a small selection of reflections varying in I/σ and duration. In practice this is performed by visual inspection and may take 15 min. Once parameters have been found that realistically represent the experiment then accurate model profiles are generated for all reflections. Integrated intensities are finally obtained from a least-squares fit of the model profiles to the observed profiles with singular value decomposition (SVD; Press et al., 1986 ▶). Following integration in _Eval_15, the main and satellite intensities can be scaled and corrected for absorption in SADABS (Sheldrick, 1996 ▶).
1.1.2. Program workflow
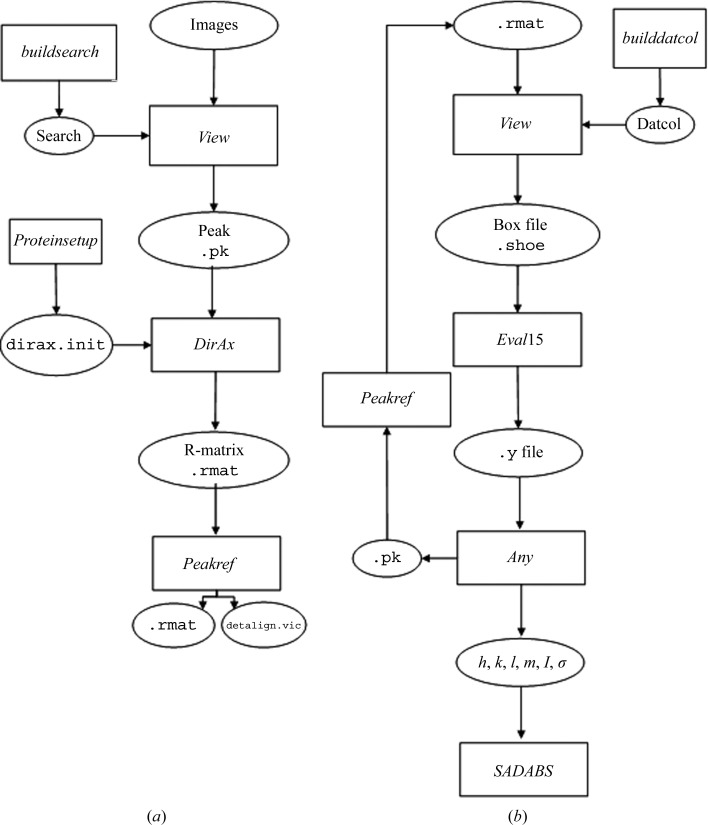
Processing incommensurately modulated diffraction data using the Eval program suite can be broken into two stages. Firstly, peak searching and indexing are performed to find the basic cell and q vector (Fig. 3 ▶ a). Secondly, the intensities are integrated and scaled (Fig. 3 ▶ b). X-ray diffraction images are read into the program View (Schreurs, 1998 ▶), which provides a graphical display for inspecting diffraction images and carrying out the peak-searching routine. A small program (buildsearch) generates scripts for the peak search. If satellite intensities are strong, the default I/σ value of 5 should be adequate for finding a sufficient number of satellite reflections (parameter peakbg). If not, then the default value will need to be lowered. Accordingly, the minimum spot separation will need to be set small enough (parameter peakmm). Once a set of suitable peaks have been found that include both satellites and mains, View outputs a peak file (.pk) that can be read directly into DirAx for indexing. Then, a list of possible unit cells for the main reflections is given together with the number of reflections that fit the basic cell. If enough alien reflections are found they are used to calculate possible q vectors, the quality of which is estimated from the figure of merit. After selection of a proper basic cell/q-vector combination, the indices h, k, l and m are assigned and the resulting R-matrix with corresponding q vector is output for peak refinement. In Peakref (Schreurs, 1999 ▶), the detector settings can be refined and written to a calibration file (detalign.vic) followed by refinement of the crystal orientation, unit cell and q vector, which are saved to an improved R-matrix file. If the results are not satisfactory, i.e. poor predictions and/or high residuals, the user can rerun View with adjusted peak-search parameters and repeat the process.
Figure 3.
Eval program workflow. (a) Steps taken to calculate and refine the basic cell and q vector. (b) Program flow for integration and scaling of experimental intensities.
With the basic cell and q vector in hand, the next stage is to integrate and scale the data. The datcol procedure in View is used to read in the R-matrix and collect three-dimensional reflection boxes; these are stored in reflection-box files that are centered on each predicted reflection, including the satellites. The main concern with building reflection boxes is that there is a sufficient amount of background for use in the least-squares fit. In the _Eval_15 graphical display, profiles which were calculated from a sample of 10 000 detector impacts for each reflection individually are shown before and after the application of a point-spread function. Adjustments can then be made to the instrument and crystal parameters such as the crystal size, shape and mosaic spread (see §1.1.1). After the proper parameters have been found they can be saved and the reflections contained in the reflection-box files are integrated. _Eval_15 outputs the integrated reflections to .y files, an XML-type file that can then be input into Any (Schreurs, 2007 ▶). Any is a versatile program that facilitates a large range of (graphical) analyses of the reflections. For example, R merge values from mains and satellites can be calculated (see Appendix A for how symmetry is applied to satellite reflections). Also, adjustments to the Laue group, reflection filters such as resolution and I/σ can be made with Any. In _Eval_15 reflection positions are refined and if after inspection in Any the shifts are considered to be too large, the new reflection positions can be written to a file that can be processed with Peakref if deemed necessary. The whole process can then be repeated. Finally, h, k, l, m, I and I/σ for all or a selection of reflections are written to a file and fed into SADABS (Sheldrick, 1996 ▶), which is used to find an error model for the standard deviations and for scaling and merging. In the scaling process the data are corrected for fluctuations in the crystal volume in the beam, incident-beam heterogeneity, absorption from the crystal and crystal decay.
2. Experimental
2.1. Cross-linking and formation of the modulated state
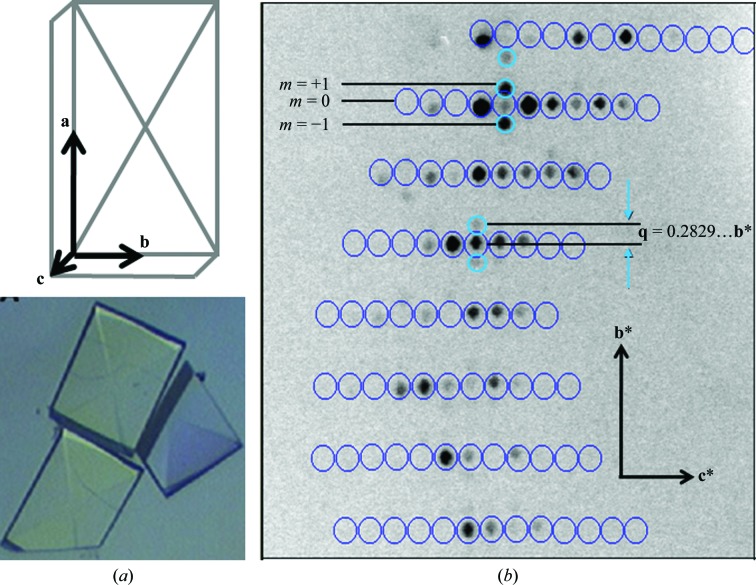
Bovine profilin–β-actin was purified and crystallized following the protocols established by Carlsson (1979 ▶) and outlined in Lovelace et al. (2008 ▶). Slightly acidic pH is known to cause the dissociation of profilin from actin and therefore promote filament formation (Oda et al., 2001 ▶; Carlsson, 1979 ▶). Cross-linking of the modulated crystal was found to be essential since the modulation of PA crystals was reversible (Lovelace et al., 2008 ▶). The reaction was optimized by testing different cross-linking reagents, pH values and reaction times. Optimal conditions for cross-linking were determined by the quality of diffraction. To induce the modulated state, the gentle vapor-diffusion method for cross-linking crystals described by Lusty was used (Lusty, 1999 ▶). Here, a profilin–actin (PA) crystal (500 × 350 × 150 µm; Fig. 4 ▶ a) was suspended over a sitting-drop reservoir that contained an acidic solution of 25% glutaraldehyde in 0.001 N HCl. The reaction was left to slowly cross-link overnight at 277 K. To obtain a full modulated data set, the crystal was mounted on a MiTeGen MicroMount, soaked in 7 M sodium formate for approximately 30 s for cryoprotection and quickly cryocooled by plunging it into liquid nitrogen.
Figure 4.
PA crystals and incommensurately modulated PA diffraction. (a) Schematic of a PA crystal with corresponding axes. Below is shown an actual PA crystal of approximate dimensions 500 × 350 × 150 µm. (b) Incommensurate diffraction in the 0_kl_ region with first-order satellite reflections.
2.2. Periodic state
To obtain normal periodic diffraction data, a PA crystal (400 × 300 × 100 µm) was soaked in a solution consisting of 1.8 M potassium phosphate pH 7.6, 5 m_M_ DTT and 1 m_M_ ATP. Calcium was intentionally omitted from the solution in order to ensure that the crystal remained nonmodulated upon cryocooling. The crystal was then soaked in a 35% solution of glycerol prepared in the same buffer and placed in a nitrogen stream (X-stream 2000) for cryocooling.
2.3. Data collection
Diffraction data were collected from the cryocooled crystal as follows. Complete data were collected at 100 K using a Rigaku FR-E Superbright Cu _K_α rotating-anode generator operating at 45 kV and 45 mA and fitted with a quarter-χ goniometer. Beam focusing was carried out with VariMaxHR optics for crystals with large unit cells. Diffraction images were collected on an R-AXIS IV++ image-plate detector and showed intense single-order satellite reflections along the b* axis (Fig. 4 ▶ b). For the modulated crystal, two swaths of data of 92 and 38 images each were collected at χ = 0 and 45°, respectively. Images were collected at a distance of 300 mm with 15 min exposures and an oscillation of Δϕ = 0.5° using CrystalClear software (Rigaku Americas Corp.) to control the X-ray system. For the periodic crystal, 360 diffraction images were collected with Δϕ = 0.5° for 5 min each.
2.4. Data processing
An initial basic cell was calculated in d*TREK (Pflugrath, 1999 ▶) using the main reflections (Fig. 4 ▶ b) and was determined to have parameters a = 37.8, b = 71.2, c = 187.3 Å, α = β = γ = 90° in the orthorhombic space group _P_212121, which is in accordance with a previously solved open-state PA structure (Chik et al., 1996 ▶). An initial start-up script Proteinsetup was run to set a maximum expected axis length and a range of volumes to limit the number of solutions output in DirAx. The calculation of q vectors has to be explicitly allowed. Peak search and indexing were carried out as described. An initial unit cell was found in an orthorhombic primitive lattice with a q vector value of 0.28 along b* and near-zero components (<0.1) along a* and c*. The unit cell and q vector were written to an R-matrix file which was then refined in Peakref. The crystal and detector positions were refined, followed by refinement of the unit cell and q vector. The q-vector values along the a* and c* dimensions were set to zero and were not refined. The refined detector and unit-cell parameters were then saved to the calibration and R-matrix files, respectively (Fig. 5 ▶). Using the updated R-matrix, the datcol procedure in View was used to build integration reflection-box files. The reflection-box size was increased to 3.5 mm to ensure that enough background was included. Each reflection-box file contained roughly 1000 reflection profiles to keep the file size manageable. The reflection-box depth was increased to 7 based on visual inspection of reflection width in ϕ; that is, over seven consecutive frames of data. Once the reflection-box files had been built in View, the simulated profiles were inspected using the _Eval_15 graphical user interface (Fig. 6 ▶). A main point of inspection here was to see that the profiles of the main and satellite reflections were properly modelled, as indicated by minimal differences between observed and calculated profiles (Fig. 6 ▶ e), and that they could be deconvoluted, which is decided by analysing the variance–covariance matrix in SVD. If satisfactory, _Eval_15 was used to integrate the reflection-box files. The .y file was read into Any to analyse the integrated intensities. Following inspection in Any, a reflection file was created which contains integrated intensities of the main and satellite reflections. The file was then input into SADABS for scaling. After scaling of the integrated intensities in SADABS, the reflection output file was analysed using Any (Table 1 ▶). The periodic diffraction data were also processed with _Eval_15 and SADABS (Table 1 ▶).
Figure 5.
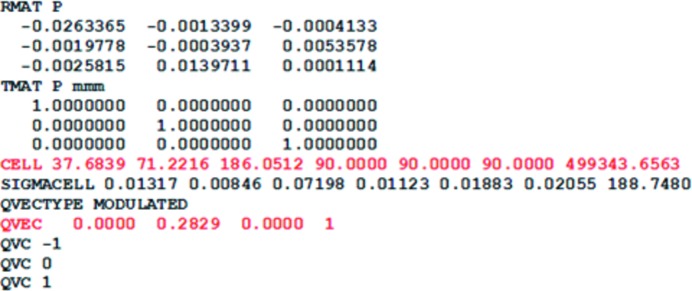
Unit cell and q vector after peak refinement in Peakref.
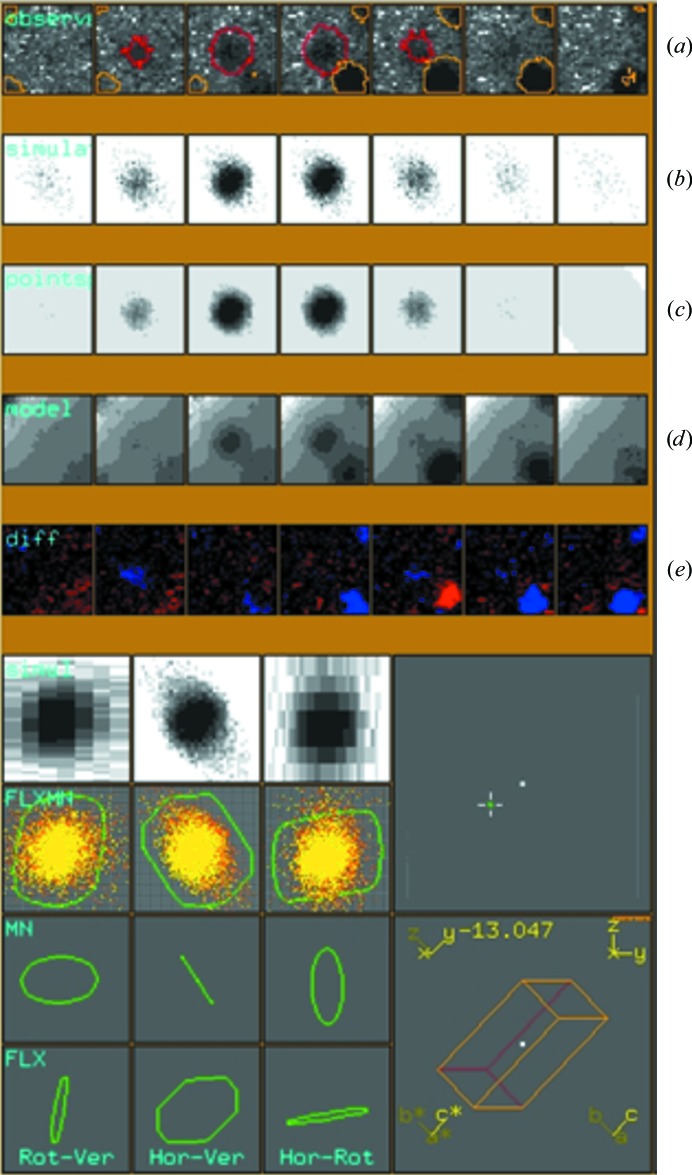
Figure 6.
_Eval_15 graphical display window showing the profile of a satellite with associated main reflection. (a) Successive observed ϕ-slices for a satellite reflection (red contour) with associated neighbors (yellow contours). (b) Resulting profile from simulated impacts. (c) Model profile after application of a pseudo-Lorentzian point-spread function. (d) Final profile after including the neighbors and application of scale factors and background parameters. (e) Difference between observed and calculated profiles.
Table 1. _Eval_15 data-processing statistics for the incommensurately modulated and periodic PA diffraction data.
Values in parentheses are for the highest resolution shell. Absorption correction and scaling were performed using SADABS.
| Criterion | Modulated | Periodic |
|---|---|---|
| Maximum resolution () | 3.0 | 2.3 |
| Completeness (%) | 98.2 (85.9) | 99.1 (96.0) |
| Unit-cell parameters | ||
| a () | 37.3 | 38.1 |
| b () | 71.1 | 72.0 |
| c () | 185.1 | 187.6 |
| = = () | 90 | 90 |
| q vector, order | 0a* + 0.2829b* + 0c*, d = 1 | NA |
| I/ (mains, satellites) | ||
| 233.0 | 15.2 (4.2), 2.2 (1.4) | 6.5 (2.7) |
| 234.0 | 15.9 (10.8), 3.1 (2.2) | |
| No. of unique reflections (mains, satellites) | 10669, 21532 | 20743 |
| Laue group | mmm | mmm |
| R sym † (%) | ||
| 233.0 | 8.2 (56.3) | 7.5 (25.7) |
| 234.0 | 7.3 (30.3) |
2.5. Satellite-reflection analysis
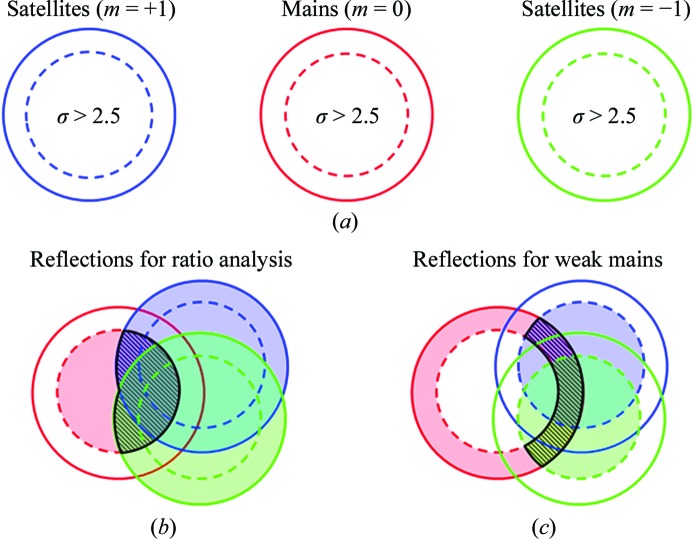
The relative intensities between the satellite and the main reflections are analysed in Table 2 ▶. For this analysis, cases in which a main and two satellites were measured were extracted from the reflection list. For this, the reflections were separated into three equal groups: satellites with m = +1, mains with m = 0 and satellites with m = −1 (Fig. 7 ▶ a, solid circles). Reflections with an I/σ of greater than 2.5 were considered ‘good’ (dashed circles inside the solid circles). Reflections having a good main and both satellites were extracted (Fig. 7 ▶ b). These reflections were sorted by resolution and grouped into ten equally sized bins. Statistical information about the ratio of the satellite intensity to the main intensity was calculated for the bins and is shown in Table 2 ▶. Reflections with ratios greater than 1 were rejected from the analysis in Table 2 ▶.
Table 2. Analysis of relative intensities between satellite and main reflections.
| Resolution bin () | No. of reflections | Average ratio† | Standard deviation ratio† | Maximum ratio | No. of rejects (ratio 1)‡ |
|---|---|---|---|---|---|
| 23.146.94 | 824 | 0.10 | 0.17 | 39.12 | 25 |
| 6.945.48 | 803 | 0.15 | 0.20 | 4.66 | 46 |
| 5.484.80 | 798 | 0.18 | 0.22 | 7.08 | 51 |
| 4.804.35 | 769 | 0.21 | 0.25 | 4.23 | 81 |
| 4.354.03 | 760 | 0.22 | 0.25 | 4.16 | 90 |
| 4.033.77 | 761 | 0.25 | 0.25 | 6.85 | 89 |
| 3.773.58 | 745 | 0.25 | 0.24 | 9.09 | 105 |
| 3.583.39 | 766 | 0.30 | 0.25 | 4.76 | 84 |
| 3.393.22 | 742 | 0.28 | 0.25 | 21.14 | 108 |
| 3.222.98 | 758 | 0.28 | 0.23 | 9.44 | 91 |
Figure 7.
Analysis of satellite reflections. Reflections that contained a measurement for the main and both satellites were separated into three sets by m value. (a) Reflections were put in the ‘good’ category if they had an I/σ of greater than 2.5 (inside the dashed circle). Weak main reflections were defined as having an I/σ of less than 2.5 (outside the dashed circle). (b) For the analysis of the relative intensities between satellite and main reflections the intersection used was good mains and all satellites (hatched area). (c) Good satellites associated with weak mains were defined as the intersection of at least one good satellite with a weak main (hatched area). Results for the strongest satellites are summarized in Table 3 ▶.
Cases in which the satellite reflections were present in the absence of a main were observed and compared with the periodic crystals in Table 3 ▶. To pull these cases out of the reflection list, cases that had at least one good satellite and a weak main or absent main (I < 2.5σ) were identified (Fig. 7 ▶ c).
Table 3. Examples of reflections where the satellite reflections are present in the absence of a main reflection.
Reflections with satellite I/ 10 were selected.
| | | | | Modulated data | Periodic data | Comparison | | | | | ----------------------------------------------------------- | --- | --- | -------------- | --------------------------- | -------------------------- | ----------- | ---------------- | -------------------------------- | | h | k | l | d () | I satellite (), m = +1 | I satellite (), m = 1 | I main () | I main () | I/ ratio |periodic/modulated| | | 4 | 1 | 18 | 6.9 | 41.7 (3.9) | 44.8 (3.8) | 3.3 (3.6) | 684.6 (137.3) | 2.3 | | 4 | 0 | 24 | 5.9 | 64.4 (3.3) | 66.7 (3.3) | 2.9 (2.9) | 2613.3 (305.3) | 4.4 | | 0 | 17 | 5 | 4.2 | 112.5 (5.4) | 114.1 (5.5) | 0.8 (4.5) | 3009.9 (275.4) | 131.2 | | 0 | 14 | 24 | 4.2 | 87.2 (3.7) | 36.1 (3.5) | 7.5 (5.6) | 1352.3 (210.0) | 3.0 | | 0 | 6 | 27 | 5.9 | 61.7 (2.7) | 67.2 (2.8) | 5.2 (2.4) | 3809.0 (510.3) | 5.6 | | 0 | 1 | 32 | 5.8 | 82.1 (4.5) | 88.1 (4.8) | 5.7 (2.6) | 40482.0 (5336.9) | 42.7 | | 0 | 4 | 23 | 7.3 | 22.6 (1.5) | 66.7 (1.9) | 5.3 (2.7) | 106.2 (53.2) | 1.1 | | 0 | 6 | 9 | 10.3 | 47.0 (1.7) | 45.6 (1.7) | 0.1 (1.2) | 814.7 (146.5) | 2.6 | | 1 | 0 | 18 | 9.9 | 79.4 (3.0) | 77.3 (3.0) | 3.6 (2.0) | 66.2 (101.4) | 0.4 | | 1 | 0 | 25 | 7.3 | 25.3 (2.6) | 27.9 (2.8) | 4.2 (2.0) | 2062.3 (242.0) | 8.5 | | 1 | 0 | 28 | 6.5 | 58.0 (3.4) | 59.2 (3.5) | 6.6 (3.6) | 1228.6 (121.3) | 11.0 | | 10 | 2 | 30 | 3.2 | 261.7 (13.0) | 464.1 (18.1) | 18.1 (10.1) | 4258.9 (407.9) | 5.8 | | | | | | | | | | | | | Systematically absent main reflections that have satellites | | | | | | | | | | 0 | 0 | 9 | 20.6 | 7.8 (0.8) | 6.7 (0.6) | 0.3 (0.4) | NA | | | 0 | 0 | 13 | 14.2 | 14.9 (1.1) | 14.9 (0.8) | 1.9 (1.3) | NA | | | 0 | 0 | 29 | 6.4 | 29.5 (2.3) | 29.0 (3.0) | 2.1 (2.2) | NA | | | 0 | 0 | 35 | 5.3 | 35.5 (2.9) | 38.0 (3.8) | 4.0 (2.8) | NA | | | 0 | 0 | 41 | 4.5 | 65.7 (3.8) | 61.5 (4.8) | 0.8 (3.5) | NA | |
3. Results and discussion
Two stumbling blocks that had prevented the evaluation of modulated PA crystals have been solved in this report: (i) obtaining a complete modulated data set and (ii) processing these data. Therefore, we sought to optimize cross-linking and cryocooling conditions that would essentially trap the modulated state in the crystal. Previous attempts at collecting a complete modulated PA data set failed since they were collected at room temperature and the reversibility of the modulated state seriously limited the amount of data that could be collected (Lovelace et al., 2008 ▶). Also, it was found that decreasing the pH below 6.0 caused the non-cross-linked crystals to crack and dissolve, most likely because of a large structural change. After testing various cross-linking agents and methods, glutaraldehyde was selected because it was the only commercially available acidic cross-linker. In the end, the gentle vapor-diffusion method for cross-linking protein crystals with acidic (pH 3.9) glutaraldehyde was employed (Lusty, 1999 ▶). It may seem counterintuitive that we selected a basic cryoprotectant (7 M sodium formate pH ∼8), but it should be noted that once the crystal is cross-linked it is no longer susceptible to the structural changes that are induced by pH fluctuations. We had previously found that 7 M sodium formate was a good cryoprotectant for normal periodic PA crystals. We chose a high-salt cryoprotectant as the crystals were grown with salt as the precipitating agent and this condition was therefore gentler on the crystal. Optimizing the above conditions allowed a complete data set to be collected and processed.
The second challenge was to process the data. In processing data from an incommensurately modulated crystal it is important to maintain a proper distinction between main and satellite reflections. An initial visual inspection of the diffraction pattern in CrystalClear using the ruler feature was helpful in estimating an approximate q vector. The most obvious feature of the satellite reflections was that they were near-perfectly aligned with the b* axis and the corresponding cell length was spaced approximately 250 Å as judged from the main reflections. This inspection already indicates that the q 2 component of q is approximately 72 Å/250 Å = 0.29. This value is in close agreement with the final refined q value of 0.2829_b_*. Although we were able to provide an initial estimate for the unit cell and q vector, it should be noted that DirAx had no problem finding the correct unit-cell/q-vector combination on its own. With q vector (0, 0.2829, 0) and mmm point-group symmetry the following equivalent reflections are generated: (h, k, l, m), (−h, −k, l, −m), (h, −k, −l, −m), (−h, k, −l, m), (−h, −k, −l, −m), (h, k, −l, m), (−h, k, l, m) and (h, −k, −l, −m) (see Appendix A for an explanation). Note that the two satellite peaks [(h, k, l, +m) and (h, k, l, −m)] on either side of a given main reflection (h, k, l, 0) are not restricted by symmetry to have the same intensity (Table 3 ▶).
For integration with _Eval_15 of satellite reflections, or any case where the reflection spacing is small, the user need not worry about overlapping reflections. These are easily deconvoluted. The quality of the profiles was analysed using the _Eval_15 graphical display window, in which the parameters (F, K, Sm, λ) that drive the calculation of simulated impacts were optimized. For example, the mosaicity was optimized by simply adjusting the value and inspecting the resultant profile. An example of a satellite profile is given in Fig. 6 ▶. The observed profile is plotted on the top line (Fig. 6 ▶ a). The satellite can be seen flanked by a main reflection at the bottom right of the reflection box. Below the observation (Fig. 6 ▶ b) is the profile which was calculated from 10 000 simulated impacts. In Fig. 6 ▶(c), a pseudo-Lorentzian point-spread function is applied and the resultant profile is shown. Finally, after the application of scale factors and background parameters, a final profile model is given (Fig. 6 ▶ d) and the difference between the observed and calculated profiles is seen (Fig. 6 ▶ e). Inspection and fine-tuning of parameters was continued for a few reflections until the results were satisfactory. Once all the parameters had been optimized, reflections in all reflection-box files were integrated.
Data statistics after scaling with SADABS are listed in Table 1 ▶. Data were 98% complete to a resolution of 3.0 Å. The I/σ ratio is greater than 3 for all reflections at 4.0 Å resolution and is greater than 2 when reflections to 3.0 Å are included. The relative intensity of the satellites to the mains increases with resolution (Table 2 ▶). The intensity of the satellites is about 10% that of the mains on average at low resolution and increases to 30% at higher resolutions. This increase in the relative intensity of satellite to the mains was also observed in our simulated data (Lovelace et al., 2010 ▶).
For a subset of the reflections the satellites are more intense than the mains. We tallied up these cases and there were 228 occasions where the main reflection was less than 2.5σ and the satellites were greater than 2.5σ (Fig. 7 ▶ c). In some cases the main is absent with very strong satellites. The cases in which the satellites were both measured and greater than 10σ are listed in Table 3 ▶. Some of these are cases in which the main is systematically absent owing to symmetry (Table 3 ▶, bottom). For the others, in most of the cases the main was present in the periodic state but becomes extinguished in the modulated state (Table 3 ▶, top). The majority of these have h = 0 or k = 0 and this may indicate something about the strength of the structural modulation along these directions.
4. Conclusions
The presence of satellites was first observed in PA crystals over twenty years ago (Schutt et al., 1989 ▶) and it was speculated that this modulation was caused by the formation of an actin filament. The mystery of what is going on inside these crystals could not be solved owing to a lack of software that could integrate the main and satellite reflections. One might think that the diffraction of the modulated PA crystals could simply be indexed and integrated as an approximately sevenfold supercell along b*. The MOSFLM, d*TREK and _HKL_-2000 (Powell, 1999 ▶; Otwinowski & Minor, 2001 ▶; Pflugrath, 1999 ▶) autoindexing routines all fail to find a supercell even when the defaults are changed to increase the maximum cell allowed and to use the weaker satellite data. Thus, the q-vector method of the Eval program suite was necessary to process the data. Data processing in Eval allowed proper indexing and integration of both main and satellite reflection intensities with the _Eval_15 method.
During data collection, it was noticed that particularly strong satellite reflections were associated with extinguished mains (Fig. 4 ▶ b). As it turns out, this is indicative of a strong structural modulation (Janssen et al., 1999 ▶). It is interesting to note that when normal periodic actin in PA crystals undergoes a transition from the ‘open’ to the ‘tight’ state the unit-cell dimension in c* changes by 14 Å, yet the crystals are stable (Chik, 1996 ▶). It is therefore possible that the structural transitions needed to bring about such a large modulation might be on a similar scale. Refinement of the basic and incommensurate PA structures will inevitably shed light on the nature of these higher order actin structures and provide insight into the early stages of actin-filament formation. This is the next step in our research.
Acknowledgments
This work was funded by NSF grant MCB-0718661 and the Nebraska Research Initiative and National Cancer Institute Eppley Cancer Center Support Grant P30CA036727. We would like to thank Clarence E. Schutt (Princeton University) and Uno Lindberg (Stockholm University) for useful discussions. We thank Lee Daniels and Christer Svensson for help with our attempts to process these diffraction data with the TwinSolve software package. We thank Sander van Smaalen for giving us the essential advice to try Eval.
Appendix A. General treatment of symmetry for q vectors
For each point group, all symmetry operations can be represented as a matrix W (International Tables For Crystallography, 2002 ▶). Reflection indices (h, k, l) are transformed to symmetry-related reflections by such a point-group operation W,
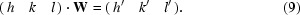
A q vector describing the modulation in our structure can be expressed as q = h a* + k b* + l c* and is transformed in a similar way: q·W = q′. Since the determinant of W is ±1, if q′ is not linearly dependent on q then they together represent a basis set {q, q′}. Applying other point-group operations or repeating the same transformation on q′ may lead to a new symmetry-related vector q′′. If this vector is not a linear combination of q and q′ then it is a third basis vector, thus forming the basis set {q, q′, q′′}. For a single q vector that is consistent with the point-group symmetry, not more than three basis vectors can be generated. Once the basis set has been established, it is stored in a matrix
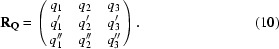
In case the basis consists of less than three q vectors the missing rows are filled with arbitrary vectors such that the matrix does not become singular.
Suppose that by application of point-group operations a symmetry-related q vector qs is obtained; it can be expressed in the basis vectors by
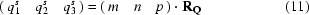
and reversely for any qs vector the indices with respect to the basis vectors are found from a set of linear equations,
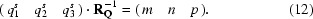
Here, m, n and p are indices of the vectors q, q′ and q′′ and are equivalent to the orders m 1, m 2 and m 3 of (2) in the main text. Now, how would the indices (m, n, p) transform by application of additional point-group operations? Suppose 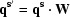 ; then, we can write
; then, we can write
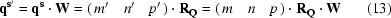
and it follows that
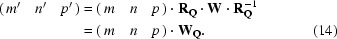
The transformation of indices (m, n, p) is thus seen to depend on the choice of the basis vectors.
In fact, in the Eval software, parallel to the point-group operations W, matrix operations WQ are generated that store the corresponding transformations of (m, n, p):
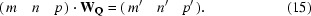
A1. Examples
A1.1. Point group 2
Matrix W is the operation of a twofold rotation. The symmetry-related reflections and q vectors are obtained by
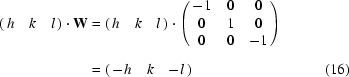
and similarly
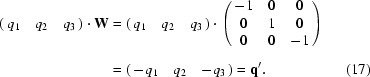
By repeating the same operation, we find q′·W = q. Thus, two basis vectors {q, q′} are found. For a one-dimensional modulation in a monoclinic crystal system admissible q vectors are (0, q 2, 0) and (q 1, 0, q 3) (see Table 3.1 in van Smaalen, 2007 ▶). For q 1 = q 3 = 0 it follows that q′ = q, so that we have only a single basis vector. It is obvious that m q transforms to m q and thus satellite reflection (h, k, l, m) with reciprocal-lattice vector h a* + k b* + l c* + m q transforms to (−h, k, −l, m). For q 2 = 0 it follows that q′ = −q, a vector collinear with q, so that again the basis is reduced to one single q vector. Now m q transforms to −m q and thus satellite reflection (h, k, l, m) with reciprocal-lattice vector h a* + k b* + l c* + m q transforms to (−h, k, −l, −m). Using matrix equations (10)–(15) the same result can be obtained. For RQ we choose
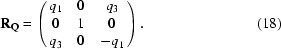
The first row contains the symmetry-restricted q vector with q 2 = 0. The second row vector is chosen not to be collinear with q and the third row vector is the vector product of the first two. Any other choice that ensures that matrix RQ is nonsingular is valid. By using W Q = R Q·W·RQ −1, we find
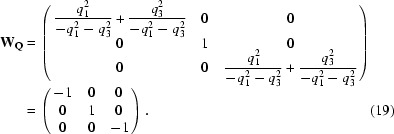
Since we have a one-dimensional modulation the indices (m n p) reduce to (m 0 0) and the result of (15) is (−m 0 0).
For a two-dimensional modulation there is no restriction on the components of the q vector.
For modulated PA crystals with mmm symmetry, only components of the q vector along the axes are allowed. If q = (0, 0.2829, 0), the following equivalent reflections are generated: (h, k, l, m), (−h, −k, l, −m), (h, −k, −l, −m), (−h, k, −l, m), (−h, −k, −l, −m), (h, k, −l, m), (−h, k, l, m) and (h, −k, l, −m).
A1.2. Point group 4
Matrix W is the operation of a fourfold rotation. The symmetry-related reflections and q vectors are obtained by
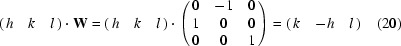
and similarly
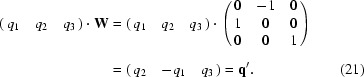
Next, we find q′·W = (−q 1 −q 2 q 3) = q′′ and q′′·W = (−q 2 q 1 q 3) = q′′′.
It is seen that q′′′ = q + q′′ − q′ and, by proceeding, no further basis q vectors are found. Our basis set consists of {q, q′, q′′}. Again, symmetry restricts the q vectors to (0, 0, q 3) for a one-dimensional modulation and to (q 1, q 2, 0) for a two-dimensional modulation. In the case of (q 1, q 2, 0) it follows that q′′ = −q, so that the basis reduces to {q, q′}. Reflection (h, k, l, m, n) transforms to its equivalent (k, −h, l, −n, m). In the case where q = (0, 0, q 3) the basis is {q} and (h, k, l, m) transforms to (k, −h, l, m).
The transformations of the indices (m, n, p) depends on the selection of the basis set {q, q′, q′′}, but if these are generated by the point-group operation from a single q vector the result is independent of the initial generating q vector.
The structure could contain a completely different additional modulation. The corresponding q vector should be treated independently and go through the same procedure as described above.
References
- Aschaffenburg, R., Fenna, R. E. & Phillips, D. C. (1972). J. Mol. Biol. 67, 529–531. [DOI] [PubMed]
- Carlsson, L. (1979). PhD thesis. Uppsala University, Sweden.
- Chik, J. K. (1996). PhD thesis. Princeton University, USA.
- Chik, J. K., Lindberg, U. & Schutt, C. E. (1996). J. Mol. Biol. 263, 607–623. [DOI] [PubMed]
- Duisenberg, A. J. M. (1992). J. Appl. Cryst. 25, 92–96.
- Duisenberg, A. J. M., Kroon-Batenburg, L. M. J. & Schreurs, A. M. M. (2003). J. Appl. Cryst. 36, 220–229.
- International Tables for Crystallography (2002). Vol. A, edited by T. Hahn, Table 11.2.2.1. Dordrecht: Kluwer Academic Publishers
- Janssen, T., Janner, A., Looijenga-Vos, A. & Wolff, P. M. D. (1999). International Tables for Crystallography, Vol. C, edited by A. J. C. Wilson & E. Prince, pp. 899–947. Dordrecht: Kluwer Academic Publishers.
- Kabsch, W. (2010). Acta Cryst. D66, 125–132. [DOI] [PMC free article] [PubMed]
- Leslie, A. G. W. (1999). Acta Cryst. D55, 1696–1702. [DOI] [PubMed]
- Lovelace, J. J., Murphy, C. R., Daniels, L., Narayan, K., Schutt, C. E., Lindberg, U., Svensson, C. & Borgstahl, G. E. O. (2008). J. Appl. Cryst. 41, 600–605.
- Lovelace, J. J., Winn, M. D. & Borgstahl, G. E. O. (2010). J. Appl. Cryst. 43, 285–292.
- Lusty, C. J. (1999). J. Appl. Cryst. 32, 106–112.
- Oda, T., Makino, K., Yamashita, I., Namba, K. & Maéda, Y. (2001). Biophys. J. 80, 841–851. [DOI] [PMC free article] [PubMed]
- Otwinowski, Z. & Minor, W. (1997). Methods Enzymol. 276, 307–326. [DOI] [PubMed]
- Otwinowski, Z. & Minor, W. (2001). International Tables for Crystallography, Vol. F, edited by M. G. Rossmann & E. Arnold, pp. 226–235. Dordrecht: Kluwer Academic Publishers.
- Petříček, V., van der Lee, A. & Evain, M. (1995). Acta Cryst. A51, 529–535.
- Pflugrath, J. W. (1999). Acta Cryst. D55, 1718–1725. [DOI] [PubMed]
- Powell, H. R. (1999). Acta Cryst. D55, 1690–1695. [DOI] [PubMed]
- Press, W. H., Flannery, B. P., Teukolsky, S. A. & Vetterling, W. T. (1986). Numerical Recipes Cambridge University Press.
- Schreurs, A. M. M. (1998). View Utrecht University, The Netherlands.
- Schreurs, A. M. M. (1999). Peakref Utrecht University, The Netherlands.
- Schreurs, A. M. M. (2007). Any Utrecht University, The Netherlands.
- Schreurs, A. M. M., Xian, X. & Kroon-Batenburg, L. M. J. (2010). J. Appl. Cryst. 43, 70–82.
- Schutt, C. E., Lindberg, U., Myslik, J. & Strauss, N. (1989). J. Mol. Biol. 209, 735–746. [DOI] [PubMed]
- Sheldrick, G. M. (1996). SADABS University of Göttingen, Germany.
- Smaalen, S. van (2007). Incommensurate Crystallography Oxford University Press.
- Svensson, C. (2003). TwinSolve Lund University, Sweden.
- Wagner, T. & Schönleber, A. (2009). Acta Cryst. B65, 249–268. [DOI] [PubMed]
- Wang, J., Kamtekar, S., Berman, A. J. & Steitz, T. A. (2005). Acta Cryst. D61, 67–74. [DOI] [PubMed]
- Yeates, T. O. (1997). Methods Enzymol. 276, 344–358. [PubMed]