Extracting a Cellular Hierarchy from High-dimensional Cytometry Data with SPADE (original) (raw)
. Author manuscript; available in PMC: 2012 Apr 2.
Published in final edited form as: Nat Biotechnol. 2011 Oct 2;29(10):886–891. doi: 10.1038/nbt.1991
Abstract
Multiparametric single-cell analysis is critical for understanding cellular heterogeneity. Despite recent technological advances in single-cell measurements, methods for analyzing high-dimensional single-cell data are often subjective, labor intensive and require prior knowledge of the biological system under investigation. To objectively uncover cellular heterogeneity from single-cell measurements, we present a novel computational approach, Spanning-tree Progression Analysis of Density-normalized Events (SPADE). We applied SPADE to cytometry data of mouse and human bone marrow. In both cases, SPADE organized cells in a hierarchy of related phenotypes that partially recapitulated well-described patterns of hematopoiesis. In addition, SPADE produced a map of intracellular signal activation across the landscape of human hematopoietic development. SPADE revealed a functionally distinct cell population, natural killer (NK) cells, without using any NK-specific parameters. SPADE is a versatile method that facilitates the analysis of cellular heterogeneity, the identification of cell types, and comparison of functional markers in response to perturbations.
1 Introduction
Multiparametric single-cell analysis has advanced our understanding of diverse biological and pathological processes, providing insights into cellular differentiation, intracellular signaling cascades and clinical immunophenotyping. Analysis by flow cytometry has increased steadily, fueled by growing interest in the identification of rare stem cell populations and the use of intracellular markers (i.e. phosphorylated proteins) for drug targeting. Modern flow cytometers typically provide simultaneous single-cell measurements of up to 12 fluorescent parameters in routine cases, and analysis of up to 17 protein parameters has been reported [1]. Recently, the first commercially available next-generation mass cytometry platform (CyTOFTM, DVS Sciences Inc., Toronto, ON, Canada) has become available and allows routine measurement of 30 or more single-cell parameters [2]. Despite increasing research in cytometric analysis and the technological advances in acquiring an increasing number of parameters per single cell, methods for analyzing multidimensional single-cell data remain inadequate. We present a novel analytical approach, Spanning-tree Progression Analysis of Density-normalized Events (SPADE), to organize high-dimensional cytometry data in an unsupervised manner, and to investigate natural and pathogenic cellular heterogeneity for biological insight.
Traditional methods for flow cytometry data analysis are often subjective and labor-intensive processes that require expert knowledge of the underlying cellular phenotypes. One common but cumbersome step is the selection of subsets of cells in a process called “gating” [3]. A gate is a region, defined in a biaxial plot of two measurements, which is used to select cells with a desired phenotype for downstream analysis. Gates are either manually drawn using software such as FlowJo (http://www.treestar.com/), FlowCore [4], or automatically defined by clustering algorithms [5, 6, 7, 8, 9, 10]. Manual gating is highly subjective and dependent on the investigator’s knowledge and interpretation of the experiment. Automatic gating algorithms cluster cells by optimizing the objective that cells in the same cluster be more similar to each other than cells from other clusters. Because these algorithms strive to define maximally different clusters, they often miss the underlying continuity of phenotypes (progression) that is inherent in cellular differentiation [11]. In addition, optimization objectives of most automatic gating algorithms are predisposed to capture the most abundant cell populations, while rare cell types, such as stem cells, are either excluded as outliers or absorbed by larger clusters. Some algorithms, such as a recent approach for automated gating termed SamSPECTRAL, have begun to include mechanisms for rare cell type identification [12].
Traditional cytometry data analysis methods also commonly suffer from limitations in scalability and visualization with increasing numbers of measurements per single cell. These limitations become more acute as the data dimensionality increases. To fully visualize an _m_-dimensional flow dataset, 12m(m−1) biaxial plots are needed, where each biaxial plot displays the correlation of only two markers at a time. It is difficult to comprehend the correlations among three or more markers from a series of biaxial plots. One recent approach that partly addresses the scalability issue is the probability state model, implemented in the GemstoneTM software package (Verity Software House, Inc.). This approach rearranges cells into a non-branching linear order, according to an investigator’s knowledge or expectation of how known markers fluctuate along a progression underlying the measured cell population [13]. Because cells are ordered in a non-branching fashion, a new model must be constructed for each mutually exclusive cell type (i.e. T cells, B cells).
SPADE is complementary to existing approaches for analyzing cytometry data by providing a visualization of multiple cell types in a branched tree structure that is constructed without requiring the user to define a known cellular ordering. Through a simple 2D visualization, SPADE shows how measured markers behave across all cell types in the data, while gating only focuses on user-selected cell types. SPADE partitions cytometry data into many hierarchically organized clusters that reflect all of the dimensions in the data, thus empowering investigators to identify and annotate known cell types, and to find unexpected ones. To demonstrate SPADE’s ability to detect a branched hierarchy underlying a heterogeneous population of real cells, we applied SPADE to a conventional (8-parameter) flow cytometry dataset of normal mouse bone marrow, a well-defined biological system with multiple known developmental transition points. The scalability of SPADE was demonstrated with a next-generation (31-parameter) mass cytometry dataset of normal human bone marrow using two staining panels and multiple experimental stimulatory conditions [14]. SPADE organized the data in a tree structure that partially recapitulated known biology of hematopoiesis, identified surrogate markers that define a functionally distinct cell type, overlaid data from complementary staining panels, and mapped intracellular signal activation of functional markers across a landscape of hematopoietic development.
2 Results
Outline of SPADE as applied to a simulated dataset
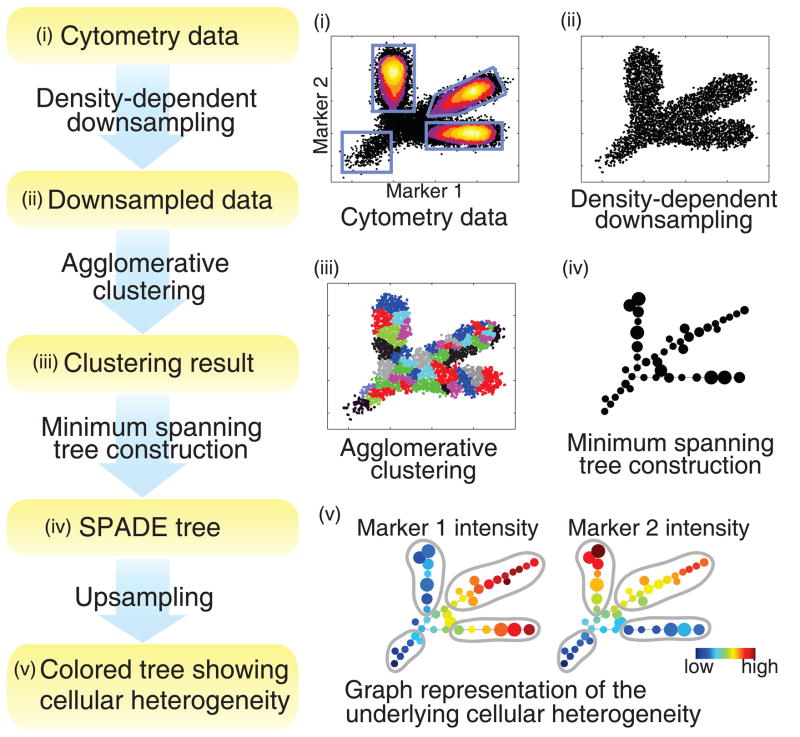
To demonstrate the SPADE algorithm (Figure 1), we simulated a 2-parameter flow cytometry dataset and analyzed it using SPADE. In the simulated cell population in Figure 1(i), the underlying cellular hierarchy originated from a rare “root” cell type and differentiated into three distinct abundant cell types. Traditional gating analysis on this dataset manually draws four gates as shown in Figure 1(i), and reports these four distinct subpopulations. Alternatively, SPADE views the data as a high-dimensional point cloud of cells, and uses topological methods to reveal the geometry of the cloud.
Figure 1.
Flowchart of SPADE, and SPADE analysis of a simulated dataset. (i) A simulated 2-parameter flow cytometry dataset, with one rare population and three abundant populations. (ii) Result of density-density downsampling of the original data. (iii) Agglomerative clustering result of the downsampled cells. (iv) Minimum spanning tree that connects the cell clusters. (v) Colored SPADE trees. Nodes are colored by the median intensities of protein markers, allowing visualization of the behaviors of the two markers across the entire heterogeneous cell population.
SPADE contains four computational modules. First, SPADE performs density-dependent downsampling to equalize the density in different parts of the cloud, and achieve equal representation of rare and abundant cell types (Figure 1(ii)). Second, SPADE performs agglomerative clustering to partition the downsampled cloud into clusters of cells with similar phenotypes. Adjacent clusters are drawn in alternating colors in Figure 1(iii). Since the downsampling step makes the abundant and rare cell types relatively equally represented, the rare “root” cells are allowed to form their own clusters and not be outnumbered by abundant cell populations during clustering. Third, SPADE performs minimum spanning tree construction to extract and summarize the geometry of the cloud. The topology of the tree structure in Figure 1(iv) reflects the shape of the cloud. Finally, SPADE performs upsampling to map each cell in the original dataset to the most similar cluster in the tree. When displaying the tree, SPADE adds another layer of information on top of the topology by varying the colors of the nodes. In Figure 1(v), nodes are colored by the median intensities of the two protein markers, allowing visualization of the behaviors of the two markers across the entire heterogeneous cell population. From the two colored trees, we can easily observe four branches with distinct phenotypes, shown by the manually drawn gray circles, which correspond to the four simulated cell types. In addition, we can also observe the gradual change along each lineage.
When visualizing the SPADE tree, an important issue is to determine its layout. In this simulated 2-parameter example, the position of each node is defined by the median intensities of the two markers, so that layout of the SPADE tree and the raw data are oriented in the same way. For data with higher dimensions, SPADE uses a modified Fruchterman and Reingold algorithm to automatically compute the layout [15]. Detailed descriptions of the visualization algorithm and the four modules of SPADE are provided in Methods.
Analysis of mouse hematopoiesis from flow cytometry data
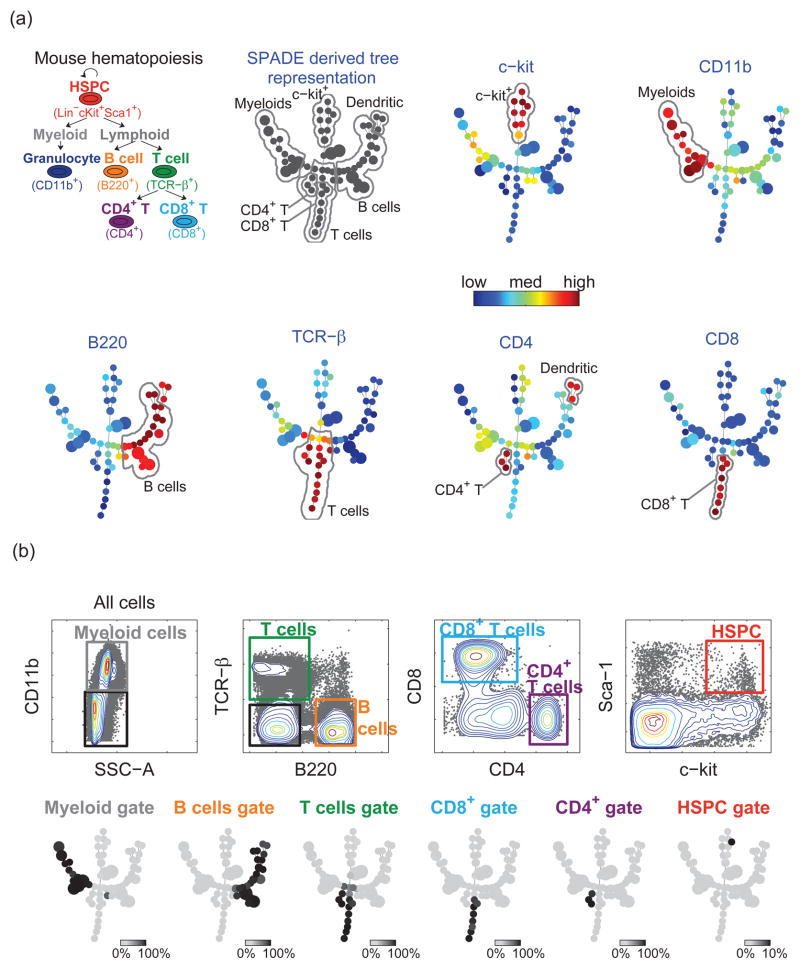
To validate its utility in representing branched cellular hierarchies, SPADE was applied to a flow cytometry dataset derived from a well-described biological hierarchy, hematopoiesis in mice (Figure 2(a)) [16, 17]. In this hierarchy, multipotent self-renewing stem and progenitor cells give rise to all of the terminally differentiated cell types. It is well known that mature myeloid cells are characterized by expression of the surface antigen CD11b, while lymphoid cells are negative for this marker. Within the lymphoid population, B-cells express B220 but not TCRβ, while the majority of T-cells express TCRβ but not B220. Finally, mature TCRβ expressing T-cells are characterized by mutually exclusive expression of CD4 or CD8.
Figure 2.
SPADE applied to mouse bone marrow flow cytometry data. (a) Known hematopoietic hierarchy in mouse bone marrow, and the colored SPADE tree derived from the mouse bone marrow data. Each tree was colored by the median intensity of one individual marker. (b) Traditional gating analysis on the mouse bone marrow data. For each gated population, one SPADE tree was drawn, where each node was colored by the percentage of gated cells in that node. Thus, the color of each tree represents which part of the tree is populated by the cells in the corresponding gate. This comparison shows the concordance between SPADE and gating results.
When applied to this mouse bone marrow flow cytometry dataset, SPADE first downsampled the data in a density-dependent manner (see Methods). The outlier and target densities were chosen empirically to be the 1st and 5th percentile of local densities of all the cells. In the clustering step, the desired number of clusters was chosen to be 50. SPADE clustered the downsampled cells, and derived the topology of the tree shown in Figure 2(a). After upsampling, the SPADE tree was colored according to the median intensity of each measured marker. The automatically generated outputs of SPADE were the tree diagrams in Figure 2(a) without the annotations.
To interpret the SPADE tree, we manually derived annotations, according to the coloration patterns of each marker. For example, when colored by c-kit, the upper branch in the middle of the SPADE tree showed a clear pattern of c-kit+. Therefore, this branch was annotated as c-kit+. Similarly, based on the SPADE tree colored by CD11b, the left branch was CD11b+. Based on the investigator’s familiarity with this immunological system, this branch was named myeloids. The remaining annotations were drawn in the same fashion, based on B220, TCRβ, CD4, and CD8. Gating and prior knowledge were not used to choose the boundaries of the annotations. From these annotations, we observed that different branches corresponded to different cell phenotypes. The interconnectivity among these phenotypes was consistent with known biology of mouse hematopoiesis.
In order to validate the SPADE tree for segregating meaningful cell populations, we compared it with the result of expert-based traditional gating analysis, in which subpopulations of cells were identified by a series of gates manually drawn on 2D plots in Figure 2(b). The manual gating analysis was performed in a blinded fashion, prior to the SPADE analysis. The SPADE tree was used to display each gated subpopulation, with each node colored by the percentage of the manually gated cells in that node. Therefore, the color of each tree in Figure 2(b) represents which part of the tree is populated by the cells in one gate. We can observe that each gated population occupied one branch of the tree. Overall, the SPADE result was consistent with traditional gating analysis in identifying biologically relevant populations.
Interestingly, manual gating did not identify the dendritic cells, because it is a subjective approach that relies on our prior knowledge, and we did not plan to find dendritic cells. Only after examining the SPADE results did we realize that manual gating could have been used to define a TCRβ-B220+ CD4+ dendritic cell population (see Supplement S1). By contrast, SPADE analysis readily identified the dendritic cell population, as three nodes on the distal end of the B220+ branch.
To quantify the difference between the two approaches, we computed the number of overlapping cells between all possible pairs of gates in the gating analysis and annotated regions in the SPADE tree. In Table 1, large values in the shaded entries indicate the consistency between gating and SPADE, while the differences are shown by the remaining entries. According to the first column, cells in the B cell gate were ascribed to B cells and dendritic cells in the SPADE analysis, which was also shown in Figure 2. From the fifth column, we observed that the myeloid gate in the gating analysis contained myeloids, B cells, T cells and c-kit+ cells in the SPADE annotations. On the contrary, the sixth row shows that few cells in the myeloid region of SPADE were regarded as other cell types by gating. In the last row, the c-kit+ branch was not intended to be specific to HSPCs (hematopoietic stem and progenitor cells). In addition to HSPCs, a significant portion of the c-kit+ branch was regarded as myeloid or T cells by the gating analysis. However the c-kit+ branch did not overlap with the CD4+ and CD8+ gates that corresponded to mature T cells. The majority of cells in the manual HSPC gate were found to be localized to the c-kit+ branch of the SPADE tree.
Table 1.
Comparison of traditional gating and SPADE, expressed in terms of the number of overlapping cells between each traditionally-derived gate and each annotated SPADE region. The total number of cells in each gate and each SPADE region are listed. The percentages are defined as the ratio between the number of overlapping cells and the total number of cells in the corresponding gate, thereby representing the percent of cells in a gate that are assigned to each SPADE region. Large values in shaded entries indicate the consistency between traditional gating and SPADE.
| Gates in the gating analysis | |||||||
|---|---|---|---|---|---|---|---|
| B cell - 150314 | T cell - 14699 | CD4+ - 2808 | CD8+ - 6055 | myeloid - 209079 | HSPC - 418 | ||
| Annotated SPADE branches | B cell - 152685 | 146017 (97.1%) | 88 (0.6%) | 0 | 0 | 2246 (1.1%) | 16 (3.8%) |
| Dendritic - 3996 | 3562 (2.4%) | 79 (0.5%) | 77 (2.7%) | 0 | 83 (<0.1%) | 0 | |
| T cell – 17538 | 364 (0.2%) | 12377 (84.2%) | 2729 (97.2%) | 6037 (99.7%) | 3033 (1.5%) | 0 | |
| CD4+ - 2931 | 0 | 2858 (19.4%) | 2713 (96.6%) | 0 | 27 (<0.1%) | 0 | |
| CD8+ - 6301 | 0 | 6174 (42%) | 0 | 5843 (96.5%) | 32 (<0.1%) | 0 | |
| myeloid - 202180 | 5 (<0.1%) | 75 (0.5%) | 0 | 0 | 199048 (95.2%) | 0 | |
| c-kit+ - 15681 | 8 (<0.1%) | 815 (5.5%) | 2 (0.1%) | 9 (<0.1%) | 1159 (0.6%) | 401 (95.9%) |
To evaluate the robustness of SPADE, numerous aspects need to be considered, including its performance with respect to clustering the cells, mapping cell clusters to phenotypically distinct cell types, and the topology of the SPADE tree that connects different cell types. A single robustness metric that simultaneously accounts for these three factors has not been established. In lieu, we qualitatively tested the robustness of SPADE. In Supplement S2, we demonstrated SPADE’s sensitivity and robustness with respect the choice of which markers to use. We started with only one marker in the analysis, and incrementally added more markers to show how the SPADE tree formed the branches shown in Figure 2. In Supplement S3, we tested SPADE under different noise levels added to the mouse bone marrow data. When the standard deviation of the added noise was small, even though parts of the SPADE tree inevitably varied, the overall topology and general interpretation were not affected.
Analysis of human hematopoiesis from mass cytometry data
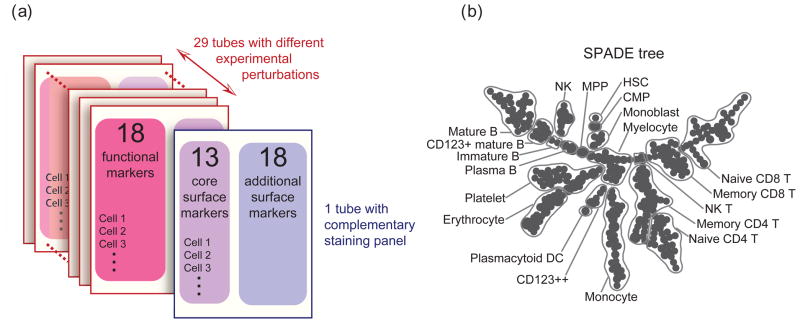
Next-generation mass cytometry technology currently provides simultaneous measurement of 31 or more markers per cell. Such a capacity allows enough surface markers to delineate nearly all cell types in human hematopoiesis, as well as additional functional markers to study cellular response to perturbations. SPADE was tested on a published mass cytometry dataset of human bone marrow from Bendall et al [14]. Single-cell data from 30 individual stimulatory conditions were obtained, as shown in Figure 3(a). In the first tube, an unstimulated aliquot of the bone marrow sample was measured with an immunophenotyping panel of 31 cell surface antibodies. The remaining 29 tubes, comprising 5 unstimulated samples and 24 samples under different perturbations, were measured by a functional staining panel of 13 core surface markers (CD3, 4, 8, 11b, 19, 20, 33, 34, 38, 45, 45RA, 90, 123, from the previous panel) and 18 intracellular targets that reflect intracellular signaling states. Bendall et al [14] demonstrated an application of SPADE on immunophenotyping without providing a detailed description and analysis of the algorithm. Here, we explain how SPADE works and how it can be extended to analyze overlapping staining panels, identify cell types, and compare multiple perturbation conditions.
Figure 3.
SPADE applied to human bone marrow dataset of 30 experiments with 2 overlapping staining panels and multiple experimental conditions. (a) Experiment and staining panel design of this human bone marrow dataset. (b) SPADE tree derived from this dataset. The SPADE tree was annotated according to the intensities of the 13 core surface markers.
SPADE was applied to extract the cellular heterogeneity underlying this high-dimensional dataset with overlapping staining panels. The 13 core surface markers were used for this analysis. Data from each tube was downsampled separately. To integrate the two staining panels, the downsampled cells of the 6 unstimulated samples were pooled (see Methods). When clustering the pooled downsampled cells, we set the desired number of clusters to be 300. The number of clusters was larger than that of the previous mouse bone marrow analysis, because the increased number of markers could capture more cell types and branch points. The resulting SPADE tree is shown in Figure 3(b). The annotations were manually derived based on the SPADE trees colored by the 13 core surface markers (see Supplement S5).
Many classically defined immune cell subsets were immediately visible in the SPADE tree (Figure 3(b) and Supplement). Multiple nodes captured the heterogeneity of abundant cell types, including B cells (CD19+), T cells (CD3+), and monocytes (CD33+). By contrast, rare cell types, such as hematopoietic stem cells (HSC), only occupied single node with high CD34 expression. The pattern of interconnectivity between these different cell types partially recapitulated established biology, as exemplified by the central positioning of the progenitor cell types, and the co-localization of multiple related T and B cell types. These results demonstrate the utility of SPADE to reduce a high-dimensional dataset to an intuitive tree diagram that reflects the relatedness of biological subsets.
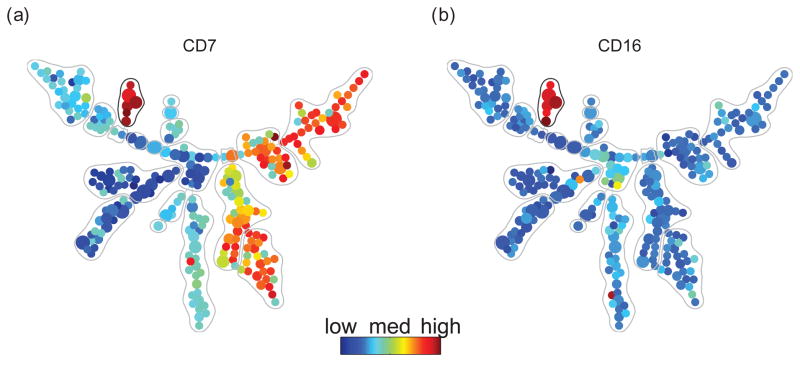
One particular group of nodes (Figure 4, gray circle) exhibited a consistent CD38+ CD45RA+ phenotype (also see Supplement S6), but the identity of this cell type was not clear based on any of the 13 core surface markers from which the SPADE tree was built. To annotate this cell type, we colored the tree with median intensities of the 18 non-core surface markers in the immunophenotyping panel that were measured in one of the six unstimulated bone marrow samples. As shown in Figure 4, the unidentified nodes were found to be positive for CD7 and CD16, markers associated with NK cells. These results indicate that SPADE clustered a biologically relevant cell type, even in the absence of markers considered to be standard immunophenotypic indicators of that cell type.
Figure 4.
SPADE tree colored by two NK specific markers CD7 and CD16, which were not used to derive the SPADE tree. The color patterns indicate that the nodes in the gray circle are NK cells. This result shows that SPADE clustered NK cells without using any NK specific markers.
Novel dynamics of intracellular markers
The SPADE tree can be used to display the dynamics of intracellular markers under different perturbations. For any combination of one intracellular marker and one perturbation, SPADE computes the ratio between the median intensities of this marker in the stimulated and unstimulated (basal) conditions for each node, and colors all of the nodes on the SPADE tree accordingly. A few examples are shown in Figure 5.
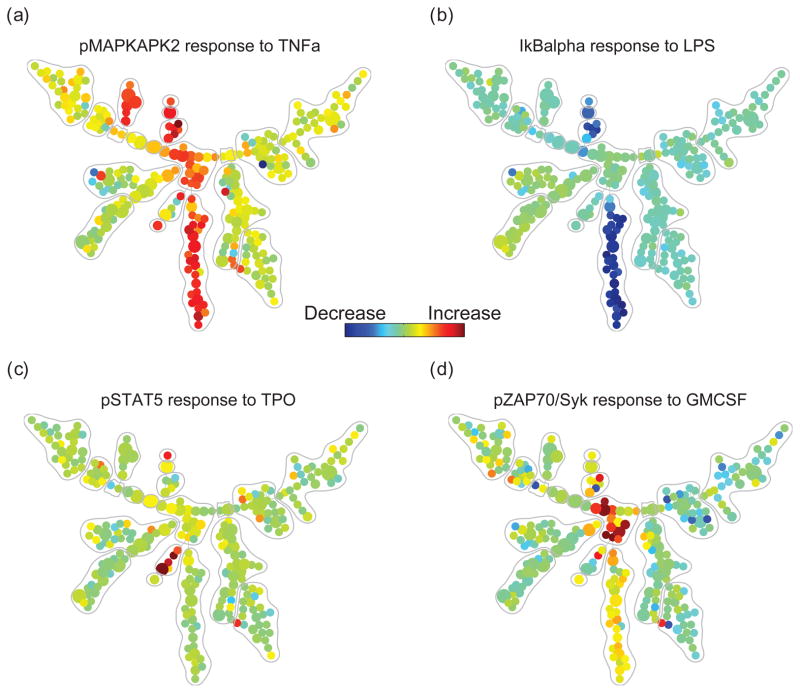
Figure 5.
SPADE tree that describes the cell-type-dependent behavior of one functional marker in response to one stimulus. (a) after stimulation with TNF, phosphorylated MAPKAPK2 was observed in myeloid and NK cell types, but not in other cell types. (b) after stimulation with LPS, degradation of total IkB was restricted to the monocytoid lineage. (c) TPO-induced phosphorylated STAT5 was observed in HSCs and CD123++, but not other cell types. (d) GM-CSF-induced phosphorylation of pSyk was observed only in myelocytes.
When colored by changes of functional markers in response to perturbations, the SPADE tree showed color patterns consistent to the annotations, meaning that the activities of the functional markers supported the annotations derived from the surface markers. Since this dataset contained measurements of 18 function markers across 24 different perturbation conditions, we could draw a total of 18*24=432 such colored trees. From these colored trees, we derived a distribution of standard deviation of functional marker activities within the annotated boundaries. By randomly permuting the tree nodes, we observed that the standard deviation of functional markers’ activities within the annotated boundaries is significantly smaller than random (two-sample student t-test p < 10–25, see Supplement S7), thus verifying the functional relevance of the boundaries defined in Figure 3(b).
From the SPADE trees colored by functional markers’ activities, we observed multiple well-established signaling functionalities that were restricted to nodes with the expected manually annotated cell phenotypes. For example, TNF induction of phosphorylated MAPKAPK2 was observed in myeloid and NK cell types (Figure 5) [18]. Similarly, the LPS-induced degradation of total IkB, an indicator of NFkB pathway activation, was restricted to cells of the monocytoid lineage, which uniquely express the receptor for LPS [19].
Such results can serve as a vehicle for data exploration and hypothesis synthesis. For example, the induction of phosphorylated STAT5 after stimulation with thrombopoietin (TPO), shown in Figure 5(c), was expected in HSCs and earlier myeloid progenitors, but not necessarily in the CD123++ population indicated in Figure 3(b). Inspection of the raw data confirmed that the presence of a rare but well-defined CD3− CD45RA− CD33mid CD38+ CD123++ population that responded to TPO through phosphorylation of STAT5 (see Supplement S8). Although this immunophenotype does not match any reported immunological population based on the markers at hand, it may be a subset of dendritic cell progenitors, which has been previously described to exhibit enhanced in vivo expansion and maturation into plasmacytoid dendritic cells when TPO is added to the traditional Flt3-containing growth media [20]. Finally, the overlay of signaling dynamics facilitated the finding of GM-CSF-induced phosphorylation of pSyk in myelocytes, as shown in Figure 5(d). Similar signaling biology has been reported in neutrophils, which are the terminally differentiated progeny of myelocytes [19], but never directly reported in the bone marrow. This analysis demonstrates how SPADE can be used to map intracellular signal activation of functional markers across the landscape of human hematopoietic development.
3 Discussions
SPADE enables the exploration of high-dimensional cytometry data in an objective manner that is scalable with increasing cellular parameters. More importantly, SPADE helps investigators infer likely cellular progressions and hierarchies. This can facilitate new biological discoveries, including the identification of unexpected signaling behaviors or the identification of rare cell types. We applied SPADE to a mouse bone marrow flow cytometry dataset and a human bone marrow mass cytometry dataset. In both datasets, SPADE was able to recover a hierarchy that resembled known biology. In addition, we demonstrated that SPADE could be used to identify functionally distinct cell types, and compare functional markers in response to perturbations.
The SPADE algorithm consists of four components: (i) density-dependent downsampling, (ii) clustering, (iii) linking clusters with a minimum spanning tree, and (iv) upsampling to restore all cells in the final result. This modularized process allows more efficient sub-algorithms to replace the current components. In this sense, SPADE can be viewed as a new framework for cytometric data analysis and visualization that has the capacity to be evolved and adapted.
Algorithmically, SPADE is complementary to, and offers certain advantages over, traditional methods for analyzing cytometric data. Firstly, SPADE does not require the user to impose a predefined hierarchical ordering of the cells using prior knowledge. Secondly, SPADE is suited for identifying rare cell types. SPADE employs a density-dependent downsampling scheme, which prevents the abundant cell types from dominating the statistics of the subsequent analysis. Finally, SPADE produces an easily visualized branching tree structure that in part recapitulates the branched cellular hierarchy that links related cell types. The resulting tree structure can be colored to display how surface and functional markers behave across the entire heterogeneous cell population.
The utility of SPADE is perhaps most limited by the choice of markers that are measured in the experiment and the subset of those that are used for building the SPADE tree. For instance, if the tree structure is built with a marker set that is not related to cellular progression, one might not expect to recover the known lineage relationships. In prior work on gene expression data analysis [21], we presented a potential approach for computationally selecting meaningful markers. Using a concept termed “progression similarity”, we identified subsets of genes that are concordant with a common hierarchical structure. As more markers can be measured on individual cells, this idea can be extended to cytometric data, as a means to select protein markers that support a common cellular hierarchy. In this manner, the utility of SPADE has the potential to increase as the number of markers per single cell increases. A focus of SPADE is to automatically produce intuitive representations of high-dimensional single-cell data that serve as an exploratory tool for analysis.
In summary, SPADE is a novel analytical approach for analyzing high-dimensional point clouds. It was tailored for cytometric data in this analysis, but it is broadly applicable to a variety of biological and non-biological datasets. We have implemented SPADE in Matlab, and made it available on the Nature Biotechnology website.
Methods
Flow Cytometry Analysis of Mouse Bone Marrow
Bone marrow was collected from the femurs and tibia of 6–10 week old C57BL/6 mice. Cells were stained for 30 minutes at 4C in FACS buffer (PBS + 0.5% BSA + 0.02% NaN3). The following markers were used in staining: c-kit, Sca-1, CD150, CD11b, B220, TCRβ, CD4, and CD8. Data was collected using the Becton-Dickinson LSR2 flow cytometer, and transformed using inverse hyperbolic sine transformation [22]. One initial gate was applied based on forward and side scatters to exclude doublets and debris.
Mass Cytometry Analysis of Human Bone Marrow
Next-generation mass cytometry data was obtained from Bendall et al, 2011 [14]. Briefly, fresh adult whole human bone marrow (BM) was stimulated using 24 unique perturbation conditions, fixed with paraformaldehyde, stained for surface markers, washed, permeabilized with methanol, stained for intracellular markers, washed, stained with an iridium-tagged DNA intercalator, and then measured on the CyTOFTM mass cytometer.
Overview of SPADE (Spanning-tree Progression Analysis of Density-normalized Events)
SPADE is performed in four steps: (i) density-dependent downsampling to equalize the density in the point cloud of cells, (ii) agglomerative clustering to partition the point cloud of cells into cell clusters, (iii) minimum spanning tree construction to link the cell clusters, and (iv) upsampling to map all the cells onto the resulting tree structure. A detailed description of each step follows:
(i) Density-dependent downsampling
SPADE views a cytometry dataset as a high-dimensional point cloud, where each point in the cloud is one cell and the dimension of the cloud is the number of cellular markers. Dense regions of the cloud correspond to abundant cell types, while low-density regions correspond to rare cell types or cells in transition between abundant cell types. Most existing clustering algorithms rely on the density variation to identify abundant cell types [6, 7, 8, 9, 10, 12]. In contrast, SPADE downsamples the data in a density-dependent fashion to remove the density variation.
SPADE estimates the local density (LDi) for cell i, defined as the number of cells within its neighborhood. We use L1 distance metric to compute the distance between cells. The size of the neighborhood is chosen such that most cells have at least one neighbor (see pseudo-code in Supplement S9). According to the target density (TD) and outlier density (OD), SPADE keeps each cell i with the following probability:
| prob(keepcelli)={0,ifLDi≤OD1,ifOD<LDi≤TDTD/LDi,ifLDi>TD | (1) |
|---|
Thus, cells whose local densities are below OD are discarded. Cells whose local densities are between OD and TD are not downsampled. Cells in high-density regions are heavily downsampled such that their local densities reduce to TD. The target density can be defined by the local density of the rare cell types of interest. In the simulated data in Figure 1, we chose OD and TD to be the 1st and 3rd percentiles of the local densities of all the cells. SPADE downsampled the dataset from 20,000 cells to ~4000 cells. Although the size of the data was significantly reduced, most cells of the rare cell type remained after downsampling, and the shape of the point cloud was preserved.
The purpose of density-dependent downsampling is to increase the prevalence of rare cells, so that SPADE is able to identify them in the subsequent clustering and tree construction steps. However, downsampling also increases the prevalence of non-specific noise events whose local densities are higher than OD. This is a trade-off between signal and noise.
(ii) Agglomerative clustering
SPADE employs a variant of agglomerative hierarchical clustering algorithm. At the beginning of the first iteration of the agglomerative process, each cell forms its own cluster. One cell is randomly chosen and grouped with its nearest neighbor, defined by single linkage L1 distance. Then, another cell is randomly chosen from the remaining cells and grouped with its nearest neighbor, if the nearest neighbor has not already been grouped with other cells in the current iteration. After all the cells are examined (i.e. either chosen or grouped with other cells), the first iteration ends and the number of clusters is reduced by approximately half. The same procedure is repeated in the second iteration to further reduce the number of clusters by approximately half. The iterative process continues until the number of remaining clusters reaches a user-defined threshold. Clustering simplifies the point cloud, distilling it into abutting cell clusters that span the full space occupied by the original cloud. The scale of the simplification can be controlled by adjusting the desired number of clusters.
(iii) Minimum spanning tree construction
SPADE uses Boruvka’s algorithm [23] to construct a minimum spanning tree (MST) that links the cell clusters. Each cell cluster is one tree node, and is represented by its median marker expressions. Briefly, we start from a graph with no edges, and iteratively add edges. In each iteration, we randomly select one connected subgraph, calculate its single linkage L1 distances to all nodes outside the randomly selected subgraph, and add an edge that corresponds to the smallest single linkage distance. This process iterates until all nodes are connected. Since the MST tends to connect clusters that are close to each other to achieve the minimum total edge length, the resulting tree approximates the shape of the point cloud.
(iv) Upsampling
To calculate the median intensity and other statistics of each cluster with high accuracy, SPADE performs upsampling by assigning each cell in the original dataset to one cluster. For each cell in the original dataset, SPADE finds its nearest neighbor in the downsampled data (subset of data used in clustering), and assigns this cell to the cluster that the nearest neighbor belongs to.
Visualization of the SPADE Tree
SPADE produces the topology of a tree structure. When visualizing the SPADE tree, we can arbitrarily rotate the layout, alter the angels between branches, or change the length of the edges. These operations change the appearance of the SPADE tree. However, as long as the topology is not changed, it still represents the same result. To automatically determine a layout of the SPADE tree, we used a modification of the Fruchterman and Reingold algorithm [15]. The layout algorithm works as follows: we first find the longest path in the tree, and fix nodes in the longest path on an arch-like curve. The rest of tree nodes are gradually appended to the main arch. When a new node and a new edge are appended to the set of nodes that are already visualized, the position of the new node is determined by simulating (i) a repelling force between each existing node and the new node, and (ii) an attracting force generated by the new edge. The simulated physics system is the reason why smaller branches are oriented pointing outwards from the main arch.
Annotation and Interpretation of the SPADE Tree
After visualizing the SPADE tree and overlaying colors on the tree nodes, we derive annotations manually, according to the colored trees. The boundaries are manually drawn to separate regions that show drastically different colors. Gating and prior knowledge are not used to draw the boundaries. Prior knowledge is used to interpret the biological relevance of each tree region. Although the annotation of the SPADE tree involves certain level of subjective interpretation, we believe that SPADE is less subjective than gating, because the interpretation is guided by the SPADE tree, which encodes an objectively derived topology among all cell types underlying the data. In contrast, gating analysis is entirely guided by user’s prior knowledge, and each gating plot only displays a 2D subset of the data where even the order that cell populations are gated in can drastically affect the endpoint subsets. SPADE “sees” all the dimensionality that even multiple 2D gating plots miss.
Parameter Selection for SPADE Analysis
The input parameters of SPADE include: markers used to build the SPADE tree, outlier density, target density, and desired number of clusters. The main tuning parameters are the markers to use and the desired number of clusters. In the following, we provide a detailed description of these parameters.
- Choice of markers used in SPADE relies on the user’s prior knowledge of which markers can be used to organize the cellular heterogeneity underlying the data. This input is important because the shape of the cell cloud may be different when different sets of markers are used (see Supplement S2). Due to the correlation among protein markers, as long as the majority of selected markers are meaningful, SPADE is robust to exclusion of a few meaningful markers or inclusion of irrelevant ones. In the human bone marrow analysis, even when NK-specific markers were not used, SPADE clustered the NK cells together (see Figure 4). In this dataset, CD90 did not provide an informative signal but was among the 13 surface markers used by SPADE, and SPADE still produced a meaningful tree.
- Outlier density is used to exclude cells with the lowest local densities. If it is set to the 1st percentile of local densities of all the cells, the bottom 1% of cells with lowest local densities are regarded as noise and discarded. NOTE that such choice does not necessarily mean that rare stem cells (i.e. 0.2% of the population) will be discarded. If the stem cells are similar to each other and form a “clique”, their local densities could be much higher than cells that represent noise. In all our current analyses, we choose outlier density to be the 1st percentile of the local densities.
- Target density determines how many cells will survive the downsampling process. The choice depends, in part, on the density of the rare population that the user aims to detect. Another purpose of this parameter is to reduce the number of cells, so that the subsequent clustering step is computationally more tractable. Ideally, we would like to set the target density comparable to the local density of the rare cells. However, when there is no prior knowledge of which cells are the rare cells, it is difficult to optimize the value of the target density. In the mouse bone marrow analysis, the choice of 5th percentile was empirical. In the human bone marrow analysis, since we were pooling multiple datasets and we wanted different datasets to contribute equal number of cells, we varied the target density such that a fixed number of 20,000 cells would survive the downsampling step for each dataset. For most of our current analyses, we choose the target density to produce 20,000 cells after downsampling.
- The desired number of clusters determines the stopping criterion of the agglomerative clustering process and the number of nodes in the SPADE tree. If the number of clusters is too small, the SPADE tree cannot correctly capture the shape of the cloud. If this number is too large, the SPADE tree is not easily interpretable. The choice of this parameter depends on the complexity of the shape of the cloud. We suggest to set this parameter much larger than the number of expected subpopulations in the data. In the mouse and human bone marrow analysis, if we double this parameter, roughly every tree node will be split into two, and the general topology of the resulting tree will remain the same. In our current practice, the desired number of clusters is usually set to be 50, 100 or 300.
SPADE for Comparing Multiple Datasets
SPADE can be used to compare multiple experiments, with overlapping staining panels. After separately downsampling the data from each individual experiment, we can pool the downsampled data into a meta-downsampled dataset, which is a meta-cloud that represents where a cell may be in the high-dimensional space defined by the markers that are common across the experiments, i.e. the 13 core surface markers in the human bone marrow dataset. The SPADE tree represents the shape of the meta-cloud. By coloring the tree using the common markers, we can annotate the tree and sketch out the phenotypic landscape of the meta-cloud. For a marker that varies across experiments, its behavior can be visualized by contrasting its intensities across different experiments. Furthermore, cells in one experiment may not populate the entire meta-cloud. We can color the tree using the change of cell frequencies between difference experiments, which allows us to observe whether any phenotypes emerge or disappear in response to perturbations.
Supplementary Material
1
2
3
4
5
Acknowledgments
The authors gratefully acknowledge funding from NCI Integrative Cancer Biology Program (ICBP), grants U56CA112973 and U54CA149145 to SP. A Damon Runyon Cancer Research Foundation Fellowship supports SCB. NSF Graduate Research Fellowship and Stanford DARE Fellowship support KG. This work is also supported by NIH grants U19 AI057229, P01 CA034233, HHSN272200700038C, 1R01CA130826, 5U54 CA143907, RB2-01592, PN2EY018228, N01-HV-00242, HEALTH.2010.1.2-1 (European Commission), as well as California Institute for Regenerative Medicine (DR1-01477) to G.P.N.
Footnotes
Note: Supplementary information is available on the Nature Biotechnology website.
Author Contributions
P.Q., G.P.N. and S.K.P. conceived the study and developed the method. E.F.S., S.C.B. and K.D.G. performed mass and flow cytometry experiments, and participated in the biological interpretation. P.Q., R.V.B., M.D.L. and K.S. performed robustness and sensitivity analysis of the method. P.Q., E.F.S., S.C.B., K.D.G., G.P.N. and S.K.P. wrote the manuscript and developed the figures.
References
- 1.Chattopadhyay P, Price D, Harper T, Betts M, Yu J, Gostick E, Perfetto S, Goepfert P, Koup R, De Rosa S, Bruchez M, Roederer M. Quantum dot semiconductor nanocrystals for immunophenotyping by polychromatic flow cytometry. Nature Medicine. 2006;12(8):972–977. doi: 10.1038/nm1371. [DOI] [PubMed] [Google Scholar]
- 2.Bandura DR, Baranov VI, Ornatsky OI, Antonov A, Kinach R, Lou X, Pavlov S, Vorobiev S, Dick JE, Tanner SD. Mass cytometry: Technique for real time single cell multitarget immunoassay based on inductively coupled plasma time-of-flight mass spectrometry. Analytical Chemistry. 2009;81(16):6813–6822. doi: 10.1021/ac901049w. [DOI] [PubMed] [Google Scholar]
- 3.Herzenberg L, Tung J, Moore W, Herzenberg L, Parks D. Interpreting flow cytometry data: a guide for the perplexed. Nat Immunol. 2006;7(7):681–685. doi: 10.1038/ni0706-681. [DOI] [PubMed] [Google Scholar]
- 4.Ellis B, Haaland P, Hahne F, Le Meur N, Gopalakrishnan N. R package version 1.10.0. Flowcore: basic structures for flow cytometry data. [Google Scholar]
- 5.Murphy RF. Automated identification of subpopulations in flow cytometric list mode data using cluster analysis. Cytometry. 1985;6(4):302–309. doi: 10.1002/cyto.990060405. [DOI] [PubMed] [Google Scholar]
- 6.Lo K, Brinkman R, Gottardo R. Automated gating of flow cytometry data via robust model-based clustering. Cytometry A. 2008;73(4):321–332. doi: 10.1002/cyto.a.20531. [DOI] [PubMed] [Google Scholar]
- 7.Boedigheimer M, Ferbas J. Mixture modeling approach to flow cytometry data. Cytometry A. 2008;73(5):421–429. doi: 10.1002/cyto.a.20553. [DOI] [PubMed] [Google Scholar]
- 8.Chan C, Feng F, Ottinger J, Foster D, West M, Kepler T. Statistical mixture modeling for cell subtype identification in flow cytometry. Cytometry A. 2008;73(8):693–701. doi: 10.1002/cyto.a.20583. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Walther G, Zimmerman N, Moore W, Parks D, Meehan S, Belitskaya I, Pan J, Herzenberg L. Automatic clustering of flow cytometry data with density-based merging. Advances in Bioinformatics. 2009 doi: 10.1155/2009/686759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Pyne S, Hu X, Kang K, Rossin E, Lin T, Maier L, Baecher-Allan C, McLachlan G, Tamayo P, Hafler D, De Jager P, Mesirov J. Automated high-dimensional flow cytometric data anlysis. PNAS. 2009;106(21):8519–8524. doi: 10.1073/pnas.0903028106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.van Lochem EG, van der Velden VHJ, Wind HK, te Marvelde JG, Westerdaal NAC, van Dongen JJM. Immunophenotypic differentiation patterns of normal hematopoiesis in human bone marrow: Reference patterns for age-related changes and disease-induced shifts. Cytometry B. 2004;60(1):1–13. doi: 10.1002/cyto.b.20008. [DOI] [PubMed] [Google Scholar]
- 12.Zare H, Shooshtari P, Gupta A, Brinkman R. Data reduction for spectral clustering to analyze high throughput flow cytometry data. BMC Bioinformatics. 2010;11(1):403. doi: 10.1186/1471-2105-11-403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bagwell BC. Probability state models. 7653509. US Patent. 2010 Jan;
- 14.Bendall SC, Simonds EF, Qiu P, Amir ED, Krutzik PO, Finck R, Bruggner RV, Melamed R, Ornatsky OI, Balderas RS, Plevritis SK, Sachs K, Pe’er D, Tanner SD, Nolan GP. Single cell mass cytometry of differential immune and drug responses across the human hematopoietic continuum. Science. 2011;332(6030):687–696. doi: 10.1126/science.1198704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fruchterman T, Reingold E. Graph drawing by force-directed placement. Softw Exp Pract. 1991;21:1129–1164. [Google Scholar]
- 16.Bryder D, Rossi D, Weissman IL. Hematopoietic stem cells: The paradigmatic tissuespecific stem cell. Am J Pathol. 2006;169(2):338–346. doi: 10.2353/ajpath.2006.060312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chao MP, Seita J, Weissman IL. Establishment of a normal hematopoietic and leukemia stem cell hierarchy. Cold Spring Harb Symp Quant Biol. 2008;73:439–449. doi: 10.1101/sqb.2008.73.031. [DOI] [PubMed] [Google Scholar]
- 18.Ashwell JD. The many paths to p38 mitogen-activated protein kinase activation in the immune system. Nature Reviews Immunology. 2006;6(7):532–540. doi: 10.1038/nri1865. [DOI] [PubMed] [Google Scholar]
- 19.Guha M, Mackman N. Lps induction of gene expression in human monocytes. Cellular Signalling. 2001;13(2):85–94. doi: 10.1016/s0898-6568(00)00149-2. [DOI] [PubMed] [Google Scholar]
- 20.Chen W, Antonenko S, Sederstrom JM, Liang X, Chan AS, Kanzler H, Blom B, Blazar BR, Liu YJ. Thrombopoietin cooperates with flt3-ligand in the generation of plasmacytoid dendritic cell precursors from human hematopoietic progenitors. Blood. 2004;103(7):2547–2553. doi: 10.1182/blood-2003-09-3058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Qiu P, Gentles AJ, Plevritis SK. Discovering biological progression underlying microarray samples. PLoS Computational Biology. 2011;7(4):e1001123. doi: 10.1371/journal.pcbi.1001123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kotecha N, Krutzik PO, Irish JM. Web-based analysis and publication of flow cytometry experiments. Current Protocols in Cytometry. 2010;Chapter 10:t10–17. doi: 10.1002/0471142956.cy1017s53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Pettie S, Ramach V. An optimal minimum spanning tree algorithm. Journal of the ACM. 1999;49:49–60. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
1
2
3
4
5