Mobility of Nonsticky Nanoparticles in Polymer Liquids (original) (raw)
. Author manuscript; available in PMC: 2012 Oct 11.
Published in final edited form as: Macromolecules. 2011 Sep 13;44(19):7853–7863. doi: 10.1021/ma201583q
Abstract
We use scaling theory to derive the time dependence of the mean-square displacement 〈Δ_r_2〉 of a spherical probe particle of size d experiencing thermal motion in polymer solutions and melts. Particles with size smaller than solution correlation length ξ undergo ordinary diffusion (〈Δ_r_2 (t)〉 ~ t) with diffusion coefficient similar to that in pure solvent. The motion of particles of intermediate size (ξ < d_ < _a_), where _a_ is the tube diameter for entangled polymer liquids, is sub-diffusive (〈Δ_r_2 (_t_)〉 ~ _t_1/2) at short time scales since their motion is affected by sub-sections of polymer chains. At long time scales the motion of these particles is diffusive and their diffusion coefficient is determined by the effective viscosity of a polymer liquid with chains of size comparable to the particle diameter _d_. The motion of particles larger than the tube diameter _a_ at time scales shorter than the relaxation time τ_e_ of an entanglement strand is similar to the motion of particles of intermediate size. At longer time scales (_t_ > τ_e) large particles (d > a) are trapped by entanglement mesh and to move further they have to wait for the surrounding polymer chains to relax at the reptation time scale τrep. At longer times t > τrep, the motion of such large particles (d > a) is diffusive with diffusion coefficient determined by the bulk viscosity of the entangled polymer liquids. Our predictions are in agreement with the results of experiments and computer simulations.
1 Introduction
Microrheology provides an important class of techniques for probing local dynamics of complex fluids,1 such as polymer solutions2,3 and melts,4–6 bio-macromolecular solutions,7–9 cells,10 and colloid suspensions11 by monitoring the motion of probe particles using diffusing wave spectroscopy,12 dynamic light scattering,11 laser deflection particle tracking,13 fluorescence correlation spectroscopy,14 or atomic force microscopy.15 These techniques are based on monitoring the time dependence of the mean-square displacement of probe objects, typically spherical particles, and relating the characteristics of particle motion to viscoelastic properties of surrounding environments by using the generalized Stokes-Einstein relation.16,17 Depending on the driving force exerted on probe particles, microrheology can be broadly classified as active or passive. Probe particles in active microrheology are driven by external forces, typically of magnetic18 or optical origin;19 while in the case of passive microrheology probe particles are undergoing thermal motion. Besides the ability to probe bulk rheological properties, microrheology can also probe local inhomogeneities of matrix materials.
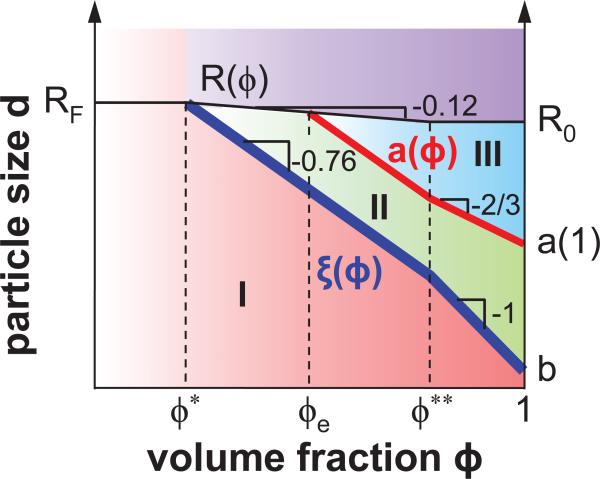
In this paper we present a theoretical description of the thermal motion (related to passive microrheology) of spherical probe particles of size d in polymer liquids (solutions and melts). We assume that there is no adsorption of polymers onto probe particles and no interaction between probe particles. Mobility of particles in polymer liquids depends on the relative particle size with respect to two important length scales. The first one is the correlation length ξ, defined as the average distance from a monomer on one chain to the nearest monomer on another chain.20 This length is on the order of polymer size at the overlap concentration (ϕ*) and decreases as a power of concentration (volume fraction) ϕ (thick line in Figure 1):
where b is the length of the Kuhn segment and v is the Flory exponent that depends on the solvent quality. The correlation length in a theta solvent (with v = 1/2) decreases with concentration as ξ ≃ _bϕ_−1, while in an athermal solvent (v = 0.588) the correlation length decreases as ξ ≃ _bϕ_−0.76. The second important length scale is the entanglement length (tube diameter) a,20–22 which is typically a factor of 5 larger than the correlation length ξ and is proportional to ξ in athermal solvent (medium line in Figure 1)
| a(ϕ)≃a(1)ϕ−ν∕(3ν−1)∼ϕ−0.76∼ξ, | (2) |
|---|
but has a different concentration dependence in a theta solvent20
| a≃a(1)ϕ−2∕3,for theta solvent | (3) |
|---|
Here a(1) is the tube diameter in polymer melt with a typical value a(1) ≃ 5 nm. The size of a polymer chain of N Kuhn segments
| R≃bN1∕2ϕ−(2ν−1)∕(6ν−2),forϕ∗<ϕ<ϕ∗∗ | (4) |
|---|
is independent of volume fraction ϕ for theta solvent (v = 1/2) and has a very weak concentration dependence in athermal (or good) solvent (v = 0.588) (see thin line in Figure 1): R ≃ _bN_1/2_ϕ_−0.12. Here ϕ** is the crossover concentration between semidilute solution regime with partially swollen chains and the concentrated solution regime with ideal chain statistics.20
Figure 1.
(Color online) Three regimes for mobility of probe particles with size d in polymer solution with volume fraction ϕ shown in the (ϕ,d) parameter space: regime I for small particles (b < _d_ < ξ), regime II for intermediate particles (ξ < _d_ < _a_), and regime III for large particles (_d_ > a). Solid lines represent the crossover boundaries between different regimes. Thick and intermediate lines correspond to the dependences of correlation length ξ and tube diameter a in good solvent on volume fraction ϕ, while thin (top) line describes concentration dependence of polymer size R(ϕ). RF is the chain size in dilute polymer solution in a good solvent and _R_0 corresponds to the chain size in a polymer melt. Dashed lines represent crossovers between regimes of polymer solution at different concentrations: (1) the dilute solution regime with 0 < ϕ < ϕ*, where ϕ* is polymer overlap concentration; (2) the semidilute unentangled solution regime with ϕ* < ϕ < ϕe, where ϕe is the concentration at which polymers start to entangle with each other; (3) the semidilute entangled solution regime with ϕe < ϕ < ϕ**; (4) the concentrated entangled solution regime with ϕ** < ϕ < 1.20 Logarithmic scales.
Considerable theoretical effort23–33 (see ref. 34 for a summary) has been devoted to describe the diffusion of spherical particles in polymer solutions. These works can be divided into two broad classes according to the physical concepts applied. The first class of theories is based on the hydrodynamic interactions between particles and polymers.23,28 In dilute polymer solutions chains with size R smaller than the particle size are considered as “hard spheres” with size equal to their hydrodynamic radii.28 Particles diffusing in dilute polymer solutions experience the hydrodynamic interaction with these effective hard spheres. Semidilute polymer solutions are modeled as a hydrodynamic medium in which polymers are treated as a background of fixed friction centers of monomer beads.23 The hydrodynamic drag between moving spherical probe particles and fixed monomer beads is assumed to be screened at length scale of solution correlation length.35 The effects of depletion of polymers near the surface of spherical particles on particle diffusion are considered in refs. 25–27. All of these theories23–27 do not take into account the relaxation of polymer matrix and predict a stretched exponential dependence of terminal particle diffusion coefficient (at long time scales) on particle size and solution concentration (see section 3.2 for the discussion). By contrast in the present work we argue that the particle mobility is determined by the dynamics of polymers and terminal particle diffusion coefficient scales as a power law of the particle size and solution concentration.
The second class of theories is based on the concept of “obstruction effect”,29–33 in which the polymer solutions are treated as a “porous” system with “pore size” characterized by the distribution of distances from an arbitrary point in the system to the nearest polymer. This distribution is obtained from a geometric consideration for a suspension of random rigid fibers.29 The diffusion coefficient of particles is assumed to be linearly proportional to the fraction of “pores” in the polymer solutions with size larger than that of probe particles. This linear assumption fails, however, when polymers overlap at high concentration as the probe particles cannot diffuse through “pores” with size smaller than the particle size. An important difference between rigid fibers and flexible polymers is that polymers are coil-like. Therefore, the concentration dependence of “pore” size in coil-like polymer solutions is different from that in solution of rigid fibers. Furthermore, polymers are mobile and therefore particles with size larger than the spacing between “obstacles” (correlation length of polymer solutions) are not permanently hindered by such “obstacles”. The mobility of such particles is determined by the polymer dynamics.
The scaling theory for mobility of probe particles of different shapes in polymer melt has been developed by Brochard-Wyart and de Gennes.36 We extend the ideas of ref. 36, in which only the terminal diffusion coefficient (at long time scales) of probe particles in polymer melt is discussed, to describe the mobility of spherical particles in polymer liquids over a wide range of concentration and time scales. In section 2 we present our prediction for the mean-square displacement of probe particles of various sizes in polymer liquids at different time scales. We show that there are three regimes depending on the particle size: 1) mobility of small particles (d < ξ) is not much affected by the surrounding polymers, 2) motion of intermediate size particles (ξ < _d_ < _a_) is coupled to segmental motion of the polymers, and 3) large particles (_d_ > a) are affected by entanglements. The contribution of hopping diffusion to the mobility of large particles (d > a) trapped in entanglement cages is not taken into account in this paper and will be discussed in a future publication.37 Section 3 deals with the dependencies of particle diffusion coefficient on solution concentration, particle size, and polymer molecular weight and these predictions are compared with existing experimental and simulation data as well as prior theoretical models. Concluding remarks and future research directions of investigations are discussed in section 4.
2 Mean-square Displacement
2.1 Small Particles (d < ξ)
If the diameter d of a probe particle is smaller than the solution correlation length ξ (see regime I in Figure 1), the motion of the particle is not much affected by polymers and is very similar to particle diffusion in a pure solvent. Mean-square displacement of particles (see dash-dotted line in Figure 2) in this regime is
Here τ0 ≃ η_sb_3/(kBT) is the monomer relaxation time, in which kB is Boltzmann constant and T is absolute temperature. The particle diffusion coefficient is determined by solvent viscosity η_s_ and is reciprocally proportional to the particle diameter d
Particle diffusion coefficient decreases by a factor on the order of two with respect to its value Ds in pure solvent as the solution concentration crosses from regime I to regime II, in which the solution correlation length ξ becomes smaller than the particle size d. Here and below we drop all numerical coefficients and keep our analysis at the scaling level.
Figure 2.
Time dependence of the product of mean-square displacement 〈Δ_r_2(t)〉 and the particle size d for small particles (b < d_ < ξ , dash-dotted line), intermediate size particles (ξ < _d_ < _a_, dashed line), and large particles (_d_ > a, solid line) in polymer solutions (ξ ≃ b in polymer melts). Here τ0 is the relaxation time of a monomer, τξ (eq. 7) is the relaxation time of a correlation blob, τ_d (eq. 11) is the relaxation time of a polymer segment with size comparable to particle size d, τ_e_ (eq. 14) is the relaxation time of an entanglement strand, and τrep (eq. 17) is the relaxation (reptation) time of a whole polymer chain. Logarithmic scales.
2.2 Intermediate Size Particles (ξ < d < a)
Motion of particles of size larger than the correlation length ξ (in polymer melt ξ ≃ b) but smaller than the tube diameter a (see regime II in Figure 1) is not affected by chain entanglements, but is affected by polymer dynamics. There are three regimes for the mean-square displacement of these intermediate size particles at different time scales. At short time scales the motion of such particles is diffusive (see eq. 5 and left part of the dashed line in Figure 2) as particles “feel” local solution viscosity comparable to that of solvent. This diffusive regime continues up to the time scale
| τξ≃ηsξ3∕(kBT)≃τ0(ξ∕b)3 | (7) |
|---|
which corresponds to the relaxation time of a correlation blob with size ξ. At time t longer than τξ the motion of intermediate size particles is sub-diffusive as it is coupled to the fluctuation modes of the polymer solution. The polymer mode with relaxation time t involves the motion of a section of the chain containing (t/τξ)1/2 correlation blobs (see Chapter 8 in ref. 20). The effective viscosity “felt” by particles at time scale t is the viscosity of a solution with polymers of size equal to the chain section size ξ(t/τξ)1/4. This effective viscosity is higher than the solvent viscosity by the factor on the order of the number of correlation blobs in the corresponding chain section
| ηeff(t)≃ηs(t∕τξ)1∕2,forτξ<t<τd | (8) |
|---|
The effective diffusion coefficient of these particles decreases with time as
| Deff(t)≃kBt∕(ηeff(t)d)≃Ds(t∕τξ)−1∕2,forτξ<t<τd | (9) |
|---|
and the mean-square displacement of the particle is proportional to the square root of time
| 〈Δr2(t)〉≃Deff(t)t≃Ds(τξt)1∕2,forτξ<t<τd | (10) |
|---|
This sub-diffusive regime (see the middle part of the dashed line in Figure 2) continues until the time scale τ_d_ at which the size of chain sections controlling viscosity is comparable with the particle size ξ(τ_d_/τξ)1/4 ≃ d.
At longer times (t > τ_d_) the motion of intermadiate size particles is diffusive (〈_r_2 (t)〉 ≃ Dtt) with a terminal diffusion coefficient (see the right part of the dashed line in Figure 2)
| Dt≃kBTηeff(τd)d≃kBTξ2ηsd3,fort>τd | (12) |
|---|
where we used equations 8 and 11 for ηeff and τ_d_. Note that the mean-square displacement of particles at the onset of this terminal Brownian diffusion (at time τ_d_) is ξ_d_ (dashed line in Figure 2), and the diffusion coefficient is proportional to the square of the correlation length and inversely proportional to the cube of the particle size (see eq. 12). The reason for this extra factor of (ξ/d)2 in the diffusion coefficient (eq. 12) is that the effective viscosity “felt” by the particles at long times is proportional to the number of correlation blobs in a chain section with size on the order of particle diameter,
| ηeff≃ηs(d∕ξ)2,fort>τd | (13) |
|---|
The correlation length in polymer melts is on the order of monomer size (ξ ≃ b) and equation 13 becomes ηeff ≃ η_s_(d/b)2.36 Note that none of the above results depends on the polymer molecular weight as long as the tube diameter a and/or polymer size R is larger than the particle size d.
2.3 Large Particles (d > a)
Particles larger than the size of entanglement mesh (d > a, where a is entanglement tube diameter20–22) are trapped by the entanglements. The arrest of particle motion occurs on time scale on the order of the relaxation time of an entanglement strand:
| τe≃τξ(a∕ξ)4≃τ0(ξ∕b)3(a∕ξ)4 | (14) |
|---|
At short time scales t < τ_e_ the motion of large particles follows the same time dependence as that of intermediate ones for the first two regimes (see section 2.2). The mean-square displacement of these large particles at time scale τ_e_
depends on all three important length scales: the tube diameter a, the correlation length ξ , and the particle size d. The plateau modulus of the semidilute solution can be obtained from this mean-square displacement (eq. 9.37 in ref. 20)
| Ge≃kBT∕(〈Δr2(τe)〉d)≃kBT∕(a2ξ) | (16) |
|---|
Note that if we consider the polymer solution as a “melt” of correlation blobs, the volume occupied by an entanglement strand is ξ3(a/ξ)2 ≃ _a_2ξ, and eq. 16 is consistent with plateau modulus corresponding to thermal energy kBT per entanglement strand. We stress out that the relation (eq. 16) between solution plateau modulus and the plateau mean-square displacement of a probe particle (eq. 15) is identical (up to numerical factors on the order of unity) to the one obtained via the generalized Stokes-Einstein relation that equates the long time limit of the mean-square displacement of a particle with the zero-frequency shear modulus in an elastic solid.17 This self-consistency between a polymer-dynamics-based scaling model and the fluctuation-dissipation theorem, that makes no assumptions about microscopic dynamics, further validates the approach relating the particle mean-square displacement to rheology.
The motion of large particles at time scales longer than τ_e_ can proceed by two mechanisms. The first one is the reptation of surrounding polymers leading to the release of topological constraints at the reptation time τrep, which is proportional to the cube of the number of entanglements (N/Ne) per chain
Here Ne is the number of monomers per entanglement strand. Tube length fluctuations20 lead to even stronger dependence of reptation time on the degree of polymerization: τrep ~ _N_3.4. The second mechanism that could lead to the motion of particles is due to fluctuations of local entanglement mesh that will allow particles to pass through entanglement gates and thus hop between neighboring entanglement cages. The contribution of hopping process will be important for diffusion of particles not significantly larger (d ≳ a) than the tube diameter of entangled polymer solutions. This hopping mechanism will be discussed in a separate publication.37 Below we focus on the motion of large particles due to chain reptation.
At time scales shorter than τrep large particles (d > a) are trapped by entanglements and their mean-square displacement is on the order of _a_2ξ/d (eq. 15)
| 〈Δr2(t)〉≃a2ξ∕d,forτe<t<τrep | (18) |
|---|
The motion of particles resulting from chain reptation at longer times (t > τrep) is Brownian with diffusion coefficient determined by the bulk solution viscosity η
| 〈Δr2(t)〉rep≃kBTηdt,fort>τrep | (19) |
|---|
where the viscosity η ≃ _Ge_τrep increases as high powers of the degree of polymerization N and solution concentration.20 Eq. 19 can also be rewritten as
| 〈Δr2(t)〉rep≃(ξa2∕d)t∕τrep,fort>τrep | (20) |
|---|
Diffusion coefficient of large probe particles due to chain reptation is
| Drep≃kBT∕(ηd)≃ξa2∕(dτrep),ford>a | (21) |
|---|
2.4 Microrheology
The viscoelastic properties of polymer liquids can be determined from the time dependence of the mean-square displacements of probe particles within a wide frequency range by using generalized Stokes-Einstein relation,16,17 which relates the viscoelastic spectrum G̃(s) of polymer liquids to the Laplace transform 〈Δ_r̃_2 (s)〉 mean-square displacement 〈Δ_r_2 (t)〉:
| G~(s)=2kBTπds〈Δr~2(s)〉 | (22) |
|---|
where s is the Laplace frequency. According to the Kramers–Kronig relations, storage modulus _G_′ (ω) and loss modulus _G_″ (ω) correspond to the real and imaginary parts of complex modulus G* (ω), which is determined by substituting _i_ω for the Laplace frequency s in eq. 22.
Figure 3 shows the viscoelastic properties of polymer liquids predicted from time-dependent mean-square displacements of particles with different sizes. Small particles (d < ξ) probe solvent-like viscosity within entire frequency range (see thin line in Figure 3). Intermediate size particles (ξ < d_ < _a_) also experience solvent-like viscosity at high frequencies (1/τξ < ω < 1/τ0). However, at frequencies lower than 1/τξ they probe segmental dynamics of polymer liquids (see medium lines in Figure 3). Particles with size larger than the tube diameter (_d_ > a) are expected to probe full dynamics of the polymer liquids (thick lines in Figure 3). Similar to intermediate size particles, large particles probe solvent-like viscosity at high frequencies (1/τξ < ω < 1/τ0) and probe the segmental dynamics of polymer liquids at frequencies 1/τ_e < ω < 1/τξ. At intermediate frequencies (1/τrep < ω < 1/τ_e_) the large particles are trapped by entanglements and probe the entanglement plateau modulus (see eq. 16). At very low frequencies (ω < 1/τrep) large particles experience bulk viscosity. It is important to point out that the probe particles in microrheology must be non-sticky, so that they do not form strong physical or chemical bonds with surrounding materials.
Figure 3.
(Color online) Viscoelastic properties of polymer liquids predicted from time-dependent mean-square displacements of small particles (d < ξ, thin line), intermediate size particles (ξ < _d_ < _a_, medium lines), and large particles (_d_ > a, thick lines). Solid lines correspond to storage moduli _G_′ and dashed lines represent loss moduli _G_″ as functions of frequency ω. Logarithmic scales.
3 Particle Diffusion Coefficient
3.1 Dependence on Particle Size
In section 2 above we have discussed the time dependence of mean-square displacements of probe particles of different sizes in polymer liquids with fixed volume fraction (concentration). The mobility of particles in polymer liquids is investigated for three main cases depending on the size of probe particles: small particles (d < ξ ) (regime I in Figure 1 and section 2.1), intermediate particles (ξ < d_ < _a_) (regime II in Figure 1 and section 2.2), and large particles (_d_ > a) (regime III in Figure 1 and section 2.3). In Figure 4 we sketch the dependence of terminal diffusion coefficient Dt on particle size d. For small probe particles with size d smaller than the solution correlation length ξ the diffusion coefficient Dt follows the classical Stokes-Einstein relation (see eq. 6) and is mainly determined by the solvent viscosity η_s, as shown by the first section of the curve in Figure 4. Terminal diffusion coefficient Dt of intermediate size particles (ξ < _d_ < _a_) has a much stronger dependence on particle size (see eq. 12) because they “feel” effective viscosity that increases as square of the particle size (eq. 13), as shown by the second section of the curve in Figure 4. As long as the particle size is smaller than the tube diameter the terminal particle diffusion coefficient is independent of polymer molecular weight. The diffusion coefficient of particles with size larger than the tube diameter (_d_ > a) (regime III in Figure 1 and section 2.3) is determined by chain reptation process and particles “feel” full solution viscosity η (see eq. 21). Note that our scaling calculation suggests a sharp drop of the terminal diffusion coefficient of particles with size on the order of the tube diameter (d ≃ a) by a large factor (N/Ne)3, as shown in Figure 4. This sharp crossover is broadened (see the dotted line in Figure 4) by the contribution to particle mobility from the hopping diffusion process.37
Figure 4.
Dependence of terminal particle diffusion coefficient Dt on particle size d in entangled polymer solutions. Dotted line corresponds to the crossover taking into account the contribution of hopping process to the particle mobility. Logarithmic scales.
As mentioned in section 2.3, the mobility of particles with size d larger than the tube diameter a is due to both chain reptation and hopping processes. To hop from one entanglement cage to a neighboring one the particle has to overcome an entropic energy barrier that increases with the ratio of particle size d to the tube diameter a. Thus, the waiting time required for the hopping process increases exponentially with this ratio d/a. This waiting time, however, can still be shorter than the relaxation of time of the whole polymer system as long as the particle size is not significantly larger than the tube diameter. Therefore, the motion of particles with size slightly larger than the tube diameter will be dominated by the hopping process with diffusion coefficient decreasing exponentially with the ratio of particle size to the tube diameter as D ~ exp(−d/a),37 shown by the dotted line in Figure 4; whereas diffusion of very large particles (d ≫ a) is primarily controlled by the chain reptation process.
It is important to point out that the hopping-controlled diffusion does not probe the macroscopic viscosity of the polymer solutions. In fact this process is possible even in entangled polymer networks with infinite zero-shear-rate viscosity. The sharp crossover with exponentially strong decrease of the diffusion coefficient of particles with size d increasing above the tube diameter a is qualitatively different from the smooth crossover of the diffusion coefficient of linear probe chains from below to above the entangled molecular weight.39 As the size of the linear probe polymers crosses from below to above the tube diameter, the molecular weight dependence of the diffusion coefficient smoothly crosses from D ~ 1/N to D ~ 1/_N_2.3, which is unlike the exponentially sharp decrease expected for particles (see Figure 4). In order to understand the reason for this qualitative difference between linear chains and particle probes, consider the limiting case with very long matrix chains of entangled polymer solutions. The linear probe chains of size larger than the tube diameter can reptate out of their original tubes and diffuse without encountering any significant entropic energy barrier.40 However, particles with size several times larger than the tube diameter (d > a) is exponentially slowed down by the free energy barrier and these particles are effectively trapped by entanglement cages.
The diffusion coefficient of intermediate size particles is predicted to be inversely proportional to the cube of particle size: Dt (d) ~ _d_−3 (see eq. 12). This prediction of our model and also earlier ref. 36 has been verified by the molecular dynamics (MD) simulations of diffusion of particles with different sizes in unentangled polymer melts.46
3.2 Dependence on Solution Concentration
Experimentally it is often easier to systematically vary polymer concentration rather than the particle size. Terminal diffusion coefficient of particles of a given size d depends on the relative value of this size d with respect to two concentration-dependent length scales: the correlation length ξ(ϕ) (thick line in Figure 1) and the tube diameter a(ϕ) (medium line in Figure 1).
Mobility of probe particles with the intermediate size d larger than the monomer size b but smaller than the tube diameter a(1) of a polymer melt crosses over from regime I to regime II (see Figure 1) as solution concentration ϕ increases. The crossover solution concentration between these two regimes is
at which the correlation length ξ(ϕ_ξ_d) is on the order of particle diameter d. In a theta solvent (v = 1/2) the crossover volume fraction is ϕ_ξ_d ≃ (d/b)−1 and in an athermal solvent (v = 0.588) it is ϕ_ξ_d ≃ (d/b)−1.32. Below this volume fraction (for ϕ < ϕ_ξ_d ) the diffusion coefficient of particles is determined by the solvent viscosity η_s_ and is almost concentration independent (see eq. 6). At volume fractions above ϕ_ξ_d particles “feel” segmental motions of polymers (see eq. 9) and particle diffusion coefficient
| Dt(ϕ)≃kBTξ2ηsd3≃kBTb2ηsd3ϕ−2ν∕(3ν−1),forϕdξ<ϕ<1andb<d<a(1) | (24) |
|---|
decreases with solution volume fraction as power −2 for theta solvent and −1.52 for athermal solvent (see dashed line in Figure 5).
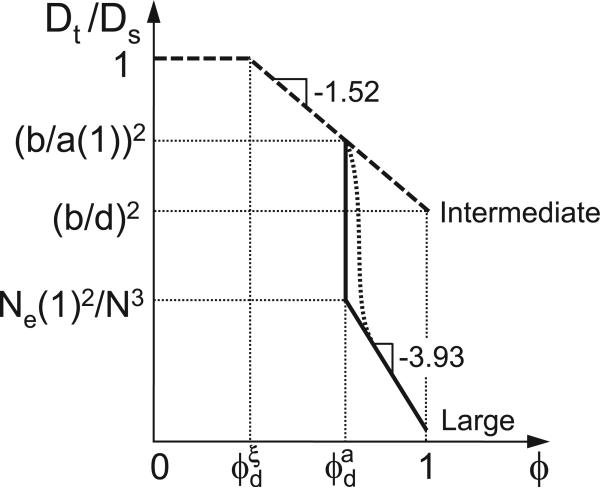
Figure 5.
Concentration dependence of terminal diffusion coefficient Dt of particles in entangled athermal polymer solutions normalized by their diffusion coefficient Ds = kBT/(η_sd_) in pure solvent (see eq. 6). Dashed line is for intermediate size particles (b < _d_ < _a_(1)) and solid line is for large particles (_d_ > a(1)). The crossover concentrations ϕ_ξ_d and ϕad, at which the correlation length ξ and the tube diameter a are on the order of particle size d, are defined in eqs. 23 and 25 respectively. Dotted line corresponds to the crossover taking into account the contribution of hopping process to the particle mobility (see discussion in section 3.1). Logarithmic scales.
If the particle size d is larger than the tube diameter a(1) in the melt, in addition to the two regimes expected for particles smaller than a(1) (see dashed line in Figure 5), there is an additional regime in which particle diffusion coefficient is determined by chain reptation. This regime begins at a solution concentration ϕad, at which the tube diameter a (see eq. 2) is on the order of the particle size d: a (ϕad) ≃ d. In a theta solvent a ≃ a(1)_ϕ_−2/3 (see eq. 3) and in an athermal solvent a ≃ a(1)_ϕ_−0.76 (see eq. 2), therefore the corresponding crossover concentrations are
| ϕda≃{(d∕a(1))−3∕2,theta(d∕a(1))−1.32,athermal} | (25) |
|---|
Large probe particles (d > a(1)) are expected to experience full solution viscosity above the crossover concentration ϕad. The terminal particle diffusion coefficient in this regime (see solid line in Figure 5) Dt (ϕ) ≃ D_rep ≃ ξ_a_2 / d_τrep is dominated by the contribution from the chain reptation process (see eq. 21). Recall the relations τ_e ≃ τ0 (ξ/b)3 (a/ξ)4 (see eq. 14) τrep ≃ τ_e (N/Ne(ϕ))3 (see eq. 17) and using eqs. 1, 2, 14, and the relation
| Ne(ϕ)≃Ne(1){ϕ−4∕3,thetaϕ−1.32,athermal} | (26) |
|---|
one can simplify eq. 21 to obtain the concentration dependence of terminal particle diffusion coefficient:
| Dt(ϕ)≃kBTηsdNe(1)2N3{ϕ−14∕3,thetaϕ−3.93,athermal}forϕda<ϕ<1andd>a(1) | (27) |
|---|
which is the reciprocal of the concentration dependence of solution viscosity η (ϕ) (eq. 9.45 in ref. 20).
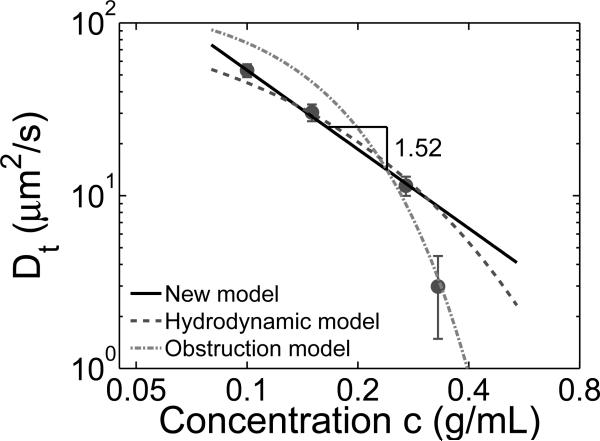
We test our scaling prediction on the concentration dependence of the diffusion coefficient of intermediate size particles (eq. 24 and Figure 5) using the data from ref. 3, in which the authors measured the diffusion coefficient of gold nanoparticles with diameter d = 5 nm in 240 kDa polystyrene/toluene (good solvent) solutions at several solution concentrations by fluctuation correlation spectroscopy. For all solution concentrations studied in ref. 3 the size of nanoparticles is larger than the solution correlation length but smaller than the tube diameter (in an entangled polystyrene melt a(1) ≃ 9 nm20), and therefore, the data points are in the intermediate particle size regime (ξ < d < a). The particle diffusion coefficients (see points in Figure 6) at low concentrations exhibit a power law dependence on concentration: Dt (c) ~ _c_−1.52±0.15, which is in good agreement with our scaling prediction (eq. 24). Note that one data point at higher concentration corresponds to lower diffusion coefficient and much larger error bar, possibly due to degradation of laser focus at such high solution concentration.41 For a good (athermal) solvent eq. 24 can be rewritten as
| Dt(c)=αDs(c∕cdξ)−1.52 | (28) |
|---|
where Ds is the particle diffusion coefficient in pure solvent, c_ξ_d (eq. 23) corresponds to the solution concentration at which the particle size d is equal to the solution correlation length ξ, and α is the scaling prefactor to be determined by fitting the scaling prediction to experimental data. The measured diffusion coefficient Ds of the 5 nm gold nanoparticles in pure solvent (toluene) is about 141μm2/s3 and the crossover concentration c_ξ_d is about 0.08 g/ml.43 The coefficient α ≃ 0.53 obtained by fitting the scaling model to the three experimental points at lower concentrations is on the order of unity confirming the consistency of the scaling estimate (eq. 28 and solid line in Figure 6).
Figure 6.
Diffusion coefficient of 5 nm gold nanoparticles in semidilute solutions of polystyrene in toluene. Solid circles are data from ref. 3 for Mw = 240 kDa polystyrene/toluene solutions above the overlap concentration. Lines are predictions of different models: solid line—our scaling model (eqs. 24 and 28 with α = 0.53), dashed line—hydrodynamic model (eq. 30 with _k_hydro = 0.96), dash-dotted line—obstruction model (eq. 31 with _k_obst = 0.43).
Earlier models23,33 predict stronger than power law concentration dependence of diffusion coefficient. The theories based on the concept of hydrodynamic interaction (hydrodynamic models)23 predict the exponential dependence of the particle diffusion coefficient on the ratio of particle size d and the solution correlation length ξ
| Dt=Dsexp(−khydrod∕ξ) | (29) |
|---|
In good solvent (eq. 1 with v = 0.588) this prediction corresponds to the stretched exponential concentration dependence of particle diffusion coefficient
| Dt(c)=Dsexp(−khydro(c∕cdξ)0.76) | (30) |
|---|
With the values of Ds = 141μm2/s and c_ξ_d = 0.08 g/ml fixed by separate experiments one can adjust parameter _k_hydro to fit this prediction (eq. 30) to experimental data. The best fit of this prediction to the three experimental points at lower concentration, shown by the dashed line in Figure 6, is qualitatively similar (slightly worse) than that of our scaling prediction.
Terminal particle diffusion coefficient predicted by the theories based on the “obstruction effect” (obstruction model)33 has an even stronger dependence on the ratio of particle size d and the correlation length ξ: Dt = Ds exp (−π((d + δ) / (ξ + δ))2 /4, where δ corresponds the effective cylindrical diameter of a polymer chain considering it as a rigid fiber. The value of δ can be estimated by δ ≃ _v_0/_b_2, where _v_0 is the Kuhn monomer volume and can be obtained from a polymer handbook.44 Typically the value of δ ~ 0.3 nm is negligible compared with both the particle size d and the correlation length ξ. Therefore, the prediction of the obstruction model can be rewritten as
| Dt(c)=Dsexp(−kobst(d∕ξ)2)=Dsexp(−kobst(c∕cdξ)1.52) | (31) |
|---|
Similar to that in hydrodynamic model the adjustable parameter _k_obst in the obstruction model is determined by fitting this prediction to the three experimental points at lower concentrations with the fixed values of Ds = 141μm2/s and c_ξ_d = 0.08 g/ml. The best fit of the data by the obstruction model, shown by the dash-dotted line in Figure 6, is qualitatively similar (slightly worse) than that of both hydrodynamic and our scaling models.
In spite of the similarities of the three fits to the experimental data at lower concentrations (Figure 6), we claim that our model is the qualitatively correct one, as it properly takes into account coupling between polymer dynamics and particle motion, which is the very basis of microrheology. Note that both hydrodynamic and obstruction models completely ignore polymer dynamics and thus are not applicable to the case of particle diffusion in polymer melts. In section Section 3.4 below we demonstrate that our scaling model describes particle diffusion both in polymer melts and polymer solutions in a consistent way by constructing a “universal” plot.
3.3 Dependence on Polymer Size
Consider the motion of probe particles of fixed size d in polymer solutions with different degrees of polymerization N but with the same concentration ϕ. Terminal diffusion coefficient of small particles with the size smaller than the correlation length is almost independent of the polymer molecular weight (dashed line in Figure 7) because these particles “feel” viscosity close to that of solvent.
Figure 7.
Dependence of the normalized terminal diffusion coefficient Dt/Ds of particles in solutions with fixed concentration on degree of polymerization N, where particle diffusion coefficient in pure solvent Ds is defined in eq. 6. Dashed line corresponds to small particles (b < _d_ < ξ), dash-dotted line corresponds to intermediate size particles (ξ < _d_ < _a_), and solid line corresponds to large particles (_d_ > a). Here _N_ξ ≃ (ξ/b)1/v is the number of monomers in a correlation volume (see eq. 32), Nd ≃ _N_ξ (d/ξ)2 is the number of monomers in a chain section on the order of intermediate particle size (see eq. 34), and Ne is the number of monomers per entanglement strand. Dotted line corresponds to the crossover taking into account the contribution of hopping process to the particle mobility (see discussion in section 3.1). Logarithmic scales.
As illustrated by the dash-dotted line in Figure 7, intermediate size particles (ξ < d < a) “feel” the viscosity close to that of solvent in dilute polymer solutions with degree of polymerization lower than _N_ξ
| Nξ≃(ξ∕b)1∕ν≃{(ξ∕b)2,theta(ξ∕b)1.76,athermal} | (32) |
|---|
The semidilute solution viscosity η increases above the solvent viscosity η_s_ linearly with degree of polymerization N: η ≃ η_s_ (N/_N_ξ). Intermediate size particles that are larger than polymers “feel” bulk solution viscosity η with terminal particle diffusion coefficient inversely proportional to the degree of polymerization N
| Dt(N)≃kBTηsd(N∕Nξ),forNξ<N<Nd | (33) |
|---|
where Nd corresponds to the degree of polymerization at which the size of polymers is comparable to the particle size d
Terminal diffusion coefficient of intermediate size particles that are smaller than polymers is independent on the degree of polymerization in solutions with N > Nd (see eq. 12)
| Dt(N)≃kBTηsd(Nd∕Nξ)≃kBTξ2ηsd3,forN>Nd | (35) |
|---|
The diffusion coefficient of large particles (d > a) is predicted to have similar molecular weight dependencies as that of intermediate size particles in dilute and in unentangled semidilute (see eq. 33) solutions. In entangled solutions large particles “feel” bulk solution viscosity at times longer than solution relaxation time (see solid line in Figure 7). The terminal particle diffusion coefficient is reciprocally proportional to the solution viscosity η and decreases with increasing degree of polymerization N as
| Dt(N)≃kBTηd∼N−3,forN>Ne | (36) |
|---|
The scaling exponent is expected to be even stronger with value of 3.4 if one takes into account tube length fluctuation.20,22
We compare our predictions for dependence of intermediate particle diffusion coefficient on molecular weight with available molecular dynamics simulation and experimental data. It is predicted that the particle diffusion coefficient DL is independent of degree of polymerization N in melts and solutions of large (L) polymers with size R larger than particles of size d (see eq. 35), whereas particles are expected to “feel” bulk viscosity in melts and solutions of short polymers (R < _d_) (see eq. 33). The ratio between diffusion coefficient _D_**S** of intermediate particles through the liquid of shorter (**S**) polymers with size _R_**S** < _d_ and degree of polymerization _N_**S** and diffusion coefficient _D_**L** of the same particles through the liquid of large polymers of size _R_**L** > d is DS/DL ≃ Nd/NS. Here Nd corresponds to the degree of polymerization at which the polymer size is on the order of the particle size. As shown in Figure 8, this prediction is verified by the simulation data from ref. 46. Diffusion coefficient of particles in polymer melts with degree of polymerization below Nd is reciprocally proportional to the degree of polymerization (see eq. 33). The diffusion coefficient DL of intermediate particles in melts with degree of polymerization N above Nd is independent of the degree of polymerization (see eq. 35 and horizontal line in Figure 8).
Figure 8.
Normalized terminal particle diffusion coefficient Dt/Ds in polymer melt. Solid circles are data from ref. 46 for diffusion of a particle with diameter d = 6σ in melts of polymers with degree of polymerization N ranging from 10 (unentangled) to 200 (entangled). Here σ corresponds to Lennard–Jones length.47Nd ≃ 24 represents the crossover degree of polymerization, below which the particle diffusion coefficient is reciprocally proportional to the degree of polymerization (see eq. 33) and above which it is independent of the degree of polymerization (see eq. 35). The root-mean-square end-to-end distance of polymer chains with degree of polymerization Nd is R ≃ √6_Rg_ ≃ 6σ, which is equal to the particle size d.
Authors of ref. 4 measured the diffusion of gold nanoparticles with diameter d ≃ 5 nm in two monodisperse poly(n-butyl methacrylate) (PBMA) melts of molecular weight 2.5 kDa and 180 kDa. The root-mean-square end-to-end distance R of 2.5 kDa PBMA chain is approximately 2.5 nm and the size of 180 kDa PBMA chain is about 21 nm as estimated based on data from refs. 4 and 45. The 5 nm gold particles are expected to experience bulk viscosity in 2.5 kDa PBMA melt but in 180 kDa melt they only “feel” effective viscosity, which is predicted by our model to be the viscosity of the PBMA melt with the chain size on the order of the particle size. It was found that the diffusion coefficient of 5 nm gold particles in 180 kDa PBMA melt is about 4 times smaller than that in 2.5 kDa PBMA melt at the same temperature above glass transition. Therefore, the 5 nm particles in 180 kDa PBMA melt probe the viscosity of an effective polymer melt with molecular weight of 10 kDa, which is 4 times higher than 2.5 kDa but 18 times lower than the actual polymer molecular weight. It turns out that the size of a 10 kDa PBMA chain in melt is about 5 nm, which is on the order of the particle size and thus verifies our prediction.
3.4 “Universal” Dependence of Diffusion Coefficient of Intermediate Size Particles
All the dependencies of diffusion coefficient of intermediate size particles described above can be combined into a single “universal” plot. To do that we define viscosity ηun,
| ηun={η(N),forN<Neη(Ne)N∕Ne,forN>Ne} | (37) |
|---|
which is the bulk viscosity η if polymer liquids are unentangled. If polymer liquids are entangled, ηun is the extrapolation of bulk viscosity from the unentangled regime, which is linearly proportional to the polymer molecular weight ηun = η (Ne)N/Ne. One can define _D_un as the naively expected particle diffusion coefficient in a polymer liquid with viscosity ηun according to classical (Stokes-Einstein) prediction:
Dependencies of terminal particle diffusion coefficient Dt on i) particle size d (eq. 12), ii) solution concentration c (eq. 24), and iii) degree of polymerization N (eqs. 33 and 35) can be rewritten in terms of the dependence of reduced diffusion coefficient Dt/_D_un on the ratio d/R of particle and polymer sizes:
| DtDun≃{(d∕R)−2,ford<R1,ford>R}forξ<d<a | (39) |
|---|
If the particle is larger than the polymer (d > R) its diffusion coefficient Dt is on the order of the classical prediction (eq. 39) where _D_un is the bulk viscosity of unentangled polymer liquid. If the particle is smaller than the polymer (d < R), the naively expected diffusion coefficient _D_un (eq. 38) with ηun—viscosity of unentangled polymer liquids (or “unentangled” extrapolation (eq. 37) for entangled polymer liquids)—underestimates the diffusion coefficient of intermediate size particles Dt by the factor (d/R)2. Below we first outline how the “universal” plot of Dt/_D_un as a function of d/R can be constructed using data from molecular dynamics simulations and experiments and then compare the resulting “universal” function with our prediction (eq. 39).
Authors of ref. 46 reported the terminal diffusion coefficient Dt of particles with size d ranging from σ to 9σ in an unentangled polymer melt with degree of polymerization N = 60, where σ is Lennard–Jones length.47 In order to construct the “universal” plot one needs to know the unentangled viscosity ηun and the polymer size R. For the unentangled polymer melt with N = 60 the unentangled viscosity ηun is equal to the bulk viscosity, which is reported to be 42.5_kBT_/σ3τ_LJ_),48 where τ_LJ_ is Lennard–Jones time.47 The diffusion coefficient _D_un is calculated using relation _D_un = kBT/(3π_dh_ηun),49 where dh = d + σ corresponds to the particle-monomer cross diameter.50 The end-to-end distance R of a linear polymer chain of degree of polymerization N > 10 in simulated melts is reported to be R = 1.22σ _N_1/2.51 Based on such information one can obtain the values of Dt/_D_un and dh/R and the results are presented by triangles in Figure 9.
Figure 9.
(Color online) Dependence of the ratio of terminal particle diffusion coefficient Dt and “unentangled” diffusion coefficient _D_un of intermediate size particles (defined by eq. 38) on the ratio of particle and polymer sizes d/R in polymer solutions and melts. Empty symbols are molecular dynamics simulation data from ref. 46 and filled circles are experimental data from ref. 3. Solid line is the prediction of our scaling model (eq. 39).
Similarly one can add to the “universal” plot the simulation data for particles of sizes d = 2σ (empty circles in Figure 9) and 6σ (empty squares in Figure 9) in melts of polymers with degree of polymerization N (from 10 to 200) ranging from unentangled to entangled regime. Within the range of N 60 the polymers are unentangled and thus the unentangled viscosity ηun is equal to the bulk melt viscosity, which is determined to be linearly proportional to degree of polymerization.48 For N > 60 the extrapolated value of ηun from the unentangled regime (eq. 38) is used to calculate _D_un. The values of Dt/_D_un and dh/R for these particles of two different sizes are calculated following the same procedure as described above.
The diffusion coefficient of 5 nm gold nanoparticles in solutions of 240 kDa polystyrene in toluene at different concentrations is reported in ref. 3. In order to add these data to the “universal” plot one can rewrite the unentangled extrapolation particle diffusion coefficient as _D_un = Ds (ξ/Rg)2, where Ds (see eq. 6) corresponds to the diffusion coefficient of a probe particle in a pure solvent. Following the procedure described in ref. 52, the concentration-dependent particle diffusion coefficients are presented by solid circles in the “universal” plot (see Figure 9). Note that all points group together because Rg is a weak function of the solution concentration.
As shown in Figure 9, all the data points for diffusion of intermediate size spherical probes in polymer liquids collapse onto a “universal” curve reasonably well. Note that the experimental point at the highest concentration (the largest value of d/R) deviates from the trend of other data points, possibly due to the error of measurements because of the degradation of laser focus at such high solution concentration.41 The “universal” curve suggests two regimes as predicted by our scaling model (eq. 39): 1) probe particles “feel” bulk viscosity if their size is larger than the polymer size, 2) particles experience local viscosity of polymer liquids, which is smaller than the unentangled viscosity ηun by a factor of (d/R)2, if their size is smaller than the polymer size and the tube diameter.
We conclude that our predictions for the mobility of intermediate size particles in polymer liquids (melts and solutions) agree with available data, but a systematic study covering a wide range of solution concentrations, polymer molecular weight, and particle sizes is needed for more systematic tests of our theory. It should be noted that our scaling calculations of particle diffusion in polymer liquids (melts and solutions) do not take into account hopping,37 the adsorption of polymer chains onto particles, and slippage at the particle-polymer interface.53
4 Conclusion
In the present paper we have developed a scaling theory for the mobility of non-sticky spherical particles in polymer liquids (solutions and melts). There are three different cases for particle diffusion in polymer liquids depending on the relation of particle size d with respect to the correlation length ξ and the tube diameter a.
(i) Small particles. Mobility of small particles (b < d < ξ ) is not strongly affected by polymers and their diffusion coefficient Ds ≃ kBT/(η_sd_) is mainly determined by the solvent viscosity η_s_.
(ii) Intermediate size particles. Motion of intermediate size particles (ξ < d_ < _a_) is not affected by entanglements. At time scales shorter than the relaxation time τξ of a correlation blob the motion of intermediate size particles is not much affected by polymers and is diffusive with diffusion coefficient mainly determined by solvent viscosity. The intermediate size particles probe modes of surrounding polymers at intermediate time scales τξ < _t_ < τ_d_, where τ_d_ is the relaxation time of a polymer segment with size comparable to particle size _d_, and therefore, the particle motion is sub-diffusive with mean-square displacement 〈Δ_r_2〉 ~ _t_1/2 (see eq. 10). At longer time scales (_t_ > τ_d) the motion of intermediate size particles is diffusive but with diffusion coefficient determined by the effective viscosity ηeff ≃ η_s_ (d/ξ )2 (see eq. 13), which is the viscosity of a polymer liquid with polymer size on the order of particle size. The effective viscosity ηeff is independent of polymer molecular weight for R > d and is only determined by the particle size and the correlation length of the polymer solution.
(iii) Large particles. Motion of particles with size larger than the entanglement length (d > a) at time scales shorter than the relaxation time τ_e_ of an entanglement strand is similar to that of intermediate size particles. At time scales longer than τ_e_ the large particles are trapped by entanglements and in order to move further they have to wait for the polymer liquid to relax during reptation time τrep. Terminal diffusion coefficient of very large particles (d ≫ a) is determined by bulk viscosity η of polymer liquids, which scales with degree of polymerization as η ~ _N_3.4. Particles slightly larger than the tube diameter (d ≳ a) do not have to wait for the whole polymer liquid to relax and can diffuse by hopping between neighboring entanglement cages.37
The results of particle mobility in polymer liquids could be applied to test the local structure and dynamics of complex fluids such as mucus.54 At the crossovers between different scaling regimes of the size-dependent particle diffusion coefficient (see section 3.1), the characteristic length scales in polymer liquids, such as correlation length ξ and entanglement mesh size a, are on the order of the particle size. It should be noted that predictions described in the present work directly apply only to non-adsorbing particles since the adsorption of polymers on particles will slow down particle motion.37 For instance, particles without proper protection will stick to the biomacromolecules in the mucus and diffuse ~ 1000 times slower than non-adsorbing particles of the same size.55 Given the time-dependent mean-square displacement of probe particles, one can describe the viscoelastic properties of probed complex environments on the length scale comparable to the particle size within a wide frequency range by using the generalized Stokes-Einstein relation.16 The probe particles can be prepared with sizes ranging from nanometer to micron scale allowing one to probe the dynamics of complex fluids over this wide range of length scales. Extensions of this work to particle mobility in reversible polymer solutions,56–58 semiflexible polymer solutions,9 and active materials like actin filament networks59 will be presented in our future publications.
Acknowledgement
We would like to acknowledge financial support from the National Science Foundation under grants NSF CHE-0911588, DMR-0907515, and CBET-0609087, the National Institutes of Health under grants NIH 1-R01-HL077546-03A2 and P01HL34322, and the Cystic Fibrosis Foundation. This research was supported in part by the National Science Foundation under Grant No. NSF PHY05-51164.
References and Notes
- 1.Waigh TA. Rep. Prog. Phys. 2005;68:685–742. [Google Scholar]
- 2.Ye X, Tong P, Fetters LJ. Macromolecules. 1998;31:5785–5793. [Google Scholar]
- 3.Omari RA, Aneese AM, Grabowski CA, Mukhopadhyay A. J. Chem. Phys. B. 2009;113:8449–8452. doi: 10.1021/jp9035088. [DOI] [PubMed] [Google Scholar]
- 4.Grabowski CA, Adhikary B, Mukhopadhyay A. Appl. Phys. Lett. 2009;94:021903–021905. [Google Scholar]
- 5.Tuteja A, Mackay ME, Narayanan S, Asokan S, Wong MS. Nano Letters. 2007;7:1276–1281. doi: 10.1021/nl070192x. [DOI] [PubMed] [Google Scholar]
- 6.Guo HY, Bourret G, Corbierre MK, Rucareanu S, Lennox RB, Laaziri K, Piche L, Sutton M, Harden JL, Leheny RL. Phys. Rev. Lett. 2009;102:075702–075705. doi: 10.1103/PhysRevLett.102.075702. [DOI] [PubMed] [Google Scholar]
- 7.Xu JY, Palmer A, Wirtz D. Macromolecules. 1998;31:6486–6492. [Google Scholar]
- 8.Chen DT, Weeks ER, Crocker JC, Islam MF, Verma R, Gruber J, Levine AJ, Lubensky TC, Yodh AG. Phys. Rev. Lett. 2003;90:108301–108304. doi: 10.1103/PhysRevLett.90.108301. [DOI] [PubMed] [Google Scholar]
- 9.Liu J, Gardel ML, Kroy K, Frey E, Hoffman BD, Crocker JC, Bausch AR, Weitz DA. Phys. Rev. Lett. 2006;96:118104–118107. doi: 10.1103/PhysRevLett.96.118104. [DOI] [PubMed] [Google Scholar]
- 10.Arrio-Dupont M, Cribier S, Foucault G, Devaux PF, d'Albis A. Biophys. J. 1996;70:2327–2332. doi: 10.1016/S0006-3495(96)79798-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mason TG, Gang H, Weitz DA. J. Mol. Struct. 1996;383:81–90. [Google Scholar]
- 12.Pine DJ, Weitz DA, Chaikin PM, Herbolzheimer E. Phys. Rev. Lett. 1988;60:1134–1137. doi: 10.1103/PhysRevLett.60.1134. [DOI] [PubMed] [Google Scholar]
- 13.Mason TG, Ganesan K, van-Zanten JH, Wirtz D, Kuo SC. Phys. Rev. Lett. 1997;79:3282–3285. [Google Scholar]
- 14.Rathgeber S, Beauvisage HJ, Chevreau H, Willenbacher N, Oelschlaeger C. Langmuir. 2009;25:6368–6376. doi: 10.1021/la804170k. [DOI] [PubMed] [Google Scholar]
- 15.Mahaffy RE, Shih CK, MacKintosh FC, Kas J. Phys. Rev. Lett. 2000;85:880–883. doi: 10.1103/PhysRevLett.85.880. [DOI] [PubMed] [Google Scholar]
- 16.Mason TG, Weitz DA. Phys. Rev. Lett. 1995;74:1250–1253. doi: 10.1103/PhysRevLett.74.1250. [DOI] [PubMed] [Google Scholar]
- 17.Mason TG. Rheol. Acta. 2000;39:371–378. [Google Scholar]
- 18.Bausch AR, Moller W, Sackmann E. Biophys. J. 1999;76:573–579. doi: 10.1016/S0006-3495(99)77225-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Helfer E, Harlepp S, Bourdieu L, Robert J, MacKintosh FC, Chatenay D. Phys. Rev. Lett. 2000;85:457–460. doi: 10.1103/PhysRevLett.85.457. [DOI] [PubMed] [Google Scholar]
- 20.Rubinstein M, Colby RH. Polymer physics. Oxford University Press; 2003. [Google Scholar]
- 21.de Gennes PG. Scaling concepts in polymer physics. Cornell University Press; Ithaca: 1979. [Google Scholar]
- 22.Doi M, Edwards SF. The theory of polymer dynamics. Oxford University Press; 1988. [Google Scholar]
- 23.Cukier RI. Macromolecules. 1984;17:252–255. [Google Scholar]
- 24.Phillies GDJ, Ullmann GS, Ullmann K, Lin TH. J. Chem. Phys. 1985;82:5242–5246. [Google Scholar]
- 25.Odijk T. Biophys. J. 2000;79:2314–2321. doi: 10.1016/S0006-3495(00)76477-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Fan TH, Dhont JKG, Tuinier R. Phys. Rev. E. 2007;75:011803–011812. doi: 10.1103/PhysRevE.75.011803. [DOI] [PubMed] [Google Scholar]
- 27.Tuinier R, Fan TH. Soft Matter. 2008;4:254–257. doi: 10.1039/b711902j. [DOI] [PubMed] [Google Scholar]
- 28.Kruger M, Rauscher M. J. Chem. Phys. 2009;131:094902–094909. doi: 10.1063/1.3216108. [DOI] [PubMed] [Google Scholar]
- 29.Ogston AG. Trans. Faraday Soc. 1958;54:1754–1757. [Google Scholar]
- 30.Ogston AG, Preston BN, Wells JD, Ogston AG, Preston BN, Snowden JM, Wells JD. Proc. R. Soc. A. 1973;333:297–316. [Google Scholar]
- 31.Altenberger AR, Tirrell M. J. Chem. Phys. 1984;80:2208–2213. [Google Scholar]
- 32.Johansson L, Elvingson C, Lofroth JE. Macromolecules. 1991;24:6024–6029. [Google Scholar]
- 33.Amsden B. Macromolecules. 1999;32:874–879. [Google Scholar]
- 34.Masaro L, Zhu XX. Prog. Polym. Sci. 1999;24:731–775. [Google Scholar]
- 35.de Gennes PG. Macromolecules. 1976;9:594–598. [Google Scholar]
- 36.Brochard-Wyart F, de Gennes PG. Eur. Phys. J. E. 2000;1:93–97. [Google Scholar]
- 37.Cai L-H, Panyukov S, Rubinstein M. To be published.
- 38.Semenov AN, Rubinstein M. Eur. Phys. J. B. 1998;1:87–94. [Google Scholar]
- 39.Brochard-Wyart F, Ajdari A, Leibler L, Rubinstein M, Viovy JL. Macromolecules. 1994;27:803–808. [Google Scholar]
- 40.For very large probe chains (N>Ne3) there is a prediction of an entropic free energy barrier.38
- 41.Mukhopadhyay A. private communication.
- 42.Hamada F, Kinugasa S, Hayashi H, Nakajima A. Macromolecules. 1985;18:2290–2294. [Google Scholar]
- 43.The crossover solution concentration cdξ≃0.08 g/ml for 5 nm gold nanoparticles is estimated by expression cdξ=c∗(Rg∕d)1.32 (refer to eq. 23), in which c*≃ 0.015 g/ml3 and the radius of gyration Rg of a 240 kDa polystyrene chain in toluene is approximately 19 nm as estimated by data from ref. 42.
- 44.Mark JE. Physical properties of polymers handbook. 2nd ed. Springer; New York: 2007. [Google Scholar]
- 45.Chinai SN, Guzzi RA. J. Polym. Sci. 1956;21:417–426. [Google Scholar]
- 46.Liu J, Cao DP, Zhang LQ. J. Phys. Chem. C. 2008;112:6653–6661. [Google Scholar]
- 47.Rapaport DC. The art of molecular dynamics simulation. 2nd ed. Cambridge University Press; Cambridge, UK: 2004. [Google Scholar]
- 48.Kroger M, Loose W, Hess S. J. Rheol. 1993;37:1057–1079. [Google Scholar]
- 49.The expression _D_un = kBT(3π_dh_ηun) applies for no-slip particle-polymer boundary condition. Slip particle-polymer boundary condition will lead to larger particle diffusion coefficient _D_un = kBT/(2π_dh_ηun).
- 50.Ould-Kaddour F, Levesque D. Phys. Rev. E. 2001;63:011205–011209. doi: 10.1103/PhysRevE.63.011205. [DOI] [PubMed] [Google Scholar]
- 51.Sen S, Kumar SK, Keblinski P. Macromolecules. 2005;38:650–653. [Google Scholar]
- 52.The values of correlation length ξ and polymer size Rg (c) at different solution concentrations are estimated by expressions ξ (c) ≃ Rg (c*)(c/c*)–0.76 and Rg (c) ≃ Rg (c*)(c/c*)–0.12, respectively. Diffusion coefficient of a particle with size on the order of the correlation length ξ in polymer solution, α_Ds_, is used for calculating DSE = α_Ds_ (ξ/Rg)2, in which Ds = 141_μ_m2/s3 is the diffusion coefficient of the 5 nm gold nanoparticles in pure solvent and the scaling prefactor α is 0.53 as determined by experimental data (see Figure 6).
- 53.Brochard F, de Gennes PG. Langmuir. 1992;8:3033–3037. [Google Scholar]
- 54.Lai SK, Wang YY, Hida K, Cone R, Hanes J. Proc. Natl. Acad. Sci. U.S.A. 2010;107:598–603. doi: 10.1073/pnas.0911748107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Lai SK, O'Hanlon DE, Harrold S, Man ST, Wang YY, Cone R, Hanes J. Proc. Natl. Acad. Sci. U.S.A. 2007;104:1482–1487. doi: 10.1073/pnas.0608611104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Leibler L, Rubinstein M, Colby RH. Macromolecules. 1991;24:4701–4707. [Google Scholar]
- 57.Rubinstein M, Dobrynin AV. Curr. Opin. Colloid Interface Sci. 1999;4:83–87. [Google Scholar]
- 58.Sprakel J, van der Gucht J, Stuart MAC, Besseling NAM. Phys. Rev. E. 2008;77:061502–061511. doi: 10.1103/PhysRevE.77.061502. [DOI] [PubMed] [Google Scholar]
- 59.Lieleg O, Claessens MMAE, Bausch AR. Soft Matter. 2010;6:218–225. [Google Scholar]