Multigait soft robot (original) (raw)

Abstract

This manuscript describes a unique class of locomotive robot: A soft robot, composed exclusively of soft materials (elastomeric polymers), which is inspired by animals (e.g., squid, starfish, worms) that do not have hard internal skeletons. Soft lithography was used to fabricate a pneumatically actuated robot capable of sophisticated locomotion (e.g., fluid movement of limbs and multiple gaits). This robot is quadrupedal; it uses no sensors, only five actuators, and a simple pneumatic valving system that operates at low pressures (< 10 psi). A combination of crawling and undulation gaits allowed this robot to navigate a difficult obstacle. This demonstration illustrates an advantage of soft robotics: They are systems in which simple types of actuation produce complex motion.

Keywords: biomimetic, mobile

Robotics developed to increase the range of motions and functions open to machines, and to build into them some of the characteristics [including autonomous motion (1–3), adaptability to the environment (4–7), and capability of decision making (8, 9)] of animals, particularly animals with skeletons. Most mobile robots are built with hard materials (hard robots), either by adding treads or wheels (10, 11) to conventional machines to increase their mobility, or by starting with conceptual models based on animals [e.g., Big Dog (12) and many others (13–15)], and replicating some of their features in hard structures. Although robotics has made enormous progress in the last 50 years, hard robots still have many limitations. Some of these limitations are mechanical, and include instability when moving in difficult terrain; some have to do with the ranges of motions afforded by actuators and structures (e.g., metal rods, mechanical joints, and electric motors); some stem from the complexity in control (especially when handling materials and structures that are soft, delicate, and complex in shape). Hard robots fabricated from metals are also often heavy and expensive, and thus are not suitable for some applications.

New classes of robots may thus find uses in applications where conventional hard robots are unsuitable. We are interested in a unique class of robots: That is, soft robots fabricated in materials (predominantly elastomeric polymers) that do not use a rigid skeleton to provide mechanical strength. The objective of this work is to demonstrate a soft robot that requires only simple design and control to generate mobility. In this demonstration, we begin to address some of the issues that have limited the development of soft robots. Instead of basing this and other designs on highly evolved animals as models, we are using simpler organisms [e.g., worms (16) and starfish (17)] for inspiration. These organisms, ones without internal skeletons, suggest designs that are simpler to make and are less expensive than conventional hard robots, and that may, in some respects, be more capable of complex motions and functions. Simple, inexpensive systems will probably not replace more complex and expensive ones, but may have different uses.

Many of the capabilities of soft robots will ultimately be defined, we believe, by the materials used in their fabrication, and the use of soft materials may simplify the more complex mechanical structures used in hard robots. A simple elastomeric structure of appropriate design, for example, can provide the function of a hinge or joint, without the complexity of a multicomponent mechanical structure (18–20). Soft robotics may, thus, initially be a field more closely related to materials science and to chemistry than to mechanical engineering.

Soft organisms, ones without endo- or exoskeletons, are ubiquitous. Many of the most interesting and versatile of these organisms (e.g., squid) live in water. The buoyancy of water obviates the need for a mechanically strong and rigid skeleton: The structural features developed by land animals to retain form and to move in a gravitational field are unnecessary (21). The mechanical characteristics of the tissues of soft-bodied marine organisms that limit them to a neutrally buoyant medium are easily circumvented by using synthetic elastomers that are structurally tougher than these tissues. Soft robots based on appropriate elastomers can move, without difficulty, in a gravitational field, without fluid support.

The most prevalent mechanisms of actuation of soft organisms [e.g., muscular hydrostats (22)] cannot currently be replicated in synthetic materials [there are still no synthetic equivalents of muscle (23)], and might not, in any event, be the most useful ones. Our work on soft robots is intended to mimic some of the motions and capabilities of soft organisms, but is not constrained to mimic the mechanisms by which these motions are achieved in vivo.

Results

We fabricated the robots using soft lithography (24); its simplicity allowed us to iterate designs rapidly. We used pneumatic actuation, with low-pressure air, in initial designs for four reasons: (i) compressed air is easily generated, (ii) it is environmentally benign, (iii) it is lightweight, and (iv) it is essentially inviscid and thus allows rapid motion. Our pneumatic channel design is based on the pneu-net (PN) architecture described previously (18), because it is simple and compatible with soft lithography (24, 25). PNs are a series of chambers embedded in a layer of extensible elastomer and bonded to an inextensible layer; these chambers inflate like balloons during actuation. The difference in strain between the extensible top layer and inextensible bottom layer causes the PN to bend when pressurized. We tuned the PN’s bending motion via the orientation, size, and number of its chambers. For example, if the chambers of the PN are oriented orthogonally to a single axis (Fig. S1_B_), the additive effect of the inflation of each chamber is to curl the PN along this axis (Fig. 1 B and C). Ecoflex (Ecoflex 00-30 or Ecoflex 00-50; Smooth-On Inc.) was our choice for the actuating layer because it is highly extensible under low stresses, and poly(dimethyl siloxane) (PDMS) (Sylgard 184, Dow Corning) was our choice of strain-limiting layer as it is relatively inextensible at the stress developed on pressurization of thePNs.

Fig. 1.

Fig. 1.

(A) Schematic representation of the soft PN channels, formed by bonding an elastomeric layer (layer 1) to the strain-limiting layer (layer 2). The independent PNs are labeled PN 1, 2, 3, 4, and 5; black arrows indicate the location at which we insert tubing, and the dashed arrow indicates the bonding of layer 2 to layer 1. (B) A cross section of a portion of PN 2 is schematically illustrated at atmospheric pressure (_P_0; Left) and actuated at PN pressure (_P_1 > _P_0; Right). (Inset, Left) Top view of the robot and the section removed from PN 2. (C) An optical micrograph with PN 2 at atmospheric pressure (Left) and at 7.0 psi (0.5 atm; Right). The rest states (Left) of PNs 1 and 2 are curved away from the surface. The scale bar is 3 cm.

To demonstrate mobility with a soft robot, we constructed a tetrapod (Fig. 1; Fig. S1 shows dimensions). This robot can lift any one of its four legs off the ground and leave the other three legs planted to provide stability (three is the minimum number of legs necessary to provide stability for a passive load). We control each leg independently by using a network of pneumatic channels (PN 1, 2, 4, 5; Fig. 1) for each limb. In addition, we placed a fifth independent PN in the spine of the robot (PN 3; Fig. 1) to lift the main body of the robot from the ground when necessary.

Each of the five PNs could be pressurized from an external source (compressed air, 7 psi; 0.5 atm) that was connected to the robot via flexible tubing, at a central hub located at one end (arbitrarily called the rear) of the robot. We connected each of the PNs to a separate, computer-controlled, solenoid valve (Fig. S2_A_). The spine of the robot (PN 3) was at a higher pressure (_P_1 = 7 psi) for undulation, or a lower pressure (_P_2 = 4 psi) for crawling. The gait sequences were empirically determined and manually written into a spreadsheet and imported into a LabVIEW script that controlled the solenoid valves.

We actuated the robot by pressurizing the PNs in sequence. Upon pressurization, each PN curled to a final actuated structure at a rate that increased with applied pressure (Fig. 1 B and C) (18). To actuate the robot at convenient rates (∼1 s actuation time per limb; Fig. S3), we applied pressures of 7 psi. By actuating the PNs with different sequences, we demonstrated two fundamentally different gaits: undulation and crawling.

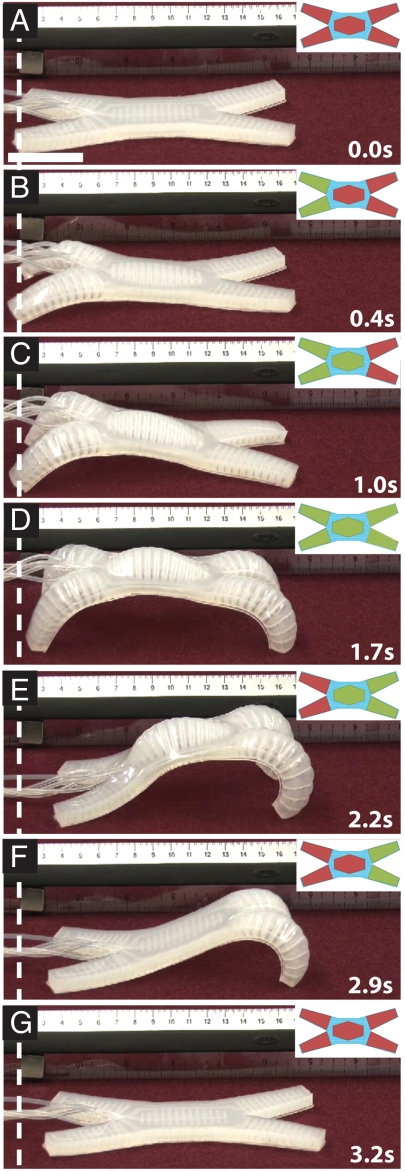
Undulation involved three steps, starting from the rest state (Fig. 2A): (i) Pressurization of PN 1 and PN 2 pulled the two hindlimbs of the robot forward (Fig. 2B); this motion anchored the robot from sliding backward. (ii) Pressurization of PN 3 lifted its spine from the surface (Fig. 2C). (iii) Pressurization of PNs 4 and 5, and sequential depressurization of PNs 1 and 2 and then PN 3 pulled the robot forward with its two forelimbs (Fig. 2 D and E). At this point, the rear two-thirds of the robot were in frictional contact with the surface; this anisotropy in frictional contact between the front and the rear half resulted in forward movement when we depressurized PNs 4 and 5 (the forelimbs; Fig. 2F). Fig. 2 shows the actuation sequence for the PNs that generates this locomotion. The complexity and fluidity of the motion that this simple sequence of binary opening and closing of valves achieves is remarkable, and reflects the nonlinearity of the transduction of pressure into shape by the two types of elastomers used in this robot (Movie S1; motion tracking data for this sequence shown in Fig. S4_A_). We drove the robot, in this gait, at 13 ± 0.6 m/h (∼93 body lengths/h; 11% of body length/cycle).

Fig. 2.

Fig. 2.

(A_–_G) Cycle of pressurization and depressurization of PNs that results in undulation. The particular PN(s) pressurized in each step are shown (Insets) as green, and inactive PN(s) are shown (Insets) as red. The scale bar in A is 4 cm.

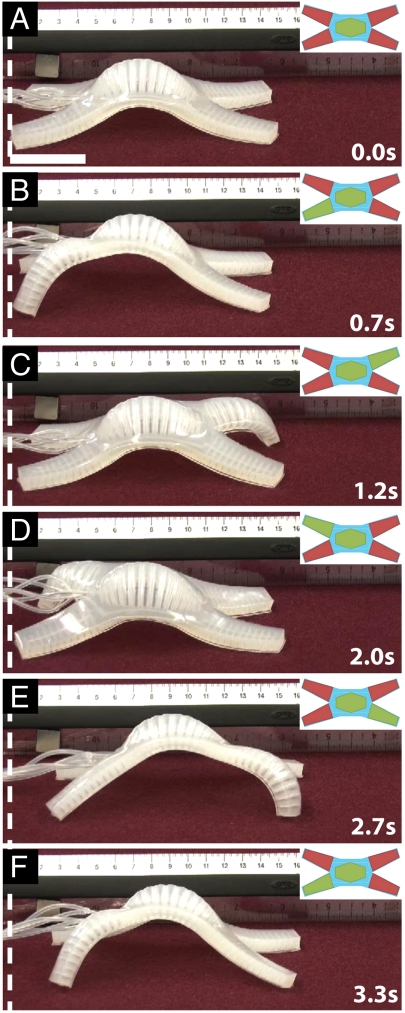
We also developed several crawl gaits for the tetrapod. One crawling sequence comprised five steps: (i) Pressurizing PN 3, the spine, lifted the core of the robot from the ground (Fig. 3A). (ii) Pressurizing PN 4 pulled the right-rear hindlimb forward (Fig. 3B). (iii) Simultaneous pressurization of PN 2 and depressurization of PN 4 then propelled the body of the tetrapod forward (Fig. 3C). (iv) Pressurizing PN 5 while depressurizing PN 2 (Fig. 3D) pulled the left-rear hindlimb forward. (v) Simultaneous pressurization of PN 1 and depressurization of PN 5 propelled, again, the body of the robot forward (Fig. 3E). Fig. 3F shows the sequence begin to repeat. Fig. 3 shows the actuation sequence for the PNs that generates this locomotion; this gait propelled the robot at 24 ± 3 m/h (∼192 body lengths/h; 12% of body length/cycle). A video of this gait is available as Movie S2 (motion tracking data for this sequence is shown in Fig. S4_B_). By using a slightly stiffer elastomer (Ecoflex 00-50; Smooth-On Inc.), we were able to drive the robot at 92 ± 4.3 m/h (Movie S3).

Fig. 3.

Fig. 3.

(A_–_F) Cycle of pressurization and depressurization of PNs that results in crawling. The particular PN(s) pressurized in each step are shown (Insets) as green, and inactive PN(s) are shown (Insets) as red. The scale bar in A is 4 cm.

To demonstrate the potential of a gait-changing soft robot to accomplish tasks that would be difficult or impossible with a hard robot, we drove the tetrapod underneath an obstacle: a glass plate elevated 2.0 cm above the ground. The robot was approximately 5.0-cm high when PN 3 (the spine) was activated for the crawling gait locomotion and each segment was approximately 2.0-cm high when actuated in the undulating gait. The thickness of the soft robot itself, however, was only 0.9 cm and therefore did not physically limit its passing underneath the 2.0-cm gap.

To drive the soft robot underneath the obstacle, we used manual control to pressurize the PNs (Fig. S2_B_); manual control simplified motion planning. Using a simplified crawl gait, we drove the robot to the obstacle, caused it to undulate under the 2-cm gap, and then resumed the crawl gait on the other side. From rest (Fig. 4A), this sequence involved four basic steps. (i) Pressurizing the spine (PN 3; Fig. 4B) and applying pressure to the hindlimbs and forelimbs for < 0.5 s elevated the robot from the surface. (ii) After pressurizing the spine, alternately actuating the left and right forelimbs caused the robot to crawl to the gap (Fig. 4C). (iii) Upon reaching the gap below the obstacle, depressurizing the spine reduced the robot’s height and allowed it to undulate under the glass plate (Fig. 4 E_–_G). (iv) Repressurizing the spine, again, lifted the body from the ground and prepared it for crawling on the other side of the gap (Fig. 4H). Fig. 4 shows the actuation sequence for the PNs that generates this locomotion. We drove the robot under the gap more than 15 times (without failure of the robot), with most attempts requiring less than 60 s to navigate under the obstacle; a significant portion of this time was due to manual control issues and disconnecting/reconnecting valves. A video of obstacle navigation is available as Movie S4.

Fig. 4.

Fig. 4.

PN actuation sequence (Left) and snapshots (Right) of a soft robot crawling to a short gap, undulating underneath it, then crawling again on the other side. (A) The robot starts unpressurized and (B) we pressurize the central channel and (C) actuate the legs to crawl toward the gap. (D) The central channel is depressurized and (E_–_G) we undulated the robot under the gap. (H) Finally, we repressurized the central channel and crawled on the other side of the gap. PN(s) actuated in each step are shown (Insets) as green, inactive PN(s) are shown (Insets) as red, and partially pressurized PNs are shown (Insets) as orange. The height of the gap is indicated by an overlaid dashed white line. The scale bar in A is 4 cm.

Discussion

A combination of techniques developed for the preparation of microfluidic systems with elastomeric materials (25) allows the convenient design and fabrication of soft robotic structures with large ranges of motions; these robots use no conventional mechanical joints or bearings. Simple soft robots, pneumatically actuated using low-pressure air (< 10 psi; 0.7 atm), are capable of locomotion in a gravitational field (unsupported by water), without an internal or external hard skeleton. Complex types of locomotion, including change in gait, emerge straightforwardly from simple PNs.

Soft robots based on elastomers and PNs have a number of attractive features. (i) Their design, and fabrication (as prototypes, and in large numbers) can be accomplished easily and inexpensively using the methods of soft lithography already highly developed for fabrication of microfluidic systems (18). (ii) The nonlinearity in their motion produces complex actuation, but requires only simple controls. (iii) They can be light, and are potentially inexpensive. (iv) The principles of design and actuation they use will scale over a range of sizes. (v) The extent to which they deform under stress can be tuned by increasing or decreasing the pressure used to actuate the PN. The structural stiffness of a PN (effectively, a balloon) drastically changes depending on its internal pressure; this capability allows the robot to change gait and/or change shape (SI Text gives the bending stiffness of a PN on pressurization; Figs. S5–S7). (vi) The large strain to failure of the silicone elastomers used to fabricate the soft robots makes them resistant to damage from many of the high-force, low strain sources that can damage the hard materials of current robot design (e.g., falling on rocks, torque from being caught in rubble, or bumps and scrapes).

Soft robots fabricated using siloxanes, relatively soft elastomers with low toughness, are more susceptible to cuts and punctures from sharp objects, such as glass or thorns, than hard robots. They also have a limited load-carrying capacity due to the low pressures that can be applied to them (given our current choice in materials and designs) before they rupture. Incorporation of other classes of materials and structures will extend their capabilities. Highly extensible materials, and structures that combine high yield stresses, Young’s moduli, and toughness (26) would make possible the application of high-force (using high pressures), make these robots more resistant to puncture, and also enable them to perform tasks requiring application of higher forces than is possible with these siloxane elastomer-based systems.

The response to actuation of elastomeric structures having embedded PNs is highly nonlinear and thus predictive modeling of their actuation is currently empirical. The development of motion control systems for these robots will require the use of nonlinear models (27–29) and may require neural-net-like learning methods (30, 31).

Materials and Methods

Details for the fabrication and control of the quadrupedal soft robot are provided in SI Materials and Methods. In brief, we fabricated the robot using soft lithography. We used a three-dimensional printer to print the mold from which the quadruped was replicated and a computer-controlled valving system to actuate the PNs. We quantified the effect of applied pressure on speed of actuation using high-speed video and we quantified the robot’s locomotion by tracking its center of mass during actuation. Additionally, the theoretical basis for PN actuation as well as a qualitative description of the structural stiffness of a PN vs. applied pressure is also provided in SI Text.

Supplementary Material

Supporting Information

Acknowledgments.

This work was supported by Defense Advanced Research Planning Agency award number W911NF-11-1-0094.

Footnotes

The authors declare no conflict of interest.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information