Evidence of a large-scale mechanosensing mechanism for cellular adaptation to substrate stiffness (original) (raw)
Abstract
Cell migration plays a major role in many fundamental biological processes, such as morphogenesis, tumor metastasis, and wound healing. As they anchor and pull on their surroundings, adhering cells actively probe the stiffness of their environment. Current understanding is that traction forces exerted by cells arise mainly at mechanotransduction sites, called focal adhesions, whose size seems to be correlated to the force exerted by cells on their underlying substrate, at least during their initial stages. In fact, our data show by direct measurements that the buildup of traction forces is faster for larger substrate stiffness, and that the stress measured at adhesion sites depends on substrate rigidity. Our results, backed by a phenomenological model based on active gel theory, suggest that rigidity-sensing is mediated by a large-scale mechanism originating in the cytoskeleton instead of a local one. We show that large-scale mechanosensing leads to an adaptative response of cell migration to stiffness gradients. In response to a step boundary in rigidity, we observe not only that cells migrate preferentially toward stiffer substrates, but also that this response is optimal in a narrow range of rigidities. Taken together, these findings lead to unique insights into the regulation of cell response to external mechanical cues and provide evidence for a cytoskeleton-based rigidity-sensing mechanism.
Keywords: actin cytoskeleton, microfabrication, mechanobiology, cell mechanics
Cell migration is not only sensitive to the biochemical composition of the environment, but also to its mechanical properties. Cells directly probe the physical properties of their environment, such as substrate stiffness, by pulling on it. Increasing evidence show that matrix or tissue elasticity has a key role in regulating numerous cell functions, such as adhesion (1), migration (2) and differentiation (3). Such functions are affected by cell-generated actomyosin forces that depend on substrate stiffness through a feedback mechanism (4). The sensitivity of cells to mechanical properties of the extracellular matrix (ECM) arises from the mechanosensitive nature of cell adhesion. Numerous plausible candidates for the transduction of mechanochemical signals have been tested (5). Among them, focal adhesions (FAs) appear to be the most prominent, as shown by the reported correlation between their area and sustained force exhibiting a constant stress (6–9). This mechanosensitivity is usually accounted for by a generic local mechanism in which a force applied to an FA induces an elastic deformation of the contact that triggers conformational and organizational changes of some of its constitutive proteins, which in turn can enhance binding with new proteins enabling growth of the contact (10–12). However, how this local mechanosensitivity can result in the ability of cells to sense and respond to the rigidity of their surroundings (2, 3, 13, 14) at a large scale remains largely unknown (5, 15). Much conflicting evidence has emerged from a variety of studies, leading to important questions. Not only FAs but also the opening of calcium ion channels (2, 16, 17) could participate in the build-up of cell tension in response to mechanical cues. Moreover, recent modeling (18) as well as indirect observations (19, 20) suggest that the contractile actomyosin apparatus can act as a global rigidity sensor (21). From a physical point of view, the deformation of the surrounding matrix in response to cell contractility is poorly understood; plausible mechanisms of cell mechanosensitivity imply that the regulation could be either mediated by the stress exerted by cells, or by the strain in the ECM (7, 22–24). These intriguing questions are currently intensively debated, because the detailed mechanisms of force transduction in response to ECM might explain the observed discrepancies in adhesion (1, 25), migration (2, 26), and differentiation (3, 27) of cells in environments of different rigidities and over different time scales.
Results and Discussion
Dynamics of Focal Adhesions and Traction Force Measurements on Substrates of Various Stiffnesses.
Here we report real-time measurements of explicit correlations between traction forces and the formation of FAs as a function of substrate stiffness. We used microforce sensor arrays (μFSA) (28) together with epifluorescence microscopy of REF52 fibroblast cells expressing a fluorescently tagged FA protein (YFP-paxillin) (Fig. 1 A and B). We seeded REF52 cells stably expressing YFP-paxillin on μFSA with pillars of various diameters and heights coated with fibronectin (13, 29, 30). These different-shaped pillars result in substrates with various spring constants, k, from 3 to 80 nN/μm (Fig. 1C, Movie S1) without altering the molecular scale properties of its surface. After allowing cells to adhere on the substrate for at least approximately 5 h, cells developed traction forces oriented toward their center that caused a deflection of the micropillars (Fig. 1B). We simultaneously analyzed the dynamics of the traction forces and FA patches over time. As a control experiment, we compared the size distributions of FAs on μFSA of different rigidities to those on a flat polydimethylsiloxane (PDMS) surface (Fig. S1). As expected from previous studies (23, 25, 31), these distributions were skewed toward larger values for substrates of increased stiffness. The topography of 2-μm pillar substrates did not significantly affect the size of FAs, as shown by the similar size distributions of FAs on μFAS and flat PDMS substrates (Fig. S1).
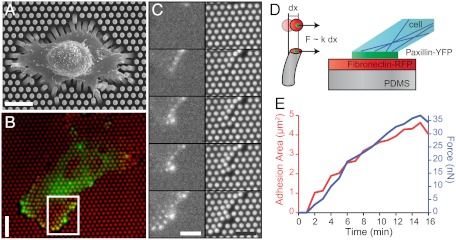
Fig. 1.
Cell adhesion and traction forces developed by REF52 fibroblasts expressing YFP-paxillin on micropillar substrates. (A) Scanning electron micrograph image of a typical REF52 cell on a micropillar substrate. (Scale bar, 15 µm.) (B) Epifluorescent image of a single cell deforming the micropillar substrate (here of spring constant k = 34 nN/μm). Micropillars are labeled by Cy3-fibronectin (red), and YFP-paxillin-rich patches are in green. (Scale bar, 15 µm.) (C) Sequential images of the insert area of B showing the dynamics of FA growth and micropillar displacements. (Scale bar, 10 µm.) (D) Schematic representation of the experimental setup showing the formation of FAs on the top of a PDMS micropillar. (E) Typical example of the formation of an FA area (red) and the buildup of force (blue) as a function of time (on a substrate of 34 nN/μm).
We analyzed traction forces in the proximity of the cell edge where the highest forces as well as the largest FAs were observed. In most cases, force generation and FA assembly over time were tightly correlated (Fig. 1 D and E): An increase of both forces and FA sizes followed by a saturation phase occurred within a time-scale of minutes (see an example on a substrate of 34 nN/μm, Fig. 1E). To characterize the dependence of such dynamics on substrate stiffness, we performed the measurements over a broad range of rigidities (from around 4 to 80 nN/μm). For each time point, we averaged the force, F, over different FAs present at the cell edge of different cells (_n_≥5). Average forces,  , exerted at paxillin sites, grew more rapidly and reached higher saturation values on substrates with higher rigidities (Fig. 2A). In contrast to the force, the dependency of FA growth (area) was less obvious although the saturation size depended on the stiffness of the pillars (Fig. 2B).
, exerted at paxillin sites, grew more rapidly and reached higher saturation values on substrates with higher rigidities (Fig. 2A). In contrast to the force, the dependency of FA growth (area) was less obvious although the saturation size depended on the stiffness of the pillars (Fig. 2B).
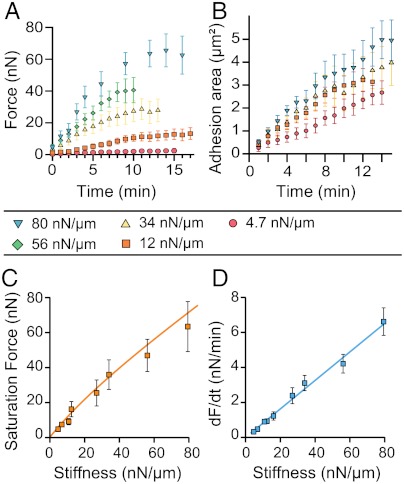
Fig. 2.
Traction forces and focal adhesion dynamics. (A) Average traction forces as a function of time for different substrate stiffnesses. Data were pooled from _n_≥5 different cells and _n_≥15 different pillars. Each curve exhibits an initial regime of fast force increase followed by a saturation regime. (B) Average focal adhesion area for different stiffnesses as a function of time. (C) Saturation force as a function of substrate stiffness. A linear relationship was observed between the maximal force and the substrate stiffness up to 80 nN/μm, showing that cells maintained a constant deformation. The fit corresponds to the theoretical model based on the active stress exerted by cytoskeleton remodeling (see SI Text). (D) Rate of increase of force with time, dF/dt, as a function of stiffness; dF/dt was obtained by fitting the slope of the initial linear regime of the force curve as a function of time (A). The rate of force with time, dF/dt, was proportional to the stiffness in the range of stiffnesses used in our study (up to 80 nN/μm).
In addition, the saturation force F p was found to be proportional to the stiffness of the substrate within our range of rigidities (Fig. 2C). This result implied that saturation forces correspond to a constant deformation of the substrate of around 0.84 ± 0.03 μm, in agreement with previous studies on other cell types (13, 23). Interestingly, the initial rate of force increase over time, dF/dt, also varied linearly with substrate rigidity, giving a speed of micropillar displacement equal to 1.3 nm/s independent of the stiffness. All together, these data suggest the existence of a mechanosensitivity mechanism that is regulated by substrate deformation.
Relationship Between Focal Adhesion Area, Force, and Stress.
To further assess the nature of force transmission, we investigated the relationship between force and focal adhesion area as a function of substrate stiffness. The relationship between force and area for all focal adhesions at all time points is plotted in Fig. 3A for substrate rigidities from 4 to 80 nN/μm (each point represents an average over at least 15 FAs of approximately equal area). This range of stiffnesses corresponds to an equivalent Young’s modulus, _E_eff, of the micropillar substrate varying from 2.8 up to 60 kPa (13). We clearly obtained a linear dependence between traction force and FA area at a given rigidity. This dependence, however, is not the same for each stiffness; surprisingly, it appears that different force values could be reached for the same FA area. For instance, an FA area of approximately 2 μm2 leads to forces that vary from 3 up to 42 nN within a stiffness range from 4.7 up to 80 nN/μm (Fig. 3A). The fact that FAs of similar areas can sustain different forces, illustrated in Fig. 3 C and D, is compatible with the results of ref. 24 where a variability of the stress between FAs at different positions was found, but only for a given substrate rigidity. These results overall contrast with the commonly accepted understanding of FA mechanosensitivity by a local force-dependent mechanism, which usually assumes a constant stress (6–8). Interestingly, the extrapolation of this linear dependence to zero gave rise to nonzero forces. This observation could be explained by invoking a second regime of tension for FAs smaller than 0.3 μm2. This residual area of 0.3 μm2 is similar to the typical size of focal complexes, which are able to sustain large traction forces that do not correlate with adhesion size (6, 32).
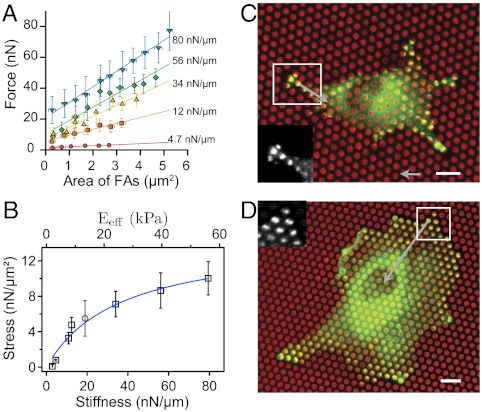
Fig. 3.
Relationship between stress and focal adhesion area. (A) Correlation between forces for different stiffnesses of the pillars and FA areas obtained by averaging data at all time points. Different forces are reached for the same size of FA on substrates of different stiffnesses. (B) Relationship between stress (σ = F/_S_FA) and substrate stiffness. An initial regime of fast increase of stress was observed for stiffness values below 34 nN/μm followed by a slow increase up to 80 nN/μm. The gray circle corresponds to the stress value obtained on soft continuous PDMS substrate with a Young’s modulus of 12 kPa by Balaban et al. (7). The equivalent rigidity of the micropillar substrate, _E_eff, was computed according to our modeling (13). The stress (σ)-stiffness (k) relationship is fitted according to our model (see SI Text). (C and D) Typical examples of an REF52 cell spread on a soft substrate (12 nN/μm) and on a stiffer substrate (54 nN/μm). Micropillars are in red and paxillin stainings in green. (Scale bar, 8 µm.) Focal adhesions of similar sizes (≈2.8 μm2) on both conditions give rise to different forces of around 41 nN on the stiff μFSA and 16 nN on the soft one (see SI Text). (Force bar, 10 nN.)
We then computed the stress, σ, defined as the force divided by the area of paxillin-rich patches. The stress corresponds to the slopes of the different curves representing the force as a function of FA area in Fig. 3A. By plotting the stress as a function of the rigidity (Fig. 3B), we discovered that the stress did not remain constant, but instead was an increasing function of the stiffness. Such an influence of substrate rigidity on the active cell response is consistent with original reports by Pelham and Wang (31). More precisely, we observed an initial regime corresponding to a fast increase of stress up to a value of 7 nN/μm2 (1 nN/μm2 = 1 kPa) below a stiffness of 34 nN/μm and was followed by a saturation phase for higher stiffnesses. In a previous study, Balaban et al. (7) concluded that the mechanical regulation of cell adhesion was governed by a constant stress, but their experiments were performed at a single stiffness. We indeed found that their result was well correlated to our stress-stiffness relationship according to the substrate stiffness used in their study (Fig. 3B). Taken together, our data indicate that the mechanosensitivity effect that we report in this study is not due to the previously reported mechanism mediated by FAs (6, 7, 33, 34), but requires a larger-scale mechanism.
Modeling of a Large-Scale Mechanosensing Process.
The mechanism usually invoked to account for a local mechanosensitivity is that a force applied to an FA induces an elastic deformation of the contact at the molecular scale that triggers conformational and organizational changes (such as unfolding) of some of its constitutive proteins, which in turn can enhance binding of new proteins enabling growth of the contact (11). Such a mechanism should therefore depend on the local stiffness of the adhesive substrate at the submicrometer scale (33) which corresponds to the surface of the top of the micropillar in our case, characterized by the elasticity of the PDMS, i.e., its Young’s modulus, E s (SI Text for more details on our phenomenological model). Consequently, if the mechanical feedback was mediated by the FA itself, then the stress applied by FAs would depend on E s only and not on k, which can be varied independently of E s in our set-up through the geometrical parameters of the pillars (SI Text). However, we show here that the stress, σ, depends on the spring constant of the pillars k (for the same E s). Such a dependency provides direct evidence that an extra feedback involving structures other than FAs must be involved. We suggest that this feedback could be mediated on a larger scale by the cytoskeleton, and in particular by the stress fibers pulling on FAs. We argue that a deformation of the cytoskeleton, such as a shortening, x, of the length of a stress fiber, has an impact on the active stress exerted by the cytoskeleton. Generally, this mechanical activation can be justified within the framework of the theory of viscoelastic active gels (35, 36). This phenomenological theory states that in nematic (or polar) media driven out of equilibrium such as the cytoskeleton, there exists an active stress  (here due to actin/myosin contractility) proportional to the nematic order parameter tensor
(here due to actin/myosin contractility) proportional to the nematic order parameter tensor  where the vector n denotes the local orientation of actin filaments. The coupling of Q ij to the strain U ij, which is standard in nematic gels (37), then implies that the stress
where the vector n denotes the local orientation of actin filaments. The coupling of Q ij to the strain U ij, which is standard in nematic gels (37), then implies that the stress  depends on U ij and therefore on the deformation x. In other words, a deformation x induces a strain U ij in the cytoskeleton and therefore a reorganization of the orientation Q ij of the filaments, which in turn yields an active stress.
depends on U ij and therefore on the deformation x. In other words, a deformation x induces a strain U ij in the cytoskeleton and therefore a reorganization of the orientation Q ij of the filaments, which in turn yields an active stress.
For this coupling of Q ij to the strain U ij to be valid, the relaxation time of Q ij has to be long, implying an elastic like rheology of the cytoskeleton. In fact, the rheology of the cytoskeleton is very complex and fluidization has been observed, but only in response to a transient stretch (38, 39). Our case is more like that of a sustained constraint, in which strain stiffening and long relaxation times have been reported (40–42), justifying our assumption.
Actin Organization Depends on Substrate Stiffness.
To evaluate Q ij for substrates of various stiffnesses, we performed experiments to image actin stress fibers on fixed cells spread on soft and stiff μFSAs. The polarization of the cell was then quantified by the scalar order parameter S defined by S = Q _n_0_n_0, where _n_0 is the average direction of stress fibers. We found that in a soft case (≈4 nN/μm), the stress fibers were fully disordered, leading to  , whereas they appeared fully polarized in a stiff case (≈100 nN/μm) leading to
, whereas they appeared fully polarized in a stiff case (≈100 nN/μm) leading to  (SI Text). At intermediate stiffness (≈40 nN/μm), we obtained
(SI Text). At intermediate stiffness (≈40 nN/μm), we obtained  . This result shows a relationship between force generation by cells and actin stress fiber alignment, yielding a semiquantitative support of the coupling between Q ij and U ij (Fig. 4). This active stress is a deformation-dependent (and therefore stiffness-dependent) contribution, enhancing the stress exerted by the FA. The existence of such coupling shows that actomyosin forces are sufficient to explain the cellular response to matrix rigidity according to a stress-dependent relationship to substrate stiffness, as recently shown for the response of stem cells to matrix stiffness (43). By assuming a linear coupling between Q ij and U ij, the model could be made explicit for the case of a single stress fiber, for which the stress,
. This result shows a relationship between force generation by cells and actin stress fiber alignment, yielding a semiquantitative support of the coupling between Q ij and U ij (Fig. 4). This active stress is a deformation-dependent (and therefore stiffness-dependent) contribution, enhancing the stress exerted by the FA. The existence of such coupling shows that actomyosin forces are sufficient to explain the cellular response to matrix rigidity according to a stress-dependent relationship to substrate stiffness, as recently shown for the response of stem cells to matrix stiffness (43). By assuming a linear coupling between Q ij and U ij, the model could be made explicit for the case of a single stress fiber, for which the stress,  at each extremity was given by the deformation of the corresponding pillar and the adhesion area, _S_FA. Based on this assumption, we made explicit the dependence of the stress, therefore the force, on the pillar rigidity and showed that this theoretical prediction, compatible with ref. 43 (SI Text), was in good agreement with our experimental data (Fig. 2C, Fig. 3B). Additionally, this large-scale mechanosensitive regulation by the contractility of actin-myosin fibers could also explain the linear relationship that we obtained between the saturation force and stiffness (Fig. 2C): The constant deformation of around 840 nm could be attributed to the simultaneous shortening of several micron-sized sarcomeric substructures within actomyosin stress fibers that, according to previous studies (44, 45), can sustain contractions of 10–25%.
at each extremity was given by the deformation of the corresponding pillar and the adhesion area, _S_FA. Based on this assumption, we made explicit the dependence of the stress, therefore the force, on the pillar rigidity and showed that this theoretical prediction, compatible with ref. 43 (SI Text), was in good agreement with our experimental data (Fig. 2C, Fig. 3B). Additionally, this large-scale mechanosensitive regulation by the contractility of actin-myosin fibers could also explain the linear relationship that we obtained between the saturation force and stiffness (Fig. 2C): The constant deformation of around 840 nm could be attributed to the simultaneous shortening of several micron-sized sarcomeric substructures within actomyosin stress fibers that, according to previous studies (44, 45), can sustain contractions of 10–25%.
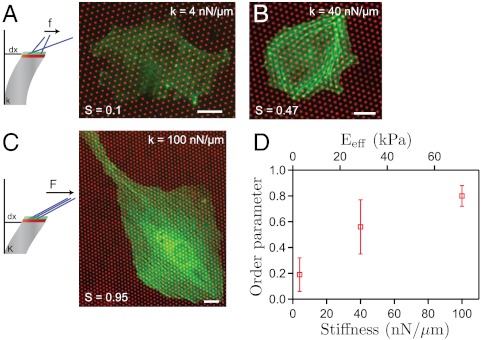
Fig. 4.
Coupling between the organization of stress fibers and the stiffness of the substrate. (A_–_C) Schematic representations and actin organization on substrates with various rigidities. Typical examples of actin staining and stress fibers organization (green) on a soft substrate (∼4 nN/μm) (A), on a substrate with an intermediate stiffness (∼40 nN/μm) (B), and on a stiffer substrate (∼100 nN/μm) (C). The scalar order parameter, S, is given here by  , where θ denotes the angle of a stress fiber with a reference axis and _θ_0 its average. Cells on stiffer substrate exhibit a more pronounced polarization of the actin stress fibers leading to an increase of S with the rigidity: S ≈ 0.1, 0.47, and 0.95, respectively. (Scale bar, 15 µm.) (D) Average order parameter for cells plated on substrates of three different stiffnesses as a function of the pillar spring constant and the effective rigidity, _E_eff, of the substrate. Data were pooled from _n_≥15 cells.
, where θ denotes the angle of a stress fiber with a reference axis and _θ_0 its average. Cells on stiffer substrate exhibit a more pronounced polarization of the actin stress fibers leading to an increase of S with the rigidity: S ≈ 0.1, 0.47, and 0.95, respectively. (Scale bar, 15 µm.) (D) Average order parameter for cells plated on substrates of three different stiffnesses as a function of the pillar spring constant and the effective rigidity, _E_eff, of the substrate. Data were pooled from _n_≥15 cells.
Substrate Stiffness Governs the Directionality of Cell Movements.
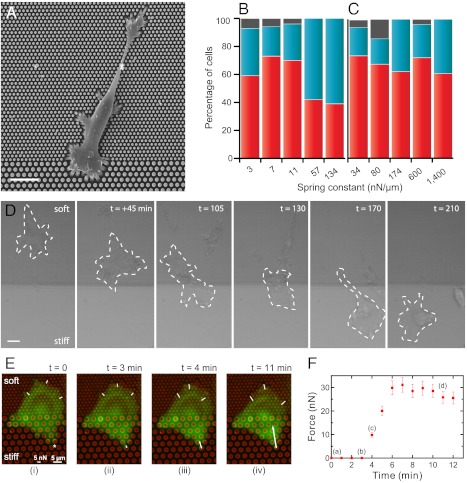
Such a large-scale mechanism driven by cell cytoskeleton polarization could also provide a plausible explanation for cell durotaxis. The combination of our observations—a faster force increase and higher saturated force values on stiffer substrates and an increasing stress with respect to substrate stiffness—led us naturally to the following prediction: polarized cells coming from a softer substrate will suddenly exert large traction forces as they touch the stiff side, and thus rotate to migrate perpendicularly to the stiff substrate. On the other hand, cells coming from the stiff side will stay along the boundary. These predictions guided the design of a durotaxis assay (2): Areas of different stiffnesses on which cells can freely move from soft to stiff and vice versa were created within the same micropillar substrate. Such substrates were composed of consecutive arrays of micropillars of diameters 1 and 2 μm (creating soft, k s, and stiff, K S, substrates, respectively) inducing a stiffness ratio of around ten between both sides (K S/k s ≈ 10) while the surface density of the micropillars was kept constant (Fig. 5A). Cells coming from the soft part or from the stiff part were considered independently. As shown in Fig. 5D and in Movie S2 for k s = 3 nN/μm and K s = 34 nN/μm, cells indeed move toward the stiff part of the substrate aligning perpendicularly to the boundary.
Fig. 5.
Durotaxis revisited with micropillar substrates. (A) Scanning electron micrograph of a cell spread between two micropillar surfaces exhibiting different stiffnesses. The diameter of the pillars vary between 1 μm (top region) and 2 μm (bottom region), but the surface density of the micropillar substrate (fraction of surface are covered by pillars) has been kept constant. (Scale bar, 10 µm.) (B) Statistics of cells migrating from the soft substrate toward the stiff one as a function of the spring constant of the soft pillars. The spring constant, k, of the pillar was varied between 3 and 134 nN/μm. A high percentage of migration events toward the stiff substrate was observed for values between 3 and 11 nN/μm, in correlation with the range of stiffnesses where a high increase of the stress is observed. For larger values of k, no preferential direction was observed. In red, percentage of cells that come from the soft part and cross the boundary. In blue, percentage of cells that do not migrate. In gray, cells with undefined movement. (C) Statistics of cells migrating from the stiff part of the substrate as a function of the spring constant of the stiff pillars. Cells prefer to stay on the stiffer substrate over a wide-range of rigidity. In red, percentage of cells that come from the stiff part and prefer to stay on it instead of crossing the boundary. In blue, percentage of cells that migrate toward the soft substrate. In gray, cells with undefined movement. (D) Brightfield images of the movement of REF52 cell at the border between stiff (K s = 34 nN/μm) and soft (k s = 3 nN/μm) substrates. The dashed line represents the cell boundary. Time = 0 is here taken arbitrarily. (Scale bar, 20 μm.) (E) Force distribution during a typical crossing event of an REF52 cell from soft to stiff substrate. Micropillars are labeled by Cy3-fibronectin (red) and the cell appears in green. (Scale bar, 5 μm.) Cell spread at the boundary between soft and stiff substrates (1-μm pillars versus 2-μm pillars) exhibits a roughly homogeneous distribution of the forces on the soft part (k s = 3 nN/μm and K s = 34 nN/μm). As the cell is probing a stiff pillar, a large deformation (i.e., high force) is peaked in the direction n, normal to the border inducing a polarized shape of the cell in this direction. (F) Variation of the force on the stiff pillar (designated by an asterisk in E, i) as a function of time.
We then used this assay to analyze the migration paths of individual cells on micropillar substrates of different stiffnesses. Our durotaxis analysis was performed by counting the preferential orientation of the cells after they touched the border between the two different parts of the substrate. We measured the number of events that corresponded to cells coming from the soft substrates and arriving at the boundary (40 < _n_cells < 80, where _n_cells is the total number of cells analyzed). By changing the rigidity of the soft micropillars from 3–134 nN/μm, we obtained an optimal durotaxis efficiency for stiffness values around 3–10 nN/μm with around 70% of cells moving toward the stiffer side (Fig. 5B). For _k_≫10 nN/μm, no preferential direction was observed (only 35–50% of cells migrate toward the stiffer substrate). On the contrary, most of the cells located on the stiffer side did not migrate toward the soft one within the tested range of stiffnesses represented by the rigidity of the stiff pillars (Histogram, Fig. 5C, Movie S3). In addition, as a control experiment to test whether cells were actually reacting to the substrate rigidity and not the adhesion geometry, we fabricated adhesive surfaces with the same geometry on glass coverslips coated with fluorescently labeled fibronectin (SI Text, Fig. S2). To limit cell adhesion to the transferred pattern, the substrates were then treated with polyethyleneglycol to passivate the rest of the surface (26), rendering it nonstick. In these conditions, we obtained an array of fibronectin patches printed on glass with the same adhesive surface and sizes as the tops of the pillars. On such surfaces presenting the same geometry but no rigidity dependency, we observed that geometry could not explain our previous results on pillar substrates. Indeed, only 37% of the cells migrated from the area of 1 μm patches to the area of 2 μm ones and 53% in the opposite direction when first placed on the 2 μm patches area.
When both sides of the substrate presented a stiffness larger than around 50 nN/μm, we observed that the migration of cells toward the stiffer part was reduced, as if cells could not sense any difference between sides (Fig. 5B). In other words, an optimal response to a step difference in matrix stiffness appeared within a narrow range of rigidities. These results could be related to the ability of cells to adapt their own stiffness to that of the substrate (27, 43, 46). Moreover, the range of stiffness that promoted migration toward the stiffer side was correlated to that of the initial regime of the stress-stiffness relationship (that of fast stress increase before reaching saturation, see Fig. 3B). By analyzing crossing events with the deformation of micropillars at the boundary between soft and stiff substrates (Fig. 5), we showed that as a cell coming from the soft part was probing the interface, the force quickly increased up to 30 nN (Fig. 5F) and peaked in the direction n normal to the border, leading to the migration of the cell body toward the stiffest region (Fig. 5E, Movie S4). In agreement with our previous observations, this behavior can be attributed to cell polarization along this axis, which in turn favored the migration from soft to stiff.
It appears that migration toward the stiffer part was enhanced when the step in stiffness corresponded to a large increase in stress between both sides of the substrate. According to Fig. 3B, the range of rigidities between 1 and 50 nN/μm corresponds to the regime of the highest cell sensitivity to substrate rigidity. However, if both sides of the substrate corresponded to similar values of stress exerted by the adherent cell, cells did not migrate from one side to the other, no matter what the rigidity step between them. Consequently, the stress-stiffness relationship that we established appeared as an interesting indicator for the durotactic behavior. As cells sense the stiff side, they exert larger forces which in turn could induce a polarization of the actin cytoskeleton toward the stiff side and thus promote durotaxis. Interestingly, qualitatively similar behavior has been observed for the durotaxis of vascular cells on defined stiffness gradients within a range of rigidities up to 80 kPa (47). The study observed a higher polarized behavior on gradient gels than on uniform substrates and a durotactic behavior enhanced by increasing the magnitude of gradients. However, they did detect an upper limit of stiffness that a cell is capable of sensing. Here we show that such a limit could be determined by the relative variations of the stress that the cell could exert on both sides.
Conclusion
We present here strong evidence that the rigidity-sensing mechanism in cell migration is not only locally driven by focal adhesion growth: The same size of FA area can lead to different forces depending on the substrate stiffness. Our results indicate clear constraints on the possible mechanisms that regulate cell mechanosensitivity. A nonconstant stress as a function of stiffness requires a large-scale mechanical feedback that involves the reorganization of actin stress fibers instead of a purely local mechanism based on FA mechanosensitivity. In our model, stress fibers may act as a force sensor that transmits a mechanical tension to FAs. Tension mediated through the actin cytoskeleton induces a polarization of actin fibers that orient along the direction of the applied force in response to substrate stiffness. Signaling pathways will help to regulate this tension by stabilizing FAs (48). We also demonstrate that durotaxis is optimal within a given range of rigidities that can be explained by our stress-rigidity relationship. The integrative mechanism we have presented here could be relevant to understanding the matrix stiffness dependence of stem cell differentiation (3, 43) and also tumor formation in vivo (49) in terms of actin reorganization and cell contractility.
Materials and Methods
Cell Culture.
REF52 cells were maintained at 37 °C in a humidified atmosphere of 5% CO2 and 95% air in DMEM containing 10% bovine calf serum, 100 U/mL penicillin, 100 μg/mL streptomycin, and 100 μg/mL glutamine. The cells were deposited on μFSA 3 to 6 h before microscopy experiments (SI Text for details).
Preparation and Calibration of Microstructured PDMS Substrates.
PDMS micropillar arrays were prepared and calibrated according to du Roure et al. (28). The SI Text provides additional details on the experimental methods.
Image Analysis.
To calculate the order parameter, the images were analyzed using ImageJ software. First the images were convolved and thresholded. Then we used the Analyze Particle tool to detect the actin filaments. Each filament was fitted with an ellipse. We then calculated the medium orientation of the filaments and the order parameter along this angle  , where the average weighting was given by the length of the filaments (SI Text).
, where the average weighting was given by the length of the filaments (SI Text).
Supplementary Material
Supporting Information
Acknowledgments.
We thank N. Biais, A. Buguin, J. Devillers, A. Nicolas, J. Prost, M.P. Sheetz, P. Silberzan, and the members of the Mechanobiology Institute (National University Singapore) for fruitful discussions and A. Richert for cell culture protocols. We thank A. Bershadsky for generously providing a stably transfected YFP-paxillin cell line. Financial support from the Association pour la Recherche sur le Cancer (ARC), the C’Nano Ile-de-France, the Ligue Contre le Cancer (Comité Ile-de-France), the Association Française contre la Myopathie (AFM), and the Agence Nationale de la Recherche [Programme Blanc 2010 (MECANOCAD) ANR 2010 BLAN 1515 and ANR Blanc International (MNVASC)] is gratefully acknowledged. The research was conducted in the scope of the International Associated Laboratory Cell Adhesion France Singapore (CAFS). L.T. acknowledges the Agence Nationale de la Recherche Programme National en Nanosciences et Nanotechnologies for a postdoctoral fellowship.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
References
- 1.Giannone G, et al. Periodic lamellipodial contractions correlate with rearward actin waves. Cell. 2004;116:431–443. doi: 10.1016/s0092-8674(04)00058-3. [DOI] [PubMed] [Google Scholar]
- 2.Lo CM, Wang HB, Dembo M, Wang YL. Cell movement is guided by the rigidity of the substrate. Biophys J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Engler AJ, Sen S, Sweeney HL, Discher DE. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–689. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 4.Discher DE, Janmey P, Wang YL. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310:1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- 5.Parsons JT, Horwitz AR, Schwartz MA. Cell adhesion: Integrating cytoskeletal dynamics and cellular tension. Nat Rev Mol Cell Biol. 2010;11:633–643. doi: 10.1038/nrm2957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tan JL, et al. Cells lying on a bed of microneedles: An approach to isolate mechanical force. Proc Natl Acad Sci USA. 2003;100:1484–1489. doi: 10.1073/pnas.0235407100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Balaban NQ, et al. Force and focal adhesion assembly: A close relationship studied using elastic micropatterned substrates. Nat Cell Biol. 2001;3:466–472. doi: 10.1038/35074532. [DOI] [PubMed] [Google Scholar]
- 8.Riveline D, et al. Focal contacts as mechanosensors: Externally applied local mechanical force induces growth of focal contacts by an mDia1-dependent and ROCK-independent mechanism. J Cell Biol. 2001;153:1175–1185. doi: 10.1083/jcb.153.6.1175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shemesh T, Geiger B, Bershadsky AD, Kozlov MM. Focal adhesions as mechanosensors: A physical mechanism. Proc Natl Acad Sci USA. 2005;102:12383–12388. doi: 10.1073/pnas.0500254102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.del Rio A, et al. Stretching single talin rod molecules activates vinculin binding. Science. 2009;323:638–641. doi: 10.1126/science.1162912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Nicolas A, Geiger B, Safran SA. Cell mechanosensitivity controls the anisotropy of focal adhesions. Proc Natl Acad Sci USA. 2004;101:12520–12525. doi: 10.1073/pnas.0403539101. and correction (2005) 102:2260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kanchanawong P, et al. Nanoscale architecture of integrin-based cell adhesions. Nature. 2010;468:580–584. doi: 10.1038/nature09621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ghibaudo M, et al. Traction forces and rigidity sensing regulate cell functions. Soft Matter. 2008;4:1836–1843. [Google Scholar]
- 14.Kasza KE, et al. Filamin A is essential for active cell stiffening but not passive stiffening under external force. Biophys J. 2009;96:4326–4335. doi: 10.1016/j.bpj.2009.02.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Keren K, et al. Mechanism of shape determination in motile cells. Nature. 2008;453:475–480. doi: 10.1038/nature06952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Glogauer M, et al. Calcium ions and tyrosine phosphorylation interact coordinately with actin to regulate cytoprotective responses to stretching. J Cell Sci. 1997;110:11–21. doi: 10.1242/jcs.110.1.11. [DOI] [PubMed] [Google Scholar]
- 17.Hayakawa K, Tatsumi H, Sokabe M. Actin stress fibers transmit and focus force to activate mechanosensitive channels. J Cell Sci. 2008;121:496–503. doi: 10.1242/jcs.022053. [DOI] [PubMed] [Google Scholar]
- 18.Walcott S, Sun SX. A mechanical model of actin stress fiber formation and substrate elasticity sensing in adherent cells. Proc Natl Acad Sci USA. 2010;107:7757–7762. doi: 10.1073/pnas.0912739107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Mitrossilis D, et al. Single-cell response to stiffness exhibits muscle-like behavior. Proc Natl Acad Sci USA. 2009;106:18243–18248. doi: 10.1073/pnas.0903994106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lam WA, et al. Mechanics and contraction dynamics of single platelets and implications for clot stiffening. Nat Mater. 2011;10:61–66. doi: 10.1038/nmat2903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Kobayashi T, Sokabe M. Sensing substrate rigidity by mechanosensitive ion channels with stress fibers and focal adhesions. Curr Opin Cell Biol. 2010;22:669–676. doi: 10.1016/j.ceb.2010.08.023. [DOI] [PubMed] [Google Scholar]
- 22.De R, Zemel A, Safran SA. Do cells sense stress or strain? Measurement of cellular orientation can provide a clue. Biophys J. 2008;94:L29–L31. doi: 10.1529/biophysj.107.126060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Saez A, Buguin A, Silberzan P, Ladoux B. Is the mechanical activity of epithelial cells controlled by deformations or forces? Biophys J. 2005;89:L52–L54. doi: 10.1529/biophysj.105.071217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Stricker J, Aratyn-Schaus Y, Oakes PW, Gardel ML. Spatiotemporal constraints on the force-dependent growth of focal adhesions. Biophys J. 2011;100:2883–2893. doi: 10.1016/j.bpj.2011.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Yeung T, et al. Effects of substrate stiffness on cell morphology, cytoskeletal structure, and adhesion. Cell Motil Cytoskeleton. 2005;60:24–34. doi: 10.1002/cm.20041. [DOI] [PubMed] [Google Scholar]
- 26.Saez A, Ghibaudo M, Buguin A, Silberzan P, Ladoux B. Rigidity-driven growth and migration of epithelial cells on microstructured anisotropic substrates. Proc Natl Acad Sci USA. 2007;104:8281–8286. doi: 10.1073/pnas.0702259104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Engler AJ, et al. Myotubes differentiate optimally on substrates with tissue-like stiffness: Pathological implications for soft or stiff microenvironments. J Cell Biol. 2004;166:877–887. doi: 10.1083/jcb.200405004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.du Roure O, et al. Force mapping in epithelial cell migration. Proc Natl Acad Sci USA. 2005;102:2390–2395. doi: 10.1073/pnas.0408482102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ladoux B, et al. Strength dependence of cadherin-mediated adhesions. Biophys J. 2010;98:534–542. doi: 10.1016/j.bpj.2009.10.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fu JP, et al. Mechanical regulation of cell function with geometrically modulated elastomeric substrates. Nat Methods. 2010;7:733–736. doi: 10.1038/nmeth.1487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Pelham RJ, Wang YL. Cell locomotion and focal adhesions are regulated by substrate flexibility. Proc Natl Acad Sci USA. 1997;94:13661–13665. doi: 10.1073/pnas.94.25.13661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Beningo KA, Dembo M, Kaverina I, Small JV, Wang YL. Nascent focal adhesions are responsible for the generation of strong propulsive forces in migrating fibroblasts. J Cell Biol. 2001;153:881–887. doi: 10.1083/jcb.153.4.881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Nicolas A, Safran SA. Limitation of cell adhesion by the elasticity of the extracellular matrix. Biophys J. 2006;91:61–73. doi: 10.1529/biophysj.105.077115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Nicolas A, Besser A, Safran SA. Dynamics of cellular focal adhesions on deformable substrates: Consequences for cell force microscopy. Biophys J. 2008;95:527–539. doi: 10.1529/biophysj.107.127399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kruse K, Joanny JF, Julicher F, Prost J, Sekimoto K. Generic theory of active polar gels: A paradigm for cytoskeletal dynamics. Eur Phys J E. 2005;16:5–16. doi: 10.1140/epje/e2005-00002-5. [DOI] [PubMed] [Google Scholar]
- 36.Voituriez R, Joanny JF, Prost J. Generic phase diagram of active polar films. Phys Rev Lett. 2006;96:028102. doi: 10.1103/PhysRevLett.96.028102. [DOI] [PubMed] [Google Scholar]
- 37.Warner M, Terentjev EM. Liquid Crystal Elastomers. Oxford: Oxford Univ Press; 2003. [Google Scholar]
- 38.Trepat X, et al. Universal physical responses to stretch in the living cell. Nature. 2007;447:592–595. doi: 10.1038/nature05824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Krishnan R, et al. Reinforcement versus fluidization in cytoskeletal mechanoresponsiveness. PLoS One. 2009;4:e5486. doi: 10.1371/journal.pone.0005486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Thoumine O, Ott A. Time scale dependent viscoelastic and contractile regimes in fibroblasts probed by microplate manipulation. J Cell Sci. 1997;110:2109–2116. doi: 10.1242/jcs.110.17.2109. [DOI] [PubMed] [Google Scholar]
- 41.Trepat X, et al. Viscoelasticity of human alveolar epithelial cells subjected to stretch. Am J Physiol. 2004;287:L1025–L1034. doi: 10.1152/ajplung.00077.2004. [DOI] [PubMed] [Google Scholar]
- 42.Desprat N, Richert A, Simeon J, Asnacios A. Creep function of a single living cell. Biophys J. 2005;88:2224–2233. doi: 10.1529/biophysj.104.050278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Zemel A, Rehfeldt F, Brown AEX, Discher DE, Safran SA. Optimal matrix rigidity for stress-fibre polarization in stem cells. Nat Phys. 2010;6:468–473. doi: 10.1038/nphys1613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kreis TE, Birchmeier W. Stress fiber sarcomeres of fibroblasts are contractile. Cell. 1980;22:555–561. doi: 10.1016/0092-8674(80)90365-7. [DOI] [PubMed] [Google Scholar]
- 45.Russell RJ, Xia SL, Dickinson RB, Lele TP. Sarcomere mechanics in capillary endothelial cells. Biophys J. 2009;97:1578–1585. doi: 10.1016/j.bpj.2009.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Solon J, Levental I, Sengupta K, Georges PC, Janmey PA. Fibroblast adaptation and stiffness matching to soft elastic substrates. Biophys J. 2007;93:4453–4461. doi: 10.1529/biophysj.106.101386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Isenberg BC, DiMilla PA, Walker M, Kim S, Wong JY. Vascular smooth muscle cell durotaxis depends on substrate stiffness gradient strength. Biophys J. 2009;97:1313–1322. doi: 10.1016/j.bpj.2009.06.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Grashoff C, et al. Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature. 2010;466:263–266. doi: 10.1038/nature09198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Paszek MJ, et al. Tensional homeostasis and the malignant phenotype. Cancer Cell. 2005;8:241–254. doi: 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information