Prognostic Model for Survival in Patients with Metastatic Renal Cell Carcinoma: Results from the International Kidney Cancer Working Group (original) (raw)
. Author manuscript; available in PMC: 2012 Aug 15.
Abstract
Purpose
To develop a single validated model for survival in metastatic renal cell carcinoma (mRCC) using a comprehensive international database.
Experimental Design
A comprehensive database of 3748 patients including previously reported clinical prognostic factors was established by pooling patient-level data from clinical trials. Following quality control and standardization, descriptive statistics were generated. Univariate analyses were conducted using proportional hazards models. Multivariable analysis using a log-logistic model stratified by center and multivariable fractional polynomials was performed to identify independent predictors of survival. Missing data were handled using multiple imputation methods. Three risk groups were formed using the 25th and 75th percentiles of the resulting prognostic index. The model was validated using an independent dataset of 645 patients treated with tyrosine kinase inhibitor (TKI) therapy.
Results
Median survival in the favorable, intermediate and poor risk groups was 26.9 months, 11.5 months, and 4.2 months, respectively. Factors contributing to the prognostic index included treatment, performance status, number of metastatic sites, time from diagnosis to treatment, and pre-treatment hemoglobin, white blood count, lactate dehydrogenase, alkaline phosphatase, and serum calcium. The model demonstrated good concordance when tested among patients treated with TKI therapy (C statistic=0.741, 95% confidence interval 0.714 to 0.768).
Conclusions
Nine clinical factors can be used to model survival in mRCC and form distinct prognostic groups. The model demonstrates utility among patients treated in the TKI era.
Keywords: Kidney Cancer, Renal Cell Carcinoma, Prognostic Factors, Risk Factors
Introduction
Renal cell carcinoma is one of the most common adult cancers, with an incidence of 58,240 new cases in the US in 2011 and 13,040 deaths1. Worldwide, there were 273,518 new cases and 116,368 deaths in 2008, the most recent year for which global statistics are available2. Although the proportion of patients with metastatic disease at diagnosis has declined due to more intense screening and incidental case ascertainment, the relationship between early diagnosis and mortality is confounded by the length and lead-time biases that accompany estimates of pre-clinical and clinical time intervals in the presence of advancing technology2. Unfortunately, approximately one-third of patients will eventually develop metastatic disease. Even with the recent introduction of vascular endothelial growth factor directed therapies, the long-term prognosis for patients with metastatic renal cell carcinoma (mRCC) is poor, with median survival under 2 years.
The natural history of mRCC is quite variable, and therefore an important consideration in the evaluation and development of new treatment strategies is the role of factors that are predictive of outcome. Use of known prognostic factors can help direct therapies to patient groups most likely to benefit from them and can help identify patients for which watchful waiting is a suitable alternative, thus potentially preserving alternatives for later use. Understanding prognostic factors can aid in the interpretation of clinical trials by helping to assess the magnitude of differences between treatments. In addition, consideration of known prognostic factors can help determine the extent to which new therapies are altering the natural history of the disease, and can be used as a backdrop against which new, potentially important prognostic factors can be evaluated to determine if they add independent information, or if their prognostic value is due simply to correlations with known factors.
A number of large retrospective studies of prognostic factors in mRCC had been reported prior to the initiation of this project3–8. These investigations focused primarily on factors prognostic for survival and generally concentrated on clinical data that were collected as part of the normal patient work-up. Unfortunately, although these investigations consistently identified several factors, such as performance status and metastasis-free interval as being independent predictors of survival, the definitions of these predictors varied, and none of the investigations evaluated the same set of factors. In addition, few investigations were validated; for example by using statistical re-sampling methods such as the bootstrap6, or by applying the results to an independent set of data3. Consequently, a comprehensive, well-characterized, validated set of prognostic factors that could be utilized to help evaluate clinical investigations of mRCC and further our understanding of the natural history of the disease remained to be defined.
Under the auspices of the Kidney Cancer Association, the International Kidney Cancer Working Group was convened and the first meeting held in October 2002, in Lyon, France to discuss this issue. The consensus of the meeting was that development of a prognostic factors scoring system for survival in mRCC was needed and a collaborative study group was formed with the objective of defining such a system.
The primary goals of this project were to establish a comprehensive database of potential prognostic factors for survival in mRCC, and to derive a single, validated prognostic scoring system that could be used to define risk groups of patients. A secondary goal was to establish the database as a resource that could be used to study the natural history of mRCC and as an aid in the design, analysis, and interpretation of clinical studies of this disease.
Materials and Methods
Project organization and database assembly
On October 17 and 18, 2002, researchers from the United States, France, England and Israel gathered in Lyon, France, to discuss how they could work together to identify prognostic factors in metastatic renal cell cancer. The meeting was organized by the Kidney Cancer Association, based in Evanston, Illinois, USA, and representatives from Centre Léon Bérard in Lyon. Participants included investigators who had previously identified prognostic factors based on retrospective experience, leaders in clinical research and pathology in renal cell cancer, and representatives from Cooperative Groups with experience conducting randomized trials in renal cell cancer. Following the meeting, an international consortium of institutions/organizations with special interest and expertise in mRCC was established. A steering committee was established to oversee the project and to prioritize use of the database once the primary goals of the project were achieved. A protocol was then written which outlined the variables to be collected, the acceptable platforms for data collection and transmission, and how patient confidentiality would be assured. Criteria for data set inclusion in the project were also specified and consisted of the following:
- Minimum of 100 patients available for submission
- Patients diagnosed with advanced renal cell cancer, defined as Stage IV disease according to the staging system in use at the time of study entry, metastatic disease, or disease with advanced tumor stage and positive lymph nodes;
- Enrolled on an institutional review board (IRB)-approved clinical trial between January 1, 1975 and December 31, 2002;
- No prior systemic therapy; and
- Data from the clinical trial should have been previously published.
An effort was made to identify all available datasets available to the consortium that met these criteria. In addition, other groups with potentially eligible data sets were also contacted. After all known groups had been given an opportunity to participate, final datasets were identified; and each participant was sent specific instructions regarding data collection and transmission. The patient-specific data collected included type of treatment on trial, year of entry, patient and disease characteristics, and laboratory parameters, with their associated normal limits. Datasets were forwarded to statisticians at Cleveland Clinic Foundation, who collated data into a single analysis dataset. The collated dataset was then forwarded to the statistical offices of the Eastern Cooperative Oncology Group (ECOG), Memorial Sloan-Kettering Cancer Institute, and the United Kingdom Medical Research Council for analysis. All analysis sites were responsible for assuring the confidentiality and security of data stored at the site, and all analysis sites operated under oversight of a local IRB. A patient index number was employed, but no patient identifiers such as name or medical record number were included in the datasets.
Data standardization and transformation
Some standardization was done to assure consistency of reporting units. Karnofsky performance status (KPS) was converted to ECOG performance status (PS) by considering KPS of 100 equal to ECOG PS of 0, KPS of 80–90 equal to ECOG PS of 1, and KPS<=70 equal to ECOG PS>=210. Values of hemoglobin, creatinine, calcium and bilirubin reported in SI units were converted to the more commonly reported standard units using published conversion factors.
Exploratory and univariate analyses
The primary endpoint was survival, defined as time from the date of entry onto the clinical trial to the date of death or the date last known alive.
Descriptive statistics such as means, medians, confidence intervals, ranges, and proportions were used to characterize patients. The method of Kaplan and Meier11 was used to estimate survival and generate plots, and the log-rank test was used to determine differences attributable to prognostic factors. Hazard ratios and 95% confidence intervals were estimated using Cox proportional hazards models12.
Multivariable analyses and model construction
Five variables (hemoglobin, white blood count, lactate dehydrogenase (LDH), alkaline phosphatase, and calcium) were standardized by dividing by their site-and gender-specific median value and then multiplying by their gender-specific median to transform the values to a common scale. Stata’s ice package13 was used to generate ten imputations of the dataset. Survival time was represented in the imputation model by the empirical cumulative hazard function for each individual, and the censoring indicator. Variables having a skew distribution (white blood count, alkaline phosphatase, days from diagnosis to study entry, and lactate dehydrogenase) were transformed toward normality using Box-Cox methodology before imputation and back-transformed afterwards.
Cox proportional hazards models were used for initial exploratory analyses. After observing significant non-proportionality of the hazard in the Cox model and exploring several other models, a log-logistic survival model, stratified by participating center, was determined to fit the data well. Next, multivariable fractional polynomial models were built for each of the 10 imputations separately, using Stata’s streg and mfp commands with option distribution(llogistic)to fit the log-logistic survival model. A significance level of 0.0044 was used for selection of variables. This significance level gives results similar to use of the BIC (Bayesian information criterion) and helps to avoid creating over-complex models. A model was selected using each imputed dataset, and the final model was obtained as the majority vote across the imputations. Rubin’s rules14 for multiply imputed estimates were used to combine the estimates and compute standard errors. Just as in a logistic regression model, each estimate (regression coefficient) represented the change in the log odds of death up to any given time point for a unit change in the prognostic factor.
Once a final model was defined, patients were divided into risk groups in two ways: 3 groups according to low, medium and high risk (placing cut points at the 25th and 75th centiles of the model’s risk score distribution); and 10 groups, using Cox’s 15 cut points. The latter minimize the loss of information for a given number of groups. Because the use of three risk groups is familiar in the clinical setting, the 3-group paradigm is used hereafter to characterize the model.
Internal and External Validation and Calibration
The model’s discriminatory value was estimated using the C index and its 95% confidence interval, as implemented by Pencina and d’Agostino16. Proportion of variability explained by the model was further explored using the D index developed by Royston and Sauerbrei17.
The model was also externally validated using an independent dataset of 645 patients treated with tyrosine kinase inhibitor (TKI) therapy16. To do this, we calculated a risk score for each patient in the validation dataset using the final model equation described above. That is, weights derived from the model were applied to the value of each factor for each patient, with factors transformed if necessary (see Table 3). Missing factors were imputed for each patient as the mean value of the (transformed) factor in the derivation dataset. The model’s discriminatory value in the validation dataset was assessed using the C index. Patients were divided into risk groups using the 25th and 75th centiles of the distribution of scores in the validation dataset.
Table 3.
Parameter Estimates and Standard Errors – Final Model
| β | SE | |
|---|---|---|
| Square Root of Days from Diagnosis to Study Entry | −0.0192 | 0.002 |
| ECOG Performance Status 0 | −1.524 | 0.11 |
| ECOG Performance Status 1 | −0.838 | 0.11 |
| Number of Metastatic Sites | 0.324 | 0.032 |
| Protocol Immunotherapy | −0.574 | 0.094 |
| Natural log of Hemoglobin | −2.47 | 0.20 |
| Natural log of LDH | 0.611 | 0.062 |
| Square Root of White Blood Count | 0.623 | 0.071 |
| 1/Square Root of Alkaline Phosphatase | −6.665 | 1.39 |
| Serum Calcium | 0.105 | 0.033 |
The model was then recalibrated using the proportional odds recalibration model described by Miller and Hui17. The fitted model contains an intercept term to represent the baseline level of risk in the population, a term representing the gradient of risk over time across all prognostic subgroups, and a term for the slope on the prognostic index, representing the predictive ability of the index. The recalibrated model was used to evaluate the fit of the prognostic index model and can be used to estimate survival probabilities for individual patients.
Results
Final database and model
A total of 3748 patients were treated by 11 groups and contributed information to the project. Table 1 summarizes the contributing groups and datasets. Patients began treatment between 1975 and 2002. European groups enrolled 39% of the patients and US groups enrolled 61%.
Table 1.
Contributing Institutions/Groups
| Institution/Group and Country or Region | Patients |
|---|---|
| Groupe Français d’Immunothérapie, France | 777 |
| Eastern Cooperative Oncology Group, United States | 743 |
| Memorial Sloan-Kettering Cancer Institute, United States | 551 |
| Cleveland Clinic Foundation, United States | 351 |
| Medical Research Council, United Kingdom | 341 |
| Cytokine Working Group, United States | 199 |
| EORTC, Europe | 176 |
| University of Washington, United States | 170 |
| UCLA, United States | 159 |
| Norwegian Radium Hospital | 153 |
| Our Lady of Mercy Cancer Center, United States | 128 |
Variables for which more than 40% of the observations were missing were not considered as potential predictors. Other variables or alternative parameterizations of factors were considered but not included in the final model-building process. Although not considered for the model, the information contained in these variables may be of use to other investigators; therefore, these are described in Supplemental Tables 1 through 4.
Table 2 provides the frequency of predictor variables tested for inclusion, including median survival, percent missing, number of events, and log-rank p-values from univariate analyses.
Table 2.
Univariate Analyses of Variables Included in the Model
| Parameter | % Missing | Level | Median Survival (yrs) | Total | Failed | Log-rank p |
|---|---|---|---|---|---|---|
| Protocol Treatment: | 0 | None | 0.55 | 1030 | 1008 | <0.0001 |
| Immunotherapy | IFN Only | 1.01 | 1034 | 918 | ||
| IL2 Only | 1.22 | 705 | 590 | |||
| IFN & IL2 | 1.19 | 979 | 796 | |||
| Prior Radiotherapy | 9.6% | No | 1.02 | 2780 | 2398 | <0.0001 |
| Yes | 0.74 | 608 | 577 | |||
| Lung Metastases | 1.0% | No | 0.96 | 1033 | 919 | 0.29 |
| Yes | 0.91 | 2676 | 2367 | |||
| Liver Metastases | 3.4% | No | 1.00 | 2915 | 2571 | <0.0001 |
| Yes | 0.59 | 706 | 657 | |||
| Bone Metastases | 4.3% | No | 1.01 | 2508 | 2198 | <0.0001 |
| Yes | 0.74 | 1077 | 996 | |||
| Retroperitoneal or Mediastinal | 38.6% | No | 0.94 | 644 | 571 | 0.13 |
| Lymph Node or Local Recurrence | Yes | 0.87 | 1656 | 1487 | ||
| 0 | 1 | 1.21 | 1387 | 1173 | <0.0001 | |
| Number of Metastatic Sites | ||||||
| 2 | 0.92 | 1392 | 1243 | |||
| 3 | 0.74 | 684 | 623 | |||
| 4 | 0.53 | 232 | 224 | |||
| 5 or more | 0.56 | 53 | 49 | |||
| Sex | 0 | Male | 0.94 | 2631 | 2305 | 0.13 |
| Female | 0.91 | 1117 | 1007 | |||
| Performance Status | 1.3% | 0 | 1.50 | 1467 | 1198 | <0.0001 |
| 1 | 0.77 | 1836 | 1686 | |||
| >=2 | 0.36 | 395 | 384 | |||
| Year on Study | 0 | 1975–1984 | 0.55 | 661 | 653 | <0.0001 |
| 1985–1994 | 0.96 | 1727 | 1580 | |||
| 1995–2002 | 1.17 | 1360 | 1079 | |||
| Age at Study Entry | 0.1% | <=58 | 0.96 | 1988 | 1740 | 0.01 |
| >58 | 0.89 | 1755 | 1569 | |||
| Days from Diagnosis to Study Entry* | 0.6% | <=134 | 0.73 | 1865 | 1685 | <0.0001 |
| >134 | 1.19 | 1862 | 1612 | |||
| Hemoglobin (g/dL)* | 5.4% | <=12.5 | 0.64 | 1801 | 1677 | <0.0001 |
| >12.5 | 1.42 | 1746 | 1472 | |||
| Alkaline Phosphatase (U/L)* | 40.8% | <=99.0 | 1.46 | 1124 | 947 | <0.0001 |
| >99.0 | 0.84 | 1093 | 975 | |||
| Lactate Dehydrogenase (U/L)* | 37.0% | <=193.0 | 1.20 | 1190 | 1059 | <0.0001 |
| >193.0 | 0.76 | 1170 | 1075 | |||
| White Blood Count (K/uL)* | 42.1% | <=7.6 | 1.37 | 1132 | 929 | <0.0001 |
| >7.6 | 0.82 | 1129 | 1003 | |||
| Calcium (mg/dL)* | 31.6% | <=9.5 | 0.94 | 1301 | 1157 | 0.16 |
| >9.5 | 0.88 | 1263 | 1110 | |||
| % Failed | ||||||
| Group | 0 | A | 1.25 | 80.6% | <0.0001 | |
| B | 0.55 | 99.2% | ||||
| C | 0.89 | 95.5% | ||||
| D | 1.09 | 84.6% | ||||
| E | 1.80 | 64.1% | ||||
| F | 0.83 | 69.9% | ||||
| G | 1.17 | 80.4% | ||||
| H | 0.67 | 94.1% | ||||
| I | 1.11 | 98.0% | ||||
| J | 1.08 | 79.9% | ||||
| K | 1.47 | 85.9% |
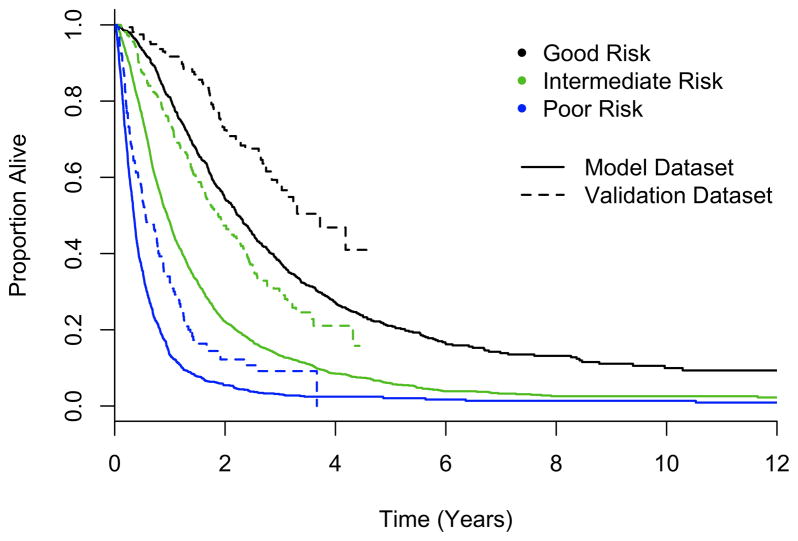
The final model was a composite derived from each of 10 imputed datasets; variables included in each of the candidate models are shown in Supplemental Table 5. Table 3 shows the form of the variables used, and the associated parameter estimates (regression coefficients or weights) and standard errors from the final model. The prognostic index from the model is the sum of the variables, each multiplied by its weight. A positive weight attached to a prognostic factor indicates higher mortality with higher levels of the factor, and a negative weight, lower mortality; similarly for the prognostic index. Three risk groups were formed by splitting at index values of −2.755 (25th percentile) and −1.253 (75th percentile), where patients with index values less than −2.755 had the most favorable outcome. Figure 1 (solid line) shows overall survival for each of the risk groups.
Figure 1.
Overall survival by risk category for the original dataset (solid line) and validation dataset (dashed line).
Internal and external validation
Internal validation of the model yielded a C index of 0.712 (95% confidence interval, 0.703 – 0.721). This indicates that the model has good discriminatory ability and suggests that subjects with longer predicted survival times actually lived longer. Using the measure proposed by Royston and Sauerbrei to estimate the proportion of variability explained by the model, we estimate that the model’s D index is 0.320 (95% confidence interval, 0.295 – 0.345), which is quite reasonable for oncology studies.
External validation was conducted using data from Heng et al18. Characteristics of the patients in the validation dataset are shown in Table 4. The regression equation resulting from the model fitting process described above was applied to each patient in the validation dataset. Weighted values used in place of missing observations are shown in Supplemental Table 6. Some differences between the dataset used to build the model and the validation dataset should be noted. First, the validation dataset did not contain information about patients’ baseline alkaline phosphatase. White blood count was not available, but neutrophils were measured. An equation was derived for estimating white blood count from neutrophils using a separate kidney cancer dataset where both were available. As a result, white blood count was defined as 0.69 times the neutrophil count plus 1.90 times the square root of neutrophils. Performance status was provided using the Karnofsky index; the rules provided in the methods section were used to transform the values to ECOG performance status. Whereas the regression equation treated the number of metastatic sites as a whole number (1, 2, 3…), the validation dataset used a binary coding, where 1 represented greater than 1 metastatic site. A value of 0 was considered to represent 1 metastatic site and a value of 1 was considered to represent 2 metastatic sites. The model contained total calcium, whereas the validation dataset contained corrected calcium.
Table 4.
Characteristics and Univariate Analyses of Model Variables for Patients in Validation Dataset
| Parameter | % Missing | Level | Median Survival (yrs) | Total | Failed | Log-rank p |
|---|---|---|---|---|---|---|
| Days from Diagnosis to Treatment Start* | 0 | <=506 | 1.31 | 212 | 111 | <0.0001 |
| >506 | 2.44 | 167 | 155 | |||
| Karnofsky Performance Status | 4.7% | <=80 | 1.07 | 336 | 243 | <0.0001 |
| >80 | 3.24 | 279 | 115 | |||
| Number of Metastatic Sites | 0 | 1 | 2.16 | 156 | 81 | 0.11 |
| >1 | 1.71 | 489 | 298 | |||
| Prior Immunotherapy | 0 | No | 1.71 | 431 | 234 | 0.82 |
| Yes | 1.83 | 214 | 145 | |||
| Hemoglobin (g/dL)* | 5.1% | <=12.9 | 1.23 | 310 | 218 | <0.0001 |
| >12.9 | 2.71 | 302 | 142 | |||
| LDH (U/L)* | 15.7% | <=197.0 | 2.21 | 273 | 144 | 0.0016 |
| >197.0 | 1.62 | 271 | 173 | |||
| Neutrophils (K/uL)* | 9.6% | <=4.86 | 2.55 | 293 | 148 | <0.0001 |
| >4.86 | 1.19 | 290 | 193 | |||
| Corrected Calcium* | 7.4% | <=9.48 | 2.41 | 305 | 159 | <0.0001 |
| >9.48 | 1.36 | 292 | 192 |
The overall C index was estimated for the validation dataset to be 0.741 (95% confidence interval, 0.714 – 0.768). The D index for the model was 0.321(95% confidence interval, 0.296 – 0.345). Thus, despite the differences between the two data sets, we conclude that the model also has good discriminatory ability among patients treated with TKI therapy. The proportion of variability explained by the model in the two datasets is quite similar. Figure 1 (dotted lines) plots survival for each of the risk groups derived from the validation dataset.
To further evaluate the model, a proportional odds recalibration model was applied to the validation dataset. If the original model fits the validation dataset well, then (a) the constant terms will be similar, reflecting similar baseline risks, (b) the gradients of risk over time in the two datasets will be similar, and (c) the slope on the prognostic index will be similar between the two datasets. Coefficients for these parameters for both datasets are shown in Supplemental Table 7. While the gradients over time were similar between the two datasets (1.733 vs. 1.737) and the coefficients corresponding to the slope were similar (1.0 vs. 1.049), the baseline risk for patients in the validation dataset was much lower than in the derivation dataset (1.019 vs. 2.005). This is consistent with Figure 1 and our belief that treatment with TKI therapy confers an improvement in overall survival compared to previous therapies.
The constant parameter from the calibrated model was used with the other parameter estimates from the derivation model to provide a prediction model suitable for use with patients treated in the TKI era.
Given evidence that the baseline risk of death is lower among patients treated in the TKI era, cutpoints for the risk categories were adjusted to balance the group sizes. Table 5 provides a summary of overall survival by risk category, showing the cutpoints for each group. Risk categories should be assigned differently for patients treated in the pre-TKI era and the TKI era. Figure 1 (dotted line) shows overall survival by risk group for the validation dataset. Table 5 also provides a summary of overall survival for each of the datasets.
Table 5.
Summary of Overall Survival by Risk Category
| Cut Points | Patients | Deaths | Median Survival (Years) | 95% Confidence Interval | ||
|---|---|---|---|---|---|---|
| Model | Overall | 3748 | 3312 | 0.93 | 0.88 – 0.98 | |
| Dataset | Good Risk | ≤ −2.755 | 937 | 698 | 2.24 | 2.10 – 2.44 |
| Intermediate Risk | > −2.755& ≤ −1.253 | 1874 | 1703 | 0.96 | 0.89 – 1.01 | |
| Poor Risk | > −1.253 | 937 | 911 | 0.35 | 0.33 – 0.37 | |
| Validation | Overall | 645 | 379 | 1.78 | 1.62 – 1.99 | |
| Dataset | Good Risk | ≤ −2.67 | 161 | 61 | 3.72 | 2.94 – nyr* |
| Intermediate Risk | > −2.67& ≤ −1.05 | 324 | 188 | 1.88 | 1.65 – 2.25 | |
| Poor Risk | >1.05 | 160 | 130 | 0.56 | 0.49 – 0.78 |
Supplemental Table 6 can be used as a worksheet to calculate the risk score for a patient treated in the TKI era. The cutpoints used for deriving and validating the model were established using datasets with patterns of missing data unlikely to exist for individual patients. For purposes of illustrating and validating the model, missing values were naively estimated, presenting a conservative portrait of the test and validation datasets. To provide more accurate cutpoints for the prediction model shown in Supplemental Table 6, we applied the previously described multiple imputation techniques to the validation dataset to minimize the impact of missing data while establishing cutpoints. The “complete-data” cutpoints shown in Supplemental Table 6 (−2.70 and −0.98) are appropriate for prospectively assigning risk categories to future patients treated in the TKI era.
Supplemental Figures 1 and 2 and Supplemental Table 8 show how the model performs in subgroups defined by protocol treatment. The model distinguishes risk groups within all of these subsets. As expected, patients in favorable subsets have improved survival within each risk category compared to those in the contrasting, less-favorable subsets.
Discussion
Through this international effort, a database of 3748 patients has been assembled. We believe that this is the largest database ever assembled for prognostic factor evaluation in metastatic renal cell carcinoma. Using this database, we proposed a single model that accurately estimates the risk of death from kidney cancer, which is based on a comprehensive assessment of previously reported clinical prognostic factors. We demonstrated that it retains value in the era of patients treated with tyrosine kinase inhibitors.
The number of reports of factors prognostic for survival among patients treated prior to the TKI era is extensive; such reports among patients treated with TKIs are only beginning to emerge as information about survival endpoints on randomized trials accumulates. The report by Heng et al.18, whose data were used to validate our model, is among the first of such reports. The model they reported, based on consecutive case series from multiple institutions, included ECOG performance status, time from diagnosis to treatment, and the laboratory parameters of hemoglobin, corrected calcium, neutrophil count, and platelet count. All of these except platelet count were represented in our model; platelets were unavailable for over half the patients in our dataset and were thus not considered. While the numbers are not directly comparable since different methods were used for calculating them, the c-index of 0.741 achieved by this model in the validation dataset was very similar to the bias-adjusted concordance statistic of 0.73 reported by Heng et al. themselves. Patil et al.20 report prognostic factors for overall survival from a phase III trial of sunitinib versus interferon-alpha as first-line therapy for mRCC. Among patients randomized to sunitinib, prognostic factors included time from diagnosis to treatment, serum LDH, corrected calcium, hemoglobin level, ECOG performance status, and the presence of bone metastases. All of these except ECOG performance status were also prognostic among patients randomized to interferon-alfa. Motzer et al.21, in their report of a second-line trial of everolimus for mRCC, identified poor performance status, high corrected calcium, low hemoglobin, and prior treatment with sunitinib as prognostic for shorter survival. These reports substantiate our finding that factors that were important before the introduction of TKI therapy remain so in the current era.
In the prior era, it was generally acknowledged that, while important in the localized setting, biologic features of the tumor were not important prognostic factors in the metastatic setting. This was suggested by the current analysis as well. Although the rate of missing information was too high to consider the factors for inclusion in the model, univariate assessments of histology and grade failed to demonstrate prognostic significance. In the modern era, the advent of molecular-based technologies has led to a better understanding of the underlying biology of RCC, and an increasing number of molecular-level factors are being reported to be of prognostic and/or predictive value in the metastatic setting. It will be important, therefore, to assess these new markers within the context of the current model in order to evaluate fully their clinical utility.
The study has limitations that should be acknowledged. Patients were treated between 1975 and 2002, representing a heterogeneous period for treatment of the disease. While the use of high-dose interleukin-2 was approved for treatment of mRCC during this time, many of the other experimental treatments were ineffective. Thus, the database may, to a great extent, represent the natural history of the disease in the absence of an effective therapy. Heterogeneity of the data sources, while enhancing the generalizability of the model, imposes some restrictions on the choice of potential prognostic factors by limiting the model to the set of commonly available factors. Use of the validation dataset required transforming some variables and making assumptions about others. The analysis is thus not ideal, but the ability of the model to demonstrate such good concordance in the face of these compromises is encouraging with respect to the model’s future utility.
While it is possible that differences or imbalances between the datasets exist, the improvement in overall survival reflected in the validation dataset suggests that patients treated today have a favorable shift in prognosis compared to previously treated patients, almost equivalent to a risk category. As illustrated in Figure 1, today’s intermediate risk patients have survival that is similar to that of good risk patients treated during the chemotherapy and cytokine eras. While this is encouraging, the need remains for additional treatment options as second-line therapy and for more effective treatments in general for patients with mRCC.
Supplementary Material
1
2
3
Statement of Translational Relevance.
Understanding of factors prognostic for survival among patients with metastatic renal cell cancer (mRCC), in particular those reported here which have been captured over many years in many parts of the globe, will contribute to more thorough understanding of mechanisms of metastasis and better treatment for the disease. Although the studies reported here predate the current era of treatment with tyrosine kinase inhibitors, the continued relevance of these factors is demonstrated.
Acknowledgments
Supporting Grants
Financial Support: Travel support for the project was provided by the Kidney Cancer Association.
The authors would like to thank the Kidney Cancer Association for its support, and in particular the family of Maita Lyn Gerber, who provided financial support for the project. We are grateful to Wanling Xie and the contributors of the International mRCC Database Consortium for their contributions related to the external validation database. The advice of Hajime Uno in the use and interpretation of concordance statistics was valuable. Finally, we extend sincere appreciation to the groups who contributed data and to the patients who were treated on the clinical trials.
References
- 1.Jemal A, Siegel R, Xu J, et al. Cancer statistics, 2010. CA Cancer J Clin. 2010;60:277–300. doi: 10.3322/caac.20073. [DOI] [PubMed] [Google Scholar]
- 2.Ferlay J, Shin HR, Bray F, Forman D, Mathers C, Parkin DM. GLOBOCAN 2008, Cancer Incidence and Mortality Worldwide: IARC CancerBase No. 10 [Internet] Lyon, France: International Agency for Research on Cancer; 2010. Available from: http://globocan.iarc.fr. [Google Scholar]
- 3.Hollingsworth JM, Miller DC, Daignault S, et al. Rising incidence of small renal masses: a need to reassess treatment effect. J Natl Cancer Inst. 2006;98:1331–1334. doi: 10.1093/jnci/djj362. [DOI] [PubMed] [Google Scholar]
- 4.Elson PJ, Witte RS, Trump DL. Prognostic factors for survival in patients with recurrent or metastatic renal cell carcinoma. Cancer Res. 1988;48:7310–7313. [PubMed] [Google Scholar]
- 5.Palmer PA, Vinke J, Philip T, et al. Prognostic factors for survival in patients with advanced renal cell carcinoma treated with recombinant interleukin-2. Ann Oncol. 1992;3:475–480. doi: 10.1093/oxfordjournals.annonc.a058239. [DOI] [PubMed] [Google Scholar]
- 6.Fossa SD, Kramar A, Droz J-P. Prognostic factors and survival in patients with metastatic renal cell carcinoma treated with chemotherapy or interferon-a. Eur J Cancer. 1994;30:1310–1314. doi: 10.1016/0959-8049(94)90179-1. [DOI] [PubMed] [Google Scholar]
- 7.Motzer RJ, Mazumdar M, Bacik J, Russo P, Berg WJ, Metz EM. Effect of cytokine therapy on survival for patients with advanced renal cell carcinoma. J Clin Oncol. 2000;18:1928–1935. doi: 10.1200/JCO.2000.18.9.1928. [DOI] [PubMed] [Google Scholar]
- 8.Negrier S, Escudier B, Gomez F, et al. Prognostic factors of survival and rapid progression in 782 patients with metastatic renal carcinomas treated by cytokines: a report from the Groupe Francais d’Immunotherapie. Ann Oncol. 2002;13:1460–1468. doi: 10.1093/annonc/mdf257. [DOI] [PubMed] [Google Scholar]
- 9.Atzpodien J, Royston P, Wandert T, et al. Metastatic renal carcinoma comprehensive prognostic system. Br J Cancer. 2003;88:348–353. doi: 10.1038/sj.bjc.6600768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ma C, Bandukwala S, Burman D, et al. Interconversion of three measures of performance status: an empirical analysis. Eur J Cancer. 2010;46:3175–3183. doi: 10.1016/j.ejca.2010.06.126. [DOI] [PubMed] [Google Scholar]
- 11.Kaplan EL, Meier Nonparametric estimation from incomplete observations. J Amer Stat Assn. 1958;53:457–481. [Google Scholar]
- 12.Cox DR. Regression models and life tables. J Royal Stat Soc B. 1972;34:181–220. [Google Scholar]
- 13.Royston P, Sauerbrei W. Building multivariable regression models with continuous covariates in epidemiology – with an emphasis on fractional polynomials. Methods Inf Med. 2005;44:561–571. [PubMed] [Google Scholar]
- 14.Rubin DB. Multiple Imputation for Nonresponse in Surveys. Wiley; New York: 1987. [Google Scholar]
- 15.Cox DR. Note on grouping. J Amer Stat Assn. 1957;52:543–547. [Google Scholar]
- 16.Pencina MJ, D’Agostino RB. Overall c as a measure of discrimination in survival analysis: model specific population value and confidence interval estimation. Stat Med. 2004;23:2109–2123. doi: 10.1002/sim.1802. [DOI] [PubMed] [Google Scholar]
- 17.Royston P, Sauerbrei W. A new measure of prognostic separation in survival. Stat Med. 2004;23:723–748. doi: 10.1002/sim.1621. [DOI] [PubMed] [Google Scholar]
- 18.Heng DYC, Xie W, Regan MM, et al. Prognostic factors for overall survival in patients with metastatic renal cell carcinoma treated with vascular endothelial growth factor-targeted agents: results from a large, multicenter study. J Clin Oncol. 2009;27:5794–5799. doi: 10.1200/JCO.2008.21.4809. [DOI] [PubMed] [Google Scholar]
- 19.Miller ME, Hui SL. Validation techniques for logistic regression models. Stat Med. 1991;10:1213–1226. doi: 10.1002/sim.4780100805. [DOI] [PubMed] [Google Scholar]
- 20.Patil S, Figlin RA, Hutson TE, et al. Prognostic factors for progression-free and overall survival with sunitinib targeted therapy and with cytokine as first-line therapy in patients with metastatic renal cell carcinoma. Ann Oncol. 2011;22(2):295–300. doi: 10.1093/annonc/mdq342. [DOI] [PubMed] [Google Scholar]
- 21.Motzer RJ, Escudier B, Oudard S, et al. for the RECORD-1 Study Group. Phase 3 trial of everolimus for metastatic renal cell carcinoma: final results and analysis of prognostic factors. Cancer. 2010;116(18):4256–4265. doi: 10.1002/cncr.25219. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
1
2
3