Exploring single-sample SNP and INDEL calling with whole-genome de novo assembly (original) (raw)
Abstract
Motivation: Eugene Myers in his string graph paper suggested that in a string graph or equivalently a unitig graph, any path spells a valid assembly. As a string/unitig graph also encodes every valid assembly of reads, such a graph, provided that it can be constructed correctly, is in fact a lossless representation of reads. In principle, every analysis based on whole-genome shotgun sequencing (WGS) data, such as SNP and insertion/deletion (INDEL) calling, can also be achieved with unitigs.
Results: To explore the feasibility of using de novo assembly in the context of resequencing, we developed a de novo assembler, fermi, that assembles Illumina short reads into unitigs while preserving most of information of the input reads. SNPs and INDELs can be called by mapping the unitigs against a reference genome. By applying the method on 35-fold human resequencing data, we showed that in comparison to the standard pipeline, our approach yields similar accuracy for SNP calling and better results for INDEL calling. It has higher sensitivity than other de novo assembly based methods for variant calling. Our work suggests that variant calling with de novo assembly can be a beneficial complement to the standard variant calling pipeline for whole-genome resequencing. In the methodological aspects, we propose FMD-index for forward–backward extension of DNA sequences, a fast algorithm for finding all super-maximal exact matches and one-pass construction of unitigs from an FMD-index.
Availability: http://github.com/lh3/fermi
Contact: hengli@broadinstitute.org
1 INTRODUCTION
The rapidly decreasing sequencing cost has enabled whole-genome shotgun (WGS) resequencing at an affordable price. Many software packages have been developed to call variants, including SNPs, short insertions and deletions (INDELs) and structural variations (SVs), from WGS data. At present, the standard approach to variant calling is to map raw sequence reads against a reference genome and then to detect differences from the reference. It is well established and has been proved to work from a single sample to thousands of samples (1000 Genomes Project Consortium, 2010). Nonetheless, a fundamental flaw in this mapping-based approach is that mapping algorithms ignore the correlation between sequence reads. They are unable to take full advantage of data and may produce inconsistent outputs which complicate variant calling. This flaw has gradually attracted the attention of various research groups who subsequently proposed several methods to alleviate the effect, including post-alignment filtering (Ossowski et al., 2008), iterative mapping (Manske and Kwiatkowski, 2009), read realignment (Albers et al., 2010; Depristo et al., 2011; Homer and Nelson, 2010; Li, 2011) and local assembly (Carnevali et al., 2011). However, because these methods still rely on the initial mapping, it is difficult for them to identify and recover mismapped or unmapped reads due to high-sequence divergence, long insertions, SVs, copy number changes or misassemblies of the reference genome. They have not solved the problem from the root.
Another distinct approach to variant calling that fundamentally avoids the flaw of the mapping-based approach is to assemble sequence reads into contigs and to discover variants via assembly-to-assemby alignment. It was probably more widely used in the era of capillary sequencing. The assembly based method became less used since 2008 due to the great difficulties in assembling 25 bp reads, but with longer paired-end reads and improved methodology, de novo assembly is reborn as the preferred choice for variant discovery between small genomes.
For variant discovery between human genomes, however, the assembly based approach has not attracted much attention. Assembling a human genome is far more challenging than assembling a bacterial genome, firstly due to the sheer size of the genome, secondly to the rich repeats and thirdly due to the diploidy of the human genome. Many heuristics effective for assembling small genomes are not directly applicable to the human genome assembly. As a result, only a few de novo assemblers have been applied on human short-read data. Among them, ABySS (Simpson et al., 2009), SOAPdenovo (Li et al., 2010) and SGA (Simpson and Durbin, 2012), as of now, do not explicitly output heterozygotes. Although in theory it is possible to recover heterozygotes from their intermediate output, it may be difficult in practice as the assemblers may not distinguish heterozygotes from sequencing errors. Cortex (Iqbal et al., 2012) is specifically designed for retaining heterozygous variants in an assembly, but it may be missing heterozygotes. ALLPATHS-LG (Gnerre et al., 2011) also paid particular attention to keep heterozygotes, but it still has a relatively low sensitivity. In addition, ALLPATHS-LG only works with reads from libraries with distinct insert size distributions and prefers read pairs with mean insert size below three times of the read length, whereas many resequencing projects do not meet these requirements and thus ALLPATHS-LG may not be applied or work to the best performance. Even if we also include de novo assemblers developed for capillary sequence reads, the version of the Celera assembler used for assembling the HuRef genome (Levy et al., 2007) is the only one that retains heterozygotes while capable of assembling a mammalian genome. At last, one may think to map sequence reads back to the assembled contigs to recover heterozygous events, but this procedure will be affected by the same flaw of read mapping. To the best of our knowledge, no existing de novo assemblers are able to achieve the sensitivity of the standard mapping-based approach for a diploid mammalian genome.
In this article, we will show that the assembly based variant calling can achieve an SNP accuracy close to the standard mapping approach and have particular strength in INDEL calling, confirming previous studies (Iqbal et al., 2012). In addition, the de novo assembly algorithm, fermi, developed for this practice is also a capable assembler for human assembly.
2 METHODS
The methods section is organized as follows. We first review the history of de novo assembly in the theoretical aspects, which leads to the rationale behind fermi: to use unitigs as a lossless representation of reads. We then summarize the notations used in the article and introduce bidirectional FM-index for DNA sequences. We will present several algorithms for assembling using the bidirectional FM-index. The key algorithm is based on previous works (Simpson and Durbin, 2010), but we need to adapt it to our new index. We also remove the recursion in the original algorithm. Finally we will discuss practical concerns in implementation.
2.1 Theoretical background
2.1.1 A history of the OLC paradigm
Computer assisted sequence assembly can be dated back to the late 1970s (Gingeras et al., 1979; Staden, 1979). In 1984, (Peltola et al., 1984) first formulated the DNA assembling problem as finding the shortest string (the assembly) such that each sequence read can be mapped to the assembly within a required error rate. To solve the problem, they proposed a three-step procedure, which is essentially the overlap-layout-consensus (OLC) approach.
Myers (1995) pointed out that reducing DNA assembly to a shortest string problem is flawed in the presence of repeat. He further proposed the concept of overlap graph, where a vertex corresponds to a read and a bidirectional edge to an overlap. Naively, the DNA assembling problem can be cast as finding a path in the overlap graph such that each vertex/read is visited exactly once (though edge/overlap caused by repeats are not required to be traversed), equivalent to a Hamilton path problem which is known to be NP-complete. This has led many to believe that the OLC approach is theoretically crippled.
However, it is worth pointing out that although the assembly problem can be reduced to a Hamilton path problem, it can be reduced to other problems as well and in practice almost no assemblers try to solve a Hamilton path problem. We note that a fundamental difference between a generic graph and an overlap graph is the latter can be transitively reduced while retaining the read relationship. More formally, if _v_1→_v_2, _v_2→_v_3 and _v_1→_v_3 are all present, edge _v_1→_v_3 is said to be reducible. When we removed all the contained reads and reducible edges, a procedure called transitive reduction, the resulting graph is still a loyal representation of the overlap graph (Myers, 1995), but the path corresponding to the assembly is not a Hamilton path any more because reads from repetitive regions need to be traversed multiple times.
In a transitively reduced graph, if there exists _v_1→_v_2 with the out-degree of _v_1 and in−degree of _v_2 both equal to 1, we are able to merge _v_1 and _v_2 into one vertex without altering the topology of the graph. After we performed all possible merges, we get a unitig graph in which each vertex corresponds to a unitig, representing a maximal linear sequence that can be resolved by reads. Multiple copies of a repeat may be collapsed to a single unitig. The concept of unitig helps to greatly simplify an assembly graph. It has played a central role in the Celera assembler (Myers et al., 2000).
Finding the optimal tour in a unitig graph is still NP-hard (Medvedev et al., 2007), but such a formulation may not be useful in practice as we can rarely assemble the entire genome into one string. A more practical solution is to compute a traversal count for each edge by solving a minimum cost network flow problem (Myers, 2005) and to drop edges with zero count as false overlaps. In the resulting graph, each unambiguous path can be considered to spell a contig.
Computing traversal counts in a transitively reduced graph can be conducted in small subgraphs separated by some unambiguous edges. The overall time complexity is not much worse than linear—the worst case almost never happens globally. However, deriving an overlap graph takes O(N2) time, where N is the number of reads, and transitive reduction takes at least O(E) time, where E is the number of edges which is usually much larger than N. This still makes an OLC-based approach less favorable in short-read assembly where N can be of the order of 109.
A breakthrough achieved by Simpson and Durbin (2010) finally solved this last remaining problem at least when we only consider exact overlaps. These authors developed an O(N) algorithm to find all the irreducible edges, effectively replacing the overlapping and transitive reduction phases.
In summary, in the OLC paradigm, contig sequences can be constructed in a time roughly linear in the total length of reads, though deriving a single-assembled sequence is NP-hard in theory.
2.1.2 De Bruijn graph and read coherence
The de Bruijn graph is an alternative graph representation of sequence reads (Idury and Waterman, 1995). It can be trivially constructed with a simple linear-time algorithm and finding the optimal tour has polynomial-time solutions. These make the de Bruijn graph approach very attractive for assembling many short reads.
However, de Bruijn is ‘lossy’. From a theoretical point view, a de Bruijn graph is equivalent to an overlap graph built by splitting a long read into overlap _k_-mers and requiring (_k_−1)-mer exact overlaps between non-redundant _k_-mers. Such a graph does not have transitive edges. Because long reads all effectively work as _k_-bp reads in a de Bruijn graph, long-range information is lost. As a result, a path in the graph may be invalidated by reads. In contrast, in a unitig graph or equivalently a string graph each path models a valid assembly from input reads. Myers (2005) called this property of path consistency as read coherence.
Losing long-range information in reads, a de Bruijn graph by itself has reduced power to resolve short repeats. This flaw is usually amended by solving a Eulerian superpath problem (Pevzner et al., 2001) whereby we map reads back to the graph and bisect repeats shorter than the reads, a procedure some also called as read threading. Many de Buijn graph-based assemblers essentially take this strategy (Chaisson et al., 2009; Li et al., 2010; Zerbino et al., 2009), though they may use different terminologies. With read threading, it is possible to transform a de Bruijn graph to a coherent graph, but finding the optimal solution is known to be NP-hard (Medvedev et al., 2007) and may be complex to implement given rich repeat structures.
2.1.3 Concluding remark
We noted that we only focused on the theoretical aspects of de novo assembly. In practice, many assemblers derived the final assembly by applying heuristics on the simplified graph instead of solving a network flow problem or a Eulerian problem. Furthermore, correcting errors, utilizing read pairs and controlling memory usage all pose challenges to large-scale de novo assembly. Many practical problems are not solved perfectly. De novo assembly is still a field under active development.
2.2 Rationale
Being coherent, a perfectly constructed unitig graph annotated with per-unitig read counts in fact encapsulates all the information of reads and encodes no information invalidated by reads. In this sense, any unitig-based analysis has an equivalent read-based analysis, and vice versa. This article just uses this property to explore the applications for which we usually rely on reads.
2.3 Strings and FM-index
2.3.1 Strings with multiple sentinels
Let Σ={$, A, C, G, T, N} be the alphabet of DNA sequences with a predefined lexicographical order $ < A < C < G < T < N, where ‘N’ represents an ambiguous base and ‘$’ is a sentinel that marks the end of a string. An element in Σ is called a symbol and a sequence of symbols is called a string. Given a string T, let |T| be the length of the string, _T_[_i_], _i_=0,…, |T|−1, be the _i_-th symbol in the string, _T_[i, _j_], 0≤_i_≤_j_≤|T|, be a substring and T _i_=_T_[i, |T|−1] be a suffix of T (Table 1). Following the definition by Siren (2009), we define a string terminated with ‘$’ as a text. A text may have multiple sentinels. In a text T, if _T_[_i_]=$ and _T_[_j_]=$, we mandate _T_[_i_]<_T_[_j_] if and only if i < j. Thus when we compare two suffixes of T, we do not need to compare beyond a sentinel because each sentinel has a different lexicographical rank.
Table 1.
Notations
| Symbol | Description |
|---|---|
| T | String: _T_=_a_0_a_1… a _n_−1 with a _n_−1 = $ |
| |T | |
| _T_[_i_] | The _i_−th symbol in string T: _T_[_i_]=a i |
| _T_[i, _j_] | Substring: _T_[i, _j_]=a _i_… a j |
| T i | Suffix: T _i_=_T_[i, _n_−1] |
| S | Suffix array; S(i) is the position of the _i_-th smallest suffix |
| B | BWT: _B_[_i_]=_T_[S(i)−1] if S(i)>0 or _B_[_i_]=$ otherwise |
| C(a) | Accumul. count array: C(a)=|{0≤_i_≤_n_−1 : _T_[_i_]<a} |
| O(a, i) | Occurrence array: O(a, i)=|{0≤j_≤_i:_B_[_j_]=a} |
| P ○ W | String concatenation of string P and W |
| Pa | String concatenation of string P and symbol a: _Pa_=P ○ a |
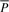 |
Watson–Crick reverse complement of DNA string P |
For two strings P and W, let P ○ W be their string concatenation. We may sometimes write P ○ W as PW if it is unambiguous in the context. Given an ordered set of texts, we call their ordered string concatenation as a collection, which is also a text. For example, suppose we have two reads. The first is ACG and the second is GTG. The collection of the two reads is T = ACG$GTG$. Suffix _T_2 < _T_6 because the first sentinel is lexicographically smaller than the second.
For convenience, we assign an integer from 0 to 5 to ‘$’, ‘A’, ‘C’, ‘G’, ‘T’ and ‘N’, respectively. We may use both the integer and the letter representations throughout the article. In addition, given a symbol a, we define  as the Watson–Crick complement of a. We regard the complement of ‘$’ and ‘N’ is identical to itself.
as the Watson–Crick complement of a. We regard the complement of ‘$’ and ‘N’ is identical to itself.
2.3.2 FM-index
The suffix array S of text T is a permutation of integers between 0 and |T|−1, where S(i), 0≤i<|T|, is the position of the _i_-th smallest suffix of T. Given a string P, the suffix array interval I l(P), I u(P)] of P in T is defined as
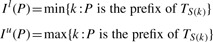
For convenience, we also define I s(P)=I u(P)−I l(P)+1 as the size of the interval.
The Burrows–Wheeler Transform (Burrows and Wheeler, 1994), or BWT, of T is a permutation of symbols in T. The BWT string B is computed as _B_[_i_]=_T_[S(i)−1] for S(i)>0 and _B_[_i_]=$ otherwise. Given a text T, also define the accumulative count array C(a) as the number of symbols in T that are lexicographically smaller than a, and the occurrence array O(a, i) as the occurrence of symbols a in _B_[0,_i_].
FM-index (Ferragina and Manzini, 2000) is a compressed representation of the BWT B, the occurrence array O(a,i) and the suffix array S(i). The key property of FM-index is
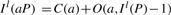 |
(1) |
|---|
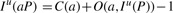 |
(2) |
|---|
and I l(aP)≤I u(aP) if and only if aP is a substring of T. We note that these two equations are different from the ones in our previous paper (Li and Durbin, 2009) in that C(a) and O(a, i) defined here include the sentinels, but the two arrays in the previous paper exclude them.
Given a collection _T_=_Q_0_Q_1… Q _n_−1, we can retrieve sequence Q i in linear time with Algorithm 1 (Mäkinen et al., 2009). The second return value is the rank of Q i which equals |{Q j : Q j<Q i}|.

2.4 FMD-index
Given DNA texts _R_0,…, R _n_−1, define 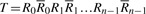 as the bidirectional collection of the texts. We call the FM-index of T as the FMD-index of _R_0,…, R _n_−1 and define the bi-interval of a string P as
as the bidirectional collection of the texts. We call the FM-index of T as the FMD-index of _R_0,…, R _n_−1 and define the bi-interval of a string P as 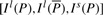 . We will show how to compute the bi-interval of aP and Pa when we know the bi-interval of P.
. We will show how to compute the bi-interval of aP and Pa when we know the bi-interval of P.
We note that when we know the bi-interval of P, I l(aP) and I s(aP) can be readily computed with Equation (1). 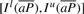 is a sub-interval of
is a sub-interval of 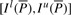 because
because 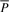 is a prefix of
is a prefix of 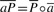 . Due to the innate symmetry of T,
. Due to the innate symmetry of T,  for all _c_∈Σ with
for all _c_∈Σ with 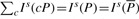 . We can compute I s(cP) for all _c_∈Σ with Equation (1), use these interval sizes to divide
. We can compute I s(cP) for all _c_∈Σ with Equation (1), use these interval sizes to divide 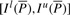 and finally derive
and finally derive 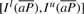 . This completes the computation of the bi-interval of aP (Algorithm 2). Furthermore, when we backward extend P, we actually forward extend
. This completes the computation of the bi-interval of aP (Algorithm 2). Furthermore, when we backward extend P, we actually forward extend 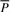 . Conversely, backward extension of
. Conversely, backward extension of 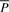 yields forward extension of P (Algorithm 3). An FMD-index is bidirectional.
yields forward extension of P (Algorithm 3). An FMD-index is bidirectional.
In comparison to the bidirectional BWT (Lam et al., 2009) which uses two FM-indices, the FMD-index builds both forward and reverse strand DNA sequences in one index. Although the FMD-index is not applicable to generic texts, it is conceptually more consistent with double-strand DNA and improves the speed of exact matching as we only need to search against one index. For example, BWA-SW (Li and Durbin, 2010) gets a 80% speedup when we adopt the FMD-index as the data structure.
2.5 Unitig construction
2.5.1 Labeling reads and overlaps
Given a bidirectional collection 
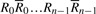 , fermi labels the _i_-th input read R i with an ordered integer pair [k, l_], where k is the rank of R i and l the rank of
, fermi labels the _i_-th input read R i with an ordered integer pair [k, l_], where k is the rank of R i and l the rank of 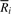 . The pair [k, l_] can be computed by GetSeq(2_i) and GetSeq(2_i+1), respectively. Obviously, if read R i is labeled by [k, _l_],
. The pair [k, l_] can be computed by GetSeq(2_i) and GetSeq(2_i+1), respectively. Obviously, if read R i is labeled by [k, _l_], 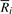 should be labeled by [l, _k_], with the two integer swapped.
should be labeled by [l, _k_], with the two integer swapped.
For two reads labeled by [k, _l_] and [_k_′, _l_′], if the tail (3′ end) of read [k, _l_] overlaps the head (5′ end) of [_k_′, l_′], we use an unordered integer pair 〈_l, _k_′〉 to label the overlap. Such is a tail-to-head overlap. Similarly, we use 〈_l_′, k_〉 for a head-to−tail overlap, 〈_l, l_′〉 for tail-to−tail and 〈_k, _k_′〉 for a head-to-head overlap. The four types of overlaps correspond to the four types of bidirectional edges in the bidirectional overlap graph (Myers, 1995).


2.5.2 Finding irreducible overlaps
Finding irreducible overlaps plays a central role in fermi as well as in SGA. Given its importance, we present a restructured version of this algorithm (SD10; Simpson and Durbin, 2010) using our notations (Algorithm 4).
In Algorithm 4, Line 1 computes the bi-interval of a single symbol. The loop at Line 2 uses backward extensions to find all the reads overlapping with the input string P. The loop at Line 3 uses forward extensions base by base to exclude reducible overlaps found at the previous step. W is this loop keeps the common substring of reads overlapping P extended from the 3′ end of P. If in an iteration we find the sentinel of a read R (Line 5), then all the reads sharing the same W with R must overlap with both R and P and therefore their overlaps with P are reducible. In this case, no further forward extensions are necessary (Lines 4 and 6).
Similar to the original algorithm, Algorithm 4 requires that there are no contained reads. Fermi actually implements a modified version that detects reads containment on the fly, but we think the algorithm is a little overcomplicated. It is probably easier to filter contained reads first and then run Algorithm 4, as SGA does.
2.5.3 Unitig construction
Unitig construction is a process of unambiguous merge of overlapped reads. If [k, _l_] and [_k_′, l_′] have an irreducible overlap 〈_l, _k_′〉 and can be unambiguously merged, we label the merged sequence with [k, _l_′]; the similar can be applied to other three types of overlaps. With this simple labeling procedure, we are able to fully keep track of the graph topology during the unitig construction and without staging the graph in RAM. This procedure can also be easily multi-threaded.
2.6 Finding the SMEMs
An FMD-index can be used to find supermaximal exact matches (SMEMs) between a reference and a query sequence. Formally, a maximal exact match (MEM) is a an exact match that cannot be extended in either direction of the match. An SMEM is a MEM that is not contained in other MEMs on the query sequence. Fermi uses SMEMs to map reads back to the unitigs.
Algorithm 5 describes the details. Basically, we use forward–backward extension to extend an exact match and detect the boundary of a maximal match by tracking the change of interval sizes. Fermi implements a variant of Algorithm 5. It finds full-length read matches and can optionally exclude matches identical to the query sequence.

2.7 Other implementation details
2.7.1 Constructing FM-index
To compute suffix arrays for strings with multiple sentinels, we modified an optimized implementation of the SA-IS algorithm (Nong et al., 2011) by Yuta Mori. We used the established algorithm to merge BWTs of subsets of reads (Ferragina et al., 2010; Hon et al., 2007; Siren, 2009). The BWT string is run-length encoded with the length in the delta encoding (Elias, 1975).
2.7.2 Error correction
Fermi corrects potential sequencing errors using an algorithm similar to solving the spectrum alignment problem (Pevzner et al., 2001), correcting bases in underrepresented _k_-mers. It also shares similarity to HiTEC (Ilie et al., 2011). Nonetheless, the fermi's algorithm differs in that it is quality aware and does not rely on a user defined threshold on the _k_-mer occurrences.
Fermi corrects errors in two phases. In the first phase, it collects all 23 mer occurring 3 or more times using a top-down traversal over the trie represented by the FMD-index. For each such 23 mer, fermi counts the occurrences of the next (i.e. the 24-th) base and stores the information in a hash table with the 23 mer being the key. In the second phase, fermi processes each read by using the 23 mer hash table to correct errors by minimizing a heuristic cost function of base quality and the occurrences of the 24-th base. Roughly speaking, fermi tries to correct a low-quality base if by looking up its 23 mer prefix we know the base is different from an overwhelmingly frequent 24-th base. This algorithm can be adapted to correct INDEL sequencing errors in principle, but this has not been done. More works are needed to perform minimization efficiently.
2.7.3 Simplifying complex bubbles
A bubble is a directed acyclic subgraph with a single source and a single sink having at least two paths between the source and the sink. A closed bubble is a bubble with no incomming edges from or outgoing edges to other parts of the entire graph, except at the source and the sink vertices. A closed bubble is simple if there are exactly two paths between the source and the sink; otherwise it is complex. In de novo assembly, a bubble is frequently caused by sequencing errors or heterozygotes. Most short-read assemblers uses a modified Dijkstra's algorithm to pop bubbles progressively. Such an algorithm works fine for haploid genomes, but it is not straightforward to distinguish heterozygotes from errors when the bubble is complex.
Fermi uses a different algorithm. It effectively performs topological sorting from the end of a vertex while keeping track of the top two paths containing most reads. A bubble is detected when every path ends at a single vertex. It then drops vertices not on the top two paths and thus turns a complex bubble to a simple one.
2.7.4 Using the paired-end information
Given paired-end reads with short-insert sizes, fermi maps reads back to the unitigs with Algorithm 5. If two unitigs are linked by at least five read pairs, fermi will locally assemble the ends of unitigs together with unpaired reads pointing to the gap under a relax setting. Fermi tries to align the ends of unitigs using the Smith–Waterman algorithm, which may reveal imperfect overlaps caused by sequencing errors or heterozygotes. Fermi also uses paired-end reads to break contigs at regions without bridging read pairs. This helps to reduce misassemblies during the unitig construction.
3 RESULTS
We evaluated fermi on 101 bp paired-end reads from NA12878 (Depristo et al., 2011). The total coverage of the original data is ~70-fold, but we only used half of them. We assembled the 35-fold reads with fermi on a machine with 12 CPUs and 96 GB memory in ~5 days. The peak memory usage is 92 GB.
We obtained unitigs of N50 1022 bp, totaling 3.83 Gb. After collapsing most heterozygotes and closing gaps with paired-end reads, we got longer contigs (Table 4). Unitigs are short and redundant mainly because they break at heterozygotes.
Table 4.
Statistics of SNP call sets
| FC | CV | SS | BS | CG | MD | |
|---|---|---|---|---|---|---|
| No. of SNPs (M) | 3.37 | 2.20 | 3.24 | 3.50 | 3.34 | 2.69 |
| No. of hets (M) | 1.97 | 1.04 | 1.94 | 2.11 | 2.04 | 1.65 |
| Ts/tv | 2.04 | 2.03 | 2.08 | 2.11 | 2.12 | 2.06 |
| DN50 (bp) | 3593 | 6662 | 3523 | 3392 | 3447 | 3992 |
| DN2/DN50 | 22.3 | 20.8 | 23.4 | 22.7 | 22.3 | 22.9 |
For SNP and INDEL calling, we aligned unitigs to the reference genome using BWA-SW (Li and Durbin, 2010) with command line options ‘-b9 -q16 -r1 -w500’. We called SNPs with the SAMtools caller and called INDELs by directly counting INDELs from the pileup output. We did not run a standard INDEL caller as short-read INDEL callers do not work well with long contig sequences.
3.1 Performance on de novo assembly
We obtained the HuRef capillary read assembly (Levy et al., 2007) and the ALLPATHS-LG NA12878 contigs (AC:AEKP01000000) from NCBI, the SGA scaffolds from http://bit.ly/jts12878 (Simpson and Durbin, 2012) and the ABySS assembly provided by Shaun Jackman (personal communication). For both SGA and ABySS scaffolds, we split at any ambiguous bases to get contigs; for the HuRef assembly, we split at contiguous ‘N’ longer than 20 bp. The ABySS, fermi and SGA assemblies are derived from essentially the same input reads. ALLPATH-LG uses a superset of reads at 100-fold coverage, including reads from multiple long-insert libraries.
From Table 2, we can see that the HuRef assembly has much better contiguity than short-read assemblies. It appears to yield more alignment break points, some of which may be caused by true SVs not easily detectable with short reads. The quality of short-read assemblies varies in terms of contiguity, misassembly rate and redundancy between contigs, but overall, they are largely comparable to each other.
Table 2.
Statistics on human whole-genome assemblies
| ABySS | AllPaths-LG | Fermi | SGA | HuRef | |
|---|---|---|---|---|---|
| Aligned contig bp | 2.73 G | 2.62 G | 2.82 G | 2.74 G | 2.88 G |
| Aligned N50 | 9.0 k | 22.6 k | 15.6 k | 9.8 k | 81.4 k |
| Covered ref. bp | 2.69 G | 2.59 G | 2.74 G | 2.70 G | 2.78 G |
| No. of type-1 breaks | 5856 | 13 738 | 5704 | 6049 | 16 318 |
| No. of type-2 breaks | 1617 | 3823 | 1120 | 1735 | 6626 |
3.2 Performance on SNP and INDEL calling
One of the key motivations of fermi is to explore the power of de novo assembly in calling short variants. We collected several SNP and INDEL call sets (Table 3) and compared the performance of fermi (Tables 4 and 5).
Table 3.
Evaluated SNP and INDEL call sets
| Label | Data | Assembler | Mapper | Caller |
|---|---|---|---|---|
| AC | 96X Illumina PEa | AllPaths-LG | BWA−SWb | SAMtoolsc |
| BS | 70X Illumina PE | BWAd | SAMtools | |
| CG | Complete Genom. | cgatools2e | cgatools2 | |
| CV | 26X Illumina SEf | Cortex | Cortex-var | |
| FC | 35X Illumina SEf | Fermi | BWA-SWb | SAMtoolsc |
| MD | 60X multiple | MAQ | 1000 g pilotg | |
| MI | Capillary readsh | |||
| SS | 35X Illumina SEf | BWA-SW | SAMtools |
Table 5.
Fraction of INDELs found in other call sets
| MD | CG | BS | CV | FC | MI | ALL | |
|---|---|---|---|---|---|---|---|
| MD | 240 424 | 0.819 | 0.937 | 0.678 | 0.947 | 0.054 | 0.977 |
| CG | 0.752 | 264 696 | 0.915 | 0.629 | 0.924 | 0.052 | 0.965 |
| BS | 0.564 | 0.597 | 404 646 | 0.498 | 0.844 | 0.044 | 0.906 |
| CV | 0.708 | 0.726 | 0.882 | 251 769 | 0.902 | 0.052 | 0.923 |
| FC | 0.588 | 0.624 | 0.873 | 0.522 | 393 841 | 0.045 | 0.952 |
| MI | 0.593 | 0.618 | 0.790 | 0.527 | 0.804 | 23 216 | 0.864 |
For SNP calling (Table 4), fermi misses 3% of SNPs called in SS, but finds more additional ones. Manual examination reveals that the additional calls are mainly caused by two factors. Firstly, in the single-end mode, BWA-SW is very conservative. It may consistently give a correct alignment a low-mapping quality which are all downweighted by samtools. Fermi is able to assemble such reads into longer sequences which increase the power of BWA-SW. Secondly, in the fermi alignment, some regions may be mapped with a high-mismatching rate. These may be due to small-scale misassemblies in fermi unitigs or in the reference assembly, or copy-number variations. It is possible that these clustered SNPs contain more errors. Such errors may lead to reduced ts/tv, but tend not to break long homozygous blocks due to very recent coalescences. That is why FC has a good DN2/DN50 ratio, which measures how often false heterozygotes arise from a long homozygous block.
Table 5 shows the comparison between different INDEL call sets. We excluded INDELs around long homopolymer runs in all call sets because INDEL sequencing errors tend to occur around long homopolymer runs and their error profile is still unclear (the 1000 Genomes Project Analysis group, personal communication). In addition, we have excluded the SS INDEL call set which is nearly contained in BS due to the use of the same INDEL caller.
For the call sets in Table 5, MD and CG are relatively small due to the use of very short reads. CV uses 26X 100 bp reads. It is a small call set due to the high-false negative rate of the calling method (Iqbal et al., 2012). The fermi call set FC is slightly smaller than BS, but it has larger overlap with other call sets than BS, and more FC calls are confirmed by others. One explanation to the lower overlapping ratio between BS and ALL is that BS is the only call set that uses 101 bp paired-end information, which gives it higher power for INDELs not detectable with single-end or very short reads. Nonetheless, purely based on Table 5, fermi appears to have higher overall accuracy.
Even with all short-read call sets combined, as many as 14% of double-hit INDELs called by (Mills et al., 2011) are missed. We manually checked 30 missing INDELs in an alignment viewer. For half of the cases, the short-read alignment and fermi alignment strongly suggest no variations, and for all these cases, the HuRef sequences are identical to GRCh37. In addition, there are a few cases called from regions under clear copy-number changes. In all, we believe INDELs called by (Mills et al., 2011) only may have high-error rate. With short reads, we can recover most of short INDELs found by capillary sequencing.
4 DISCUSSIONS
In this article, we derived FMD-index by storing both forward and reverse complement DNA sequences in FM-index. This simple modification enables faster forward–backward search than bi-directional BWT (Lam et al., 2009) and makes FMD-index a more natural representation of DNA sequences. Based on FMD-index, we developed a new de novo assembler, fermi, which achieves similar quality to other mainstream assemblers.
We demonstrated that it is possible to call SNPs and short INDELs by aligning assembled unitigs to the reference genome. This approach has similar SNP accuracy to the standard mapping-based SNP calling and arguably outperforms the existing methods on INDEL calling in terms of both sensitivity and precision. Assembly based variant calling is a practical and beneficial complement to mapping-based calling.
In the course of evaluating INDEL accuracy, we found that outside long homopolymer regions, INDEL call sets do not often contain false positives, but they may have high-false negative rate, which leads to the apparent small overlap between call sets (Lam et al., 2012).
As a theoretical remark, we note that with read counts kept, unitigs are a lossless but reduced representation of sequence reads. They are ‘reduced’ in that individual reads are lost; they are ‘lossless’ in that all the information in reads, such as small variants, copy numbers and structural changes are fully preserved in unitigs, as long as they are constructed correctly. For single-end reads, it is theoretically possible to ‘compress’ reads to unitigs, which are largely non-redundant and much smaller in size. Accurately and efficiently constructing unitigs might provide an interesting alternative to data storage and downstream analyses in future, though practical challenges, such as the high-computational cost and the lack of accuracy of unitigs, remain at present.
ACKNOWLEDGEMENTS
We are grateful to David Reich, Evan Eichler and Peter Sudmant for providing additional data and computing resources for evaluating fermi, to David Altshuler and the GSA group at Broad for the helpful discussions and to Richard Durbin and Jared Simpson for their comments on the initial draft of the manuscript. We also thank Shaun Jackman for providing the ABySS assembly and Michael Brudno for his insight into the algorithm time complexity.
Funding: NIH Joint SNP and CNV calling in 1000 Genomes sequence data grant (1U01HG005208-01).
Conflict of Interest: none declared.
REFERENCES
- Albers C.A., et al. Dindel: accurate indel calls from short-read data. Genome Res. 2010;21:961–973. doi: 10.1101/gr.112326.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burrows M., Wheeler D.J. A block-sorting lossless data compression algorithm. Palo Alto, CA: Digital Equipment Corporation; 1994. Technical Report 124. [Google Scholar]
- Carnevali P., et al. Computational techniques for human genome resequencing using mated gapped reads. J. Comput. Biol. 2011;19:279–292. doi: 10.1089/cmb.2011.0201. [DOI] [PubMed] [Google Scholar]
- Chaisson M.J., et al. De novo fragment assembly with short mate-paired reads: Does the read length matter? Genome Res. 2009;19:336–346. doi: 10.1101/gr.079053.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Depristo M.A., et al. A framework for variation discovery and genotyping using next-generation DNA sequencing data. Nat. Genet. 2011;43:491–498. doi: 10.1038/ng.806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drmanac R., et al. Human genome sequencing using unchained base reads on self-assembling DNA nanoarrays. Science. 2010;327:78–81. doi: 10.1126/science.1181498. [DOI] [PubMed] [Google Scholar]
- Elias P. Universal codeword sets and representations of the integers. IEEE Trans. Inf. Theory. 1975;21:194–203. [Google Scholar]
- Ferragina P., Manzini G. FOCS. Redondo Beach, California, USA: IEEE Computer Society; 2000. Opportunistic data structures with applications; pp. 390–398. [Google Scholar]
- Ferragina P., et al. Lightweight data indexing and compression in external memory. In: López-Ortiz A., editor. LATIN. Vol. 6034. Oaxaca, Mexico: Springer; 2010. pp. 697–710. of Lecture Notes in Computer Science. [Google Scholar]
- Gingeras T. R., et al. Computer programs for the assembly of DNA sequences. Nucleic Acids Res. 1979;7:529–545. doi: 10.1093/nar/7.2.529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gnerre S., et al. High-quality draft assemblies of mammalian genomes from massively parallel sequence data. Proc. Natl. Acad. Sci. USA. 2011;108:1513–1518. doi: 10.1073/pnas.1017351108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Homer N., Nelson S.F. Improved variant discovery through local re-alignment of short-read next-generation sequencing data using SRMA. Genome Biol. 2010;11:R99. doi: 10.1186/gb-2010-11-10-r99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hon W.-K., et al. A space and time efficient algorithm for constructing compressed suffix arrays. Algorithmica. 2007;48:23–36. [Google Scholar]
- Idury R.M., Waterman M.S. A new algorithm for DNA sequence assembly. J. Comput. Biol. 1995;2:291–306. doi: 10.1089/cmb.1995.2.291. [DOI] [PubMed] [Google Scholar]
- Ilie L., et al. HiTEC: accurate error correction in high-throughput sequencing data. Bioinformatics. 2011;27:295–302. doi: 10.1093/bioinformatics/btq653. [DOI] [PubMed] [Google Scholar]
- Iqbal Z., et al. De novo assembly and genotyping of variants using colored de bruijn graphs. Nat. Genet. 2012;44:226–232. doi: 10.1038/ng.1028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lam T.W., et al. BIBM. Washington, DC, USA: 2009. High throughput short read alignment via bi-directional BWT; pp. 31–36. [Google Scholar]
- Lam H.Y.K., et al. Performance comparison of whole-genome sequencing platforms. Nat. Biotechnol. 2012;30:78–82. doi: 10.1038/nbt.2065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy S., et al. The diploid genome sequence of an individual human. PLoS Biol. 2007;5:e254. doi: 10.1371/journal.pbio.0050254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Durbin R. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics. 2009;25:1754–1760. doi: 10.1093/bioinformatics/btp324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Durbin R. Fast and accurate long-read alignment with Burrows-Wheeler transform. Bioinformatics. 2010;26:589–595. doi: 10.1093/bioinformatics/btp698. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. Improving SNP discovery by base alignment quality. Bioinformatics. 2011;27:1157–1158. doi: 10.1093/bioinformatics/btr076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R., et al. De novo assembly of human genomes with massively parallel short read sequencing. Genome Res. 2010;20:265–272. doi: 10.1101/gr.097261.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mäkinen V., et al. Storage and retrieval of individual genomes. In: Batzoglou S., editor. RECOMB. Vol. 5541. Tucson, AZ, USA: Springer; 2009. pp. 121–137. of Lecture Notes in Computer Science. [Google Scholar]
- Manske H.M., Kwiatkowski D.P. SNP-o-matic. Bioinformatics. 2009;25:2434–2435. doi: 10.1093/bioinformatics/btp403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Medvedev P., et al. Computability of models for sequence assembly. In: Giancarlo R., Hannenhalli S., editors. WABI. Vol. 4654. Philadelphia, PA, USA: Springer; 2007. pp. 289–301. of Lecture Notes in Computer Science. [Google Scholar]
- Mills R.E., et al. Natural genetic variation caused by small insertions and deletions in the human genome. Genome Res. 2011;21:830–839. doi: 10.1101/gr.115907.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers E.W. Toward simplifying and accurately formulating fragment assembly. J. Comput. Biol. 1995;2:275–290. doi: 10.1089/cmb.1995.2.275. [DOI] [PubMed] [Google Scholar]
- Myers E.W., et al. A whole-genome assembly of drosophila. Science. 2000;287:2196–2204. doi: 10.1126/science.287.5461.2196. [DOI] [PubMed] [Google Scholar]
- Myers E.W. The fragment assembly string graph. Bioinformatics. 2005;21(Suppl. 2):ii79–ii85. doi: 10.1093/bioinformatics/bti1114. [DOI] [PubMed] [Google Scholar]
- Nong G., et al. Two efficient algorithms for linear time suffix array construction. IEEE Trans. Comput. 2011;60:1471–1484. [Google Scholar]
- Ossowski S., et al. Sequencing of natural strains of arabidopsis thaliana with short reads. Genome Res. 2008;18:2024–2033. doi: 10.1101/gr.080200.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peltola H., et al. SEQAID: a DNA sequence assembling program based on a mathematical model. Nucleic Acids Res. 1984;12:307–321. doi: 10.1093/nar/12.1part1.307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pevzner P.A., et al. An eulerian path approach to DNA fragment assembly. Proc. Natl. Acad. Sci. USA. 2001;98:9748–9753. doi: 10.1073/pnas.171285098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson J.T., Durbin R. Efficient construction of an assembly string graph using the FM-index. Bioinformatics. 2010;26:i367–i373. doi: 10.1093/bioinformatics/btq217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson J.T., Durbin R. Efficient de novo assembly of large genomes using compressed data structures. Genome Res. 2012;22:549–556. doi: 10.1101/gr.126953.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simpson J.T., et al. ABySS: a parallel assembler for short read sequence data. Genome Res. 2009;19:1117–1123. doi: 10.1101/gr.089532.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siren J. String Processing and Information Retrieval. Saariselkä, Finland: 2009. Compressed suffix arrays for massive data; pp. 63–74. [Google Scholar]
- Staden R. A strategy of DNA sequencing employing computer programs. Nucleic Acids Res. 1979;6:2601–2610. doi: 10.1093/nar/6.7.2601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zerbino D.R., et al. Pebble and rock band: heuristic resolution of repeats and scaffolding in the velvet short-read de novo assembler. PLoS ONE. 2009;4:e8407. doi: 10.1371/journal.pone.0008407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 1000 Genomes Project Consortium. A map of human genome variation from population-scale sequencing. Nature. 2010;467:1061–1073. doi: 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]