The effect of correlation in false discovery rate estimation (original) (raw)
Summary
The objective of this paper is to quantify the effect of correlation in false discovery rate analysis. Specifically, we derive approximations for the mean, variance, distribution and quantiles of the standard false discovery rate estimator for arbitrarily correlated data. This is achieved using a negative binomial model for the number of false discoveries, where the parameters are found empirically from the data. We show that correlation may increase the bias and variance of the estimator substantially with respect to the independent case, and that in some cases, such as an exchangeable correlation structure, the estimator fails to be consistent as the number of tests becomes large.
Keywords: High-dimensional data, Microarray data, Multiple testing, Negative binomial
1. Introduction
Large-scale multiple testing is a common statistical problem in the analysis of high-dimensional data, particularly in genomics and medical imaging. An increasingly popular global error measure in these applications is the false discovery rate (Benjamini & Hochberg, 1995), defined as the expected proportion of false discoveries among the total number of discoveries. High-dimensional data are often highly correlated; in the microarray data example below, the raw pairwise correlations range from −0.9 to 0.96. Correlation may greatly inflate the variance of both the number of false discoveries (Owen, 2005) and common false discovery rate estimators (Qiu & Yakovlev, 2006). While there exist procedures that control the false discovery rate under arbitrary dependence (Benjamini & Yekutieli, 2001), they have substantially less power than procedures that assume independence (Farcomeni, 2008) and the latter are often preferred. Because of the current widespread use of the false discovery rate, it is important to understand the effect of correlation in the analysis as it is typically done in practice, both for correct inference using current methods and as a guide for developing new methods for correlated data.
The goal of this paper is to quantify the effect of correlation in false discovery rate analysis. As a benchmark, we use the false discovery rate estimator of Storey et al. (2004) and Genovese & Wasserman (2004), originally proposed by Yekutieli & Benjamini (1999) and Benjamini & Hochberg (2000). This estimator is appealing because it provides estimates of the false discovery rate at all thresholds simultaneously. Furthermore, thresholding of this estimator is equivalent to the original false discovery rate controlling algorithm (Benjamini & Hochberg, 1995) under independence (Benjamini & Hochberg, 2000), and under specific forms of dependence such as positive regression dependence (Benjamini & Yekutieli, 2001) and weak dependence such as dependence in finite blocks (Storey et al., 2004). However, the generality of the estimator makes it conservative under correlation (Yekutieli & Benjamini, 1999) and it can perform poorly in genomic data (Qiu & Yakovlev, 2006). We show that correlation increases both the bias and variance of the estimator substantially compared with the independent case, but less so for small error levels. From a theoretical point of view, we show that in some cases, such as an exchangeable correlation structure, the estimator fails to be consistent as the number of tests increases.
As related work, Efron (2007a) and Schwartzman (2008) estimated the variance of the false discovery rate estimator by the delta method but did not consider the bias and skewness of the distribution. Owen (2005) quantified the variance of the number of discoveries given an arbitrary correlation structure, but did not provide results about the false discovery rate. Qiu & Yakovlev (2006) showed the strong effect of correlation on the false discovery rate estimator via simulations only.
Our contributions are as follows. First, we provide approximations for the mean, variance, distribution and quantiles of the false discovery rate estimator given an arbitrary correlation structure. This is achieved by modelling the number of discoveries with a negative binomial distribution whose parameters are estimated from the data based on the empirical distribution of the pairwise correlations. Our results are derived for test statistics whose marginal distribution is either normal or _χ_2. Secondly, we identify a necessary condition for consistency of the false discovery rate estimator as the number of tests increases and show that it is violated in situations such as exchangeable correlation.
2. Theory
2.1. The false discovery rate estimator
Let H_1, . . . , Hm_ be m null hypotheses with associated test statistics T_1, . . . , Tm_. The test statistics are assumed to have marginal distributions Tj ∼ F_0 if Hj is true and Tj ∼ Fj if Hj is false, where F_0 is a common distribution under the null hypothesis and F_1, F_2, . . . are specific alternative distributions for each test. The test statistics may be dependent with corr(Ti , Tj) = ρij. In particular, if the test statistics are _z_-scores, then this is the same as the correlation between the original observations.
The fraction p_0 = m_0/m of tests where the null is true is called the null proportion. The complete null model is the one where _p_0 = 1 and Tj ∼ _F_0 for all j. Without loss of generality, we focus on one-sided tests, where for each hypothesis Hj and a threshold u, the decision rule is Dj (u) = I (Tj > u). Two-sided tests may be incorporated, for example, by defining Tj = T˜j2 or Tj = |T̃j|, where T̃j is a two-sided test statistic.
The false discovery rate is the expectation, under the true model, of the proportion of false positives among rejected null hypothesis or discoveries, i.e.
| FDR(u)=E{Vm(u)Rm(u)∨1}, | (1) |
|---|
where Vm(u)=∑j=1mDj(u)I(Hj is true) is the number of false positives and Rm(u)=∑j=1mDj(u) is the number of rejected null hypotheses or discoveries (Benjamini & Hochberg, 1995). The maximum operator ∨ sets the fraction inside the expectation to zero when Rm(u) = 0. When m is large, fdr(u) is estimated by
| FD^Rm(u)=Ep^0mα(u)Rm(u)∨1, | (2) |
|---|
where _p̂_0 is an estimate of the null proportion _p_0, and α(u) is the marginal type-I-error level α(u) = E{Dj (u)} = pr(Tj > u), computed under the assumption that Hj is true. This estimator was proposed by Yekutieli & Benjamini (1999) and its asymptotic properties were studied by Storey et al. (2004) and Genovese & Wasserman (2004). A heuristic argument for this estimator is that the expectation of the false discovery proportion numerator, E{Vm(u)}, is equal to p_0_mα(u) under the true model. There are several ways to estimate _p_0 (Genovese & Wasserman, 2004; Storey et al., 2004; Efron, 2007b; Jin & Cai, 2007). In applications _p_0 is often close to 1 and setting _p̂_0 = 1 biases the estimate only slightly and in a conservative fashion (Efron, 2004). In this article, we focus on the effect that correlation has on the estimator (2) via the number of discoveries Rm(u).
2.2. The number of discoveries
As a stepping stone towards studying the estimator (2), we first study the number of rejected null hypotheses or discoveries Rm(u). Under the complete null model, and if the tests are independent, Rm(u) is binomial with number of trials m and success probability α(u). In general, under the true model and allowing dependence, we have
| E{Rm(u)}=∑i=1mE{Di(u)}=∑i=1mβi(u),var{Rm(u)}=∑i=1m∑j=1mcov{Di(u),Dj(u)}=∑i=1m∑j=1mψij(u), | (3) |
|---|
where
| βi(u)=pri(Ti>u), ψij(u)=pr(Ti>u,Tj>u)−pr(Ti>u)pr(Tj>u). | (4) |
|---|
The quantity βi (u) is the per-test power. For those tests where the null hypothesis is true, this is equal to the marginal type-I-error level α(u). Summing over the diagonals in (3) reveals the mean-variance structure
| E{Rm(u)}=mβ¯(u), var{Rm(u)}=m{β¯(u)−β¯2(u)}+m(m−1)Ψm(u), | (5) |
|---|
where
| β¯(u)=1m∑i=1mβi(u), β¯2(u)=1m∑i=1mβi2(u), Ψm(u)=2m(m−1)∑i<jψij(u). | (6) |
|---|
The quantities β̄(u) and β̄_2(u) are empirical moments of the power, while Ψ_m(u) is the average covariance of the decisions Di (u) and Dj (u) for i ≠ j, a function of the pairwise correlations {ρij}.
The dependence between the test statistics does not affect the mean of Rm(u) but does affect its variance. It does so by adding the overdispersion term m(m − 1)Ψ_m_(u) to the independent-case variance m{β̄(u) − _β̄_2(u)}. Expression (5) under the complete null is an unconditional version of the conditional variance in expression (8) of Owen (2005). Similar expressions have appeared before in estimation problems with correlated binary data (Crowder, 1985; Prentice, 1986).
Another observation from (4) is that ψij (u) vanishes asymptotically as u → ∞, so the effect of the correlation becomes negligible for very high thresholds. We will see in § 2.4 that the rate of decay is a quadratic exponential times a polynomial.
2.3. Inconsistency of the false discovery rate estimator
The overdispersion of the number of discoveries Rm(u) has implications for the behaviour of the estimator (2). We consider the asymptotic case m → ∞ in this section and treat the finite m case in § 2.4 and 2.5.
As m → ∞, a sufficient condition for consistency of the estimator (2) is that the test statistics are independent or weakly dependent, e.g. dependent in finite blocks (Storey et al., 2004). On the other hand, taking m in (2) to the denominator, we see that a necessary condition for consistency is that the fraction of discoveries Rm(u)/m has asymptotically vanishing variance. By (5), the variance of Rm(u)/m is
| var{Rm(u)m}=β¯(u)−β¯2(u)m+(1−1m)Ψm(u) | (7) |
|---|
and is asymptotically zero if and only if the overdispersion Ψ_m_ is asymptotically zero, provided that β̄ and _β̄_2 grow slower than linearly with m.
Theorem 1. Assume {β̄(u) − β̄_2(u)}/m_ → 0 as m → ∞_. Fix an ordering of the test statistics T_1_, . . . , Tm_ and assume the autocovariance sequence ψi,i+k(u) = ψi+k,i (u) in (7) has a limit Ψ∞(u) ⩾ 0 as k → ∞ for every i. Then, as m → ∞_,_ var{Rm(u)/m}→ Ψ∞(u) ⩾ 0.
Example 1. Exchangeable correlation. Suppose the test statistics Ti have an exchangeable correlation structure so that ρij = ρ > 0 is a constant for all i ≠ j. For any fixed threshold, u, ψij (u) = ψ(u) > 0 in (6) does not depend on i, j. As a consequence, Ψ_m_(u) = ψ(u) = Ψ∞(u) > 0, and the estimator (2) is inconsistent. The case ρ <_ 0 is asymptotically moot because positive definiteness of the covariance of the _Ti_ s requires _ρ > −1_/_(m − 1), so ρ cannot be negative in the limit m → ∞.
Example 2. Stationary ergodic covariance. Suppose the index i represents time or position along a sequence, and suppose the test statistic sequence Ti is a stationary ergodic process, e.g., M-dependent or autoregressive moving average, with Toeplitz correlation ρij = ρi_−_j. Then ρi,i+k = ρk → 0 for all i as k → ∞, and so Ψ∞(u) = 0, pointwise for all u. By Theorem 1, the variance (7) converges to zero as m → ∞.
Example 3. Finite blocks. Suppose the test statistics Ti are dependent in finite blocks, so that they are correlated within blocks but independent between blocks. Suppose the largest block has size K. If K increases with m such that K/m → 0 as m → ∞ then Ψ∞(u) = 0 for all u. On the other hand, if K/m → γ > 0 then Ψ∞(u) > 0 and the estimator (2) is inconsistent.
Example 4. Strong mixing. Suppose the test statistics Ti have a strong mixing or α_-mixing dependence; that is, the supremum over k of |pr(A ∩ B) − pr(A)pr(B)|, where A is in the σ_-field generated by T_1, . . . , Tk and B is in the σ_-field generated by Tk+1, Tk+2_, . . ._, tends to 0 as m → ∞ (Zhou & Liang, 2000). By taking A = {Ti > u} and B = {Tj > u} in (4), we have that Ψ∞ = 0 and therefore, by Theorem 1, the variance (7) converges to zero as m → ∞.
Example 5. Sparse dependence. Suppose the test statistics Ti are pairwise independent except for M_1 out of the M = m(m − 1)/2 distinct pairs. If the dependence is asymptotically sparse in the sense that M_1/M → 0 as m → ∞, then Ψ∞(u) = 0 and the variance (7) goes to zero. However, if M_1/M_ → γ > 0, then the result will depend on the dependence structure among the _M_1 dependent pairs. If this dependence goes away asymptotically as in one of the cases above, then the variance (7) goes to zero. Otherwise, if the dependence persists such that Ψ∞(u) > 0, the estimator (2) is inconsistent.
2.4. Quantifying overdispersion for finite m
We are interested in estimating the distributional properties of the false discovery rate estimator. This requires estimating the overdispersion Ψ_m_(u) in (5) and (7). This quantity is easy to write in terms of the pairwise correlations between the decision rules, as in (3), but not necessarily as a function of the pairwise test statistic correlations ρij. In this section we provide expressions for Ψ_m_(u) for finite m assuming a specific bivariate probability model for every pair of test statistics, but without the need to assume a higher order correlation structure. We consider commonly used z and _χ_2 tests.
Suppose first that every pair of test statistics (Ti , Tj) has the bivariate normal density with marginals N(μi , 1) and N(μj , 1), and corr(Ti , Tj) = ρij. Denote by ϕ(t) and _ϕ_2(ti , tj; ρij) the univariate and bivariate standard normal densities. Mehler’s formula (Patel & Read, 1996; Kotz et al., 2000) states that the joint density fij (ti , tj) = _ϕ_2(ti − μi , tj − μj; ρij) of (Ti , Tj) can be written as
| fij(ti,tj)=ϕ(ti−μi)ϕ(tj−μj)∑k=1∞ρijkk!ℋk(ti−μi)ℋk(tj−μj), | (8) |
|---|
where ℋk(t) are the Hermite polynomials: _ℋ_0(t) = 1, _ℋ_1(t) = t, _ℋ_2(t) = _t_2 − 1 and so forth.
Theorem 2. Let μ = (μ_1, . . . , μm_)T_. Under the bivariate normal model_ (8), the overdispersion term in (6) is
| Ψm(u;μ)=∑k=1∞ρk*(u;μ)k!, | (9) |
|---|
where
| ρk*(u;μ)=2m(m−1)∑i<jρijkϕ(u−μi)ϕ(u−μj)ℋk−1(u−μi)ℋk−1(u−μj). | (10) |
|---|
Under the complete null model μ = 0_,_ (9) reduces to
| Ψm(u)=Ψm(u;0)=ϕ2(u)∑k=1∞ρ¯kk!ℋk−12(u), | (11) |
|---|
where ρ̄k (k = 1_,_ 2_, . . .) are the empirical moments of the m(m − 1)/_2 correlations ρij(i < j).
Another common null distribution in multiple testing problems is the _χ_2 distribution. Let fν (t) and Fν (t) be the density and distribution functions of the _χ_2(ν) distribution with ν degrees of freedom. Under the complete null, the pair of test statistics (Ti , Tj) admits a Lancaster bivariate model where Ti and Tj have the same marginal density fν, their correlation is ρij, and their joint density is
| fν(ti,tj;ρij)=fν(ti)fν(ti)∑k=0∞ρijkk!Γ(ν/2)Γ(ν/2+k)ℒk(ν/2−1)(tj2),ℒk(ν/2−1)(tj2), | (12) |
|---|
where ℒk(ν/2−1)(t) are the generalized Laguerre polynomials of degree _ν/_2 − 1: ℒ0(ν/2−1)(t)=1, ℒ1(ν/2−1)(t)=−t+ν/2, ℒ2(ν/2−1)(t)=t2−2(ν/2+1)t+(ν/2)(ν/2+1) and so forth (Koudou, 1998). The _χ_2 distribution is not a location family with respect to the non-centrality parameter, so the Lancaster expansion does not hold in the non-central case.
Theorem 3. Assume the complete null. Under the bivariate χ_2 model (12), the overdispersion term in_ (6) is
| Ψm(u)=fν+22(u)∑k=1∞ρ¯kk!ν2Γ(ν/2)k2Γ(ν/2+k){Lk−1(ν/2)(u2)}2, | (13) |
|---|
where ρ̄k (k = 1_,_ 2_, . . .) are the empirical moments of the m(m − 1)/_2 correlations ρij(i < j).
Theorems 2 and 3 show that the overdispersion is a function of modified empirical moments of the pairwise correlations ρij and depends on m only through these moments. This provides an efficient way to evaluate Ψ_m_(u) for a given set of pairwise correlations, as the expansions (11) and (13) may be approximated evaluating only the first few terms. This is in contrast to direct computation of (6), which requires m(m − 1)/2 evaluations of the bivariate probabilities in (4), one for each value of ρij. In addition, as a function of u, both (11) and (13) decay as a quadratic exponential times a polynomial, implying that the effect of correlation quickly becomes negligible for high thresholds. Finally, under the complete null, (11) and (13) indicate that the overdispersion, and thus also the variance (7), vanish asymptotically as m → ∞ for all u if and only if ρ̄k → 0 as m → ∞ for all k = 1, 2_, . . ._.
2.5. Distributional properties of the false discovery rate estimator
We now apply the above results towards quantifying the distributional properties of the false discovery rate estimator (2). Our strategy is to model Rm(u) as a negative binomial variable and derive the properties of the estimator based on this model.
Seen as a function of m, the mean-variance structure (5) resembles that of the beta-binomial distribution, which has been used to model overdispersed binomial data (Prentice, 1986; McCullagh & Nelder, 1989). Because the beta-binomial distribution is difficult to work with, we propose instead to model Rm(u) using a negative binomial distribution. The rationale is as follows. A binomial distribution with number of trials n and success probability p can be approximated by a Poisson distribution with mean parameter np when n is large and p is small. If p has a beta distribution with mean μ, then when n is large and μ is small, the distribution of np can be approximated by a gamma distribution with mean nμ. Therefore, the beta-binomial mixture model can be approximated by a gamma-Poisson mixture model, which is equivalent to a negative binomial distribution (Hilbe, 2007).
It is convenient to parameterize the negative binomial distribution with parameters λ ⩾ 0 and ω ⩾ 0, such that the mean and variance of R ∼ N B(λ, ω) are
| E(R)=λ, var(R)=λ+ωλ2. | (14) |
|---|
See the proof of Theorem 4 below for details. Here λ is a mean parameter, whereas ω controls the overdispersion with respect to the Poisson distribution. When ω → 0 with λ constant, the negative binomial distribution becomes Poisson with mean λ; when λ = 0, it becomes a point mass at R = 0.
We describe how to estimate λ and ω from data in § 2.6. Given λ and ω, the moments, distribution and quantiles of the estimator (2) can be obtained directly from the negative binomial model as follows. For simplicity of notation, we omit the indices m and u.
Theorem 4. Suppose R ∼ N B(λ, ω) if λ ⩾ 0_, ω >_ 0_, or R_ ∼ Po(λ) if λ ⩾ 0_, ω_ = 0_, with moments_ (14), cumulative distribution function F(k) = pr(R ⩾ k), and quantiles F_−1(q) = inf{x : pr(R ⩽ x) ⩾ q}. Assume p_0 is known and define the probability of discovery to be
γ(λ,ω)=pr(R>0)={1−(1+ωλ)−1/ω(ω>0),1−exp(−λ)(ω=0).
The mean and variance of fd^r = p_0_mα/(R ∨ 1) are
E(FD^R)=p0mα{1−γ(λ,ω)+γ(λ,ω)ζ(λ,ω)},var(FD^R)=(p0mα)2{1−γ(λ,ω)+γ(λ,ω)ζ2(λ,ω)}−E2(FD^R),
where
ζ(λ,ω)=E(1R|R>0)=∫0λγ−1(λ,ω)−1γ−1(x,ω)−1.dxx(1+ωx),ζ2(λ,ω)=E(1R2|R>0)=∫0λγ−1(λ,ω)−1γ−1(x,ω)−1.ζ(x,ω)dxx(1+ωx).
The distribution and quantiles of fd^r = p_0_mα/(R ∨ 1) are
pr(FD^R⩽x)={1−F(k)(ak+1⩽x<ak;k=1,2,…),1(a1⩽x),inf{x:pr(FD^R⩽x)⩾q}={aF−1(1−q)+1(q⩽1−F(1)),a1(q>1−F(1)),
where ak = p_0_mα/ k.
As a notational choice, the functions ζ (λ, ω) and _ζ_2(λ, ω) above were defined so that both are bounded, tend to 0 as λ → 0, and tend to 1 as λ → ∞. When ω = 0, they are the same as (27) in Schwartzman (2008) divided by λ.
2.6. Estimation of the distributional properties of the false discovery rate estimator
We estimate the parameters λ and ω of the negative binomial model for Rm(u) by the method of moments. Based on (5) but respecting the form (14), we use the approximations E{Rm(u)} ∼ mα(u) and var{Rm(u)} ∼ mα(u) + m_2Ψ_m(u; 0) for large m under the complete null. The form of the variance ensures that it is greater or equal to the mean as required by the negative binomial model. In the normal case, using (11), the overdispersion term Ψ_m_(u; 0) is estimated by
Ψ^m(u;0)=ϕ2(u)∑k=1Kρ^¯kk!ℋk−12(u),
where ρ^¯ (k = 1_, . . . , K_) denote the empirical moments of the m(m − 1)_/_2 empirical pairwise correlations ρ̂ij (i < j), after correction for sampling variability. In practice, K = 3 suffices. The overdispersion (13) is estimated similarly in the _χ_2 case.
Matching the estimated moments of Rm(u) to those of the negative binomial model (14) leads to the parameter estimates
| λ^m(u)=mα(u), ω^m(u)=Ψ^m(u;0)α2(u). | (15) |
|---|
Finally, the moments and quantiles of fd^r are estimated using the formulas in Theorem 4 by plugging in the parameter estimates (15).
3. Numerical studies and data examples
3.1. Numerical studies
The following simulations illustrate the effect of correlation on the estimator (2) and show the accuracy of the negative binomial model in quantifying that effect. In the following simulations, N = 10 000 datasets were drawn at random from the model Yj = μj + Zj (j = 1_, . . . , m_), where each Zj has marginal distribution N (0_,_ 1). The tests were set up as _H_0 : μj = 0 vs. Hj : μj > 0. The test statistics were taken as the z_-scores Tj = Yj, the signal-to-noise ratio being controlled by the strength of the signal μj. The true false discovery rate was computed according to (1) where the expectation was replaced by an average over the N simulated datasets. Similarly, the true moments and distribution of Rm(u) and fd^r_m(u) (2) were obtained from the N simulated datasets.
Example 6. Sparse correlation, complete null. A sparse correlation matrix Σ = {ρij} was generated as follows. First, a lower triangular matrix A was generated with diagonal entries equal to 1 and 10% of its lower off-diagonal entries randomly set to 0.6, zero otherwise. Then, Σ was computed as the covariance matrix AA_′, normalized to be a correlation matrix. This process guarantees that Σ is positive definite. The resulting matrix Σ had 68% of its off-diagonal entries equal to zero, and empirical moments ρ̄ = 0.0588, ρ̄_2 = 0.0134, ρ̄_3 = 0.0037. The correlated observations Z = (Z_1, . . . , Zm)′ were generated as Z = Σ1/2_ɛ, where ɛ ∼ N(0, Im_). The signal was set to μj = 0 for all j = 1_, . . . , m_.
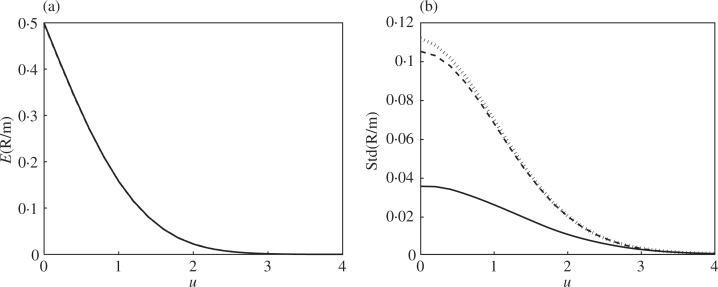
Figure 1 shows the effect of dependence on the discovery rate Rm(u)/m for m = 100 under the complete null. According to (5), dependence does not affect the mean, as all the lines overlap in Figure 1(a), but affects the variance substantially for low thresholds. The estimated negative binomial mean and standard deviation coincide with the true values by design because the moments were matched, except that only three terms were used in the polynomial expansion (11) for Ψ_m_(u). The first of these terms is the largest by far.
Fig. 1.
Simulation results for Example 6: number of discoveries under the complete null, sparse correlation, m = 100. Expectation (a) and standard deviation (b) of Rm (u)/m. Plotted in both panels: the true value under independence (solid), the true value under dependence (dashed) and the value calculated using the polynomial expansion (11) (dotted).
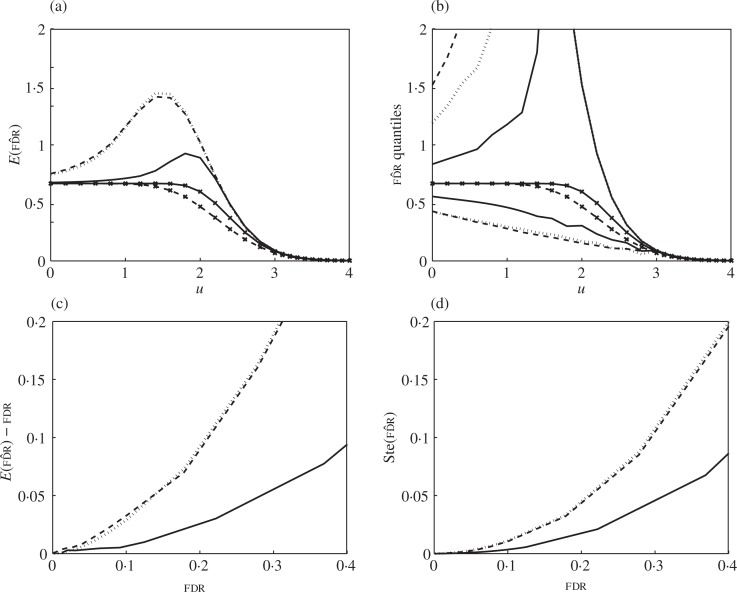
Figure 2 shows the effect of dependence on the false discovery rate estimator (2) for m = 100 under the complete null. Figure 2(a) shows that the estimator is always positively biased. It may even be greater than 1 if the denominator is smaller than the numerator. Dependence causes the true false discovery rate to go down, further increasing the bias. Dependence also causes the variability of the estimator to increase dramatically, as indicated by the 0.05 and 0.95 quantiles in Fig. 2(b). Here, the ragged and non-monotone lines are a consequence of the discrete nature of the distribution. In both panels (a) and (b), the expectation and quantiles of fd^r under dependency are reasonably well approximated by the negative binomial model.
Fig. 2.
Simulation results for Example 6: false discovery rate estimator under the complete null, sparse correlation, m = 100. (a) and (b) Expectation and quantiles 0.05 and 0.95 of fd^r as a function of threshold under independence (solid plain), under dependence (dashed plain) and estimated by the negative binomial model (dotted). Also plotted: true false discovery rate under independence (solid crossed) and under dependence (dashed crossed). (c) and (d) Bias and standard error of fd^r as a function of the true false discovery rate under independence (solid), under dependence (dashed) and estimated by the negative binomial model (dotted).
The bias and standard error of the false discovery rate estimator (2) are easier to assess when plotted against the true false discovery rate in each case, as shown in Fig. 2(c) and (d). At practical false discovery rate levels such as 0.2, the bias of the estimator under independence is about 10% while under correlation is 25%, about 2.5 times larger. Similarly, the standard error under independence is about 9% while under correlation is 14%, about 1.7 times larger. The negative binomial model gives slight overestimates.
Other simulations for increasing m from m = 10 to m = 10 000 indicate that, when plotted against the true false discovery rate as in Fig. 2(c) and (d), the bias and standard error of the estimator increase slightly as a function of m both under independence and correlation. This is because increasing m increases the expectation and variance of the estimator for any fixed threshold, but the threshold required for controlling false discovery rate at a given level also increases accordingly.
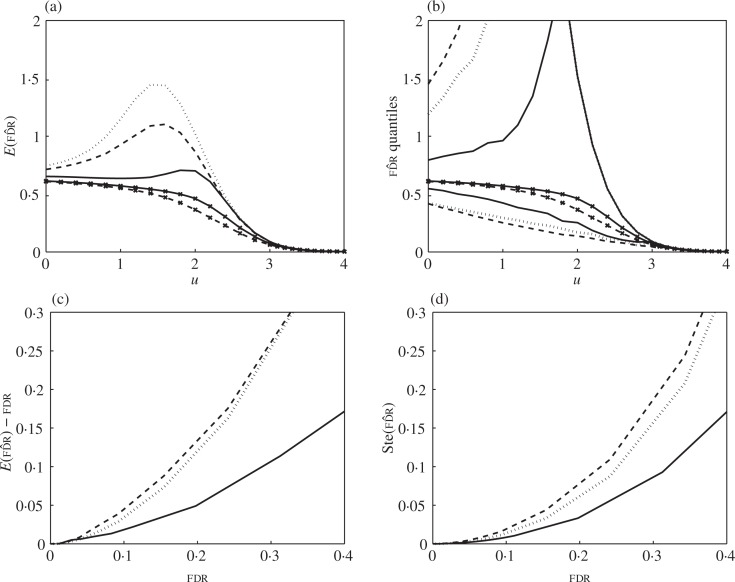
Example 7. Sparse correlation, non-complete null. Keeping the same correlation structure as before with m = 100, the signal was set to μj = 1 (j = 1_, . . . ,_ 5), providing a null fraction _p_0 = 0.95. Figure 3 shows the effect of dependence on the false discovery rate estimator (2). Figure 3(a) shows that the bias up persists as in the complete null case, while the overshoot has been diminished. Figure 3(b) shows that correlation increases the variability of the estimator. This is visible in this panel mostly in terms of the 0.05 quantile, as the 0.95 quantile lines coincide.
Fig. 3.
Simulation results for Example 7: false discovery rate estimator with 5% signal at μ = 1, sparse correlation, m = 100. Same quantities plotted as in Fig. 2. The negative binomial line (dotted) was fitted assuming the complete null.
When plotted against the true false discovery rate, Fig. 3(c) and (d) shows that the bias and variance of the estimator are higher than in the complete null case, about twice as much at a false discovery rate level of 0.2. This is a consequence of the increased variance of Rm(u)/m at medium-high thresholds, itself a consequence of the increased mean of Rm(u)/m according to (5). In this regard, the effect of the signal is stronger than that of dependence. This explains why the negative binomial line, which was fitted assuming the complete null, does not match the simulations as well as when no signal is present.
3.2. Data example
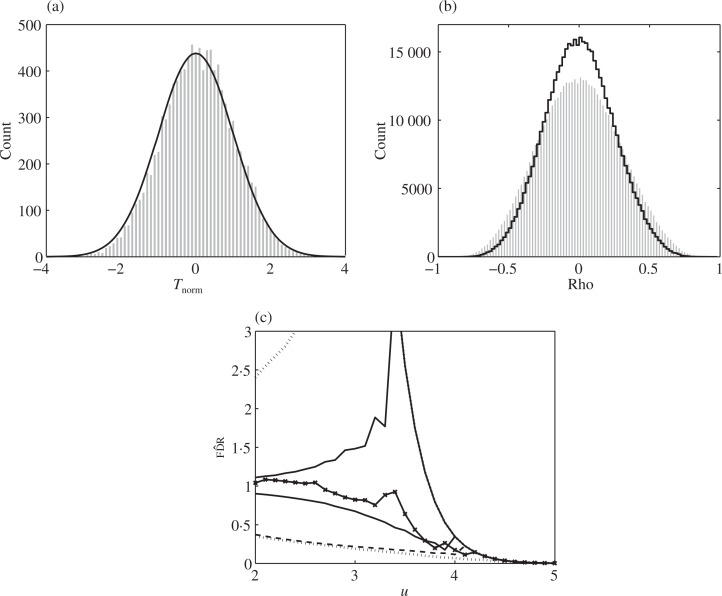
We use the genetic microarray dataset from Mootha et al. (2003), which has m = 10 983 expression levels measured among diabetes patients. For the purposes of this article, standard two-sample _t_-statistics were computed at each gene between the group with Type 2 diabetes mel-litus, _n_1 = 17, and the group with normal glucose tolerance, _n_2 = 17. The _t_-statistics, having 32 degrees of freedom, were converted to the normal scale by a bijective quantile transformation (Efron, 2004, 2007a). The histogram of the m = 10 983 test statistics in Fig. 4(a) is almost standard normal; its mean and standard deviation are 0.059 and 0.977. Thus the effect of correlation on the null distribution (Efron, 2007a) is minimal.
Fig. 4.
The diabetes microarray data. (a) Histogram of the m = 10 983 test statistics converted to normal scale; superimposed is the N(0_,_ 1) density times m. (b) Histogram of 499 500 pairwise sample correlations from 1000 randomly sampled genes; superimposed in black: histogram corrected for sampling variability. (c) False discovery rate curves: fd^r (solid crossed); quantiles 0.05 and 0.95 estimated by the negative binomial model assuming independence (solid) and assuming the pairwise correlations from the data (dashed); 0.05 and 0.95 quantiles estimated by permutations (dotted). All the 0.95 quantile lines overlap at the right edge.
Figure 4(b) shows a histogram of 499 500 sample pairwise correlations computed from 1000 randomly sampled genes out of m = 10 983. The pairwise correlations were computed between the gene expression levels across all 34 subjects after subtracting the means of both groups separately. These are approximately the same as the correlations between the _z_-scores given the moderate sample size of 34. The first three empirical moments of the sample pairwise correlations, obtained from a random sample of 2000 genes, were 0.0044, 0.0846 and 0.0020. To correct for sampling variability, empirical Bayes shrinking of the sample correlations towards zero (Owen, 2005; Efron, 2007a) resulted in the superimposed black histogram, with first three empirical moments 0.0029, 0.0586 and 0.0012.
Figure 4(c) shows the false discovery rate estimator (2) as a function of the threshold u. Superimposed are the 0.05 and 0.95 quantiles of the estimator according to the negative binomial model under the complete null. The 0.05 quantile line is much lower when correlation is taken into account, while the 0.95 quantile lines coincide. At u = 4, the estimated false discovery rate is 0.17, but the bands under correlation indicate that with 90% probability it could have been as low as 0.12 or as high as 0.35. For reference, we superimposed the 0.05 and 0.95 quantiles of the empirical distribution of the estimator obtained by permuting the subject labels between the two groups, while keeping genes belonging to the same subject together. We see that the permutation estimates closely resemble those of the negative binomial model under correlation.
4. Discussion
The distribution of the false discovery rate estimator (2) is discrete and highly skewed, so rather than standard errors, as in Efron (2007a) and Schwartzman (2008), we chose to indicate the variability of the estimator by its quantiles. The 0.05 quantile indicates how deceptively low the estimates can be even when there is no signal. The 0.95 quantile is almost always equal to mα(u), the Bonferroni-adjusted level, showing that the estimator can be sometimes as conservative as the Bonferroni method. We emphasize that the negative binomial bands between the 0.05 and 0.95 quantiles describe the behavior under the complete null and are not 90% confidence bands for the true false discovery rate. It is interesting that, in our data example, correlation played an important role but did not cause a departure from the null distribution, as may have been predicted by Efron (2007a).
The negative binomial parameters can be computed via (5) and (15) for any pairwise distribution of the test statistics. The main motivation for assuming the normal and _χ_2 models was to reduce computations, as the Mehler and Lancaster expansions of § 2.4 allowed reducing the correlation structure to the first few empirical moments of the pairwise correlations. A similar reduction was used by Owen (2005) and Efron (2007a). As shown in the data example, _t_-statistics can be handled easily by a quantile transformation to _z_-scores (Efron, 2007a). Similarly, F statistics can be transformed to _χ_2-scores (Schwartzman, 2008).
Summarizing the effect of the pairwise correlations by their empirical moments allows a gross comparison between different correlation structures. For example, the simulated scenario in Examples 6 and 7 of a sparse correlation structure with 68% pairwise correlations equal to zero has nearly the same first moment but higher second moment as a fully exchangeable correlation with ρ = 0.06. Simulations show that both correlation structures have similar effects on the false discovery rate estimator.
Further work is required for the estimation of λ_m_(u) and ωm(u) in the negative binomial model, not assuming the complete null. This is difficult but important because the effect of the signal may be stronger than that of the correlation. Since λ_m_(u) is the expected number of discoveries, one could estimate it by Rm(u), but this estimate is too noisy. In terms of ωm(u), one could estimate the required overdispersion term using Theorem 2, but the provided expression depends on the true signal, which is unknown. Estimating the signal as null may be appropriate if the signal is weak and/or _p_0 is close to 1. Other options include using a highly regularized estimator of the signal vector μ. From the form of (10), it is expected that more weight would be given to pairwise correlations where the signal is large.
The negative binomial model was based on an approximation to a beta-binomial model when m is large and α is small. For larger α, the approximation may continue to hold as both distributions approach normality. Another approach sometimes used when strong dependency is suspected is to first transform the data to weak dependency via linear combination and then apply the false discovery rate procedure (Klebanov et al., 2008). This approach does not test the original marginal means but linear combinations of them. We chose not to do this so that the inference would continue to be about the original hypotheses.
The false discovery rate estimator is inherently biased and highly variable. It has been recognized before that under high correlation, the estimator ‘might become either downward biased or grossly upward biased’ (Yekutieli & Benjamini, 1999). The exchangeable correlation structure is a special case of positive regression dependence and therefore thresholding of the estimator guarantees control of the false discovery rate control (Benjamini & Yekutieli, 2001). The conservativeness of the thresholding procedure is reflected in the positive bias of the estimator, a consequence of overdispersion in the number of discoveries. In general, however, a positive bias is not enough to guarantee false discovery rate control as it makes the thresholding procedure conservative only on average, not uniformly over thresholds (Yekutieli & Benjamini, 1999). A correlation structure that produced underdispersion and negative bias might not provide control of the false discovery rate. Because the false discovery rate estimator was derived from the point of view of control, it is possible that better estimators might be found in the future by approaching the problem directly as an estimation problem.
Acknowledgments
This work was partially supported by a U.S. National Institutes of Health grant, the Claudia Adams Barr Program in Cancer Research, and the William F. Milton Fund.
Appendix
Technical details
Proof of Theorem 1. Define a mapping of the matrix {ψij} to the unit square [0_,_ 1)2 by the function
gm(x,y)=∑i=1m∑j=1mψij1(i−1m⩽x<im,j−1m⩽y<im).
Then the variance (3) is equal to the integral ∫01∫01gm(x,y)dxdy. The limit assumptions on ψij imply that as m → ∞, gm (x, y) → Ψ∞ pointwise for every (x, y). Therefore, by the bounded convergence theorem, the integral converges to ∫01∫01Ψ∞dxdy=Ψ∞.
Proof of Theorem 2. Let Φ+(u) be the standard normal survival function and Φ2+ (u, υ; ρ) be the bivariate standard normal survival function with marginals N(0_,_ 1) and correlation ρ. Integrating (8) over the quadrant [ti − μi , ∞] × [tj − μj , ∞] gives
Φ2+(ti−μi,tj−μj;ρij)=Φ+(ti−μi)Φ+(tj−μj)+ϕ(ti−μi)ϕ(tj−μj)∑k=1∞ρijkk!ℋk−1(ti−μi)ℋk−1(tj−μj),
where we have used the property that the integral of ϕ(t)ℋk (t) over [_u,_ ∞) is −_ϕ_(_u_)_ℋk_−1(_u_) for _k_ ⩾ 1. Replacing in (4) and then (6) gives the overdispersion term (11).
Proof of Theorem 3. Let Fν (u, υ; ρ) denote the bivariate _χ_2 survival function with ν degrees of freedom corresponding to the density (12). Integrating (12) over the quadrant [u, ∞] × [υ, ∞] gives
Fν(u,υ;ρij)=Fν(u)Fν(υ)+fν+2(u)fν+2(υ)∑k=1∞ρijkk!ν2Γ(ν/2)k2Γ(ν/2+k)ℒk−1(ν/2)(u2)ℒk−1(ν/2)(υ2),
where we have used the property that the integral of fν(t)ℒk(ν/2−1)(t/2) over [_u,_ ∞) is (ν/k)fν+2(u)ℒk−1(ν/2)(u/2) for _k_ ⩾ 1. Replacing in (4) and then (6) gives the overdispersion term (13).
Proof of Theorem 4. Let R ∼ N B(r, p) denote the common parameterization of the negative binomial distribution with probability mass function
| pr(R=k)=Γ(k+r)k!Γ(r)pr(1−p)k (k=0,1,2,…), | (A1) |
|---|
where 0 < p < 1 and r ⩾ 0. This parameterization is related to ours by
| λ=r1−pp⩾0, ω=1r>0⇔r=1ω, p=11+ωλ. | (A2) |
|---|
The case ω = 0, R ∼ Po(λ), is obtained as the limit of the above negative binomial distribution as ω → 0 such that λ remains constant. The same is true for the moments of R, which are continuous functions of ω.
From (A1), γ (λ, ω) = pr(R > 0) = 1 − p r = 1 − (1 + ω_λ)−1/ω_, which becomes 1 − exp(−λ) in the limit as ω → 0. For the mean, we have that
E(FD^R)=E(p0mαR∨1)=p0mα{pr(R=0)+E(1R|R>0)pr(R>0)},
where pr(R > 0) = γ (λ, ω) and pr(R = 0) = 1 − γ (λ, ω) by definition. All that remains is the conditional expectation, which for ω > 0 is equal to
E(1R|R>0)=11−pr∑k=1∞1kΓ(k+r)k!Γ(r)pr(1−p)k=pr1−pr∑k=1∞Γ(k+r)k!Γ(r)∫p1(1−t)k−1dt=pr1−pr∫p1dt(1−t)tr∑k=1∞Γ(k+r)k!Γ(r)tr(1−t)k=pr1−pr∫p11−tr(1−t)trdt.
Replacing (A2) and making the change of variable t = 1_/_(1 + ωx) gives the expression for ζ (λ, ω). The case ω = 0 is obtained by similar calculations for the Poisson distribution or by taking the limit as ω → 0.
For the second moment, we have
E(FD^R2)=E{(p0mαR∨1)2}=(p0mα)2{pr(R=0)+E(1R2|R>0)pr(R>0)}.
Again, we only need the conditional expectation, which for ω > 0 is equal to
E(1R2|R>0)=11−pr∑k=1∞1k2Γ(k+r)k!Γ(r)pr(1−p)k=pr1−pr∑k=1∞Γ(k+r)k!Γ(r)∫p1(1−t)k−1kdt=pr1−pr∫p1dt(1−t)tr∑k=1∞1kΓ(k+r)k!Γ(r)tr(1−t)k.
Following the argument in part (ii) of the proof, the last sum above is equal to (1 − t r)E{(1_/S_)|S > 0}, where S ∼ N B(r, t). Then the change of variable t = 1_/_(1 + ωx) and replacing (A2) gives the expression for _ζ_2(λ, ω).
For the distribution, fd^r takes values the discrete values ak = p_0_mα/ k (k = 1_,_ 2_, . . .). If ak+1 ⩽ x < ak (k = 1,_ 2_, . . ._), then
pr(FD^R⩽x)=P(p0mαR∨1⩽p0mαk+1)=pr(R⩾k+1)=1−pr(R⩽k)=1−F(k).
If x ⩾ _a_1 = p_0_mα, then x is greater than the largest value that fd^r can take, so pr(fd^r ⩽ x) = 1.
For the quantiles, let ɛ > 0. If q ⩽ 1 − F(1), k = _F_−1(1 − q), then
pr(FD^R⩽ak+1)=pr(FD^R⩽p0mαk+1)=pr(R⩾k+1)=1−F(k)⩾q,pr(FD^R⩽ak+1−ε)=pr(FD^R⩽p0mαk+2)=pr(R⩾k+2)=1−F(k+1)<q.
If q > 1 − F(1),
pr(FD^R⩽a1)=pr(FD^R⩽p0mα)=pr(R∨1⩾1)=1⩾q,pr(FD^R⩽a1−ε)=pr(FD^R⩽p0mα2)=pr(R⩾2)=1−F(1)<q.
References
- Benjamini Y, Hochberg Y. Controlling the false discovery rate: a practical and powerful approach to multiple testing. J. R. Statist. Soc. B. 1995;57:289–300. [Google Scholar]
- Benjamini Y, Hochberg Y. On the adaptive control of the false discovery rate in multiple testing with independent statistics. J Behav Educ Statist. 2000;25:60–83. [Google Scholar]
- Benjamini Y, Yekutieli D. The control of the false discovery rate in multiple testing under dependency. Ann Statist. 2001;29:1165–88. [Google Scholar]
- Crowder M. Gaussian estimation for correlated binomial data. J. R. Statist. Soc. B. 1985;47:229–37. [Google Scholar]
- Efron B. Large-scale simultaneous hypothesis testing: the choice of a null hypothesis. J Amer Statist Assoc. 2004;99:96–104. [Google Scholar]
- Efron B. Correlation and large-scale simultaneous hypothesis testing. J Amer Statist Assoc. 2007a;102:93–103. [Google Scholar]
- Efron B. Size, power and false discovery rates. Ann Statist. 2007b;35:1351–77. [Google Scholar]
- Farcomeni A. A review of modern multiple hypothesis testing, with particular attention to the false discovery proportion. Stat Methods Med Res. 2008;17:347–88. doi: 10.1177/0962280206079046. [DOI] [PubMed] [Google Scholar]
- Genovese CR, Wasserman L. A stochastic process approach to false discovery control. Ann Statist. 2004;32:1035–61. [Google Scholar]
- Hilbe JM. Negative Binomial Regression. Cambridge, UK: Cambridge University Press; 2007. [Google Scholar]
- Jin J, Cai TT. Estimating the null and the proportion of nonnull effects in large-scale multiple comparisons. J Amer Statist Assoc. 2007;102:495–506. [Google Scholar]
- Klebanov L, Qiu X, Yakovlev A. Testing differential expression in nonoverlapping gene pairs: a new perspective for the empirical Bayes method. J Bioinform Comput Biol. 2008;6:301–16. doi: 10.1142/s0219720008003436. [DOI] [PubMed] [Google Scholar]
- Kotz S, Balakrishnan N, Johnson NL. Continuous Multivariate Distributions, Vol 1: Models and Applications. New York: John Wiley & Sons; 2000. Bivariate and trivariate normal distributions; pp. 251–348. [Google Scholar]
- Koudou AE. Lancaster bivariate probability distributions with Poisson, negative binomial and gamma margins. Test. 1998;7:95–110. [Google Scholar]
- McCullagh P, Nelder JA. Generalized Linear Models. 2nd ed. Boca Raton, FL: Chapman & Hall/CRC; 1989. [Google Scholar]
- Mootha VK, Lindgren CM, Eriksson FK, Subramanian A, Sihag S, Lehar J, Puigserver P, Carlsson E, Ridderstraale M, Laurila E, et al. PGC-1-responsive genes involved in oxidative phosphorylation are coordinately downregulated in human diabetes. Nature Genetics. 2003;34:267–73. doi: 10.1038/ng1180. [DOI] [PubMed] [Google Scholar]
- Owen AB. Variance of the number of false discoveries. J. R. Statist. Soc. B. 2005;67:411–26. [Google Scholar]
- Patel JK, Read CB. Handbook of the Normal Distribution. 2nd ed. New York: Marcel Dekker Inc; 1996. [Google Scholar]
- Prentice RL. Binary regression using an extended beta-binomial distribution, with discussion of correlation induced by covariate measurement errors. J Amer Statist Assoc. 1986;81:321–27. [Google Scholar]
- Qiu X, Yakovlev A. Some comments on instability of false discovery rate estimation. J Bioinform Comput Biol. 2006;4:1057–68. doi: 10.1142/s0219720006002338. [DOI] [PubMed] [Google Scholar]
- Schwartzman A. Empirical null and false discovery rate inference for exponential families. Ann Appl Statist. 2008;2:1332–59. [Google Scholar]
- Storey JD, Taylor JE, Siegmund D. Strong control, conservative point estimation and simultaneous conservative consistency of false discovery rates: a unified approach. J. R. Statist. Soc. B. 2004;66:187–205. [Google Scholar]
- Yekutieli D, Benjamini Y. Resampling-based false discovery rate controlling multiple test procedures for correlated test statistics. J Stat Plan Inf. 1999;82:171–96. [Google Scholar]
- Zhou Y, Liang H. Asymptotic normality for L1 norm kernel estimator of conditional median under a-mixing dependence. J Mult Anal. 2000;73:136–54. [Google Scholar]