Late Pleistocene climate change and the global expansion of anatomically modern humans (original) (raw)

Abstract

The extent to which past climate change has dictated the pattern and timing of the out-of-Africa expansion by anatomically modern humans is currently unclear [Stewart JR, Stringer CB (2012) Science 335:1317–1321]. In particular, the incompleteness of the fossil record makes it difficult to quantify the effect of climate. Here, we take a different approach to this problem; rather than relying on the appearance of fossils or archaeological evidence to determine arrival times in different parts of the world, we use patterns of genetic variation in modern human populations to determine the plausibility of past demographic parameters. We develop a spatially explicit model of the expansion of anatomically modern humans and use climate reconstructions over the past 120 ky based on the Hadley Centre global climate model HadCM3 to quantify the possible effects of climate on human demography. The combinations of demographic parameters compatible with the current genetic makeup of worldwide populations indicate a clear effect of climate on past population densities. Our estimates of this effect, based on population genetics, capture the observed relationship between current climate and population density in modern hunter–gatherers worldwide, providing supporting evidence for the realism of our approach. Furthermore, although we did not use any archaeological and anthropological data to inform the model, the arrival times in different continents predicted by our model are also broadly consistent with the fossil and archaeological records. Our framework provides the most accurate spatiotemporal reconstruction of human demographic history available at present and will allow for a greater integration of genetic and archaeological evidence.

Keywords: human dispersals, colonization, population bottlenecks, net primary productivity, most recent common ancestor

Anatomically modern humans (AMHs) first appear in the fossil record almost 200 kya in Africa (1), but all remains found in other continents are considerably more recent (2, 3). Based on existing fossil and archaeological records, it has been proposed that AMHs left Africa 60–70 kya and spread across Asia relatively quickly (2, 3), reaching Southeast Asia at least 45 kya (4) and crossing into Sahul (Australia, New Guinea, and Tasmania) at some point between 60 and 40 kya (3). The similarity of the tropical climate in the southern part of Asia to the ancestral home in sub-Saharan Africa has been suggested as an important factor aiding the fast rate of spread (5). Movement into Southern Europe was also relatively fast, with AMHs reaching Italy 45 kya (6), and Northern Europe was reached as early as 42–43 kya (7). Conversely, the spread into North Asia and eventually, the Americas was considerably slower, possibly because of the large ice sheets that covered North America (8). However, after AHMs reached the plains of North America, their spread accelerated again, and they expanded rapidly into South America (9). Although many key events during the spread of AMHs seem to coincide with favorable climatic conditions and the occurrence of land bridges because of low sea levels, the incompleteness of the fossil record during the initial stages of human arrival into different areas makes it difficult to formally quantify the effect of climate on past human demography. Moreover, archaeological assemblages do not always provide unequivocal evidence in terms of the taxonomic status of their makers, further exacerbating the task of understanding the role of climate change in the demographic expansion of AMHs.

In this paper, we take a unique approach to this problem (a schematic representation is shown in Fig. S1). We quantify the effects of past climate change on the demography of AMHs by exploiting the signals left in the worldwide distribution of genetic variation in modern human populations. Past demographic events, such as colonization events, migrations, population bottlenecks, and expansions, have affected genetic variation within populations as well as genetic differences between populations. Thus, any estimated effect of climate on such events need to be compatible with the distribution of these genetic metrics in modern populations. To describe the global patterns of neutral genetic variation, we used the human genome diversity panel-Centre d'Etude du Polymorphisme Humain (HGDP-CEPH) panel of 51 populations distributed around the world (10) (Fig. S2), a dataset that has been used several times in the past to investigate past human demography (11, 12). We built a detailed reconstruction of worldwide climate for the last 120 ky based on the Hadley Centre model HadCM3 (based on ref. 13; details in Materials and Methods). To link climate to human demography, we used annual net primary productivity (NPP), which provides a general proxy for food availability, and it has been shown to be a powerful predictor of demographic patterns in many ecological studies (14). Estimates of temperature and precipitation from our climate reconstructions were used to predict annual NPP based on the Miami vegetation model (15). The world was represented by a hexagonal lattice with cells of equal area (∼100 km wide). The human expansion out of sub-Saharan Africa was computed over the lattice using a model of local population growth and dispersal (a schematic representation is shown in Fig. S3). This approach is analogous to the approach adopted by ref. 16, but in our model, demographic parameters were linked to primary productivity. We explored a wide range of parameter values, representing scenarios that spanned from climate having no effect on demography (the standard approach used by most population genetics models) to primary productivity having a strong positive effect on population density. Model fit was assessed using approximate Bayesian computation (ABC) (17) based on regional estimates of pairwise time to most recent common ancestor (TMRCA) (Materials and Methods).

Results

Effect of Climate on Demography.

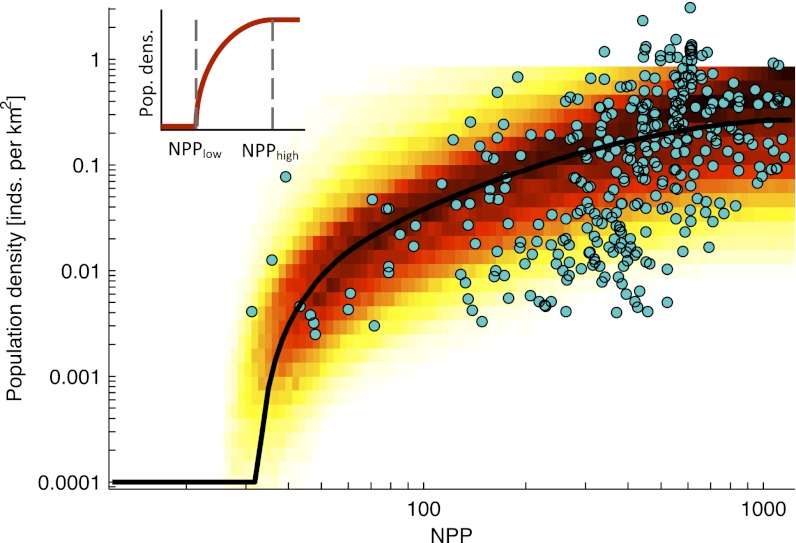
All demographic parameter combinations compatible with the present worldwide distribution of genetic diversity (Fig. S4) indicated a clear effect of climate on demography, generating the expected positive relationship between primary productivity and carrying capacities (Fig. 1). The pattern implied by the model is qualitatively similar to the relationship between primary productivity and population densities in modern hunter–gatherers (18) (Fig. S5), and populations were not recorded in areas where NPP falls below the minimum threshold for human presence selected by the model (_NPP_low) (Materials and Methods and Fig. S4 have detailed descriptions of the model parameters). Because densities of modern hunter–gatherers were not used to inform on the parameters of the model, they provide a strong validation of the realism of our simulations in reconstructing the role of resource availability on demography.

Fig. 1.

Fig. 1.

The effect of NPP on population density (individuals per kilometer squared) plotted on a log–log scale. The relationships selected by fitting the model to the current patterns of genetic variation are represented by shading, with darker colors representing more frequently selected values and the median of the relationships shown as a black line. Population densities for modern hunter–gatherers (not used to inform on the parameters of the model) are plotted as blue circles. Inset shows the role of the two model parameters (NPP _l_ow and _NPP_high) on the same log–log scale as the figure.

Predicted Arrival Times.

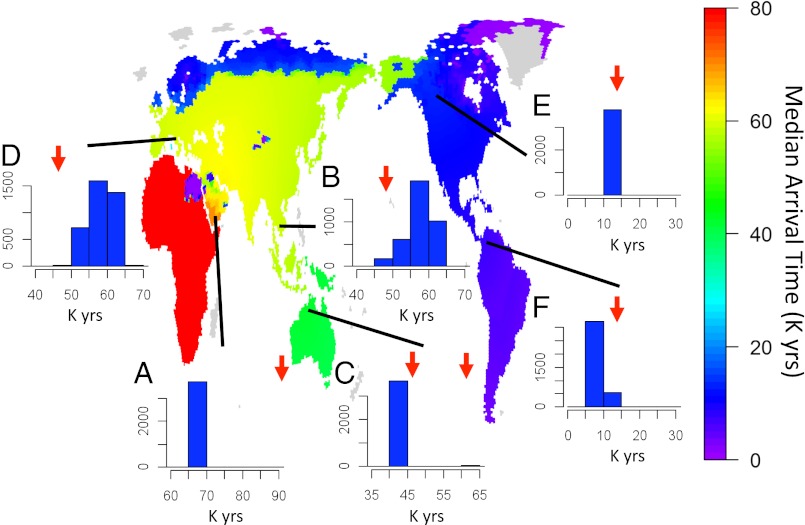
Given that no archaeological or fossil data were used to inform our model, it is especially interesting to investigate how compatible our predicted arrival times into different continents are with the fossil record. Overall, fitting our model to the genetic data produces a most likely chronology (Fig. 2 and Movie S1 shows a typical example of the expansion dynamics) broadly consistent with widely accepted archaeological and fossil data (SI Text). Crucially, such credible scenarios can only be retrieved when climate is taken into consideration; runs of the model with parameter combinations that correspond to no link between carrying capacity and NPP gave a decrease in the fit to the genetic data and unrealistic timings. Our climate-informed model reconstructs an expansion throughout sub-Saharan Africa starting ∼150–160 kya (Fig. S4_A_), resulting from the oldest pairwise TMRCA between any pair of populations found in Dataset S1. This timing is in line with other genetic models, and it is very close to the earliest dated AMH fossils found in Ethiopia (1, 19). Because of the lack of climatic information before 120 kya, which forces us to treat earlier dates as climatically homogeneous, it was not possible to reconstruct the initial dynamics of AMH expansion within Africa in detail. Moreover, the presence of AMHs in Southwest Asia at 130–90 kya suggests an early but ephemeral expansion outside of Africa (Materials and Methods). However, it is clear that, until 60–70 kya, the global colonization by humans ancestral to modern populations was prevented by the arid climate in Northeast Africa and much of the Arabian Peninsula (Fig. 2_A_). At this time, a combination of lowered sea level and more favorable climatic conditions allowed extensive migration of AMHs to the Arabic peninsula and subsequent movement through an otherwise harsh area. Our model suggests that AMHs mostly followed the so-called southern route out of Africa (20), crossing into the Arabic Peninsula at the Bab-el-Mandeb strait (Fig. 2).

Fig. 2.

Fig. 2.

Median arrival times (thousands of years ago) as predicted by the model. Histograms show the distribution [frequency (f)] of times for key areas of the world: (A) the Arabian Peninsula (the exit point out of Africa), (B) Southeast Asia, (C) Australia, (D) Europe, (E) North America, and (F) Central and South America. Red arrows show key archaeological findings commonly referred to as the earliest evidence for AMHs in those areas (SI Text, Fig. S7, and Tables S1 and S2). Gray areas were never colonized, either because of extreme climatic conditions or a lack of connections to the mainland (sea voyages of more than 100 km were not allowed in our model). For clarity, arrival times were capped to 80 kya.

After moving out of Africa, AMHs are predicted to have moved quickly through the southern part of the Asian continent, reaching Southeast Asia around 45–50 kya, consistent with the findings at the Niah caves, Malaysia, dated ca. 45 kya (4) (Fig. 2_B_). For most combinations of demographic parameters compatible with modern genetic data (Fig. S4), the predicted arrival in Southeast Asia is too late for an immediate crossing into Sahul because of higher sea levels at that time. This finding would suggest that expansion into Australasia was prevented until 45–40 kya, when sea levels lowered again (Fig. 2_C_). However, in a minority of scenarios, which are characterized by the earliest exit time out of Africa and faster rates of spread, AMHs would have been able to reach Sahul ∼60 kya. Although recent genetic work provides some support for an early colonization of Australia (21), current fossil and archaeological evidence favors the more recent expansion date into Australasia of ca. 45 kya (22, 23). However, it should be noted that our genetic dataset does not include any Australian Aboriginal population, limiting our ability to resolve the details of the spread into this continent.

Our model also predicts a rapid migration into Europe after the exit out of Africa, arriving ∼55 kya (Fig. 2_D_). This timing is somewhat earlier than the remains at the Grotta del Cavallo in Italy dated at 45 kya (6). We expect a possible delay in the appearance of fossil remains after the arrival of AMHs in any given area (the Signor–Lipps effect), and given that recent findings have pushed back the arrival in Europe by over 5 ky, the mismatch between our model and the currently known archaeological and fossil records does not seem to be very large for this region. Another interesting possibility is that the initial wave of expansion into Europe might have also been slowed down by competition with Neanderthals, a factor that our global model does not take into account. Possible admixture with Neanderthals (24) is unlikely to explain the mismatch; other than being estimated at most to be very low (25, 26), it should affect both the European and Asian branches of the out-of-Africa expansion (24), and the latter is well-reconstructed by our model.

For the colonization of the Americas, the model suggests that the main demographically significant influx of people, which accounts for contemporary genetic data, occurred ∼15 kya (Fig. 2_E_). The model parameters suggest that the end of the last glacial cycle provided favorable conditions for a rapid expansion into the Americas, with AMHs reaching South America ∼10 kya (just a few thousand years later than the most accepted dates for the presence of AMHs in the Americas) (Fig. 2_F_ and Table S2). The timing is strongly affected by the extent of the ice sheets in North America 10–20 kya, an aspect of past climate that is still relatively poorly constrained (27), and adopting different reconstructions could easily push back arrival times by a few thousands of years. It must be noted that only a limited number of genetic samples are available in the Americas; although an expanded genetic dataset of Native American populations is available in the literature (28), the additional populations have undergone varying degrees of admixture with Europeans. Moreover, given the evidence from Monte Verde, another caveat is that, although all of the alleles in the genetic dataset have ancestors, not all fossils or producers of artifacts will necessarily have descendents in these genetic data (29). Hence, the inconsistency between the archaeological evidence and the model parameters for this region could be accounted for by a number of reasons.

Routes of Gene Flow Through Time.

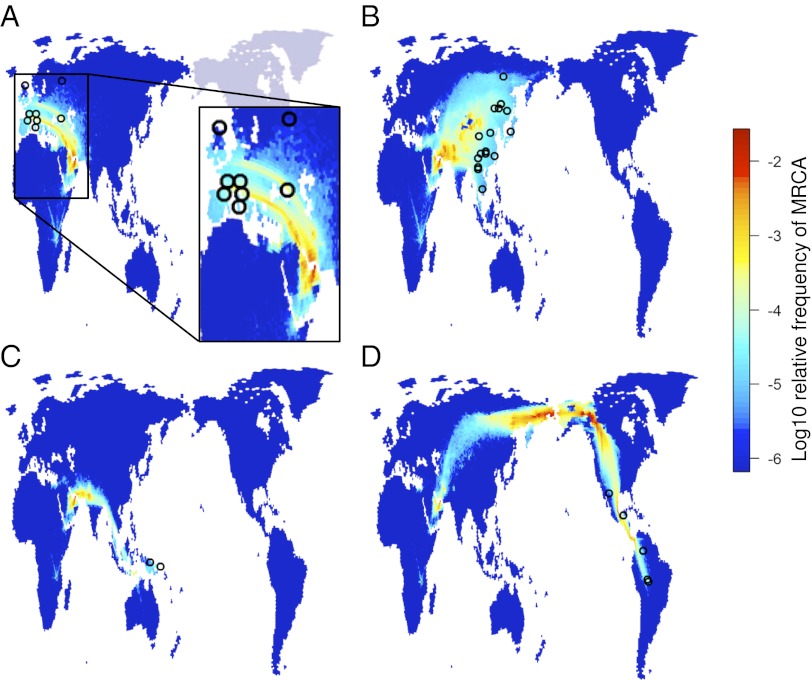
The reconstructions of human demography presented in this paper are the most realistic available to date. This unprecedented level of detail allows us to reconstruct the shared history of any set of population across time and space, integrating the effect of colonizations, migrations, and population bottlenecks and expansions. The simplest way to visualize shared ancestry is to trace the history of lineages back in time and find the location where two lineages coalesce (the site of the most recent common ancestor). High densities of coalescence events reflect areas that played a key role in defining the genetic makeup of present day populations. Using our spatial framework, we simulated haplotypes for the HGDP-CEPH populations and traced the lineages for pairs of haplotypes coming from the same continent. We obtained an intriguing picture that highlights Southwestern Asia as a major hub, from which lines spread out into Europe (Fig. 3_A_), the rest of Asia (Fig. 3_B_), Australasia (Fig. 3_C_), and the Americas (Fig. 3_D_). Surprisingly, the key area where most lines meet is not found at any of the two exit points out of Africa (the Suez strait and the Bab-el-Mandeb strait) but somewhat beyond that area, spanning modern Iraq and Iran. Because of the harsh conditions in the Arabian Peninsula, this area imposed severe constraint on the movement of people out of Africa. There is also a clear signal for two separate axes of gene flow into Europe on either side of the Black Sea (Fig. 3_A_, Inset), one into the southern part of the continent and another one to the northern part (bounded to the north by the harsh Arctic climate). In Asia, the migration routes split around the Himalayas, with the northern route crossing eastern Siberia en route to the Americas (Fig. 3_B_) and the southern route crossing Southeast Asia into Australia (Fig. 3_C_). This finding is consistent with an early split between early Australian and Eurasian populations, which was found in the recent analyses of the first complete Aboriginal genome (21). We also find an interesting hotspot on the Siberian side of the Bering Strait (Fig. 3_D_), revealing its role as a locus for the expansion into the Americas consistent with the Beringian Incubation Model (30, 31).

Fig. 3.

Fig. 3.

Routes of gene flow during the expansion represented by the distribution of coalescence events; 100 gene trees were sampled from each of the best-fitting combinations of demographic parameters. Each population was represented by a single, randomly sampled haplotype. The four panels show coalescence events for populations from (A) Europe, (B) East Asia, (C) Australasia, and (D) the Americas.

Discussion

Our model highlights specific times and geographic regions that represent milestones in the peopling of the world. A particular strength of our approach is that the explicit spatial and temporal nature of our model generates a set of predictions regarding the nature and timing of human dispersal that can be tested against the available archaeological and fossil records. Areas where empirical evidence indicates an earlier dispersal suggest that our estimates of carrying capacity for those regions might be too stringent or that modern genetic diversity does not encapsulate the diversity of these ancient human populations, some of which will have presumably gone extinct without contributing directly to modern levels of genetic variation. To build a global model, we had to leave out several region-specific factors, such as local adaptation to new climatic conditions (32, 33), the depletion of important food sources such as megafauna (34), the advent of new techniques such as agriculture (35) and domestication (36, 37), or the possible competition with Neanderthals during the colonization of Europe (38). Moreover, given that as much as two-thirds of the history of Homo sapiens took place within sub-Saharan Africa, we should not forget the combined effects of demographic and cultural evolution within Africa before expansion (39), which may ultimately have had profound effects on our ability to adapt culturally to a range of novel environments and successfully outcompete archaic populations (2).

Future work should concentrate on regional studies, which would require producing more detailed climatic reconstructions for the appropriate times and places. It will then be possible to implement more refined demographic models, which might, for example, capture changes in technology and our ancestors’ ability to survive and reproduce under different climates and ecological settings or incorporate more complex demographic rules, such as allowing colonization events to occur before reaching carrying capacity in a neighboring deme (40). Parameterizing such localized reconstructions will require the inclusion of genetic data from key populations, and some of these populations may reside outside of the area of primary interest, which was revealed by the broad spatial spread of coalescent events described by our global model (Fig. 3). Furthermore, archaeological and anthropological evidence could be used combined with the genetic data to further constrain demographic parameters of the expansion (in a manner analogous to ref. 36). Ultimately, this generation of spatial models will allow an unprecedented integration of genetic, fossil, and archaeological evidence and hopefully foster a meaningful and integrated conversation between these disciplines as scenarios are generated, evaluated, and revised.

Materials and Methods

Genetic Dataset and Summary Statistics.

We used genotype data comprising 54 di- and 166 trinucleotide microsatellite markers from 51 populations (Fig. S2) in the HGDP-CEPH panel to represent global present day genetic variation (published in ref. 41). This subset of the genotype data is from unrelated individuals in the HGDP-CEPH panel (published in refs. 10, 42, and 43) filtered for alleles consistent with gains and losses of whole units of the repeat motifs of each marker (41). The tetranucleotide markers were removed because of their bias in global trends in genetic diversity compared with di- and trinucleotide markers, consistent with ascertainment bias (41). In addition, we removed the Bantu-South population (because of recent long-range movement) and merged the two Han-Chinese populations into a single population.

From the genotype data, we estimated the average pairwise number of generations to pairwise TMRCA within and between populations for di- and trinucleotide loci separately using the standard stepwise mutation model (44, 45). For dinucleotide markers (the average pairwise TMRCA between populations a and b), we use (Eq. 1)

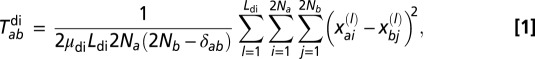
graphic file with name pnas.1209494109eq1.jpg

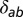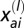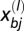where L_di is the number of dinucleotide loci, μ_di is the dinucleotide mutation rate, Inline graphic is Kronecker’s Δ (which is one when a = b and zero otherwise), 2_N a and 2_N b are the number of genotypes from populations a and b, respectively (N a and N b are the corresponding sample sizes), and Inline graphic and Inline graphic are the _i_th and _j_th genotypes (number of repeat units) in populations a and b, respectively, of locus l. The corresponding calculation for trinucleotide loci (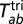Inline graphic) is analogous.

The dinucleotide stepwise mutation model mutation rate for these markers was estimated in the work by Dib et al. (46) to _μ_di = 1.52 × 10−3 mutations per generation. We scaled the average of all pairwise trinucleotide TMRCA estimates within and between populations to match the corresponding quantity calculated from the dinucleotide markers. Finally, we combined the estimates from di- and trinucleotide markers into a single estimate using the weighted average (Eq. 2)

graphic file with name pnas.1209494109eq2.jpg

Estimates of pairwise TMRCA for all populations can be found in Dataset S1.

Climate and Net Primary Productivity Reconstructions.

Climate reconstructions were based on the Hadley Centre Model HadCM3 (13), and we computed annual NPP based on the Miami model (15). Details on the climate models are in SI Text.

Spatially Explicit Demography.

We built a spatially explicit model, in which the world is divided into hexagonal cells of equal area ∼100 km wide [this scheme avoids distortion at large latitudes (47)]. Cells are either entirely on land or sea. The cells on land depend on the global sea level, which itself depends on the climate and thus, changes through time. Some cells at high latitudes were completely covered in ice and considered uninhabitable (the temporal extent of ice sheets were reconstructed as described above).

The carrying capacity K of a cell is a continuous, piecewise linear function of the NPP. For NPP values below the lower threshold, _NPP_low, the carrying capacity is zero; above the upper threshold, _NPP_high, the carrying capacity is given by the parameter _K_max, and between the two thresholds, the carrying capacity increases linearly from zero at _NPP_low to K at _NPP_high. By adjusting the thresholds, it is possible to represent both high and low climate sensitivity as well as different options for the NPP value where the model is most sensitive to variation in climate.

Our climate reconstructions used 62 snapshots of global climate spaced every 1,000 y between the present (0 kya) and 22 kya, every 2,000 y between 24 and 80 kya, and every 4,000 y between 84 and 120 kya. For each climate snapshot, we classified cells as land or sea, and we calculated yearly NPP for each land cell. For generations between snapshots, we interpolated the land/sea classification using the nearest snapshot, and NPP values were calculated using the function (Eq. 3)

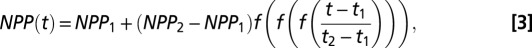
graphic file with name pnas.1209494109eq3.jpg

where 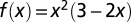Inline graphic is a function symmetric around x = 1/2, the first and second derivatives equal to zero at x = 0 and x = 1, _t_1 and _t_2 are the times of the two snapshots (_t_1 < t < _t_2), and _NPP_1 and _NPP_2 are the corresponding NPP values [Fig. S6 shows an illustration of NPP(t)]. This NPP interpolation is approximately constant around the points in time where reconstructions are available, and consecutive reconstruction points are separated by a region of smooth transition from one to the other, covering approximately one-half of the interval between the reconstruction points.

We used a simple growth model for the population dynamics (Fig. S3 shows a schematic representation). The demographic simulation is started _T_start generations ago by seeding a single cell in sub-Saharan Africa (11°7′ S, 34°21′ E) with _cK_0 individuals randomly from a hypothetical ancestral population with _K_0 individuals (assumed to be constant leading up to the start of the simulation). In each subsequent generation, the population within the cell grows linearly with rate rK individuals per generation until reaching the carrying capacity K. Thereafter, if K increases, population growth is resumed, and if K decreases, the population is reduced to the new carrying capacity. When the population is at carrying capacity, it sends cK colonizers to each neighboring empty, habitable cell. In addition, neighboring cells exchange _mN_min migrants per generation, where _N_min is the smaller population size of the two cells.

To facilitate efficient simulation of the Wright–Fisher genetic model (local random mating, diploid nonoverlapping generations, and selectively neutral mutations) (48), we needed the number of individuals to be integer numbers. We found that simply rounding to the nearest integer in a deterministic model can produce strong artifacts, especially when the number of colonizers or the carrying capacity is small. To avoid this problem, we use a simple stochastic population model. Given population sizes in generation t, the number of individuals in the cell in generation t + 1 is calculated as follows. First, we use the population model described above to calculate expected population growth, migration between cells, and colonization of empty cells. Second, the actual number of individuals in the cells and the number of migrants and colonizers are taken as independent Poisson distributed random numbers generated using the corresponding expected values. When the population size is large, there is little difference between the stochastic and deterministic formulations of the population dynamic, but for low migration and colonization rates, the stochastic formulation works much better.

Generating Gene Genealogies from Simulated Demographies.

To generate stochastic gene genealogies for individuals sampled at different locations, we proceed in two stages. First, the global population dynamic is simulated forward in time as described above. In each generation, we record the number of individuals in each cell and the number of migrants or colonizers moving from a cell to another. Second, we simulate gene genealogies for each locus (independently because they are unlinked). We simulate local random mating according to the Wright–Fisher dynamic conditional on the population dynamic recorded in the first stage. Starting with the present, we trace the ancestral lines of our sampled individuals back through time generation by generation, keeping track of which line belongs to each cell. Each line is randomly assigned to a gamete within the individuals in the cell. If the individual is a migrant or colonizer, the line moves to the cell of origin. Whenever two lines are assigned to the same gamete, we record the data, and the two lines coalesce into a single line (their common ancestor). This process proceeds until there is only a single line left, corresponding to the common ancestors of the whole sample.

Model Fitting by ABC.

We fitted our model in the ABC framework using the ABC-GLM algorithm implemented in the ABCtoolbox software (17). We generated six summary statistics from the average pairwise TMRCA between continents: we treated Europe and Central Asia as one continent (Eurasia) and East Asia as a separate continent. Because Oceania only has two populations (in Papua New Guinea), we included these populations in the East Asian set. Our summary statistics are, thus, _T_Africa,Eurasia, _T_Africa,EastAsia, _T_Africa,America, _T_Eurasia,EastAsia, _T_Eurasia,America, and _T_America,America. These statistics were selected to capture the most important features of the full matrix of pairwise TMRCA values. Although there is a gradual decline in genetic diversity (and thus, a decline in pairwise TMRCA within populations) with increasing distance from Africa, the decrease is not linear (12), and there are some discontinuities between continents (49). Pairwise TMRCAs between adjacent pairs of continents capture both the overall shape of the decline (including the different slopes at different distances from Africa) and any discontinuity caused by major bottlenecks during the initial spread into new continents; they also keep the number of summary variables reasonably low, which is required by ABC (17).

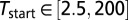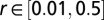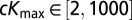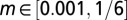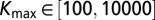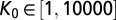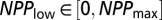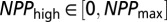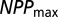We started by randomly sampling 1.5 million parameter values from the following ranges: Inline graphic (in thousands of years ago), Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, Inline graphic, and Inline graphic (where Inline graphic is the largest NPP value observed in the climate dataset). The parameters t, _NPP_low, and _NPP_high were sampled according to a uniform distribution over the interval, whereas all other parameters were sampled from a uniform distribution of their log-transformed values. We also imposed (through rejection sampling) the constraints 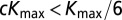Inline graphic (cannot send out more colonists than individuals) and 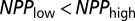Inline graphic. We then ran ABC-GLM on the accepted parameter combinations (based on the 0.25 percentile of Euclidean distances between simulated and observed statistics) to estimate posterior distributions of the model parameters.

Supplementary Material

Supporting Information

Acknowledgments

We acknowledge financial support from the Biotechnology and Biological Sciences Research Council (F.B. and A.M.) and the Leverhulme Trust (A.M.).

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information