Strain history dependence of the nonlinear stress response of fibrin and collagen networks (original) (raw)

Abstract

We show that the nonlinear mechanical response of networks formed from un–cross-linked fibrin or collagen type I continually changes in response to repeated large-strain loading. We demonstrate that this dynamic evolution of the mechanical response arises from a shift of a characteristic nonlinear stress–strain relationship to higher strains. Therefore, the imposed loading does not weaken the underlying matrices but instead delays the occurrence of the strain stiffening. Using confocal microscopy, we present direct evidence that this behavior results from persistent lengthening of individual fibers caused by an interplay between fiber stretching and fiber buckling when the networks are repeatedly strained. Moreover, we show that covalent cross-linking of fibrin or collagen inhibits the shift of the nonlinear material response, suggesting that the molecular origin of individual fiber lengthening may be slip of monomers within the fibers. Thus, a fibrous architecture in combination with constituents that exhibit internal plasticity creates a material whose mechanical response adapts to external loading conditions. This design principle may be useful to engineer novel materials with this capability.

Keywords: ECM, nonlinear rheology, factor XIII, blood clot

Networks of stiff biopolymer fibers are a major component of the structural architecture of multicellular organisms; their unique material properties provide rigidity and protect structural integrity. These networks are particularly important in the extracellular matrix (ECM) where they provide mechanical support to living cells and form many of the load-carrying structures in the body. One important example is fibrin, which forms the underlying scaffold of blood clots and the provisional matrix (1). Another important example is collagen type I, the major structural constituent of all connective tissue, tendons, ligaments, and bone (2). Because the in vivo structure of these fiber networks is so complex, investigations of in vitro networks of both proteins have been used to explore their structure and unique mechanical properties, and to elucidate their underlying design principles. Interestingly, fibrin and collagen exhibit many similar features: Both proteins self-assemble into thick, hierarchically ordered, rather stiff fibers through electrostatic and hydrophobic interactions (3, 4); these fibers associate into sparse, 3D networks that possess unusual mechanical properties not seen in synthetic polymers. In both cases, these networks display highly nonlinear mechanics and stiffen significantly as the strain increases (5–8). In addition, they are both also viscoelastic: They partially store elastic energy and partially relax internal stress through dissipative processes (9–12). All of these properties are delicately influenced by the structure of the networks, by the molecular interactions between monomers, and by the addition of covalent cross-links (7, 13, 14). This creates a delicate interplay between the viscoelastic and nonlinear mechanical properties of these networks. However, the underlying nature of this interplay remains elusive; this is particularly important when a network is strained into its nonlinear regime where the material is exposed to very high stresses. In this case, little is known about how the complex viscoelastic behavior affects the internal structure and whether this leads to a modification of the bulk mechanics. In particular, it is unclear whether the mechanical bulk response remains unchanged when the network is strained several times. In fact, it is just this repeated straining that is important for an ECM: Blood clots must withstand the pulsatory flow of blood (1). Similarly, tendons and ligaments are subjected to repeated stretch with every motion of the body; indeed, collagen-rich tissues are known to exhibit mechanics that are dependent on their loading history (15–18). However, detailed rheological measurements of pure collagen or fibrin biopolymer networks under repeated large-strain loading have never been reported. This is essential to assess whether these biopolymer networks exhibit mechanics that depend on loading history and to elucidate the interplay between viscoelastic properties and nonlinear bulk mechanics of stiff ECM biopolymer networks. This may also help determine how these structures behave in the body.

Here, we show that the mechanical response of networks formed from fibrin or collagen type I continually changes in response to repeated large-strain loading. This change shows many characteristics of weakening; however, by collapsing this response onto a master curve, we demonstrate that the dynamic evolution arises from a shift of a characteristic nonlinear stress–strain response to higher strains. Therefore, the imposed loading does not weaken the underlying matrices but instead delays the onset of the strain-stiffening response. Using confocal microscopy, we present direct evidence that this behavior does not arise from damage to the material, such as rupture of the constituent fibers or detachment of their branch points; instead, it results from persistent lengthening of the individual fibers. Furthermore, we show that covalent cross-linking of fibrin or collagen inhibits this workability of both materials, suggesting that the molecular origin of individual fiber lengthening is slip of monomers within the fibers.

Results

Repeated Large-Strain Loading of Fibrin Networks.

We initiate polymerization of a fibrin network by addition of 0.2 NIH units/mL human α-thrombin to a 1 mg/mL fibrinogen solution at 25 °C in situ in a strain-controlled rheometer equipped with a plate–plate geometry. To ensure that the resulting network is completely free of covalent cross-links, we remove any traces of human factor XIII from our fibrinogen stock solution by affinity chromatography (19). We measure the nonlinear mechanical response by imposing a series of sinusoidal, large-strain oscillations of fixed amplitude while continuously recording the resulting stress. The stress–strain response of each cycle exhibits a sharp upturn of the stress with increasing strain, reflecting the nonlinearity of the material, and a closed loop on decreasing the strain, reflecting the dissipative loss in the network as seen in Fig. 1_A_.

Fig. 1.

Fig. 1.

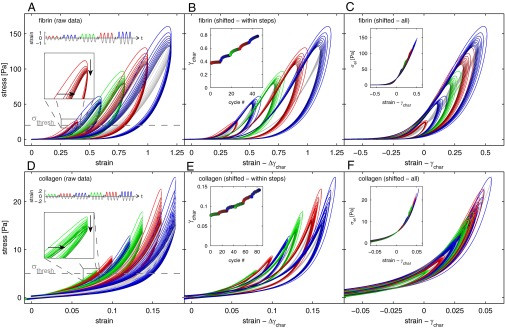
Evolution of the nonlinear viscoelastic stress response of fibrin (A–C) and collagen networks (D –F) in response to large amplitude strain cycles. (A) Sets of 10 strain oscillations with stepwise increasing strain amplitude (0.4, 0.6, 0.8, 1, 1.2) are imposed on a 1 mg/mL fibrin network free of covalent cross-links. (Upper Inset) Colored loops show the stress vs. strain response of half-cycles (sets of cycles at different amplitudes are represented by different colors; later cycles are indicated by darker shades of each color). (Lower Inset) Enlarged view of the evolution of the first set of cycles at a strain of 0.4; the stresses decrease with each subsequent cycle (vertical arrow), and the onset of nonlinearity occurs at higher strains (horizontal arrow). Gray lines represent the elastic midlines of each cycle; the intersect strain γchar with the threshold stress σthresh is calculated for each midline (Inset in B). (B) Stress vs. strain loops from cycles at the same strain amplitude are replotted by subtracting Δγchar, the increase of γchar of each cycle with respect to γchar of the first cycle at each strain amplitude. (C) All stress vs. strain loops are collapsed onto a single master curve by replotting each cycle subtracted by γchar. (Inset) Collapse of the elastic midlines σel by replotting each curve subtracted by γchar. Colors correspond to the viscoelastic loops in the main panel. (D –F) A similar strain protocol (0.06, 0.08, 0.1, 0.12, 0.14, 0.16, and 0.18 strain amplitude) is performed on a 0.9 mg/mL collagen network; this shows a similar shift of the material’s stress–strain response that can also be collapsed onto a single master curve. (All panels and Insets correspond to those in A–C.)

However, the stress–strain response changes with each subsequent cycle: The stress is lower at each value of the strain, and the upturn due to the nonlinearity occurs at a higher strain (Fig. 1_A_, Lower Inset). After 10 cycles, we increase the strain amplitude of the oscillations (Fig. 1_A_, Upper Inset). The stress–strain behavior of the first cycle at the increased strain amplitude closely follows that of the last cycle at lower strain levels; however, because the maximum strain is now larger, the maximum stress the nonlinear loop reaches is also larger. With all subsequent cycles at this strain amplitude, the stress decreases and the network again undergoes weakening (Fig. 1_A_). As we increase the amplitude further, the material responds similarly, and this can be repeated until the network eventually breaks (Fig. S1_A_). This response contains many intriguing features; however, it is particularly striking that the shapes of the nonlinear mechanical response of all cycles are very similar, with the distinguishing characteristic that the nonlinear strain stiffening occurs at successively higher strain.

To compare the stress–strain relation between cycles of fixed strain amplitude, we quantify the shift in the nonlinear response of the elastic portion of the viscoelastic stress–strain relation. We average the stresses during loading and unloading to determine the elastic component of the complex stress, σel (20) (for further details, see Fig. S2 and SI Text). To parameterize the shift of the onset of the nonlinearity in each cycle, we chose a threshold stress σthresh and calculate the characteristic strain, γchar, at which σel(γchar) = σthresh. We find that γchar increases with each cycle; the amount of the increase slows with successive cycles of the same strain amplitude (Fig. 1_B_, Inset). To compare the similarities in the shifted mechanical response, we determine the increased shift for each successive cycle 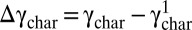Inline graphic, where 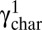Inline graphic is the characteristic strain for the first cycle of each amplitude. We then shift the data for each cycle by subtracting Δγchar from the strain at every point on the cycle, and plot these shifted data in Fig. 1_B_. Remarkably, the σel for each strain amplitude collapse onto a master curve as shown by the gray curves in Fig. 1_B_. Moreover, we can collapse all stress curves from all steps at all strain amplitudes onto a single, universal master curve by subtracting γchar, thus plotting σel(γ − γchar) (Fig. 1_C_ and Inset). We confirm that this collapse is not affected by the geometry of the rheometer tool by repeating the experiment and analysis using a cone–plate geometry where the strain is constant across the whole geometry of the tool (Fig. S3). Remarkably, this master curve is similar to that obtained for a virgin network when strained immediately to the highest amplitude (Fig. S1_A_, Inset). Thus, the shapes of the nonlinear mechanical response of a fibrin network remain identical after repeated straining or working, demonstrating that the effect of the working of the material is to shift its nonlinear stress response to a higher strain. The shift occurs equally in both directions of the symmetrically applied sinusoidal deformations (Fig. S1). However, when the network is strained by several cyclic half-sine deformations in one direction, only that half of a full sinusoidal strain cycle is shifted, whereas the response in the other half of the cycle is unaffected (Fig. S4). Such unusual shift of the material response cannot be explained by any conventional concept of viscoelasticity. Instead, it is reminiscent of an inelastic material change that introduces an excess length into the network. This can occur through various processes: Branch points may detach (21, 22), and fibers may slide with respect to one another (23), may bundle (24), or may rupture.

Confocal Imaging of a Fibrin Network Held Under Shear.

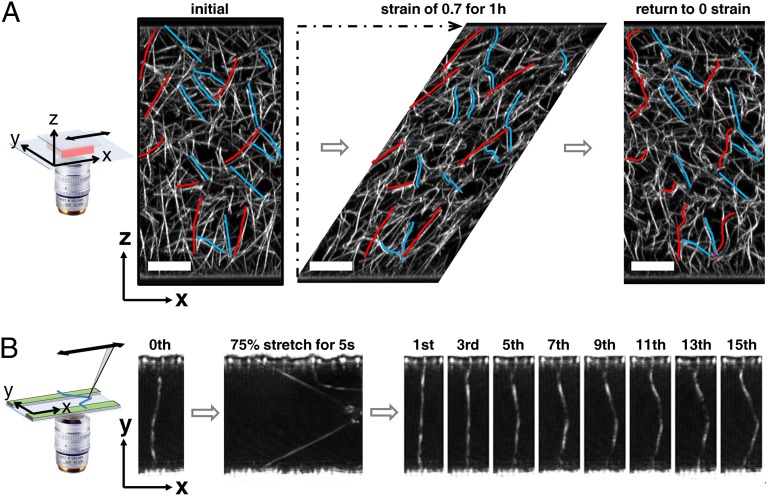
To elucidate the nature of this lengthening, we polymerize a fluorescently labeled fibrin network between two parallel glass plates on a confocal microscope and directly image the network structure while we perform a strain hold experiment: We impose a sudden shear deformation of a strain of 0.7 by translating the top plate and acquire a full 3D image every minute for 1 h; thereafter, we release the shear by returning the plate to its initial, 0-strain position and immediately acquire another 3D image. The unstrained, virgin fibrin network is composed of sparse, randomly oriented fibers, which are initially nearly straight (Fig. 2_A_). Upon being sheared, the deformation of individual fibers depends on their orientation in the network: Fibers stretch and their length increases when oriented in the direction of shear; whereas, rather than being compressed, they buckle when oriented perpendicular to the direction of shear as highlighted by the red and blue lines, respectively, in Fig. 2_A_. When we perform a similar strain hold experiment with the rheometer, we find that the network stress decreases significantly, to less than 20% of its initial value, over the course of 1 h (Fig. S5_A_). Surprisingly, however, when we examine the evolution of the structure of the network under shear, there are no obvious changes in the sheared structure visible during the entire period; instead the network appears completely static (Movie S1): We observe no rupture of individual fibers or branch points, no detachment of fibers from the plates, and no significant sliding of fibers with respect to one another. Thus, network stress is relaxed, yet the network structure remains fully static. Therefore, stress relaxation must occur within the fibers themselves; this is consistent with atomic force microscopy experiments on single fibers (25).

Fig. 2.

Fig. 2.

Structural changes of an un–cross-linked fibrin network held under shear deformation, and the effect of repeated stretching of an individual fibrin fiber. (A) A fluorescently labeled 1 mg/mL fibrin network free of covalent cross-links is polymerized in a custom-built shear cell consisting of two parallel glass plates. Its 3D network structure is imaged before (Left), during (Center), and after (Right) a shear deformation of a strain of 0.7 is applied for 1 h by translating the top plate horizontally while the bottom stays stationary. The colored lines highlight fibers in the direction of shear (right of red lines) and perpendicular to the direction of shear (left of blue lines). All images are x–z projections of a volume spanning 15 µm in the y direction. (Scale bar: 20 µm.) (B) An individual fibrin fiber suspended perpendicularly over a 20-µm–wide micropatterned channel is stretched 15 times for 5 s to 175% of its original length with a pulled glass capillary. With ongoing cycles, the fiber appears increasingly bowed, indicating that it becomes successively longer.

When the imposed strain is removed, the branch points of the network return approximately to their initial position; however, the shapes of the fibers differ significantly from their initial state: Fibers that were buckled under shear return relatively straight, whereas fibers that were stretched under shear now appear buckled and curved as shown in Fig. 2_A_ and Movie S2. This buckling suggests that stretched fibers do not fully retract to their original rest length but instead become longer.

To confirm that fibers do indeed lengthen after they have been temporarily stretched, we image an individual fibrin fiber suspended perpendicularly over a microchannel (26) and repeatedly stretch it with a glass capillary pulled to a 1-μm diameter tip and mounted onto a micromanipulator. The initially straight fiber is stretched laterally along the channel until its length is increased by ∼75%. After holding this deformation for 5 s, we release the fiber and then repeat this procedure 15 times in 10-s intervals. After each stretch, the shape of the fiber becomes increasingly bowed as seen in Fig. 2_B_. This demonstrates that the fiber rest length does indeed increase when it is stretched.

Microscopic Origin of the Bulk Response.

We can use these observations to understand the bulk network behavior on an individual-fiber basis: When the network is sheared, each fiber of the subset oriented in the direction of shear is stretched, putting it under tension (Fig. 3_A_, I–II). However, the rest lengths of these fibers increase over time, thereby relaxing most of this tension (Fig. 3_A_, III). As the applied strain returns to zero, the system returns to its initial position, putting the lengthened fibers under compression; instead of shortening to their original rest lengths they buckle and remain lengthened (Fig. 3_A_, IV). Thus, when the fibrin network is sheared again, these lengthened fibers do not contribute to the total network shear stress until their undulations are pulled out and they become taut (Fig. 3_A_, V–VI). This delayed engagement of these fibers leads to the observed shift of the shear response of the entire system to higher strains. The amount fibers lengthen during each cycle is a fraction of their relative stretch; therefore, as the rest length of these fibers increases, their successive relative stretch becomes less, leading to the asymptotic approach to their maximum increase in length. Thus, for a constant strain amplitude, the successive shift of the stress response slows as does the decrease of the maximum stress. However, when the strain amplitude is increased, fibers are again stretched beyond the increased length to which they have been worked, and, hence, the lengthening and corresponding shift in the stress response begins anew. Moreover, once the lengthened fibers are pulled taut, the stress–strain response of the network is again similar to the virgin network. This provides a fiber-level account of the stress–strain response behavior of the bulk and its scaling, as observed in Fig. 1. For symmetrically applied shear deformations, the fibers of each of the two orthogonal subpopulations are lengthened during the respective half-cycles and, hence, the response of the fibrin network shifts in a similar fashion in each strain direction. By contrast, when the network is sheared asymmetrically in one direction, only fibers in the subpopulation that is stretched are lengthened; those in the subpopulation of orthogonal fibers remain unaltered. This explains our observation that an asymmetrically worked network displays a shift of its mechanical response only in the direction that it is worked, while its properties remain unaltered in the other direction.

Fig. 3.

Fig. 3.

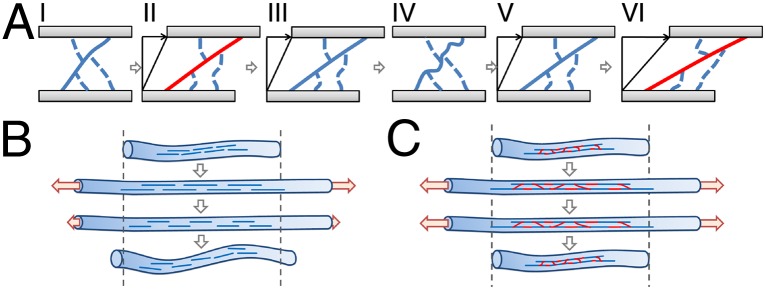
Lengthening of viscoelastic fibers due to stretching followed by buckling. (A) (I) Fibers oriented in the direction of shear (solid line) and fibers oriented perpendicular to it (dashed lines) behave differently when the bulk is sheared. (II) Upon shear, fibers in the direction of shear are stretched, putting them under tension (red line), whereas fibers perpendicular to it buckle. (III) The tension within the stretched fibers relaxes quickly due to internal viscoelastic processes, leading to an increase of their rest lengths. (IV) Upon return of the bulk deformation to the initial 0-strain position, lengthened fibers remain so, because they do not become compressed, but instead buckle. (V) When the network is sheared again, the lengthened fibers do not contribute to the bulk shear stress until they are pulled taut. (VI) Once the shear amplitude exceeds those of previous cycles, fibers contribute to the shear stress as before, which accounts for the observed shift of the bulk stress response to higher strains. (B) When an un–cross-linked fiber is put under tension, slip of protofibrils (blue lines) leads to a strong relaxation of the internal stress and causes the rest length of the fiber to increase. (C) By contrast, in a fiber fully cross-linked, adjacent protofibrils are covalently bound to one another (red links) and do not slip under tension leading to a suppressed relaxation; therefore, the fiber retains its initial rest length upon stress release.

Effect of Covalent Cross-Linking.

The stress relaxation and lengthening of the fibrin fibers under stretch can be explained by their microscopic nature: Fibrin fibers are self-assembled arrays of fibrin protofibrils whose mechanical properties, as well as their interaction with each other, determine the mechanics of the fibers (1, 13). Slippage between protofibrils or the breaking of knob-hole bonds drive stress relaxation in fine fibrin clots (5, 27, 28) and may occur within the fibers themselves in coarse clots (29) (Fig. 3_B_). Furthermore, the dissociation of oligomers (30) could also contribute to stress relaxation and fiber lengthening. All of these mechanisms are inhibited with the introduction of physiologically important covalent cross-links by activated factor XIII (factor XIIIa), which catalyzes the formation of covalent bonds that not only link fibrin monomers within protofibrils to each other but also link adjacent protofibrils (30, 31). If protofibrils neither slip nor break, the fibers will not lengthen and the stress response of the system should not shift (Fig. 3_C_). We therefore hypothesize that a fibrin network that is covalently cross-linked by factor XIIIa will show a decreased shift of the stress response under cyclic loading.

To test this hypothesis, we repeat the same measurement protocol on an equivalent fibrin network that has not been depleted of factor XIII and, hence, is completely cross-linked (Fig. S6). In this case, the stress–strain response is unchanged with subsequent cycles at constant amplitude and the data loops fully overlap each other (Fig. 4_A_, same colors). Moreover, upon increase of the strain amplitude, the loading branches of each stress–strain response exactly follow the same trace, whereas the unloading branches return at correspondingly higher strains (Fig. 4_A_, different colors). These data demonstrate that the onset of nonlinearity of the cross-linked system always occurs at the same strain, regardless of the previous loading history of the material. This confirms our hypothesis that covalent cross-linking of the system inhibits the shift of the bulk mechanics to higher strains (Fig. 4_A_, Inset); moreover, these data suggest that, in the absence of covalent cross-links, the nonpermanent coupling of monomers is the origin of the observed change of the mechanical properties of the un–cross-linked fibrin network.

Fig. 4.

Fig. 4.

Nonlinear viscoelastic stress response of covalently cross-linked fibrin and collagen networks in response to large-amplitude strain cycles. (A) The stress vs. strain loops of a 1 mg/mL fibrin network cross-linked by factor XIII all overlap and do not display a pronounced shift to larger strains as indicated by the strongly inhibited evolution of γchar with cycles (Inset). (B) The stress response of a 0.9 mg/mL collagen network cross-linked by 0.2% glutaraldehyde displays a similarly suppressed working behavior. (Inset) Evolution of γchar with cycles. (The strain protocols for both systems are identical to those in Fig. 1. The gray lines represent the midlines of the viscoelastic loops from which γchar is determined for each cycle.)

Similarity with Collagen Networks.

Self-assembly of monomers into fibers is a common strategy not only inherent to fibrin networks but shared by many other biopolymers. Fibers of other proteins constructed in such a way may also be susceptible to slip of their monomers with respect to one another and, thus, may be susceptible to working of their bulk response. To ascertain whether the mechanical behavior reported here is limited to fibrin or shared by other biopolymers of this class, we repeat our measurements on another important example of a biopolymer network that is composed of nonpermanently coupled, self-assembled fibers: collagen type I (2, 3). We use a similar cyclic-strain protocol on a reconstituted network of 0.9 mg/mL collagen type I, polymerized at 25 °C in situ (Fig. 1_D_, Upper Inset). Like fibrin, collagen is viscoelastic and exhibits highly nonlinear loading and unloading cycles, with each oscillation featuring closed loops with sharp upturns (Fig. 1_D_ and Lower Inset). However, unlike fibrin, the strain-stiffening response of the collagen networks occurs at smaller strains and the networks break earlier (Fig. S1_C_). We therefore adjust the strain amplitudes in our experiment accordingly. In response to repeated straining, the nonlinear response of the collagen network also evolves with every newly imposed cycle (Fig. 1_D_, same color). When the strain amplitude is increased after 15 oscillations, the network displays an equivalent strain-stiffening response at the higher strains and subsequently undergoes a working behavior (Fig. 1_D_, different colors). This is consistent with previous work on fibroblast-populated collagen matrices, where uniaxial stretching led to similar responses (32). Once again, we can collapse all recorded stress–strain responses by subtracting an offset strain γchar, and thereby obtain a single nonlinear master curve as shown in Fig. 1 E and F. These data demonstrate that collagen networks also undergo working similar to fibrin networks.

We can also test the influence of covalent cross-linking on collagen networks by an alternative method: We add a solution of 0.2% glutaraldehyde after a network has fully polymerized; glutaraldehyde is a small molecule that can incorporate into protein fibers and covalently binds amino acid residues of neighboring monomers together. Analogous to the fibrin network cross-linked by factor XIIIa, when we repeat our measurements using a collagen network cross-linked with glutaraldehyde, the evolution of the bulk nonlinearity is completely inhibited (Fig. 4_B_) and each of the loading branches follows the same nonlinear stress–strain response. These findings confirm that covalent cross-linking has a similarly strong effect on the working behavior of collagen networks as it has for fibrin.

Discussion and Conclusion

In this report, we show that the nonlinear mechanical response of in vitro fibrin and collagen networks can change dramatically when these networks are repeatedly strained, provided the intrafibrillar bonds are not permanently cross-linked. This leads to a pronounced working behavior of the network characterized by a shift of the nonlinear stress response to higher strains. We have shown using confocal microscopy that the working of un–cross-linked fibrin networks results from lengthening of individual fibers without altering the network architecture and, thus, the stress–strain response data can be shifted onto a universal master curve when this additional length is subtracted. Because of their similar fiber architecture and rheological response, it is reasonable to expect that fiber lengthening also underlies the mechanical evolution of collagen networks.

Many aspects of this working behavior in un–cross-linked fibrin and collagen networks are also observed in other materials. A weakening of the stress–strain response during repeated straining, known as the “Mullins effect,” is observed for carbon-filled rubbers (33); similar behavior is observed in the “shakedown” of elastomers or hydrogels (34, 35), in the “fluidization” of living cells (36), in the “preconditioning” of tissues (15–18), and in the “dynamic softening” of cross-linked actin biopolymer networks (22, 24). For these materials, however, the mechanical response weakens dramatically between the first and subsequent straining cycles; this finding contrasts with the gradual shift of the entire nonlinear curve to higher strains, which we observe for fibrin and collagen, and which is reminiscent of the preconditioning of collagenous tissues. Furthermore, the underlying mechanisms responsible for strain-induced softening have not been established for the majority of these other materials. By contrast, because we can directly image the individual fibers of fibrin networks using confocal microscopy, we can unambiguously attribute the origin of the behavior in fibrin networks to the lengthening of individual fibers. The only other system for which the underlying mechanism has been identified by direct visualization is reconstituted actin networks; surprisingly, depending on conditions, actin networks exhibit both softening and hardening during cyclic loading. However, the mechanical alterations of actin networks arise mainly from unbinding and rebinding of cross-linking proteins, combined with structural rearrangements of the network, including fiber bundling, unbundling, or detachment from the plates (22,24).

The gradual working of un–cross-linked fibrin networks results from a successive lengthening of stretched fibers. Such lengthening, or plasticity, at the fiber level is observed in many biopolymer systems, including actin (37), intermediate filaments (38), or microtubules (37), and in the results of molecular dynamics simulations for collagen fibers (39). We demonstrate the consequences of such fiber plasticity on the bulk behavior when these networks are repeatedly strained: Because fibers do not rupture and, thus, the network structure remains unchanged, the shape of the nonlinear response also remains unchanged. Consequently, the data collapse best when shifted through subtraction to scale them onto a master curve. This scaling method is distinct from that commonly used to obtain master curves for other biopolymer networks or living cells (40, 41), where the scaling is achieved through multiplication by a scaling factor. It is possible that scaling through subtraction of a distinct strain may help to describe the data obtained with other materials; this possibility deserves further investigation.

The observed working behavior of fibrin and collagen networks provides a very different material property for a network that is continually subjected to cyclical strain of constant amplitude: Because the individual fibers cannot lengthen beyond their stretched length, the shift of the nonlinear response of the material will be confined to strains at or below the amplitude of the imposed cyclic strain; therefore, the mechanical response of these networks will adapt in such a way that the nonlinearity occurs at this amplitude. In the event of an increase of the strain amplitude, the immediate response will be characterized by a strong nonlinearity of the material; this might help protect the structural integrity of the network by preventing overstretch. This automatic adaptation of the mechanical bulk properties to loading conditions may be a useful design principle for the engineering of bio-inspired materials.

Our results also demonstrate that covalent cross-linking of fibrin and collagen networks controls whether the bulk mechanics of these materials shift under loading or remain fixed. Currently, the two major functions associated with human factor XIII activity are stiffening of the clots and an increase in resilience to lysis (1, 31). We, however, show that factor XIII might also have this third important function of modulating the workability of fibrin. This may have important physiological consequences for blood clots: The complete cross-linking of a blood clot during coagulation takes longer than the formation of its fibrillar backbone (31). Thus, after the initial clot has formed, its mechanical response may be slowly worked by the repeated straining and adapt to the exact mechanical environment; the subsequent cross-linking would then ultimately stabilize these adapted properties and prevent the clot from further working and rupture.

Finally, the influence of cross-linking on the mechanics of collagen may also play a role when living cells migrate through the collagen-rich interstitial space of the ECM during processes such as tissue development, wound healing, or metastasis of cancer. To migrate, cells attach to the fibers of the ECM and create traction forces that propel them (42). These forces put collagen fibers under tension; if the fibers are un–cross-linked, this tension might relax, causing the fibers to lengthen. As a result, un–cross-linked fibers may not be able to support enough tension for the cells to migrate. By contrast, cross-linked fibers may not relax their internal tension as much, thereby supporting traction forces that would facilitate cell migration. Indeed, recent results have implicated covalent cross-linking in tumor progression (43). Hence, not only the stiffening of the ECM caused by the cross-linking of collagen, but also the inhibition of fiber lengthening might play an important role for the increased ability of cancer cells to invade the surrounding ECM. Thus, the full consequences of the working behavior of fibrin and collagen networks remain to be further investigated.

Materials and Methods

Polymerization of Fibrin and Collagen Networks.

We dilute human fibrinogen and α-thrombin (Enzyme Research Labs) in a buffer containing 150 mM NaCl, 20 mM CaCl, and 20 mM Hepes at a pH of 7.4. We create a batch of factor XIII-free fibrinogen by purifying the stock solution as described in the SI Text. We polymerize un–cross-linked and cross-linked fibrin networks at 25 °C by mixing 1 vol of 0.4 NIH units/mL thrombin with 1 vol of a 2 mg/mL fibrinogen solution of the factor XIII-free or factor XIII-containing fibrinogen stock, respectively. We quantify the degree of covalent cross-linking by denaturing polyacrylamide gel electrophoresis as described in the SI Text and shown in Fig. S6.

For collagen networks, we dilute type I collagen (BD Biosciences) at 4 °C to a final concentration of 0.9 mg/mL in 1× DMEM (Sigma-Aldrich), 25 mM Hepes, and adjust the pH to 9.0 by addition of 1 M NaOH. We initiate polymerization by heating the solution to 25 °C. To covalently cross-link the samples, we pipette a solution of 0.2% glutaraldehyde (Sigma) in 1× PBS (Lonza) around the rheometer geometry once the networks have polymerized for at least 45 min. We incubate the samples for 3 h before performing experiments.

Rheometry.

We perform all rheological experiments on an ARES-G2 (TA Instruments) strain-controlled rheometer equipped with a 25-mm plate–plate geometry set to a gap of 400 µm. For fibrin experiments, we use commercial roughened stainless-steel plates; for collagen experiments, we use a custom-cut 25-mm poly(methyl methacrylate) disk as top plate and a petri dish as the bottom plate. We prevent evaporation by sealing the samples with mineral oil, except for experiments on cross-linked collagen. Here, we use a custom-built solvent trap, which allows for the addition of the cross-linking solution.

We monitor the polymerization of all samples by continuous oscillations with a strain amplitude of 0.005 at a frequency of 1 rad/s. For fibrin samples, we impose oscillatory cycles at 0.01 Hz in 0.2 strain steps beginning at a strain of 0.4. For collagen samples, we impose cycles at 0.1 Hz in steps of 0.02, beginning at a strain of 0.06. Additional measurements are described in SI Text. All data are smoothed with a cubic spline interpolation for plotting.

Confocal Imaging.

We perform all confocal experiments on a Leica SP5 equipped with a 63×/1.2 N.A. water immersion lens. For the confocal strain hold experiment, we polymerize a 1 mg/mL fibrin network from a 1:5 mixture of fibrinogen labeled with 5-(and 6)-carboxytetramethylrhodamine succinimidyl ester (TAMRA-SE) (Invitrogen) and unlabeled fibrinogen in a custom-built shear cell and visualize the full 3D structure with fluorescence confocal scanning microscopy. For single fiber pulling experiments, we create microstructured channels on a #1 coverslip by imprinting polydimethylsiloxane stamps of ridges (20 µm wide, 10 µm high) into a drop of Norland Optical adhesive #81 and curing the adhesive in 350-nm UV light. After removal of the stamp, we briefly treat the channels in an oxygen plasma and polymerize unlabeled fibrin networks over them. We remove the majority of the network and visualize the remaining single fibers suspended over the channels by confocal reflection imaging. For fiber manipulation, we sharpen a borosilicate capillary with a commercial capillary puller and coat its tip with PEG-silane to avoid adhesion to the fibers. We mount the capillary onto an Eppendorff Transferman II, which we control via custom software.

Supplementary Material

Supporting Information

Acknowledgments

We thank D. A. Vader, C. P. Broedersz, and F. C. MacKintosh for valuable discussions. This work was supported by the “Emerging Fields Initiative” of the University Erlangen-Nuremberg (Project: TOPBiomat) (to S.M. and B.F.) and by the National Science Foundation through the Harvard Materials Research Science and Engineering Center (DMR-0820484) (to D.A.W.).

Footnotes

The authors declare no conflict of interest.

This article is a PNAS Direct Submission.

See Commentary on page 12164.

References

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information