Regression-Based Quantitative-Trait–Locus Mapping in the 21st Century (original) (raw)

In the beginning, there was Haseman-Elston regression. This tool for human QTL mapping, developed in 1972, was simple and inspired. The idea was to take pairs of siblings and regress the squared differences in their trait values on their identity-by-descent (IBD) sharing at a marker. If the marker is linked to the trait, high levels of IBD sharing should be associated with a small difference in trait values, and the regression slope should be negative. Thus, linkage can be tested with a regression t test. This method (with some extensions) was predominant in human studies for >20 years, which was primarily a reflection of the fact that too little human QTL mapping was being performed to prompt the development of more sophisticated methods.

In the mid-1990s, we saw the first important alternative to Haseman-Elston regression, maximum-likelihood–based variance-components estimation (see, e.g., Amos 1994; Almasy and Blangero 1998). Variance components is seamlessly applicable to any type of pedigree, whereas Haseman-Elston regression is not, and it has substantially higher power than Haseman-Elston when trait distributions are approximately Gaussian. It has superseded Haseman-Elston as the method of choice for most studies, particularly when large pedigrees are used. However, variance components relies heavily on normality assumptions and can fail dramatically when those assumptions are violated either by nonnormality of the trait distribution or by selected sampling. Attempts to “robustify” variance components have had mixed success (see Feingold [2001] for a more complete discussion), so there is still a role for regression-based methods, which are intrinsically more robust.

In the past 5 years, there has been an avalanche of attempts to improve the power of Haseman-Elston regression and to bring regression-based QTL mapping up to date. This was set off by Wright's (1997) Letter to the Editor suggesting that it is beneficial to use the trait values of both members of a sib pair rather than just the squared difference (although this was, in fact, pointed out by Gaines and Elston [1969]). Since then, there have been six articles suggesting “revised Haseman-Elston” (regression-based) methods that use the bivariate data—by Drigalenko (1998), Elston et al. (2000), Xu et al. (2000), Forrest (2001), Sham and Purcell (2001), and Visscher and Hopper (2001). I believe that this is a complete list, but I offer profound apologies to anyone I may have omitted. There have also been three new articles discussing score statistics that have properties similar to the regression-based methods, by Tang and Siegmund (2001), Putter et al. (2002), and Wang and Huang (2002). The best of these new methods have succeeded in matching the power of variance components while retaining the robustness of the regression framework. However, they are all limited to sibships, or, in some cases, to sib pairs. In this issue of the Journal, Sham et al. (2002) take the logical next step, by developing a regression-based method that can be applied to extended pedigrees.

Those of us trying to map human QTLs have a much richer set of tools available to us than we did 5 years ago. However, the abundance of new methods has made it difficult to make choices. Only true aficionados can keep up with the literature. In this editorial, I briefly review the newest options. I will describe the new regression-based methods and score statistics, compare their strengths and weaknesses, and conclude by describing how the current offering from Sham et al. (2002 [in this issue]) fits in. I will start, however, with a disclaimer. Because all of these methods are very new, they have not been tested extensively. Most of my observations below are based on statistical theory, and I'm sure that further study of the statistics will prove at least some of my guesses wrong. A related caveat is that all of the theory I rely on is large-sample theory, and even among statistics that are asymptotically identical there may be important differences in small-sample behavior.

Description of the New Methods

Original Haseman-Elston Regression

The method proposed by Haseman and Elston (1972) is as follows. Let the _i_th sibling pair have trait values (X i,1, X i,2), and define the squared trait difference as Y D i_=(X i,1-X i,2)2. Summarize the estimated mean IBD sharing at the locus for the pair as π_i. Perform a simple linear regression of Y D i on π i. Under the null hypothesis of no linkage, the regression slope is zero. Under the alternative hypothesis that the locus is linked to the trait, the regression slope is negative. Linkage can be tested with a one-sided t test of the regression slope estimate.

New Regression-Based Methods

Wright (1997) pointed out that Haseman and Elston’s choice of Y D _i_=(X i,1-X i,2)2 discards some useful information. He showed, in a simple likelihood context, that a nontrivial amount of linkage power can be gained if information from the trait sum is also included. This observation led to the six articles mentioned above (i.e., Drigalenko 1998; Elston et al. 2000; Xu et al. 2000; Forrest 2001; Sham and Purcell 2001; Visscher and Hopper 2001), as well as to a number of other articles that studied the issue without proposing new methods. All of the new regression-based methods combine the squared trait sum and the squared trait difference in some way, in an attempt to find the function of the trait values that is most highly correlated with the IBD sharing.

Define the mean-corrected squared trait sum Y S _i_=[(X i,1-μ)+(X i,2-μ)]2. Drigalenko (1998) showed that regressions of Y D on π and Y S on π produce separate estimates of the same slope (at least for population samples). Thus, a naive approach to combining the sum and the difference is to perform separate regressions for each and to average the resulting slope estimates. Drigalenko (1998) also showed that such an approach is equivalent to performing a single regression using the mean-corrected trait product, Y P _i_=[(X i,1-μ)(X i,2-μ)], as the dependent variable. The trait-product regression idea was developed further by Elston et al. (2000), who expanded it to consider larger sibships, covariates, and other complexities.

Xu et al. (2000) and Forrest (2001) pointed out that weighting the two slope estimates equally is not optimal. On the basis of standard statistical theory, they should be weighted by the inverses of their variances. That is, the overall slope estimate should be something like

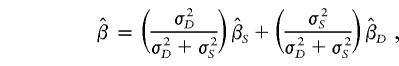
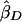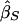where and are the slope estimates from the separate squared difference and squared sum regressions, and σ2_D_ and σ2_S_ are the corresponding variances. Forrest (2001) calculated an estimate like this, by using least-squares iteratively to simultaneously estimate the two intercepts, the single slope, and the two variances. Visscher and Hopper (2001) used a very similar method, performing the two regressions separately and then weighting the slope estimates by the separate empirical variance estimates. Xu et al. (2000) used essentially the same approach as Visscher and Hopper (2001), but they modified the weights to allow for a covariance between the two slope estimates. Sham and Purcell (2001) pointed out that σ2_D_ and σ2_S_ can be written as functions of the sib correlation and proposed a version of the estimate above with weights calculated from the correlation rather than estimated empirically. Their method is equivalent to performing a single regression of the variable

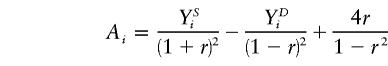
on π_i_ , where r is the sib correlation. The regression is performed with the intercept fixed at zero. They also assume that the trait values have been standardized to have mean zero and variance one before calculation of Y D and Y S.

Score Statistics

The three score statistics (Tang and Siegmund 2001; Putter et al. 2002; Wang and Huang 2002) are very similar to each other and very similar to the regression-based method of Sham and Purcell (2001), and they have the important advantage of having natural extensions to larger sibships. The score statistics are based on more or less the same likelihood used for variance components, but they are “robustified” through use of an empirical variance estimate in the denominator of the statistic. (It is also possible to use the score statistics without the empirical variance estimate, in which case they are essentially equivalent to variance components but are computationally simpler.) Tang and Siegmund's (2001) version of the score statistic is

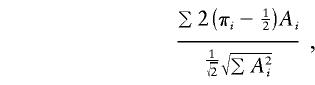
where A i is the same function defined above for Sham and Purcell's (2001) method. (Note that there are minor errors in the formulas for this score statistic in both the article by Feingold [2001] and the one by Tang and Siegmund [2001].) The other score statistics are similar, but there are minor differences among them. One difference that might be important is whether the factor 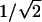is used in the denominator, as shown above, or whether the empirical standard deviation of (π_i_-1/2) is used, instead. It is also possible to make the statistic even more empirical, by using 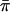instead of 1/2 to normalize π_I_ in both numerator and denominator.

Comparison of the New Methods

I have three primary criteria for evaluating the QTL mapping statistics (and, indeed, just about any statistic). The first is the power of the statistic under ideal conditions, which, for the QTL-mapping problem, means a population sample from a trait that is approximately normally distributed. The second criterion is robustness of the type I error—that is, is the type I error level of the test correct regardless of the characteristics of the data? The third criterion is the robustness of the power—that is, when the trait is not normally distributed and/or we do not have a population sample, is the statistic still powerful?

For the first criterion, variance components sets the standard. It is probably possible to eke out a little more power than variance components does, but not much more. Therefore, all of the methods are judged by whether their power equals that of variance components for population samples from normally distributed traits. On the second and third criteria (robustness of the type I error and of the power), variance components performs very poorly. When assumptions are violated, the type I error can be very wrong and the power can be very low. The regression t test, on the other hand, has type I error that is quite robust to deviations from normality for reasonably sized samples. Miller (1986) presents a general statistical discussion of this property, and Tang and Siegmund (2001) make remarks specific to the QTL-mapping setting. The robustness of the power of the t test in the presence of nonnormality is not as well-guaranteed as the robustness of the type I error (Miller 1986), though it theoretically should be better than variance components.

To be precise, I should point out that the normality assumption in regression is actually that the residuals of the regression equation are normally distributed. In fact, the Haseman-Elston method departs substantially from the regression normality assumption, because if the environmental variance in the trait model is normally distributed, then the squared trait difference (and, thus, the residuals of the regression) will have a fairly skewed distribution. Similarly, the normality assumption in the variance components model is that the trait distribution within families is multivariate normal, given the IBD configuration; however, in fact, we depart from this in standard applications, because we are really hoping that the conditional distribution given the genotype at the major locus is Gaussian. In practice, this does not seem to have an adverse effect on the power.

Criterion #1: Power for a Population Sample from a Gaussian Trait Distribution

The regression-based methods of Xu et al. (2000), Forrest (2001), Sham and Purcell (2001), and Visscher and Hopper (2001), as well as the three score statistics, are all essentially equivalent to variance components for large population samples from approximately Gaussian distributions. The original Haseman-Elston (1972) and the trait-product regression proposed by Drigalenko (1998) and Elston et al. (2000) both have lower power for certain trait distributions, because of the suboptimal weighting of the information from the squared trait sum and the squared trait difference. This is the cause of the now fairly well-known fact that the “revised Haseman-Elston” regression is more powerful than the original Haseman-Elston when the sib correlation is small but is less powerful when the correlation is large (e.g., see Palmer et al. 2000; Forrest 2001).

Criterion #2: Robustness of the Type I Error

All of the regression-based methods have type I error that is robust to departures from assumptions, at least for large sample sizes. As I discussed above, this is an intrinsic property of the regression procedure. The method proposed by Forrest (2001) departs slightly from standard regression methods, but limited studies of my own have shown it to have robust type I error. The score statistics should also have robust type I error, although they should be used with an empirical variance of the IBD estimate (as discussed above) to protect the type I error when markers are not fully informative.

Criterion #3: Power for Selected Samples and/or Non-Gaussian Trait Distributions

There are several factors that affect the robustness of the power. Probably the most important issue is the fact that Xu et al. (2000), Forrest (2001), and Visscher and Hopper (2001) weight the two slope estimates through use of empirical variance estimates, whereas Sham and Purcell (2001) and all of the score statistics use weights based on the sibling trait correlation. I would expect the latter approach (i.e., that of Sham and Purcell [2001] and the score statistics) to be more powerful when one has a population sample phenotyped (if not genotyped), so that it is possible to get a good estimate of the sib correlation. If one is not in a position to estimate the sib correlation from one's own sample or from previous studies, the methods of Xu et al. (2000), Forrest (2001), and Visscher and Hopper (2001) should do better. This certainly deserves empirical study to verify my guesses, however.

A second factor affecting the robustness of the power is whether the method allows for a covariance between the two slope estimates. Xu et al.'s (2000) method is the only one that does so. This issue has been the source of a great deal of confusion, even among those developing the methods, so I will briefly clarify the theory here. First, under any statistical model whatsoever, the (unsquared) trait sum and (unsquared) trait difference are uncorrelated. If the sib-pair trait values are a random sample from a bivariate normal distribution, then the unsquared sum and unsquared difference are also bivariate normal. If two bivariate normal variables are uncorrelated, they are independent. If they are independent, then any functions of them are independent. The slope estimates from the two regressions are such functions. Thus, if the trait values are bivariate normal, the two slope estimates are independent. However, if the trait values are not bivariate normal (because of either their basic distribution or selected sampling), we do not have independence of the sum and difference and, thus, do not have independence of the slope estimates.

Yet a third factor is that all of the new methods require that one specify the overall trait mean, μ. It appears that, for highest power, this should always be the population trait mean, even when one is not using a population sample. Again, this issue deserves further study. I note that in some selected sampling situations, an appropriate population estimate might not be available, which raises the interesting question of whether the original Haseman-Elston (the only method that does not require an estimate of μ) might actually have an advantage in such situations. Wang et al. (2001) suggest the use of a family-wise mean rather than an overall population mean. They show that this is powerful when there is etiological heterogeneity—for example, when there are family-wise covariates. They apply this idea to trait-product regression, but it would be interesting to study its behavior when it is incorporated into the other methods.

Some of the methods additionally require that one specify the trait variance. Again, this should probably be the population value.

How Do the Methods Handle More Than Two Siblings?

A final item that should be mentioned is how the statistics are extended to larger sibships. Forrest (2001), Sham and Purcell (2001), and Visscher and Hopper (2001) developed their methods only for sibling pairs. Xu et al. (2000) extended their method to larger sibships through use of generalized estimating equations with an independent working model. Elston et al. (2000) proposed to handle larger sibships by directly calculating covariances between pairs. In addition, the score tests are very similar to Sham and Purcell's (2001) method, but they extend to larger sibships. In general, the different methods for handling larger sibships are not equivalent and not well studied. This is a very important area for future work, since it is well established that large sibships are more powerful than small ones for QTL mapping.

The Bottom Line

There is no reason to use the original Haseman-Elston or trait-product (Drigalenko 1998; Elston et al. 2000) regression. If you have a perfect population sample from a normally distributed trait, all of the other methods (including variance components) should be about equivalent. If you are in a situation where substantial departures from normality are likely, don't use variance components, Forrest's (2001) method, or Visscher and Hopper's (2001) method. The best choice for such data should be Sham and Purcell's (2001) method or a score statistic, if you can get a population estimate of the sib correlation; otherwise, Xu et al.'s (2000) method is probably the best option. This is the best advice I have to offer right now, but, as I said above, many details remain to be studied.

The Current Contribution by Sham et al.

Since all of the new methods discussed above are only applicable to sibships, we are still left with the need to develop robust methods for extended pedigrees. Sham et al. (2002 [in this issue]) offer us such a method. The basic idea is to reverse the original Haseman-Elston paradigm and regress the IBD sharing on an appropriate function of the trait values. The actual regression that is performed is a multivariate (not multiple) regression, within each family, of the pairwise IBD sharing scores on the pairwise squared sums and squared differences. This yields an estimate of the additive genetic variance, and those estimates can be combined across families in a natural way. This method is computationally manageable (that is, it should be much faster than variance components) and is implemented in the software package Merlin (Abecasis et al. 2002). However, it is mathematically complex enough that not all of its properties are readily apparent. Sham et al. (2002 [in this issue]) provide extensive simulation results, which suggest that the method does indeed have many of the properties we would like.

Their first simulation (their table 2) is of the type I error for population samples from an approximately normal distribution, and it shows, as would be expected, that their test has correct type I error. The second simulation (their table 3) examines the power of the test for population samples from an approximately normal distribution. For sib pairs, the power is very similar to that of variance components. For larger sibships, they actually see higher power than variance components. The third simulation (their table 4) looks at selected sampling. The type I error is correct in this case, and the power appears to be reasonable, although there is no comparison with any other method. The fourth simulation (their tables 5 and 6) looks at nonnormally distributed traits. The type I error rate is inflated in some cases. It appears that it is correct asymptotically but that fairly large sample sizes are needed for the asymptotics to hold (see the article for more detail). Some power is definitely lost when dealing with a nonnormally distributed trait, although, again, it is a little hard to judge this without comparison to other methods. The fifth simulation (their fig. 2) looks at the effect of misspecification of the population trait parameters. The type I error appears to be robust to this. Misspecification of the mean has a large effect on power, whereas misspecification of the variance or heritability does not. (Perhaps this is also true for the methods I discussed above?) The final simulation (their table 7) looks at cousin pedigrees instead of sibships, and it verifies that the type I error is mostly correct (see below for further discussion) and that the power is equal to that of variance components.

This method is an important step toward what I think will be the next generation of human QTL-mapping methods. It solves many of the major problems that have been outstanding. Of course, it still needs further study, and there are some situations in which there may be problems. In particular, as Sham et al. (2002 [in this issue]) note in their discussion, there is some hint of inflated type I error when there are small sample sizes, nonnormal trait distributions, or highly skewed contributions from some pedigrees. This leads me to wonder whether this method will indeed turn out to be appropriate for a study that consists of, say, a few very large pedigrees. However, the method is computationally easy enough that P values for such a study could be computed quickly by simulation, which means it may still be an improvement over variance components. An additional minor concern about applying this method to very large pedigrees is that one must specify the correlation between each type of relative pair. The results of Sham et al.'s (2002 [in this issue]) simulations suggest that it will be good enough if these correlations can be specified fairly approximately, but this issue probably deserves further scrutiny.

A final obvious question is whether this method makes the sibship methods discussed above obsolete. That is, for sibship data, should one use this method or one of the previous ones? The power results in table 3 of Sham et al. (2002 [in this issue]) certainly suggest that this method might be a significant improvement over all the previous methods. However, we have not actually seen power comparisons between this method and the others for selected samples and/or nonnormally distributed traits. It is also not clear whether the type I error is as robust as that of the previous methods. Therefore, I don't think we can answer this question yet.

Acknowledgments

This work was supported by National Institutes of Health grant R01 HG02374-01 and was partially completed while I was visiting the Institute for Mathematical Sciences, National University of Singapore, in 2002. The visit was supported by the Institute and by Biomedical Research Council–National Science and Technology Board (Singapore) grant 01/1/21/19/217. I would also like to offer my gratitude to the many colleagues who gave me comments on drafts of this editorial.

References

1. Abecasis G, Cherny S, Cookson W, Cardon L (2002) Merlin—rapid analysis of dense genetic maps using sparse gene flow trees. Nat Genet 30:97–101 [DOI] [PubMed] [Google Scholar]
2. Almasy L, Blangero J (1998) Multipoint quantitative-trait linkage analysis in general pedigrees. Am J Hum Genet 62:1198–1211 [DOI] [PMC free article] [PubMed] [Google Scholar]
3. Amos CI (1994) Robust variance-components approach for assessing genetic linkage in pedigrees. Am J Hum Genet 54:535–543 [PMC free article] [PubMed] [Google Scholar]
4. Drigalenko E (1998) How sib pairs reveal linkage. Am J Hum Genet 63:1242–1245 [PMC free article] [PubMed] [Google Scholar]
5. Elston RC, Buxbaum S, Jacobs KB, Olson JM (2000) Haseman and Elston revisited. Genet Epidemiol 19:1–17 [DOI] [PubMed] [Google Scholar]
6. Feingold E (2001) Methods for linkage analysis of quantitative trait loci in humans. Theor Popul Biol 60:167–180 [DOI] [PubMed] [Google Scholar]
7. Forrest W (2001) Weighting improves the “new Haseman-Elston” method. Hum Hered 52:47–54 [DOI] [PubMed] [Google Scholar]
8. Gaines RE, Elston RC (1969) On the probability that a twin pair is monozygotic. Am J Hum Genet 21:457–465 [PMC free article] [PubMed] [Google Scholar]
9. Haseman, JK, Elston RC (1972) The investigation of linkage between a quantitative trait and a marker locus. Behav Genet 2:3–19 [DOI] [PubMed] [Google Scholar]
10. Miller R G (1986) Beyond ANOVA, basics of applied statistics. John Wiley & Sons, New York [Google Scholar]
11. Palmer LJ, Jacobs KB, Elston RC (2000) Haseman and Elston revisited: the effects of ascertainment and residual familial correlations on power to detect linkage. Genet Epidemiol 19:456–460 [DOI] [PubMed] [Google Scholar]
12. Putter H, Sandkuijl LA, van Houwelingen JC (2002) Score test for detecting linkage to quantitative traits. Genet Epidemiol 22:345–355 [DOI] [PubMed] [Google Scholar]
13. Sham PC, Purcell S (2001) Equivalence between Haseman-Elston and variance-components linkage analyses for sib pairs. Am J Hum Genet 68:1527–1532 [DOI] [PMC free article] [PubMed] [Google Scholar]
14. Sham PC, Purcell S, Cherny SS, Abecasis GR (2002) Powerful regression-based quantitative-trait linkage analysis of general pedigrees. Am J Hum Genet 71:238–253 (in this issue) [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Tang H-K, Siegmund D (2001) Mapping quantitative trait loci in oligogenic models. Biostatistics 2:147–162 [DOI] [PubMed] [Google Scholar]
16. Visscher PM, Hopper JL (2001) Power of regression and maximum likelihood methods to map QTL from sib-pair and DZ twin data. Ann Hum Genet 65:583–601 [DOI] [PubMed] [Google Scholar]
17. Wang D, Lin S, Cheng R, Gao X, Wright FA (2001) Transformation of sib-pair values for the Haseman-Elston method. Am J Hum Genet 68:1238–1249 [DOI] [PMC free article] [PubMed] [Google Scholar]
18. Wang K, Huang J (2002) A score-statistic approach for the mapping of quantitative-trait loci with sibships of arbitrary size. Am J Hum Genet 70:412–424 [DOI] [PMC free article] [PubMed] [Google Scholar]
19. Wright FA (1997) The phenotypic difference discards sib-pair QTL linkage information. Am J Hum Genet 60:740–742 [PMC free article] [PubMed] [Google Scholar]
20. Xu X, Weiss S, Xu X, Wei LJ (2000) A unified Haseman-Elston method for testing linkage with quantitative traits. Am J Hum Genet 67:1025–1028 [DOI] [PMC free article] [PubMed] [Google Scholar]