Major Recessive Gene(s) with Considerable Residual Polygenic Effect Regulating Adult Height: Confirmation of Genomewide Scan Results for Chromosomes 6, 9, and 12 (original) (raw)
Abstract
Segregation and linkage analyses were performed for adult height in a population of 200 Dutch families, each of which was ascertained through a proband with asthma. The best-fit model from the segregation analysis was a major recessive gene with a significant residual polygenic background. Models without a polygenic component were rejected. A genomewide scan was performed, and it confirmed previous linkage results for chromosomes 6q25 (LOD = 3.06, D6S2436), 9p1 (LOD = 2.09, D9S301), and 12q1 (LOD = 1.86, D12S375). Our results provide evidence that a combination of segregation and linkage approaches is valuable in understanding genetic determination of common complex traits.
In the July issue of the Journal, Hirschhorn et al. (2001) reported evidence that several chromosomal regions, including chromosomes 6, 7, 12, and 13, were linked to adult height. The evidence is based on data from four different European populations examined by use of a genomewide-scan approach. Here, we present new evidence, from a segregation analysis of 200 Dutch families, for a major recessive gene regulating adult height, and we provide strong confirmation for the loci on 6q25, 9p1, and 12q1 from our genomewide scan. The results from the studies of Hirschhorn et al. (2001), together with our own results, provide strong evidence for major genes with considerable residual polygenes regulating the normal variation of adult height. In addition, these results clearly suggest that a combination of segregation and linkage approaches is valuable in understanding genetic determination of complex traits.
In an effort to understand the genetics of pulmonary function and asthma, we measured height in 1,184 subjects from 200 families. These families were ascertained through probands with asthma from Beatrixoord Hospital, Haren, The Netherlands (Postma et al. 1995; Xu et al. 2000). The spouse and all the offspring were then recruited, regardless of asthma status. Among the 200 families, 166 families consisted of two generations, 33 families of three generations, and 1 family of four generations. All participants gave written informed consent. This study design provided an optimal sample for segregation analysis.
As expected, height among our subjects increases with age in children and adolescents, reaches the maximum at age 14 years in girls and at age 16 years in boys, and then decreases slightly after age 16, reflecting either a secular trend or a longitudinal decrease in height with age in the same individual. Because we are interested in the genetic determinants of adult height, we limited our analyses of height to the 962 individuals who were age ⩾16 years at the time of examination. The residual of height, after adjusting for the effect of age (in males and females, separately), was used in all analyses. Height in this population varied between 1.5 and 2.0 m.
We first estimated correlation coefficients (_r_2) of height from the sums of squares and cross-products in relative pairs by use of the familial correlation computer program of S.A.G.E. (Statistical Analysis for Genetic Epidemiology) using an option of equal weights to all pairs (table 1). In the first-degree relative pairs, _r_2=0.4; in the second-degree relative pairs, _r_2=0.2; and in the third-degree relative pairs, _r_2=0.06, suggesting a strong familial aggregation of height. The _r_2 values between same-sex pairs of individuals were higher than those between individuals of the opposite sex, with mother-daughter pairs having the highest (_r_2=0.49). There was considerable correlation between spouses (_r_2=0.16), indicating the phenomenon of assortative mating. Heritability estimates were fairly stable, with ∼0.8 derived from most relative pairs.
Table 1.
Correlation Coefficients of Height (Adjusted for Age and Sex) among Various Relative Pairs (Age ⩾16 Years)
| Relationship | No.of Pairs | CorrelationCoefficient |
|---|---|---|
| 1st-degree relatives: | ||
| Parent-offspring | 1,354 | .41 |
| Mother-daughter | 370 | .49 |
| Mother-son | 309 | .41 |
| Father-daughter | 368 | .32 |
| Father-son | 307 | .45 |
| Siblings: | 695 | .41 |
| Sister-sister | 197 | .43 |
| Sister-brother | 347 | .38 |
| Brother-brother | 151 | .44 |
| 2nd-degree relatives: | ||
| Grandparent-grandchild | 258 | .21 |
| Avuncular | 559 | .25 |
| 3rd-degree relatives: | ||
| 1st cousin | 405 | .06 |
| Unrelated spouses | 276 | .16 |
We then performed a segregation analysis to evaluate the mode of inheritance and to estimate the potential genetic variance due to a major gene. Segregation analysis was performed using a maximum-likelihood method, as implemented in the computer package, Pedigree Analysis Package (PAP). We calculated the likelihood of finding the observed height in these families under various models, ranging from a general model to major-gene Mendelian models and including an environmental model, a polygenic model, and a combination of polygenic models with either major-gene models or an environmental model. Two criteria were employed to compare the likelihoods of these models. When models are nested, twice the difference in natural-log (ln) likelihoods (−2ln_L_) between a restricted and an unrestricted model approximately follows a χ2 statistic, with degrees of freedom equal to the difference in the number of parameters estimated in the two models. The best-fitting model is the one that requires the fewest estimated parameters while giving an ln likelihood that is not significantly smaller than the unrestricted model. When comparing nonnested models, the Akaike’s information criterion (AIC) was used (Akaike 1974). AIC is equal to -2_lnL_+2_k_, where k is the number of parameters estimated in the models. By this criterion, the most parsimonious model is the one with the smallest AIC score. Our results suggest that the mixed-recessive model (i.e., a major recessive gene and residual polygenic effect) was the best fit for the observed distribution of height in these families (table 2; _AIC_=5866.14). It should be noted that statistical analysis showed that the fit of several models—including a mixed recessive (_P_=.79), mixed codominant (_P_=.8), and polygenic model (_P_=.098)—was not significantly worse than that of the general model. However, on the basis of a likelihood-ratio test, the fit of the “polygenic only” model was significantly worse than that of the mixed-recessive model (χ2=9.0, _df_=2, _P_=.01).
Table 2.
Segregation Analysis of Height (Adjusted for Age and Sex) among Individuals ⩾16 Years of Age in 200 Dutch Families[Note]
| TransmissionProbability | Mean | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | qA | AA | Aa | aa | AA | Aa | aa | SD | _h_2 | −2ln_L_ | AIC | χ2 | df | P |
| General | .31 | .07 | .72 | .02 | −.58 | −3.91 | 3.69 | 4.74 | .82 | 5854.45 | 5872.45 | |||
| Env Only | .74 | .51 | =AA | =AA | 2.40 | −4.40 | 6.00 | 4.36 | [0] | 6063.65 | 6075.65 | 209.20 | 3 | 4.3359 × 10−45 |
| Mix Env (Env + Poly) | .995 | .34 | =AA | =AA | .09 | −1.90 | 2.24 | 5.75 | .84 | 5861.52 | 5875.52 | 7.07 | 2 | .029 |
| Major Cod Only | .500 | [1] | [.5] | [0] | −6.49 | .05 | 6.66 | 3.57 | [0] | 5888.07 | 5898.07 | 33.62 | 4 | 8.91607 × 10−7 |
| Major Rec Only | .27 | [1] | [.5] | [0] | −4.38 | =AA | 3.98 | 4.24 | [0] | 5928.90 | 5936.90 | 74.45 | 5 | 1.21167E-14 |
| Mix Cod (Cod + Poly) | .28 | [1] | [.5] | [0] | −1.92 | −3.80 | 3.50 | 4.80 | .84 | 5855.46 | 5867.46 | 1.01 | 3 | .8 |
| Mix Dom (Dom + Poly) | .66 | [1] | [.5] | [0] | −2.70 | 2.17 | =Aa | 5.41 | .81 | 5864.72 | 5874.72 | 1.27 | 4 | .036 |
| Mix Rec (Rec + Poly) | .28 | [1] | [.5] | [0] | −3.60 | =AA | 3.56 | 4.75 | .78 | 5856.14 | 5866.14 | 1.69 | 4 | .79 |
| Polygenic | [1] | n/a | n/a | n/a | .07 | =AA | =AA | 5.90 | .81 | 5865.14 | 5871.14 | 10.69 | 6 | .098 |
| Sporadic | [1] | n/a | n/a | n/a | −.05 | =AA | =AA | 5.95 | [0] | 6079.22 | 6083.22 | 224.77 | 7 | 6.40753 × 10−45 |
The maximum-likelihood estimate (MLE) of allele frequency A (corresponding to a low value of height) under the mixed-recessive model was 0.28 (95% CI 0.20–0.36), which resulted in frequencies of 0.48 for genotype AA/Aa and of 0.52 for genotype aa, under Hardy-Weinberg equilibrium. When genotypic probability estimators were used (Hasstedt and Moll 1989), this hypothetical gene had a large effect on height and was responsible for 38.1% of the total variation of residual height in these families. The means of the residual height in these two groups were significantly different (−3.60 for AA/Aa and 3.56 for aa, with _SD_=4.75, t _statistic_=24.5, _P_≈0).
Because there is evidence of assortative mating with regard to height (table 1), it is of concern that assortative mating may have an effect on the result of segregation analysis. To examine this issue, we used a class D regressive model, as implemented in the regressive models for continuous traits program of S.A.G.E. (Bonney 1986), to perform a segregation analysis that included the effect of the residual spouse correlation. The conclusion from the segregation analysis, using a class D regressive model, was similar to that from PAP (data not shown). The best-fitting and most-parsimonious model was the mixed-recessive model. Neither the mixed-recessive model (-2_lnL_=5853.94, χ2=4.51, _df_=3, _P_=.21), nor the polygenic model (-2_lnL_=5860.98, χ2=11.55, _df_=6, _P_=.07) fit the data significantly worse than did the general model (-2_lnL_=5849.43). Interestingly, the polygenic-only model did not fit the data significantly worse than did the mixed recessive model (χ2=7.04, _df_=3, _P_=.07), when the residual spouse correlation was included in the model. The MLE spouse correlation coefficient was 0.22 (_P_=.01) under the mixed-recessive model.
It is worth noting that there is a considerable polygenic effect on height. This was evident from the following: First, all of the models without a polygenetic component, such as the environmental-only, major-gene–only, and sporadic models, were clearly rejected, compared with the general model. Second, the recessive-only model fit the data significantly worse than the mixed recessive model (χ2=63.76, _df_=1, _P_=1.4×10-15). The MLE of heritability was 0.78 under the mixed-recessive model. Third, when the residual spouse correlation was included, the polygenic-only model did not fit the data significantly worse than did the mixed-recessive model.
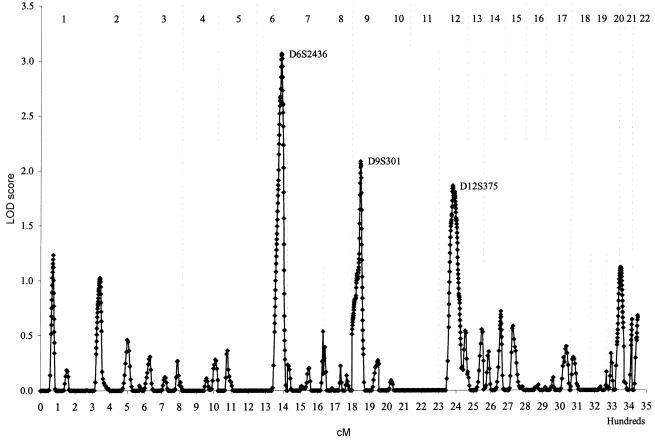
Finally, we used a genomewide-scan approach to search for the chromosomal regions that are likely to contain genes that regulate adult height. We genotyped 366 autosomal markers of the Weber set (version 8), which spans the human genome at an average interval of 10 cM, with an average marker heterozygosity of 76%. Linkage analysis was performed using a variance-components method as implemented in the computer program package Sequential Oligogenic Linkage Analysis Routines (SOLAR) (Almasy and Blangero 1998). By calculating and comparing the likelihood of models with and without a genetic marker (major gene), it is possible to infer the localization and effect sizes of a major gene. The difference between the log10 likelihoods of two models produces a LOD score that is equivalent to the classical LOD score for linkage. Results of the multipoint linkage analyses are presented in figure 1. Strikingly, the top three linkage peaks in the present study overlap with the linkage peaks observed in the families from Finland (Hirschhorn et al. 2001). In the present study, the highest LOD was 3.06 (nominal _P_=.0002), near the marker D6S2436 at 6q25, which overlaps with the highest linkage signal (_LOD_=3.85 at D6S1007) in the 58 families from Botnia, Finland (Hirschhorn et al. 2001). The distance between the markers D6S2436 and D6S1007 is ∼5 cM. This locus contributed to 44% of the height variance. The second highest LOD in our study was 2.09 (nominal _P_=.002) near the marker D9S301 at 9p1, which overlaps with the linkage signal at D9S1868 (_LOD_=2.01) in the same 58 families from Botnia, Finland. The distance between the markers D9S301 and D9S1868 is ∼14 cM. The third highest LOD in our study was 1.86 (nominal _P_=.003), near the marker D12S375 at 12q1, which overlaps with the linkage signal at D12S398 (_LOD_=3.35) observed in 183 families from other parts of Finland (Hirschhorn et al. 2001). The distance between the markers D12S375 and D12S398 is ∼12 cM.
Figure 1.
Genomewide scan for loci regulating height (adjusted for age and sex; all subjects age ⩾16 years) in 200 Dutch families, using variance component analysis; 344 evenly spaced autosomal markers were genotyped. Vertical dotted lines divide the genome into 22 chromosomes.
To examine the source of the families that contributed to the positive linkage results at 6q25, linkage analyses were reperformed separately for the first 100 and the second 100 families. Both subsets of families provided a positive LOD at this region; the first 100 families had a LOD of 2.1, and the second 100 families had a LOD of 1.5. These results suggest that the evidence for the linkage at 6q25 is consistent in our sample and that sampling variation is limited. We also examined the impact of outliers on the results by reanalyzing the linkage data for chromosome 6 markers with the exclusion of six outliers, the three highest and three lowest (two of the highest and two of the lowest were >3 SD from the mean). The LOD decreased from 3.06 to 2.84 at 6q25, suggesting the results were stable and were not driven by the few outliers.
Height has been shown in numerous studies to be controlled largely by genetic factors, with heritability estimates ranging from 76% to 90% in different populations, similar to the heritability of 78% observed in our population (Phillips and Matheny 1990; Carmichael and McGue 1995; Preece 1996; Silventoinen et al. 2000). Because it is a normally distributed quantitative trait, the genetic component of height has generally been considered to be purely polygenic, that is, influenced by multiple, probably undetectable genes, each with a small effect on height.
Review of the literature on the genetics of height shows a long-standing interest in this trait. Early researchers demonstrated significant parent-offspring and sibling correlations (Pearson and Lee 1903). Later studies, utilizing path analysis and segregation modeling, confirmed high heritability estimates but were unable to provide evidence for major gene effects (Province and Rao 1985). To our knowledge, our study is the first segregation analysis to provide evidence for a major height gene with significant residual polygenic effect. Although each of the 200 Dutch families was ascertained through an asthmatic proband, the results obtained from the present study can be generalized, because there is no statistically significant difference in height between asthmatic and nonasthmatic individuals in our sample. Among the probands and their spouses, the mean heights were the same (178 cm) in asthmatic and nonasthmatic male subjects (_P_=.64); and mean heights were the same (166 cm) in asthmatic and nonasthmatic female subjects (_P_=0.31).
Further fine-mapping and gene-identification studies in the 6q25, 9p1, and 12q1 chromosomal regions are warranted by the significant linkage findings from Hirschhorn et al. (2001) and by our confirmatory results. It is worth noting that the estrogen receptor α gene (ESR1) lies in the middle of 6q25. Association studies to test the effect of ESR1 sequence variants on height are a reasonable next step. Meanwhile, two other directions are worth pursuing. First, because multiple major height genes are implicated by these linkage studies, it is important to include oligogenic models (e.g., two-locus models, in the segregation analysis, to improve our understanding of genetic regulation of height (Villard et al. 1996). Second, because height is clearly influenced by environmental factors (e.g., nutrition), the inclusion of relevant environmental variables in the segregation and linkage analyses will be important to future studies.
The complexity of gene mapping for complex traits remains apparent, because different linkage results for adult height have been observed in several studies. In a genomewide scan for adult height in five Finnish populations ascertained for hypertension, obesity, osteoarthritis, migraine, and familial combined hyperlipidemia, Perola et al. (2001) found a strong linkage between stature and markers at 7pter. Positive linkage to the 7pter region was also found by Hirschhorn et al. (2001). In another genomewide scan from 593 pedigrees ascertained for a study of type 2 diabetes in the United Kingdom, Wiltshire et al. (2002) provided evidence of height linkage at 3p26 and in several other chromosomal regions. Although differences in ethnicity, sources of subjects, and statistical fluctuations may contribute to the varied findings (Altmuller et al. 2001; Hirschhorn et al. 2001), other unknown factors have yet to be identified. Clearly, as with genetic studies of common traits both as qualitative and quantitative measures, replication of genomewide screen results is often not observed. However, it is important to note that our study did confirm three previously identified chromosomal regions and did not identify additional regions that were not detected in other studies.
The significance of the present study and the study by Hirschhorn et al. (2001) extends beyond the scope of the genetics of height. Together, we have successfully demonstrated the use of segregation analysis to provide evidence of major genes regulating complex traits and the use of linkage studies to identify chromosomal regions linked to the traits.
Acknowledgments
We thank all of the families whose participation made this project possible. This work was supported by Dutch Asthma Funds grant AF 95.09 and by National Institutes of Health grants R01-HL48341 and R01-HL66393. Some of the results of this article were obtained by use of the program package S.A.G.E., which is supported by U.S. Public Health Service Resource grant 1-P41-RR03655 from the National Center for Research Resources.
Electronic-Database Information
Accession numbers and URLs for data presented herein are as follows:
- Human Genetics Analysis Resource, http://darwin.cwru.edu/octane/sage/sage.php (for S.A.G.E.)
- PAP: Pedigree Analysis Package, http://hasstedt.genetics.utah.edu/
- SOLAR: Sequential Oligogenic Linkage Analysis Routines, http://www.sfbr.org/sfbr/public/software/solar/index.html
References
- Akaike H (1974) A new look at the statistical model identification. IEEE Trans Automatic Control AC 19:719–723 [Google Scholar]
- Almasy L, Blangero J (1998) Multipoint quantitative-trait linkage analysis in general pedigrees. Am J Hum Genet 62:1198–1211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altmuller J, Palmer LJ, Fischer G, Scherb H, Wjst M (2001) Genomewide scans of complex human diseases: true linkage is hard to find. Am J Hum Genet 69:936–950 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonney GE (1986) Regressive logistic models for familial disease and other binary traits. Biometrics 42:611–625 [PubMed] [Google Scholar]
- Carmichael CM, McGue M (1995) A cross-sectional examination of height, weight, and body mass index in adult twins. J Gerontol A Biol Sci Med Sci 50:B237-B244 [DOI] [PubMed] [Google Scholar]
- Hasstedt SJ, Moll PP (1989) Estimation of genetic model parameters: variables correlated with a quantitative phenotype exhibiting major locus inheritance. Genet Epidemiol 6:319–332 [DOI] [PubMed] [Google Scholar]
- Hirschhorn JN, Lindgren CM, Daly MJ, Kirby A, Schaffner SF, Burtt NP, Altshuler D, Parker A, Rioux JD, Platko J, Gaudet D, Hudson TJ, Groop LC, Lander ES (2001) Genomewide linkage analysis of stature in multiple populations reveals several regions with evidence of linkage to adult height. Am J Hum Genet 69:106–116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearson K, Lee A (1903) On the laws of inheritance in man. I. Inheritance of physical characters. Biometrika 2:357–462 [Google Scholar]
- Perola M, Ohman M, Hiekkalinna T, Leppavuori J, Pajukanta P, Wessman M, Koskenvuo M, Palotie A, Lange K, Kaprio J, Peltonen L (2001) Quantitative-trait-locus analysis of body-mass index and of stature, by combined analysis of genome scans of five Finnish study groups. Am J Hum Genet 69:117–123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phillips K, Matheny AP Jr (1990) Quantitative genetic analysis of longitudinal trends in height: preliminary results from the Louisville Twin Study. Acta Genet Med Gemellol 39:143–163 [DOI] [PubMed] [Google Scholar]
- Postma DS, Bleecker ER, Amelung PJ, Holroyd KJ, Panhuysen CIM, Xu J, Meyers DA, Levitt RC (1995) Genetic susceptibility to asthma: bronchial hyperresponsiveness coinherited with a major gene for atopy. N Engl J Med 333:894–900 [DOI] [PubMed] [Google Scholar]
- Preece MA (1996) The genetic contribution to stature. Horm Res 45:56–58 [DOI] [PubMed] [Google Scholar]
- Province MA, Rao DC (1985) Path analysis of family resemblance with temporal trends: applications to height, weight, and Quetelet index in northeastern Brazil. Am J Hum Genet 37:178–192 [PMC free article] [PubMed] [Google Scholar]
- Silventoinen K, Kaprio J, Lahelma E, Koskenvuo M (2000) Relative effect of genetic and environmental factors on body height: differences across birth cohorts among Finnish men and women. Am J Public Health 90:627–630 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villard E, Tiret L, Visvikis S, Rakotovao R, Cambien F, Soubrier F. (1996) Identification of new polymorphisms of the angiotensin I-converting enzyme (ACE) gene and study of their relationship to plasma ACE levels by two-QTL segregation-linkage analysis. Am J Hum Genet 58:1268–1278 [PMC free article] [PubMed] [Google Scholar]
- Wiltshire S, Frayling TM, Hattersley AT, Hitman GA, Walker M, Levy JC, O'Rahilly S, Groves CJ, Menzel S, Cardon LR, McCarthy MI (2002) Evidence for linkage of stature to chromosome 3p26 in a large UK family data set ascertained for type 2 diabetes. Am J Hum Genet 70:543–546 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J, Postma DS, Howard TD, Koppelman GH, Zheng SL, Stine OC, Bleecker ER, Meyers DA (2000) Major genes regulating total serum immunoglobulin E levels in families with asthma. Am J Hum Genet 67:1163–1173 [DOI] [PMC free article] [PubMed] [Google Scholar]