Robust methods for differential abundance analysis in marker gene surveys (original) (raw)
. Author manuscript; available in PMC: 2014 Jun 1.
Published in final edited form as: Nat Methods. 2013 Sep 29;10(12):1200–1202. doi: 10.1038/nmeth.2658
Abstract
We introduce a novel methodology for differential abundance analysis in sparse high-throughput marker gene survey data. Our approach, implemented in the metagenomeSeq Bioconductor package, relies on a novel normalization technique and a statistical model that accounts for under-sampling: a common feature of large-scale marker gene studies. We show, using simulated data and several published microbiota datasets, that metagenomeSeq outperforms the tools currently used in this field.
Marker gene surveys have recently been applied to clinical settings with the intent of understanding the structure and function of healthy microbial communities and the association of the microbiota with diseases such as: Crohn’s disease1, bacterial vaginosis2, diabetes3, 4, eczema5, obesity6 and periodontal disease.7 The identification of potentially pathogenic or probiotic bacteria, characterized by significant differences in their abundance within a disease population, is critical in this setting. While methods for whole-scale community comparisons are commonly used8, 9 there is a need for tools that discern taxon-specific disease associations in marker gene surveys.
We focus here on the targeted sequencing of the 16S ribosomal RNA gene from selected samples. ‘Universal’ primers amplify specific hyper-variable regions within the 16S rRNA gene, and the corresponding segments are sequenced. Sequence reads are first clustered into operational taxonomic units (OTUs)10 and representative sequences from each cluster are then annotated against a database of 16S rDNA reference sequences.11
While data preprocessing and differential abundance analysis have been extensively studied in high-throughput experiments measuring gene expression with microarray technology and sequencing-based assays (e.g., SAGE, RNAseq), marker gene data have specific characteristics that need to be considered, leading to the development of specialized analytical tools12–14. Principally, most taxonomic features in marker gene studies are rare (absent from a large number of samples) in contrast to RNAseq studies where a much more complete representation of features is encountered.
Here, we present two complementary methods for the analysis of large-scale marker gene microbial survey data implemented in the publicly available metagenomeSeq Bioconductor package (http://cbcb.umd.edu/software/metagenomeSeq). Our first contribution is a novel normalization technique, the cumulative sum scaling (CSS) normalization, which corrects the bias in the assessment of differential abundance introduced by total-sum normalization (TSS), the most commonly used approach. TSS normalizes count data by dividing feature read counts by the total number of reads in each sample, i.e., converts feature counts to appropriately scaled ratios. TSS has been shown to incorrectly bias differential abundance estimates in RNAseq data derived through high-throughput technologies15, 16 since a few measurements (e.g., taxa or genes) are sampled preferentially as sequencing yield increases, and have an undue influence on normalized counts. A recent proposal for normalization of RNAseq data is to scale counts by the 75th percentile of each sample’s non-zero count distribution15. The percentile cutoff that appropriately captures the segment of the count distribution that is relatively invariant across samples varies across 16S rDNA datasets (Supplementary Fig. 1). Our CSS method is an adaptive extension of the quantile normalization approach that is better suited for marker gene survey data whereby raw counts are divided by the cumulative sum of counts up to a percentile determined using a data-driven approach.
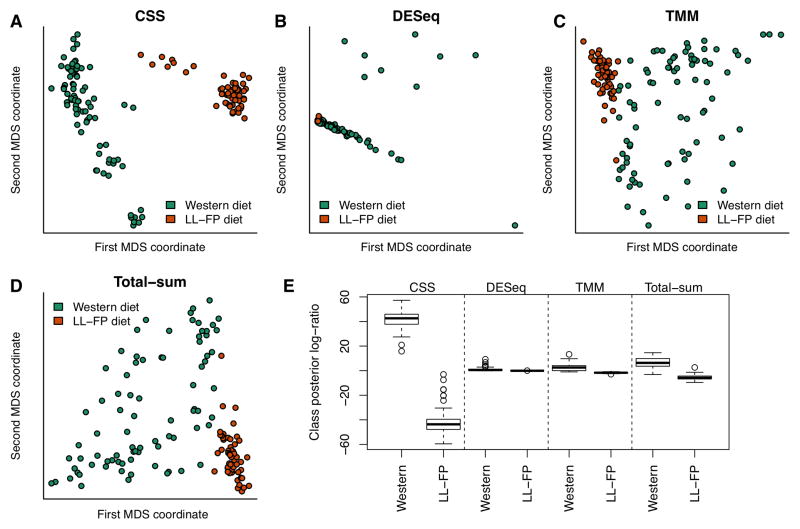
We applied the CSS normalization procedure on data from a longitudinal study tracking the gut microbial community of twelve gnotobiotic mice.17 To assess the effect of normalization on distinguishing samples by phenotypic similarity we performed a multi-dimensional scaling analysis of data normalized using CSS, DESeq18 size factors, TMM19 and total-sum normalization (Fig. 1A–D). CSS normalization was able to best separate samples based on diet while controlling within-group variance. We quantified this observation using linear discriminant analysis (Online Methods) and observed that CSS normalization performed the best in distinguishing samples by phenotypic similarity (Fig. 1E). We observed similar results when comparing CSS normalization to other frequently used normalization methods (Supplementary Fig. 2).
Figure 1. Clustering analysis is improved substantially by CSS normalization.
We plot the first two principal coordinates in a multi-dimensional scaling analysis of mouse stool data normalized by (A) CSS, (B) DESeq size factors, (C) trimmed mean of M-values, and (D) total-sum. Colors indicate clinical phenotype (diet). CSS normalization data successfully separates samples by diet while controlling within-group variability. (E) Class posterior probability log-ratio for Western diet obtained from linear discriminant analysis (LDA). Each box corresponds to the distribution of leave-one-out posterior probability of assignment to the “Western” cluster across normalization methods (whiskers indicate 1.5 times inter-quartile range). Samples were best distinguished by phenotypic similarity using CSS normalization.
Our second contribution is a zero-inflated Gaussian distribution mixture model that accounts for biases in differential abundance testing resulting from under-sampling of the microbial community. We found a strong correlation between the number of OTUs detected in a sample and the corresponding sequencing depth in high-throughput 16S rDNA studies (R2=0.92–0.97, Supplementary Fig. 3) consistent with previous reports.20–22 This suggests that measurements of differential abundance suffer from biases resulting from the misinterpretation of zero counts in samples with low coverage as taxonomic features not present in the microbial community, as opposed to interpreting their absence as the result of under-sampling. The degree of sparsity observed in marker gene experiments (1–3%) is much higher than usually seen in other abundance assays such as transcriptome profiling from single genomes23 (15–85%, Supplementary Fig. 4).
To explicitly account for under-sampling, we include in our analysis a mixture model that implements a zero-inflated Gaussian (ZIG) distribution of mean group abundance for each taxonomic feature (Supplementary Fig. 5). The effect of this model is exemplified on one OTU from the Human Microbiome Project24 (Supplementary Fig. 6). Using posterior probability estimates that account for community under-sampling as weights to estimate count distribution parameters reduces the estimated fold-change between the two groups under study. Furthermore, counts after accounting for under-sampling are better fit by a log-normal distribution (Shapiro-Wilks test P=0.78) than normalized counts (Shapiro-Wilks test P=0.08).
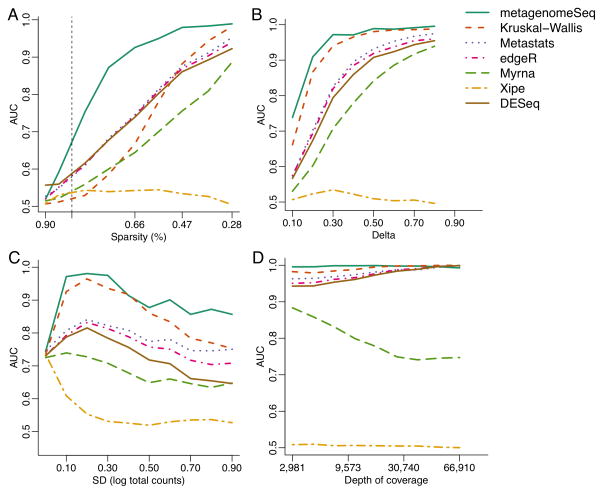
We evaluated metagenomeSeq using simulated data and compared it to existing tools for metagenomic analysis: Metastats13, Xipe12, and a Kruskal-Wallis test as used in Lefse.14 We also compared to representative methods for RNAseq analysis. MetagenomeSeq and, to a lesser degree, the Kruskal-Wallis test consistently produced high area under the curve (AUC) scores across most simulation settings (Fig. 2). However, metagenomeSeq obtains the highest AUC compared to all other methods (includings Lefse’s Kruskal-Wallis test) in datasets with high sparsity similar to actual metagenomic datasets (greater than 85%, Fig. 2A). Metastats, edgeR19 and DESeq18 have similar performance characteristics with smaller AUC scores. Xipe performed poorly across most simulation settings, as expected, since this method does not account for population variability.
Figure 2. Simulation results indicate that metagenomeSeq has greater sensitivity and specificity in a variety of settings.
We use area under the receiver operating characteristic curve (AUC) to compare Metastats13, Xipe12, Kruskal-Wallis test as used in Lefse14, a non-zero inflated log-normal model30, edgeR19 and DESeq18. (A) AUC as dataset sparsity decreases. MetagenomeSeq achieves larger AUC values than any other method in datasets with high sparsity (vertical dashed line represents the least sparse metagenomic dataset). (B) AUC as the effect-size between two conditions increases. Both metagenomeSeq and Lefse are better at detecting features with small effect size. (C) AUC as the variability in depth of sequencing increases. MetagenomeSeq and Kruskal-Wallis are robust to high variability in sequencing depth. (D) AUC as average sequencing depth increases. All models (except the non-zero inflated log-normal model and XIPE) perform similarly well at sufficient depth of coverage.
Our ZIG model uses linear modeling following standard conventions in methods for testing differential abundance in gene expression25 that control for confounding factors. In contrast, Lefse uses an ad-hoc heuristic approach to account for subpopulations in large marker studies that is overly conservative and prone to low sensitivity. We observed by simulation (Supplementary Fig. 7, Supplementary Table 1) that metagenomeSeq was more sensitive than Lefse (0.95, 0.01 respectively) while retaining high specificity (0.96 vs. 1) in settings where groups tested include confounding subpopulations.
We also compared these methods using oral microbiota data from the Human Microbiome Project24 (Supplementary Fig. 8) to identify OTUs that are differentially abundant between tongue and subgingival plaque samples. Metastats and edgeR identified the largest number of OTUs to be significant (533 and 524, respectively), while metagenomeSeq (360) and, especially, DESeq (20) and Lefse (8) identified much fewer significant OTUs (Supplementary Table 2). Organisms found enriched in subgingival plaque by metagenomeSeq but missed by DESeq or Lefse are fairly abundant well-known members of the periodontal microbiome and include sulfate-reducing bacteria, which have been proposed as potential pathogenicity factors in periodontal disease.26 In general, the poor performance of Metastats and Lefse was due to their lack of robust modeling of confounding factors, while for DESeq and edgeR the assumptions upon which these models are based are not met by these data. We provide a detailed comparison of these results in Supplementary Note and Supplementary Figs. 9–11.
We further compared our results at the species level with those obtained by Segata, et al.27 who applied Lefse to the same oral dataset. While we confirmed all species detected as differentially abundant by Lefse, we also identified three additional differentially abundant species missed by their analysis. Specifically, we find Atopobium parvulum, Lautropia sp., and Desulfotomaculum sp. to be enriched in subgingival plaque (Supplementary Fig. 12). All of these were fairly abundant in the samples, representing at least 4% the population, and represent previously characterized members of the normal subgingival microbiota.26, 28, 29
In summary, our methods yield a more precise biological interpretation of the data – in mouse stool data the CSS normalization helps distinguish clinical phenotypes that are confounded by commonly used normalization methods, while in the oral microbiome, the combined differential abundance modeling approach identifies additional associations that were missed by commonly used tools. To accurately estimate differential abundance, we explicitly model the effect of under-sampling on the ability to detect a particular feature. Although under-sampling is ubiquitous in marker gene survey data, to our knowledge, the approach presented here is the first to correct for this phenomenon. While our focus is on data generated in microbial community surveys, sparsity may also be an issue in some RNAseq experiments, and thus our methods may have broader applicability (Fig. 2A). The evaluation of our methods in that context is, however, beyond the scope of this work and will be addressed in future studies.
This work directly addresses some of the main challenges to robust analysis of marker gene surveys in clinical and epidemiological settings: variable depth of coverage across samples and the resulting rarefaction effect; and confounding due to technical and population characteristics. We have demonstrated that our methods outperform approaches that are widely used in the field, and expect that the improved analysis approaches we propose will help practitioners achieve the full promise of marker gene surveys in clinical research.
Online Methods
Cumulative sum scaling normalization
Assume raw data is given as count matrix M(m, n) where m and n are the number of features and samples, respectively. The raw data in this matrix is represented by counts cij representing the number of times taxonomic feature i was observed in sample j. Denote the sum of counts for sample i as sj = Σ_i cij_. The usual normalization procedure for marker gene survey data corresponds to producing normalized counts cij∼=cijsj. We refer to this procedure as total-sum normalization.
We introduce a new normalization method, cumulative sum scaling normalization (CSS), to remove biases in the count data. The biases come from features that are preferentially amplified in a sample-specific manner. Denote the _l_th quantile of sample j as qjl, that is, in sample j there are l taxonomic features with counts smaller than qjl. For l = ⌊.95 * _m_⌋, qjl corresponds to the 95th percentile of the count distribution for sample j.
Also denote sjl=∑i∣cij≤qjlcij as the sum of counts for sample j up to the l_th quantile. Using this notation, the total sum sj=sjm. Our normalization chooses a value l̂ ≤ m to define a normalization scaling factor for each sample to produce normalized counts cij∼=cijsjl^N where N is an appropriately chosen normalization constant. We scale all samples using the same constant N so normalized counts have interpretable units. We recommend using the median scaling factor sjl^ across samples. Counts for samples with scaling factor close to N can be interpreted as reference samples, and counts for other samples are interpreted relative to the reference. In our datasets the median sjl^ was close to 1,000 and thus used this value in our analysis. Note that ratios are also used in this procedure, assuming there is a finite capacity to the size of microbial communities. This is the same assumption that underlies total-sum normalization. However, our method seeks to avoid placing undue influence on features that are preferentially sampled. The relative proportion of the features is unaffected by the normalization as sj = Σ_i cij and s∼j=∑icijsjl^, this implies pi=cijsj=sjl^∗cijsjl^∗∑icij=cij∼sj∼=pi∼.
The choice of the appropriate quantile given by l̂ above is critical for ensuring that the normalization approach does not introduce normalization-related artifacts in the data. At a high level, the count distribution of samples should all be roughly equivalent and independent of each other up to this quantile under the assumption that, at this range, counts are derived from a common distribution. The specific value for the chosen quantile is project-specific and likely depends on the complete experimental details (including all the sample preparation, sequencing, and subsequent bioinformatics analysis).
We use an adaptive, data-driven, method to determine l̂ based on the observation above. We find a value l̂ where sample-specific count distributions deviate from an appropriately defined reference distribution. Specifically, denote ql¯=medj{qjl}, the median _l_th quantile across samples, as the _l_th quantile of the reference distribution. Note that this is exactly the way a reference distribution is defined in the commonly used quantile normalization approach.15 Denote as dl=medj|qjl-ql¯|. This is the median absolute deviation of sample-specific quantiles around the reference. Under the methods assumptions, this quantity dl is stable for low quantiles and shows high instability in high quantiles. Our method defines l̂ as the smallest value where high instability is detected (Supplementary Figure 1). We measure instability in this case by using relative first differences. Specifically, we set l̂ to the smallest l that satisfies dl+1 − dl ≥ 0.1 dl. The value 0.1 is set arbitrarily and may be substituted by another value to determine high instability.
We found that CSS-normalized sample abundance measurements are well approximated by a log-normal distribution in studies with large number of samples (Supplementary Fig. 13A) and therefore applied a logarithmic transform to the normalized count data. This transformation controls the variability of taxonomic feature measurements across samples (Supplementary Fig. 13B).
Assessment of normalization methods
To assess the effect of normalization on distinguishing samples by phenotype we performed a multi-dimensional scaling analysis of count data normalized by using CSS, total-sum scaling, logged total-sum scaling, geometric mean, trimmed mean by M values, quantile scaling, and quantile normalization.
We calculated the 1000 taxonomic features with largest variance after each normalization method and used those normalized feature counts in the MDS analysis. We also used linear discriminant analysis (LDA) to distinguish samples by diet. We calculated the log-ratio of class posterior probabilities for each sample x using leave-one-out cross-validation:
where πw is the proportion of samples on the “Western” diet, and fw and fl are normal densities for each of the diets, with a common variance. Parameters in each leave-one-out fold are estimated from the remaining samples. The class posterior probability should be large and positive for “Western” samples and small and negative for samples in the other group. We measure the performance of each normalization method by the difference in the distribution of the class posterior probabilities (Figure 1E and Supplementary Fig. 2E).
Zero-inflated Gaussian Model
Our zero-inflated Gaussian (ZIG) mixture model is motivated by the observed relationship between depth of coverage and the number of OTUs detected (Supplementary Fig. 3). The components of the mixture model correspond to normally distributed log-abundances in each group of interest, e.g., case or control (represented as the count distribution in Supplementary Fig. 5) and a spike-mass at zero indicating absence of the feature due to under-sampling (represented as the detection distribution in Supplementary Fig. 5). Our model seeks to directly estimate the probability that an observed zero is generated from the detection distribution due to under-sampling or from the count distribution (absence of the taxonomic feature in the microbial community). We estimate the expected value of latent component indicators based on sample sequencing depth of coverage using an expectation maximization algorithm (see Supplementary note). A detailed description of the model is available in the Supplementary note.
Simulation study
We simulated OTU level datasets with 1,000 features. A sample’s total count was sampled from a log-normal distribution with μ = 7.5 and a standard deviation of 0.3. These values represent similar total counts to those observed in data. The first 50 features were chosen to be “significant”. In one of the populations, for the first 25 significant features, we changed the proportion of the total counts for those features by adding 1×10−3 · δ percentage of the particular sample’s total counts. For the remaining 25 we subtracted 1×10−3 · δ percentage of the sample’s total counts. We used a logistic regression model of the proportion of zeros as a function of depth of coverage in a standard marker gene survey to build a plausible simulation model for sparsity. Given a sample’s depth of coverage sj an expected proportion of zero features πj is obtained from the logistic regression fit. For each feature we randomly drew from a Bernoulli trial with probability πj to spuriously set the feature to zero. Finally, we assigned randomly to 5% of the data an additional 1.3% (a value obtained from a standard marker gene survey) of the mean of the total counts to introduce extremely abundant features.
Subgroup Simulation
We simulated data from two populations where each population consisted of two subpopulations. This example represents a case-control study where cases and controls were collected from differing sites. We simulated OTU level datasets with 1,000 features. A sample’s total count was sampled from a log-normal distribution with μ = 7.5 and a standard deviation of 0.3. These values represent similar total counts to those observed in data. The first 50 features were chosen to be “significant”. In one of the populations, for the first 25 significant features, we changed the proportion of the total counts for those features by adding 1×10−3 · δ percentage of the particular sample’s total counts. For the remaining 25 we subtracted 1×10−3 · δ percentage of the sample’s total counts. The second subgroup had a relatively larger expression of the significant features. This represents potential greater feature enrichment in a site’s sub population. The trend though across populations in either subgroup is to either increase or decrease in cases or controls. Finally, 5% of the data is randomly given an additional 1.3% (a value obtained from a standard marker gene survey) of the mean of the total counts to introduce extremely abundant features.
Materials
Marker gene survey data
Humanized gnotobiotic mouse gut
Twelve germ-free adult male C57BL/6J mice were fed a low-fat, plant polysaccharide-rich diet. Each mouse was gavaged with healthy adult human fecal material. Following the fecal transplant, mice remained on the low-fat, plant polysacchaaride-rich diet for four weeks, following which a subset of 6 were switched to a high-fat and high-sugar diet for eight weeks. Fecal samples for each mouse went through PCR amplification of the bacterial 16S rRNA gene V2 region weekly. Details of experimental protocols and further details of the data can be found in Turnbaugh et al.17 OTUs were classified by RDP11 and annotated (minimum confidence level of 0.8). Sequences can be found at: http://gordonlab.wustl.edu/TurnbaughSE_10_09/STM_2009.html.
Subgingival plaque and tongue dorsum
Subgingival plaque and tongue dorsum samples were a part of the Human Microbiome Project24 dataset used in this analysis. The samples were part of a larger study aimed at cataloging the healthy human microbiome. Reads were deposited into the Data Analysis and Coordination Center (DACC) at http://www.hmpdacc.org/. In particular, reads and metadata were downloaded from http://www.hmpdacc.org/HMR16S/. Further information on data collection protocol and samples is available at http://www.hmpdacc.org/ and in HMP. Only patients from their earliest visit were considered as were only samples properly annotated. Following OTU propagation (described below), singletons (up to 5 positive samples) were trimmed. To consider solely differential abundance estimates, we report on OTUs present in at least approximately 2% of the population. For each differential abundance method compared, differentially abundant OTUs were determined at FDR<0.05 where the OTU is at least twice as abundant in one group compared to the other (absolute estimated fold-change greater than 1). We used Lefse’s default detection method (as no fold-change estimate is provided).
Human Microbiome Project data
Data used in Supplementary Figure 3 was a part of the Human Microbiome Project24 dataset used in this analysis. The samples were a catalog of the healthy human microbiome. Reads were organized into OTUs by QIIME8 and deposited in the Data Analysis and Coordination Center (DACC) at http://www.hmpdacc.org/. In particular, OTUs and metadata was downloaded from http://www.hmpdacc.org/HMQCP/. Further information on data collection protocol and samples is available at http://www.hmpdacc.org/ and in HMP.
Lung microbiome
The lung microbiome consisted of respiratory flora sampled from six healthy individuals. Three healthy nonsmokers and three healthy smokers. The upper lung tracts were sampled by oral wash and oro-nasopharyngeal swabs. Up to a patients’ glottis, samples were taken using two bronchoscopes a serial bronchoalveolar lavage and lower airway protected brushes. More detailed information about the lung Microbiome samples, collection and protocols is available in Charlson et al.31 Reads and barcodes were provided by Frederic Bushman. Following OTU propagation (described below), OTUs were trimmed if they were not present in approximately 8% of the population.
Analysis pipeline
OTU identification and annotation
454 SFF files and barcode dictionaries were downloaded and run through the same pipeline. Conservative Operational Taxonomic Units (OTUs) were constructed by pooling together the sequences from all samples, then clustered using DNAclust10 with default parameters (99% identity clusters) to ensure that the definition of an OTU is consistent across all samples. To obtain taxonomic identification, a representative sequence from each OTU was aligned to Ribosomal Database (rdp.cme.msu.edu, release 10.4) using Blastn with long word length (-W 100) in order to only detect nearly-identical sequences. Sequences without a nearly-identical match to RDP were marked as having “no match” and assigned an OTU identifier. The resulting data was organized into a collection of tables at many different taxonomic levels containing each taxonomic group as a row and each sample as a column. These tables formed the substrate for the statistical analyses described. This process was performed for the human microbiome project and the human lung microbiome datasets. After removing OTUs present in less than 5 samples, the HMP dataset consisted of 23,685 OTUs, whereas the human lung microbiome consisted of 2,365 OTUs. We explored the effect of ambiguosly assigned reads (sequences that have good matches to two or more OTUs) by running DNAclust in ‘non-overlapping’ mode – a mode that ensures high separation between clusters and eliminates ambiguous reads. We also ran the HMP dataset using this option and confirmed all results shown in the paper (Supplementary Figs. 14A–B, 15A–B). We provide further discussion of the ambiguity of mapping reads to OTUs in the supplementary material.
RNAseq data
RNA sequencing counts were downloaded from ReCount23, http://bowtie-bio.sourceforge.net/recount/. Only datasets with at least 15 samples were considered.
Software
The following software versions were used for analysis on the following platform.
DESeq version 1.8.318 and edgeR version 2.6.1219 and limma version 3.12.325 were used in the comparisons. Personalized R scripts were written for the other methods and all analyses were performed on R version 2.15.1 on a Red Hat Enterprise Linux Server release 5.9 (Tikanga) 64-bit platform.
Supplementary Material
1
Acknowledgments
Individuals were partially supported by the following awards: US National Science Foundation Graduate Research Fellowship (award DGE0750616 to JNP). JNP, OCS and MP were supported in part by the Bill and Melinda Gates Foundation (award 42917 to OCS). HCB was supported in part by the US National Institutes of Health grant 5R01HG005220. We would like to thank B. Lindsay and L. Magder for discussion of the methods and C. M. Hill for help with clustering of OTUs.
Footnotes
Author Contributions
J.N.P and H.C.B. developed the algorithms and wrote the software. J.N.P. collected results. O.C.S. and M.P. contributed to discussions of the methods. J.N.P., H.C.B. and M.P. analyzed results. J.N.P, H.C.B. and M.P. wrote the manuscript. All authors read and approved of the manuscript.
Competing financial interests
The authors declare no competing financial interests.
References
- 1.Morgan XC, et al. Dysfunction of the intestinal microbiome in inflammatory bowel disease and treatment. Genome Biol. 2012;13:R79. doi: 10.1186/gb-2012-13-9-r79. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ravel J, et al. Vaginal microbiome of reproductive-age women. Proc Natl Acad Sci U S A. 2011;108 (Suppl 1):4680–4687. doi: 10.1073/pnas.1002611107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Larsen N, et al. Gut microbiota in human adults with type 2 diabetes differs from non-diabetic adults. PLoS One. 2010;5:e9085. doi: 10.1371/journal.pone.0009085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kåhrström CT. Microbiome: Gut microbiome as a marker for diabetes. Nature Reviews Microbiology. 2012;10 [Google Scholar]
- 5.Harris JK, Wagner BD. Bacterial identification and analytic challenges in clinical microbiome studies. J Allergy Clin Immunol. 2012;129:441–442. doi: 10.1016/j.jaci.2011.12.969. [DOI] [PubMed] [Google Scholar]
- 6.Turnbaugh PJ, et al. A core gut microbiome in obese and lean twins. Nature. 2009;457:480–484. doi: 10.1038/nature07540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Scher JU, et al. Periodontal disease and the oral microbiota in new-onset rheumatoid arthritis. Arthritis Rheum. 2012;64:3083–3094. doi: 10.1002/art.34539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Caporaso JG, et al. QIIME allows analysis of high-throughput community sequencing data. Nat Methods. 2010;7:335–336. doi: 10.1038/nmeth.f.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lozupone C, Knight R. UniFrac: a new phylogenetic method for comparing microbial communities. Appl Environ Microbiol. 2005;71:8228–8235. doi: 10.1128/AEM.71.12.8228-8235.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ghodsi M, Liu B, Pop M. DNACLUST: accurate and efficient clustering of phylogenetic marker genes. BMC Bioinformatics. 2011;12:271. doi: 10.1186/1471-2105-12-271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang Q, Garrity GM, Tiedje JM, Cole JR. Naive Bayesian classifier for rapid assignment of rRNA sequences into the new bacterial taxonomy. Appl Environ Microbiol. 2007;73:5261–5267. doi: 10.1128/AEM.00062-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rodriguez-Brito B, Rohwer F, Edwards RA. An application of statistics to comparative metagenomics. BMC Bioinformatics. 2006;7:162. doi: 10.1186/1471-2105-7-162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.White JR, Nagarajan N, Pop M. Statistical methods for detecting differentially abundant features in clinical metagenomic samples. PLoS Comput Biol. 2009;5:e1000352. doi: 10.1371/journal.pcbi.1000352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Segata N, et al. Metagenomic biomarker discovery and explanation. Genome Biol. 2011;12:R60. doi: 10.1186/gb-2011-12-6-r60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bullard JH, Purdom E, Hansen KD, Dudoit S. Evaluation of statistical methods for normalization and differential expression in mRNA-Seq experiments. BMC Bioinformatics. 2010;11:94. doi: 10.1186/1471-2105-11-94. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dillies MA, et al. A comprehensive evaluation of normalization methods for Illumina high-throughput RNA sequencing data analysis. Brief Bioinform. 2012 doi: 10.1093/bib/bbs046. [DOI] [PubMed] [Google Scholar]
- 17.Turnbaugh PJ, et al. The effect of diet on the human gut microbiome: a metagenomic analysis in humanized gnotobiotic mice. Sci Transl Med. 2009;1:6ra14. doi: 10.1126/scitranslmed.3000322. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Anders S, Huber W. Differential expression analysis for sequence count data. Genome Biol. 2010;11:R106. doi: 10.1186/gb-2010-11-10-r106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Robinson MD, McCarthy DJ, Smyth GK. edgeR: a Bioconductor package for differential expression analysis of digital gene expression data. Bioinformatics. 2010;26:139–140. doi: 10.1093/bioinformatics/btp616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.White JR, et al. Alignment and clustering of phylogenetic markers--implications for microbial diversity studies. BMC Bioinformatics. 2010;11:152. doi: 10.1186/1471-2105-11-152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Friedman J, Alm EJ. Inferring correlation networks from genomic survey data. PLoS Comput Biol. 2012;8:e1002687. doi: 10.1371/journal.pcbi.1002687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Faust K, et al. Microbial co-occurrence relationships in the human microbiome. PLoS Comput Biol. 2012;8:e1002606. doi: 10.1371/journal.pcbi.1002606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Frazee AC, Langmead B, Leek JT. ReCount: a multi-experiment resource of analysis-ready RNA-seq gene count datasets. BMC Bioinformatics. 2011;12:449. doi: 10.1186/1471-2105-12-449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Human Microbiome Project C. A framework for human microbiome research. Nature. 2012;486:215–221. doi: 10.1038/nature11209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Smyth GK. Bioinformatics and Computational Biology Solutions using R and Bioconductor. Springer; 2005. pp. 397–420. [Google Scholar]
- 26.Langendijk-Genevaux PS, Grimm WD, van der Hoeven JS. Sulfate-reducing bacteria in relation with other potential periodontal pathogens. J Clin Periodontol. 2001;28:1151–1157. doi: 10.1034/j.1600-051x.2001.281210.x. [DOI] [PubMed] [Google Scholar]
- 27.Segata N, et al. Composition of the adult digestive tract bacterial microbiome based on seven mouth surfaces, tonsils, throat and stool samples. Genome Biol. 2012;13:R42. doi: 10.1186/gb-2012-13-6-r42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Paster BJ, et al. Bacterial diversity in human subgingival plaque. J Bacteriol. 2001;183:3770–3783. doi: 10.1128/JB.183.12.3770-3783.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Colombo AP, et al. Comparisons of subgingival microbial profiles of refractory periodontitis, severe periodontitis, and periodontal health using the human oral microbe identification microarray. J Periodontol. 2009;80:1421–1432. doi: 10.1902/jop.2009.090185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Langmead B, Hansen KD, Leek JT. Cloud-scale RNA-sequencing differential expression analysis with Myrna. Genome Biol. 2010;11:R83. doi: 10.1186/gb-2010-11-8-r83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Charlson ES, et al. Topographical continuity of bacterial populations in the healthy human respiratory tract. American journal of respiratory and critical care medicine. 2011;184:957–963. doi: 10.1164/rccm.201104-0655OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
1