PCAP: A Whole-Genome Assembly Program (original) (raw)
Abstract
We describe a whole-genome assembly program named PCAP for processing tens of millions of reads. The PCAP program has several features to address efficiency and accuracy issues in assembly. Multiple processors are used to perform most time-consuming computations in assembly. A more sensitive method is used to avoid missing overlaps caused by sequencing errors. Repetitive regions of reads are detected on the basis of many overlaps with other reads, instead of many shorter word matches with other reads. Contaminated end regions of reads are identified and removed. Generation of a consensus sequence for a contig is based on an alignment of reads in the contig, in which both base quality values and coverage information are used to determine every consensus base. The PCAP program was tested on a mouse whole-genome data set of 30 million reads and a human Chromosome 20 data set of 1.7 million reads. The program is freely available for academic use.
The whole-genome shotgun strategy (WGS) is an efficient method to produce draft sequences of a mammalian genome, whereas the clone-based strategy is an accurate method to produce high-quality sequences of a mammalian genome. The most challenging problem in WGS is to assemble tens of millions of reads into long sequences. A few whole-genome assembly programs have recently been developed: Celera Assembler (Myers et al. 2000), ARACHNE (Batzoglou et al. 2002), RePS (Wang et al. 2002), JAZZ (Aparicio et al. 2002), and Phusion (Mullikin and Ning 2003). Those programs are based on the experiences of previous sequence assembly programs (Staden 1980; Peltola et al. 1984; Huang 1992; Green 1995; Kececioglu and Myers 1995; Sutton et al. 1995; Huang and Madan 1999; Kim and Segre 1999; Chen and Skiena 2000; Pevzner et al. 2001). The existing programs have made WGS successful in several genome sequencing projects. Nevertheless, continued development of new and improved whole-genome assembly programs is required to produce more accurate sequences with the WGS strategy.
We have developed a parallel contig assembly program (PCAP) for assembling tens of millions of reads into long sequences. The PCAP program has several features to address issues in whole-genome assembly. The program has an ability to locate and remove contaminated end regions of reads, which are from sequencing vectors or other foreign sources. The two-hit idea of BLAST2 (Altschul et al. 1997) is used in PCAP as an initial screening requirement for finding pairs of reads with a potential overlap. If two reads have two word matches with at most a few base differences between the matches, the pair of reads is selected for consideration in overlap computation. Identification of repetitive regions in reads is based on deep coverage by longer approximate matches, instead of by shorter exact matches. The score of every overlap is adjusted to reflect the depths of coverage for the two regions in the overlap. The consensus sequence of a contig is generated by constructing an alignment of reads in the contig.
The PCAP program was tested on a mouse whole-genome data set of 30 million reads. The assembly computation was performed on a cluster of Compaq ES40 servers. The test shows that PCAP is efficient enough to handle a whole-genome data set. The accuracy of PCAP was evaluated by performing an assembly on a human Chromosome 20 data set of 1.7 million reads and comparing the PCAP assembly with the finished sequences of Chromosome 20. The evaluation indicates that PCAP is acceptably accurate.
METHODS
The assembly algorithm consists of two major phases. In the first phase, repetitive regions of reads are identified, and overlaps between reads are computed. In the second phase, overlaps are evaluated to identify unique overlaps. Poor end regions of each read are identified and removed. Reads are assembled into contigs by using unique overlaps. Contigs are corrected and linked into scaffolds with constraints. A multiple sequence alignment of reads is constructed, and a consensus sequence is computed for each contig. Below we describe each phase in detail.
Repeat Identification and Overlap Computation
An efficient method is designed to find and mask repetitive regions of reads during computation of overlaps between reads. The method allows the computation of overlaps to be performed in parallel on multiple processors. It also avoids computing overlaps involving repetitive read regions that have already been found. Let _f_0, _f_1, _f_2,... be a list of all input reads in given orientation and let rx be the reverse complement of read fx.
The entire data set S of reads is partitioned into m subsets of similar sizes, which are referred to as _S_0, _S_1,..., Sm – 1, respectively. The set S is compared with every subset Sk on a processor to compute overlaps between reads in S and reads in Sk. An overlap between reads fx and fy occurs twice in the comparisons, once in the comparison of S with the subset containing fy and once in the comparison of S with the subset containing fx. An additional requirement is placed to ensure that every overlap is computed at most once in the comparisons. Specifically, an overlap between reads fx and fy and an overlap between reads rx and fy are computed in the comparison of the set S with a subset Sk if x < y, fx is in S, and fy is in Sk. Pairs of reads fx and fy that satisfy the condition are called potential read pairs.
The set S should be partitioned in such a way that the comparisons of the set S with the subsets are balanced in load. If the numbers of potential read pairs considered in every comparison are equal or very close, then it is likely that the comparisons are balanced in load. It follows from the definition of potential read pairs that the numbers of potential read pairs considered in every comparison are very close if the indices of reads in every subset have the same distribution pattern. The following partition of the set S into subsets meets the requirement. For 0 ≤ k < m, subset Sk consists of reads fy with k = y mod m, where y mod m is the remainder when y is divided by m (Qian 1999).
Because of the huge size of the set S, S is stored only on a hard disk accessible by all processors. Every subset and its data structures are stored in the main memory of a processor. To compare S with the subset, the reads in S are considered one at a time, with the current read in S read into the main memory and compared with the subset. The set S is compared with every subset in parallel.
The computation involving the set S and the subset consists of three major steps. First, repetitive regions of reads in the subset are identified by comparing the subset with itself. Second, additional repetitive regions of reads in the subset are identified by comparing the set S with the subset. The repetitive regions of reads in the subset are reported in a file. Third, overlaps between reads in S and unique read regions in the subset are computed. The overlaps are reported in a file. Note that the order in which repetitive regions of reads in the subset are found depends on how the subset is constructed. Repetitive regions that are highly represented in the subset are first found in the comparison within the subset. On the other hand, repetitive regions that are not highly represented in the subset are later found in the comparison between the set S and the subset. Below we describe each step in detail.
A region of a read is repetitive if it is highly similar to regions of many reads. Repetitive regions of reads in the subset are identified by computing coverage arrays of reads in the subset. The coverage array of a read is an integer array of the same length, in which the value at a position of the array is the number of overlaps between the read and other reads that cover the position. A region of a read is repetitive if the values at every position of the corresponding region of the coverage array are greater than a repeat coverage cutoff.
Identification of repetitive regions of reads depends on computation of overlaps involving the reads. However, it may not be computationally feasible to compute all overlaps because there are a huge number of overlaps between repetitive regions. Our strategy is to alternate computation of overlaps and identification of repetitive regions. Initially, some overlaps are computed. Then repetitive regions are identified based on the overlaps. The repetitive regions are processed so that no overlap involving any of the repetitive regions is computed again. The two-step procedure is performed many times until all repetitive regions are identified.
Specifically, the coverage arrays of the reads in the subset are computed as follows. Initially, for each read in the subset, its coverage array is set to zero at every position. A look-up table is constructed for all regions of the reads in the subset, and the table is used to compute quickly overlaps involving regions in the table. Then for each read fy in the subset, overlaps between the read fy and other reads in the subset and overlaps between the read ry and other reads in the subset are computed using the look-up table. Whenever an overlap involving fy is computed, the coverage array of fy is incremented by 1 at every position covered by the overlap. An overlap involving ry is transformed into an overlap involving fy, which is used to update the coverage array of fy. After all overlaps between reads in the subset are computed, repetitive regions of reads in the subset are identified using the coverage array of every read in the subset. Then the look-up table is replaced by a new look-up table, which is constructed for the unique regions of reads in the subset. Because the repetitive regions are not in the look-up table, no overlap completely covered by any of the repetitive regions can be computed using the look-up table.
Next, each read fx from the set S is compared in both orientations with the subset. Overlaps between the read fx and reads in the subset are computed using the look-up table. For every overlap between the read fx and a read fy in the subset, the coverage array of the read fy is updated over the corresponding region. The look-up table is replaced by a new look-up table after every ns reads from S are compared, where ns is the number of reads in the subset. After all reads from S are compared with the subset, the repetitive regions of reads in the subset are reported in a file. A final look-up table is constructed for the unique regions of reads in the subset.
Finally, each read fx from the set S is compared in both orientations with the subset. Overlaps between the read fx and reads in the subset are computed using the final look-up table. The overlaps are reported in a file.
Below we describe how to compute quickly overlaps between a read g and reads in the subset with a BLAST-like method. The sequences of all reads fy in the subset are concatenated together with a special character inserted at every read boundary (Huang and Madan 1999). The resulting sequence is called the combined sequence. A look-up table with a word length w is constructed for the combined sequence, where for any word of length w, the table gives an ordered list of positions of each unique occurrence of the word in the combined sequence (Huang 2002). An occurrence of a word in a read fy is unique if the coverage array of fy is less than or equal to the repeat coverage cutoff at every position covered by the occurrence. Let wd(i) denote a word of length w starting at position i of the read g. The look-up table can be used to locate quickly the occurrences of wd(i) in the combined sequence. Each occurrence corresponds to an exact match of length w between the read g and a read in the subset. Two close word matches between the read g and a read in the subset are required to extend a word match into a segment pair (Altschul et al. 1997).
Consider two words wd(i) and wd(j) in the read g, where the words are separated by d bases with d > 0, that is, j – i = w + d. An occurrence of wd(i) and an occurrence of wd(j) in reads in the subset are close if the two occurrences are in the same read, the occurrence of wd(i) is before the occurrence of wd(j), and the two occurrences are separated by 0 to 2_d_ bases. The definition of close word occurrences is intended to deal with one sequencing error involving at most d consecutive bases. A separation of 2_d_ bases between the occurrences of wd(i) and wd(j) may be caused by a sequencing error, where d bases are either deleted between the words wd(i) and wd(j), or inserted between their occurrences. In other words, the sequencing error either reduces the number of bases between wd(i) and wd(j) from 2_d_ to d, or increases the number of bases between the occurrences of wd(i) and wd(j) from d to 2_d_. Similarly, a separation of 0 bases between the occurrences of wd(i) and wd(j) may be caused by a sequencing error, where d bases are either inserted between the words wd(i) and wd(j), or deleted between their occurrences. A small value of 4 is selected for the parameter d because a sequencing error usually involves 1 to 2 bases and very rarely involves more than 4 bases.
For every pair of positions i and j of the read g with j – i = w + d, the look-up table is used to locate pairs of close occurrences of words wd(i) and wd(j). For each pair of close occurrences, the word match corresponding to the occurrence of wd(i) is extended into a high-scoring segment pair. Segment pairs of scores greater than a cutoff from the same read are combined into a high-scoring chain by dynamic programming (Huang 2002). The segment pair score cutoff is set to 40, the score of a segment pair of 20 exact base matches with each exact base match given a score of 2. If the score of a high-scoring chain of segment pairs from a read fy is greater than a cutoff value of 80, the chain is taken as an overlap between the read g and read fy. The values for the parameters in the chain computation and the following alignment computation are selected based on evaluation of assembly results on BAC data sets. For computation of repetitive regions, a chain of segment pairs between two reads serves as an overlap between the reads. For computation of reported overlaps, a chain of segment pairs between two reads is refined into a high-scoring alignment, which is computed by performing the Smith-Waterman computation in a matrix band covering all segment pairs of the chain.
The matrix band is determined as follows. A diagonal of the matrix is named by a number k such that the diagonal consists of all entries (i, j) with j – i = k. A segment pair beginning with position i of one read and position j of the other read is said to occur on diagonal j – i. A band of diagonals from numbers low to upp with low ≤ upp consists of diagonals low, low + 1, low + 2,..., upp. A band of diagonals in the matrix covers a chain of segment pairs if each segment pair in the chain occurs on a diagonal inside the band. For a high-scoring chain of segment pairs, a minimum band of diagonals from low to upp is determined, where low is the smallest number of diagonals on which the segment pairs occur and upp is the largest number of diagonals on which the segment pairs occur. The minimum band is expanded in both directions by 15 diagonals, and the resulting band is used for the Smith-Waterman computation. The exact score and start–end positions of the overlap are computed by a banded Smith-Waterman algorithm (Chao et al. 1992), in which the scoring system consists of a match score of 2, a mismatch score of –5, a gap open score of –6, and a gap extension score of –2.
Construction of Contigs and Scaffolds
The second phase consists of the following major steps. First, the depths of coverage of the reads at every position are computed using the files of overlaps and files of repetitive regions. Each overlap is evaluated based on the depths of coverage of the two regions in the overlap. Second, the clipping positions of each read are determined based on unique overlaps. Poor ends of every read are removed at the clipping positions of the read. Chimeric reads are identified and removed. Finally, reads are assembled into contigs using unique overlaps. Contigs are corrected and linked into scaffolds with constraints. A consensus sequence is constructed for each contig. Below we describe each step in detail.
The coverage arrays of the reads in given orientation are computed using the files of repetitive regions and files of overlaps. Each coverage array is initialized to zero at every position. For each repetitive region of a read f, the coverage array of f is increased by the repeat coverage cutoff at every position in the region. For each overlap involving reads gx and gy, if gx = rx, then the region of rx in the overlap is transformed into a region of fx; the coverage array of fx is increased by 1 at every position in the region of fx; and the same procedure is performed for read gy.
The score of each overlap is adjusted to reflect the depths of coverage of the regions in the overlap. This is done by multiplying the overlap score by the smaller of the average coverage scores of the two regions in the overlap. Let repcocut denote the repeat coverage cutoff. The parameter repcocut should be set to the maximum depth of coverage in unique regions. A default value of 60 is used for repcocut. The coverage score array, denoted by csax, of a read fx is computed from the coverage array cax as follows. For a position i of fx,
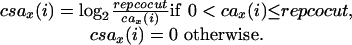
The log ratio function, which is commonly used in discriminatory models, is used to turn depths of coverage into additive coverage scores. For example, if cax(i) = repcocut/8 for a position i, then csax(i) = 3. The average coverage score of a region of fx is the sum of coverage scores of each position in the region divided by the length of the region. If an overlap involves a region with depths of coverage greater than repcocut at every position, then the average coverage score of the region is 0 and the adjusted score of the overlap is 0. On the other hand, if both regions of an overlap have low depths of coverage, then the adjusted score of the overlap is much higher. Only overlaps with an adjusted score greater than an overlap score cutoff are considered in the subsequent steps. We found through experimental tests that using the value 5000 for the overlap score cutoff achieves a good tradeoff between missing true overlaps and admitting false overlaps.
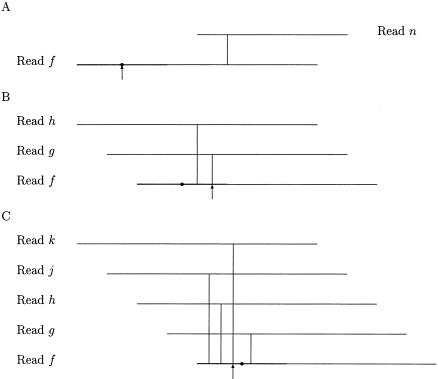
Poor ends of each read f are located and removed by computing the 5′ and 3′ clipping positions of f. The computation is based on the quality values of f and overlaps involving f. The quality values of f are used to determine 5′ and 3′ ranges for potential 5′ and 3′ clipping positions of f, whereas overlaps are used to select the 5′ and 3′ clipping positions of f in the 5′ and 3′ ranges. Let qstart(f) and qend(f) be the start and end positions of a high-quality region of f with respect to a quality value cutoff. Let rsize be the maximum number of high-quality bases allowed in any range. Then the 5′ range of f is defined as a 5′-end region of f from base 1 to base min{qstart(f) + rsize, len(f)}, where len(f) is the length of f. The parameter rsize should be set to a length that is longer than most of the 5′ contaminated end regions. A default value of 300 was found to meet the requirement in our test and is used for rsize. Let cdep be the maximum number of overlaps that can be used to select a clipping position. Let mdep5(f) be the maximum depth of coverage by overlaps in the 5′ range of f. If no position in the 5′ range of f is covered by any overlap, that is, mdep5(f) = 0, then the 5′ clipping position of f is qstart(f). Otherwise, the 5′ clipping position of f is defined as a smallest position in the 5′ range of f such that the position is covered by min{cdep, mdep5(f)} overlaps. The parameter cdep is related to the average depth of coverage for the input data set, and a default value of 3 is used for the parameter cdep. Figure 1 illustrates three cases in computation of the 5′ clipping position of a read f. The overlaps in Figure 1 are drawn such that the order of the start positions of the overlaps in the read f is somewhat consistent with the order of the other reads involved in the overlaps. The 3′ range and clipping position of f are similarly defined.
Figure 1.
Three cases in computation of the 5′ clipping position of a read f. A vertical line shows the start position of an overlap between two reads. The thick line indicates the 5′ clipping range of f. The dot marks the start position of a high-quality region of f. The arrow points to the 5′ clipping position of f. Assume that cdep, the maximum number of overlaps that can be used for computing any clipping position, is set to 3. (A) The maximum depth of coverage by overlaps in the 5′ range of f, denoted by mdep5(f), is 0. (B) We have mdep5(f) = 2 < 3 = _cdep_. (_C_) We have _mdep5_(_f_) = 4 > 3 = cdep.
Consider computing the positions qstart(f) and qend(f) of a high-quality region of read f with respect to a quality value cutoff. A high-quality region of f is defined as a region with the maximum quality score, where the quality score of a base position is the quality value of the position minus the quality value cutoff, and the quality score of a region is the sum of quality scores of each position in the region. A high-quality region of f is found by the maximum-consecutive-subsequence algorithm (Bentley 1986). The quality value cutoff is set to 12 because bases of quality values greater than 12 are often useful for generation of consensus sequences.
Chimeric reads are identified based on an existing method (Huang 1996). A chimeric read consists of two pieces from different parts of the genome. A pair of similar regions between two reads ends (starts) with an overhang if the regions of the reads after (before) the similar regions are sufficiently long and different. A pair of similar regions between a chimeric read and a real read often ends or starts with an overhang. A read f is identified as a chimeric read if it has an internal position pos satisfying the following requirements. A region of the read f immediately before the position pos is similar to a number of other reads. All the similarities end around pos, and a majority of them end with an overhang. A region of the read f immediately after pos is similar to a number of other reads. All the similarities start around pos, and a majority of them start with an overhang. Chimeric reads are not used in construction of contigs.
An initial construction of contigs and scaffolds is performed on a processor with a large amount of main memory. The unique overlaps are read into the main memory. Reads are assembled into contigs by processing the overlaps in a decreasing order of their adjusted scores. Then contigs are corrected and connected into scaffolds with forward–reverse constraints (Huang and Madan 1999). The length of each gap between two contigs in a scaffold is estimated using the distances of the constraints that link the two contigs. The scaffolds are arranged in a decreasing order of sizes, which are referred to as scaffold 0, scaffold 1, scaffold 2, and so on. Next, the scaffolds are partitioned into m groups, where for 0 ≤ k < m, group k consists of scaffolds q with k = q mod m. This partition ensures that the groups are balanced in scaffold sizes. Finally, each group of scaffolds is reported in a separate file.
The memory requirement of an implementation of the procedure described above consists of two parts. The first part is equal to 36 bytes times the number of overlaps saved in the main memory, where each overlap takes 36 bytes of memory. The second part is close to 340 bytes times the total number of reads in the entire data set, where the value 340 is obtained by calculating the total number of bytes per read required by all data structures except the overlap data structure.
From now on, the m groups of scaffolds are processed in parallel. Each group of scaffolds is read from its file to the main memory of a processor. For each scaffold, a set of repetitive reads that are linked by constraints to unique reads in the scaffold is identified. For each gap in the scaffold, a subset of repetitive reads that may fall into the gap are selected from the set for the scaffold. The selection is based on the orientations of unique reads in contigs, the lengths of contigs, and the estimated lengths of gaps in the scaffold. For example, consider a constraint involving reads fx and ry with a maximum distance of d. First, assume that fx is a unique read in a contig C and that ry is a repetitive read. Then the read ry may fall into a gap G downstream of the contig C if the sum of lengths of the contigs and gaps exclusively between the contig C and the gap G is less than d. The distance from the start position of the read fx in the contig C to the end of C is included in the sum. Next, consider the case in which fx is a repetitive read and ry is a unique read in a contig C. The read fx may fall into a gap G upstream of the contig C if the sum of lengths of the contigs and gaps exclusively between the gap G and the contig C is less than d. The distance from the start of the contig C to the end position of the read ry in C is included in the sum.
An attempt is made to close the gap with the subset R of repetitive reads as follows. A 3′-end region of the contig before the gap, where the end region is longer than any overlap, is located. Let U5 denote the set of unique reads that end in the region. Similarly, let U3 denote the set of unique reads that start in a proper 5′-end region of the contig after the gap. Then overlaps are computed for reads in the union of R, U5, and U3. If the gap can be closed with the overlaps, then the contigs before and after the gap are joined into a new contig. Otherwise, no change is made to the contigs before and after the gap.
After all gaps in the group of scaffolds are considered for closure, multiple alignments of reads and consensus sequences are constructed for the contigs in the group with a method used in the CAP3 program (Huang and Madan 1999). Files of contig alignments and consensus sequences are reported in both CAP3 and ace formats.
RESULTS
We first describe results produced by PCAP on a large whole-genome data set. A mouse whole-genome shotgun data set of 33 million reads was downloaded from NCBI in December 2001. A high-quality region of every read was determined with respect to a quality value cutoff of 9, and the low-quality end regions before and after the high-quality region were trimmed. The resulting read was retained if its length was at least 150 bp. The computation of a high-quality region of the read is described in Methods in the context of computing the clipping positions of the read. The selection of 9 for the quality value cutoff was based on the observation that bases of quality values smaller than 9 are useless for assembly. A data set of 30 million reads was produced by the trimming step. The entire set of reads was stored in 68 pairs of base and quality files in compressed form, which took a total of 19 Gb of disk space. A total of 12.9 million forward–reverse constraints involving 25.8 million reads were identified. Although no distance information was provided for some constraints, most of the constraints were from short subclones of 1–6 kb. Thus, a distance range of 500–6000 bp was used when subclone lengths were not available.
The platform for the assembly computation consisted of 21 Compaq ES40 servers, each with four processors. One server had 16 Gb of main memory, and each of the 20 other servers had 4 Gb of main memory. There was a common file system accessible by each server. There was a 32-Gb disk quota on the common file system. Each server had a local scratch disk of 17 Gb.
The assembly computation on the mouse data set was performed by many jobs, each running on one processor. Only jobs of the same type could run in parallel. There were no communications between jobs of the same type. Jobs of different types communicated through input and output files.
All jobs except the one for construction of contigs and scaffolds took <4 Gb of main memory. The contig construction job required 16 Gb of main memory. By saving input and output files in compressed form, all the jobs were completed within the 32-Gb disk quota on the common file system, 19 Gb of which were used to keep the original base and quality files.
The overlap computation was performed by 80 jobs of the same type. Each job took as input the whole set of reads, selected a subset of reads, compared the subset with the whole set, and produced as output a file of repetitive regions for the subset and a file of overlaps between the subset and the whole set. The word length w was set to 12. Each job took 7 d on a processor, spending a majority of the time on automatic identification of repetitive regions of reads. The number of overlap jobs was determined such that each job required <4 Gb of main memory. The memory requirement of each overlap job was 14 times the size of the subset. The overlap jobs produced a total of 273 million overlaps.
The computation of average coverage scores for overlap regions was performed by 20 jobs of the same type. The whole set of reads was partitioned into 20 groups of similar sizes. Each job took as input the 80 files of repetitive regions and 80 files of overlaps, computed the depths of coverage for reads in its group, computed the average coverage scores for overlap regions of reads in its group, and generated as output a file of average coverage scores for overlap regions. The number of jobs was determined based on the memory requirement to save the depths of coverage for reads in each group. Each job took 10 h on a processor.
The construction of contigs and scaffolds was performed by one job. The job took as input the 80 files of overlaps and 20 files of average coverage scores for overlap regions, computed the adjusted score of every overlap, and saved the overlaps with adjusted scores greater than a cutoff in the main memory. Then the job assembled reads into contigs by processing the overlaps in a decreasing order of adjusted scores, took as input the file of constraints, and linked contigs into scaffolds with constraints. Finally, the job produced as output 80 files of scaffolds. The job took 10 h and 16 Gb of main memory on a processor. The cutoff was selected such that there was enough main memory to save the overlaps with adjusted scores greater than the cutoff and to carry out the computation. The cutoff was 8000. The number of overlaps that could be processed within the memory limit of 16 Gb was 135 million, nearly half of the input overlaps. Because of the lack of main memory, ∼12 million overlaps of adjusted scores between 5000 and 8000 were not considered for construction of contigs. The cutoff value 5000 would have been used if there were an additional 0.5 Gb of main memory to save the 12 million overlaps, where each overlap took 36 bytes of memory. About half an hour more time would have been required to process the 12 million overlaps.
Closure of gaps and generation of consensus sequences were performed by 80 jobs of the same type. Each job took as input a group of scaffolds and the whole set of reads, selected a subset of reads that are in the group of scaffolds, and saved the base sequences and quality sequences of the subset in the main memory. Then the job attempted to close, with repetitive reads, gaps between contigs linked by constraints, constructed a multiple alignment of reads for each contig in the group, and generated a consensus sequence for each contig in the group. Finally, the job reported files of multiple alignments and consensus sequences for the group in two formats. The job took 30 h on a processor. A total of 114,215 gaps were closed by the 80 jobs. The entire assembly computation took ∼36 d on the Compaq cluster with at most 20 processors in use at any time.
A summary of contigs and scaffolds produced by PCAP on the mouse data set is shown in Table 1. Of the 30 million reads, 24 million reads appeared in the assembly. There are three reasons that the 6 million reads did not appear in the assembly. First, if a read did not have any overlap of an adjusted score greater than the cutoff and the read was not linked by any constraint to another read in the assembly, then the read could not appear in the assembly. Reads from highly repetitive regions of the genome had overlaps of low adjusted scores. Second, reads that had no overlaps with other reads could not appear in the assembly. Third, chimeric reads were not used in the assembly. The assembly results are available on the Web at http://seq.cs.iastate.edu.
Table 1.
Summary Statistics for Mouse Contigs and Scaffolds
| Type | Numbera | N50 lengthb (bp) | Maximum length (bp) | Total length (Mb) |
|---|---|---|---|---|
| Contigs | 274,201 | 13,696 | 197,544 | 2189.7 |
| Scaffolds | 96,789 | 55,527 | 536,751 | 2240.4 |
It is difficult to evaluate the quality of the PCAP mouse assembly because the mouse genome is not finished. To assess the accuracy of PCAP, we tested PCAP on a data set for human Chromosome 20, which is finished. The data set was made available by ftp from Sanger Center for evaluation of assembly programs in 2001. However, the data set is no longer available at the previous ftp address. The data set contains 1.68 million reads with an average of 12-fold coverage. The reads are free of low-quality bases at ends. The data set was created by combining all reads from clone-based shotgun sequencing projects. A set of seven finished genomic sequences with a total of 59.4 Mb for human Chromosome 20 was obtained from NCBI at ftp://ftp.ncbi.nih.gov/genomes/H_sapiens/CHR_20. We made an artificial set of 370,321 constraints for the data set based on comparison of the reads with the finished genomic sequences. About half of the constraints are of short distances smaller than 5 kb, a quarter are of medium distances between 8 and 20 kb, and a quarter are of long distances between 80 and 130 kb. The data set along with the set of constraints were provided to PCAP as a whole-chromosome shotgun data set. No clone-based information was used by PCAP for assembly.
The assembly computation took 1 d on a computer with eight processors. At most 2 Gb of main memory was used by each of the eight processors. A summary of contigs and scaffolds produced by PCAP on the human Chromosome 20 data set is shown in Table 2. Of the 1.68 million reads, 1.45 million reads appeared in the assembly. Most of the reads that did not appear in the assembly are from highly repetitive regions of human Chromosome 20.
Table 2.
Summary Statistics for Chromosome 20 Contigs and Scaffolds
| Type | Numbera | N50 length (bp) | Maximum length (bp) | Total length (Mb) |
|---|---|---|---|---|
| Contigs | 3486 | 41,343 | 325,806 | 52.4 |
| Scaffolds | 1505 | 2,002,049 | 5,693,424 | 52.6 |
To evaluate the quality of the PCAP assembly, the PCAP contig sequences were compared with the seven finished genomic sequences by Cross_Match (Green 1995). Matches of score at least 3000 between PCAP contig sequences and finished sequences were computed, where the cutoff value 3000 is the score of a perfect match of 3000 bp. The large cutoff value had to be used to keep the number of matches manageable. Unique matches between PCAP contig sequences and finished genomic sequences were selected from the high-scoring matches. Each unique match consists of a pair of corresponding regions between a PCAP contig sequence and a finished sequence. About 80% or 47.7 Mb of the finished genomic sequences were covered by PCAP contig regions from the unique matches. The numbers of misjoins were computed for the PCAP contigs and scaffolds with unique matches to finished sequences. A misjoin in a PCAP contig was detected when two adjacent regions of the contig were found to correspond to nonadjacent regions of a finished sequence or regions of different finished sequences. A mislink in a PCAP scaffold was detected when the order or orientation of two adjacent contigs in the scaffold was found to be inconsistent with that of their counterparts in finished sequences. The number of misjoins made by PCAP in the contigs is 96, and the number of mislinks made by PCAP in the scaffolds is 306. The total length of the PCAP contigs with unique matches to finished sequences is 47.95 Mb. Thus, the misjoin rate for the contigs is one misjoin every 500 kb, and the mislink rate for the scaffolds is one mislink every 157 kb.
The accuracy of the PCAP assembly at the base level was evaluated by using the base quality values of the PCAP contig sequences. The quality value of a PCAP consensus base is a weighted sum of input base quality values (Huang and Madan 1999). The PCAP contig sequences of at least 1500 bp were included in the evaluation. Because a contig sequence often has low coverage and low base quality values in end regions, the bases in the 300-bp ends of the contig sequence were not considered. We found that 99.8% of the bases in the PCAP contig sequences are of quality values at least 30. We chose to do the evaluation based on quality values because the percent identity information was not generated for the matches between PCAP contig sequences and finished sequences.
DISCUSSION
We have developed a whole-genome assembly program named PCAP for processing tens of millions of reads. The PCAP program uses multiple processors to perform overlap and consensus computations, most time-consuming parts in assembly. The program has a number of features to address assembly issues. Two shorter word matches, instead of a longer word match, are used as a seed for finding an overlap. This feature allows the program to miss fewer overlaps because of sequencing errors. Repetitive regions of reads are defined as regions covered by many overlaps with other reads, instead of many shorter exact matches with other reads. The definition leads to more accurate identification of repetitive regions. Contaminated end regions of reads are identified and removed. Generation of a consensus sequence for a contig is based on an alignment of reads in the contig, where both base quality values and coverage information are used to determine every consensus base. The efficiency of PCAP was tested on a mouse whole-genome data set of 30 million reads, and the accuracy of PCAP was evaluated on a human Chromosome 20 data set.
The N50 contig and scaffold lengths for the PCAP mouse assembly are much smaller than those for the ARACHNE mouse assembly (Mouse Genome Sequencing Consortium 2002) for three reasons. First, the PCAP mouse assembly was produced by an early version of PCAP, in which constraints were not used to correct misjoins in contigs. Contigs with misjoins resulted in short scaffolds. Note that the PCAP human Chromosome 20 assembly was produced by the present version of PCAP, in which constraints are used to find and correct misjoins in contigs (Huang and Madan 1999). In the ARACHNE mouse assembly, several effective techniques were used to find and correct errors in scaffolds (Jaffe et al. 2003). Second, BAC end reads and other constraints of distance >7 kb were not provided to PCAP for the mouse assembly. Those long constraints were necessary for construction of long scaffolds (Jaffe et al. 2003). Third, the PCAP mouse assembly started with a raw data set of 33 million reads, instead of a raw data set of 41 million reads. Because of the 16-Gb memory limitation, PCAP was not able to consider 12 million overlaps in construction of contigs.
As powerful computers become available to ordinary labs in the future, powerful assembly programs will be required to process millions of genomic and EST reads in ordinary labs. Sequence assembly programs with different features will better serve the various needs of users. This has been the case with existing assembly programs. For example, Phrap (Green 1995) is suitable for assembly of genomic reads with quality values, whereas CAP3 (Huang and Madan 1999) is suitable for assembly of EST reads without quality values (Liang et al. 2000).
Availability
The PCAP program is freely available for academic use at xqhuang@cs.iastate.edu. The PCAP program can be used with the CONSED program. Additional information on PCAP is available at http://seq.cs.iastate.edu.
Acknowledgments
We thank Ray Hookway and Eamonn O'Toole of Compaq Computer Corp. for giving us access to the Compaq computer cluster; Nat Goodman of Compaq Computer Corp. for lending us an ES40 Compaq server; Asif Chinwalla and Rick Wilson for encouragement; Haining Lin for programming assistance; the Mouse Genome Sequencing Consortium for the mouse data set; David Jaffe for information on the mouse paired reads; James Mullikin for the human Chromosome 20 data set; Oliver Eulenstein, Paul Havlak, and Suraj Kothari for discussions; and the reviewers for helpful suggestions. X.H. and J.W. are supported by NIH grants R01 HG01502 and R01 HG01676. S.A. is supported by NSF grant ACI-0203782. S.-P.Y. and L.H. are supported by NIH grants U54 HG02042 and U01 HG02155.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
[The following individuals kindly provided reagents, samples, or unpublished information as indicated in the paper: the Mouse Genome Sequencing Consortium 2002; J. Mullikin. The assembled mouse sequences are available at our Web site, http://seq.cs.iastate.edu.\]
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.1390403.
References
- Altschul, S.F., Madden, T.L., Schaffer, A.A., Zhang, J., Zhang, Z., Miller, W., and Lipman, D.J. 1997. Gapped BLAST and PSI-BLAST: A new generation of protein database search programs. Nucleic Acids Res. 25**:** 3389–3402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aparicio, S., Chapman, J., Stupka, E., Putnam, N., Chia, J.M., Dehal, P., Christoffels, A., Rash, S., Hoon, S., Smit, A.F., et al. 2002. Whole-genome shotgun assembly and analysis of the genome of Fugu rubripes. Science 297**:** 1301–1310. [DOI] [PubMed] [Google Scholar]
- Batzoglou, S., Jaffe, D., Stanley, K., Butler, J., Gnerre, S., Mauceli, E., Berger, B., Mesirov, J.P., and Lander, E.S. 2002. ARACHNE: A whole-genome shotgun assembler. Genome Res. 12**:** 177–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bentley, J. 1986. Programming pearls. Addison-Wesley, Reading, MA.
- Chao, K.-M., Pearson, W.R., and Miller, W. 1992. Aligning two sequences within a specified diagonal band. Comput. Applic. Biosci. 8**:** 481–487. [DOI] [PubMed] [Google Scholar]
- Chen, T. and Skiena, S.S. 2000. A case study in genome-level fragment assembly. Bioinformatics 16**:** 494–500. [DOI] [PubMed] [Google Scholar]
- Green, P. 1995. Phrap and Cross_Match at http://www.phrap.org.
- Huang, X. 1992. A contig assembly program based on sensitive detection of fragment overlaps. Genomics 14**:** 18–25. [DOI] [PubMed] [Google Scholar]
- ____. 1996. An improved sequence assembly program. Genomics 33**:** 21–31. [DOI] [PubMed] [Google Scholar]
- ____. 2002. Bio-sequence comparison and applications. In Current topics in computational molecular biology (eds. T. Jiang et al.), pp. 45–69. The MIT Press, Cambridge, MA.
- Huang, X. and Madan, A. 1999. CAP3: A DNA sequence assembly program. Genome Res. 9**:** 868–877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaffe, D.B., Butler, J., Gnerre, S., Mauceli, E., Lindblad-Toh, K., Mesirov, J.P., Zody, M.C., and Lander, E.S. 2003. Whole-genome sequence assembly for mammalian genomes: ARACHNE 2. Genome Res. 13**:** 91–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kececioglu, J.D. and Myers, E.W. 1995. Combinatorial algorithms for DNA sequence assembly. Algorithmica 13**:** 7–51. [Google Scholar]
- Kim, S. and Segre, A.M. 1999. AMASS: A structured pattern matching approach to shotgun sequence assembly. J. Comp. Biol. 6**:** 163–186. [DOI] [PubMed] [Google Scholar]
- Liang, F., Holt, I., Pertea, G., Karamycheva, S., Salzberg, S., and Quackenbush, J. 2000. An optimized protocol for analysis of EST sequences. Nucleic Acids Res. 28**:** 3657–3665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mouse Genome Sequencing Consortium. 2002. Initial sequencing and comparative analysis of the mouse genome. Nature 420**:** 520–562. [DOI] [PubMed] [Google Scholar]
- Mullikin, J.C. and Ning, Z. 2003. The Phusion assembler. Genome Res. 13**:** 81–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Myers, E.W., Sutton, G.G., Delcher, A.L., Dew, I.M., Fasulo, D.P., Flanigan, M.J., Kravitz, S.A., Mobarry, C.M., Reinert, K.H., Remington, K.A., et al. 2000. A whole-genome assembly of Drosophila. Science 287**:** 2196–2204. [DOI] [PubMed] [Google Scholar]
- Peltola, H., Soderlund, H., and Ukkonen, E. 1984. SEQAID: A DNA sequence assembling program based on a mathematical model. Nucleic Acids Res. 12**:** 307–321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pevzner, P.A., Tang, H., and Waterman, M.S. 2001. An Eulerian path approach to DNA fragment assembly. Proc. Natl. Acad. Sci. 98**:** 9748–9753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qian, J. 1999. “Parallel DNA sequence assembly.” M.S. thesis, Michigan Technological University, Houghton, MI.
- Staden, R. 1980. A new computer method for the storage and manipulation of DNA gel reading data. Nucleic Acids Res. 8**:** 3673–3694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutton, G.G., White, O., Adams, M.D., and Kerlavage, A.R. 1995. TIGR Assembler: A new tool for assembling large shotgun sequencing projects. Genome Sci. Tech. 1**:** 9–19. [Google Scholar]
- Wang, J., Wong, G.K., Ni, P., Han, Y., Huang, X., Zhang, J., Ye, C., Zhang, Y., Hu, J., Zhang, K., et al. 2002. RePS: A sequence assembler that masks exact repeats identified from the shotgun data. Genome Res. 12**:** 824–831. [DOI] [PMC free article] [PubMed] [Google Scholar]
WEB SITE REFERENCES
- ftp://ftp.ncbi.nih.gov/genomes/H_sapiens/CHR_20; human Chromosome 20 sequences.
- http://seq.cs.iastate.edu; PCAP mouse assembly and PCAP program.
- http://www.ncbi.nlm.nih.gov/Traces; mouse raw data set.