Stability Approach to Regularization Selection (StARS) for High Dimensional Graphical Models (original) (raw)
. Author manuscript; available in PMC: 2014 Aug 20.
Published in final edited form as: Adv Neural Inf Process Syst. 2010 Dec 31;24(2):1432–1440.
Abstract
A challenging problem in estimating high-dimensional graphical models is to choose the regularization parameter in a data-dependent way. The standard techniques include _K_-fold cross-validation (_K_-CV), Akaike information criterion (AIC), and Bayesian information criterion (BIC). Though these methods work well for low-dimensional problems, they are not suitable in high dimensional settings. In this paper, we present StARS: a new stability-based method for choosing the regularization parameter in high dimensional inference for undirected graphs. The method has a clear interpretation: we use the least amount of regularization that simultaneously makes a graph sparse and replicable under random sampling. This interpretation requires essentially no conditions. Under mild conditions, we show that StARS is partially sparsistent in terms of graph estimation: i.e. with high probability, all the true edges will be included in the selected model even when the graph size diverges with the sample size. Empirically, the performance of StARS is compared with the state-of-the-art model selection procedures, including _K_-CV, AIC, and BIC, on both synthetic data and a real microarray dataset. StARS outperforms all these competing procedures.
1 Introduction
Undirected graphical models have emerged as a useful tool because they allow for a stochastic description of complex associations in high-dimensional data. For example, biological processes in a cell lead to complex interactions among gene products. It is of interest to determine which features of the system are conditionally independent. Such problems require us to infer an undirected graph from i.i.d. observations. Each node in this graph corresponds to a random variable and the existence of an edge between a pair of nodes represent their conditional independence relationship.
Gaussian graphical models [4, 23, 5, 9] are by far the most popular approach for learning high dimensional undirected graph structures. Under the Gaussian assumption, the graph can be estimated using the sparsity pattern of the inverse covariance matrix. If two variables are conditionally independent, the corresponding element of the inverse covariance matrix is zero. In many applications, estimating the the inverse covariance matrix is statistically challenging because the number of features measured may be much larger than the number of collected samples. To handle this challenge, the graphical lasso or glasso [7, 24, 2] is rapidly becoming a popular method for estimating sparse undirected graphs. To use this method, however, the user must specify a regularization parameter λ that controls the sparsity of the graph. The choice of λ is critical since different _λ_’s may lead to different scientific conclusions of the statistical inference. Other methods for estimating high dimensional graphs include [11, 14, 10]. They also require the user to specify a regularization parameter.
The standard methods for choosing the regularization parameter are AIC [1], BIC [19] and cross validation [6]. Though these methods have good theoretical properties in low dimensions, they are not suitable for high dimensional problems. In regression, cross-validation has been shown to overfit the data [22]. Likewise, AIC and BIC tend to perform poorly when the dimension is large relative to the sample size. Our simulations confirm that these methods perform poorly when used with glasso.
A new approach to model selection, based on model stability, has recently generated some interest in the literature [8]. The idea, as we develop it, is based on subsampling [15] and builds on the approach of Meinshausen and Bühlmann [12]. We draw many random subsamples and construct a graph from each subsample (unlike _K_-fold cross-validation, these subsamples are overlapping). We choose the regularization parameter so that the obtained graph is sparse and there is not too much variability across subsamples. More precisely, we start with a large regularization which corresponds to an empty, and hence highly stable, graph. We gradually reduce the amount of regularization until there is a small but acceptable amount of variability of the graph across subsamples. In other words, we regularize to the point that we control the dissonance between graphs. The procedure is named StARS: Stability Approach to Regularization Selection. We study the performance of StARS by simulations and theoretical analysis in Sections 4 and 5. Although we focus here on graphical models, StARS is quite general and can be adapted to other settings including regression, classification, clustering, and dimensionality reduction.
In the context of clustering, results of stability methods have been mixed. Weaknesses of stability have been shown in [3]. However, the approach was successful for density-based clustering [17]. For graph selection, Meinshausen and Bühlmann [12] also used a stability criterion; however, their approach differs from StARS in its fundamental conception. They use subsampling to produce a new and more stable regularization path then select a regularization parameter from this newly created path, whereas we propose to use subsampling to directly select one regularization parameter from the original path. Our aim is to ensure that the selected graph is sparse, but inclusive, while they aim to control the familywise type I errors. As a consequence, their goal is contrary to ours: instead of selecting a larger graph that contains the true graph, they try to select a smaller graph that is contained in the true graph. As we will discuss in Section 3, in specific application domains like gene regulatory network analysis, our goal for graph selection is more natural.
2 Estimating a High-dimensional Undirected Graph
Let X = (X(1), …, X(p))T be a random vector with distribution P. The undirected graph G = (V, E) associated with P has vertices V = {X(1), …, X(p)} and a set of edges E corresponding to pairs of vertices. In this paper, we also interchangeably use E to denote the adjacency matrix of the graph G. The edge corresponding to X(j) and X(k) is absent if X(j) and X(k) are conditionally independent given the other coordinates of X. The graph estimation problem is to infer E from i.i.d. observed data X_1,_ …, Xn where Xi = (Xi(1), …, Xi(p))T.
Suppose now that P is Gaussian with mean vector μ and covariance matrix Σ. Then the edge corresponding to X(j) and X(k) is absent if and only if Ω_jk_ = 0 where Ω = Σ−1. Hence, to estimate the graph we only need to estimate the sparsity pattern of Ω. When p could diverge with n, estimating Ω is difficult. A popular approach is the graphical lasso or glasso [7, 24, 2]. Using glasso, we estimate Ω as follows: Ignoring constants, the log-likelihood (after maximizing over μ) can be written as ℓ(Ω) = log |Ω| − trace (Σ̂Ω) where Σ̂ is the sample covariance matrix. With a positive regularization parameter λ, the glasso estimator Ω̂(λ) is obtained by minimizing the regularized negative log-likelihood
| Ω^(λ)=argminΩ≻0{−ℓ(Ω)+λ||Ω||1} | (1) | | -------------------------------- | --- |
where ||Ω||1 = Σ_j,k_ |Ω_jk_| is the elementwise ℓ1-norm of Ω. The estimated graph Ĝ(λ) = (V, Ê(λ)) is then easily obtained from Ω̂(λ): for i ≠ j, an edge (i, j) ∈ Ê(λ) if and only if the corresponding entry in Ω̂(λ) is nonzero. Friedman et al. [7] give a fast algorithm for calculating Ω̂(λ) over a grid of _λ_s ranging from small to large. By taking advantage of the fact that the objective function in (1) is convex, their algorithm iteratively estimates a single row (and column) of Ω in each iteration by solving a lasso regression [21]. The resulting regularization path Ω̂(λ) for all _λ_s has been shown to have excellent theoretical properties [18, 16]. For example, Ravikumar et al. [16] show that, if the regularization parameter λ satisfies a certain rate, the corresponding estimator Ω̂(λ) could recover the true graph with high probability. However, these types of results are either asymptotic or non-asymptotic but with very large constants. They are not practical enough to guide the choice of the regularization parameter λ in finite-sample settings.
3 Regularization Selection
In Equation (1), the choice of λ is critical because λ controls the sparsity level of Ĝ(λ). Larger values of λ tend to yield sparser graphs and smaller values of λ yield denser graphs. It is convenient to define Λ = 1/λ so that small Λ corresponds to a more sparse graph. In particular, Λ = 0 corresponds to the empty graph with no edges. Given a grid of regularization parameters 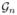 = {Λ1_,_ …, Λ_K_}, our goal of graph regularization parameter selection is to choose one Λ̂ ∈
= {Λ1_,_ …, Λ_K_}, our goal of graph regularization parameter selection is to choose one Λ̂ ∈ 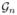 , such that the true graph E is contained in Ê(Λ̂) with high probability. In other words, we want to “overselect” instead of “underselect”. Such a choice is motivated by application problems like gene regulatory networks reconstruction, in which we aim to study the interactions of many genes. For these types of studies, we tolerant some false positives but not false negatives. Specifically, it is acceptable that an edge presents but the two genes corresponding to this edge do not really interact with each other. Such false positives can generally be screened out by more fine-tuned downstream biological experiments. However, if one important interaction edge is omitted at the beginning, it’s very difficult for us to re-discovery it by follow-up analysis. There is also a tradeoff: we want to select a denser graph which contains the true graph with high probability. At the same time, we want the graph to be as sparse as possible so that important information will not be buried by massive false positives. Based on this rationale, an “underselect” method, like the approach of Meinshausen and Bühlmann[12], does not really fit our goal. In the following, we start with an overview of several state-of-the-art regularization parameter selection methods for graphs. We then introduce our new StARS approach.
, such that the true graph E is contained in Ê(Λ̂) with high probability. In other words, we want to “overselect” instead of “underselect”. Such a choice is motivated by application problems like gene regulatory networks reconstruction, in which we aim to study the interactions of many genes. For these types of studies, we tolerant some false positives but not false negatives. Specifically, it is acceptable that an edge presents but the two genes corresponding to this edge do not really interact with each other. Such false positives can generally be screened out by more fine-tuned downstream biological experiments. However, if one important interaction edge is omitted at the beginning, it’s very difficult for us to re-discovery it by follow-up analysis. There is also a tradeoff: we want to select a denser graph which contains the true graph with high probability. At the same time, we want the graph to be as sparse as possible so that important information will not be buried by massive false positives. Based on this rationale, an “underselect” method, like the approach of Meinshausen and Bühlmann[12], does not really fit our goal. In the following, we start with an overview of several state-of-the-art regularization parameter selection methods for graphs. We then introduce our new StARS approach.
3.1 Existing Methods
The regularization parameter is often chosen using AIC or BIC. Let Ω̂(Λ) denote the estimator corresponding to Λ. Let d(Λ) denote the degree of freedom (or the effective number of free parameters) of the corresponding Gaussian model. AIC chooses Λ to minimize −2ℓ(Ω̂(Λ)) + 2_d_(Λ) and BIC chooses Λ to minimize −2ℓ(Ω̂(Λ)) + d(Λ) · log n. The usual theoretical justification for these methods assumes that the dimension p is fixed as n increases; however, in the case where p > n this justification is not applicable. In fact, it’s even not straightforward how to estimate the degree of freedom d(Λ) when p is larger than n. A common practice is to calculate d(Λ) as d(Λ) = m(Λ)(m(Λ) − 1)/2 + p where m(Λ) denotes the number of nonzero elements of Ω̂(Λ). As we will see in our experiments, AIC and BIC tend to select overly dense graphs in high dimensions.
Another popular method is _K_-fold cross-validation (_K_-CV). For this procedure the data is partitioned into K subsets. Of the K subsets one is retained as the validation data, and the remaining K − 1 ones are used as training data. For each Λ ∈ 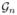 , we estimate a graph on the K − 1 training sets and evaluate the negative log-likelihood on the retained validation set. The results are averaged over all K folds to obtain a single CV score. We then choose Λ to minimize the CV score over he whole grid
, we estimate a graph on the K − 1 training sets and evaluate the negative log-likelihood on the retained validation set. The results are averaged over all K folds to obtain a single CV score. We then choose Λ to minimize the CV score over he whole grid 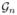 . In regression, cross-validation has been shown to overfit [22]. Our experiments will confirm this is true for graph estimation as well.
. In regression, cross-validation has been shown to overfit [22]. Our experiments will confirm this is true for graph estimation as well.
3.2 StARS: Stability Approach to Regularization Selection
The StARS approach is to choose Λ based on stability. When Λ is 0, the graph is empty and two datasets from P would both yield the same graph. As we increase Λ, the variability of the graph increases and hence the stability decreases. We increase Λ just until the point where the graph becomes variable as measured by the stability. StARS leads to a concrete rule for choosing Λ.
Let b = b(n) be such that 1 < b(n) < n. We draw N random subsamples S_1,_ …, SN from X_1,_ …, Xn, each of size b. There are (nb) such subsamples. Theoretically one uses all (nb) sub-samples. However, Politis et al. [15] show that it suffices in practice to choose a large number N of subsamples at random. Note that, unlike bootstrapping [6], each subsample is drawn without replacement. For each Λ ∈ 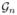 , we construct a graph using the glasso for each subsample. This results in N estimated edge matrices E^1b(Λ),…,E^Nb(Λ). Focus for now on one edge (s, t) and one value of Λ. Let _ψ_Λ(·) denote the glasso algorithm with the regularization parameter Λ. For any subsample Sj let ψstΛ(Sj)=1 if the algorithm puts an edge and ψstΛ(Sj)=0 if the algorithm does not put an edge between (s, t). Define θstb(Λ)=P(ψstΛ(X1,…,Xb)=1). To estimate θstb(Λ), we use a U-statistic of order b, namely, θ^stb(Λ)=1N∑j=1NψstΛ(Sj).
, we construct a graph using the glasso for each subsample. This results in N estimated edge matrices E^1b(Λ),…,E^Nb(Λ). Focus for now on one edge (s, t) and one value of Λ. Let _ψ_Λ(·) denote the glasso algorithm with the regularization parameter Λ. For any subsample Sj let ψstΛ(Sj)=1 if the algorithm puts an edge and ψstΛ(Sj)=0 if the algorithm does not put an edge between (s, t). Define θstb(Λ)=P(ψstΛ(X1,…,Xb)=1). To estimate θstb(Λ), we use a U-statistic of order b, namely, θ^stb(Λ)=1N∑j=1NψstΛ(Sj).
Now define the parameter ξstb(Λ)=2θstb(Λ)(1−θstb(Λ)) and let ξ^stb(Λ)=2θ^stb(Λ)(1−θ^stb(Λ)) be its estimate. Then ξstb(Λ), in addition to being twice the variance of the Bernoulli indicator of the edge (s, t), has the following nice interpretation: For each pair of graphs, we can ask how often they disagree on the presence of the edge: ξstb(Λ) is the fraction of times they disagree. For Λ ∈ 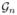 , we regard ξstb(Λ) as a measure of instability of the edge across subsamples, with 0≤ξstb(Λ)≤1/2.
, we regard ξstb(Λ) as a measure of instability of the edge across subsamples, with 0≤ξstb(Λ)≤1/2.
Define the total instability by averaging over all edges: D^b(Λ)=∑s<tξ^stb/(p2). Clearly on the boundary D̂b(0) = 0, and D̂b(Λ) generally will increase as Λ increases. However, when Λ gets very large, all the graphs will become dense and D̂b(Λ) will begin to decrease. Subsample stability for large Λ is essentially an artifact. We are interested in stability for sparse graphs not dense graphs. For this reason we monotonize D̂b(Λ) by defining D̄b(Λ) = sup0≤_t_≤Λ D̂b(t). Finally, our StARS approach chooses Λ by defining Λ̂s = sup{Λ : D̄b(Λ) ≤ β} for a specified cut point value β.
It may seem that we have merely replaced the problem of choosing Λ with the problem of choosing β, but β is an interpretable quantity and we always set a default value β = 0.05. One thing to note is that all quantities Ê, θ̂, ξ̂, D̂ depend on the subsampling block size b. Since StARS is based on subsampling, the effective sample size for estimating the selected graph is b instead of n. Compared with methods like BIC and AIC which fully utilize all n data points. StARS has some efficiency loss in low dimensions. However, in high dimensional settings, the gain of StARS on better graph selection significantly dominate this efficiency loss. This fact is confirmed by our experiments.
4 Theoretical Properties
The StARS procedure is quite general and can be applied with any graph estimation algorithms. Here, we provide its theoretical properties. We start with a key theorem which establishes the rates of convergence of the estimated stability quantities to their population means. We then discuss the implication of this theorem on general gaph regularization selection problems.
Let Λ be an element in the grid 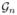 = {Λ1_,_ …, Λ_K_} where K is a polynomial of n. We denote Db(Λ) =
= {Λ1_,_ …, Λ_K_} where K is a polynomial of n. We denote Db(Λ) = 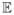 (D̂b(Λ)). The quantity ξ^stb(Λ) is an estimate of ξstb(Λ) and D̂b(Λ) is an estimate of Db(Λ). Standard U -statistic theory guarantees that these estimates have good uniform convergence properties to their population quantities:
(D̂b(Λ)). The quantity ξ^stb(Λ) is an estimate of ξstb(Λ) and D̂b(Λ) is an estimate of Db(Λ). Standard U -statistic theory guarantees that these estimates have good uniform convergence properties to their population quantities:
Theorem 1
(Uniform Concentration) The following statements hold with no assumptions on P. For any δ ∈ (0, 1), w_ith probability at least_ 1 − δ, we have
| ∀Λ∈Gn,maxs<t∣ξ^stb(Λ)−ξstb(Λ)∣≤18b(2logp+log(2/δ))n, | (2) |
|---|
| maxΛ∈Gn∣D^b(Λ)−Db(Λ)∣≤18b(logK+4logp+log(1/δ))n. | (3) |
|---|
Proof
Note that θ^stb(Λ) is a U -statistic of order b. Hence, by Hoeffding’s inequality for U –statistics [20], we have, for any ε > 0,
| P(∣θ^stb(Λ)−θstb(Λ)∣>ε)≤2exp(−2nε2/b). | (4) |
|---|
Now ξ^stb(Λ) is just a function of the U -statistic θ^stb(Λ). Note that
| ∣ξ^stb(Λ)−ξstb(Λ)∣=2∣θ^stb(Λ)(1−θ^stb(Λ))−θstb(Λ)(1−θstb(Λ))∣ | (5) |
|---|
| =2∣θ^stb(Λ)−(θ^stb(Λ))2−θstb(Λ)+(θstb(Λ))2∣ | (6) |
|---|
| ≤2∣θ^stb(Λ)−θstb(Λ)∣+2∣(θ^stb(Λ))2−(θstb(Λ))2∣ | (7) |
|---|
| ≤2∣θ^stb(Λ)−θstb(Λ)∣+2∣(θ^stb(Λ)−θstb(Λ))(θ^stb(Λ)+θstb(Λ))∣ | (8) |
|---|
| ≤2∣θ^stb(Λ)−θstb(Λ)∣+4∣θ^stb(Λ)−θstb(Λ)∣ | (9) |
|---|
| =6∣θ^stb(Λ)−θstb(Λ)∣, | (10) |
|---|
we have ∣ξ^stb(Λ)−ξstb(Λ)∣≤6∣θ^stb(Λ)−θstb(Λ)∣. Using (4) and the union bound over all the edges, we obtain: for each Λ ∈ 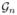 ,
,
| P(maxs<t∣ξ^stb(Λ)−ξstb(Λ)∣>6ε)≤2p2exp(−2nε2/b). | (11) |
|---|
Using two union bound arguments over the K values of Λ and all the p(p − 1)/2 edges, we have:
| P(maxΛ∈Gn∣D^b(Λ)−Db(Λ)∣≥ε)≤∣Gn∣·p(p−1)2·P(maxs<t∣ξ^stb(Λ)−ξstb(Λ)∣>ε) | (12) |
|---|
| ≤K·p4·exp(−nε2/(18b)). | (13) |
|---|
Equations (2) and (3) follow directly from (11) and the above exponential probability inequality.
Theorem 1 allows us to explicitly characterize the high-dimensional scaling of the sample size n, dimensionality p, subsampling block size b, and the grid size K. More specifically, we get
| nblog(np4K)→∞⇒maxΛ∈Gn∣D^b(Λ)−Db(Λ)∣→P0 | (14) |
|---|
by setting δ = 1/n in Equation (3). From (14), let c_1, c_2 be arbitrary positive constants, if b=c1n, K = n c_2, and p ≤ exp (nγ) for some γ < 1/_2, the estimated total stability D̂b(Λ) still converges to its mean Db(Λ) uniformly over the whole grid 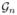 .
.
We now discuss the implication of Theorem 1 to graph regularization selection problems. Due to the generality of StARS, we provide theoretical justifications for a whole family of graph estimation procedures satisfying certain conditions. Let ψ be a graph estimation procedure. We denote Êb(Λ) as the estimated edge set using the regularization parameter Λ by applying ψ on a subsampled dataset with block size b. To establish graph selection result, we start with two technical assumptions:
- (A1)
∃Λo ∈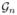 , such that maxΛ≤Λo∧Λ∈
, such that maxΛ≤Λo∧Λ∈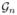 Db(Λ) ≤ _β/_2 for large enough n.
Db(Λ) ≤ _β/_2 for large enough n. - (A2)
For any Λ ∈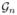 and Λ ≥ Λo, ℙ(E ⊂ Êb(Λ)) → 1 as n → ∞.
and Λ ≥ Λo, ℙ(E ⊂ Êb(Λ)) → 1 as n → ∞.
Note that Λo here depends on the sample size n and does not have to be unique. To understand the above conditions, (A1) assumes that there exists a threshold Λo ∈ 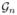 , such that the population quantity Db(Λ) is small for all Λ ≤ Λo. (A2) requires that all estimated graphs using regularization parameters Λ ≥ Λo contain the true graph with high probability. Both assumptions are mild and should be satisfied by most graph estimation algorithm with reasonable behaviors. More detailed analysis on how glasso satisfies (A1) and (A2) will be provided in the full version of this paper. There is a tradeoff on the design of the subsampling block size b. To make (A2) hold, we require b to be large. However, to make D̂b(Λ) concentrate to Db(Λ) fast, we require b to be small. Our suggested value is b=⌊10n⌋, which balances both the theoretical and empirical performance well. The next theorem provides the graph selection performance of StARS:
, such that the population quantity Db(Λ) is small for all Λ ≤ Λo. (A2) requires that all estimated graphs using regularization parameters Λ ≥ Λo contain the true graph with high probability. Both assumptions are mild and should be satisfied by most graph estimation algorithm with reasonable behaviors. More detailed analysis on how glasso satisfies (A1) and (A2) will be provided in the full version of this paper. There is a tradeoff on the design of the subsampling block size b. To make (A2) hold, we require b to be large. However, to make D̂b(Λ) concentrate to Db(Λ) fast, we require b to be small. Our suggested value is b=⌊10n⌋, which balances both the theoretical and empirical performance well. The next theorem provides the graph selection performance of StARS:
Theorem 2
(Partial Sparsistency): Let ψ to be a graph estimation algorithm. We assume (A1) and (A2) hold for ψ using b=⌊10n⌋ and |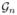 | = K = nc1 for some constant c1 > 0. Let Λ̂s ∈
| = K = nc1 for some constant c1 > 0. Let Λ̂s ∈ 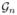 be the selected regularization parameter using the StARS procedure with a constant cutting point β. Then, if p ≤ exp (nγ) for some γ < 1/2, we have
be the selected regularization parameter using the StARS procedure with a constant cutting point β. Then, if p ≤ exp (nγ) for some γ < 1/2, we have
| P(E⊂E^b(Λ^s))→1asn→∞. | (15) |
|---|
Proof
We define 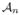 to be the event that maxΛ∈
to be the event that maxΛ∈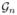 |D̂b(Λ) − D̂b(Λ)| ≤ _β/_2. The scaling of n, K, b, p in the theorem satisfies the L.H.S. of (14), which implies that ℙ(
|D̂b(Λ) − D̂b(Λ)| ≤ _β/_2. The scaling of n, K, b, p in the theorem satisfies the L.H.S. of (14), which implies that ℙ(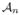 ) → 1 as n → ∞.
) → 1 as n → ∞.
Using (A1), we know that, on 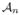 ,
,
| maxΛ<Λo∧Λ∈GnD^b(Λ)≤maxΛ∈Gn∣D^b(Λ)−Db(Λ)∣+maxΛ≤Λo∧Λ∈GnDb(Λ)≤β. | (16) |
|---|
This implies that, on 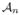 , Λ̂s ≥ Λo. The result follows by applying (A2) and a union bound.
, Λ̂s ≥ Λo. The result follows by applying (A2) and a union bound.
5 Experimental Results
We now provide empirical evidence to illustrate the usefulness of StARS and compare it with several state-of-the-art competitors, including 10-fold cross-validation (_K_-CV), BIC, and AIC. For StARS we always use subsampling block size b(n)=⌊10·n⌋ and set the cut point β = 0.05. We first quantitatively evaluate these methods on two types of synthetic datasets, where the true graphs are known. We then illustrate StARS on a microarray dataset that records the gene expression levels from immortalized B cells of human subjects. On all high dimensional synthetic datasets, StARS significantly outperforms its competitors. On the microarray dataset, StARS obtains a remarkably simple graph while all competing methods select what appear to be overly dense graphs.
5.1 Synthetic Data
To quantitatively evaluate the graph estimation performance, we adapt the criteria including precision, recall, and _F_1-score from the information retrieval literature. Let G = (V, E) be a _p_-dimensional graph and let Ĝ = (V, Ê) be an estimated graph. We define precision = |Ê ∩ E|/|Ê|, recall = |Ê ∩ E|/|E|, and _F_1-score = 2 · precision · recall/(precision + recall). In other words, Precision is the number of correctly estimated edges divided by the total number of edges in the estimated graph; recall is the number of correctly estimated edges divided by the total number of edges in the true graph; the _F_1-score can be viewed as a weighted average of the precision and recall, where an _F_1-score reaches its best value at 1 and worst score at 0. On the synthetic data where we know the true graphs, we also compare the previous methods with an oracle procedure which selects the optimal regularization parameter by minimizing the total number of different edges between the estimated and true graphs along the full regularization path. Since this oracle procedure requires the knowledge of the truth graph, it is not a practical method. We only present it here to calibrate the inherent challenge of each simulated scenario. To make the comparison fair, once the regularization parameters are selected, we estimate the oracle and StARS graphs only based on a subsampled dataset with size b(n)=⌊10n⌋. In contrast, the _K_-CV, BIC, and AIC graphs are estimated using the full dataset. More details about this issue were discussed in Section 3.
We generate data from sparse Gaussian graphs, neighborhood graphs and hub graphs, which mimic characteristics of real-wolrd biological networks. The mean is set to be zero and the covariance matrix Σ = Ω−1. For both graphs, the diagonal elements of Ω are set to be one. More specifically:
- Neighborhood graph: We first uniformly sample y_1, …, yn from a unit square. We then set Ω_ij = Ω_ji_ = ρ with probability (2π)−1exp(−4||yi−yj||2). All the rest Ω_ij_ are set to be zero. The number of nonzero off-diagonal elements of each row or column is restricted to be smaller than ⌊1/ρ_⌋. In this paper, ρ is set to be 0.245.
2. Hub graph: The rows/columns are partitioned into J equally-sized disjoint groups: V_1 ∪ V_2 … ∪ VJ = {1, … p}, each group is associated with a “pivotal” row k. Let |V_1| = s. We set Ω_ik = Ω_ki = ρ for i ∈ Vk and Ω_ik = Ω_ki = 0 otherwise. In our experiment, J = ⌊p/s_⌋, k = 1, s + 1, 2_s + 1, …, and we always set ρ = 1/(s + 1) with s = 20.
We generate synthetic datasets in both low-dimensional (n = 800, p = 40) and high-dimensional (n = 400, p = 100) settings. Table 1 provides comparisons of all methods, where we repeat the experiments 100 times and report the averaged precision, recall, _F_1-score with their standard errors.
Table 1.
Quantitative comparison of different methods on the datasets from the neighborhood and hub graphs.
| Methods | Neighborhood graph: n =800, p=40 | Neighborhood graph: n=400, p =100 | ||||
|---|---|---|---|---|---|---|
| Precision | Recall | _F_1-score | Precision | Recall | _F_1-score | |
| Oracle | 0.9222 (0.05) | 0.9070 (0.07) | 0.9119 (0.04) | 0.7473 (0.09) | 0.8001 (0.06) | 0.7672 (0.07) |
| StARS | 0.204 (0.8) | 0.9530 (0.05) | 0.8171 (0.05) | 0.6366 (0.07) | 0.8718 (0.06) | 0.7352 (0.07) |
| K-CV | 0.1394 (0.02) | 1.0000 (0.00) | 0.2440 (0.04) | 0.1383 (0.01) | 1.0000 (0.00) | 0.2428 (0.01) |
| BIC | 0.9738 (0.03) | 0.9948 (0.02) | 0.9839 (0. 01) | 0.1796 (0.11) | 1.0000 (0.00) | 0.2933 (0.13) |
| AIC | 0.8696 (0.11) | 0.9996 (0.01) | 0.9236 (0.07) | 0.1279 (0.00) | 1.0000 (0.00) | 0.2268 (0.01) |
| Methods | Hub graph: n =800, p=40 | Hub graph: n=400, p =100 | ||||
| Precision | Recall | _F_1-score | Precision | Recall | _F_1-score | |
| Oracle | 0.9793 (0.01) | 1.0000 (0.00) | 0.9895 (0.01) | 0.8976 (0.02) | 1.0000 (0.00) | 0.9459 (0.01) |
| StARS | 0.4377 (0.02) | 1.0000 (0.00) | 0.6086 (0.02) | 0.4572 (0.01) | 1.0000 (0.00) | 0.6274 (0.01) |
| K-CV | 0.2383 (0.09) | 1.0000 (0.00) | 0.3769 (0.01) | 0.1574 (0.01) | 1.0000 (0.00) | 0.2719 (0.00) |
| BIC | 0.4879 (0.05) | 1.0000 (0.00) | 0.6542 (0.05) | 0.2155 (0.00) | 1.0000 (0.00) | 0.3545 (0.01) |
| AIC | 0.2522 (0.09) | 1.0000 (0.00) | 0.3951 (0.00) | 0.1676 (0.00) | 1.0000 (0.00) | 0.2871 (0.00) |
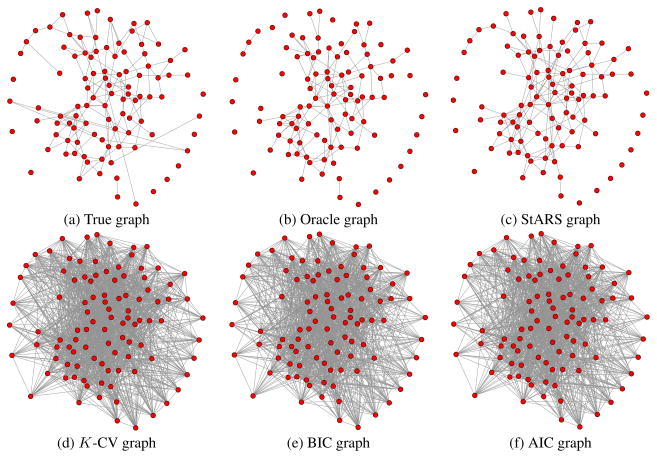
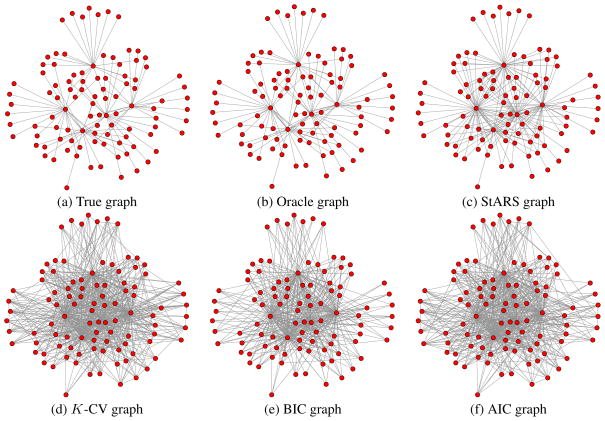
For low-dimensional settings where n ≫ p, the BIC criterion is very competitive and performs the best among all the methods. In high dimensional settings, however, StARS clearly outperforms all the competing methods for both neighborhood and hub graphs. This is consistent with our theory. At first sight, it might be surprising that for data from low-dimensional neighborhood graphs, BIC and AIC even outperform the oracle procedure! This is due to the fact that both BIC and AIC graphs are estimated using all the n = 800 data points, while the oracle graph is estimated using only the subsampled dataset with size b(n)=⌊10·n⌋=282. Direct usage of the full sample is an advantage of model selection methods that take the general form of BIC and AIC. In high dimensions, however, we see that even with this advantage, StARS clearly outperforms BIC and AIC. The estimated graphs for different methods in the setting n = 400, p = 100 are provided in Figures 1 and 2, from which we see that the StARS graph is almost as good as the oracle, while the _K_-CV, BIC, and AIC graphs are overly too dense.
Figure 1.
Comparison of different methods on the data from the neighborhood graphs (n = 400, p = 100).
Figure 2.
Comparison of different methods on the data from the hub graphs (n = 400, p = 100).
5.2 Microarray Data
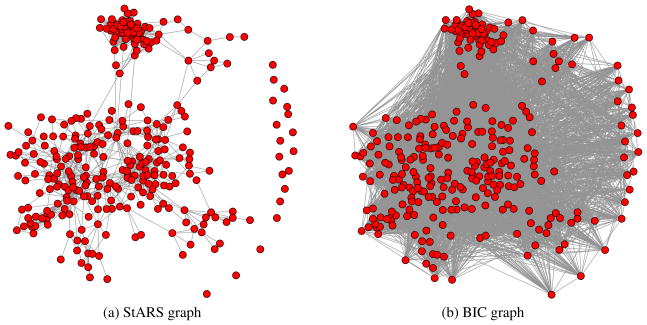
We apply StARS to a dataset based on Affymetrix GeneChip microarrays for the gene expression levels from immortalized B cells of human subjects. The sample size is n = 294. The expression levels for each array are pre-processed by log-transformation and standardization as in [13]. Using a sub-pathway subset of 324 correlated genes, we study the estimated graphs obtained from each method under investigation. The StARS and BIC graphs are provided in Figure 3. We see that the StARS graph is remarkably simple and informative, exhibiting some cliques and hub genes. In contrast, the BIC graph is very dense and possible useful association information is buried in the large number of estimated edges. The selected graphs using AIC and _K_-CV are even more dense than the BIC graph and will be reported elsewhere. A full treatment of the biological implication of these two graphs validated by enrichment analysis will be provided in the full version of this paper.
Figure 3.
Microarray data example. The StARS graph is more informative graph than the BIC graph.
6 Conclusions
The problem of estimating structure in high dimensions is very challenging. Casting the problem in the context of a regularized optimization has led to some success, but the choice of the regularization parameter is critical. We present a new method, StARS, for choosing this parameter in high dimensional inference for undirected graphs. Like Meinshausen and Bühlmann’s stability selection approach [12], our method makes use of subsampling, but it differs substantially from their approach in both implementation and goals. For graphical models, we choose the regularization parameter directly based on the edge stability. Under mild conditions, StARS is partially sparsistent. However, even without these conditions, StARS has a simple interpretation: we use the least amount of regularization that simultaneously makes a graph sparse and replicable under random sampling.
Empirically, we show that StARS works significantly better than existing techniques on both synthetic and microarray datasets. Although we focus here on graphical models, our new method is generally applicable to many problems that involve estimating structure, including regression, classification, density estimation, clustering, and dimensionality reduction.
References
- 1.Akaike Hirotsugu. Information theory and an extension of the maximum likelihood principle. Second International Symposium on Information Theory. 1973;(2):267–281. [Google Scholar]
- 2.Banerjee Onureena, El Ghaoui Laurent, d’Aspremont Alexandre. Model selection through sparse maximum likelihood estimation. Journal of Machine Learning Research. 2008 Mar;9:485–516. [Google Scholar]
- 3.Ben-david Shai, Von Luxburg Ulrike, Pal David. Proceedings of the Conference of Learning Theory. Springer; 2006. A sober look at clustering stability; pp. 5–19. [Google Scholar]
- 4.Dempster Arthur P. Covariance selection. Biometrics. 1972;28:157–175. [Google Scholar]
- 5.Edwards David. Introduction to graphical modelling. Springer-Verlag Inc; 1995. [Google Scholar]
- 6.Efron Bradley. The jackknife, the bootstrap and other resampling plans. SIAM [Society for Industrial and Applied Mathematics]; 1982. [Google Scholar]
- 7.Friedman Jerome H, Hastie Trevor, Tibshirani Robert. Sparse inverse covariance estimation with the graphical lasso. Biostatistics. 2007;9(3):432–441. doi: 10.1093/biostatistics/kxm045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Lange Tilman, Roth Volker, Braun Mikio L, Buhmann Joachim M. Stability-based validation of clustering solutions. Neural Computation. 2004;16(6):1299–1323. doi: 10.1162/089976604773717621. [DOI] [PubMed] [Google Scholar]
- 9.Lauritzen Steffen L. Graphical Models. Oxford University Press; 1996. [Google Scholar]
- 10.Liu Han, Lafferty John, Wainwright J. The nonparanormal: Semiparametric estimation of high dimensional undirected graphs. Journal of Machine Learning Research. 2009;10:2295–2328. [Google Scholar]
- 11.Nicolai Meinshausen and Peter Bühlmann. High dimensional graphs and variable selection with the Lasso. The Annals of Statistics. 2006;34:1436–1462. [Google Scholar]
- 12.Nicolai Meinshausen and Peter Bühlmann. Stability selection. 2010 To Appear in Journal of the Royal Statistical Society, Series B, Methodological. [Google Scholar]
- 13.Nayak Renuka R, Kearns Michael, Spielman Richard S, Cheung Vivian G. Coexpression network based on natural variation in human gene expression reveals gene interactions and functions. Genome Research. 2009 Nov;19(11):1953–1962. doi: 10.1101/gr.097600.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Peng Jie, Wang Pei, Zhou Nengfeng, Zhu Ji. Partial correlation estimation by joint sparse regression models. Journal of the American Statistical Association. 2009;104(486):735–746. doi: 10.1198/jasa.2009.0126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Politis Dimitris N, Romano Joseph P, Wolf Michael. Subsampling (Springer Series in Statistics) 1. Springer; Aug, 1999. [Google Scholar]
- 16.Ravikumar Pradeep, Wainwright Martin, Raskutti Garvesh, Yu Bin. Advances in Neural Information Processing Systems. Vol. 22. Cambridge, MA: MIT Press; 2009. Model selection in Gaussian graphical models: High-dimensional consistency of ℓ1-regularized MLE. [Google Scholar]
- 17.Rinaldo Alessandro, Wasserman Larry. Generalized density clustering. 2009. arXiv/0907.3454. [Google Scholar]
- 18.Rothman Adam J, Bickel Peter J, Levina Elizaveta, Zhu Ji. Sparse permutation invariant covariance estimation. Electronic Journal of Statistics. 2008;2:494–515. [Google Scholar]
- 19.Schwarz Gideon. Estimating the dimension of a model. The Annals of Statistics. 1978;6:461–464. [Google Scholar]
- 20.Serfling Robert J. Approximation theorems of mathematical statistics. John Wiley and Sons; 1980. [Google Scholar]
- 21.Tibshirani Robert. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society, Series B, Methodological. 1996;58:267–288. [Google Scholar]
- 22.Wasserman Larry, Roeder Kathryn. High dimensional variable selection. Annals of statistics. 2009 Jan;37(5A):2178–2201. doi: 10.1214/08-aos646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Whittaker Joe. Graphical Models in Applied Multivariate Statistics. Wiley; 1990. [Google Scholar]
- 24.Yuan Ming, Lin Yi. Model selection and estimation in the Gaussian graphical model. Biometrika. 2007;94(1):19–35. [Google Scholar]