Probing the stochastic, motor-driven properties of the cytoplasm using force spectrum microscopy (original) (raw)

. Author manuscript; available in PMC: 2015 Aug 14.

SUMMARY

Molecular motors in cells typically produce highly directed motion; however, the aggregate, incoherent effect of all active processes also creates randomly fluctuating forces, which drive diffusive-like, non-thermal motion. Here we introduce force-spectrum-microscopy (FSM) to directly quantify random forces within the cytoplasm of cells and thereby probe stochastic motor activity. This technique combines measurements of the random motion of probe particles with independent micromechanical measurements of the cytoplasm to quantify the spectrum of force fluctuations. Using FSM, we show that force fluctuations substantially enhance intracellular movement of small and large components. The fluctuations are three times larger in malignant cells than in their benign counterparts. We further demonstrate that vimentin acts globally to anchor organelles against randomly fluctuating forces in the cytoplasm, with no effect on their magnitude. Thus, FSM has broad applications for understanding the cytoplasm and its intracellular processes in relation to cell physiology in healthy and diseased states.

INTRODUCTION

The cytoplasm of living cells is not a static environment, but is instead subjected to a wide variety of forces (Howard, 2001). For example, molecular motors such as kinesin and dynein generate forces that directionally transport cargo along microtubule tracks, while myosin II motors actively contract actin filaments (Vale, 2003). These active processes all have clearly established functions in the cell, and their individual forces have been precisely quantified (Svoboda and Block, 1994; Vale, 2003). Collectively, these forces have important consequences in the cytoplasm: Several motors operating coherently can generate large forces for directional transport (Hendricks et al., 2012; Rai et al., 2013). On an even larger scale, the cooperative activity of a large number of motors and other active processes collectively drive critical functions at the level of the whole cell, such as division, migration and contraction (Doyle and Yamada, 2010; Dufrene et al., 2011; Grashoff et al., 2010; Gundersen and Worman, 2013; Heisenberg and Bellaïche, 2013). However, the aggregate effect of all the motors and active processes also contribute an incoherent background of fluctuating forces, and the ensemble aggregate of the forces from the incoherent effects of all cellular activities is directly associated with the functional efficiency and the overall metabolic state of the cell (Doyle and Yamada, 2010). In the cytoplasm, these fluctuating forces can give rise, for instance, to random motion of vesicles, mitochondria and signaling proteins (Ananthanarayanan et al., 2013; Brangwynne et al., 2008a; del Alamo et al., 2008; Hammar et al., 2012; Han et al., 1999; Jaqaman et al., 2011; Kyoung and Sheets, 2008), and may drive an even broader range of intracellular dynamics.

Because the motion that arises from fluctuating forces in the cytoplasm is random, little previous effort has been made to quantify these forces. Indeed, many researchers have interpreted random cytoplasmic motion as arising primarily from thermally-induced diffusion, not recognizing the role of overall, aggregate forces. The ensemble forces from overall cellular activity are likely to have a large effect on overall motion within the cytoplasm and would change as the biochemical processes giving rise to these forces are altered during different cell conditions. These forces could thus be a critical readout of the dynamic state of the cell. Because of this, we sought out a direct way to measure aggregate forces within the cytoplasm, aiming to devise methodology for quantifying these forces and testing how they impact different cell states and control motion of cytoplasmic components.

Toward this end, we introduce force spectrum microscopy (FSM), an approach that probes the frequency-dependence of the aggregate, incoherent cytoplasmic forces within a cell. To accomplish this, we combine independent measurements of the intracellular fluctuating movement of injected particles with measurements of the mechanics of the cytoplasm performed with active microrheology using laser tweezers. With these measurements, we determine the temporal spectrum of the ensemble of the random, fluctuating forces, demonstrating that this ubiquitous fluctuating motion in cells is not thermally induced, but is instead a consequence of random forces. We then exploit FSM to probe the intracellular micromechanical behavior of malignant and benign cells, and show that cancer cells exhibit a significantly enhanced level of forces, albeit with the same frequency dependence, as predicted by our model. Moreover, we show that these active forces strongly dominate thermal Brownian forces in the cellular interior, impacting motion of objects from nanometers to microns in scale, providing a fundamental mechanism for transport of objects of all scales. Thus, FSM is a valuable new tool for characterizing the dynamic state of a cell.

RESULTS

Random intracellular movement appears diffusive

To measure the fluctuating motion in the cytoplasm of eukaryotic cells, we microinjected sub-micron colloidal particles into A7 melanoma cells (Cunningham et al., 1992) and measured their time-dependent motion with confocal microscopy. The particles were rendered inert by attaching a short polyethylene-glycol (PEG) brush layer to their surface to eliminate interactions with biopolymers or proteins (Valentine et al., 2004). Moreover, because they were microinjected, the particles were not surrounded by a lipid membrane. Unlike smaller tracers that travel freely through the cytoskeletal network, the injected sub-micron particles were larger than the typical cytoskeletal mesh size, which is about 50 nm (Luby-Phelps, 2000; Lubyphelps et al., 1987). Thus, their motion reflects the fluctuations of the cytoplasm itself. To avoid cell-boundary effects, we imaged particles that are greater than ~1 μm deep within the cell; we also imaged particles away from both the thin lamellar region and the nucleus to avoid any interactions with the mechanically distinct cell cortex and nucleus (Supplemental Information). Particle centers were determined in each image with an accuracy of 22 nm. We tracked their trajectories and calculated the time- and ensemble-averaged mean-square displacement (MSD), <Δ_r_2(τ_)>, where Δ_r(τ)=r(t+τ)−r(t).

At shorter time scales (t ≤ 0.1 s), the MSD of the probe particles was nearly constant in time; however, the fluctuations were always at least 5 times larger than the noise floor. At longer time scales (t ≥ 0.1 s), the MSD increased approximately linearly with time, as shown in Figure 1 and Figure S1. Particles of different size, d, exhibited a similar time dependence, as shown in Figure 1B. Moreover, the amplitude of the fluctuations scaled as 1/d, as shown in Figure 1C; this is consistent with motion in the continuum viscoelastic environment of the cytoplasm (Hoffman et al., 2006). Such motion is often interpreted as thermal Brownian motion (Baker et al., 2010; del Alamo et al., 2008; Gupton et al., 2005; Hale et al., 2009; Wu et al., 2012; Yamada et al., 2000). However, a MSD that increases linearly with time is only consistent with Brownian motion in a purely viscous liquid and at thermal equilibrium, neither of which applies to the cytoplasm (Brangwynne et al., 2008a; Bursac et al., 2005; Hoffman et al., 2006; MacKintosh, 2012; Wilhelm, 2008). As the cytoplasm is neither a pure viscous liquid or at thermal equilibrium, we concluded that the observed cytoplasmic fluctuations must derive from some other source than thermal-based diffusion.

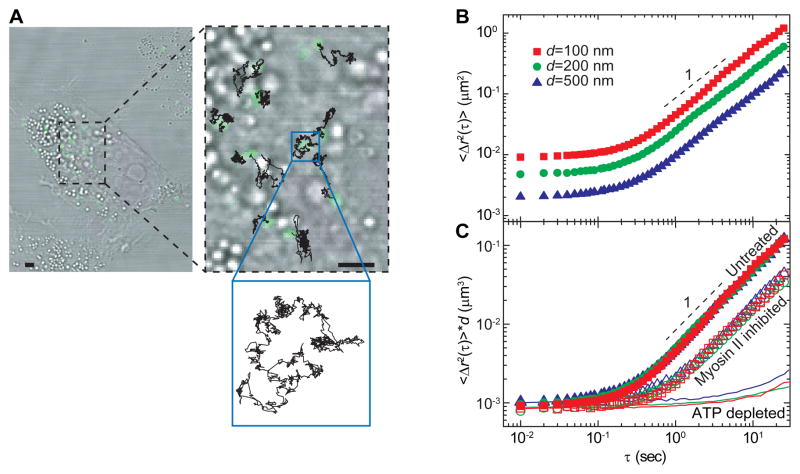
Figure 1. Movements of microinjected tracer particles in living cells.

(A) Bright-field image of a A7 cell with microinjected 200-nm-diameter fluorescence particles (green) and two-minute trajectories (black) superimposed on top. PEG coated particles are microinjected into cells grown on collagen I coated glass-bottom dish. Particle trajectories in the cytoplasm look very similar with thermal Brownian motion. Scale bar, 5 μm.

(B) Two dimensional ensemble-averaged mean-square displacement (MSD) <Δ_r_2(τ)> of PEG-coated tracer particles of various sizes are plotted against lag time on a log-log scale, in living A7 cells. Red, green and blue symbols and lines represent particles that are 100 nm, 200 nm and 500 nm in diameter, respectively. Dashed lines indicate a logarithmic slope of 1. Measurements are done with more than 200 tracer particles in about 25 individual cells for each particle size.

(C) Ensemble-averaged MSD scaled with particle diameter, in untreated (solid symbols), blebbistatin treated (open symbols) and ATP-depleted (solid lines) A7 cells.

Cytoplasmic diffusive-like movement results from active processes

To clarify the active character of the cytoplasmic fluctuating motion, we examined the effect of inhibiting myosin II activity in cells. Myosin II is a nonprocessive motor protein that binds to actin filaments and undergoes a power stroke upon ATP hydrolysis (Howard, 2001). We treated cells with 10 μM blebbistatin, which inhibits myosin II motor activity. After inhibition, we observed a marked decrease in the MSD of injected particles in the diffusive-like regime (t ≥ 0.1 s), while the shorter time-scale movement remained essentially unchanged. When we inhibited general motor and polymerization activity by depleting cells of ATP using 2 mM sodium azide and 10 mM 2-deoxyglucose, the MSD became nearly time independent over our experimental time scales (Figure 1C; Figure S1A; Movie S1). Thus, the motion of the particles is driven by active, ATP-dependent processes. Such active behavior is not limited to the cytoplasm or to eukaryotic cells; ATP-dependent random fluctuating motion has also been observed in prokaryotic cells and yeast (Parry et al., 2014; Weber et al., 2012).

To account for this active behavior, we adapted recent theoretical work suggesting that diffusive motion in the cytoskeleton can arise from random motor activity (Lau et al., 2003; MacKintosh and Levine, 2008): In a filamentous actin network, acto-myosin contractile forces exerted by myosin II motors can drive fluctuating deformations. These myosin motors do not act individually but form aggregates, or minifilaments, which bind to the actin network and act as “disordered muscle fibers”, applying random contractile forces in the network (Koenderink et al., 2009). These forces can result in random fluctuations of the network, similar to that observed in reconstituted networks (Brangwynne et al., 2008b; Mizuno et al., 2009; Mizuno et al., 2007). However, the theoretical framework of actively-driven fluctuations requires a network to be nearly elastic, rather than viscous, to account for the diffusive-like motion observed for _t_≥0.1 s. Thus, a direct measure of the intracellular mechanics is essential to ascertain whether the observed particle motion is due to thermal or active effects (MacKintosh, 2012).

The cytoplasm is a weak elastic solid

To directly measure the micromechanical properties of the cytoplasm, we performed active microrheology measurements using optical tweezers to impose a sinusoidal oscillation as a function of frequency, υ, on a 500-nm-diameter probe particle within a cell. The trap stiffness was 0.05 pN/nm as determined using the equipartition theorem to describe Brownian motion of a bead trapped in water (Veigel et al., 1998). By measuring the resultant displacement of the bead, x(υ), subjected to an applied sinusoidal trap oscillation with a force F at frequency υ, we extracted the effective spring constant, K(υ)=F(υ)/x(υ), for the intracellular environment (Guo et al., 2013; Mizuno et al., 2007). The complex shear modulus _G_=G′+iG″ is related to the spring constant through a generalization of the Stokes relation K_=3_πGd. Thus, we can determine the full frequency-dependent modulus of the cytoplasm.

Our active measurements yielded a resultant displacement that was almost in phase with the applied force; therefore, the micromechanical response of A7 cells was predominantly elastic rather than viscous (Figure 2). Consistent with this, the measured elastic modulus G′ was significantly larger than the loss modulus G″ over the frequency range from 0.3 to 70 Hz (Figure S2). The elastic modulus follows a power-law form, |G(υ)| ~ υβ, with β ≈ 0.15, in agreement with other measurements (Fabry et al., 2001; Guo et al., 2013). We also noted that the measured cytoplasmic modulus is approximately 1 Pa (Figure S2), much lower than that measured on the actin cortex (Fabry et al., 2001); presumably this reflects the denser cross-linked actin structure in the cell cortex, whereas the beads probe the cytoplasm which is much more dilute and hence lower in elasticity. Thus, our tweezers measurements confirmed that the cytoplasm is an elastic solid, on the time scale measured.

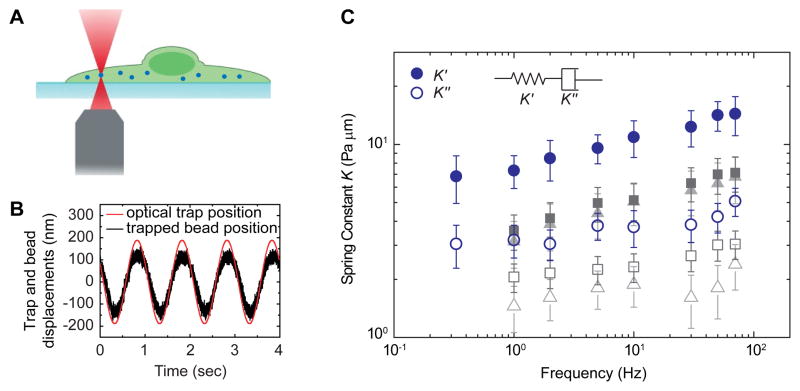
Figure 2. Optical-tweezer active microrheology measurement shows that the cytoplasm is a weak elastic gel.

(A) Schematic shows the experimental setup used to measure the intracellular mechanics.

(B) Typical displacements of the trapped bead and the optical trap oscillating at 1Hz.

(C) Effective spring constant _K_0 of the intracellular environment measured directly with active microrheology using optical tweezers shows that the intracellular elastic stiffness (solid symbols) dominates over the dissipative resistance (open symbols). Blue circles, grey squares, light grey triangles represent untreated, 10 mM blebbistatin treated, and ATP depleted A7 cells, respectively. Both the blebbistatin treatment and ATP depletion reduce the cytoplasmic stiffness by about two folds. Error bars represent standard deviation (_n_=15). The corresponding shear moduli of the cytoplasm are shown in Figure S2.

Model of diffusive-like motion in a nearly elastic medium

The motion of tracer particles directly reflects the fluctuations driven by random motor activity throughout the cell. This provides a basis for an assay that characterizes the average effect of all motor forces; this cannot be done with any other existing technique. To develop this assay, a quantitative description of the random fluctuating motion is required. To do this, we adopted the fundamental force-displacement relationship of any medium, Hooke’s law, _f_=Kx, where f and x are the driving force and the resulting displacement. The material properties are frequency dependent, and the forces are stochastic; thus we consider the quadratic form of the averaged quantities in the frequency domain, <_x_2(_υ_)> = <_f_2(_υ_)>/|K(υ)|2. The MSD, <Δ_x_2(_t_)>, is obtained through the Fourier transform of <_x_2(_υ_)>.

To illustrate the application of the formalism, we consider the simple case of thermally induced Brownian motion in a viscous fluid. In this case, the stochastic thermal forces exerted on the particle are equivalent to white noise and independent of frequency. Furthermore, for a viscous fluid |K|2 ∝ _υ_2, since K″ ∝ ηυ, with η denoting the fluid viscosity. Therefore, <_x_2(_υ_)> ∝ _υ−_2; after Fourier transform, the MSD becomes <Δ_x_2(_t_)> ∝ t, as expected for thermally driven Brownian diffusion in a viscous fluid.

However, the laser-tweezer measurements reveal that the cytoplasm is not a simple fluid, but is instead a weak elastic gel; thus, the tracer particle movement directly reflects the average motor activity. Within this picture, the effect of uncorrelated molecular motors, such as those of myosin filament contractions, is to generate random intracellular forces; these drive fluctuating deformations of the elastic network. This in turn drives the fluctuating motion of objects embedded within the network, as illustrated schematically in Figure 3A. Molecular motors generate force during their processivity time, _τ_p, which characterizes the typical period of binding and coherent motion of a motor; at times longer than this, the motor unbinds, and the tension is instantaneously released, as sketched by the time-evolution of the force, f(t), in the inset of Figure S1B. A force with this step-like behavior in time leads to a power spectrum of force fluctuations, <_f_2(_υ_)>, that varies with frequency as _υ_−2 (Lau et al., 2003; MacKintosh and Levine, 2008). For a purely elastic medium, K is independent of frequency, leading to <_x_2(_υ_)> ∝ _υ−_2, which again becomes <Δ_x_2(_t_)> ∝ t. Interestingly, this temporal dependence of x is the same as that of thermal motion in a viscous fluid; however, in this case, the motion reflects the random active motor forces in an elastic medium, rather than stochastic thermal agitation in a viscous fluid.

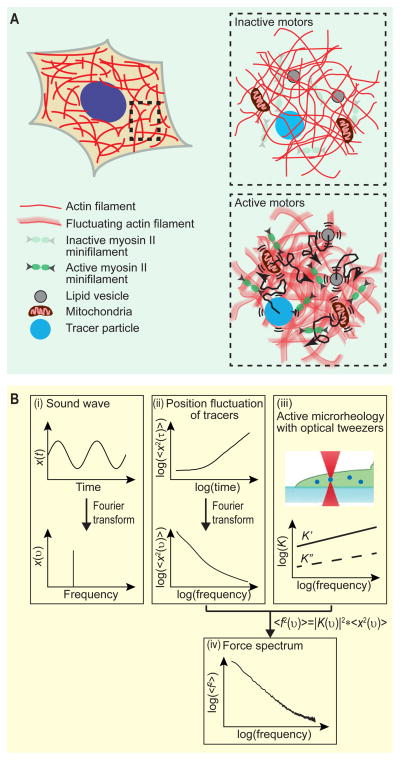
Figure 3. Conceptual basis of FSM.

(A) Schematic illustration of cytoplasmic fluctuating forces enhancing intracellular movements. The aggregate effect of all the motors and active processes working at random directions and random times contribute an incoherent background of fluctuating forces. These active forces drive fluctuating deformations of the cytoplasmic network and substantially enhance intracellular movement over a broad range of length scales, from sub-micron organelles to nanometer-sized proteins.

(B) Basic procedure of FSM. (i) A sound wave in the time domain can be represented in the frequency domain by taking its Fourier transform, thereby revealing its frequency composition. (ii) By analogy to the sound wave, we Fourier transform the MSD and express it in the frequency domain. (iii) The cytoplasmic material property, specifically the spring constant, is measured directly using optical tweezers, also in the frequency domain. (iv) Analogous to a stretched spring, if the spring deformation and spring constant are known, the stretching force can be calculated; in cells, the randomly fluctuating force at each frequency is calculated as <_f_2(_υ_)> = |K(υ)|2<_x_2(_υ_)>.

The laser-tweezer measurements of the elastic modulus (Figures 2, S2 and S3A) show that the local micromechanical environment experienced by probe particles is in fact not purely elastic, but is instead viscoelastic, with a frequency-dependent spring constant |K(υ)|=K_0_υβ, where _β_≈0.15. Furthermore, in the measured frequency range, we find no apparent change in the time behavior of the spring constant; therefore, we assume the same time dependence persists. In this case, the frequency- and force-dependent displacement spectrum becomes <_x_2(_υ_)> ∝ _υ−_2(1+β). Thus, for times less than the processivity time _τ_p, the MSD becomes <Δ_x_2(_t_)> ∝ t_1+2_β/_K_02. This is in stark contrast to the thermal motion expected in such a viscoelastic environment as <Δ_x_2(_t_)> ∝ tβkT/_K_0. Indeed, the observed plateau in the MSD at short time scales (Figure 1B) is consistent with <Δ_x_2(_t_)> ∝ tβ with _β_≈0.15, indicating that the short time regime can be understood as thermal motion in a nearly elastic medium.

Force spectrum microscopy (FSM) probes ensemble aggregate intracellular forces

The fluctuating motion of the tracer particles is a direct readout of the average random fluctuations due to the aggregate motor activity in the cell. If both the particle motion and the cytoplasmic viscoelasticity are measured, the spectrum of the average fluctuating force due to these motors, which drives this motion, can be directly determined, through <_f_2(_υ_)> = |K(υ)|2<_x_2(_υ_)>. This provides a new tool for characterizing the frequency-dependent spectrum of the average force, which is due to the aggregate, yet random effects of all active processes in the cell. While these forces are inherently time-dependent, it is more convenient to describe their frequency-dependent spectrum. We call this new assay Force Spectrum Microscopy (FSM), as summarized schematically in Figure 3B.

To demonstrate the applicability of FSM, we quantified the average aggregate cytoplasmic forces due to active processes in A7 cells. The resultant force spectrum exhibited two distinct frequency regimes, as shown by the red data in Figure 4A: In the low frequency range, corresponding to time scales _t_≥0.1 s, <_f_2(_υ_)> is proportional to _υ_−2; by contrast, in the high-frequency range, corresponding to _t_≤0.1 s, <_f_2(_υ_)> has a weaker frequency dependency. These observations are consistent with a low frequency regime dominated by active forces, and a high frequency regime dominated by thermal forces (Brangwynne et al., 2008a; Lau et al., 2003; MacKintosh and Levine, 2008; Mizuno et al., 2007). Moreover, based on our model, we estimate that a density of myosin filaments of ~1/μm3, each generating a force of order 10 pN, can account for the observed force spectrum (see details in Supplemental Information). This is the first experimental assessment of this important global measurement of the overall enzymatic activity in the cell.

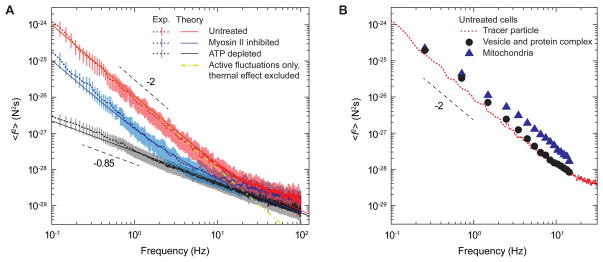
Figure 4. Ensemble aggregate intracellular force spectrum probed by FSM.

(A) Cytoplasmic force spectrum calculated from spontaneous fluctuations of tracer particles and the active microrheology measurement, through <_f_2(_υ_)>=|K(υ)|2<_x_2(_υ_)>, inside control untreated (red), myosin II inhibited (blue) and ATP-depleted (black) A7 cells. Data are shown as mean values (dotted lines) and vertical error bars (_n_>). For comparison, theoretical predictions are shown for an elastic medium with a shear modulus as shown in Figure S2, with three levels of activities; the red solid line corresponds to about 1/μm3 density of myosin II filaments applying a force ~ pN, the blue solid line corresponds to a 90% reduction of myosin motor activity by 10 μM blebbistatin (Kovacs et al., 2004), and the black solid line corresponds to no active motors. The yellow dash dotted line represents the theoretical prediction of only active contributions and excludes thermal effects. Dashed lines indicate logarithmic slopes of −0.85 and −2. Vertical bars represent standard error (_n_=15).

(B) Comparison of force spectra probed by FSM in untreated A7 cells, using the spontaneous fluctuations of injected tracer particles (red dotted line, same as that in Figure 4A), endogenous vesicles and protein complexes (black circle) and mitochondria (blue triangle). The spring constant is measured by active microrheology with probe particles, as shown in Figure 2. The force spectrum measured with vesicles and protein complexes is in excellent accord with that measured for probe particles. The force spectrum for mitochondria exhibits the same frequency dependence as that for probe particles, but is larger in amplitude; this is consistent with mitochondria are also occasionally directly transported by specific motors within the cell.

To further establish the applicability of FSM in quantifying active forces in the cell, we suppressed the level of actin-based cytoskeletal forces by inhibiting myosin II motors through the addition of 10 μM blebbistatin to the cell culture medium. As a result, the low-frequency, active component of the force spectrum was suppressed, although the same overall _υ_−2 dependence remained, as shown by the blue data in Figure 4A. Furthermore, when we depleted cells of ATP through addition of 2 mM sodium azide and 10 mM 2-deoxyglucose, we observed a force spectrum that is consistent with purely thermal fluctuations over the full frequency range for the viscoelasticy medium measured directly for these cells, as shown by the black data in Figure 4A. This suggested that, while actomyosin contractions are a significant source of intracellular forces, other enzymatic activities also contribute to the forces and hence the motion experienced by intracellular objects. Moreover, above 10 Hz, the force spectra measured in all cases had the same time dependence and nearly the same amplitudes, consistent with a common thermal origin of the motion in this regime (Figure 4A). These results demonstrate the ability of FSM to quantify the degree of motor activity in a cell, and to distinguish these active forces from thermal forces.

To further explore the utility and sensitivity of FSM, we increased the cytoplasmic stiffness by applying osmotic stress to compress cells (Zhou et al., 2009). We observe a marked reduction in the amplitude of particle fluctuations, although the frequency dependence remains unchanged, reflecting the consequences of the increased cytoplasmic stiffness (Figure S3). Surprisingly, however, when the force spectrum was calculated, we found that the amplitude of intracellular forces did not change, at least within the range of osmotic pressures applied (see details in Supplemental Information).

FSM reveals differences in the intracellular forces within benign and malignant cells

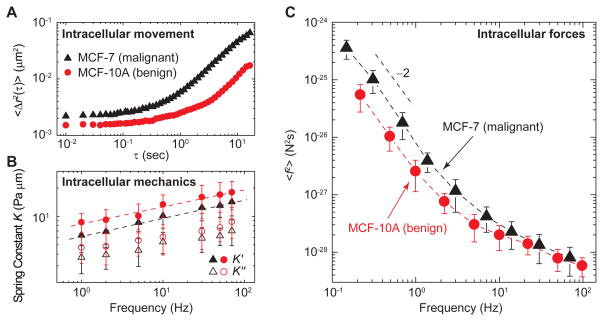
Since FSM probes the consequences of the aggregate forces due to active processes in the cell, it can be used to directly quantify changes in intracellular activity and the dynamic state of cytoplasm in response to changes in conditions such as drug treatment, external stimuli, or even the disease state of a cell. To illustrate this, we compared the force spectrum of malignant and benign cells. Malignant cells exhibit reduced cell stiffness (Cross et al., 2007; Plodinec et al., 2013) and increased traction forces (Kraning-Rush et al., 2012), which may provide potential biophysical markers for metastatic progression. Using FSM, we compared the force spectrum in benign (MCF-10A) to that in malignant (MCF-7) breast cancer cells which are known to exhibit enhanced motility (Chan et al., 2008; Nagaraja et al., 2006). Tracer-particle motion is significantly enhanced in malignant MCF-7 cells relative to benign cells, as shown in Figure 5A, whereas the cytoplasmic stiffness was only ~30% smaller in the malignant MCF-7 cells (Figure 5B). When we calculated the force spectrum, we indeed found a significant difference between malignant and benign cells, with malignant cells having a force spectrum with approximately 3 times larger magnitude than the benign cells; however, the frequency dependence of the spectra remained unchanged (Figure 5C). A similar behavior was observed for another pair of malignant and benign cells, M6C and M28 (Holzer et al., 2003), as shown in Figure S4. The results suggested, therefore, that highly motile cancer cells have a more active cytoplasm. The enhanced motor activity reflected by the larger magnitude in the force spectrum measured with FSM is consistent with cancer cells exerting increased traction force on the extracellular matrix (Agus et al., 2013), despite their decreased stiffness; this observation also fits well with biochemical studies showing changes in metabolic and proliferative rates of cancer cells (DeBerardinis et al., 2008; Sherr, 1996). Therefore, FSM provides a tool to identify changes in ensemble intracellular forces and dynamic states of the cytoplasm, even though the origin of these changes is complex. Moreover, our results with malignant cells provide an additional metastatic signature at the sub-cellular scale, and may help elucidate the physical and chemical forces that shape and govern the progression of cancer.

Figure 5. Intracellular mechanics, dynamics and forces in benign and malignant tumor cells.

(A) Two dimensional MSD <Δ_r_2(τ)> of 500 nm tracer particles are plotted against lag time on a log-log scale, in the benign breast cells MCF-10A (red circle) and malignant breast tumor cells MCF-7 (black triangle), respectively. The fluctuating movement of tracer particles is stronger in the malignant cells, as compared to the benign cells.

(B) Cytoplasmic mechanics measured by active microrheology using optical tweezers. The effective spring constant of the cytoplasm is larger in the MCF-10A (red circle), as compared to the MCF-7 (black triangle); this suggests that the cytoplasm of benign cells is stiffer than malignant cells.

(C) The spectrum of intracellular forces calculated based on the fluctuating movement of tracer particles and the cytoplasmic mechanics measurement. The intracellular forces are stronger in the malignant tumor cells MCF-7 (black triangle), than the benign cells MCF-10A (red circle).

Error bars represent standard deviation (_n_=6).

Force spectrum microscopy reveals that expression of vimentin intermediate filaments does not affect intracellular forces

Force spectrum microscopy can identify the contribution of specific cellular components to the overall level of intracellular activity. To demonstrate this, we apply FSM to measure the effect of vimentin intermediate filaments (VIFs) in mesenchymal cells. Vimentin is a type-III IF protein that is typically expressed in cells of mesenchymal origin and is widely used as a marker of the epithelial to mesenchymal transition (EMT). VIFs have been shown to induce changes in cell shape, motility and adhesion during EMT (Mendez et al., 2010); however, the role of VIFs in the level of aggregate intracellular forces is unknown because no technique has been able to quantify this property. We used FSM to probe intracellular force spectrum in mouse embryonic fibroblasts (mEFs) from wild type (WT) and vimentin knockout (Vim−/−) mice; we found no significant difference in the intracellular force spectrum between WT and Vim−/− mEFs, as shown in Figure S5. In contrast, the force spectrum was markedly reduced when we depolymerize actin filaments with 5 μg/mL cytochalasin D in WT mEFs. These results suggested that vimentin IFs are mainly structural polymers that are an important contributor to the internal stiffness of cells, but do not affect the aggregate intracellular forces.

Force spectrum reveals motor processivity time

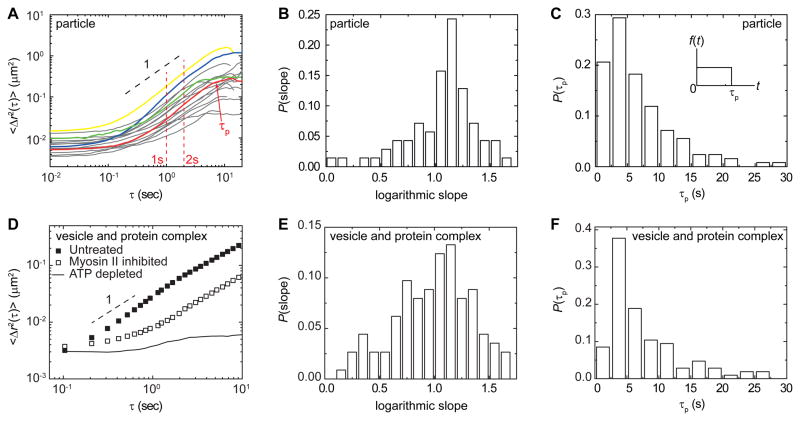
The frequency spectrum can quantify additional important, but heretofore unresolved, features of motor activity. This is seen in a more precise investigation of the time dependence of the MSD. At long times, _t_≥0.1 s, we observe an approximately linear time dependence in the MSD averaged over many particles. By contrast, our model predicts a stronger time dependence, as given by <Δ_x_2(_t_)> ∝ t_1+2_β/_K_02. This difference arises from the ensemble averaging over different trajectories; indeed when we examine the MSDs of individual particles, we find that most trajectories exhibit a markedly larger maximum local slope reflecting a stronger time dependence. However, they also exhibit clear evidence of a roll-off or saturation at the longest times, on the order of 10 s, as shown in Figures 6A and S1B. This roll-off behavior is consistent with the finite processivity of motor contractions, at a processivity time, τp; processive forces are generated by motors with an average duration, τp, and result in finite displacements in the cytoplasm over corresponding timescales. To quantify this, we measure the distribution of logarithmic slopes of the MSD and find a peak near 1.2, as shown in Figure 6B; this is in excellent agreement with the prediction of <Δ_x_2(_t_)> ∝ t_1+2_β with β ≈ 0.15. Moreover, the distribution of processivity times is peaked around 5 s, as shown in Figure 6C; this is the first experimental measure of processivity times for the ensemble aggregate forces. The processivity time is not apparent in the ensemble average data, due to the large distribution in processivity times, _τ_p, obscures the effect of individual turnover.

Figure 6. Logarithmic slope and processivity time analyzed from MSD of single tracer particles and cytoplasmic organelles.

(A) Individual MSD curves of single 100-nm particles. Colored lines highlight representative deviations from the ensemble average. The full data set is shown in Figure S1B.

(B) Distribution of the average logarithmic slopes of single particle’s MSD curve in untreated A7 cells, calculated between 1 to 2 second lag time as indicated by the red dashed lines in the inset. The mean and standard deviation of the slopes are 1.1 and 0.26, respectively, and the mode is about 1.2.

(C) Distribution of processivity times τp associating with the random intracellular fluctuations, calculated from the transition between the diffusive-like regime and the long time saturation of the time-averaged MSD of each single particle, as pointed by a red arrow in (A). Inset, schematic of the time-dependent force due to activity of myosin filament.

(D) Two dimensional MSD of the movement of intracellular vesicles and protein complexes, in untreated (solid squares) and blebbistatin treated (open squares) A7 cells, tracked by bright-field microscopy.

(E, F) Logarithmic slopes (E) and distribution of processivity times (F) are calculated from MSD curves of single vesicle and protein complex in the untreated cells.

Active force fluctuations increase vesicle and organelle motion

FSM provides a powerful assay to probe the consequences of the aggregate random forces due to motor activity within cells. In particular, it can be used to explore the consequences of these forces on motion of vesicles, protein complexes and organelles within the cell, providing new insight into the origin of their random motion. We used FSM to probe the effects of random forces on the overall movements of these various structures. The motion of vesicles and protein complexes were tracked using bright-field microscopy in A7 cells. Occasionally, the movement was directed, with these structures moving along a straight path at a constant velocity; however, the majority of the motion was random in nature, with the MSD increasing approximately linearly in time (Figure 6D). We inferred the force spectrum acting on these vesicles and protein complexes using a combination of their MSD and the cytoplasmic mechanics measured with active microrheology using laser tweezers on tracer beads. We found that the force spectrum was in excellent accord, both in magnitude and frequency dependence, with that measured for injected probe particles (Figure 4B). Moreover, when we suppressed the random cytoplasmic force by inhibiting acto-myosin contraction with 10 μM blebbistatin, we observed a marked decrease in their movements in direct analogy to the behavior observed for probe particles (Figure 6D; Movie S2). These results show that the random aggregate motor forces within the cell act on endogenous cytoplasmic structures in the exact same fashion as they do on the probe particles. This illustrates the ubiquity of the effects of the active random forces, and suggests that they may also contribute to intracellular transport.

We also applied FSM to probe the movement of mitochondria within the cell (see details in Supplemental Information). Interestingly, we observed a force spectrum that exhibits the same frequency dependence as that of the probe particles, but is larger in amplitude by about a factor of 2, as shown in Figure 4B. By carefully observing the shape of mitochondria over time, we identified significant changes in their local configuration. This has an effect of shifting the center of the mitochondria identified during the tracking, thereby adding to the fluctuations, and is likely to contribute to the additional amplitude of the force spectrum. Moreover, it is known that mitochondria are occasionally transported by specific motors along microtubules (Wang and Schwarz, 2009). Therefore, the observed movement includes contributions from both random force fluctuations and effects from mitochondria specific motors; this is also consistent with larger amplitude of forces observed on mitochondria. Thus, FSM is also able to probe the consequences of shape changes of the objects induced by the random forces, and might also provide a way to distinguish the specific and non-specific effects of motor activity on certain organelles.

Active force fluctuations increase protein movement

The force spectra revealed by FSM show that active processes dominate the ensemble cytoplasmic forces at relatively low frequencies (Figure 4A), which corresponds to long time scales. In contrast to micron-sized organelles and particles, smaller objects such as nanometer-sized proteins that are smaller than typical cytoplasmic mesh size, are much more mobile, and the role of the random forces on individual proteins is unclear. To investigate this, we examined both short and long time-scale diffusive-like behavior of nm-sized proteins. To examine short time-scale behavior, we transfected HeLa cells with green fluorescent protein (GFP), and perform fluorescent correlation spectroscopy (FCS) to measure the local dynamics of GFP, over timescales of tens of μs. At this scale, we did not resolve significant differences in the apparent diffusion coefficient of GFP between untreated and ATP depleted cells (Figure S6), implying that the random active forces do not affect the motion of individual proteins on short time scales.

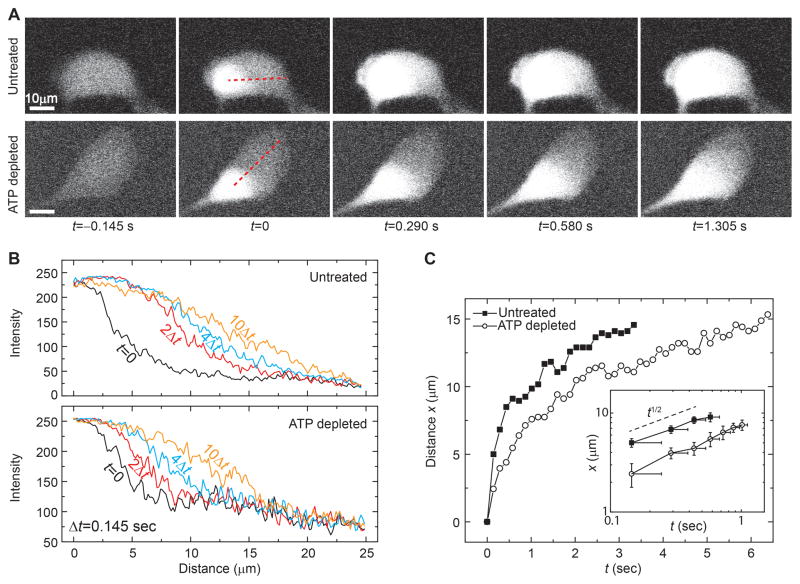
Since many signaling proteins and even nutrients travel across larger parts of the cell, over time scales of seconds, this is likely to be affected by the active fluctuating forces at long time scales. To investigate this, we transfected HeLa cells with Dendra2, a 26-kDa fluorescent protein that switches from green GFP-like fluorescence to red RFP-like fluorescence when flashed with 405 nm light (Chudakov et al., 2007). By tracking the RFP signal after local photoconversion, we visualize the Dendra2-protein movement throughout the cell which takes a few seconds; we observe a marked decrease of the spreading of the RFP signal in the ATP depleted cells as compared to the untreated cells (Figure 7A; Movie S3). This is confirmed by plotting the time-dependence of the fluorescence intensity profile of the proteins. In the presence of ATP, the profile spreads more rapidly (Figure 7B) with the width of the profile exhibiting more rapid expansion with time (Figure 7C). This result confirms that active forces contribute to the large-scale transport of individual proteins, suggesting that even the transport of small molecules or nutrients can be enhanced by random active processes.

Figure 7. Movement of Dendra2 in cells is increased with ATP.

(A) Typical confocal fluorescence images of the red-channel of Dendra2 during photoconversion by a 405 nm pulse. Before photoconversion, cells have low background red fluorescence; the flashed region rapidly converts to red, and begins to move throughout the cell over several seconds. Comparing the untreated and ATP depleted conditions, we see that red fluorescence spreads more quickly in cells with ATP.

(B) By quantifying the red fluorescence intensity as a function distance (along the red dashed line in (A)) at several different times, we see that ATP approximately doubles Dendra2 transport over longer length scales.

(C) Plotting the spatial width of the red fluorescence intensity as a function of time demonstrates that, without ATP, photoconverted Dendra2 spreads more slowly. (Inset) Replotting in log-log format shows that with or without ATP Dendra2 spreads proportional to _t_1/2, demonstrating that both cases movement appears random. Error bars, 145 ms (based on measurement uncertainty from limited imaging frequency).

DISCUSSION

We introduce a new assay, force spectrum microscopy (FSM), which directly quantifies the magnitude and frequency-dependence of the aggregate random active processes in the cell. We determine the force spectrum by tracking the random fluctuations of objects combined with the micromechanical characterization of the intracellular environment. This technique provides a direct measure of the forces within cells, which is very challenging by comparison to making measurements of position or motion using microscopy. Furthermore, FSM provides the first direct measure of the random aggregate forces attributable to active processes inside the cell, and enables these to be distinguished from purely mechanical effects. This provides new insight into the consequences of the overall activity within the cell. Using FSM, we show that malignant cancer cells have significantly larger intracellular activity as compared to benign cells, demonstrating its utility in probing the internal dynamic state of cells. We confirm that vimentin IFs contribute mainly to structural mechanics, and not to the forces within the cell. These results demonstrate the ability of FSM to isolate the effects of cellular activity and distinguish it from the effects of cytoplasmic viscoelastic properties on intracellular dynamics. We further show that FSM can be performed on intracellular organelles to investigate random forces experienced by organelles or different objects in cells. These results suggest that FSM may be used as a general assay to quantify the role of the random forces in driving many cellular and developmental processes, such as proliferation and the epithelial to mesenchymal transition. In addition, the information provided by FSM on both the amplitude and frequency spectrum of the random aggregate forces in the cell may yield new insights into the dynamic nature of cytoplasm, which may help resolve some long-standing issues in disease development and progression and may provide the basis for new diagnostic and therapeutic approaches.

Furthermore, our findings alter the way that we view the cytoplasm of eukaryotic cells. We demonstrate that force fluctuations driven by motor activity play an important, even dominant role in intracellular motion over a broad range of length and time scales, from micron-sized organelles to nanometer-sized proteins and nutrients. These results also confirm that random motion, so ubiquitous in cells, is not a result of thermally-induced fluctuations, but is instead the result of the random forces due to the aggregate motor activity in cells. Thus, interpretation of intracellular motion based on equilibrium thermal fluctuations, such as is done for passive microrheology (Baker et al., 2010; del Alamo et al., 2008; Wu et al., 2012; Yamada et al., 2000) is incorrect. Moreover, this random motion driven by intracellular force fluctuations can have important consequences for many aspects of cell physiology. For example, many cellular components, such as protein filaments and complexes, storage granules, and intracellular organelles, will be impacted by these active fluctuations in the cytoplasm; these components are involved in processes that are essential for life in natural environments, and their functions depends on their ability to move in the cytoplasm. More specifically, these random fluctuations are likely to be crucial for spatially distributing key cellular machineries, such as ribosomes and proteasomes, to facilitate efficient translation and degradation of proteins. They also could be vital for quick removal of enzyme products from their site of synthesis in metabolic reactions to avoid local concentration effects. Finally, growth and remodeling of the cytoskeleton may depend on these random force fluctuations, which may help ensure, for example, that actin monomers are in continual supply to rapidly growing filaments in the cell periphery.

EXPERIMENTAL PROCEDURES

Cell Culture, Microinjection, and Pharmacological Interventions

Cells are maintained under 5% CO2 at 37°C in a humidified incubator. A7 cells (Cunningham et al., 1992) (gift from Tom Stossel lab at Harvard Medical School) are cultured in Dulbecco’s minimal essential medium (DMEM) supplemented with 2% fetal calf serum, 8% newborn calf serum (Invitrogen), 10 mM HEPES buffer, 100 U/ml penicillin and 100 μg/ml streptomycin. WT and Vim−/− mEFs (Guo et al., 2013) are cultured in DMEM with 10% fetal calf serum, 5mM nonessential amino acids, 100 U/ml penicillin and 100 μg/ml streptomycin. MCF-10A cells are cultured in 1:1 DMEM:F12 media (Invitrogen) with 5% house serum (Invitrogen), 20 mM HEPEs, 10 μg/ml insulin, 0.1 μg/ml Cholera Toxin, 500 ng/ml hydrocortisone, 100 U/ml penicillin and 100 μg/ml streptomycin. MCF-7 cells and HeLa cells are cultured in DMEM with 10% fetal calf serum. Cells are plated on collagen I coated MatTek dishes at a density of 20 per mm2 overnight before experiment.

Microinjection is performed using a glass needle and a FemtoJet microinjector (Eppendorf) mounted on a bright-field microscope. About 50 cells are injected per dish; each cell is injected up to 50 tracer particles to eliminate the interference to cell function. Cells are then allowed to recover in culture medium for 6 hours, and are imaged on a confocal microscope at 37 °C and 5% CO2. Organelles and injected tracer particles are imaged with bright-field or confocal microscopy using a 63x/1.2NA water immersion lens on a Leica TSC SP5. Please refer to Extended Experimental Procedures for more details.

To inhibit myosin II motor activity, blebbistatin (Toronto Research Chemicals) is dissolved in DMSO and added to cell culture media to a 10 μM final concentration, incubating for 30 minutes. ATP depletion is achieved by incubating cells with 2 mM NaN3 and 10 mM deoxyglucose in PBS for 1 hour.

Particle Surface Chemistry

Fluorescent carboxylate-modi ed polystyrene spherical particles (100 nm, 200 nm and 500 nm, from Molecular Probes) are rendered inert by grafting short amine-terminated methoxy-poly(ethylene glycol) to the surface of carboxylated microspheres, as described previously (Valentine et al., 2004). PEG coated particles are stored at 4°C and used within two weeks. Both yellow-green and far red particles for each size are used in this study.

Particle Tracking and Analysis

The trajectories of the fluorescent particles are recorded every 10 ms for about 2 minutes. The images are processed with particle tracking software written by J. Crocker, D. Grier and E. Weeks, in IDL (http://www.physics.emory.edu/~weeks/idl/). Particle centers are found in each image with an accuracy of 22 nm. The MSD of the probe particles is nearly constant in time at short time scales (t ≤ 0.1 s), and is about an order of magnitude greater than the noise floor, as shown in Figure S1A. Please refer to Extended Experimental Procedures for more details.

Optical Tweezers Setup

To optically trap and manipulate 500 nm beads in the cytoplasm of living cells, the beam from a variable-power Nd:YAG solid-state laser (4 W, 1064 nm; Spectra Physics) is steered through a series of Keplerian beam expanders to overfill the back aperture of a 100x 1.3 numerical aperture microscope objective (Nikon S-fluor; Nikon). To steer the beam and manipulate the trapped bead, two acousto-optic deflectors (NEOS Technologies) are used to manipulate the beam in the plane of the microscope glass slide. For detection, the bead is centered on a high-resolution position detection quadrant detector (MBPS; Spectral Applied Research) and illuminated using brightfield illumination from a 75 W Xe lamp. The linear region of the detector is calibrated by trapping a bead identical to those used in the cells in water and moving it across the detector using the acousto-optic deflectors in known step sizes. The trap stiffness is calibrated to 0.05 pN/nm using the mean-squared Brownian motion of a trapped bead in water at various laser power settings using the principle of energy equipartition as previously described (Veigel et al., 1998). A trapped bead is oscillated across a frequency range of 0.3–70 Hz using the acousto-optic deflectors, and the laser position and bead displacement are recorded simultaneously, from which the elastic and viscous shear moduli are determined.

Osmotic Stress

Hyperosmotic stress is applied by adding polyethylene glycol 300 (PEG300) to isotonic culture medium. Cells are then allowed to equilibrate for 10 min at 37 °C and 5% CO2, before we perform the imaging or optical-tweezer measurement. The cell size and mechanics equilibrate in 2 minutes after adding PEG based on our imaging and previous studies (Zhou et al., 2009).

Measurement of Protein Movement with Photoconvertable Dendra2

To measure the large length scale movement of small proteins, we use the photonically switchable fluorescent proteins Dendra2, a photoconvertible fluorescent protein which irreversibly switches from green (GFP-like) to red (RFP-like) when exposed to a brief flash of 405 nm light (Chudakov et al., 2007). We transfect HeLa cells with Dendra2 (Evrogen), then perform fluorescence loss after photoconversion (FLAC) measurements as described previously (Ehrlicher et al., 2011). In FLAC measurements using Dendra2, we start with the green fluorescence of unconverted Dendra2, which allows us to identify cells with high expression that are bright. We then flash the cell with a brief (~50 ms) flash of 405 light, while monitoring both the green and red fluorescence. A dip in the green fluorescence is observed, but a bright spot of red fluorescence in the pulsed region is clearly visible. By monitoring the increase of red fluorescence at different distances from the pulsed region, we can quantify the movement of the Dendra2 probe throughout the cell. Please refer to Extended Experimental Procedures for more details.

Supplementary Material

01. Movie S1.

Three-minute movie of injected 500nm PEG-coated particles movement in wild type (left), blebbistatin treated (middle), and ATP depleted (right) A7 cells, respectively. The movie is about 20X speed up, and the actual time is shown on the upper left. Related to Figure 1.

02. Movie S2.

30-second movie of vesicles movement in A7 wild type (left) and blebbistatin traeated (right) A7 cells. The movie is about 6X speed up, and the actual time is shown on the upper left. Related to Figure 6.

03. Movie S3.

20-second movie of Dendra2 spread out through wild type (left) and ATP depleted (right) HeLa cells, after activated by a 405nm laser. The actual time is shown on the upper left. Related to Figure 7.

Figure S1. Movement of 100 nm tracer particles in living A7 cells. Related to Figures 1 and 6.

(A) Two dimensional mean-square displacement (MSD) <Δ_r_2(τ)> of PEG-coated 100 nm tracer particles measured with particle tracking method are plotted against lag time on a log-log scale, in wild-type (solid symbols), blebbistatin treated (open symbols) and ATP-depleted (solid lines) A7 cells. Noise level is shown as the black star, which is measured by imaging and tracking the same beads fixed on a glass coverslip.

(B) Full data set of individual MSD curves of single 100 nm particles. Colored lines highlight representative deviations from the ensemble average. Inset, schematic of the time-dependent force due to activity of myosin filament. Part of this data are shown in Figure 6A.

Figure S2. Mechanical properties of the cytoplasm measured by optical-tweezer acitve microrheology in A7 cells. Related to Figure 2.

The frequency dependent elastic and viscous moduli are extracted via the Stokes relation K_=3_πGd, if a homogenerous intracellular material is assumed, where K is directly calculated by measuring the resultant displacement x of the bead in the trap oscillation, as f/x. as plotted in Figure 2. The cytoplasm shows predominantly elastic behavior (G′ > G″) for the untreated cells (blue circles), blebbistatin treated cells (gray squares), and ATP depleted cells (light gray triangles). Blebbistatin treatment and ATP depletion reduces both the cytoplasmic G′ and G″ about 50 percent, as compared to the untreated cells.

Figure S3. Osmotic compression increases cytoplasmic stiffness and reduces intracellular movement. Related to Figure 2.

(A) The effective spring constant of the cytoplasm increases as PEG concentration goes up, from 0% PEG300 (green circles), to 3%w/w PEG300 (black triangles), then to 6%w/w PEG300 (magenta squares) in addition of culture medium. The in-phase (elastic) components are fitted using K (ω) ≅ K_0_ωβ, as shown by solid lines. Fitted values for K_0 are used for scaling in (C) and (D). Here ω is the angular frequency, that equals 2π_v where v denotes the natural frequency.

(B) Two dimensional MSD <Δ_r_2(τ)> of 200 nm PEG-coated tracer particles are plotted against lag time on a log-log scale, in A7 cells, under varying levels of osmotic compression. Beads fluctuating movement slows done as cells are compressed by adding PEG.

(C) The MSD data shown in (B) is rescaled by _K_0, for different concentrations of PEG (_K_0=10.1, 12.4, 16 Pa μm for 0% PEG300, to 3%w/w PEG300, 6%w/w PEG300, respectively). The collapse of all curves at short time scales when scaled by _K_0 suggests that this elastic plateau is thermally dominated.

(D) Same data as shown in (B) rescaled by _K_02 collapse at long time-scales suggests that the diffusive-like regime is actively driven.

Figure S4. Intracellular mechanics, dynamics and forces in benign and malignant tumor cells. Related to Figure 5.

(A) Two dimensional MSD <Δ_r_2(τ)> of 500 nm tracer particles are plotted against lag time on a log-log scale, in the benign cells M28 (grey circle) and malignant tumor cells M6C (black square), respectively. The fluctuating movement of tracer particles is stronger in the malignant cells, as compared to the benign cells.

(B) Cytoplasmic mechanics measured by active microrheology using optical tweezers. The effective spring constant of the cytoplasm is slightly larger in the M28 (grey circle), as compared to the M6C (black square); this suggests that the cytoplasm of benign M28 cells is slightly stiffer than malignant M6C cells, almost indistinguishable.

(C) The spectrum of intracellular forces calculated based on the fluctuating movement of tracer particles and the cytoplasmic mechanics measurement. The intracellular forces are stronger in the malignant tumor cells M6C (black square), than the benign cells M28 (grey circle).

Error bars represent standard deviation (_n_=5).

Figure S5. Ensemble aggregate intracellular force spectrum probed by FSM in wild-type and vimentin-null cells. Related to Figure 5.

Spectrum of intracellular fluctuating forces calculated in wild-type and vimentin-null mouse embryonic fibroblasts (mEFs), using the spontaneous fluctuations of endogenous vesicles, through 〈_f_2 (ω)〉 = 〈_x_2 (ω)〉|K(ω)|2. The spring constant K is measured with optical-tweezer active microrheology manipulating a 500 nm injected particle in the cytoplasm. The force spectra measured in wild-type and vimentin-null mEFs are essentially same; however, they are both significantly higher than that measured in mEFs with F-actin depolymerized by 5 μg/mL Cytochalasin D. These results suggest that vimentin intermediate filament is important for stabilizing cytoplasmic mechanics, but is not involved in the generation of intracellular fluctuating force, as compared to actin which is a more dynamic cytoplasmic component.

Figure S6. Local mobility of GFP oligomers in the absence and presence of 2-DG and Na-azide as assessed by FCS over timescales of tens of μs. Related to Figure 7.

(A) Data is analyzed using a two-componential fit taking into account a apparently freely diffusing and a transiently bound species. The apparent diffusion coefficient, D [μm2/s], of the first freely diffusing component is calculated using the measured diffusion time of the GFP oligomer as well as measured diffusion time and known diffusion coefficient of a calibration probe. Differences in dynamics of GFP oligomers in the absence (−) and presence (+) of 2-DG and Na-azide could not be resolved. All measurements are performed in untreated and 2-DG and Na-azide treated cells at 37°C.

(B) The same data is analyzed using a fit considering anomalous diffusion of only one component. Alphas is plotted. Again, no differences in apparent diffusibility of GFP oligomers in the absence (−) and presence (+) of 2-DG and Na-azide are resolbed.

HIGHLIGHTS.

Random intracellular motion is driven by active force fluctuations in the cytoplasm
The aggregate random forces enhance motion of small proteins and large organelles
We develop Force Spectrum Microscopy to probe aggregate random cytoplasmic forces
The aggregate random forces are larger in malignant cancer cells than benign cells

Acknowledgments

We thank A. Rowat, S. Lindström, K. Kasza for helpful discussions; we thank F. Deng and A. Pegoraro for comments on the manuscript. This work was supported by the NIH (PO1GM096971), the Harvard Materials Research Science and Engineering Center (DMR-0820484), the NSF (DMR-1310266). AJE was supported by NIH grant DK083592; MHJ and JRM were supported by NIH grant HL86655; FCM was supported in part by FOM/NWO. RG was supported by NIH PO1GM096971 and Hannah’s Hope Fund.

Footnotes

Conflict of Interest statement.

The authors declare no conflict of interests.

SUPPLEMENTAL INFORMATION

Supplemental information includes Extended Experimental Procedures, Supplemental Information, six figures and three movies.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

Agus DB, Alexander JF, Arap W, Ashili S, Aslan JE, Austin RH, Backman V, Bethel KJ, Bonneau R, Chen WC, et al. A physical sciences network characterization of non-tumorigenic and metastatic cells. Scientific Reports. 2013:3. doi: 10.1038/srep01449. [DOI] [PMC free article] [PubMed] [Google Scholar]
Ananthanarayanan V, Schattat M, Vogel Sven K, Krull A, Pavin N, Toli-Nørrelykke Iva M. Dynein Motion Switches from Diffusive to Directed upon Cortical Anchoring. Cell. 2013;153:1526–1536. doi: 10.1016/j.cell.2013.05.020. [DOI] [PubMed] [Google Scholar]
Baker EL, Lu J, Yu DH, Bonnecaze RT, Zaman MH. Cancer Cell Stiffness: Integrated Roles of Three-Dimensional Matrix Stiffness and Transforming Potential. Biophysical Journal. 2010;99:2048–2057. doi: 10.1016/j.bpj.2010.07.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brangwynne CP, Koenderink GH, MacKintosh FC, Weitz DA. Cytoplasmic diffusion: molecular motors mix it up. Journal of Cell Biology. 2008a;183:583–587. doi: 10.1083/jcb.200806149. [DOI] [PMC free article] [PubMed] [Google Scholar]
Brangwynne CP, Koenderink GH, MacKintosh FC, Weitz DA. Nonequilibrium microtubule fluctuations in a model cytoskeleton. Phys Rev Lett. 2008b:100. doi: 10.1103/PhysRevLett.100.118104. [DOI] [PubMed] [Google Scholar]
Bursac P, Lenormand G, Fabry B, Oliver M, Weitz DA, Viasnoff V, Butler JP, Fredberg JJ. Cytoskeletal remodelling and slow dynamics in the living cell. Nature Materials. 2005;4:557–561. doi: 10.1038/nmat1404. [DOI] [PubMed] [Google Scholar]
Chan SW, Lim CJ, Guo K, Ng CP, Lee I, Hunziker W, Zeng Q, Hong WJ. A role for TAZ in migration, invasion, and tumorigenesis of breast cancer cells. Cancer Res. 2008;68:2592–2598. doi: 10.1158/0008-5472.CAN-07-2696. [DOI] [PubMed] [Google Scholar]
Chudakov DM, Lukyanov S, Lukyanov KA. Tracking intracellular protein movements using photoswitchable fluorescent proteins PS-CFP2 and Dendra2. Nat Protoc. 2007;2:2024–2032. doi: 10.1038/nprot.2007.291. [DOI] [PubMed] [Google Scholar]
Cross SE, Jin YS, Rao J, Gimzewski JK. Nanomechanical analysis of cells from cancer patients. Nat Nanotechnol. 2007;2:780–783. doi: 10.1038/nnano.2007.388. [DOI] [PubMed] [Google Scholar]
Cunningham CC, Gorlin JB, Kwiatkowski DJ, Hartwig JH, Janmey PA, Byers HR, Stossel TP. Actin-binding protein requirement for cortical stability and efficient locomotion. Science. 1992;255:325–327. doi: 10.1126/science.1549777. [DOI] [PubMed] [Google Scholar]
DeBerardinis RJ, Sayed N, Ditsworth D, Thompson CB. Brick by brick: metabolism and tumor cell growth. Curr Opin Genet Dev. 2008;18:54–61. doi: 10.1016/j.gde.2008.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
del Alamo JC, Norwich GN, Li YSJ, Lasheras JC, Chien S. Anisotropic rheology and directional mechanotransduction in vascular endothelial cells. Proc Natl Acad Sci U S A. 2008;105:15411–15416. doi: 10.1073/pnas.0804573105. [DOI] [PMC free article] [PubMed] [Google Scholar]
Doyle AD, Yamada KM. CELL BIOLOGY Sensing tension. Nature. 2010;466:192–193. doi: 10.1038/466192a. [DOI] [PubMed] [Google Scholar]
Dufrene YF, Evans E, Engel A, Helenius J, Gaub HE, Muller DJ. Five challenges to bringing single-molecule force spectroscopy into living cells. Nature Methods. 2011;8:123–127. doi: 10.1038/nmeth0211-123. [DOI] [PubMed] [Google Scholar]
Ehrlicher AJ, Nakamura F, Hartwig JH, Weitz DA, Stossel TP. Mechanical strain in actin networks regulates FilGAP and integrin binding to filamin A. Nature. 2011;478:260–U154. doi: 10.1038/nature10430. [DOI] [PMC free article] [PubMed] [Google Scholar]
Fabry B, Maksym GN, Butler JP, Glogauer M, Navajas D, Fredberg JJ. Scaling the microrheology of living cells. Phys Rev Lett. 2001;87:148102. doi: 10.1103/PhysRevLett.87.148102. [DOI] [PubMed] [Google Scholar]
Grashoff C, Hoffman BD, Brenner MD, Zhou RB, Parsons M, Yang MT, McLean MA, Sligar SG, Chen CS, Ha T, et al. Measuring mechanical tension across vinculin reveals regulation of focal adhesion dynamics. Nature. 2010;466:263–U143. doi: 10.1038/nature09198. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gundersen Gregg G, Worman Howard J. Nuclear Positioning. Cell. 2013;152:1376–1389. doi: 10.1016/j.cell.2013.02.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
Guo M, Ehrlicher Allen J, Mahammad S, Fabich H, Jensen Mikkel H, Moore Jeffrey R, Fredberg Jeffrey J, Goldman Robert D, Weitz David A. The Role of Vimentin Intermediate Filaments in Cortical and Cytoplasmic Mechanics. Biophysical Journal. 2013;105:1562–1568. doi: 10.1016/j.bpj.2013.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
Gupton SL, Anderson KL, Kole TP, Fischer RS, Ponti A, Hitchcock-DeGregori SE, Danuser G, Fowler VM, Wirtz D, Hanein D, et al. Cell migration without a lamellipodium: translation of actin dynamics into cell movement mediated by tropornyosin. Journal of Cell Biology. 2005;168:619–631. doi: 10.1083/jcb.200406063. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hale CM, Sun SX, Wirtz D. Resolving the Role of Actoymyosin Contractility in Cell Microrheology. PLoS One. 2009:4. doi: 10.1371/journal.pone.0007054. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hammar P, Leroy P, Mahmutovic A, Marklund EG, Berg OG, Elf J. The lac Repressor Displays Facilitated Diffusion in Living Cells. Science. 2012;336:1595–1598. doi: 10.1126/science.1221648. [DOI] [PubMed] [Google Scholar]
Han WP, Ng YK, Axelrod D, Levitan ES. Neuropeptide release by efficient recruitment of diffusing cytoplasmic secretory vesicles. Proceedings of the National Academy of Sciences of the United States of America. 1999;96:14577–14582. doi: 10.1073/pnas.96.25.14577. [DOI] [PMC free article] [PubMed] [Google Scholar]
Heisenberg CP, Bellaïche Y. Forces in Tissue Morphogenesis and Patterning. Cell. 2013;153:948–962. doi: 10.1016/j.cell.2013.05.008. [DOI] [PubMed] [Google Scholar]
Hendricks AG, Holzbaur ELF, Goldman YE. Force measurements on cargoes in living cells reveal collective dynamics of microtubule motors. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:18447–18452. doi: 10.1073/pnas.1215462109. [DOI] [PMC free article] [PubMed] [Google Scholar]
Hoffman BD, Massiera G, Van Citters KM, Crocker JC. The consensus mechanics of cultured mammalian cells. Proceedings of the National Academy of Sciences. 2006;103:10259–10264. doi: 10.1073/pnas.0510348103. [DOI] [PMC free article] [PubMed] [Google Scholar]
Holzer R, MacDougall C, Cortright G, Atwood K, Green J, Jorcyk C. Development and Characterization of a Progressive Series of Mammary Adenocarcinoma Cell Lines Derived from the C3(1)/SV40 Large T-antigen Transgenic Mouse Model. Breast Cancer Res Treat. 2003;77:65–76. doi: 10.1023/a:1021175931177. [DOI] [PubMed] [Google Scholar]
Howard J. Mechanics of motor proteins and the cytoskeleton. Sunderland, MA 01375 USA: Sinauer Associates, Inc; 2001. [Google Scholar]
Jaqaman K, Kuwata H, Touret N, Collins R, Trimble WS, Danuser G, Grinstein S. Cytoskeletal Control of CD36 Diffusion Promotes Its Receptor and Signaling Function. Cell. 2011;146:593–606. doi: 10.1016/j.cell.2011.06.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
Koenderink GH, Dogic Z, Nakamura F, Bendix PM, MacKintosh FC, Hartwig JH, Stossel TP, Weitz DA. An active biopolymer network controlled by molecular motors. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:15192–15197. doi: 10.1073/pnas.0903974106. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kovacs M, Toth J, Hetenyi C, Malnasi-Csizmadia A, Sellers JR. Mechanism of blebbistatin inhibition of myosin II. J Biol Chem. 2004;279:35557–35563. doi: 10.1074/jbc.M405319200. [DOI] [PubMed] [Google Scholar]
Kraning-Rush CM, Califano JP, Reinhart-King CA. Cellular Traction Stresses Increase with Increasing Metastatic Potential. PLoS One. 2012:7. doi: 10.1371/journal.pone.0032572. [DOI] [PMC free article] [PubMed] [Google Scholar]
Kyoung M, Sheets ED. Vesicle Diffusion Close to a Membrane: Intermembrane Interactions Measured with Fluorescence Correlation Spectroscopy. Biophysical Journal. 2008;95:5789–5797. doi: 10.1529/biophysj.108.128934. [DOI] [PMC free article] [PubMed] [Google Scholar]
Lau AWC, Hoffman BD, Davies A, Crocker JC, Lubensky TC. Microrheology, stress fluctuations, and active behavior of living cells. Phys Rev Lett. 2003:91. doi: 10.1103/PhysRevLett.91.198101. [DOI] [PubMed] [Google Scholar]
Luby-Phelps K. Cytoarchitecture and physical properties of cytoplasm: Volume, viscosity. diffusion, intracellular surface area. International Review of Cytology - a Survey of Cell Biology. 2000;192:189–221. doi: 10.1016/s0074-7696(08)60527-6. [DOI] [PubMed] [Google Scholar]
Lubyphelps K, Castle PE, Taylor DL, Lanni F. Hindered diffusion of inert tracer particles in the cytoplasm of mouse 3T3 cells. Proc Natl Acad Sci U S A. 1987;84:4910–4913. doi: 10.1073/pnas.84.14.4910. [DOI] [PMC free article] [PubMed] [Google Scholar]
MacKintosh FC. Active diffusion: The erratic dance of chromosomal loci. Proceedings of the National Academy of Sciences of the United States of America. 2012;109:7138–7139. doi: 10.1073/pnas.1204794109. [DOI] [PMC free article] [PubMed] [Google Scholar]
MacKintosh FC, Levine AJ. Nonequilibrium mechanics and dynamics of motor-activated gels. Phys Rev Lett. 2008:100. doi: 10.1103/PhysRevLett.100.018104. [DOI] [PubMed] [Google Scholar]
Mendez MG, Kojima SI, Goldman RD. Vimentin induces changes in cell shape, motility, and adhesion during the epithelial to mesenchymal transition. Faseb J. 2010;24:1838–1851. doi: 10.1096/fj.09-151639. [DOI] [PMC free article] [PubMed] [Google Scholar]
Mizuno D, Bacabac R, Tardin C, Head D, Schmidt CF. High-Resolution Probing of Cellular Force Transmission. Phys Rev Lett. 2009;102:168102. doi: 10.1103/PhysRevLett.102.168102. [DOI] [PubMed] [Google Scholar]
Mizuno D, Tardin C, Schmidt CF, MacKintosh FC. Nonequilibrium mechanics of active cytoskeletal networks. Science. 2007;315:370–373. doi: 10.1126/science.1134404. [DOI] [PubMed] [Google Scholar]
Nagaraja GM, Othman M, Fox BP, Alsaber R, Pellegrino CM, Zeng Y, Khanna R, Tamburini P, Swaroop A, Kandpal RP. Gene expression signatures and biomarkers of noninvasive and invasive breast cancer cells: comprehensive profiles by representational difference analysis, microarrays and proteomics. Oncogene. 2006;25:2328–2338. doi: 10.1038/sj.onc.1209265. [DOI] [PubMed] [Google Scholar]
Parry BR, Surovtsev IV, Cabeen MT, O’Hem CS, Dufresne ER, Jacobs-Wagner C. The Bacterial Cytoplasm Has Glass-like Properties and Is Fluidized by Metabolic Activity. Cell. 2014;156:183–194. doi: 10.1016/j.cell.2013.11.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
Plodinec M, Loparic M, Monnier CA, Obermann EC, Zanetti-Dallenbach R, Oertle P, Hyotyla JT, Aebi U, Bentires-Alj M, Schoenenberger CA, et al. The Nanomechanical Signature of Breast Cancer. Biophysical Journal. 2013;104:321A–321A. doi: 10.1038/nnano.2012.167. [DOI] [PubMed] [Google Scholar]
Rai AK, Rai A, Ramaiya AJ, Jha R, Mallik R. Molecular Adaptations Allow Dynein to Generate Large Collective Forces inside Cells. Cell. 2013;152:172–182. doi: 10.1016/j.cell.2012.11.044. [DOI] [PubMed] [Google Scholar]
Sherr CJ. Cancer cell cycles. Science. 1996;274:1672–1677. doi: 10.1126/science.274.5293.1672. [DOI] [PubMed] [Google Scholar]
Svoboda K, Block SM. Force and velocity measured for single kinesin molecules. Cell. 1994;77:773–784. doi: 10.1016/0092-8674(94)90060-4. [DOI] [PubMed] [Google Scholar]
Vale RD. The molecular motor toolbox for intracellular transport. Cell. 2003;112:467–480. doi: 10.1016/s0092-8674(03)00111-9. [DOI] [PubMed] [Google Scholar]
Valentine MT, Perlman ZE, Gardel ML, Shin JH, Matsudaira P, Mitchison TJ, Weitz DA. Colloid surface chemistry critically affects multiple particle tracking measurements of biomaterials. Biophysical Journal. 2004;86:4004–4014. doi: 10.1529/biophysj.103.037812. [DOI] [PMC free article] [PubMed] [Google Scholar]
Veigel C, Bartoo ML, White DCS, Sparrow JC, Molloy JE. The stiffness of rabbit skeletal actomyosin cross-bridges determined with an optical tweezers transducer. Biophysical Journal. 1998;75:1424–1438. doi: 10.1016/S0006-3495(98)74061-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang X, Schwarz TL. The Mechanism of Ca2+-Dependent Regulation of Kinesin-Mediated Mitochondrial Motility. Cell. 2009;136:163–174. doi: 10.1016/j.cell.2008.11.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
Weber SC, Spakowitz AJ, Theriot JA. Nonthermal ATP-dependent fluctuations contribute to the in vivo motion of chromosomal loci. Proc Natl Acad Sci U S A. 2012;109:7338–7343. doi: 10.1073/pnas.1119505109. [DOI] [PMC free article] [PubMed] [Google Scholar]
Wilhelm C. Out-of-Equilibrium Microrheology inside Living Cells. Phys Rev Lett. 2008;101:028101. doi: 10.1103/PhysRevLett.101.028101. [DOI] [PubMed] [Google Scholar]
Wu PH, Hale CM, Chen WC, Lee JSH, Tseng Y, Wirtz D. High-throughput ballistic injection nanorheology to measure cell mechanics. Nat Protoc. 2012;7:155–170. doi: 10.1038/nprot.2011.436. [DOI] [PMC free article] [PubMed] [Google Scholar]
Yamada S, Wirtz D, Kuo SC. Mechanics of living cells measured by laser tracking microrheology. Biophysical Journal. 2000;78:1736–1747. doi: 10.1016/S0006-3495(00)76725-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Zhou EH, Trepat X, Park CY, Lenormand G, Oliver MN, Mijailovich SM, Hardin C, Weitz DA, Butler JP, Fredberg JJ. Universal behavior of the osmotically compressed cell and its analogy to the colloidal glass transition. Proc Natl Acad Sci U S A. 2009;106:10632–10637. doi: 10.1073/pnas.0901462106. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials