Long-Range Force Transmission in Fibrous Matrices Enabled by Tension-Driven Alignment of Fibers (original) (raw)
Abstract
Cells can sense and respond to mechanical signals over relatively long distances across fibrous extracellular matrices. Recently proposed models suggest that long-range force transmission can be attributed to the nonlinear elasticity or fibrous nature of collagen matrices, yet the mechanism whereby fibers align remains unknown. Moreover, cell shape and anisotropy of cellular contraction are not considered in existing models, although recent experiments have shown that they play crucial roles. Here, we explore all of the key factors that influence long-range force transmission in cell-populated collagen matrices: alignment of collagen fibers, responses to applied force, strain stiffening properties of the aligned fibers, aspect ratios of the cells, and the polarization of cellular contraction. A constitutive law accounting for mechanically driven collagen fiber reorientation is proposed. We systematically investigate the range of collagen-fiber alignment using both finite-element simulations and analytical calculations. Our results show that tension-driven collagen-fiber alignment plays a crucial role in force transmission. Small critical stretch for fiber alignment, large fiber stiffness and fiber strain-hardening behavior enable long-range interaction. Furthermore, the range of collagen-fiber alignment for elliptical cells with polarized contraction is much larger than that for spherical cells with diagonal contraction. A phase diagram showing the range of force transmission as a function of cell shape and polarization and matrix properties is presented. Our results are in good agreement with recent experiments, and highlight the factors that influence long-range force transmission, in particular tension-driven alignment of fibers. Our work has important relevance to biological processes including development, cancer metastasis, and wound healing, suggesting conditions whereby cells communicate over long distances.
Introduction
Cells in fibrous matrices sense and respond to mechanical forces over distances many times their diameter. Although cells cultured on polyacrylamide gels fail to sense substrate stiffness or the presence of other cells beyond a distance of ∼20–25 _μ_m (1–3), long-range force sensing (250–1000 _μ_m) between cells in fibrous gels has been appreciated for decades. Stopak and Harris and later Miron-Mendoza et al. placed fibroblast explants into collagen gels and observed collagen realignment parallel to the connecting axes between explants, with translocation of collagen fibrils toward the explants, shortening of the axes, and fibroblast migration across the newly aligned collagen-fibril bridges (4,5). Others have shown that single cells, as well as cell colonies, are able to align and compact collagen fibers over long distances (6,7) and that these aligned fibers are required for long-range cell-cell interactions (7,8). More recently, Winer et al. showed that single cells in fibrin gels were able to stiffen the gels both locally and globally (9).
Long-range force transmission has significant relevance in normal physiology and pathophysiology over a range of length scales. At the level of single cells, mechanically based cell-cell communication over long distances regulates patterning, including both tube formation and the detachment of cells from multicellular aggregates (7,9,10). At the tissue level, long-range force transmission may drive the development of tendons, ligaments, and muscle (4); it has the potential to mediate other large-scale architectural rearrangements typical of developmental processes as well (11). Long-distance force transmission between groups of cells, or cells and the matrix, may also mediate tissue-scale rearrangements in pathological settings such as pulmonary fibrosis and liver cirrhosis (12,13). There are some experimental data implicating it in cancer metastasis (7,14,15), although other work suggests caveats to these findings (16).
Previous studies attempting to explain the mechanism of long-range force transmission have implicated applied strain and the presence of a fibrous network (6). Although some investigators suggest that the strain-hardening properties of fibrous materials could explain long-range mechanical communication (9,17), more recent evidence (8,18) suggests that the fibrous nature of the extracellular matrix (ECM), specifically the presence of cross-linked fibers (primarily collagen), is critical for transmission of force over scales that are 10–20 times the diameters of the cells. Ma et al. used microscopy images to develop finite-element models that included fibers that bridge pairs of interacting cells in a collagen matrix (8). They found that including discrete fibers along with a nonlinear strain-hardening matrix leads to long-range transmission of forces, with the fibers carrying most of the loads and nonlinear and isotropic matrix mechanics playing a relatively minor role. In other words, the fibrous nature of the collagen matrix, rather than a nonlinear response to force, determined the extent of force transmission. It should be noted that since the fiber distribution in the model of Ma et al. was obtained from experiments, the model cannot predict how an initially random fiber network under strain yields reinforcing fibrous structures in response to forces from contractile cells. Multiscale finite-element models, where discrete fiber networks are employed to determine forces at nodes, have also been used to study force transmission in fibrous gels (18). It has also been observed that the shapes of cells play a crucial role in the transmission of forces. Fabry and co-workers reported that invasive tumor cells are elongated and spindle-shaped compared to their noninvasive counterparts and they observed, through displacements of beads in the matrices, that force transmission is much longer-ranged in the former than in the latter case (19). Elongated cells have also been found to be polarized (i.e., the forces they exert are aligned with their long axes). Although these and other studies (20,21) have considered the role of individual-cell and matrix elements in force transmission, none have addressed in an integrated way the impact of fiber realignment, the shape of cells, the anisotropy and magnitude of contractile forces, and the mechanical properties of fibrous gels on the long-range nature of force transmission.
In this work, we develop to our knowledge a new nonlinear and anisotropic constitutive description of fibrous materials that accounts for long-range force transmission. We incorporate the fact that these fibrous materials stiffen preferentially along the directions of tensile principal stretches. We start from random and isotropic distributions of fibers, and from there study how mechanical anisotropy evolves as loads are applied. We have developed a finite-element implementation of this constitutive law and have used it to study interactions of cells in three-dimensional (3D) matrices and on fibrous substrates. In the case of simple cell geometries (spheres, ellipsoids, polarized versus nonpolarized), we solve for the stress fields by analytic methods. Thus, we describe here an approach to systematic determination of the role of fiber alignment, nonlinear elasticity of fibers, cell shape, and polarization of contraction in long-range force transmission. We show that collagen fiber alignment is critical and that anisotropy in cell shape and contraction result in significantly greater collagen alignment and force transmission.
A New Constitutive Law for Fibrous Matrices
We first developed a new constitutive law to explain the behavior of fibrous matrices and to serve as the foundation for further simulations examining the impact of cells and their contractility on these matrices. To start, we carried out discrete fiber simulations (see Section A in the Supporting Material). We assume that when a fibrous matrix undergoes stretch, there are two families of fibers: the set of fibers that align with the direction of the maximum principal stretch as the material is loaded (Fig. 1 b, red) and the set of fibers that do not align with the applied load and thus display an isotropic mechanical response. When we plot stress versus strain for such collagen networks (Fig. 1 c), we find that there is a knee in the curve representing strain stiffening. This knee, which according to our simulations requires the presence of both families of fibers, is in good accord with experimental data (22) (Fig. 1 c). For strains below a typical threshold (typically 5–10%, depending on collagen concentration and cross-linking), the network shows a nearly isotropic response, without stiffening. Beyond this threshold, there is a transition to a stiffening response concomitant with the formation of aligned fibers in the direction of maximal tensile stretch. With increased loading, the numbers of these highly aligned fibers increase, leading to the observed stiffening and to the alignment shown in the inset of Fig. 1 b.
Figure 1.
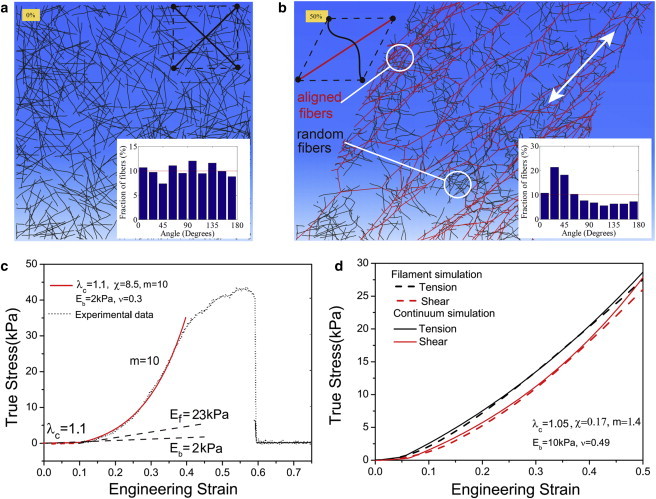
(a and b) Discrete fiber simulations of a random fiber network before (a) and after (b) shear deformation (50% shear strain). Insets show that the initial random distributions of fibers (a) develop a peak close to the 45° orientation (b), which coincides with the direction of maximum principle stretch. Fibers (with axial strain >1%) that reorient along the tensile loading axis are colored red. The white arrow in b indicates the direction of principle tensile stretch. (c) The stress-strain curves of collagen I under uniaxial deformation derived experimentally (from Roeder et al. (22)) (black) are in good accord with those predicted from our constitutive law (red). The knee indicates strain stiffening at strains of ∼10%. The material parameters that provide the best fit to the experimental data are λc=1.1,χ=(1+ν)(1−2ν)Ef/(1−ν)Eb=8.5,m=10,Eb=2kPa,ν=0.3. (d) Stress-strain curves under uniaxial tension (black) and shear (red) deformations from discrete fiber simulations and from our constitutive law. The material parameters that provide the best fit to the discrete simulations are λc=1.05,χ=0.17,m=1.4,Eb=10kPa,ν=0.49. To see this figure in color, go online.
To capture the presence of these two distinct families of aligned and isotropic fibers when developing our constitutive law, we assume that the overall energy density, W, of the collagen network consists of two contributions (23):
| W=Wb+WfWb=μ2(I¯1−3)+κ2(J−1)2Wf=∑a=13f(λa). | (1) |
|---|
Here, the first term, Wb(I¯1,J), captures the isotropic response, which we describe using the neo-Hookean hyperelastic model, where κ and μ are the initial bulk and shear moduli, respectively, and _W_f is the contribution from the aligned fibers. In the above equation, F ij = ∂x i/∂X j is the deformation gradient tensor, where X and x represent the reference and deformed coordinates, respectively, and C = F T F and B = FF T are the right and left Cauchy-Green deformation tensors, respectively. The invariants J, C, and B can be defined as (23)
| J=det(F)C=∑a=13λa2Na⊗NaB=∑a=13λa2na⊗na, | (2) |
|---|
where _λ_1, _λ_2, _λ_3 are the principle stretches, I¯1 is the first invariant of the deviatoric part of C, and N a and n a are the unit vectors in the principle stretch orientations in the reference state and deformed state, respectively. The functional form f(λ a) is chosen such that the system stiffens only in the direction of tensile principal stretches (beyond a critical value of tensile stretch, as observed in experiments and discrete fiber simulations). This is accomplished by decomposing the Cauchy stress (true stress), σ, into isotropic (σ b) and fibrous contributions (σ f) (23):
| σ=2F⋅(∂W/∂C)⋅FT/J,σ=σb+σfσb=κ(J−1)I+μdev(B¯)/Jσf=1J∑a=13∂f(λa)∂λaλa(na⊗na), | (3) |
|---|
where I is the identity tensor and B¯=B/J2/3 is the left modified Cauchy-Green tensor. The principal components of the filamentous contribution can be obtained from
| ∂f(λa)∂λa={0λa<λ1Ef(λa−λ1λ2−λ1)n(λa−λ1)n+1,λ1≤λa<λ2Ef[λ2−λ1n+1+(1+λa−λ2)m+1−1m+1],λa≥λ2, | (4) |
|---|
chosen such that the principal stresses vanish below the critical (tensile) principal stretch, _λ_c, and show a stiffened response characterized by the modulus _E_f and a strain hardening exponent, m. To ensure that the derivative of the stress-strain curve is continuous near the transition point, a smooth interpolation function is used between (_λ_c − _λ_t/2,_λ_c + _λ_t/2), where the transition width is _λ_t = 0.25_λ_c and the transition exponent is n = 5, and we have defined _λ_1 = _λ_c − _λ_t/2, _λ_2 = _λ_c + _λ_t/2. The functional form f(λ a), which leads to Eq. 4, is provided in Section B of the Supporting Material.
Biophysical basis for the constitutive law
The strain energy function and the stresses we propose depend on two parameters (the initial bulk and shear moduli) for the isotropic response and three parameters (the critical stretch, λ c; the initial modulus of the fibrous phase, E f; and the strain-hardening exponent of the fibrous phase, m) for the anisotropic response. We have determined these parameters for collagen networks by comparing the stress-strain curves for uniaxial and shear deformation from discrete network simulations with our constitutive model (Fig. 1 d). The biophysical basis underlying the constitutive law postulated here is the presence of two families of fibers, clearly evident from the discrete fiber simulations: the first family (Fig. 1 b, red) is aligned with the principal axes (Fig. 1 b, white arrow) and the fibers are in a state of tension, whereas the second family of fibers (black, in compression) provide an isotropic background stress that opposes alignment. The stress at any material point is the sum of the stresses from these two components (Eq. 3). The degree of the interaction between the two families of fibers is determined by the parameter E f/E b: when this ratio is large, the isotropic part provides little resistance to alignment. A systematic study of the range of force transmission as a function of this parameter is given below. With the two families of fibers, our model captures the key features of the response of a collagen network to force, in particular the knee and the subsequent hardening response.
Results
Having developed a constitutive law, we use it in analytical calculations and finite-element simulations to study the impact of the material parameters of the isotropic and fibrous components of the matrix, the shape of cells, and the polarization of cell contractile forces on force transmission in fibrous matrices. We have simulated cells on fibrous as well as linear and nonlinear substrates to identify the key factors that allow for long-range force transmission in fibrous matrices. All simulations were carried out using the finite-element package Abaqus (24) by implementing the material model of the new fibrous constitutive law in a user material subroutine (details of the implementation are given in Section B of the Supporting Material). The numerical simulations were performed in a finite-deformation setting (i.e., the effects of geometry changes on force balance and rigid-body rotations are explicitly taken into account).
Force transmission in 3D matrices depends on the fibrous components and the magnitude of the contractile strains
To determine the impact of the fibrous component of the matrix on force transmission, we consider matrices that are linearly elastic, hyperelastic (neo-Hookean), and fibrous (characterized by the constitutive law (Eq. 4)). We consider the case of a spherical cell or contractile explant of radius R in a 3D matrix contracting isotropically and inwardly by an amount _u_0 (contractile strain = _u_0/R). In our calculations, we apply the boundary condition on the radial displacement (u_0) at the cell-matrix interface and determine the elastic fields in the matrix by applying both symmetry (or periodic) and fixed (where all displacements and rotations vanish) conditions at the top and bottom surfaces of the matrix located at a distance L ∼ 10_R from the center of the cell. In the case of the linearly elastic material, the scaled displacement fields (u/_u_0) are independent of the magnitude of the contractile strain, _u_0, whereas this is not the case for nonlinear materials. For both the neo-Hookean and the isotropic response of the fibrous material, the material parameters are chosen such that the Young’s moduli and Poisson ratios are the same as that of the linear elastic material at small strains.
We find that the displacement fields decay rapidly within a distance on the order of the cell diameter in nonfibrous materials (Fig. 2 a, black, blue, and green curves), whereas the displacement fields are long-range in the fibrous matrix (Fig. 2 a, red and orange curves). The range of interaction in the fibrous matrix is >20 times the radius of the cell, as demonstrated by the fact that the boundary condition (periodic versus fixed) has an impact on the displacement fields; the cells in this case are able to feel its periodic image, since the displacement field does not completely vanish at the boundaries.
Figure 2.
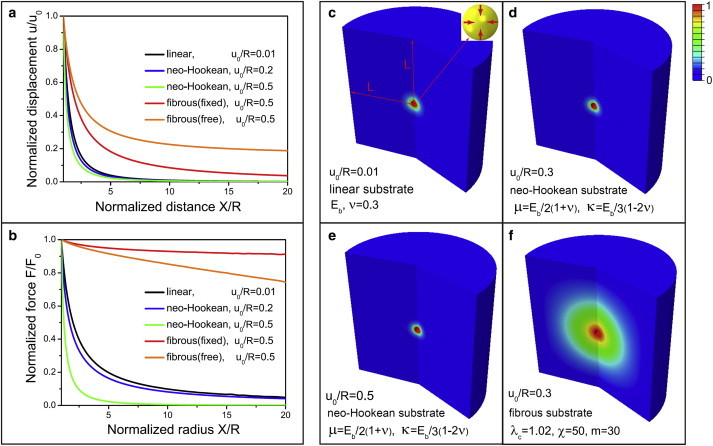
Displacement and force profiles in 3D linearly elastic, neo-Hookean, and fibrous matrices with a spherical and isotropically contracting cell of radius R. (a and b) Normalized radial displacement u(X)/u(R) and force F(X)/F(R) as functions of the normalized distance X/R (the boundaries are located at a distance L = 100_R_) from the center. We have chosen the critical stretch, λ c = 1, fibrous modulus χ = 50, and strain-stiffening parameter m = 0 for the fibrous matrix. (c_–_f) Contour plots of normalized radial displacement u(X)/u(R) for fibrous matrices with χ = 50 and m = 30, E b = 2 kPa, and Poisson’s ratio ν = 0.3 (where the latter two parameters are the same as E b and ν for linear matrices). For neo-Hookean matrices, μ/E b = 1/2(1 + ν), κ/E b = 1/3(1 − 2_ν_). To see this figure in color, go online.
To gain further insight into the range of elastic fields, we plotted the total force, F(X) = σ(X)4_πX_2, normalized by the force at the cell-matrix interface (Fig. 2 b). We find that the decay of the total force in strain-hardening hyperelastic matrices is more rapid than in the case of the linearly elastic material, whereas the transmission of force is very long-range in fibrous matrices. In Section C of the Supporting Material, we have derived a closed-form expression for the decay of force distribution as a function of the material parameters of the fibrous phase. These analytical calculations and the simulations in Fig. 2, c_–_f, clearly show that the fibrous components, and not the isotropic strain-hardening response, lead to long-range force transmission.
Force transmission in 3D matrices depends on the shape of cells or explants and cell polarization
Next, we consider the effect of shape and contraction anisotropy on force transmission in elastic and fibrous matrices. Unlike prior work that focused on the role of shape and cell polarization in linear elastic materials (25,26), here we consider fibrous materials described by the constitutive laws derived above (A New Constitutive Law for Fibrous Matrices). We model elongated cells as prolate spheroids described by the shape (x/a)2 + (y/a)2 + (z/b)2 = 1. Here, a and b represent the length of the semiminor and semimajor axes, respectively, of the prolate spheroid. The polarization of active forces is modeled by assuming that the contractile strains (determined by molecular motors and regulation of adhesion sites) along the long axis of the spheroid, ε b, are greater than the strain along the short axis, ε a. To compare shapes with different aspect ratios, α = 1 − a/b, and strain polarizations, β=(1−(1−εb)/(1−εa))/(1−V1/V0), we assume that the volume of the cells before (V0=4πa2b/3=4πR3/3) and after contraction (V1=4π(1−εa)2(1−εb)R3) is the same in all cases. Note that α = 0 corresponds to a sphere, whereas α ∼ 1 is a highly elongated prolate spheroid. In a similar way, β = 0 corresponds to isotropic contraction, whereas β = 1 represents a fully polarized cell (Fig. 3, a_–_d)). Here, R is the radius of the sphere as α = 0. The above definitions also provide a definition for the size of a cell, R = _a_2/3_b_1/3, which is the geometric mean of the lengths of the semimajor and semiminor axes of the elongated cell (which can be considerably shorter than the length of the semimajor axis for a highly elongated cell).
Figure 3.
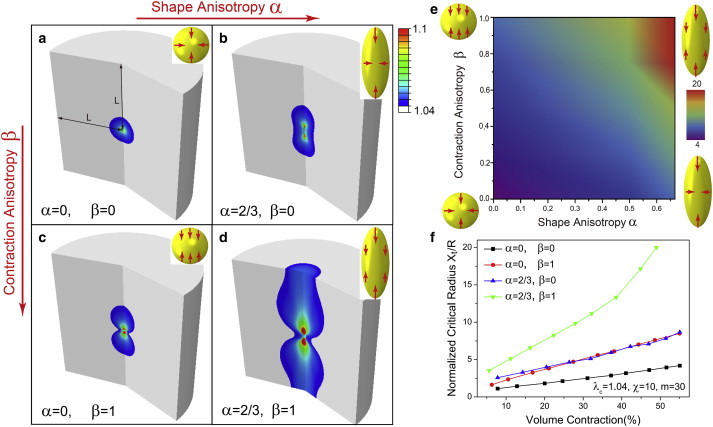
Influence of shape and contraction anisotropies (α and β, respectively) of contractile cells on distance X t/R over which forces are transmitted (measured by the extent of aligned fibrous regions in the matrices). (a_–_d) Contour plots of aligned (colored) and isotropic (white) regions for the four cases with α = 1, 2/3, and β = 0, 1. Colors (blue to red) represent maximum principle stretches (1.04–1.1). (e) Contour plots of X t/R as a function of shape anisotropy, α, and contraction anisotropy, β. Colors (blue to red) represent X t/R(4–20). (f) Normalized transmission distance X t/R versus volume contraction for the four cases in a_–_d. Yellow ellipsoids with red arrows represent contractile cells with different values of α and β. Material parameters for the fibrous matrix are λ c = 1.04, χ = 50, and m = 30. The volume contraction is 55% for all the cases (a_–_d). The matrix size is 20 × the contractile cell radius (L/R = 20) and the symmetry boundary conditions are applied at all boundaries. To see this figure in color, go online.
The effect of shape and contraction and shape anisotropies on the range of force transmission in fibrous matrices is shown in Fig. 3, a_–_d. Here, the colored regions represent the extent of the aligned fibrous region, where the fibers are aligned with the tensile principal axis of strain tensor. We find that whereas shape and contraction anisotropies lead to an increase in the extent of the fibrous region, the effect is significantly amplified when both these factors are present simultaneously. We can understand this by noting that both shape and contraction anisotropies lead to concentration of tensile strains along the long axes of the cells. However, this effect is considerably magnified when the shape is elongated and the cell is polarized; significant concentration of tensile stresses in this case (Fig. 3 d) leads to formation of extended regions where fibers are aligned. A heat map of the range of force transmission as a function of these parameters is given in Fig. 3 e for the case where the volume contraction is 1 − _V_1/_V_0 = 55%. We find that the extent of the fibrous region can be as high as 20 times the characteristic size of the fully polarized cells for α = 2/3, as has been observed in several studies (8,18). The influence of the magnitude of volume contraction of the cell on the range of force transmission is plotted in Fig. 3 f: our simulations show that the range of force transmission generally increases with an increase in overall contractile strain, although the effect is much more pronounced in elongated and polarized cells on account of the stress concentration effects discussed above. Thus, our analytical calculations and simulations collectively show that in addition to the fibrous components of the matrix, elongated cells and polarized contraction lead to long-range force transmission.
Long-range transmission in 3D matrices varies with the stiffness and strain-hardening exponent of the fibrous component and the critical strain for fiber formation
We show in this section that in the material model we have developed, the relative contributions of the fibrous and isotropic strain-hardening components to the overall mechanical response depends on three parameters: the ratio of the initial elastic moduli of the two components, _E_f/_E_b, the strain-hardening exponent of the fibrous phase, m, and the critical strain for the onset of the fibrous response. A more pronounced fibrous response is obtained when _E_f/_E_b and m are large and when the critical stretch, _λ_c, is small (leading to an early transition to the aligned fiber phase). The extent of the aligned fibrous region that surrounds an elongated (α = 2/3) and fully polarized (β = 1) cell is shown in Fig. 4, a_–_d, as a function of the material parameters that characterize the fibrous phase. The simulations show that the range of force transmission increases with increasing modulus and the strain-hardening exponent of the fibrous phase and with decreasing values of the critical strain for transitioning to the fibrous phase. These parameters are determined by the density of fibers, the numbers of cross-linkers per fiber, and the porosity of the fibrous gels, as discussed above.
Figure 4.
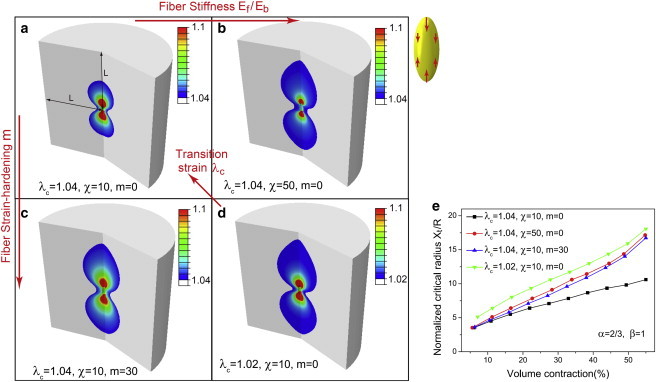
Influence of material parameters of fibrous matrices on the transmission distance X t/R. (a_–_d) Contour plots of aligned (colored) and isotropic (gray) regions for the four cases with λ c = 1.02 − 1.04, χ = 10 − 50, and m = 0 − 30. Colors represent maximum principle stretch (1.04 − 1.1) (blue to red). (e) Normalized transmission distance, X t/R, versus volume contraction for the four cases in a_–_d. Shape and contraction anisotropies are α = 2/3 and β = 1, and the volume contraction is 55% for all the cases. The matrix size is 20 × the contractile cell radius (L/R = 20) and the symmetry boundary conditions are applied at all boundaries. To see this figure in color, go online.
Cells sense farther into fibrous substrates than into linear and strain-hardening substrates
Recent work has demonstrated that fibroblasts sense deeper into collagen and fibrin gels (typically >65 μ_m) than they do into polyacrylamide gels (characteristically <5 μ_m) (18). To determine the characteristics of these gels responsible for characteristic sensing distances, we carried out calculations to determine cell sensing distance as a function of the thickness of gels constrained on one of the sides by a rigid (glass) substrate. Following methods used in an earlier work (1), we assume that the cell is circular and that it contracts radially inward by pulling on the cell-substrate boundary. We apply displacement boundary conditions to this boundary (radial displacement of u(R)/R = 0.2) and the bottom surface is clamped to the underlying glass substrate. All other surfaces are free of any traction. As in earlier work (1), we find that in both linear elastic and nonlinear strain-hardening materials, the sensing distance is close to the radius of the cell, R. Increasing the gel thickness, H, by a factor of 5, from 2_R/3 to 10_R/3, has very little impact on the spatial profiles of the displacement fields. On the other hand, cells are able to sense much deeper into fibrous gels, as evidenced by the slower decay of the displacement fields of cells on thicker substrates. Our results for the sensing distances (Fig. 5 g) show that cells can sense up to 8 times their radii on fibrous gels compared to 1.8 times their radii on strain-hardening substrates.
Figure 5.
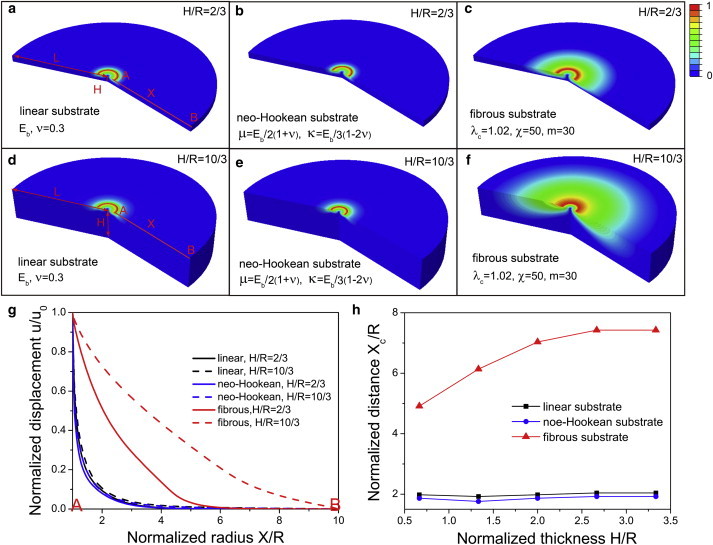
Mechanosensing distances for contractile cells on linear, neo-Hookean, and fibrous substrates with thickness H = 2_R_/3–10_R_/3, where R is the radius of the cell: (a_–_f) Contour plots of the normalized radial displacement, u(X)/_u_0 (_u_0 = u (R)), with normalized thickness H/R = 2/3 (a_–_c) and H/R = 10/3 (d_–_f). (g) Normalized radial displacement, u(X)/_u_0, on the substrate surface as a function of the normalized distance X/R. (h) Normalized force-transmission distance X c/R as a function of the normalized-thickness, H/R (chosen with the criterion that the displacement fields decay by 90%, or u(X c)/_u_0 = 0.1). Circles (black line), squares (blue line), and triangles (red line) indicate linear, neo-Hookean, and fibrous substrates, respectively. Material parameters for the fibrous matrix are λ c = 1.02, χ = 50, and m = 30. The substrate radius is 10 × the cell radius (L/R = 10) and the bottom boundary is clamped. To see this figure in color, go online.
Cells sense other cells located at distances ∼20 times their size in fibrous 3D matrices
Interactions between pairs of cells play a key role in cell clustering during morphogenesis, as well as in pathological processes such as fibrosis, wound healing, and metastasis. Based on our results (presented above) regarding the elastic fields of cells in different types of matrices, it is reasonable to guess that cell-cell interactions are significant when their separations are of the order of twice the sensing distance of a single cell. We verified this hypothesis by explicitly simulating the interactions between two cells in 3D fibrous and nonfibrous matrices, as well as on substrates. The clear role of fibrous matrices in mediating cell-cell interactions is shown in Fig. 6, where significant overlap and alignment of strain fields are observed for pairs of cells located in fibrous matrices at a distance of 10 times their size. There is no overlap of strain fields for cells on nonfibrous substrates. Using these simulations, we confirm that cell-cell interactions become significant when cell spacing is twice the sensing distance, which is in agreement with the results shown in Fig. 6. Color represents the normalized radial displacement (0 − 1) (increasing from blue to red). The geometry and boundary conditions in Fig. 6, b and e, are the same as those in Figs. 2 f and 5 f, respectively. Our simulations also clearly show the formation of collagen lines observed experimentally between pairs of cells (4,5); we find that that the alignment of fibers coincides with the line that connects the centers of the two contractile cells both in 3D matrices and on substrates (Fig. 6, c and e). Thus, we find that fibrous, but not neo-Hookean, matrices enable cells to form collagen lines and interact mechanically with other cells at long range.
Figure 6.
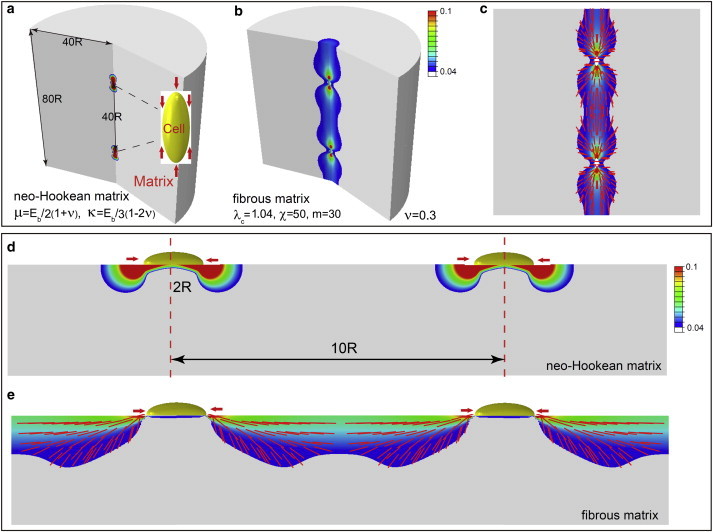
Interactions of pairs of contractile cells in neo-Hookean and fibrous matrices: (a and b) Contour plots of maximum principle strain in 3D matrices. (c) Vector plots of maximum principle strain (which coincides with the orientation of the collagen lines) in a 3D fibrous matrix. (d and e) Contour plots of maximum principle strain on 2D substrates. Colors (blue to red) represent maximum principle strain (0.04–0.1). Lengths of red lines represent the magnitude of the maximum principle strain (0.04–1) and their orientations show the directions of fiber alignment. For the fibrous matrices, colored and gray regions represent aligned fibrous and isotropic regions, respectively. We have chosen λ c = 1.04, χ = 50, and m = 30 for the fibrous material. To see this figure in color, go online.
Summary and Discussion
In summary, we have developed a new constitutive law for fibrous matrices that predicts several key cell behaviors.
- Both shape and contraction anisotropy are important for long-range force transmission. These features of cells lead to stress concentration at the poles, which in turn leads to fiber alignment. Elongated prolate spheroidal cells with polarized contraction are able to sense the mechanical environment over much larger distances than spherical cells exhibiting diagonal contraction.
- Tension-driven fiber alignment plays a crucial role in mechanosensing: small critical stretch for fiber alignment (_λ_c), large fiber stiffness (χ), and fiber strain-hardening behavior (m) enable long-range interactions.
- Cells in 3D fibrous matrices and cells on 2D fibrous substrates sense rigid boundaries and other cells over relatively long distances compared to cells in and on linear and strain-hardening isotropic materials. The range of force transmission increases with increasing contractility for cells in fibrous matrices, whereas increasing contractility of cells cannot lead to enhancement of mechanosensing distances in linear and strain-hardening materials.
- Cells in 3D fibrous matrices sense rigid boundaries over 10 times their diameters and other cells over 20 times their diameters. Cells on 2D fibrous substrates sense radial rigid boundaries up to 8 times their radii and thicknesses up to 3.5 times their radii. Sensing distances can be further enhanced by increasing cell elongation, polarization, and contractility.
These findings are highly relevant biologically. They suggest that the presence of a fibrous matrix, as well as the material properties of that matrix, determine the nature of the mechanical interactions between groups of cells and between cells and boundaries in a range of settings including development, cancer metastases, and wound healing and fibrosis. This is consistent with the experimental observation that increased collagen cross-linking is associated with many of these processes, and it suggests that studying the impact of other matrix proteins on fibrous collagen matrices may yield important insights into normal biology and pathology. In a similar way, elongated cell shape and polarized cell contractility enhance long-range mechanical interactions; our results are consistent with experimental observations that cells involved in many of these processes are elongated and contractile (and may have undergone an epithelial to mesenchymal transition).
Derivation of the constitutive law
The constitutive law for fibrous matrices we have proposed is nonlinear with respect to the orientation and magnitudes of the principal strains. The direction of the stiffened fibrous response coincides with the principal orientations whose principal strains are above a critical threshold. As we show below, these two features are critical for capturing the key features of long-range force transmission observed in experiments. In this regard, the detailed form of the constitutive law of the matrix is not crucial as along as it captures the orientational anisotropy and stiffening that naturally arises along the principal directions upon loading. We have verified this idea by studying force transmission in matrices (Fig. 7) with other functional forms of response (see Section D in the Supporting Material), but those retain the general features of anisotropic stiffening that coincides with the principal strain orientations. In particular, our constitutive law shares some common features with modified Cauchy-Green deformation tensors (23,27), but there are some crucial differences that are essential to obtaining long-range force transmission. In the previously published works, the collagen network is modeled as a hyperelastic material reinforced by two families of fibers whose orientations depend on the directions of principal stress (see Section D of the Supporting Material). Note, however, that unlike our formulation, their constitutive laws are based on the invariants of the modified Cauchy-Green deformation tensor. As we show in Section E of the Supporting Material, long-range force transmission cannot be observed when modified Cauchy-Green deformation tensors are used. We have therefore modified the constitutive law such that we use the principal stretches, which are the eigenvalues of the Cauchy-Green deformation. However, we have retained the condition that collagen fibers form only along those directions where the stretches are tensile. In essence, the law previously proposed relies on the deviatoric components of the dyadic ni⊗ni (n i being the principal stretch), which, as we show in Section E of the Supporting Material, cannot give long-range force transmission, since an incompressible material is similar to an isotropic material without tension-driven alignment of collagen fibers (Eq. C10 in the Supporting Material).
Figure 7.
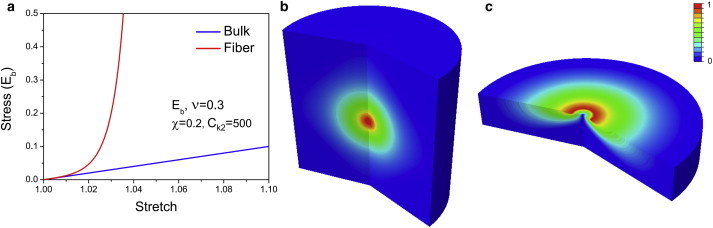
Force transmission for the material with strain energy function similar to that given in works by Holzapfel and colleagues (23,27). (Eb,ν=0.3,χ=0.2,Ck2=500). (a) Blue and red curves represent bulk and fibrous contributions, respectively, to the stress. (b) Contour plot of normalized radial displacement u(X)/u(R) in fibrous matrices (which is similar to the result in Fig. 2f). (c) Contour plot of normalized radial displacement u(X)/u(R) on a fibrous substrate, which is similar to the result in Fig. 5f. Colors (blue to red) represent the normalized radial displacement (0–1). The geometry and boundary conditions for b and c are the same as in Figs. 2f and 5f, respectively. To see this figure in color, go online.
Sensing of thickness and lateral boundaries by cells on substrates
Our results are consistent with published experimental data on cell sensing distances. Both computational modeling (1,2) and experimental observations (3,28,29) suggest that cells cultured on polyacrylamide gels (linear elasticity) cannot sense nearby cells beyond one cell length apart (<40 _μ_m) (1) and substrate thickness beyond half a cell length away (<20 _μ_m) (2). In contrast to cells on polyacrylamide gels, human mesenchymal stem cells and 3T3 fibroblasts on fibrin gels were shown to sense and respond to mechanical signals up to five cell lengths away (9), consistent with the results shown in Fig. 5 g. Leong et al. (17) studied the role of collagen I gel thickness on the fate of human mesenchymal stem cells and found that the mechanosensing distance for these cells is ∼130 _μ_m, which corresponds to ∼4.3 times cell radii, also in agreement with our work. Recently, Rudnicki et al. designed sloped collagen and fibrin gel cultures to investigate thickness sensing. They found that human lung fibroblast and 3T3 fibroblast cell areas gradually decrease as gel thickness increases from 0 to 150 _μ_m, with spreading affected on gels as thick as 150 _μ_m (18). Since the spreading radius in the case of the 150-_μ_m-thick gel is 20 _μ_m, the mechanosensing distance for substrate thickness is 7.5 times cell radii (18). Although these multiscale simulations suggest sensing distances of 3.7 times cell radii (sensing distance of 50 _μ_m for a cell radius of 13.4 _μ_m), our results show that cells sense boundaries up to 3.5 times their radii on fibrous substrates compared to 1.8 times their radii on strain-hardening substrates (Fig. 5 h). Thus, our work provides a good estimate for sensing distances on fibrous substrates. Although most of the experimental work has focused on thickness sensing, recently Mohammadi et al. developed a model system to examine sensing of lateral boundaries in floating thin collagen gels populated with 3T3 fibroblasts (30). They found that cell-induced deformation fields extended to, and were resisted by, the grid boundaries 250 _μ_m away (30), suggesting a sensing distance for lateral rigid boundaries of ∼8 times cell radii. These results are consistent with our calculations in Fig. 5, g_–_h, that show that lateral and thickness sensing distances are similar in magnitude.
Mechanosensing in 3D gels
Our results are consistent with published experimental work on the importance of cell shape, cell contractility, contractile strains, and local fiber alignment on long-range force transmission. Gjorevsk and Nelson examined the strain fields around engineered 3D epithelial tissues in collagen I gels. They found that linear elasticity cannot explain the long-range nature of the strain fields but reported that mechanical heterogeneities caused by stiffening near the poles of elongated contractile epithelial tissues can explain the decay of strain fields (31). Our results clearly show that long-range displacement fields within matrices can be captured by tension-driven local fiber alignment, and that heterogeneities result from the anisotropic shape of the cell domain and the anisotropic contraction of cells (Fig. 3). Cell contractility results in reorganization of the ECM to provide contact guidance that facilitates 3D migration and invasion (4,5,32). The fiber alignments observed between nearby cells in 3D matrices (4,5,32) are clearly shown in our FEM simulations (Fig. 6 c). Experimental work has shown that treatment of cells to abolish actomyosin contractility leads to dissolution of the collagen lines, in agreement with our results that show that the magnitude of contractile strains plays an important role in determining the range of force transmission. Recent experiments on mammary acini in collagen gels show that they can interconnect by forming long collagen lines up to ∼10 times acini size (7). Guo et al. find that these lines and interactions are initiated by traction forces created by the cells and not by diffusive factors (10). They also found collagen-density-dependent transmission of force up to 10 times cell radii for interacting acini. Our results show that cells in 3D fibrous matrices can sense the radial rigid boundaries up to 10 times their diameters and other cells up to 20 times their diameters (Fig. 3 and Fig. 6, a_–_c), in very good agreement with results from the experiments mentioned here. Furthermore, Ma et al. suggest that the fibrous nature of the ECM leads to reorganization of the collagen fibers, leading to areas of higher fiber density near the cells over relatively long distances (10 cell diameters) (8). The mechanism by which this reorganization proceeds (starting from a random network) is discussed in our work.
Koch et al. studied the effect of anisotropic cell shape and contractility on the range of force transmission in invasive and noninvasive cancer cells (19). They found that both lung and breast carcinoma cells were significantly elongated compared to the noninvasive cells, which were observed to have rounder shapes. Cell shape anisotropy was accompanied by a larger sensing distance, suggesting that directionality of traction forces is important for cancer cell invasion, consistent with our results (Fig. 3).
In sum, we present a new constitutive law that describes the behavior of cells in matrices. All of the parameters for our constitutive law can be obtained either from experiments or from fiber simulations, as shown in Fig. 1, c and d. Our findings are relevant to a variety of normal and pathological processes and, it is important to note, are consistent with an extensive body of experimental work, as highlighted in detail above. We hope that this work will inspire further experiments where the mechanical properties of the ECM are tuned by varying the fiber density and degree of cross-linking to validate our predictions.
Acknowledgments
We thank Tom Lubensky for insightful discussions on fibrous constitutive laws.
Research reported in this publication was supported by the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health under award number R01EB017753 and the U.S. National Science Foundation Grant CMMI-1312392.
The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health or the National Science Foundation.
Supporting Material
Document S1. Model description
Document S2. Article plus Supporting Material
Supporting Citations
References (33–41) appear in the Supporting Material.
References
- 1.Sen S., Engler A.J., Discher D.E. Matrix strains induced by cells: computing how far cells can feel. Cell. Mol. Bioeng. 2009;2:39–48. doi: 10.1007/s12195-009-0052-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Buxboim A., Rajagopal K., Discher D.E. How deeply cells feel: methods for thin gels. J. Phys. Condens. Matter. 2010;22:194116. doi: 10.1088/0953-8984/22/19/194116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Reinhart-King C.A., Dembo M., Hammer D.A. Cell-cell mechanical communication through compliant substrates. Biophys. J. 2008;95:6044–6051. doi: 10.1529/biophysj.107.127662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Harris A.K., Stopak D., Wild P. Fibroblast traction as a mechanism for collagen morphogenesis. Nature. 1981;290:249–251. doi: 10.1038/290249a0. [DOI] [PubMed] [Google Scholar]
- 5.Miron-Mendoza M., Seemann J., Grinnell F. Collagen fibril flow and tissue translocation coupled to fibroblast migration in 3D collagen matrices. Mol. Biol. Cell. 2008;19:2051–2058. doi: 10.1091/mbc.E07-09-0930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Vader D., Kabla A., Mahadevan L. Strain-induced alignment in collagen gels. PLoS ONE. 2009;4:e5902. doi: 10.1371/journal.pone.0005902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Shi Q., Ghosh R.P., Liphardt J.T. Rapid disorganization of mechanically interacting systems of mammary acini. Proc. Natl. Acad. Sci. USA. 2014;111:658–663. doi: 10.1073/pnas.1311312110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Ma X., Schickel M.E., Hart R.T. Fibers in the extracellular matrix enable long-range stress transmission between cells. Biophys. J. 2013;104:1410–1418. doi: 10.1016/j.bpj.2013.02.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Winer J.P., Oake S., Janmey P.A. Non-linear elasticity of extracellular matrices enables contractile cells to communicate local position and orientation. PLoS ONE. 2009;4:e6382. doi: 10.1371/journal.pone.0006382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Guo C.-L., Ouyang M., Shen C.Y. Long-range mechanical force enables self-assembly of epithelial tubular patterns. Proc. Natl. Acad. Sci. USA. 2012;109:5576–5582. doi: 10.1073/pnas.1114781109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ladoux B. Biophysics: cells guided on their journey. Nat. Phys. 2009;5:377–378. [Google Scholar]
- 12.Hinz B., Phan S.H., Gabbiani G. Recent developments in myofibroblast biology: paradigms for connective tissue remodeling. Am. J. Pathol. 2012;180:1340–1355. doi: 10.1016/j.ajpath.2012.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bates J.H.T., Davis G.S., Suki B. Linking parenchymal disease progression to changes in lung mechanical function by percolation. Am. J. Respir. Crit. Care Med. 2007;176:617–623. doi: 10.1164/rccm.200611-1739OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Conklin M.W., Eickhoff J.C., Keely P.J. Aligned collagen is a prognostic signature for survival in human breast carcinoma. Am. J. Pathol. 2011;178:1221–1232. doi: 10.1016/j.ajpath.2010.11.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Levental K.R., Yu H., Weaver V.M. Matrix crosslinking forces tumor progression by enhancing integrin signaling. Cell. 2009;139:891–906. doi: 10.1016/j.cell.2009.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Beck J.N., Singh A., Ewald A.J. The independent roles of mechanical, structural and adhesion characteristics of 3D hydrogels on the regulation of cancer invasion and dissemination. Biomaterials. 2013;34:9486–9495. doi: 10.1016/j.biomaterials.2013.08.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Leong W.S., Tay C.Y., Tan L.P. Thickness sensing of hMSCs on collagen gel directs stem cell fate. Biochem. Biophys. Res. Commun. 2010;401:287–292. doi: 10.1016/j.bbrc.2010.09.052. [DOI] [PubMed] [Google Scholar]
- 18.Rudnicki M.S., Cirka H.A., Billiar K.L. Nonlinear strain stiffening is not sufficient to explain how far cells can feel on fibrous protein gels. Biophys. J. 2013;105:11–20. doi: 10.1016/j.bpj.2013.05.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Koch T.M., Münster S., Fabry B. 3D Traction forces in cancer cell invasion. PLoS ONE. 2012;7:e33476. doi: 10.1371/journal.pone.0033476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Oster G.F., Murray J.D., Harris A.K. Mechanical aspects of mesenchymal morphogenesis. J. Embryol. Exp. Morphol. 1983;78:83–125. [PubMed] [Google Scholar]
- 21.Barocas V.H., Tranquillo R.T. A finite element solution for the anisotropic biphasic theory of tissue-equivalent mechanics: the effect of contact guidance on isometric cell traction measurement. J. Biomech. Eng. 1997;119:261–268. doi: 10.1115/1.2796090. [DOI] [PubMed] [Google Scholar]
- 22.Roeder B.A., Kokini K., Voytik-Harbin S.L. Tensile mechanical properties of three-dimensional type I collagen extracellular matrices with varied microstructure. J. Biomech. Eng. 2002;124:214–222. doi: 10.1115/1.1449904. [DOI] [PubMed] [Google Scholar]
- 23.Holzapfel G.A. Wiley, Chichester; United Kingdom: 2000. Nonlinear Solid Mechanics: A Continuum Approach for Engineering. [Google Scholar]
- 24.Dassault Systemes . Version 6. Dassault Systemes; Providence, RI: 2010. ABAQUS. [Google Scholar]
- 25.Zemel A., Rehfeldt F., Safran S.A. Cell shape, spreading symmetry and the polarization of stress-fibers in cells. J. Phys. Condens. Matter. 2010;22:194110. doi: 10.1088/0953-8984/22/19/194110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zemel A., Rehfeldt F., Safran S.A. Optimal matrix rigidity for stress fiber polarization in stem cells. Nat. Phys. 2010;6:468–473. doi: 10.1038/nphys1613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Holzapfel G.A., Gasser T.C., Ogden R.W. A new constitutive framework for arterial wall mechanics and a comparative study of material models. J. Elast. 2000;61:1–48. [Google Scholar]
- 28.Maloney J.M., Walton E.B., Van Vliet K.J. Influence of finite thickness and stiffness on cellular adhesion-induced deformation of compliant substrata. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;78:041923. doi: 10.1103/PhysRevE.78.041923. [DOI] [PubMed] [Google Scholar]
- 29.Merkel R., Kirchgessner N., Hoffmann B. Cell force microscopy on elastic layers of finite thickness. Biophys. J. 2007;93:3314–3323. doi: 10.1529/biophysj.107.111328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Mohammadi H., Janmey P.A., McCulloch C.A. Lateral boundary mechanosensing by adherent cells in a collagen gel system. Biomaterials. 2014;35:1138–1149. doi: 10.1016/j.biomaterials.2013.10.059. [DOI] [PubMed] [Google Scholar]
- 31.Gjorevski N., Nelson C.M. Mapping of mechanical strains and stresses around quiescent engineered three-dimensional epithelial tissues. Biophys. J. 2012;103:152–162. doi: 10.1016/j.bpj.2012.05.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Provenzano P.P., Inman D.R., Keely P.J. Contact guidance mediated three-dimensional cell migration is regulated by Rho/ROCK-dependent matrix reorganization. Biophys. J. 2008;95:5374–5384. doi: 10.1529/biophysj.108.133116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chen P., Shenoy V.B. Strain stiffening induced by molecular motors in active crosslinked biopolymer networks. Soft Matter. 2011;7:355–358. [Google Scholar]
- 34.Christiansen D.L., Huang E.K., Silver F.H. Assembly of type I collagen: fusion of fibril subunits and the influence of fibril diameter on mechanical properties. Matrix Biol. 2000;19:409–420. doi: 10.1016/s0945-053x(00)00089-5. [DOI] [PubMed] [Google Scholar]
- 35.Gentleman E., Lay A.N., Dee K.C. Mechanical characterization of collagen fibers and scaffolds for tissue engineering. Biomaterials. 2003;24:3805–3813. doi: 10.1016/s0142-9612(03)00206-0. [DOI] [PubMed] [Google Scholar]
- 36.Sander E.A., Stylianopoulos T., Barocas V.H. Image-based multiscale modeling predicts tissue-level and network-level fiber reorganization in stretched cell-compacted collagen gels. Proc. Natl. Acad. Sci. USA. 2009;106:17675–17680. doi: 10.1073/pnas.0903716106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Stein A.M., Vader D.A., Sander L.M. An algorithm for extracting the network geometry of three-dimensional collagen gels. J. Microsc. 2008;232:463–475. doi: 10.1111/j.1365-2818.2008.02141.x. [DOI] [PubMed] [Google Scholar]
- 38.Nair, A. 2012. Discrete micromechanics of random fibrous architectures. PhD Thesis. National University of Singapore, Singapore. (http://scholarbank.nus.edu.sg/handle/10635/36146).
- 39.Stein A.M., Vader D.A., Sander L.M. The micromechanics of three-dimensional collagen-I gels. Complexity. 2011;16:22–28. [Google Scholar]
- 40.Sun W., Chaikof E.L., Levenston M.E. Numerical approximation of tangent moduli for finite element implementations of nonlinear hyperelastic material models. J. Biomech. Eng. 2008;130:061003. doi: 10.1115/1.2979872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sander L.M. Alignment localization in nonlinear biological media. J. Biomech. Eng. 2013;135:71006. doi: 10.1115/1.4024199. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Document S1. Model description
Document S2. Article plus Supporting Material