Toward an evolutionary model of cancer: Considering the mechanisms that govern the fate of somatic mutations (original) (raw)
Abstract
Our understanding of cancer has greatly advanced since Nordling [Nordling CO (1953) Br J Cancer 7(1):68–72] and Armitage and Doll [Armitage P, Doll R (1954) Br J Cancer 8(1):1–12] put forth the multistage model of carcinogenesis. However, a number of observations remain poorly understood from the standpoint of this paradigm in its contemporary state. These observations include the similar age-dependent exponential rise in incidence of cancers originating from stem/progenitor pools differing drastically in size, age-dependent cell division profiles, and compartmentalization. This common incidence pattern is characteristic of cancers requiring different numbers of oncogenic mutations, and it scales to very divergent life spans of mammalian species. Also, bigger mammals with larger underlying stem cell pools are not proportionally more prone to cancer, an observation known as Peto’s paradox. Here, we present a number of factors beyond the occurrence of oncogenic mutations that are unaccounted for in the current model of cancer development but should have significant impacts on cancer incidence. Furthermore, we propose a revision of the current understanding for how oncogenic and other functional somatic mutations affect cellular fitness. We present evidence, substantiated by evolutionary theory, demonstrating that fitness is a dynamic environment-dependent property of a phenotype and that oncogenic mutations should have vastly different fitness effects on somatic cells dependent on the tissue microenvironment in an age-dependent manner. Combined, this evidence provides a firm basis for understanding the age-dependent incidence of cancers as driven by age-altered systemic processes regulated above the cell level.
Keywords: somatic evolution, cancer, aging, oncogenic mutations, fitness
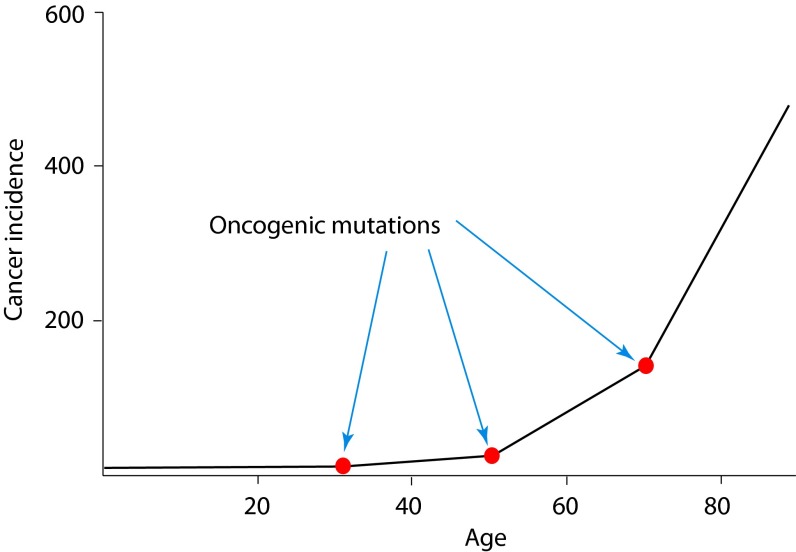
Cancer is believed to develop as a multistage disease driven by oncogenic mutations (also called driver mutations) that occur in stem cells (SCs) or progenitor cells. Each such mutation is thought to confer to the recipient cell a certain fitness advantage over other cells in a competitive stem/progenitor pool, leading to proliferation of the cell’s progeny (clone) in the pool. The successive clonal expansions driven by oncogenic mutations multiply the number of cells representing an oncogenic mutation-bearing clone, and thus increase the odds of the occurrence of the subsequent driver mutations in the premalignant genetic background. In this way, carcinogenesis is viewed as a Darwinian process of successive rounds of selection leading to the formation of a malignant cell phenotype produced by a certain number of driver mutations (1–7). SC fitness, being the ability of a SC of a particular genotype/epigenotype to be maintained, expand, or contract within the SC compartment, is thus a central phenomenon determining somatic evolution. Because cancer incidence increases exponentially with age, successive clonal expansions are thought to follow the occurrence of oncogenic mutations and increase the likelihood of subsequent drivers over time, such that carcinogenesis is rate-limited by the occurrence of oncogenic mutations over a lifetime (Fig. 1). Based on this model, investigators have used curves of cancer incidence with age to calculate the number of driver mutations needed to form a certain type of cancer (2, 8, 9), as well as the magnitude of the fitness effects conferred by some typical drivers (10). Since early published ideas (2, 6), this model has been advanced but largely held within the framework of this general scheme [an extended summary of the development of the theory of carcinogenesis is provided by Frank (11)].
Fig. 1.
Armitage and Doll’s model of sequential oncogenic mutation accumulation over time (2). Each oncogenic mutation is thought to add a certain fitness advantage to the recipient cell, which is believed to explain the exponential increase in cancer incidence. General mutation accumulation probability over time is considered. The effect of tissue-specific clonal dynamics on the probability of sequential mutation accumulation in one cell (Fig. 4 and Eq. 3), necessary for multistage carcinogenesis, as opposed to the general probability of oncogenic mutations over time, is not accounted for. Dynamic, microenvironment-dependent fitness effects of mutations (Fig. 3), which should affect clonal dynamics of premalignant contexts in an age-dependent manner, are not considered.
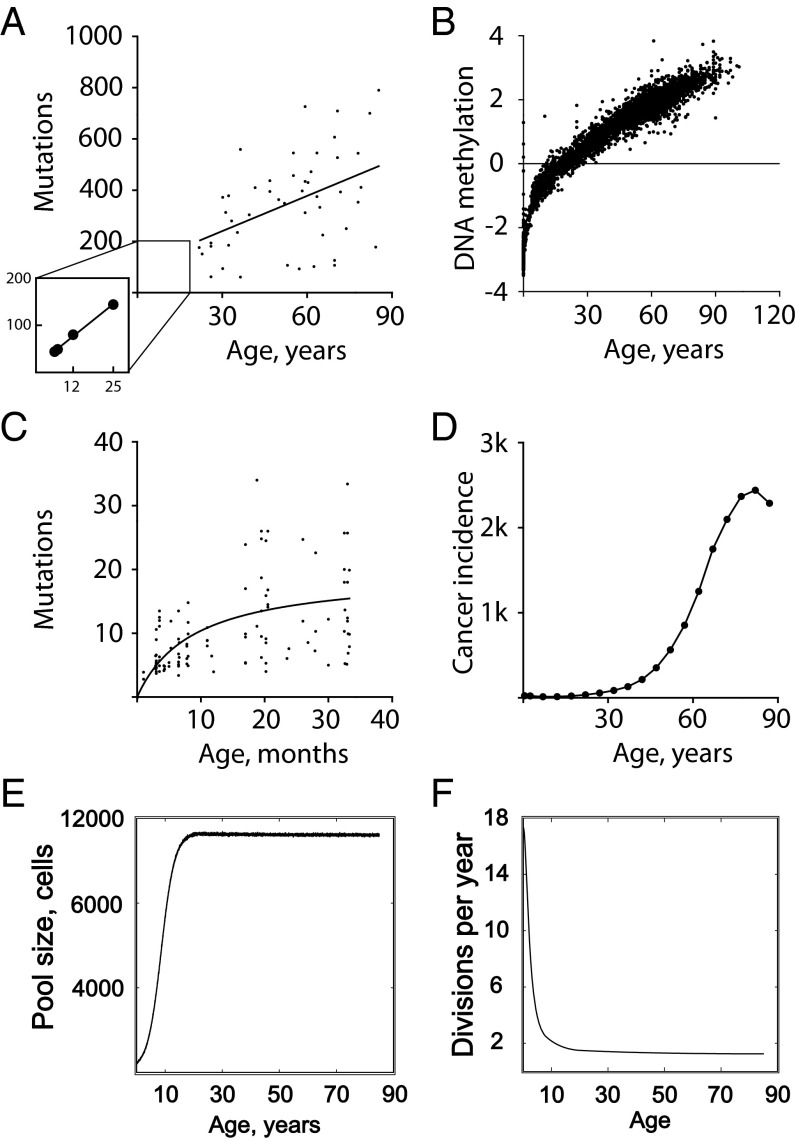
Although the general multistage oncogenic mutation-driven nature of cancer development is generally accepted and supported by experimental evidence, a number of observations have so far been difficult to explain within this paradigm. First, evidence from mammalian tissues and genomes indicates that a substantial portion (40–50%) of mutations and epigenetic changes accumulate early in life before body growth stops (12–15), consistent with a rapid slowdown in SC division rates after body maturation (16, 17) (Fig. 2). Because most cancer diagnoses happen at advanced ages (roughly after the age of 50 y in humans; www.seer.cancer.gov), cancer development is largely delayed for several decades from the time when a substantial portion of oncogenic mutations occur. Delayed cancer incidence is particularly difficult to explain in cancers, such as acute myeloid leukemia, that are known to develop quickly (within 1–2 y). Another conundrum appears from the observation that various types of cancers in humans exhibit exponential incidence increases at similar ages. Some cancers, such as colon carcinomas and leukemia, originate from vastly different underlying SC pools, having (i) different numbers of SCs (thus different target sizes for oncogenic mutations), (ii) different rates of cell division and mutagen exposure (both engendering differences in the speed of mutation accumulation), and (iii) different SC pool compartmentalization (differentially limiting early expansions of oncogenically initiated clones). These, and perhaps some other, parameters should clearly have an impact on the absolute incidence of cancers, and they should likewise affect the timing of disease onset with age. Nevertheless, the majority of cancers have similar late-age timing for the onset of elevated incidence. The late-life exponential age-dependent incidence of chronic myeloid leukemia that appears to develop with a single oncogenic mutation (18) represents the most difficult case to explain within the current multistage paradigm.
Fig. 2.
Nonlinear changes in genetic damage accumulation, cancer incidence, and SC dynamics with age. (A) Accumulation of neutral mutations (tier 3 genome) in acute megakaryoblastic leukemia (early postnatal phase) and acute myeloid leukemia (adult ages) genomes (15, 68). (B) Accumulation of DNA methylation in hematopoietic tissues (a similar pattern was found for other tissues as well) (14). (C) Accumulation of mutations in mouse tissues (combined data for spleen, intestine, heart, brain, and liver) (13, 61, 69). (D) Total cancer incidence in humans (www.seer.cancer.gov). (E) Rapid increase in the size of HSC pools during body growth in humans (21, 64). (F) HSC division rates slow down dramatically before body maturation in humans (17); a similar pattern has been found in mice (16).
Furthermore, increased cancer incidence seems to be largely universally postponed until the postreproductive portion of life spans across mammalian taxa. Mice demonstrate an exponential rise in cancer rates starting around 1.5 y of age (19), which is ∼30-fold earlier than humans. Partially, this difference can be ascribed to different rates of SC division, which are faster in mice (16, 17, 20, 21). However, the target sizes of murine SC pools for mutations in most tissues are likely manifoldly smaller than their human counterparts due to body size. Various mechanisms have been proposed to suppress cancer incidence in larger mammals (22–24), such as the possible evolution of multiple copies of tumor suppressor genes or suppression of telomerase activity with the evolution of larger body size. These mechanisms could help explain Peto’s paradox, whereby larger mammals having much larger SC pool sizes do not develop proportionally more cancers. However, these mechanisms doubtfully explain the temporal scaling of elevated cancer incidence to the postreproductive portion of vastly different life spans, such as the 30-fold difference between humans and mice.
Below, we will address a number of factors beyond the occurrence of oncogenic mutations that have not been thoroughly explored. These factors should greatly affect the odds of cancer development and should be considered in building a new evolutionary model of cancer that could explain the above-mentioned quandaries.
Fitness Effects of Mutations
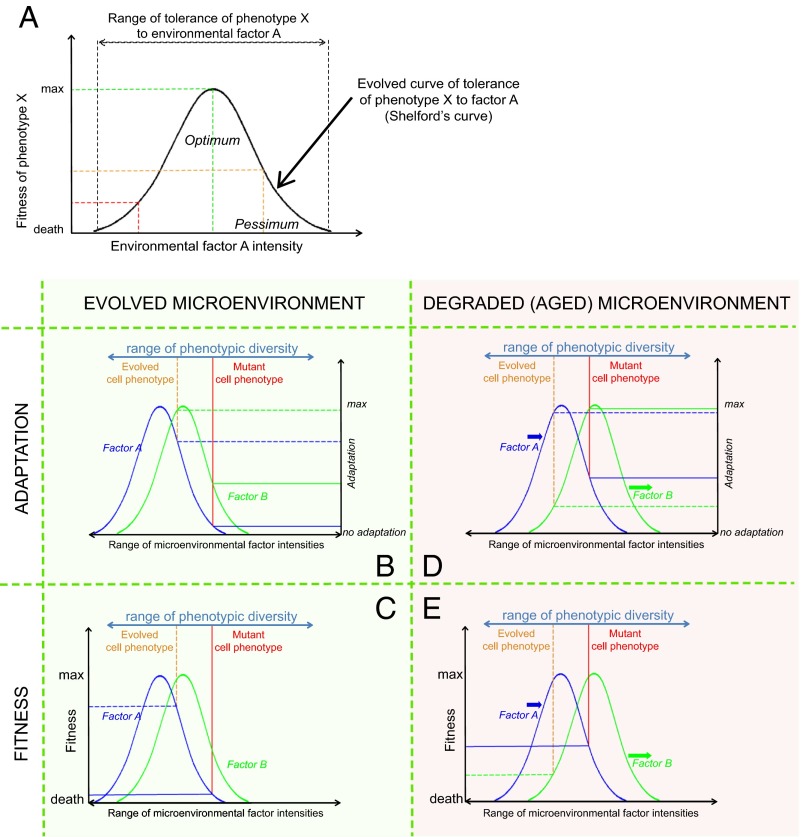
Because carcinogenesis is thought to be a Darwinian process of multiple rounds of selection within SC and progenitor cell pools, the concept of cell fitness applied to intercellular competition within self-renewing tissues is central to the theory of cancer development. At the SC population level, fitness can thus be defined as the ability of a cell to persist within a competitive pool. Cells with lower fitness will decrease in representation in the pool, either by dividing less or by increased rates of cell differentiation or death. Cells with higher fitness will, on average, increase in frequency in the pool either by dividing more and/or differentiating and dying less. Fitness thus will ultimately depend on a cell’s rate of division and its likelihood to differentiate or die. Oncogenic mutations are generally thought to increase cellular fitness and lead to clonal expansions of the recipient cells. However, there exists a marked discrepancy between cancer theory and evolutionary biology in how the concept of fitness is understood. Selection acts on phenotype and is blind to mutations that have no phenotypic manifestations. Likewise, oncogenic mutations can have defined phenotypic effects, making oncogenically initiated cells pliable to selection. However, fitness effects are not a fixed attribute of phenotype-altering mutations. Instead, fitness is a dynamic property of a phenotype imposed by environment and is determined by the match between the current environmental demand and the phenotypic manifestation of mutations (how fitness is defined is reviewed in refs. 25, 26) (Fig. 3). A hypothetical example in terms of cancer development would be a mutation that confers to a cell better resistance to hypoxia. This resistance is a cellular phenotype that can be measured by the difference in tolerance to reductions in oxygen concentration. However, in a normoxic tissue, such a mutation is likely to be selectively neutral (zero effect on cell fitness) or even disadvantageous, whereas it will be advantageous in a hypoxic tissue of a developing tumor. The effect of such a mutation on the cell’s relative fitness will be proportional to the severity of hypoxia, and thus is not a stationary attribute of a given mutation. Similarly, a mutation producing a cell phenotype with enhanced sensitivity to proliferative cues will have a defined phenotypic effect, but its selective value may depend on the concentration of specific proliferative cues within the SC niche, as well as potential consequences of enhanced proliferation toward cell differentiation and survival.
Fig. 3.
Definition of fitness in natural populations based on the Shelford’s law of tolerance and the Sprengel–Liebig law of the minimum. (A) Illustration of Shelford’s law of tolerance (70). Every factor in the environment has the optimum intensity that a species (or a phenotype) is best adapted to; the optimum intensity ensures highest fitness of the phenotype, and extreme intensities of the factor (also called pessima) lead to a decrease in the phenotype’s fitness within the range of the phenotypes’s tolerance to the factor. (B) Illustration of two phenotypes’ adaptation to environmental factors A and B based on Shelford’s law of tolerance. Evolution leads to higher adaptation (here called “evolved cell phenotype”), reducing the probability of a randomly mutated phenotype improving its adaptation relative to evolved phenotypes. (C) Following the Sprengel–Liebig law of the minimum, a phenotype’s fitness is limited by the environmental factor the phenotype is worst adapted to (phenotypes’ adaptations in this example are shown in B). (D) In an altered environment (degraded/aged tissue microenvironment in this example), environmental factor intensities change relative to the ones that the evolved phenotype is best adapted to, thus changing the adaptation of both phenotypes in this example to factors A and B. (E) Altered tissue microenvironment increases the probability that a randomly mutated phenotype will have higher fitness relative to the evolved phenotype. Note that in a normal microenvironment (C), the fitness of both phenotypes is limited by factor A; in an altered environment (E), the fitness of the evolved phenotype is now limited by factor B, whereas the fitness of the mutant phenotype still remains limited by factor A. Alteration of the environment a phenotype is adapted to may lead to changes in its fitness-limiting factors. The term “evolved microenvironment” signifies the tissue microenvironment during early and reproductive portions of the life span shaped by evolution at the germ-line level for optimal tissue performance.
In line with these theoretical examples, multiple studies have shown that oncogenic mutations indeed confer varying selective advantage/disadvantage to recipient cells, depending on external environment (27–34). Given the complexity of tissue microenvironments, with multiple chemical cues governing SC fate decisions, and the dramatic changes in tissues with age, it can be reasoned that the fitness effects of one and the same mutation producing one and the same cellular phenotype can dynamically change with age based on the current state of its niche. Other contexts that change tissue microenvironments, such as smoking, other carcinogenic exposures, or certain inherited syndromes, should have a similar impact on the fitness value of somatic mutations. Indeed, a number of studies demonstrate that selection differentially acts on an oncogenically initiated SC under different microenvironmental conditions, such as altered inflammatory status (32, 35, 36), irradiation (27, 29–31), and general tissue fitness decline with age (28, 33, 34). This dynamic fitness phenomenon leads to the hypothesis that delayed cancer incidence may be due, in part, to the reduced fitness value of oncogenically initiated cell phenotypes in young and healthy SC pools. Their fitness advantage may be promoted later by aging-altered microenvironments (Fig. 3). This concept is consistent with evolution and adaptation at the germ-line level, whereby the selective (fitness) value of a given phenotype in a complex and changing environment is dynamic and depends on the degree of deviation of particular environmental factors from the optimum at any given time (25).
Consideration of the mechanisms of how fitness is determined therefore calls for the question as to how much somatic evolution is affected by cell-autonomous processes, such as the occurrence of oncogenic mutations per se, relative to the role of external factors. Stochastic modeling of somatic evolution in hematopoietic stem cell (HSC) pools provides evidence that tissue microenvironmental determinants prevail in their effect on somatic evolution over pure cell-intrinsic processes (37).
Fitness in SCs
Although cell fitness is a central notion to the theory of carcinogenesis, there is no consistency in its use so far. Sometimes the notion is only applied to transformed malignant and premalignant cells (38). However, clonal competition in SC pools is a well-established phenomenon (39, 40), indicating that somatic evolution is a continuous process in normal tissues beyond carcinogenesis. From this perspective, carcinogenesis driven by differences in SC and progenitor cell fitness is just one particular type of somatic evolution.
Capitalizing on early ideas by Fischer (41), Haldane (42) and Wright (43), absolute fitness in population genetics is generally viewed as the likelihood that a given genotype will be transmitted to subsequent generations, and is the product of the probability of survival and the rate of reproduction. Another expression of fitness is the ratio of the frequency of a given genotype in the population after selection to its frequency before selection, usually measured per generation. This general principle can be applied to SCs, for which [1 − (differentiation rate + death rate + senescence rate)] would reflect the “probability of survival” in an SC pool and cell division frequency would represent the reproduction rate. However, some adaptation of this general principle to SCs and progenitor cells is needed for a number of reasons. Fitness in populations is considered to be an averaged measure that relates to groups or populations, and it is generally measured in a temporally discrete manner. In cancer biology, specific effects of many oncogenic mutations on cell cycle and self-renewal are known, and it is therefore more interesting to know what would be the fitness effects of these mutations from a single-cell perspective to predict the likelihood and timing of the ensuing clonal expansion. We have previously shown that the following equation can provide a useful measure of fitness in SCs (29):
where _F_′ reflects a measure of fitness; D is the combined probability of SC differentiation, death, and senescence per cell per division; and C is cell division rate. Essentially the equation measures the rate at which new SCs of a given genetic descent appear or disappear. From Eq. 1, it can be inferred that D = 0.5 leads to a stationary clone size irrespective of cell division rates. It should be noted, however, that the use of Eq. 1 is largely limited to comparative experimental studies, such as when comparing the fitness of oncogenically initiated cells vs. normal cells under certain conditions. Its applicability to natural in vivo processes may be limited in some cases. For example, body growth early in life leads to an increase in the SC pool capacity, providing room for clonal expansions unrelated to fitness but resulting from increased niche space due to body growth. This expansion may affect the accuracy of fitness measurement in vivo using Eq. 1 during early periods before animal maturity. Cells in such clones will demonstrate a different ratio between differentiation and cell division rates, which can lead to incorrect conclusions about fitness if judged by Eq. 1. Nonetheless, relative fitness of SCs in adult pools is suitable for comparison using this equation.
We have shown that this approach to measuring SC fitness can generally be applied and is easily transferrable to in vitro experiments to elucidate the net fitness of oncogenic mutations under various contexts (29). The cell cycle rate can be measured by traditional methods, and D can be calculated using the following equation:
| D=1−12(StS0)1log2(PtS0), | [2] |
|---|
where _S_0 is the initial number of SCs, S t is the number of SCs at the time of measurement, and P t is the total number of cells (SCs + differentiated/committed to differentiate + dead cells) at the time of measurement. This equation could also be used in vivo, where such parameters can be measured or estimated.
Methods of measuring SC fitness, as well as the underlying theory, are important as a tool to investigate further how somatic evolution actually works in animal tissues. For example, from the observation that they often positively regulate the cell cycle, it is tempting to speculate that oncogenic mutations lead to fitness gain in recipient cells (44). However, a summary of a large number of studies demonstrates that many typical cancer driver mutations decrease SC self-renewal capacity in vivo by elevating the cell’s proclivity to differentiate (45). These observations, combined with the dynamic evolutionary concept of mutation fitness effects discussed above (Fig. 3), provide clues toward an evolutionary explanation for why most cancer incidence is delayed until the postreproductive portion of life spans across mammalian taxa. The mechanism underlying such an explanation could lie in the microenvironment-dependent definition of mutation fitness effects. SCs are subject to two levels of selection, at the germ-line level for optimally maintaining high body fitness and at the somatic/tissue level through competition for niche space. Selection at the germ-line level for body fitness during the reproductive portion of the life span drives coevolution of SCs and the tissue microenvironment for optimal tissue maintenance. Just how effective selection at this level is can be inferred from substantial differences in the life spans of some species within closely related groups. Such differences can be substantial even within one species, such as the ∼1.5-fold difference in rates of aging between the mainland and island populations of Virginia opossums (Didelphis virginiana) that have been separated only for several thousand years (46).
Coevolution of SCs and the tissue microenvironment at the germ-line level does not automatically mean that SCs are at peak fitness at the somatic/tissue level of selection. However, based on the fitness definition shown in Fig. 3, adaptation of SCs to their tissue niches should still reduce the probability that any random genetic change can improve SC fitness relative to that probability in aged tissues for which decline is not “visible” to natural selection. As SCs become better adapted to their microenvironment, the probability that a random mutation can improve the adaptation becomes progressively reduced. Thus, stabilizing selection should favor the evolved phenotype (the inherited phenotype not phenotypically affected by somatic mutations) through reproductive periods, thus inhibiting somatic evolution. In contrast, being substantially less directed by natural selection, aging processes during the postreproductive period have a greater stochastic (random) component. It follows then that irrespective of the general frequency of the occurrence of mutations capable of driving somatic evolution, their abundance within somatic cell populations should increase during postreproductive periods of life spans by means of the increasing fitness value of some previously accumulated mutations. In other words, SCs do not have means of adapting to a degraded aged microenvironment other than via somatic evolution, and the frequency of somatic cell clones bearing such adaptive mutations will increase in old age. Just as changes in environments can stimulate organismal evolution (by promoting adaptation to the new environment), microenvironmental changes in tissues in old age will engender positive selection for adaptive mutations (whether oncogenic or not), thus promoting somatic evolution (and, in some cases, cancer). Such an explanation also predicts that SC pools should become progressively more clonal during the postreproductive period, because increased positive selection should lead to increased rates of somatic evolution (clonal expansions) and elimination of many small nonadaptive clones. Evidence actually corroborates this prediction. For example, in HSC pools, clonality (when the major portion of hematopoiesis derives from one or a few expanded clones) has recently been shown to increase exponentially with age, resembling the cancer incidence curve (47–51).
Tissue Architecture: Drift vs. Selection
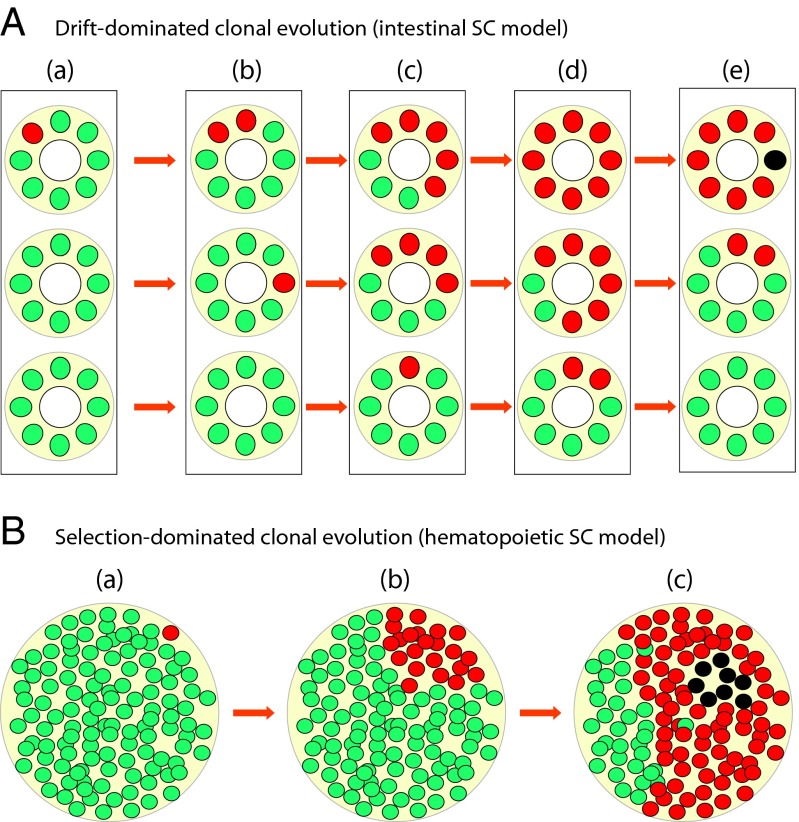
The organization of SC pools has been argued to affect processes, such as mutation accumulation and carcinogenesis, significantly via differences in cell division and self-renewal (52, 53). The architecture of SC and progenitor cell pools, which serve as the initial targets for oncogenesis, in different tissues should also have a significant impact on selection processes, and is thus an important consideration toward building an evolutionary model of cancer. HSC pools, for example, have been effectively shown to be one large population (with estimates ranging from 11,000 to hundreds of thousands of cells) competing for a limited niche space (20, 54, 55). Parabiosis experiments with mice (using shared blood circulation) confirm that HSCs do intermix to a substantial degree (56). Just as for other mammalian SC systems, HSCs are thought to make cell fate decisions stochastically, with some probability of asymmetric vs. symmetric cell division (at least at homeostasis). A similar model would likely apply to mesenchymal SCs, because they are known to migrate and to have a similar spatial geometry of their pool organization in the bone marrow (57). In contrast, epithelial tissues exhibit a different compartmental organization for their SCs. For example, intestinal epithelia are continuously renewed from isolated clusters (∼14–20 cells each in mice) of SCs sequestered in intestinal crypts (Fig. 4). This striking difference in SC pool architecture has been proposed to impose drastic effects on selection processes (58). Whereas the large adult HSC pools potentially allow for significant clonal expansions driven by selection for beneficial mutations, the fate of mutations in intestinal SC, including oncogenic mutations, such as in the gene encoding the p53 tumor suppressor protein (TP53), has been shown to be greatly affected by random drift (32, 59, 60). These findings are in accord with data on evolution at the germ-line level, whereby population size is known to determine the drift–selection balance. The smaller the effective population size, the larger the change in phenotype need be to be “visible” to selection. Thus, in large enough populations, the drift–selection barrier is low and minute phenotypic changes produced by mutations can be acted on by selection. In small or fragmented populations, such as intestinal crypt SC pools, oncogenic mutations would have to have substantially greater fitness effects to be influenced by selection compared with pools of HSCs or mesenchymal SCs.
Fig. 4.
Illustration of the effect of tissue architecture on sequential oncogenic mutation accumulation in SC pools. (A) Schematic representation of fragmented SC pools, such as those fragmented SC pools in gut epithelia. (a) Schematic section of the gut epithelium with three crypts shown as circles containing green (nonmutated) cells and one red (mutant) cell. (b_–_e) Stages of somatic evolution within the three crypts. The power of random drift is increased in each crypt due to the small SC pool size in the crypts, leading to drift-driven clonal dynamics. The chances of mutation α (red cells) fixation in a crypt are heavily influenced by drift, and the total number of the mutation α-affected cells depends on the rate of mutation α fixation and the number of crypts in which mutation α independently occurred; the black cell in e represents a double mutant that bears mutation α and has acquired a second mutation β. (B) In large nonfragmented pools, such as HSCs, the power of drift is limited by the large population size and clonal dynamics are mostly governed by selection driven by fitness differences between normal cells (green cells) and cells bearing mutation α (red cells). Following Eq. 3, the selection-enriched pool of mutant α cells increases the chances that mutation β will occur in a cell already bearing mutation α; selection can further enrich the pool of αβ mutants (black cells in c) to promote the next selection rounds of multistage carcinogenesis.
Moreover, the expansion of an oncogenically initiated, premalignant clone is typically limited by the crypt niche capacity. This limitation should effectively render many functional mutations “neutral” in terms of selection, at least if their impact on SCs is relatively small. However, given the vast expanses of mammalian gut epithelia, mutations that have a similar impact on the same gene or pathway should appear over time in many crypts independently. Therefore, the effective size of an oncogenically initiated context may well exceed the limits of a crypt. Unlike in HSCs, however, where an exponential increase in the size of advantageous clones can be expected, the intestinal SC system architecture will probably allow only linear increases over time for premalignant contexts that are not capable of breaking through the crypt (Fig. 4). Given that the accumulation of mutations in the mouse intestine (61) and epigenetic changes in the human intestine (14) slow down with age, explanation of the exponential age-dependent cancer incidence for gut carcinomas, where positive selection is limited, becomes problematic. However, if positive effects on cell fitness by oncogenic mutations increase in aged microenvironments, this effect could overcome drift in intestinal crypts. With the large area of gut epithelia, an improved fitness value conferred by a given mutation, if sufficient to overcome the drift barrier, will lead to a faster and nonlinear total expansion of cells containing a similar mutation (in terms of phenotypic impact, an effective intestinal “clone”), because a supposedly linear increase in the number of crypts containing such mutations will be amplified by more frequent fixations of the mutations in particular crypts. Because tissue decline is progressing exponentially after reproductive ages, the frequency of fixation of adaptive mutations within crypts should thus also increase exponentially and determine a similar curve for the probability of sequential acquisition of oncogenic drivers. This dynamic fitness phenomenon would thus be able to generate an exponential rise in gut carcinomas with age. Such factors as increasing inflammation, a hallmark of aging (62), have actually been shown to increase the positive effect on fitness by mutant TP53 in SC pools in the crypt (32). Moreover, aging-associated conditions, such as inflammation, might also increase mutation rates and/or increase selection for cells with mutator phenotypes (e.g., mismatch repair deficiency in colon cancers), further fueling somatic evolution (63). In contrast, the simple model of multiple rounds of oncogenic event-limited positive selection leading to multistage carcinogenesis will likely fail when one considers the complexities of intestinal SC organization.
However, another discrepancy between SC systems, such as HSCs and intestinal SCs, might be a difference in their total pool sizes in mammals with different body sizes. There is evidence that HSC pool size may be conserved across mammalian taxa (64) (i.e., HSC pool sizes do not appear to scale to body size). However, the total number of intestinal SCs should be proportional to the surface area of gut epithelia, which is immensely different for mammals of different sizes. If the described effect of SC pool architecture is operative in affecting cancer odds, the different ratios of the HSC pool size to the epithelial SC pool size between small and large mammals could explain the relative rarity of carcinomas in small mammals like mice (with a greater frequency of hematopoietic malignancies), which contrasts with the prevalence of carcinomas in humans (and perhaps other large animals having much larger total epithelial surfaces) (65).
SC Divisions and the Odds of Accumulating Multiple Oncogenic Mutations
The characteristics considered above, such as SC pool size and fragmentation, which determine the relative roles of drift and selection (the drift–selection barrier), as well as the state of the tissue microenvironment, which should alter mutation fitness effects, and thus the balance of stabilizing and directional (positive) selection, should have significant effects on SC clonal dynamics and somatic evolution in general. However, the mechanisms that translate somatic evolutionary processes into the actual cancer risk need to be addressed.
Most cancers are known to require multiple genetic and/or epigenetic changes in cells. Thus, a series of oncogenic events needs to occur in one cell to lead to full malignancy. Mutations appear over time, mostly as cells divide, and specific types of cancers require certain sets of oncogenic mutations as the basic condition for cancer to develop. However, the current cancer paradigm likely oversimplifies the probabilities that govern mutation accumulation in particular cells, assuming that their probability simply rises with time and cell divisions (Fig. 1). The current paradigm of cancer development is based on the view that the occurrence of oncogenic mutations is inevitably followed by rounds of positive selection leading to expansion of the recipient clones. These expansions are thought to multiply the probability of the next oncogenic mutation occurring within the clone, which further promotes selection for these clones. This general scheme is believed to explain the exponential increase in cancer incidence with age (Fig. 2_D_). However, a growing body of experimental data indicates that a substantial portion of mutations and epigenetic changes (up to 40–50%), and thus a similar share of oncogenic mutations, occur before adulthood (14, 15, 66) (∼18 y for humans or 2 mo for mice). This pattern can be explained by evidence from both humans and mice at least for some SCs, such as HSCs, that the frequency of SC divisions is substantially reduced postnatally as body growth slows (16, 17). This pattern is drastically discrepant with the typical age-dependent curve of cancer incidence.
As we have argued earlier (37), the probability of multiple oncogenic mutations occurring in a single cell is a function of the product of mutation rate and the number of cell divisions, and can be summarized in the following equation:
| Pd1…dn(t)= D(t)×∫0t(∏i=1npi)(t)dt, | [3] |
|---|
where P d_1…_dn(t) is the probability of acquiring n drivers in one cell by time t, D(t) is the total number of cell divisions within a clonal context by time t, and p i is the probability of acquiring a driver d i ∈ {d 1, …, d n} per cell per division as a linear function of the effective mutation rate. Eq. 1 indicates that fitness/selection-driven proliferation/shrinkage of clones will exponentially depend on rates of SC differentiation per cell division (as long as D ≠ 0.5), thus ensuring that fitness/selection has an exponential effect on clonal size. Based on Eq. 3, the character of selection should thus have a far greater effect on the odds of multidriver cancers than the mutation rate by exponentially increasing the number of dividing cells, and thus the total number of cell divisions within a proliferating clone [D(_t_) in Eq. 3] by a certain time t. Evidence for the effects of generally increased positive selection on cancer risk comes from the above-mentioned studies that reveal a greater risk for hematopoietic malignancies in aged people with clonal hematopoiesis (47, 48, 50, 51, 67). Increased clonality in HSC pools is expected to result from clonal expansions driven by positive selection. Consistent with Eq. 3, this clonal expansion should lead to an elevated probability of sequential oncogenic mutation accumulation, because some of the expanding clones already contain initiating oncogenic mutations, and thus propagate these genetic contexts. However, following the same logic, if positive fitness effects of oncogenic mutations are reduced in the healthy (evolved) microenvironment during reproductive ages relative to the older degraded microenvironment, positive selection and somatic evolution will be suppressed before postreproductive age, thus reducing the probability of accumulating multiple cancer drivers in one cell.
Combining this logic with theory addressed in previous sections, we can conclude that such factors as SC pool structure (tissue architecture) and aging (deviation from evolved/optimal state of microenvironment/SC niche), which affect the balance of drift vs. selection and stabilizing vs. directional selection, respectively, should have dramatic effects on the net probability and timing of the appearance of cells that contain multiple oncogenic drivers (premalignant or malignant cells) in a tissue. However, fitness alteration-driven selection is not the only force that can affect the probability of multiple driver accumulation. Given the evidence of much faster SC division rates during early life before body maturation (16, 17) (Fig. 2_F_), child SC clones of much smaller size compared with adult clones can thus generate significantly higher total numbers of cell divisions per clone of a given size. However, individual clones should be smaller in children due to the generally smaller size of SC pools and the body (Fig. 2_E_). These two factors counteract in producing the D(t) parameter in Eq. 3. We do not yet know the net result of this counteraction for any SC system in the human body, but one can speculate, based on this logic, that the relative role of clonal expansions (selection) in affecting the odds of multidriver cancers by affecting D(t) will differ between children and adults. Thus, the nonlinear change in SC division rates and pool size from ontogeny into adulthood is another factor that should act to determine the risk of cancer throughout life.
Conclusions
The recognition of cancer as a somatic evolutionary process requiring multiple rounds of selection for adaptive oncogenic mutations has armed cancer modeling with parametric approaches and led to the foundation of the current multistage model of carcinogenesis operating with mutation fitness effects as the pivotal element of the theory. Although the general model of multistage carcinogenesis has been corroborated, it still lacks consideration of a number of known evolutionary phenomena that could help explain experimental evidence. Since its origin, the multistage model has operated with the assumption that mutations accumulate linearly with age, which is now known not to be true. It also assumes that cancer driver mutations confer a fixed fitness advantage to recipient cells, which is in conflict with the evolutionary mechanism of fitness definition, whereby fitness is a dynamic property imposed on phenotype and modulated by environment, and thus is not a cell-intrinsic stationary characteristic imposed by mutations. By assuming that rounds of positive selection follow each occurrence of oncogenic mutations, the multistage model of carcinogenesis overlooks population parameters that affect selection as a phenomenon. The factors that govern the balance of drift and selection (e.g., SC pool size and structure) or the balance of stabilizing and positive selection (which should depend to a large extent on the state of tissue microenvironment) need to be incorporated into an evolutionary theory of cancer.
What from the perspective of the predominant cancer paradigm appear as conundrums, such as Peto’s paradox and the scaling of cancer to vastly different mammalian life spans, is easier to explain by recognizing that the power of stabilizing selection depends on population size (SC pool size) and that the magnitude of positive selection, which drives somatic evolution, depends to a large extent on the state of the tissue microenvironment. In the case of SCs, these dependencies entail that a healthy (evolved state) tissue microenvironment within the reproductive period of a mammal’s life span should act to prevent somatic evolution and the selective advantage conferred by oncogenic mutations within such a microenvironment should be reduced relative to an older, degraded state. In a postreproductive microenvironment deviating from the evolved one, the balance shifts from stabilizing to positive selection, and thus, irrespective of life span, this aging-induced change should trigger somatic evolution driven by previously accumulated mutations. The exponentially increasing clonality shown to develop during human postreproductive ages in the hematopoietic system (47, 48, 50, 51, 67), in fact, provides a strong line of evidence that the balance between stabilizing and positive selection changes in SCs pools in an age-dependent manner in normal tissues, irrespective of carcinogenesis. It also supports the idea that the selective value of oncogenic mutations should change (increase) with age. From this perspective, Peto’s paradox is also easier to explain, because stabilizing selection should be more powerful in larger SC pools, which should counteract the increased risk of oncogenic mutations conferred by larger SC pools and more lifetime divisions for larger long-lived animals.
Understanding the principles of somatic evolution could have profound implications for cancer therapy and drug design. The key transition here should be from therapies and drugs targeting malignant cellular phenotypes to therapies and drugs targeting cell fitness. For example, inflammation has been shown in multiple studies to promote carcinogenesis. Inflammation essentially represents altered tissue microenvironmental signaling and is likely to affect SC fate decisions. Thus, identification of the most important inflammation-related signaling molecules, which are critical in elevating the fitness of malignant cell phenotypes, could lead to novel approaches in therapy, whereby drugs targeting malignant phenotypes could be combined with strategies targeting/suppressing specific microenvironmental factors promoting somatic evolution in specific types of cancer or tissue. One additional advantage of targeting the microenvironment is that, unlike the cancer, the resident tissue cells will not be under selective pressure to evolve escape mechanisms from the therapy.
Acknowledgments
We thank Subhajyoti De, Hannah Scarborough, and Kelly Higa of the University of Colorado for critical review of the manuscript. These studies were supported by National Cancer Institute Grant R01CA180175 (to J.D.).
Footnotes
The authors declare no conflict of interest.
This paper results from the Arthur M. Sackler Colloquium of the National Academy of Sciences, “In the Light of Evolution IX: Clonal Reproduction: Alternatives to Sex,” held January 9–10, 2015, at the Arnold and Mabel Beckman Center of the National Academies of Sciences and Engineering in Irvine, CA. The complete program and video recordings of most presentations are available on the NAS website at www.nasonline.org/ILE_IX_Clonal_Reproduction.
This article is a PNAS Direct Submission.
References
- 1.Armitage P. Multistage models of carcinogenesis. Environ Health Perspect. 1985;63:195–201. doi: 10.1289/ehp.8563195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Armitage P, Doll R. The age distribution of cancer and a multi-stage theory of carcinogenesis. Br J Cancer. 1954;8(1):1–12. doi: 10.1038/bjc.1954.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nowell PC. The clonal evolution of tumor cell populations. Science. 1976;194(4260):23–28. doi: 10.1126/science.959840. [DOI] [PubMed] [Google Scholar]
- 4.Reiter JG, Bozic I, Allen B, Chatterjee K, Nowak MA. The effect of one additional driver mutation on tumor progression. Evol Appl. 2013;6(1):34–45. doi: 10.1111/eva.12020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Vogelstein B, et al. Cancer genome landscapes. Science. 2013;339(6127):1546–1558. doi: 10.1126/science.1235122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nordling CO. A new theory on cancer-inducing mechanism. Br J Cancer. 1953;7(1):68–72. doi: 10.1038/bjc.1953.8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Luebeck EG, Moolgavkar SH. Multistage carcinogenesis and the incidence of colorectal cancer. Proc Natl Acad Sci USA. 2002;99(23):15095–15100. doi: 10.1073/pnas.222118199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Michor F, Iwasa Y, Nowak MA. The age incidence of chronic myeloid leukemia can be explained by a one-mutation model. Proc Natl Acad Sci USA. 2006;103(40):14931–14934. doi: 10.1073/pnas.0607006103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Vickers M. Estimation of the number of mutations necessary to cause chronic myeloid leukaemia from epidemiological data. Br J Haematol. 1996;94(1):1–4. doi: 10.1046/j.1365-2141.1996.d01-1751.x. [DOI] [PubMed] [Google Scholar]
- 10.Bozic I, et al. Accumulation of driver and passenger mutations during tumor progression. Proc Natl Acad Sci USA. 2010;107(43):18545–18550. doi: 10.1073/pnas.1010978107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Frank SA. Dynamics of Cancer: Incidence, Inheritance, and Evolution. Princeton Univ Press; Princeton: 2007. [PubMed] [Google Scholar]
- 12.Finette BA, et al. Determination of hprt mutant frequencies in T-lymphocytes from a healthy pediatric population: Statistical comparison between newborn, children and adult mutant frequencies, cloning efficiency and age. Mutat Res. 1994;308(2):223–231. doi: 10.1016/0027-5107(94)90157-0. [DOI] [PubMed] [Google Scholar]
- 13.Giese H, et al. Age-related mutation accumulation at a lacZ reporter locus in normal and tumor tissues of Trp53-deficient mice. Mutat Res. 2002;514(1-2):153–163. doi: 10.1016/s1383-5718(01)00329-1. [DOI] [PubMed] [Google Scholar]
- 14.Horvath S. DNA methylation age of human tissues and cell types. Genome Biol. 2013;14(10):R115. doi: 10.1186/gb-2013-14-10-r115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Anonymous; Cancer Genome Atlas Research Network Genomic and epigenomic landscapes of adult de novo acute myeloid leukemia. N Engl J Med. 2013;368(22):2059–2074. doi: 10.1056/NEJMoa1301689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bowie MB, et al. Hematopoietic stem cells proliferate until after birth and show a reversible phase-specific engraftment defect. J Clin Invest. 2006;116(10):2808–2816. doi: 10.1172/JCI28310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sidorov I, Kimura M, Yashin A, Aviv A. Leukocyte telomere dynamics and human hematopoietic stem cell kinetics during somatic growth. Exp Hematol. 2009;37(4):514–524. doi: 10.1016/j.exphem.2008.11.009. [DOI] [PubMed] [Google Scholar]
- 18.Mullighan CG, et al. BCR-ABL1 lymphoblastic leukaemia is characterized by the deletion of Ikaros. Nature. 2008;453(7191):110–114. doi: 10.1038/nature06866. [DOI] [PubMed] [Google Scholar]
- 19.Frith CH, Ward JM, Chandra M. The morphology, immunohistochemistry, and incidence of hematopoietic neoplasms in mice and rats. Toxicol Pathol. 1993;21(2):206–218. doi: 10.1177/019262339302100213. [DOI] [PubMed] [Google Scholar]
- 20.Abkowitz JL, Golinelli D, Harrison DE, Guttorp P. In vivo kinetics of murine hemopoietic stem cells. Blood. 2000;96(10):3399–3405. [PubMed] [Google Scholar]
- 21.Catlin SN, Busque L, Gale RE, Guttorp P, Abkowitz JL. The replication rate of human hematopoietic stem cells in vivo. Blood. 2011;117(17):4460–4466. doi: 10.1182/blood-2010-08-303537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Caulin AF, Maley CC. Peto’s Paradox: Evolution’s prescription for cancer prevention. Trends Ecol Evol. 2011;26(4):175–182. doi: 10.1016/j.tree.2011.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gorbunova V, Seluanov A. Coevolution of telomerase activity and body mass in mammals: From mice to beavers. Mech Ageing Dev. 2009;130(1-2):3–9. doi: 10.1016/j.mad.2008.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gorbunova V, Seluanov A, Zhang Z, Gladyshev VN, Vijg J. Comparative genetics of longevity and cancer: Insights from long-lived rodents. Nat Rev Genet. 2014;15(8):531–540. doi: 10.1038/nrg3728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gorban AN, Pokidysheva LI, Smirnova EV, Tyukina TA. Law of the Minimum paradoxes. Bull Math Biol. 2011;73(9):2013–2044. doi: 10.1007/s11538-010-9597-1. [DOI] [PubMed] [Google Scholar]
- 26.Orr HA. Fitness and its role in evolutionary genetics. Nat Rev Genet. 2009;10(8):531–539. doi: 10.1038/nrg2603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Bondar T, Medzhitov R. p53-mediated hematopoietic stem and progenitor cell competition. Cell Stem Cell. 2010;6(4):309–322. doi: 10.1016/j.stem.2010.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Henry CJ, Marusyk A, Zaberezhnyy V, Adane B, DeGregori J. Declining lymphoid progenitor fitness promotes aging-associated leukemogenesis. Proc Natl Acad Sci USA. 2010;107(50):21713–21718. doi: 10.1073/pnas.1005486107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fleenor CJ, et al. Contrasting Roles for C/EBPalpha and Notch in Irradiation-Induced Multipotent Hematopoietic Progenitor Cell Defects. Stem Cells. 2015;33(4):1345–1358. doi: 10.1002/stem.1936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Marusyk A, et al. Irradiation alters selection for oncogenic mutations in hematopoietic progenitors. Cancer Res. 2009;69(18):7262–7269. doi: 10.1158/0008-5472.CAN-09-0604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Marusyk A, Porter CC, Zaberezhnyy V, DeGregori J. Irradiation selects for p53-deficient hematopoietic progenitors. PLoS Biol. 2010;8(3):e1000324. doi: 10.1371/journal.pbio.1000324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vermeulen L, et al. Defining stem cell dynamics in models of intestinal tumor initiation. Science. 2013;342(6161):995–998. doi: 10.1126/science.1243148. [DOI] [PubMed] [Google Scholar]
- 33.Vas V, Senger K, Dörr K, Niebel A, Geiger H. Aging of the microenvironment influences clonality in hematopoiesis. PLoS ONE. 2012;7(8):e42080. doi: 10.1371/journal.pone.0042080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Vas V, Wandhoff C, Dörr K, Niebel A, Geiger H. Contribution of an aged microenvironment to aging-associated myeloproliferative disease. PLoS ONE. 2012;7(2):e31523. doi: 10.1371/journal.pone.0031523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Toomer KH, Chen Z. Autoimmunity as a double agent in tumor killing and cancer promotion. Front Immunol. 2014;5:116. doi: 10.3389/fimmu.2014.00116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.de Visser KE, Eichten A, Coussens LM. Paradoxical roles of the immune system during cancer development. Nat Rev Cancer. 2006;6(1):24–37. doi: 10.1038/nrc1782. [DOI] [PubMed] [Google Scholar]
- 37.Rozhok AI, Salstrom JL, DeGregori J. Stochastic modeling indicates that aging and somatic evolution in the hematopoetic system are driven by non-cell-autonomous processes. Aging (Albany, NY Online) 2014;6(12):1033–1048. doi: 10.18632/aging.100707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gatenby RA, Cunningham JJ, Brown JS. Evolutionary triage governs fitness in driver and passenger mutations and suggests targeting never mutations. Nat Commun. 2014;5:5499. doi: 10.1038/ncomms6499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Amoyel M, Bach EA. Cell competition: How to eliminate your neighbours. Development. 2014;141(5):988–1000. doi: 10.1242/dev.079129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Levayer R, Moreno E. Mechanisms of cell competition: Themes and variations. J Cell Biol. 2013;200(6):689–698. doi: 10.1083/jcb.201301051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Fischer RA. The Genetical Theory of Natural Selection. Clarendon; Oxford: 1930. [Google Scholar]
- 42.Haldane JBS. The Causes of Evolution. Longmans, Green, and Co.; London: 1932. [Google Scholar]
- 43.Wright S. Evolution in Mendelian Populations. Genetics. 1931;16(2):97–159. doi: 10.1093/genetics/16.2.97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hanahan D, Weinberg RA. Hallmarks of cancer: The next generation. Cell. 2011;144(5):646–674. doi: 10.1016/j.cell.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 45.DeGregori J. Challenging the axiom: Does the occurrence of oncogenic mutations truly limit cancer development with age? Oncogene. 2013;32(15):1869–1875. doi: 10.1038/onc.2012.281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Austad SN. Retarded senescence in an insular population of Virginia opossums (Didelphis virginiana) J Zool. 1993;229(4):695–708. [Google Scholar]
- 47.Genovese G, et al. Clonal hematopoiesis and blood-cancer risk inferred from blood DNA sequence. N Engl J Med. 2014;371(26):2477–2487. doi: 10.1056/NEJMoa1409405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jaiswal S, et al. Age-related clonal hematopoiesis associated with adverse outcomes. N Engl J Med. 2014;371(26):2488–2498. doi: 10.1056/NEJMoa1408617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.McKerrell T, et al. Understanding Society Scientific Group Leukemia-associated somatic mutations drive distinct patterns of age-related clonal hemopoiesis. Cell Reports. 2015;10(8):1239–1245. doi: 10.1016/j.celrep.2015.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Laurie CC, et al. Detectable clonal mosaicism from birth to old age and its relationship to cancer. Nat Genet. 2012;44(6):642–650. doi: 10.1038/ng.2271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Jacobs KB, et al. Detectable clonal mosaicism and its relationship to aging and cancer. Nat Genet. 2012;44(6):651–658. doi: 10.1038/ng.2270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Komarova NL. Cancer, aging and the optimal tissue design. Semin Cancer Biol. 2005;15(6):494–505. doi: 10.1016/j.semcancer.2005.07.003. [DOI] [PubMed] [Google Scholar]
- 53.Rodriguez-Brenes IA, Wodarz D, Komarova NL. Minimizing the risk of cancer: Tissue architecture and cellular replication limits. J R Soc Interface. 2013;10(86):20130410. doi: 10.1098/rsif.2013.0410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Abkowitz JL, Catlin SN, Guttorp P. Evidence that hematopoiesis may be a stochastic process in vivo. Nat Med. 1996;2(2):190–197. doi: 10.1038/nm0296-190. [DOI] [PubMed] [Google Scholar]
- 55.Wang JC, Doedens M, Dick JE. Primitive human hematopoietic cells are enriched in cord blood compared with adult bone marrow or mobilized peripheral blood as measured by the quantitative in vivo SCID-repopulating cell assay. Blood. 1997;89(11):3919–3924. [PubMed] [Google Scholar]
- 56.Wright DE, Wagers AJ, Gulati AP, Johnson FL, Weissman IL. Physiological migration of hematopoietic stem and progenitor cells. Science. 2001;294(5548):1933–1936. doi: 10.1126/science.1064081. [DOI] [PubMed] [Google Scholar]
- 57.Sohni A, Verfaillie CM. Mesenchymal stem cells migration homing and tracking. Stem Cells Int. 2013;2013:130763. doi: 10.1155/2013/130763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Frank SA. Somatic mutation: Early cancer steps depend on tissue architecture. Curr Biol. 2003;13(7):R261–R263. doi: 10.1016/s0960-9822(03)00195-7. [DOI] [PubMed] [Google Scholar]
- 59.Lopez-Garcia C, Klein AM, Simons BD, Winton DJ. Intestinal stem cell replacement follows a pattern of neutral drift. Science. 2010;330(6005):822–825. doi: 10.1126/science.1196236. [DOI] [PubMed] [Google Scholar]
- 60.Snippert HJ, et al. Intestinal crypt homeostasis results from neutral competition between symmetrically dividing Lgr5 stem cells. Cell. 2010;143(1):134–144. doi: 10.1016/j.cell.2010.09.016. [DOI] [PubMed] [Google Scholar]
- 61.Dollé ME, Snyder WK, Gossen JA, Lohman PH, Vijg J. Distinct spectra of somatic mutations accumulated with age in mouse heart and small intestine. Proc Natl Acad Sci USA. 2000;97(15):8403–8408. doi: 10.1073/pnas.97.15.8403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Goto M. Inflammaging (inflammation + aging): A driving force for human aging based on an evolutionarily antagonistic pleiotropy theory? Biosci Trends. 2008;2(6):218–230. [PubMed] [Google Scholar]
- 63.Komarova NL, Wodarz D. Evolutionary dynamics of mutator phenotypes in cancer: Implications for chemotherapy. Cancer Res. 2003;63(20):6635–6642. [PubMed] [Google Scholar]
- 64.Abkowitz JL, Catlin SN, McCallie MT, Guttorp P. Evidence that the number of hematopoietic stem cells per animal is conserved in mammals. Blood. 2002;100(7):2665–2667. doi: 10.1182/blood-2002-03-0822. [DOI] [PubMed] [Google Scholar]
- 65.DePinho RA. The age of cancer. Nature. 2000;408(6809):248–254. doi: 10.1038/35041694. [DOI] [PubMed] [Google Scholar]
- 66.Vijg J, Busuttil RA, Bahar R, Dollé ME. Aging and genome maintenance. Ann N Y Acad Sci. 2005;1055:35–47. doi: 10.1196/annals.1323.007. [DOI] [PubMed] [Google Scholar]
- 67.Aghili L, Foo J, DeGregori J, De S. Patterns of somatically acquired amplifications and deletions in apparently normal tissues of ovarian cancer patients. Cell Reports. 2014;7(4):1310–1319. doi: 10.1016/j.celrep.2014.03.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Gruber TA, et al. An Inv(16)(p13.3q24.3)-encoded CBFA2T3-GLIS2 fusion protein defines an aggressive subtype of pediatric acute megakaryoblastic leukemia. Cancer Cell. 2012;22(5):683–697. doi: 10.1016/j.ccr.2012.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Dollé ME, et al. Rapid accumulation of genome rearrangements in liver but not in brain of old mice. Nat Genet. 1997;17(4):431–434. doi: 10.1038/ng1297-431. [DOI] [PubMed] [Google Scholar]
- 70.Shelford VE. Some concepts in bioecology. Ecology. 1931;12(3):455–467. [Google Scholar]