Cell and nanoparticle transport in tumour microvasculature: the role of size, shape and surface functionality of nanoparticles (original) (raw)
Abstract
Through nanomedicine, game-changing methods are emerging to deliver drug molecules directly to diseased areas. One of the most promising of these is the targeted delivery of drugs and imaging agents via drug carrier-based platforms. Such drug delivery systems can now be synthesized from a wide range of different materials, made in a number of different shapes, and coated with an array of different organic molecules, including ligands. If optimized, these systems can enhance the efficacy and specificity of delivery compared with those of non-targeted systems. Emerging integrated multiscale experiments, models and simulations have opened the door for endless medical applications. Current bottlenecks in design of the drug-carrying particles are the lack of knowledge about the dispersion of these particles in the microvasculature and of their subsequent internalization by diseased cells (Bao et al. 2014 J. R. Soc. Interface 11, 20140301 (doi:10.1098/rsif.2014.0301)). We describe multiscale modelling techniques that study how drug carriers disperse within the microvasculature. The immersed molecular finite-element method is adopted to simulate whole blood including blood plasma, red blood cells and nanoparticles. With a novel dissipative particle dynamics method, the beginning stages of receptor-driven endocytosis of nanoparticles can be understood in detail. Using this multiscale modelling method, we elucidate how the size, shape and surface functionality of nanoparticles will affect their dispersion in the microvasculature and subsequent internalization by targeted cells.
Keywords: drug delivery, multiscale modelling, fluid–structure interaction
1. Introduction
A number of biophysical barriers can prevent circulating agents from accumulating at tumour sites at satisfactory levels. Thus, the delivery efficiency of drug molecules as well as imaging agents can be very low. The biophysical barriers include the sequestration in the reticulo-endothelial system (RES) organs [1,2], cellular uptake by immune cells [3,4], degradation by protein absorption (opsonization) within the blood flow [5], low permeability of the blood vessels and adverse interstitial fluid pressure in solid tumours [6–10]. Therefore, the freely administrated drug molecules cannot be efficiently delivered into the tumour site. For instance, only less than 0.1% of the injected drug molecules can be found in 1 g of tumour tissue, signalling the inefficient delivery of these free molecules. However, when these molecules are encapsulated into liposomes, their peak accumulation can be improved by one or two orders of magnitude. Thus, it opens a new avenue for the nanoparticle (NP)-based drug carriers to efficiently deliver the drug molecules or imaging agents into the diseased sites.
In cancer treatment and imaging, the standard strategy for maximizing NP accumulation at the tumour sites relies on the enhanced permeation and retention (EPR) effect [11–14]. At the tumour sites, the vessel walls tend to be discontinuous with fenestrations. The size of these fenestrations is approximately 100–200 nm for mice, depending on the tumour type, stage and location [11]. Therefore, sufficiently small NPs (smaller than the size of fenestrations) can passively exit tumour vessels and diffuse into the tumour tissue. The accumulation of these NPs usually reaches a peak 12–24 h after injection. Then, these NPs should be sterically stabilized and opsonization-resistant within the blood flow, in order to allow long circulation times (hours to days). However, major RES organs, such as the liver and spleen, are also characterized by a fenestrated endothelium and adopt the same mechanism to sequester the foreign circulating objects, i.e. drug molecules and NPs. Thus, not surprisingly, most of the systemically injected drug molecules and NPs accumulate in the RES organs. In addition to this, we should emphasize that the EPR-based delivery strategy is solely and exclusively limited to cancer therapy and imagining, and does not provide a general method for drug delivery, as discussed by Nie [15]. Therefore, the design principle for drug carriers has been extended by not only considering the EPR effect (passive targeting) but also the local environment (active targeting), such as pH value [16,17], for targeted drug delivery.
Up to date, there are several classes of NPs demonstrating promising properties as therapeutic carriers, such as solid lipid NPs, liposomes, quantum dots, dendrimers and polymer micelles. By loading the drug molecules into these NPs, their bio-distribution, pharmacokinetics and toxicity can be dramatically improved, in comparison to their freely administrated counterparts [19–21]. Nevertheless, the accumulation of these NPs in the diseased sites is still undesirably low and can be improved. To resolve this issue, there are many strategies developed for designing efficient NP-based drug carriers [22–24]. For example, vascular targeting has been proposed as a general strategy to enhance the concentration of NPs and the associated drug molecules, within the diseased tissue. In this case, injected NPs are decorated with targeting moieties (ligands) that specifically recognize and firmly bind to the over-expressed specific receptors on the abnormal vessels walls [25–27].
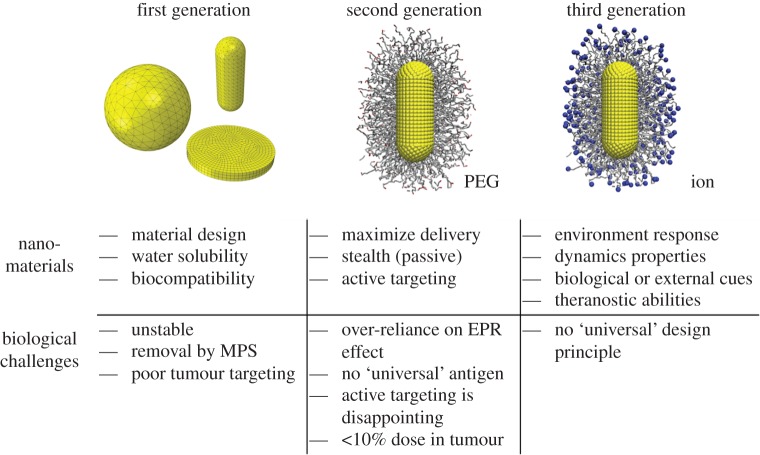
The physiochemical properties of NPs, such as size, shape, surface functionality and stiffness (4S parameters), can affect their biological clearance [18,23,24,28,29]. Therefore, NPs can be modified in various ways to extend their circulation time [13,14]. In the past decades, the design of NPs for biomedical applications has been advanced by studying their biological responses. The evolution of the NP carriers has followed advances in understanding of how 4S parameters affect their efficacy. As shown in figure 1, there are three generations of NPs developed for biomedical applications [18,23]. In the first generation of NPs, they are functionalized with basic surface chemistries (charges/ligands) and are evaluated through their biocompatibility and toxicity. However, these NPs are unstable and usually internalized by the immune cells (macrophages) during circulation. To overcome these problems, in the second generation, the surfaces of NPs are grafted with polymer chains, improving their water solubility and allowing them to avoid aggregation and opsonization. Compared with the first generation, the second generation of NPs demonstrate improved stability and targeting in biological systems. However, the active targeting of these NPs to the tumour cells or other diseased cells is still disappointing. Thus, the third-generation NPs shifts the design paradigm from stable materials to ‘intelligent’ and environmentally responsive materials with improved targeting capabilities. Local environmental (i.e. pH value) changes cause the properties of these NPs to change in a prescribed way. Here we should emphasize that although the design of NPs shifts from the first generation to the third generation, the first- and second-generation NPs still have many applications in different areas, but their behaviours are still poorly understood. Moreover, a comprehensive understanding on the first- and second-generation NPs will help us to efficiently design the third-generation NPs, which will be pursued in this study.
Figure 1.
Evolution of the design of nanoparticles with their properties and biological challenges. MPS, EPR and PEG denote mononuclear phagocyte system, enhanced permeation and retention and polyethylene glycol, respectively. See the main text for more discussions. Adapted from [18]. (Online version in colour.)
When the NP-based drug carriers are injected into the blood flow, they will experience several important steps during their life journey to be delivered into the diseased site [28]: (i) microcirculation with red blood cells (RBCs), white blood cells (WBCs), platelets and many others in the blood flow, (ii) firm absorption by the vessel wall around the tumour site, (iii) diffusing to the tumour site, and (iv) recognition and uptake by the tumour cells. Owing to the complexity of drug delivery process, it is usually difficult to trace the behaviours of NPs step by step in this process and understand their behaviours. On the contrary, with the advancements in computational modelling, the behaviours of NPs within blood flow and their interactions with disease cells can be more accurately quantified [18,28,30–32]. Therefore, the detailed physical mechanisms underpinning the NP-mediated drug delivery can be understood through these simulations, which will be useful in guiding the design of NPs with high efficacy.
This paper is organized as follows. Section 2 summarizes the current knowledge of NP-mediated drug delivery by focusing on the transport of NPs within the blood flow and their subsequent internalization by diseased cells. The effects of NP size and shape will be further explored through immersed molecular finite-element method (IMFEM) simulations in §3. Section 4 will demonstrate how the NPs’ shape and surface functionalization will influence their internalization behaviours. Finally, §5 concludes the present study and discusses the future research directions with the advancements in multiscale modelling.
2. State of knowledge
2.1. Vascular dynamics of nanoparticles
2.1.1. Margination behaviour of nanoparticles
Blood is a dense suspension of deformable cells in plasma, with RBCs comprising approximately 35–45% by volume while WBCs and platelets occupy less than 1%. The volume fraction of RBCs is called haematocrit. In large vessels, due to the high shear rates, blood can simply be modelled as a Newtonian fluid. However, in the microcirculation and near the vessel walls, the transport, rolling and adhesion dynamics of NPs are affected by the presence of RBCs. In particular, it is well documented that fast moving RBCs tend to push circulating WBCs and NPs laterally, thus affecting their dynamics and wall deposition [26,33]. Therefore, in the microcirculation and in proximity of the vessel walls, the potential importance of non-Newtonian effects warrants careful investigation.
In experiments, different components in the blood flow, including the RBCs, WBCs, platelets and NPs, are found to segregate under normal physiological conditions [34,35]. The RBCs tend to migrate away from the vessel wall and concentrate in the middle of the vessel. Thus, a ‘cell-free layer’ is formed near the vascular wall, which is approximately 1 µm thick [36]. However, the WBCs, platelets and some of the NPs prefer to migrate into this ‘cell-free layer’. This behaviour is called ‘margination’. In NP-mediated drug delivery, the drug molecules can be more efficiently delivered to the tumour through the margination behaviour of NPs, which increases NPs' interaction with the vascular wall. This allows the NPs to better ‘sense’ the biophysical and biological abnormalities, such as the presence of fenestrations or the expression of specific receptors, on the surface of endothelial cells. Afterwards, the NP can firmly adhere to the vessel wall under flow, if the hydrodynamic forces are balanced out by the interfacial adhesive interactions between the NP and vessel wall. The adhesive interaction can be specific, i.e. formation of ligand–receptor bonds, and non-specific, i.e. van der Waals, electrostatic and steric interactions. Margination and the subsequent adhesion of NPs to the endothelium allow the NPs to transmigrate across the endothelial wall and enter a diseased area of tissue, eventually delivering the drug molecules. Therefore, irrespective of the targeting mechanism (specific or non-specific), an efficient drug carrier should be able to migrate into the ‘cell-free layer’ at the tumour site, thereby maximizing its interaction with the tumour vascular wall.
2.1.2. 4S parameter effects on margination propensity
Margination propensity depends on the 4S parameters of NPs. The effects of these parameters on NP margination are summarized in table 1. The size of the NP is an important parameter in designing drug carriers. The NPs smaller than 10 nm will be cleaned from the blood stream through the kidney or via extravasation from a tumour [49]. However, the NPs larger than 200 nm are at risk of being filtered out by the liver or spleen or destroyed by the bone marrow. Charoenphol et al. [40] studied the NP size effect by using spheres with diameters ranging from 0.5 to 10 µm in the blood. The margination propensity is found to increase with the sphere diameter. Recently, Lee et al. [38] explored the NP size effect through combined in vivo and in silico studies, by using spherical polystyrene NPs with diameters of 10–1000 nm. The simulation and experimental results confirm that larger NPs (greater than 500 nm) can migrate into the ‘cell-free layer’, while smaller NPs (less than 200 nm) are mostly trapped between RBCs in the core region. However, to date, there is not a consensus on an optimal NP size for margination [31,34,37,38,40].
Table 1.
Summary of the effects of 4S parameters on NP margination.
| parameter | key observations | key references |
|---|---|---|
| size | 500 nm and larger diameter spherical NPs exhibit margination behaviour, while 200 nm and smaller NPs are trapped between RBCs within the core of the blood flow | [34,35,37–40] |
| shape | non-spherical NPs with a higher aspect ratio marginate more readily than spherical NPs | [34,37,41,42] |
| surface | studies are too different to draw any meaningful conclusions | [43,44] |
| stiffness | conflicting simulation results have been reported for WBCs | [45–48] |
The margination and adhesion of different shaped NPs have been theoretically and experimentally (in vitro) studied. Spherical, quasi-hemispherical and discoidal NPs have been compared [34,35]. Thin discoidal NPs are found to exhibit larger lateral drift velocities (migration rate) than other NPs, under the influence of hydrodynamic forces [34,35]. These results indicate that thin discoidal NPs more probably interact with the vascular wall. Some of the theoretical, in vitro and in vivo experimental results have revealed that thin discoidal particles can more firmly adhere to the lateral walls under shear flow when compared with spherical and slender cylindrical particles [26,50,51]. The thin discoidal NPs are observed to offer a larger surface of adhesion and a smaller cross section, leading to lower hydrodynamic forces and larger adhesive interaction. Similarly, Gentile et al. [35] found that disc-shaped and hemispherical NPs migrated more compared with their spherical counterparts. Moreover, gold nanorods exhibit much higher margination propensity than gold nanospheres, as revealed by Toy et al. [37]. The evidence clearly demonstrates that NP shape can dramatically affect their vascular dynamics.
The effect of NP stiffness has been explored through the margination of WBCs. Freund studied the mixture of RBCs and WBCs in flow [45]. When the stiffness of RBCs was enlarged by a factor of 10, the observed change of margination propensity for WBCs was negligible. Thus, the author concluded that the deformability of RBCs does not affect the margination behaviours of WBCs. Kumar & Graham [46] modelled a dilute suspension of elastic capsules under simple shear flow. Contradictory to the results reported by Freund [45], they found that stiff particles (such as WBCs) tend to marginate, while the soft (‘floppy’) particles (such as RBCs) accumulate near the centre of the channel [46]. Later, they studied a system containing both type of particles and found that the stiff and soft particles mimicked the behaviours of WBCs and RBCs in the blood flow [47], respectively. The margination of stiff particles is attributed to the heterogeneous collisions between these particles [48]. Recently, the deformability (stiffness) of particles and its effect on transport in blood circulation has been noted by the group of DeSimone [52]. They adopted the PRINT approach, which is similar to the hydrogel-template strategy, to demonstrate that deformable microparticles (5 µm) with concave shape can circulate longer than their rigid counterparts [52].
Through Monte Carlo simulations, Wang & Dormidontova [53,54] have studied the binding between a spherical NP tethered with ligands and a planar cell surface with mobile receptors. The core size of the NP, grafting density, tether length and the per cent of functionalization by ligands are found to play important roles in the binding affinity of NPs for the cell surface. Radhakrishnan and co-workers [55,56] have developed a Monte Carlo method to calculate the binding free energy between functionalized NPs and endothelial cell surfaces. The obtained results demonstrate that there exists a critical antibody density, below which the binding affinity drops dramatically. All these results demonstrate the important role played by the surface properties of NPs, i.e. grafted chains and their length, grafting density and ligand density. In addition, the shape and size of NPs are also theoretically found to have great influence on the adhesive strength [26,50]. Thus, studying the binding affinity between NPs and vessel wall under the combined influence of the 4S parameters and the shear flow is essential to fully understand the mechanisms controlling drug-delivery efficacy [57].
Although extensive experimental studies have been carried out to understand the effect of 4S parameters of NPs on their drug-delivery efficacy, many conflicting results have been reported for varied conditions. For example, Toy et al. [37] measured the margination of spherical NPs with diameters ranging from 60 to 130 nm in a bloodless solution. They found that the smaller NPs diffused much faster than larger NPs due to the Brownian motion [21]. However, through a combined in vivo and in silico study, Lee et al. [38] found that 1 µm NPs exhibited near wall dispersion, whereas 200 nm NPs were distributed randomly in the blood vessel when RBCs were present. The smaller NPs appear to get trapped within the spaces between RBCs, slowing their diffusion toward the vascular wall and suggesting that smaller NPs may not always be better. The different results reported by these studies are induced by different haematocrit. To resolve above controversy and provide a unified picture of how to design efficient NPs, we need to create a multiscale computational method for studying the vascular transport and deposition of NPs with different 4S properties, under the same relevant physiological conditions such as vessel diameter, shear rate and haematocrit.
2.2. Internalization of nanoparticles
After the NP approaches the surface of tumour cells, it has to be internalized to deliver the attached drug molecules into the interior of the cell. This process, so-called ‘endocytosis’, involves several important steps: (i) NPs are specific-bound to the cell membrane, (ii) NPs are wrapped by the membrane and a membrane-bound NP complex is formed, (iii) an early stage endosome is formed due to the pinching-off of the membrane budding, and (iv) endosomal release of the NP during the late stage of the endosome. Note that endocytosis is also an important process for cells to internalize small molecules, such as proteins and other macromolecules.
The size and shape of NPs have been identified as two key parameters to control their internalization behaviours [58–60]. Aoyama and co-workers explored the size effect of endocytosis in the subviral region, by using the lipophilic CdSe quantum dot coated with trioctylphosphine oxide [59]. Comparing the NPs with different diameters, i.e. 5, 15 and 50 nm, they found a dramatic size effect as 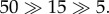 Later on, Chan and co-workers have systematically studied the NP size effect by using Au NPs with different diameters from 10 to 100 nm [60]. The uptake half time of Au NPs with diameters of 14, 50 and 74 nm is 2.1, 1.90 and 2.24 h, respectively. Again, they find that Au NPs with diameter of 50 nm can be most efficiently taken up by the diseased cells. Thus, both the kinetics and saturation concentrations of NPs can be highly influenced by their physical dimensions. They also explored the potential NP shape effect by using the spherical and rod-like NPs. The NP uptake is found to be dependent on the shape and uptake of rod-like NPs is less efficient than their spherical counterparts [60]. For instance, 500 and 375% more 74 and 14 nm spherical NPs can be internalized by cells than 74 × 14 nm rod-like NPs, respectively. Further studies reveal that the local curvature of non-spherical NPs controls the endocytic kinetics when the NPs approach the cell surface [61,62].
Later on, Chan and co-workers have systematically studied the NP size effect by using Au NPs with different diameters from 10 to 100 nm [60]. The uptake half time of Au NPs with diameters of 14, 50 and 74 nm is 2.1, 1.90 and 2.24 h, respectively. Again, they find that Au NPs with diameter of 50 nm can be most efficiently taken up by the diseased cells. Thus, both the kinetics and saturation concentrations of NPs can be highly influenced by their physical dimensions. They also explored the potential NP shape effect by using the spherical and rod-like NPs. The NP uptake is found to be dependent on the shape and uptake of rod-like NPs is less efficient than their spherical counterparts [60]. For instance, 500 and 375% more 74 and 14 nm spherical NPs can be internalized by cells than 74 × 14 nm rod-like NPs, respectively. Further studies reveal that the local curvature of non-spherical NPs controls the endocytic kinetics when the NPs approach the cell surface [61,62].
To understand the NP size and shape effects, both theoretical and computational studies have been pursued in the past years [63–68]. The pioneering work done by Gao et al. [63] points out that the endocytosis of NPs relies on competition between the bending of membrane and diffusion of free receptors to the docking site when the NP approaches cell surface. Therefore, both small and large NPs cannot be efficiently taken up due to the energy barrier of membrane bending and limitation of free receptors, respectively. Their theoretical model predicts the optimal size of NP of approximately 25–50 nm [63], which agrees well with previous experimental observations. However, due to the complex kinetic process involved during the endocytosis of non-spherical NPs, the theoretical study can only be used to qualitatively explain the NP shape effect. More information has been revealed through large scale molecular simulations (e.g. [67,69–71]). These simulation results show that the spherical NPs are the most efficient carriers to be accepted by diseased cells. The membrane bending energy is the major reason why the non-spherical NPs are less efficient to be delivered into the diseased cell. The kinetics of endocytosis plays an important role in design of drug carriers. For instance, the efficacy of drug carriers does not only depend on how many, but also relies on how fast they can enter the diseased cell. As demonstrated in the present study, both the NP surface property and shape can dramatically affect the endocytic kinetics, which should be taken into consideration in the design of drug carriers.
In recent years, the stiffness of NPs has also been recognized as a key parameter to control their endocytic kinetics. Theoretical [74], computational [75] and experimental [76,77] studies have uncovered that the stiff NPs can be more easily internalized by cells, comparing with their soft counterparts. The theoretical model developed by Yi et al. [74] has excellently explained how the stiffness of NPs can control their internalization. For example, when a soft NP approaches the cell membrane, it can spread out on the cell surface with a large wet angle. Then, the highly spread out NP introduces a large local curvature at the spreading front. In this way, the endocytosis of a soft NP encounters a very large membrane bending energy barrier akin to the spread shape. Eventually, the membrane wrapping of the soft NP may be prevented by the large energy barrier (table 2).
Table 2.
Summary of the effects of 4S parameters on NP internalization.
| parameter | key observations | key references |
|---|---|---|
| size | spherical NPs with diameter about 25–50 nm can be most efficiently delivered | [58–60] |
| shape | non-spherical NPs are less efficient comparing with their spherical counterparts due to large membrane bending energy | [60–62] |
| surface | controversial results have been reported | [15,72,73] |
| stiffness | stiff NPs are more efficient than soft ones | [74–76] |
Molecular-specific NPs have been developed with the goal of improving tumour-specific accumulation. The surface of these NPs is coated with ligand molecules capable of recognizing and binding receptors expressed on the target cells [72]. Despite their extraordinary in vitro efficiency, this approach has demonstrated limited success in vivo. Potential reasons include changes in ligand binding affinity, ligand immunogenicity and constraints on the ligand presentation, particularly on small NPs with limited surface area. As a result, tumour targeting with molecular-specific NPs remains controversial, as highlighted by Nie and co-workers [15,73]. Therefore, designing the surface functionality of the NPs is still a challenge, which needs to be further explored in detail.
3. Vascular transport of nanoparticles predicted by immersed molecular finite-element method
3.1. Model and methodology
The IMFEM [78–83] is a computational framework to concurrently deal with the relevant physical interactions in biological environments [80,84,85], including fluid–structure interaction (FSI) [82,86,87], cell–cell interaction [81,88,89], thermal fluctuation [78,79,90], electrokinetics [83,91,92], self-assembly behaviour [79,93–95] and other mesoscale and molecular effects [96]. In this work, the IMFEM will be used to simulate the blood flow as well as the microcirculation of NPs. In this case, the deformable RBCs will be immersed into a Newtonian fluid, representing the blood plasma. The microcirculation of NPs within the blood will be analysed as a function of the 4S parameters, and the local vascular conditions, i.e. vessel diameter and flow velocity. Then, the cell–cell, cell–NP and NP–NP interactions will be explicitly accounted for as described below and will be coupled with an Eulerian fluid domain within IMFEM. The NPs are treated as Lagrangian solids in the Eulerian fluid domain, as described in figure 2. The FSI forces are calculated on the surfaces of RBCs and NPs, and subsequently distributed onto the surrounding fluid domain through a Dirac delta function or reproducing kernel particle method (RKPM) [97,98]. The underlying governing equation for the Eulerian fluid is the Navier–Stokes equation, which can be directly solved by a fluid solver. The movement of RBCs and NPs is determined by the hydrodynamic forces and thermal fluctuations, as well as their interactions.
Figure 2.
Mathematical framework for immersed molecular finite-element method, which is based on a Navier–Stokes equation solver. The structural equation is treated as a fluid–structure interaction force distributed into the fluid domain by the reproducing kernel particle method function. (Online version in colour.)
The initial shape of the RBC is a biconcave discoid with its cross-sectional profile defined by a mathematical expression [81]. The deformation of RBCs is defined by a hyper-elastic, Mooney–Rivlin, strain energy function. The material properties of the RBC membrane have been calibrated from the experimental results on the uniaxial tension of a single RBC [99], as given in figure 3. The RBC–RBC interaction is described by a Morse-type potential, which has been theoretically provided by Neu et al. [100,101]. To prevent overlap between RBCs and NPs in the simulations, we adopt a Lennard-Jones potential for RBC–NP and NP–NP interactions [31,38]. To correctly capture the multiphase nature of the plasma–cell–NP mixtures, their interactions are also coupled with the Navier–Stokes equation for the fluid domain. The interaction forces are calculated for each element on the surfaces of RBCs or NPs by using a cut-off distance to determine which elements of nearby cells are within the domain of influence. The interactions forces are integrated over the surface area within the affected domain. The calculated forces on the surfaces of RBCs and NPs are distributed onto the surrounding fluid domain through the RKPM [97,98]. These FSIs are also included into the equations of motion for the fluid domain. After solving the governing equations, the velocities of the fluid domain are interpolated onto the surfaces of RBCs and NPs, which ensures the no-slip boundary condition on the surfaces of RBCs or NPs. Here we should emphasize that although the fluid domain is modelled as a Newtonian fluid, the non-Newtonian behaviour in the microcirculation emerges from the multiphase mixture of RBCs and NPs, and is correctly captured through our IMFEM simulations.
Figure 3.
Validation of immersed finite-element method on a single red blood cell (RBC): (a) deformation behaviour of the RBC under uniaxial tension, (b) deformation of RBC along the tensile and transverse directions when it is under uniaxial tension and (c) tank-treading behaviour of RBC under a shear flow (maximum shear velocity is 100 µm s–1). The experimental assumptions and results in (a) and (b) are reproduced with permission from [99]. The tank-treading behaviour of RBC under the shear flow has been observed in experiments by [102]. (Online version in colour.)
The IMFEM simulation of blood flow has been validated and verified through comparisons with the following experiments: (i) RBC deformation along the tensile and transverse directions when it is under uniaxial tension [99], (ii) tank-treading behaviour of RBC under a shear flow [102,103], (iii) discharge haematocrit out of the vessel [104], (iv) discharge haematocrit out of the vessel [104], and (v) cell-free-layer thickness at different haematocrits [105,106], as discussed in our recent study [38]. For all of these cases, experimental results are found to be in good agreement with our simulations, supporting the accuracy and validity of the proposed approach. After the model and methods are validated, the coefficient of radial dispersion _D_r of NPs regulating their near-wall accumulation in blood vessels can be determined through the IMFEM simulations. For a given number of NPs, N, the dispersion coefficient _D_r is defined as
 |
3.1 |
|---|
where ri(t) and ri(0) are the distances of NPs to the centre of vessel at the time t and 0, respectively. Here the dispersion coefficient _D_r of NPs is obtained by averaging over all the NPs in the microcirculation. If the dispersion coefficient is positive, it indicates that NPs tend to accumulate near the blood vessel wall in the circulation. Otherwise, they will tend to circulate with RBCs in the blood flow. In this way, the dispersion coefficient provides an important characterization of a NP's efficiency as a drug carrier. The larger the dispersion coefficient, the better the drug carrier, as NPs that spend more time in the cell-free layer are more likely to adhere to vessel walls.
3.2. Effects of nanoparticle size and shape on microcirculation behaviour
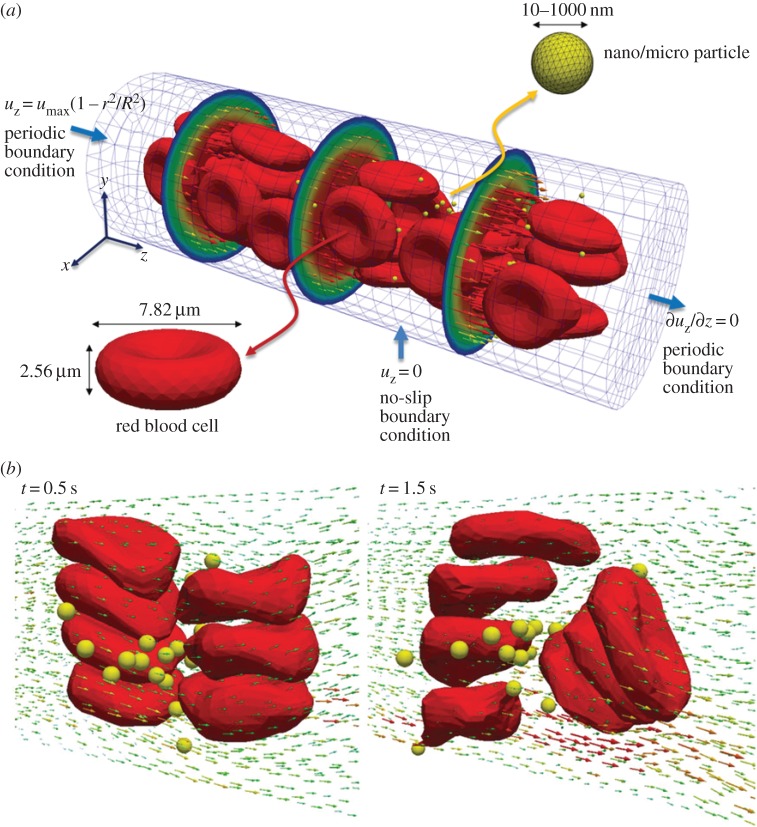
To understand the NP size effect on its microcirculation behaviour, 100 rigid, spherical NPs with equal diameter (varying between simulations from 20 to 1000 nm) are randomly distributed within the capillary in the initial configurations, as described in figure 4. Under the normal physiological conditions, we find that the deformation of RBCs modifies the local surrounding flow field. Specifically, the deformed RBCs are pushed away from the vessel wall and tend to accumulate within the centre of the blood vessel, leading to the formation of a ‘cell-free layer’. The modified local flow field around RBCs dramatically changes the microcirculation behaviours of the NPs (cf. figure 4). When the diameter of NPs is larger than 500 nm, the NPs are pushed away from the centre of blood vessel, due to the tumbling of RBCs. Thus, the large NPs migrate into the ‘cell-free layer’ and tend to accumulate near the vessel wall. Such margination behaviour of large NPs mimics WBCs and platelets during circulations. When the diameters of the NPs are smaller than 500 nm, they can stay within the space between RBCs during circulation. Interestingly, the NPs distributed within the centre of the blood vessel cannot escape away, as their movements are blocked by the RBCs. The radial dispersion coefficients _D_r of different sized NPs are also calculated during the simulations. _D_r of NPs with 1000 nm diameters are found to be six times larger than those of 100 nm NPs, indicating the important role played by the size of NPs.
Figure 4.
(a) Initial configuration of deformable red blood cells (RBCs) and spherical rigid particles dispersed within a 20 × 60 µm capillary. A parabolic velocity profile is assigned at the inlet section with a maximum velocity of 100 µs−1. (b) Complex flow field is formed around the particles, in the vicinity of RBCs. Adapted from [38]. (Online version in colour.)
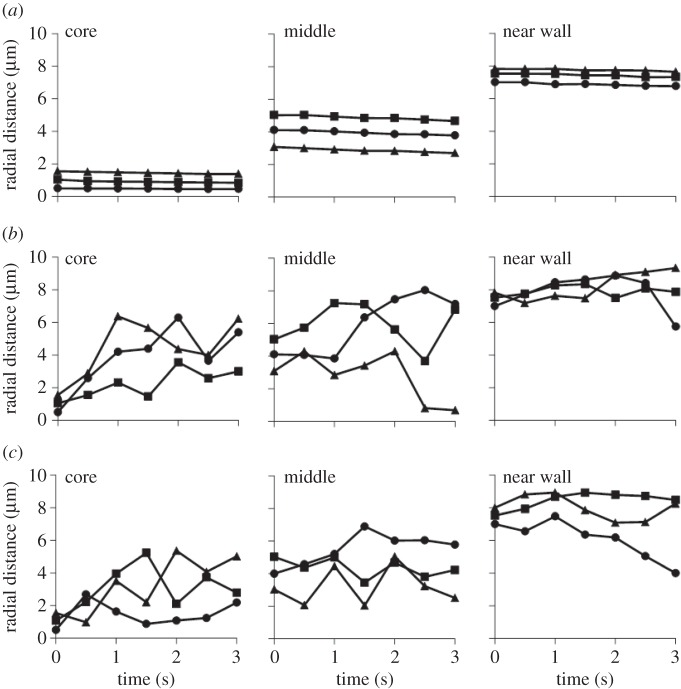
The concentration of the RBCs is also found to play an important role in this process. For example, the trajectories of 100 and 1000 nm NPs in a capillary with different haematocrits, namely 0, 15 and 30%, are given in figures 5 and 6. Clearly, in the absence of RBCs (0% haematocrit), the NPs follow the streamlines without appreciable lateral drifting, regardless of the NP size. However, for the case with 15 and 30% haematocrits, lateral motions for NPs are found to deviate away from the core region and move toward the midline. The largest and more rapid fluctuations along the radial direction of the vessel were observed for the small NPs (100 nm in diameter), at the lower haematocrit (15%). Indeed, with a lower RBC volume fraction, the separation distance between adjacent cells is larger and NPs can more easily move through the circulating cells, thus leading to a more hectic NP dynamics. Overall, these results further demonstrate that larger, sub-micrometre- and micrometre-sized NPs can be more efficiently excluded by the vessel core, pushed laterally by the fast moving RBCs, whereas the smallest NPs would benefit far less from this exclusion mechanism and would stay confined with the vessel core for a longer time.
Figure 5.
Trajectories for spherical particles with 100 nm diameter in a capillary with different haematocrits: (a) 0%, (b) 15% and (c) 30%.
Figure 6.
Trajectories for spherical particles with 1000 nm diameter in a capillary with different haematocrits: (a) 0%, (b) 15% and (c) 30%.
To quantify the effective dispersion of NPs during microcirculation, we further introduce the effective radial dispersion coefficient, defined as _D_r/_D_B, where _D_B is the diffusion coefficient of NPs induced by the Brownian motion. According to the classical Stokes–Einstein relation, we have
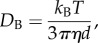 |
3.2 |
|---|
where _k_B and T are the Boltzmann constant and temperature, respectively, d is the diameter of particles and η is the viscosity of the fluid. Then, the effective radial dispersion coefficients for NPs with diameters of 100 and 1000 nm can be obtained and are given in figure 7a with haematocrits of 15%. The effective dispersion ratio _D_r/_D_B is larger for NPs in the vessel core and reduced for NPs in the ‘cell-free layer’. Comparing with the 1000 nm NPs, the effective dispersion ratio is always smaller for the 100 nm NPs, signalling that the larger sized NPs are more efficient. Moreover, the contribution of RBCs to the dispersion of smaller NPs is relatively small. Finally, the NP shape effect can be explored by the same method. As given in figure 7b, the different shaped NPs, such as sphere, capsule and ellipsoid, can be studied and their lateral drifting velocities are calculated. The ellipsoid-shaped NP is found to more efficiently drift away from the core region of the vessel. Further studies will be pursued to understand the NP shape effect in detail.
Figure 7.
(a) Effective radial dispersion coefficients for particles of 100 and 1000 nm in diameter with 15% haematocrit. (b) Drift velocity of the different shaped particles in a capillary with 30% haematocrit. (Online version in colour.)
4. Molecular simulation on internalization of nanoparticles
4.1. Model and methodology
To study the internalization behaviour of the NPs, we adopt the dissipative particle dynamics (DPD) method [107,108], which can accurately account for the hydrodynamic interactions by considering the water molecules explicitly. In the DPD method, a single bead represents a group of atoms or molecules. Thus, DPD can approach larger temporal and spatial scales in comparison to classical molecular simulations. Additionally, the interactions between different molecular species can be accurately reproduced by the conservative force in the DPD simulations [71,109]. As a result, the DPD method is well suited to study the endocytosis of NPs as different molecules involved.
As presented in figure 8, the lipid molecule is represented by the H3(T5)2 model. Each lipid molecule consists of a lipid head with two tails, formed by three hydrophilic (H) and five hydrophobic (T) beads, respectively. Then, the neighbouring beads are connected together by a simple harmonic spring. To ensure the linearity of the lipid heads and tails, a harmonic bending potential is applied on the adjacent three beads. To represent the hydrophilic/hydrophobic property of the head and tail beads, the repulsive interaction parameters for the same type of beads are the same; while it has been enlarged for different beads. Then, the lipid molecules can self-assemble into a stable lipid bilayer in the water environment. For the detailed set-up of the DPD simulation, the readers are referred to our previous studies [71,109]. For the model of NPs, we consider that the NP is formed by a rigid core with a surface coated polymer [110]. A typical model system will be the PEGylated Au NPs, with the core and shell representing Au NP and PEG polymer, respectively. In the DPD simulation, the relative position of the core beads for the NP is fixed by considering a rigid core. The tethered polymer chains are rather flexible and hydrophilic, preventing the clustering of NPs in the solution. Each pair of beads on a tethered polymer chain is connected through a harmonic bond with adjacent three beads constrained through a harmonic bending potential, ensuring the persistent length of the polymer chains is realistic. The potentials of the bond and angle are calibrated through the statistical distributions of the bond and angle of the PEG polymer immersed into the water, which are obtained through the all-atomic simulations [109]. In this way, the conformation of the tethered PEG polymers can be accurately represented in our DPD simulations. All the potential parameters for the grafted PEG polymers and their interactions with lipid molecules are reported in our recent studies [71,109]. The representative DPD models for PEGylated NPs are shown in figure 8. With these models at hand, the internalization of PEGylated NPs can be studied by our DPD simulations.
Figure 8.
(a) H3(T5)2 model for the lipid molecule and corresponding lipid bilayer in the simulation box. The hydrophilic heads and hydroponic tails of lipid molecules are coloured by blue beads and silver lines, respectively. For clarity, the solvent (water) molecules are made invisible. (b) Models for PEGylated NPs with grafted PEG chain length N = 18, corresponding to molecular weight of 815 Da. The core diameter of the NP is approximately 8 nm, coloured by yellow. The grafted PEG chains and targeting moieties bound to their free ends are coloured by cyan and blue, respectively. For clarity, the solvent molecules are made invisible. (Online version in colour.)
Here we assume that the NPs have already reached the tumour cells in simulations. Therefore, the endocytosis of these NPs by the cell can directly indicate the efficacy of these drug carriers in treating the disease. To mimic the receptor-mediated endocytosis in our simulations, the cell membrane is considered to contain rich-receptor embedded regimes, which is the typical situation for tumour cells. Then, the free ends of tethered PEG chains are covalently bound with specific ligands, which can recognize and bind with these receptors. In this way, our simulation model could well reproduce the receptor-mediated endocytosis pathway [71,109].
4.2. Effects of nanoparticle surface functionality and shape on internalization behaviour
The endocytoic kinetics of the PEGylated NPs with spherical core are given in figure 9. The diameter of the core is approximately 8 nm and the molecular weight of tethered chain is approximately 838 Da, which falls within the experimentally relevant range. Owing to the different grafting density of PEG, we can observe quantitatively different behaviours of these PEGylated NPs. For example, when the grafting density is low, e.g. 0.2 chains nm−2, the PEGylated NP can be absorbed on the surface of cell membrane at the beginning. However, after a long simulation time (more than 2000 ns), the PEGylated NP is still on the surface of membrane and cannot be delivered into the interior of the cell. When the grafting density has been increased to 1.6 chains nm−2, the PEGylated NP will be wrapped by the cell membrane at the beginning, which is the so-called ‘membrane-bending’ stage. This is followed by the ‘membrane-extruding’ stage, as the upper leaflet of the membrane will extrude to wrap around the surface of the NP. Eventually, the NP will be fully wrapped by the membrane and form a NP–membrane complex. In this way, the PEGylated NP can be delivered into the diseased cell for targeted drug delivery.
Figure 9.
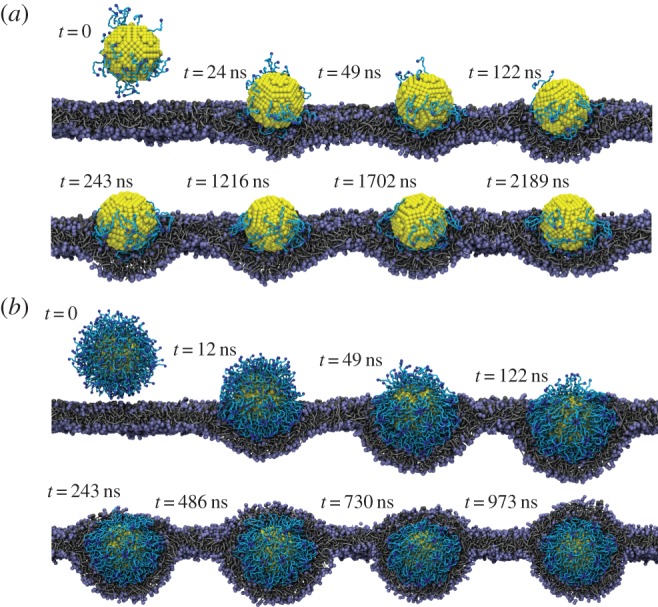
Representative DPD simulation snapshots for the internalization process of PEGylated NP with grafting densities of (a) 0.2 and (b) 1.6 chains nm−2. The core diameter is approximately 8 nm. The grafted PEG chain length is N = 18. Same colour scheme as in figure 8 is used. (Online version in colour.)
Given these different behaviours of PEGylated NPs, we may wonder why the different grafting densities of PEG polymer play an important role. In our recent studies [28,71,109], it has been revealed that three major free energy changes are involved during endocytosis: (i) specific ligand–receptor interactions, (ii) membrane bending energy, and (iii) non-specific entropy change of tethered chains. In these free energy contributions, the specific ligand–receptor interaction provides the driving force for the PEGylated NP to be wrapped by the lipid bilayer and eventually delivered into the cell. However, the bending energy change and the entropy loss of tethered chains create energy barriers, preventing the internalization of NPs. In this case, if the driving force provided by the ligand–receptor interaction is not strong enough to overcome the energy barrier created by the membrane bending and entropy loss of tethered chains, the NP cannot be internalized. According to the above argument, we have developed a theoretical method (mean-field approach) to estimate the entropy loss of the tethered chains [71,109]. The free change per chain during this process is found to be approximately 1_k_B_T_, where _k_B and T are the Boltzmann constant and temperature, respectively. When the grafting density is low, i.e. 0.2 chains nm−2, the corresponding entropy loss is also small. However, the ligand–receptor interaction is also weak, as the ligands are conjugated to the free ends of tethered chains. Thus, the PEGylated NPs cannot be internalized. On the contrary, the PEGylated NPs with large grafting density can be quickly accepted by the cell, as the specific ligand–receptor interaction is strong enough to overcome the energy barriers. These observations highlight the important role played by the surface functionalization of NPs during endocytosis.
The simulation results have also been compared with experimental studies on the J774A.1 uptake of PEGylated Au NPs in serum-free media, done by Walkey et al. [111], as shown in figure 10. When the grafting density of PEG polymer is high, the interaction between the PEGylated NP and cell membrane is very strong, due to the direct interactions between the distal methoxy group at the free ends of the PEG chains and the membrane surface proteins or lipids [111]. However, when the grafting density is low, the interaction between PEGylated NPs and cell membrane becomes very weak. Thus, the PEGylated NPs with high grafting densities could be easily accepted by the cell; whereas low grafting density ones cannot. All these phenomena have been confirmed by molecular simulations and experimental results (cf. figure 10). Nevertheless, the PEGylated NPs could enter the cell through other pathways, such as clathrin-mediated endocytosis, which is beyond the scope of this study [106].
Figure 10.
Effect of grafting density on the cellular uptake efficiency, which is proportional to the internalization rate of PEGylated NPs. (a) Experimental results by Walkey et al. [111] for J774A.1 uptake of PEGylated Au NPs are shown for comparison with our DPD results. (b) Representative transmission electron microscopy images of the intracellular distribution of PEGylated Au NPs with grafting density of 0.96 chains nm−2 and core diameter of 15 nm (B1: scale bar, 1000 nm. B2–B4: scale bar, 100 nm). Images B1–B4 are reproduced with permission from [111]. (Online version in colour.)
The NP shape is also an important design parameter for internalization. As demonstrated in figure 11, the different shaped NPs display different endocytic kinetics, although they have the same ligand–receptor interaction with equal amount of grafted PEG polymers. The spherical, rod-like, cubic and disc-like NPs are compared with the same surface areas for their cores. Under a fixed grafting density, 0.6 chains nm−2, the spherical NP can be most efficiently accepted by the cell, followed by cubic and rod-like NPs, while the disc-like NP can only be found on the surface of cell membrane. The related membrane bending energies are found to be about 8_π_ κ, [8,12)_π_ _κ_, 12_π_ _κ_ and 27.33_π_ _κ_ for spherical, cubic, rod- and disc-like NPs [71], respectively. κ is the membrane bending modulus, of the order of 10–20 k_B_T [71]. Therefore, the different membrane bending energies for these NPs determine their efficiency during endocytosis.
Figure 11.
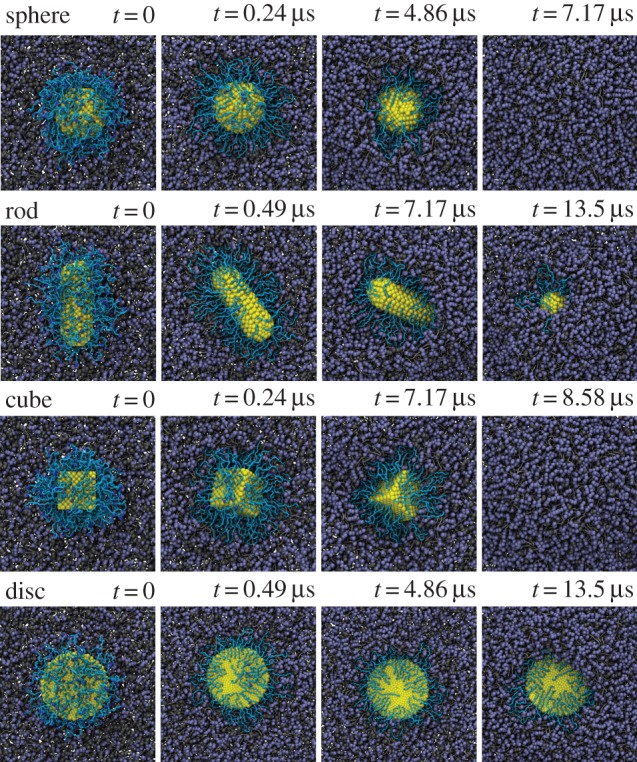
Representative DPD simulation snapshots for the internalization process of PEGylated NPs with different shaped cores: sphere, rod, cube and disc. All these cores have equal surface area. The grafted PEG chain length is N = 30. Same colour scheme as in figure 8 is used. Adapted from [71]. (Online version in colour.)
We should emphasize that the effect of NP shape is always ambiguously evaluated in the experiments due to the interplay between the NP shape and its surface properties. For example, the different shaped NPs have different surface area-to-volume ratios, which makes discerning size effect from surface effect difficult, especially when only a few different shapes are considered. Besides, different shaped NPs have different numbers of ligands per grafted chain due to their different surface curvatures [112]. To clarify the shape effect of NPs, we can first fix the size (diameter) of spherical NPs, and then study the rod or disc NPs under equal surface area-to-volume ratio and ligand-to-grafted-chain ratio. Such precisely defined conditions will allow us to unambiguously explore the shape effect of NPs during endocytosis, which is only achievable through computer simulations.
5. Concluding remarks and perspective
In this work, we have demonstrated that the transport of NPs within the tumour microvasculature can be greatly influenced by their 4S parameters, such as size, shape, surface functionality and stiffness. The microcirculation of NPs and their subsequent internalization by disease cells can be understood through IMFEM and DPD simulations, respectively. The important roles played by the 4S parameters can be elucidated through these simulations. Thus, by combing the IMFEM with DPD simulations, the life journey of the NP-based drug carriers can be predicted through our multiscale modelling approach.
Through these multiscale simulations, fundamental mechanisms underpinning the NP-mediated drug delivery can be elucidated. These detailed physical insights can provide useful guidelines in the design of NPs. For instance, larger sized NPs are found to be able to migrate into the ‘cell-free layer’ through IMFEM simulations, whereas smaller sized NPs could be more efficiently taken up by the diseased cells through theoretical analysis and computer simulations. Based on these observations, a multistage delivery platform has been designed by Ferrari and co-workers [113]. In the design of this platform, biodegradable and biocompatible mesoporous silicon particles are used to carry nano-sized quantum dots or carbon nanotubes. During the microcirculation process, these mesoporous silicon particles can be more easily accumulated at the tumour sites due to the EPR and margination effects. Then, the carried NPs can be gradually released and diffuse into the tumour cells. Through receptor-mediated endocytosis and other pathways, these NPs will be internalized by tumour cells. Comparing with traditional design of NPs, this multistage platform has considered different physical mechanisms during the NP-mediated drug-delivery process. Note that the traditional design of NPs relies on the slow and inefficient ‘Edisonian’ approaches. Such a process is very time-consuming and cost-inefficient. According to the multiscale modelling approach, the design of NPs can be more easily achieved through these computer simulations. In the near future, we hope that simulation-based design paradigms can guide experimental design of next-generation NPs, with enhanced active targeting, low toxicity and limited side effects.
Acknowledgements
We are grateful to Stephen E. Lin for critical reading of the manuscript. Yi.L. acknowledges support from the Department of Mechanical Engineering at University of Connecticut. This research was supported in part through the computational resources and staff contributions provided for the Quest high performance computing facility at Northwestern University and Booth Engineering Center for Advanced Technology (BECAT) at University of Connecticut.
Competing interests
We declare we have no competing interests.
Funding
W.K.L. was partially funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, under grant no. (7-135-1434 HiCi). Ya.L. thanks the support by the Office of China Postdoctoral Council under the International Postdocotral Exchange Fellowship Program 2014.
References
- 1.Cho K, Wang X, Nie S, Chen Z, Shin DM. 2008. Therapeutic nanoparticles for drug delivery in cancer. Clin. Cancer Res. 14, 1310–1316. ( 10.1158/1078-0432.CCR-07-1441) [DOI] [PubMed] [Google Scholar]
- 2.Siepmann J, Siegel RA, Rathbone MJ. 2011. Fundamentals and applications of controlled release drug delivery. Berlin, Germany: Springer Science & Business Media. [Google Scholar]
- 3.De Jong WH, Hagens WI, Krystek P, Burger MC, Sips AJAM, Geertsma RE. 2008. Particle size-dependent organ distribution of gold nanoparticles after intravenous administration. Biomaterials 29, 1912–1919. ( 10.1016/j.biomaterials.2007.12.037) [DOI] [PubMed] [Google Scholar]
- 4.Immordino ML, Dosio F, Cattel L. 2006. Stealth liposomes: review of the basic science, rationale, and clinical applications, existing and potential. Int. J. Nanomed. 1, 297–315. ( 10.2217/17435889.1.3.297) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Muller RH, Keck CM. 2004. Challenges and solutions for the delivery of biotech drugs—a review of drug nanocrystal technology and lipid nanoparticles. J. Biotechnol. 113, 151–170. ( 10.1016/j.jbiotec.2004.06.007) [DOI] [PubMed] [Google Scholar]
- 6.Jain RK, Stylianopoulos T. 2010. Delivering nanomedicine to solid tumors. Nat. Rev. Clin. Oncol. 7, 653–664. ( 10.1038/nrclinonc.2010.139) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Narang AS, Chang R-K, Hussain MA. 2013. Pharmaceutical development and regulatory considerations for nanoparticles and nanoparticulate drug delivery systems. J. Pharm. Sci. 102, 3867–3882. ( 10.1002/jps.23691) [DOI] [PubMed] [Google Scholar]
- 8.Li L, Sun J, He Z. 2013. Deep penetration of nanoparticulate drug delivery systems into tumors: challenges and solutions. Curr. Med. Chem. 20, 2881–2891. ( 10.2174/09298673113209990004) [DOI] [PubMed] [Google Scholar]
- 9.Keck CM, Müller RH. 2013. Nanotoxicological classification system (NCS)—a guide for the risk-benefit assessment of nanoparticulate drug delivery systems. Eur. J. Pharm. Biopharm. 84, 445–448. ( 10.1016/j.ejpb.2013.01.001) [DOI] [PubMed] [Google Scholar]
- 10.Leucuta SE. 2013. Systemic and biophase bioavailability and pharmacokinetics of nanoparticulate drug delivery systems. Curr. Drug Deliv. 10, 208–240. ( 10.2174/1567201811310020007) [DOI] [PubMed] [Google Scholar]
- 11.Hobbs SK, Monsky WL, Yuan F, Roberts WG, Griffith L, Torchilin VP, Jain RK. 1998. Regulation of transport pathways in tumor vessels: role of tumor type and microenvironment. Proc. Natl Acad. Sci. USA 95, 4607–4612. ( 10.1073/pnas.95.8.4607) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yuan F, Leunig M, Huang SK, Berk DA, Papahadjopoulos D, Jain RK. 1994. Mirovascular permeability and interstitial penetration of sterically stabilized (stealth) liposomes in a human tumor xenograft. Cancer Res. 54, 3352–3356. [PubMed] [Google Scholar]
- 13.Oltra NS, Nair P, Discher DE. 2014. From stealthy polymersomes and filomicelles to self peptide-nanoparticles for cancer therapy. Annu. Rev. Chem. Biomol. Eng. 5, 281–299. ( 10.1146/annurev-chembioeng-060713-040447) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Prabhu RH, Patravale VB, Joshi MD. 2015. Polymeric nanoparticles for targeted treatment in oncology: current insights. Int. J. Nanomed. 10, 1001–1018. ( 10.2147/IJN.S56932) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nie S. 2010. Understanding and overcoming major barriers in cancer nanomedicine. Nanomedicine (Lond.) 5, 523–528. ( 10.2217/nnm.10.23) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Poon Z, Chang D, Zhao X, Hammond PT. 2011. Layer-by-layer nanoparticles with a pH-sheddable layer for in vivo targeting of tumor hypoxia. ACS Nano 5, 4284–4292. ( 10.1021/nn200876f) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lee ES, Gao Z, Bae YH. 2008. Recent progress in tumor pH targeting nanotechnology. J. Controlled Rel. 132, 164–170. ( 10.1016/j.jconrel.2008.05.003) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bao G, et al. 2014. USNCTAM perspectives on mechanics in medicine. J. R. Soc. Interface 11, 20140301 ( 10.1098/rsif.2014.0301) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Allen TM, Cullis PR. 2004. Drug delivery systems: entering the mainstream. Science 303, 1818–1822. ( 10.1126/science.1095833) [DOI] [PubMed] [Google Scholar]
- 20.Gabizon A, Papahadjopoulos D. 1988. Liposome formulations with prolonged circulation time in blood and enhanced uptake by tumors. Proc. Natl Acad. Sci. USA 85, 6949–6953. ( 10.1073/pnas.85.18.6949) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Torchilin VP. 2005. Recent advances with liposomes as pharmaceutical carriers. Nat. Rev. Drug Disc. 4, 145–160. ( 10.1038/nrd1632) [DOI] [PubMed] [Google Scholar]
- 22.Lazarovits J, Chen YY, Sykes EA, Chan WCW. 2015. Nanoparticle–blood interactions: the implications on solid tumour targeting. Chem. Commun. 51, 2756–2767. ( 10.1039/C4CC07644C) [DOI] [PubMed] [Google Scholar]
- 23.Albanese A, Tang PS, Chan WCW. 2012. The effect of nanoparticle size, shape, and surface chemistry on biological systems. Annu. Rev. Biomed. Eng. 14, 1–16. ( 10.1146/annurev-bioeng-071811-150124) [DOI] [PubMed] [Google Scholar]
- 24.Walkey CD, Chan WCW. 2012. Understanding and controlling the interaction of nanomaterials with proteins in a physiological environment. Chem. Soc. Rev. 41, 2780–2799. ( 10.1039/C1CS15233E) [DOI] [PubMed] [Google Scholar]
- 25.Choi HS, Liu W, Liu F, Nasr K, Misra P, Bawendi MG, Frangioni JV. 2010. Design considerations for tumour-targeted nanoparticles. Nat. Nanotechnol. 5, 42–47. ( 10.1038/nnano.2009.314) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Decuzzi P, Pasqualini R, Arap W, Ferrari M. 2009. Intravascular delivery of particulate systems: does geometry really matter? Pharm. Res. 26, 235–243. ( 10.1007/s11095-008-9697-x) [DOI] [PubMed] [Google Scholar]
- 27.Schmitt-Sody M, Strieth S, Krasnici S, Sauer B, Schulze B, Teifel M, Michaelis U, Naujoks K, Dellian M. 2003. Neovascular targeting therapy paclitaxel encapsulated in cationic liposomes improves antitumoral efficacy. Clin. Cancer Res. 9, 2335–2341. [PubMed] [Google Scholar]
- 28.Li Y, Stroberg W, Lee T-R, Kim HS, Man H, Ho D, Decuzzi P, Liu WK. 2014. Multiscale modeling and uncertainty quantification in nanoparticle-mediated drug/gene delivery. Comput. Mech. 53, 511–537. ( 10.1007/s00466-013-0953-5) [DOI] [Google Scholar]
- 29.Jiang W, Huang Y, An Y, Kim BYS. 2015. Remodeling tumor vasculature to enhance delivery of intermediate-sized nanoparticles. ACS Nano 9, 8689–8696. ( 10.1021/acsnano.5b02028) [DOI] [PubMed] [Google Scholar]
- 30.Zhang S, Gao H, Bao G. 2015. Physical principles of nanoparticle cellular endocytosis. ACS Nano 9, 8655–8671. ( 10.1021/acsnano.5b03184) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tan J, Thomas A, Liu Y. 2012. Influence of red blood cells on nanoparticle targeted delivery in microcirculation. Soft Matter 8, 1934–1946. ( 10.1039/C2SM06391C) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Liu Y, Shah S, Tan J. 2012. Computational modeling of nanoparticle targeted drug delivery. Rev. Nanosci. Nanotechnol. 1, 66–83. ( 10.1166/rnn.2012.1014) [DOI] [Google Scholar]
- 33.Fedosov DA, Fornleitner J, Gompper G. 2012. Margination of white blood cells in microcapillary flow. Phys. Rev. Lett. 108, 028104 ( 10.1103/PhysRevLett.108.028104) [DOI] [PubMed] [Google Scholar]
- 34.Lee S-Y, Ferrari M, Decuzzi P. 2009. Shaping nano-/micro-particles for enhanced vascular interaction in laminar flows. Nanotechnology 20, 495101 ( 10.1088/0957-4484/20/49/495101) [DOI] [PubMed] [Google Scholar]
- 35.Gentile F, Chiappini C, Fine D, Bhavane RC, Peluccio MS, Cheng MM-C, Liu X, Ferrari M, Decuzzi P. 2008. The effect of shape on the margination dynamics of non-neutrally buoyant particles in two-dimensional shear flows. J. Biomech. 41, 2312–2318. ( 10.1016/j.jbiomech.2008.03.021) [DOI] [PubMed] [Google Scholar]
- 36.Firrell JC, Lipowsky HH. 1989. Leukocyte margination and deformation in mesenteric venules of rat. Am. J. Physiol. Heart Circ. Physiol. 256, H1667–H1674. [DOI] [PubMed] [Google Scholar]
- 37.Toy R, Hayden E, Shoup C, Baskaran H, Karathanasis E. 2011. The effects of particle size, density and shape on margination of nanoparticles in microcirculation. Nanotechnology 22, 115101 ( 10.1088/0957-4484/22/11/115101) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Lee T-R, Choi M, Kopacz AM, Yun S-H, Liu WK, Decuzzi P. 2013. On the near-wall accumulation of injectable particles in the microcirculation: smaller is not better. Sci. Rep. 3, 2079 ( 10.1038/srep02079) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Namdee K, Thompson AJ, Charoenphol P, Eniola-Adefeso O. 2013. Margination propensity of vascular-targeted spheres from blood flow in amicrofluidic model of human microvessels. Langmuir 29, 2530–2535. ( 10.1021/la304746p) [DOI] [PubMed] [Google Scholar]
- 40.Charoenphol P, Huang RB, Eniola-Adefeso O. 2010. Potential role of size and hemodynamics in the efficacy of vascular-targeted spherical drug carriers. Biomaterials 31, 1392–1402. ( 10.1016/j.biomaterials.2009.11.007) [DOI] [PubMed] [Google Scholar]
- 41.Tan J, Shah S, Thomas A, Ou-Yang HD, Liu Y. 2013. The influence of size, shape and vessel geometry on nanoparticle distribution. Microfluidics Nanofluidics 14, 77–87. ( 10.1007/s10404-012-1024-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Doshi N, Prabhakarpandian B, Rea-Ramsey A, Pant K, Sundaram S, Mitragotri S. 2010. Flow and adhesion of drug carriers in blood vessels depend on their shape: a study using model synthetic microvascular networks. J. Controlled Rel. 146, 196–200. ( 10.1016/j.jconrel.2010.04.007) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Yuan F, Dellian M, Fukumura D, Leunig M, Berk DA, Torchilin VP, Jain RK. 1995. Vascular permeability in a human tumor xenograft: molecular size dependence and cutoff size. Cancer Res. 55, 3752–3756. [PubMed] [Google Scholar]
- 44.Perrault SD, Walkey C, Jennings T, Fischer HC, Chan WCW. 2009. Mediating tumor targeting efficiency of nanoparticles through design. Nano Lett. 9, 1909–1915. ( 10.1021/nl900031y) [DOI] [PubMed] [Google Scholar]
- 45.Freund JB. 2007. Leukocyte margination in a model microvessel. Phys. Fluids 19, 023301 ( 10.1063/1.2472479) [DOI] [Google Scholar]
- 46.Kumar A, Graham MD. 2012. Margination and segregation in confined flows of blood and other multicomponent suspensions. Soft Matter 8, 10 536–10 548. ( 10.1039/c2sm25943e) [DOI] [PubMed] [Google Scholar]
- 47.Kumar A, Graham MD. 2011. Segregation by membrane rigidity in flowing binary suspensions of elastic capsules. Phys. Rev. E 84, 066316 ( 10.1103/PhysRevE.84.066316) [DOI] [PubMed] [Google Scholar]
- 48.Kumar A, Graham MD. 2012. Mechanism of margination in confined flows of blood and other multicomponent suspensions. Phys. Rev. Lett. 109, 108102 ( 10.1103/PhysRevLett.109.108102) [DOI] [PubMed] [Google Scholar]
- 49.Liu Y, Tan J, Thomas A, Ou-Yang D, Muzykantov VR. 2012. The shape of things to come: importance of design in nanotechnology for drug delivery. Ther. Deliv. 3, 181–194. ( 10.4155/tde.11.156) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Decuzzi P, Ferrari M. 2006. The adhesive strength of non-spherical particles mediated by specific interactions. Biomaterials 27, 5307–5314. ( 10.1016/j.biomaterials.2006.05.024) [DOI] [PubMed] [Google Scholar]
- 51.van de Ven AL, et al. 2012. Rapid tumoritropic accumulation of systemically injected plateloid particles and their biodistribution. J. Controlled Rel. 158, 148–155. ( 10.1016/j.jconrel.2011.10.021) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Merkel TJ, et al. 2011. Using mechanobiological mimicry of red blood cells to extend circulation times of hydrogel microparticles. Proc. Natl Acad. Sci. USA 108, 586–591. ( 10.1073/pnas.1010013108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Wang S, Dormidontova EE. 2010. Nanoparticle design optimization for enhanced targeting: Monte Carlo simulations. Biomacromolecules 11, 1785–1795. ( 10.1021/bm100248e) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Wang S, Dormidontova EE. 2012. Selectivity of ligand-receptor interactions between nanoparticle and cell surfaces. Phys. Rev. Lett. 109, 238102 ( 10.1103/PhysRevLett.109.238102) [DOI] [PubMed] [Google Scholar]
- 55.Liu J, Weller GER, Zern B, Ayyaswamy PS, Eckmann DM, Muzykantov VR, Radhakrishnan R. 2010. Computational model for nanocarrier binding to endothelium validated using in vivo, in vitro, and atomic forcemicroscopy experiments. Proc. Natl Acad. Sci. USA 107, 16 530–16 535. ( 10.1073/pnas.1006611107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Liu J, Agrawal NJ, Calderon A, Ayyaswamy PS, Eckmann DM, Radhakrishnan R. 2011. Multivalent binding of nanocarrier to endothelial cells under shear flow. Biophys. J. 101, 319–326. ( 10.1016/j.bpj.2011.05.063) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Vahidkhah K, Bagchi P. 2015. Microparticle shape effects on margination, near-wall dynamics and adhesion in a three-dimensional simulation of red blood cell suspension. Soft Matter 11, 2097–2109. ( 10.1039/C4SM02686A) [DOI] [PubMed] [Google Scholar]
- 58.Aoyama Y, Kanamori T, Nakai T, Sasaki T, Horiuchi S, Sando S, Niidome T. 2003. Artificial viruses and their application to gene delivery. Size-controlled gene coating with glycocluster nanoparticles. J. Am. Chem. Soc. 125, 3455–3457. ( 10.1021/ja029608t) [DOI] [PubMed] [Google Scholar]
- 59.Osaki F, Kanamori T, Sando S, Sera T, Aoyama Y. 2004. A quantum dot conjugated sugar ball and its cellular uptake on the size effects of endocytosis in the subviral region. J. Am. Chem. Soc. 126, 6520–6521. ( 10.1021/ja048792a) [DOI] [PubMed] [Google Scholar]
- 60.Chithrani BD, Ghazani AA, Chan WCW. 2006. Determining the size and shape dependence of gold nanoparticle uptake into mammalian cells. Nano Lett. 6, 662–668. ( 10.1021/nl052396o) [DOI] [PubMed] [Google Scholar]
- 61.Gratton SEA, Ropp PA, Pohlhaus PD, Luft JC, Madden VJ, Napier ME, DeSimone JM. 2008. The effect of particle design on cellular internalization pathways. Proc. Natl Acad. Sci. USA 105, 11 613–11 618. ( 10.1073/pnas.0801763105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Champion JA, Mitragotri S. 2006. Role of target geometry in phagocytosis. Proc. Natl Acad. Sci. USA 103, 4930–4934. ( 10.1073/pnas.0600997103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gao H, Shi W, Freund LB. 2005. Mechanics of receptor-mediated endocytosis. Proc. Natl Acad. Sci. USA 102, 9469–9474. ( 10.1073/pnas.0503879102) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Decuzzi P, Ferrari M. 2008. The receptor-mediated endocytosis of nonspherical particles. Biophys. J. 94, 3790–3797. ( 10.1529/biophysj.107.120238) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Decuzzi P, Ferrari M. 2007. The role of specific and non-specific interactions in receptor-mediated endocytosis of nanoparticles. Biomaterials 28, 2915–2922. ( 10.1016/j.biomaterials.2007.02.013) [DOI] [PubMed] [Google Scholar]
- 66.Zhang S, Li J, Lykotrafitis G, Bao G, Suresh S. 2009. Size-dependent endocytosis of nanoparticles. Adv. Mater. 21, 419–424. ( 10.1002/adma.200801393) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Huang C, Zhang Y, Yuan H, Gao H, Zhang S. 2013. Role of nanoparticle geometry in endocytosis: laying down to stand up. Nano Lett. 13, 4546–4550. ( 10.1021/nl402628n) [DOI] [PubMed] [Google Scholar]
- 68.Ding H-M, Ma Y-Q. 2015. Theoretical and computational investigations of nanoparticle–biomembrane interactions in cellular delivery. Small 11, 1055–1071. ( 10.1002/smll.201401943) [DOI] [PubMed] [Google Scholar]
- 69.Shi X, von Dem Bussche A, Hurt RH, Kane AB, Gao H. 2011. Cell entry of one-dimensional nanomaterials occurs by tip recognition and rotation. Nat. Nanotechnol. 6, 714–719. ( 10.1038/nnano.2011.151) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Li Y, Yue T, Yang K, Zhang X. 2012. Molecular modeling of the relationship between nanoparticle shape anisotropy and endocytosis kinetics. Biomaterials 33, 4965–4973. ( 10.1016/j.biomaterials.2012.03.044) [DOI] [PubMed] [Google Scholar]
- 71.Li Y, Kröger M, Liu WK. 2015. Shape effect in cellular uptake of pegylated nanoparticles: comparison between sphere, rod, cube and disk. Nanoscale 7, 16 631–16 646. ( 10.1039/C5NR02970H) [DOI] [PubMed] [Google Scholar]
- 72.Wang MD, Shin DM, Simons JW, Nie S. 2007 doi: 10.1586/14737140.7.6.833. Nanotechnology for targeted cancer therapy. Expert Rev. Anticancer Ther. 7 , 833–837. ( ) [DOI] [Google Scholar]
- 73.Huang X, Peng X, Wang Y, Wang Y, Shin DM, El-Sayed MA, Nie S. 2010. A reexamination of active and passive tumor targeting by using rod-shaped gold nanocrystals and covalently conjugated peptide ligands. ACS Nano 4, 5887–5896. ( 10.1021/nn102055s) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Yi X, Shi X, Gao H. 2011. Cellular uptake of elastic nanoparticles. Phys. Rev. Lett. 107, 098101 ( 10.1103/PhysRevLett.107.098101) [DOI] [PubMed] [Google Scholar]
- 75.Li Y, Zhang X, Cao D. 2015. Nanoparticle hardness controls the internalization pathway for drug delivery. Nanoscale 7, 2758–2769. ( 10.1039/C4NR05575F) [DOI] [PubMed] [Google Scholar]
- 76.Sun J, et al. 2015. Tunable rigidity of (polymeric core)–(lipid shell) nanoparticles for regulated cellular uptake. Adv. Mater. 27, 1402–1407. ( 10.1002/adma.201404788) [DOI] [PubMed] [Google Scholar]
- 77.Zhang L, et al. 2015. Microfluidic synthesis of hybrid nanoparticles with controlled lipid layers: understanding flexibility-regulated cell-nanoparticle interaction. ACS Nano 9, 9912–9921. ( 10.1021/acsnano.5b05792) [DOI] [PubMed] [Google Scholar]
- 78.Kopacz AM, Liu WK. 2013. Immersed molecular electrokinetic finite element method. Comput. Mech. 52, 193–199. ( 10.1007/s00466-012-0806-7) [DOI] [Google Scholar]
- 79.Kopacz AM, Patankar NA, Liu WK. 2012. The immersed molecular finite element method. Comput. Methods Appl. Mech. Eng. 233, 28–39. ( 10.1016/j.cma.2012.04.005) [DOI] [Google Scholar]
- 80.Liu WK, et al. 2006. Immersed finite element method and its applications to biological systems. Comput. Methods Appl. Mech. Eng. 195, 1722–1749. ( 10.1016/j.cma.2005.05.049) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Liu Y, Liu WK. 2006. Rheology of red blood cell aggregation by computer simulation. J. Comput. Phys. 220, 139–154. ( 10.1016/j.jcp.2006.05.010) [DOI] [Google Scholar]
- 82.Zhang L, Gerstenberger A, Wang X, Liu WK. 2004. Immersed finite element method. Comput. Methods Appl. Mech. Eng. 193, 2051–2067. ( 10.1016/j.cma.2003.12.044) [DOI] [Google Scholar]
- 83.Liu Y, Zhang L, Wang X, Liu WK. 2004. Coupling of Navier-Stokes equations with protein molecular dynamics and its application to hemodynamics. Int. J. Numer. Methods Fluids 46, 1237–1252. ( 10.1002/fld.798) [DOI] [Google Scholar]
- 84.Gay M, Zhang L, Liu WK. 2006. Stent modeling using immersed finite element method. Comput. Methods Appl. Mech. Eng. 195, 4358–4370. ( 10.1016/j.cma.2005.09.012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Zhang LT, Gay M. 2008. Characterizing left atrial appendage functions in sinus rhythm and atrial fibrillation using computational models. J. Biomech. 41, 2515–2523. ( 10.1016/j.jbiomech.2008.05.012) [DOI] [PubMed] [Google Scholar]
- 86.Liu WK, Tang S, Kim DW. 2007. Mathematical foundations of the immersed finite element method. Comput. Mech. 39, 211–222. ( 10.1007/s00466-005-0018-5) [DOI] [Google Scholar]
- 87.Wang XS, Zhang LT, Liu WK. 2009. On computational issues of immersed finite element methods. J. Comput. Phys. 228, 2535–2551. ( 10.1016/j.jcp.2008.12.012) [DOI] [Google Scholar]
- 88.Kopacz AM, Liu WK, Liu SQ. 2008. Simulation and prediction of endothelial cell adhesion modulated by molecular engineering. Comput. Methods Appl. Mech. Eng. 197, 2340–2352. ( 10.1016/j.cma.2008.01.016) [DOI] [Google Scholar]
- 89.Lee T-R, Greene MS, Jiang Z, Kopacz AM, Decuzzi P, Chen W, Liu WK. 2014. Quantifying uncertainties in the microvascular transport of nanoparticles. Biomech. Model. Mechanobiol. 13, 515–526. ( 10.1007/s10237-013-0513-0) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Kopacz AM, Yeo W-H, Chung J-H, Liu WK. 2012. Nanoscale sensor analysis using the immersed molecular electrokinetic finite element method. Nanoscale 4, 5189–5194. ( 10.1039/c2nr31279d) [DOI] [PubMed] [Google Scholar]
- 91.Liu Y, Liu WK, Belytschko T, Patankar N, To AC, Kopacz A, Chung JH. 2007. Immersed electrokinetic finite element method. Int. J. Numer. Methods Eng. 71, 379–405. ( 10.1002/nme.1941) [DOI] [Google Scholar]
- 92.Yeo W-H, Kopacz AM, Kim J-H, Chen X, Wu J, Gao D, Lee K-H, Liu W-K, Chung J-H. 2012. Dielectrophoretic concentration of low-abundance nanoparticles using a nanostructured tip. Nanotechnology 23, 485707 ( 10.1088/0957-4484/23/48/485707) [DOI] [PubMed] [Google Scholar]
- 93.Liu Y, Chung J-H, Liu WK, Ruoff RS. 2006. Dielectrophoretic assembly of nanowires. J. Phys. Chem. B 110, 14 098–14 106. ( 10.1021/jp061367e) [DOI] [PubMed] [Google Scholar]
- 94.Oh K, Chung J-H, Riley JJ, Liu Y, Liu WK. 2007. Fluid flow-assisted dielectrophoretic assembly of nanowires. Langmuir 23, 11 932–11 940. ( 10.1021/la701755s) [DOI] [PubMed] [Google Scholar]
- 95.Liu Y, Oh K, Bai JG, Chang C-L, Yeo W, Chung J-H, Lee K-H, Liu WK. 2008. Manipulation of nanoparticles and biomolecules by electric field and surface tension. Comput. Methods Appl. Mech. Eng. 197, 2156–2172. ( 10.1016/j.cma.2007.08.012) [DOI] [Google Scholar]
- 96.Tefft BJ, Kopacz AM, Liu WK, Liu SQ. 2015. Enhancement of endothelial cell retention on ePTFE vascular constructs by siRNA-mediated SHP-1 or SHP-2 gene silencing. Cell. Mol. Bioeng. 8, 507–516. ( 10.1007/s12195-015-0392-9) [DOI] [Google Scholar]
- 97.Liu WK, Jun S, Zhang YF. 1995. Reproducing kernel particle methods. Int. J. Numer. Methods Fluids 20, 1081–1106. ( 10.1002/fld.1650200824) [DOI] [Google Scholar]
- 98.Zhang LT, Liu WK, Li SF, Qian D, Hao S. 2003. Survey of multi-scale meshfree particle methods. In Meshfree methods for partial differential equations, pp. 441–457. Berlin, Germany: Springer. [Google Scholar]
- 99.Suresh S, Spatz J, Mills JP, Micoulet A, Dao M, Lim CT, Beil M, Seufferlein T. 2005. Connections between single-cell biomechanics and human disease states: gastrointestinal cancer and malaria. Acta Biomater. 1, 15–30. ( 10.1016/j.actbio.2004.09.001) [DOI] [PubMed] [Google Scholar]
- 100.Neu B, Meiselman HJ. 2002. Depletion-mediated red blood cell aggregation in polymer solutions. Biophys. J. 83, 2482–2490. ( 10.1016/S0006-3495(02)75259-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Neu B, Sowemimo-Coker SO, Meiselman HJ. 2003. Cell-cell affinity of senescent human erythrocytes. Biophys. J. 85, 75–84. ( 10.1016/S0006-3495(03)74456-7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Tran-Son-Tay R, Sutera SP, Rao PR. 1984. Determination of red blood cell membrane viscosity from rheoscopic observations of tank-treading motion. Biophys. J. 46, 65–72. ( 10.1016/S0006-3495(84)83999-5) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Skotheim JM, Secomb TW. 2007. Red blood cells and other nonspherical capsules in shear flow: oscillatory dynamics and the tank-treading-to-tumbling transition. Phys. Rev. Lett. 98, 078301 ( 10.1103/PhysRevLett.98.078301) [DOI] [PubMed] [Google Scholar]
- 104.Pries AR, Secomb TW, Gessner T, Sperandio MB, Gross JF, Gaehtgens P. 1994. Resistance to blood flow in microvessels in vivo. Circ. Res. 75, 904–915. ( 10.1161/01.RES.75.5.904) [DOI] [PubMed] [Google Scholar]
- 105.Maeda N, Suzuki Y, Tanaka J, Tateishi N. 1996. Erythrocyte flow and elasticity of microvessels evaluated by marginal cell-free layer and flow resistance. Am. J. Physiol. Heart Circ. Physiol. 271, H2454–H2461. [DOI] [PubMed] [Google Scholar]
- 106.Kim S, Kong RL, Popel AS, Intaglietta M, Johnson PC. 2007. Temporal and spatial variations of cell-free layer width in arterioles. Am. J. Physiol. Heart Circ. Physiol. 293, H1526–H1535. ( 10.1152/ajpheart.01090.2006) [DOI] [PubMed] [Google Scholar]
- 107.Hoogerbrugge PJ, Koelman JMVA. 1992. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 19, 155–160. ( 10.1209/0295-5075/19/3/001) [DOI] [Google Scholar]
- 108.Groot RD, Warren PB. 1997. Dissipative particle dynamics: bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 107, 4423–4435. ( 10.1063/1.474784) [DOI] [Google Scholar]
- 109.Li Y, Kröger M, Liu WK. 2014. Endocytosis of PEGylated nanoparticles accompanied by structural and free energy changes of the grafted polyethylene glycol. Biomaterials 35, 8467–8478. ( 10.1016/j.biomaterials.2014.06.032) [DOI] [PubMed] [Google Scholar]
- 110.Kim HR, et al. 2007. Low-density lipoprotein receptor-mediated endocytosis of PEGylated nanoparticles in rat brain endothelial cells. Cell. Mol. Life Sci. 64, 356–364. ( 10.1007/s00018-007-6390-x) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Walkey CD, Olsen JB, Guo H, Emili A, Chan WCW. 2012. Nanoparticle size and surface chemistry determine serum protein adsorption and macrophage uptake. J. Am. Chem. Soc. 134, 2139–2147. ( 10.1021/ja2084338) [DOI] [PubMed] [Google Scholar]
- 112.Xia X, Yang M, Wang Y, Zheng Y, Li Q, Chen J, Xia Y. 2011. Quantifying the coverage density of poly(ethylene glycol) chains on the surface of gold nanostructures. ACS Nano 6, 512–522. ( 10.1021/nn2038516) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Tasciotti E, et al. 2008. Mesoporous silicon particles as a multistage delivery system for imaging and therapeutic applications. Nat. Nanotechnol. 3, 151–157. ( 10.1038/nnano.2008.34) [DOI] [PubMed] [Google Scholar]