GeneWise and Genomewise (original) (raw)
Abstract
We present two algorithms in this paper: GeneWise, which predicts gene structure using similar protein sequences, and Genomewise, which provides a gene structure final parse across cDNA- and EST-defined spliced structure. Both algorithms are heavily used by the Ensembl annotation system. The GeneWise algorithm was developed from a principled combination of hidden Markov models (HMMs). Both algorithms are highly accurate and can provide both accurate and complete gene structures when used with the correct evidence.
The Ensembl gene prediction pipeline (Curwen et al. 2004) follows a widespread approach of maximizing the use of experimental evidence of mature mRNA structures to produce accurate gene prediction. There are two streams of evidence for genes: (1) the direct placement of cDNA and EST on the genome of the same species, and (2) the use of evidence from a related gene in another species which is then used as a template for the homologous gene. For both of these cases the pipeline can be divided into two parts; the collection of evidence for a particular transcript, and then the final construction of a valid transcript structure. In the Ensembl pipeline after this transcript-generation phase, the final gene builder rationalizes the usually heavily redundant cDNA and EST set and uses a final set of heuristics to accept or discard different transcripts and form final genes. This paper focuses on the two main tools used in the Ensembl pipeline for detailed generation of transcript structures given evidence: GeneWise for the use of homologous protein sequences as evidence, and Genomewise for the use of EST and cDNA information.
GeneWise is a relatively mature tool with implementations available since 1997 (Birney and Durbin 1997) and has been used in numerous genome projects, both as part of the Ensembl pipeline (The International Human Genome Sequencing Consortium 2001; Aparicio et al. 2002; Waterston et al. 2002) and as a standalone tool (Dehal et al. 2002; Galagan et al. 2003). It has also been assessed by a number of authors (Birney and Durbin 2000; Guigo et al. 2000; Yeh et al. 2001; Meyer and Durbin 2002). However, there has been no paper on the theory by which the GeneWise algorithm was developed, nor details on the precise implementation of aspects of the algorithm. This paper therefore is the first explicit detailing of the method. In contrast, Genomewise is a far newer method, and is only being used in production in the Ensembl system. Genomewise is a far more pragmatic method developed explicitly to solve problems encountered in the Ensembl pipeline; it may or may not prove useful outside of this context.
Both GeneWise and Genomewise were implemented using the dynamic programming language Dynamite (Birney and Durbin 1997) which was written for this use case. Dynamite provides a higher-level language for specifying hidden Markov models (HMMs) and dynamic programming recursions commonly used in sequence analysis, and it provides efficient and bug-free code; this allows us to generate new variations of algorithms quickly with the confidence that all of the mechanics of the code will work flawlessly.
The process of eukaryotic gene prediction is a well understood though by no means solved problem, with many successful algorithms using different approaches. There has been a long history of successful ab initio programs which do not use any additional evidence to predict genes on genomic DNA, of which Genscan (Burge and Karlin 1997) and Fgenesh (Solovyev and Salamov 1997) are two of the most successful cases. In both cases the authors used the HMM framework to provide the parameterization and decoding of a probabilistic model of gene structure (for review, see Zhang 2002). The development of evidenced-based gene prediction can be traced back to the PairWise program (Birney et al. 1996), a forerunner of GeneWise, and a similar approach in concept to GeneWise was developed in Procrustes (Gelfand et al. 1996). In essence, though, GeneWise is a pair-HMM style method, with strong similarities to the more recent dual genome predictors DoubleScan (Meyer and Durbin 2002) and SLAM (Alexandersson et al. 2003). Another class of evidence-based gene prediction programs are ones which use external evidence to influence the scoring of potential exons, including SGP-2 (Parra et al. 2003), Genie (Kulp et al. 1996), Genomescan (Yeh et al. 2001), HMMGene (Krogh 2000), and Fgenesh++ (Solovyev and Salamov 1997). Twinscan (Flicek et al. 2003) takes an “informant” approach to the prediction of genes from two genomes, and multiple genome-prediction machinery is likely to be developed fully from ideas proposed by the Hein group (Pedersen and Hein 2003) and the Haussler (Siepel and Haussler 2003) group. Finally there are pure feature-based programs, which have no inherent probabilistic model or knowledge of the underlying DNA, but provide a framework for the integration of component features which do have knowledge of the DNA sequence, such as GAZE (Howe et al. 2002). Genomewise is more akin to GAZE than other methods, but does integrate a highly simplistic gene model with feature parsing in a novel manner.
Given such a diversity in methods, it is unsurprising that individual bioinformatics groups use a mosaic of different gene prediction methods for different tasks. GeneWise and Genome-wise are used in the Ensembl pipeline because (1) the methods are heavily biased towards high-specificity predictions— effectively neither method will predict exons outside of the available evidence for them; (2) both methods are focused on producing transcript structures which have valid protein coding products on the genome sequence; (3) the methods are robustly implemented, and finally (4) as the program writer for GeneWise and Genomewise was part of the broader Ensembl team, we were able to have a fast-feedback loop for bugs and feature additions. As such we do not claim in any way that GeneWise and Genome-wise are the last word in metozoan gene prediction, but rather that they are useful programs for the final detailed transcript prediction from experimental evidence.
RESULTS
GeneWise Theory
GeneWise solves the problem of taking a single protein sequence or HMM and comparing it directly to genomic DNA, taking into account the known statistical properties of gene structures and the presence of sequencing error. One could build classical dynamic programming recursions representing this process by hand, as was done in the PairWise (Birney et al. 1996) method and Est2Genome (Mott 1997), but this seemed to us an overly specific approach. Instead we took a more abstract stance at first, noticing that both the alignment process of two protein sequences and the process of predicting a protein-coding gene structure could be well represented as HMMs. If it was possible to formally combine the sequential application of two HMMs into a single method, then we would have a general process of producing a combined algorithm for any HMM model of gene structure and any HMM model of alignment. For the rest of this discussion we explicitly use pair-HMMs, which are HMMs that convert one sequence of letters to another, that is, alignment-style HMMs (also known as transducing grammars or Probabilistic Finite State Machines).
Consider two pair-HMMs S and T, where S maps a sequence of letters from the alphabet A to a sequence of letters from the alphabet B, and T maps letters from B to C. To help understand the process, for the case of GeneWise, A is the genomic sequence, B its predicted protein sequence, and C is the homologous protein sequence which is being used to guide the gene prediction. Figure 1 provides a pictorial illustration of the merging process, which will merge the S (gene prediction) and T (protein comparison) HMMs into a single HMM. The following notation is used to describe the pair-HMMs.
Figure 1.
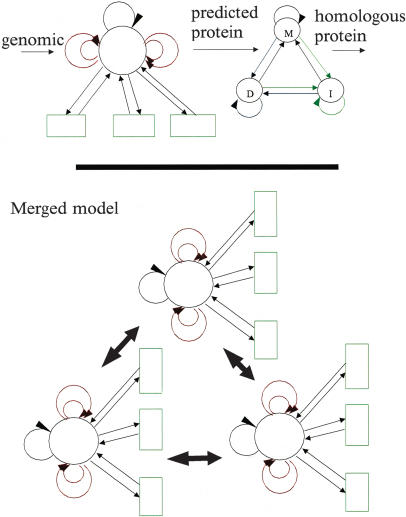
The merging process between the gene prediction model and the homology model (written out in the top panel) and the merged model (lower panel). The large black arrows indicate that between each set of four states, all possible transitions exist. This model will be later pruned to a small set of states: See the text for more details.
S has states 1...ns. The transition from state i to state j, emitting a finite string of letters a in one sequence and b in another sequence has probability Sijab. a is a finite string of letters drawn from the alphabet A with 0 representing a non-emitting spacer. b is a single letter drawn from the alphabet B with the additional string 0 representing a non-emitting spacer. There is a requirement for b to be a single letter to allow the merging process to work. Similarly the T pair-HMM is defined with states 1...nt, and the probability of the transition k to l emitting a single b and any finite length of c letters is Tklbc.
We wish to construct the state machine U which will map a sequence of A letters to a sequence of C letters, considering all possible sequences of B intermediates. We propose that U has nsnt states, each of which can be characterized by a pair of states in each of the original machines. i and j will be used for state index from the S machine, and k and l as the state indexes from the T machine. Thus the transition U(i,k)(j,l)ac is the transition from the state (i,k) in U derived from i in S and k in T to the state (j,l) derived from j and l states respectively, emitting a in one sequence and c in another sequence. We need to construct the definitions of the probability for each of these transitions in U in terms of the transitions defined in S and T. The following equations provide that definition (δ_ij_ being 1 if i = j and 0 if i ≠ j).
For neither a nor c being 0
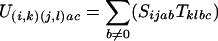 |
1 |
|---|
For a being 0 but not c
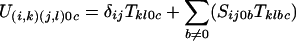 |
2 |
|---|
For c being 0 but not a
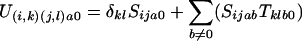 |
3 |
|---|
Equation 1 sums over all possible b intermediates for this transition, using the underlying transitions from the S and T machines. The two other cases are when no letter is generated for one of the sequences. In each case the blank could have been generated from either S or the T machines. For the case of generating a blank in the a stream of letters, if it was generated by the S machine, then that means that there is an intermediate b sequence which has to account for the c string. However, if the blank was generated by the T machine, then there is no possible b letter, and furthermore this case can only occur when the transition remains silent in the S machine index (hence the δ_ij_). The symmetrical argument applies for c emitting 0. We need not worry ourselves about the case when S emits an a,0 pair and T emits a 0,c pair, as this contains no b sequence, and so is not permitted.
The requirement that the two machines emit at most a single b letter per transition is so that we can do the summations in equations 1, 2, and 3 over all b. If b was longer than a single letter, it would be possible to have the S machine produce a b string which was out of phase with the b string that the T machine would produce. We can see no clean way to provide the derivative U machine transitions in this case. One could claim that longer b strings could be allowed as long as the two machines were emitting “in-phase” strings, but this simply means that there is a new alphabet, _B_′ where each “in-phase” string is mapped to a single _b_′ letter.
Notice that the U machine represents a sort of model “product” of S and T. This means that for even modestly sized machines, the product will be quite large. However the combined machine allows us to ignore the identity of intermediate sequences in standard calculations of, for example, the likelihood of two sequences, A and C being generated by the combined machine, and the most likely path through both S and T. The additional bulk of the combined machine is easily justified when one considers the alternative of listing all possible B sequences which, depending on the architecture of the machine, might in fact be infinite.
This theory has been built up for first-order HMMs. Extending this theory to higher-order HMMs is easy, as one can use the fact that any HMM can be represented as a first-order HMM at the cost of more states in the machine. This provides us with a principled way of combining any two machines. However, notice that the expansion of a nonfirst-order machine to a first-order machine is also a “product”-type operation. If one does want to merge two nonfirst-order machines, the number of states required to model all of the independent paths through each machine will rapidly become impractical.
The GeneWise model was created to be the integration of two separate models, a gene prediction model and a protein homology model, using the ideas outlined above. The genomic sequence is equivalent to the A sequence, the predicted protein sequence of the gene is the B sequence, and the homologous protein sequence to which it is being compared to is C. The aim is to compare genomic sequence directly to the homologous protein sequence considering all possible intermediates of the predicted protein.
To be able to use the model combination theory effectively, high-order Markov dependencies must be removed from the two models. The protein model, which is a probabilistic Smith-Waterman model, is 0th order and is conceptually identical to the profile-HMM models used in HMMER (Eddy 1998). This Match, Insert, and Delete model has three states with seven transitions. Gene prediction models, however, are generally of a higher order, and it this model which has simplifications to make the merging process achievable. There are two approximations made to make the model usable. First, amino acids which are split by introns are ignored. This is similar to what happens in most gene prediction programs, which make the same approximation to avoid having a high-order Markov dependency. Second, high-order Markov dependencies in the coding sequence model are shortened. Most gene prediction programs use fifth-order Markov chains to model coding regions, whereas we use a simpler model that emits triplets (equivalent in some sense to a second-order Markov chain). This has the nice feature that there is a simple mapping to the letters of the intermediate sequence, the predicted protein, fulfilling the requirement that b is a single letter.
The gene prediction model is similar to the Genscan-style HMM but simpler. It has a single state representing exons which emits a series of independent codons. The intron states are differentiated by which phase the intron occurs in (phase being the place in the codon which the intron interrupts). For phase 1 and phase 2 introns, the fact that this interrupts a codon is ignored, and is not scored. Each intron is considered to be made from five sections: the 5′ splice site, a central intron section, a poly-pyrimidine tract, a spacer following the poly-pyrimidine tract, and the 3′ splice site. As the 5′ and 3′ splice sites are considered to be ungapped motifs, they can be represented by single transitions which “emit” 10 or six base pairs, respectively.
Given these two models, the combination using the rules outlined above is simple. The combined model should have 10×3 states, expanding each homology model state into 10 separate gene-finding states. This process is shown pictorially in Figure 1. However, not all of these states are actually required in the comparison, as we know that some transitions are forced to zero. This is because it is impossible to get an intermediate protein sequence letter with no genomic DNA sequence: in other words, the combination 0_b_ in the previous notation does not occur. Applying this to equation 2 means that we can remove a number of states.
Because transitions which emit 0_c_ are all directed to the “Delete” state of the homology model, this means that all the transitions which are directed to the intron states of the delete state in the combined model have probability zero, as i_≠_j for these states. The result is that we can remove them. This is intuitively correct, as the Delete-state models positions in the homologous protein sequence which have no sequence in its protein counterpart. With no protein sequence in the predicted protein, there is no possibility of an intron at this position. Notice that the Delete state still has transitions to the Match and Insert introns, as these transitions do emit a protein sequence.
The inter-intron transitions can also be removed. The intron states all have transitions which emit _a_0, producing genomic sequence with no corresponding protein sequence. For these transitions the sum in equation 3 is zero, as all the transitions ab,b_≠0 are zero. The other, δ_kl term is also zero, as movement between different introns implies k_≠_l. Again this marries well with the observation that one cannot change from being in a “Match” intron to an “Insert” intron in the middle of an intron.
The pruned model, called GeneWise 21:93, is shown in Figure 2. The name reflects the number of states (21) and number of transitions (93) used in the model.
Figure 2.
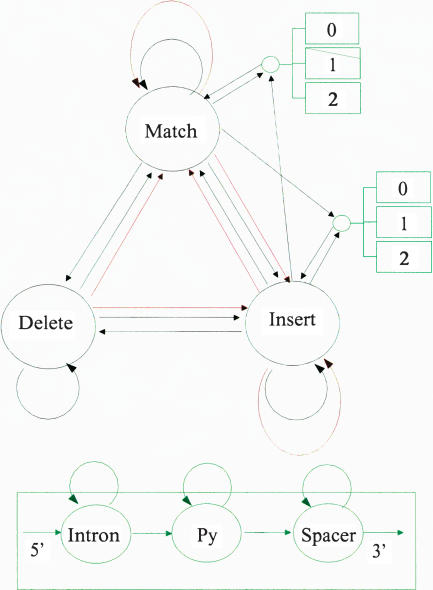
The GeneWise21:93 algorithm. The circles represent states, and the arrows between them transitions. Black transitions are standard protein transitions, red transitions are frameshifting transitions, and green transitions are intronic transitions. Introns are each built of three states, listed at the bottom of the figure.
It was clear from the start of this work that GeneWise21:93 was an overly ambitious model, and probably not useful for practical work. Using Dynamite we experimented with a number of different machines, and a good compromise between speed and sensitivity was achieved with the GeneWise6:23 model, shown in Figure 3. Compared to the GeneWise21:93 model, the differences are:
Figure 3.
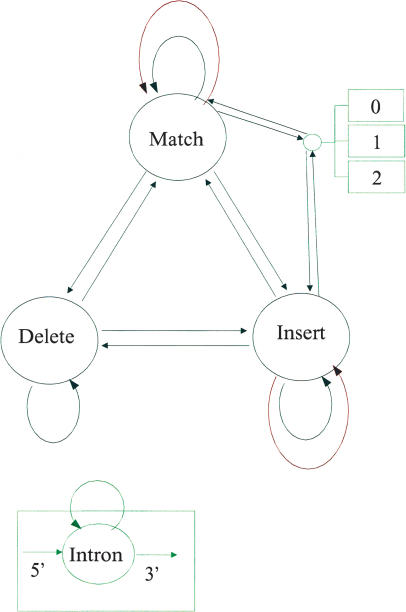
The GeneWise6:23 algorithm. The circles and rectangles represent states, and the arrows between them transitions. For simplicity the three intron states are gathered into one node; in each case there is a unique transition state from either Match or Insert into each of the intron states (each state representing a different phase).
- The poly-pyrimidine states are removed, providing a saving of 12 states and 36 transitions.
- The Match/Insert information is lost in the introns. This means that for the cases where a Match to Insert or Insert to Match transition occurs in the protein in the same position as an intron, it will not be scored correctly. As both introns and Match/Insert switches are rare, this should not be a significant problem.
- The sequencing error transitions are removed from the Match/Insert and Delete to Match and Delete to Insert transitions. This means that sequencing error which falls at a switch in the protein state will not be modeled, and will probably occur a base pair before or after the real position.
Heavy use of the GeneWise6:23 model has shown excellent results (see below), and has become the workhorse for GeneWise methods. We have tried even further reductions in GeneWise4: 21, in which the different phases of the introns were merged into a single state, resulting in only four states and 21 transitions, but this has not been as widely used.
Parameterization
We expected most of the power of this method to come from the application of accurate protein profile-HMMs to the gene prediction model (i.e., the protein homology model would force the gene model to take certain parses as the gene prediction was a better fit to the protein homology). The gene model would only be used to provide good edge detection of exons, principally splice sites. Therefore the approach was to take the established profile HMMs from Sean Eddy's HMMER (Eddy 1998) package for the protein homology model. When we used a single sequence, not a profile HMM, we parameterized it as if it was a protein profile HMM, providing parameters deduced from the standard Smith-Waterman parameters routinely used. For the gene model, we wanted to make it simple. The approach was to make maximum likelihood estimates of the fixed length motifs of the splice sites from known splice sites, and parameterize almost all the rest of the gene model as if it was background.
The emissions of codons in the Match and Insert transitions in the model are due to three different effects: (1) the amino acid distribution of the protein homology model, (2) the codon bias of the organism, and (3) the substitution of the base pairs due to possible sequencing error.
We considered this process to be the transformation of the vector of 20 amino acid probabilities in the homology model to the 64 possible codons. The codon probability given a particular amino acid is decomposed as coming from two possibilities:
- There was no substitution error, in which case the probability is 0 for codons which are not translated to this amino acid, or P(codon|aminoacid) for the codon bias in this organism.
- There was a substitution error, meaning that the observed codon is actually a different codon in the real DNA sequence. In this case, we considered every possible single base pair substitution, but not double substitutions inside one codon.
Due to every possible base being substituted, in most cases this means that codons combine information from a number of different amino acid positions. The effect of the substitution error therefore is to smudge out the amino acid distribution over a number of different codons, mainly the ones which encoded the amino acid, but also “nearby” codons, which are related by a single sequencing error. An upshot of this is that stop codons do have some small probability associated with them, but this probability is greater when the homology positions are more likely to emit amino acids which are a single base substitution away. For example, strong tryptophan-emitting positions (codon TGG) have a relatively large chance of matching TAG and TGA stop codons, compared to other positions. Default parameters for substitution error was one error in 10,000 base pairs, the quoted accuracy for genome sequencing projects.
Insertion or Deletion Errors
GeneWise's approach to handling insertion or deletion errors in the sequencing process is deliberately naive. This is because handling the insertion/deletion errors correctly is difficult. When one considers the theory outlined above, it would be attractive to consider sequencing error to be the action of another machine, which substitutes, inserts, or deletes bases of the DNA sequence before it is used in the gene prediction process. This unfortunately breaks the rule that the intermediate B sequence as protein is only emitted as single bases, and one would need to expand the homology machines into base pair-aware machines, using the fact that any N-order Markov chain (in this case second order) can be represented by a 0-order machine. This complete resulting HMM would have an impressive 70 states and 837 transitions in each protein unit. Effectively most of the transitions would be modeling the combination of a sequencing error and an intron occurring in the same codon, or two independent sequencing errors occurring. As well as being highly unlikely, the parameterization of the transitions means that most combinations are going to have almost indistinguishable likelihoods, and that the most likely path through such multiple events will be arbitrary.
Instead, GeneWise considers sequencing error to be a 1-, 2-, 4-, or 5-base codon. The base composition of the deletion or insertion is ignored completely, which is a gross approximation. For example, if one observes a TTTT in a putative sequencing error, a strong phenalanine-emitting position (codon TTT) is a far more likely position to emit this than Glycine (codon GGN). Ignoring the base composition was really to prevent excessive calculation. Deriving the potential probability for base deletions is relatively easy to do, as one is considering only one or two bases, and one can build a look-up table for each position of all combinations. However, one cannot take this approach for four or five base pairs, as the tables become too large. An alternative is to call a function which would on-the-fly calculate the probability of a four- or five-base pair insertion of particular bases to a probability distribution of amino acids. However such a function would be called at every cell in the dynamic programming matrix, making it an extremely expensive solution.
Flanking Regions
One issue we did not account for at first were the flanking regions of genomic DNA outside of a homology region that we were interested in predicting. These regions could of course contain genes, either as part of the gene we wished to predict which was outside the region of homology, or entirely different genes. These genes might not have any similarity to the protein homology model we were using, but they do have gene features which would score well against the gene prediction portion of the GeneWise model. These additional fragments often caused mispredictions at the end of the homology region. In particular, if the homology region ended near an intron, as introns have a very broad length distribution, GeneWise could ignore the correct end of the intron and simply choose the best start or end splice site respectively for the start or end of the region within the rest of the sequence. For large clones, this gave rise to “stretched” gene predictions which spanned almost the entire length of the clone. They would start with a first very large intron leaving at the best 5′ splice site in the clone, joining to the homology region and continuing to near the end of the homology region when another large intron would jump to the best 3′ splice site in the remainder of the DNA sequence. Unsurprisingly, the biologists who saw these early results were not impressed.
The solution is to somehow make the flanking regions less attractive to the homology model. The most principled way of doing this is to provide flanking models which represent the content of genomic DNA in the absence of the homology model. These regions would then score at least as highly as a homology + gene prediction model in the absence of homology, and in general much better, causing the homology model to be kept in its correct place. The most natural way to build the flanking models is to duplicate the gene prediction model in the absence of the homology model. This is what was done in the Gene-Wise21:93 model.
A major drawback to this approach is that now every genomic DNA will score well against this model, even if the genomic DNA does not contain a gene with homology to a particular HMM or protein sequence. Thus using this model for the detection of the presence of homology requires the path information of where the most likely path went through the model, in particular if it crossed into the homology part of the larger, complete model of both flanking regions and homology model. Ideally one also wants the likelihood score of just the homology portion. Although there are ways to computationally achieve this without requiring the calculation of the entire path, it is an additional computational step in an already expensive operation.
For GeneWise6:23 we provided the reverse solution, by toning down the gene prediction parts of the model so that any potential benefit of producing an erroneous intron would be more than outweighed by the additional penalties for misaligning a homology region. As GeneWise6:23 does not have a poly-pyrimidine tract model, a considerable gene prediction signal is removed. In addition, no intronic bias (where the base composition of the intron is different from the intergenic DNA sequence) was provided. The only remaining gene signals were the actual splice sites, and in tests, these were not sufficient to cause this error in practical use.
An additional parameterization problem related to the flanking regions was how to score the start and end of the homology sequence. By analogy to protein alignments, the default is to have protein sequences behave in a “local” manner, with start and end transitions from every protein position, and profile-HMMs using the built-in start/end transitions provided in the model. In both cases however these can be overridden. In addition, two other modes were provided. For profile-HMMs, a relatively common occurrence was to have somewhat poorly defined edges to the profile-HMM, which in protein alignments harmlessly match the adjoining regions to a well conserved protein domain. However in GeneWise, when such poorly defined regions are in the profile-HMM in a global mode, the algorithm can optimize the placement of these columns to large DNA sequences, giving rise again to stretched gene predictions with excessive first and last intron sizes. A “wing” mode, which allows starts in any of the first five positions and ends in any of the last five positions, gives more freedom for marginally truncating the profile-HMM without losing the strong constraint that the core domain must be matched. The second mode is for the opposite case in close protein sequence matching, where it is hoped that the homologous sequence stretches from start to end of the target gene. However, because the edges of sequences are often less well conserved, interruption by an intron compounds the challenge of matching these tail regions. The endbias mode attempts to correct this by rewarding matches that account for all of the homologous sequence. This idea is extended even further by the algorithm 623S, which has additional pure ab initio states at the two tail regions, modeling the start codon to start of homology and the end of homology to stop codon. This is a relatively new algorithm which is currently undergoing testing; we expect this to work well in genomes such as Anopheles gambiae and C. briggsae where terminal exons are longer and so the homology match is far more likely to have a trivial extension to find valid starts and stops.
GeneWise Results
To assess Genewise, we took 500 human transcripts from separate genes which had a protein sequence identical throughout its amino acid sequence to a human SWISS-PROT or RefSeq protein; we assumed due to this perfect identity that the spliced structure was correct. We then found sequences in SWISS-PROT/SPTREMBL that matched the protein sequence in different similarity bands—55%–65% identical, 65%–75% identical, 75%–85% identical, and 85%–95% identical. In each case the protein was used with GeneWise6:23 to predict the gene model, and the resulting structure was assessed with reference to the human gene, using common criteria of specificity and sensitivity at the base pair, exon overlap, and exact exon level (this follows the standard conventions for assessing gene prediction accuracy; see, e.g., Guigo et al. 2000). The results are shown in Table 1. As GeneWise only predicts where there is similarity evidence, the fact that the terminal exons of the prediction do not extend to the start or end (respectively) on the exon is expected. Therefore the terminal exons were not used in the calculation of exact exon specificity, though they were included for the overlap statistics.
Table 1.
The Specificity and Sensitivity for GeneWise Predictions Made With Different Classes of Similarity Data
| Similarity | Exon spec. | Base spec. | Wrong exon | Exon sens. (exact) | Exon sens. (over) | Base sens. |
|---|---|---|---|---|---|---|
| 85-95, Long | 92.8 | 97.2 | 3.4 | 75.2 | 95.8 | 98.2 |
| 85-85 | 90.1 | 96.4 | 4.8 | 40.2 | 58.4 | 51.3 |
| 75-85 | 81.8 | 88.8 | 9.1 | 41.4 | 62.2 | 55.8 |
| 65-75 | 76.5 | 94.0 | 11.6 | 36.1 | 56.9 | 46.7 |
| 55-65 | 72.9 | 87.6 | 18.1 | 34.5 | 53.2 | 44.7 |
As expected, Genewise has a outstanding record in specificity with base pair specificity from 87% when distant sequences are used, up to 96% when close sequences are employed. Compared to the ab initio predictors (Genscan quoted here as an exemplar), the specificity levels are considerably better, as one would expect. What seems far more of concern is the low sensitivity of GeneWise. However, this is not directly a function of the method but rather a consequence of the protein sequences used to build the gene models. The homologous proteins often either naturally have only a small portion which aligns or are artificially truncated due to the high number of fragments in the protein database. When we restricted the protein sequences used as models to those which were both in the 85%–95% similarity band and have alignments to the human protein that stretch to within 20 amino acids of the termini of the protein, the sensitivity increases from ∼60% to 98% (on the exon overlap statistic).
No matter which similarity class is used, there is a stubborn residual set of “wrong” exons, that is, predicted exons which were not present in the human gene. We examined a number of these by hand. The main explanation seemed to be low-complexity sequences (e.g., polyglycine) possibly combining with alternative splicing through such regions, where there was more than one candidate human exon with a corresponding low-complexity region. Other examples were clearly explained by conserved alternative splicing (e.g., a mouse transcript predicting an alternative exon conserved between human and mouse). However there were a large number of complex cases where there was no obvious explanation of the pattern; perhaps clone errors in the similar gene's cDNA, for example leading to a short random run of amino acids that is then arbitrarily placed by Gene-Wise in the DNA sequence.
Genomewise
Genomewise was written to solve the problem of parsing a final gene structure from a set of overlapping EST or cDNA fragments which have already been aligned to the genome. This problem at first sight looks trivial, as the only problem is to assign start and stop codons to the longest open reading frame in the set of exons. However, there are two minor issues that make the problem more challenging. First, errors in either the EST or genome sequencing can throw off EST alignments, in particular close to splice junctions due to “edge wander” of the introns (Holmes and Durbin 1998). This can result in the erroneous alignment making a frameshift in the coding region, with catastrophic results in trying to find the correct open reading frame. A second problem is that often ESTs extend only partially into exons, and, when such matches are close they clearly delineate the exon without actually overlapping.
This problem is solved in Genomewise by having a simple HMM-like model of transcript structure, with 5′ UTR, coding regions, and 3′ UTR states, each potentially interrupted by introns. In the case of the coding exon, three possible introns (representing the three possible phases of relative placement of intron with respect to the codon) are modeled to provide the maintenance of the open reading frame. This model is then dragged over a number of different “strands” of evidence, each evidence strand providing a putative, partial transcript structure of exons and introns, and generally coming from cDNA or EST evidence. The model can switch between any different evidence strands at any position at some cost, the “switching” penalty (but must remain within the same model state), and progression along the DNA strand is scored with respect to the model. The model is not allowed to progress in the intron or UTR states without evidence, but can progress in the coding exon state without evidence. As the coding exon heavily penalizes stop codons, this “unconstrained” gene model can only continue through open reading frames between evidence-based exons.
Genomewise's parameterization is with raw numbers generated by trial and error—a pragmatic though not very rigorous approach. Current parameters are +10 for every non-stop codon amino acid, -1000 for a stop codon, and -20 for each switch. Splice sites are +30 for each splice site taken precisely at the same point as the evidence, and -30 for splice sites taken within three base pairs of them. It is this “smell space” splice site which allows Genomewise to fix slightly erroneous splice site positions. Assessing Genomewise is problematic, as it is a “finishing” gene prediction tool that finds the final ATG to stop signals inside a series of exon structures. Table 2 shows the performance of Genomewise parsing as more (artifical) splice-site positioning error is introduced into otherwise perfect gene structures. As the table shows, Genomewise is able to “fix” small splice site errors, but as the error in splice-site positioning grows it loses the ability to find the right splice site just due to reading frame constraints. This is particularly true for small exons, where often more than one reading frame will be open.
Table 2.
The Sensitivity (Number of Correct Bases) of Genomewise Parsers Through Correct Gene Structures With Differing Levels of Error Introduced at the Positioning of Splice Sites
| Error | 0% | 1% | 2% | 5% | 10% |
|---|---|---|---|---|---|
| Base | 99.7% | 99.7% | 99.2% | 98.6% | 94.2% |
| Exon | 97.4% | 97.4% | 94.8% | 92.1% | 89.1% |
DISCUSSION
GeneWise and Genomewise both adhere to the Ensembl perspective of high-specificity gene prediction at the expense of some loss of sensitivity; this is most dramatically illustrated by the progressive loss of coverage by GeneWise for lower-similarity genes with virtually no loss in accuracy; this is the classic trade-off between sensitivity and specificity at the exon level, and in GeneWise we have chosen to emphasize specificity. However, this decision to stress the specificity must be put in the context where we can choose whichever protein sequence from the many available in the protein databases, and so for genomes which are reasonably close to a well studied genome (with extensive cDNA or manual annotation), GeneWise can provide highly accurate and sensitive predictions. For example, in the mouse genome over 80% of the genes have a protein of at least 85% similarity. The main drawback is in terminal exons, which often have short coding regions (there are, for example, a significant number of genes where the initial methionine is adjacent or even split by the end splice site of the exon). This terminal exon problem is partially mitigated by the endbias option to reward alignments which extend to the start and end of the provided protein sequence, and furthermore by the “stretch” algorithm which extends terminal exons to find Met and STOP signals. It is worth noting that the ability to model frameshifts has also been an important aspect for GeneWise; tolerance towards errors has allowed GeneWise to be used in many phases of genome analysis and also provides a tool to investigate pseudogene structure, as has been used by Torrance and Bork (e.g., Hillier et al. 2003).
GeneWise has been the workhorse of much of the final prediction in Ensembl and elsewhere, and as such is a robust and well tested solution. We expect to be making small improvements to the GeneWise method, but the core system is unlikely to change. One major drawback for using GeneWise is its large computational cost. As described by Curwen et al. (2004), this has been solved by using the miniseq system. More improvements in speed are likely to come from systems such as the Exonerate framework (G. Slater, unpubl.), which provide a formal way to integrate heuristic-based speed-ups with any formal pair-HMM-like model.
In theory, GeneWise could also be used to enhance the sensitivity of gene prediction when used with profile-HMMs on “distant” genomes. This is because the important signal aspects of a profile HMM might be split across exons, and so only a combined gene prediction and HMM model will have the power to detect such genes. This approach has not been tested yet, mainly because there are currently only a few genomes where such “deep homology” is required; usually there is a closer protein sequence which makes a far better “homology model” than the deeper HMM model for that particular gene. However, with the advent of deeper sequencing in the metozoan and broader eukaryotic tree, this approach might become useful. One clear confounding factor will be degrading pseudogenes, which will have a lingering homology signal similar to such distantly similar genes.
Genomewise, as mentioned in the introduction, is a far more pragmatic program with dramatically fewer users than GeneWise. One can certainly imagine many uses for Genomewise in helping to combine different evidence types into gene structures, and the code has been deliberately written to be flexible and allow different “plug-ins” of models.
Finally we would like to stress that both GeneWise and Genomewise are used in the final “polishing” stage of gene prediction. Despite the rather elaborate justification of the GeneWise model detailed in this paper, overall by far the more complex aspect of gene prediction is knowing which algorithm to call with which piece of evidence. Given a protein highly similar to a particular gene, there are likely to be many good enough solutions to predicting its gene structure. The pragmatic decision-making for Ensembl is detailed in the Gene Prediction paper by Curwen et al. (2004), and is where the majority of the decisions for gene structure are made.
Acknowledgments
Ensembl is principally funded by the Wellcome Trust, with additional funding from EMBL and NIH-NIAID. A large portion of this work was completed when E.B. was funded by the Wellcome Trust Prize Studentship scheme. We thank the Ensembl team for their help during the development of these algorithms, in particular Val Curwen, Steve Searle, and Eduardo Eyras. We also thank Mor Amatai, Ian Holmes, and David Kulp for helpful discussions during the development of these methods.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.1865504.
References
- Alexandersson, M., Cawley, S., and Pachter, L. 2003. SLAM: Cross-species gene finding and alignment with a generalized pair hidden Markov model. Genome Res. 13**:** 496-502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aparicio, S., Chapman, J., Stupka, E., Putnam, N., Chia, J.-M., Dehal, P., Christoffels, A., Rash, S., Hoon, S., Smit, A., et al. 2002. Whole-genome shotgun assembly and analysis of the genome of Fugu rubripes. Science 297**:** 1301-1310. [DOI] [PubMed] [Google Scholar]
- Birney, E. and Durbin, R. 1997. Dynamite: A flexible code generating language for dynamic programming methods used in sequence comparison. ISMB 97**:** 56-64. [PubMed] [Google Scholar]
- Birney, E. and Durbin, R. 2000. Using GeneWise in the Drosophila annotation experiment. Genome Res. 10**:** 547-548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birney, E., Thompson, J.D., and Gibson, T.J. 1996. Pairwise and searchwise: Comparison of a protein profile to all three translation frames simultaneously. Nucleic Acids Res. 24**:** 2730-2739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burge, C. and Karlin, S. 1997. Prediction of complete gene structures in human genomic DNA. J. Mol. Biol. 268**:** 78-94. [DOI] [PubMed] [Google Scholar]
- Curwen, V., Eyras, E., Andrews, D., Clarke, L., Mongin, E., Searle, S., and Clamp, M. 2004. The ensembl automatic gene annotation system. Genome Res. (this issue). [DOI] [PMC free article] [PubMed]
- Dehal, P., Satou, Y., Campbell, R.K., Chapman, J., Degnan, B., De Tomaso, A., Davidson, B., Di Gregorio, A., Gelpke, M., Goodstein, D.M., et al. 2002. The draft genome of Ciona intestinalis: Insights into chordate and vertebrate origins. Science 298**:** 2157-2167. [DOI] [PubMed] [Google Scholar]
- Eddy, S.R. 1998. Profile hidden Markov models. Bioinformatics 14**:** 755-763. [DOI] [PubMed] [Google Scholar]
- Flicek, P., Keibler, E., Hu, P., Korf, I., and Brent, M.R. 2003. Leveraging the mouse genome for gene prediction in human: From whole-genome shotgun reads to a global synteny map. Genome Res. 13**:** 46-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galagan, J.E., Calvo, S.E., Borkovich, K.A., Selker, E.U., Read, N.D., Jaffe, D., FitzHugh, W., Ma, L.-J., Smirnov, S., Purcell, S., et al. 2003. The genome sequence of the filamentous fungus Neurospora crassa. Nature 422**:** 859-868. [DOI] [PubMed] [Google Scholar]
- Gelfand, M.S., Mironov, A.A., and Pevzner, P.A. 1996. Gene recognition via spliced sequence alignment. Proc. Natl. Acad. Sci. 93**:** 9061-9066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guigo, R., Agarwal, P., Abril, J.F., Burset, M., and Fickett, J.W. 2000. An assessment of gene prediction accuracy in large DNA sequences. Genome Res. 10**:** 1631-1642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hillier, L.W., Fulton, R.S., Fulton, L.A., Graves, T.A., Pepin, K.H., Wagner-McPherson, C., Layman, D., Maas, J., Jaeger, S., Walker, R., et al. 2003. The DNA sequence of human chromosome 7. Nature 424**:** 157-164. [DOI] [PubMed] [Google Scholar]
- Holmes, I. and Durbin, R. 1998. Dynamic programming alignment accuracy. J. Comp. Biol. 5**:** 493-504. [DOI] [PubMed] [Google Scholar]
- Howe, K.L., Chothia, T., and Durbin, R. 2002. GAZE: A generic framework for the integration of gene-prediction data by dynamic programming. Genome Res. 12**:** 1418-1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The International Human Genome Sequencing Consortium 2001. Initial sequencing and analysis of the human genome. Nature 409**:** 860-921. [DOI] [PubMed] [Google Scholar]
- Krogh, A. 2000. Using database matches with HMMGene for automated gene detection in Drosophila. Genome Res. 10**:** 523-528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulp, D., Haussler, D., Reese, M.G., and Eeckman, F.H. 1996. A generalized hidden Markov model for the recognition of human genes in DNA. In Proceedings of the fourth international conference on intelligent systems for molecular biology (eds. D.J. States et al.), pp. 134-142. AAAI Press, Menlo Park, CA. [PubMed]
- Meyer, I.M. and Durbin, R. 2002. Comparative ab initio prediction of gene structures using pair HMMs. Bioinformatics 18**:** 1309-1318. Evaluation Studies. [DOI] [PubMed] [Google Scholar]
- Mott, R. 1997. EST_GENOME: A program to align spliced DNA sequences to unspliced genomic DNA. Comp. Appl. Biosci. 13**:** 477-478. [DOI] [PubMed] [Google Scholar]
- Parra, G., Agarwal, P., Abril, J.F., Wiehe, T., Fickett, J.W., and Guigo, R. 2003. Comparative gene prediction in human and mouse. Genome Res. 13**:** 108-117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedersen, J.S. and Hein, J. 2003. Gene finding with a hidden Markov model of genome structure and evolution. Bioinformatics 19**:** 219-227. [DOI] [PubMed] [Google Scholar]
- Siepel, A. and Haussler, D. 2003. Combining phylogenetic and hidden markov models in biosequence analysis. In Proceedings of the seventh annual international conference on research in computational biology (RECOMB'03) 277-286. [DOI] [PubMed]
- Solovyev, V.V. and Salamov, A.A.S. 1997. The Gene-Finder computer tools for analysis of human and model organisms genome sequences. ISMB 97**:** 294-302. [PubMed] [Google Scholar]
- Waterston, R.H., Lindblad-Toh, K., Birney, E., Rogers, J., Abril, J.F., Agarwal, P., Agarwala, R., Ainscough, R., Alexandersson, M., An, P. et al. 2002. Initial sequencing and comparative analysis of the mouse genome. Nature 420**:** 520-562. [DOI] [PubMed] [Google Scholar]
- Yeh, R.F., Lim, L.P., and Burge, C.B. 2001. Computational inference of homologous gene structures in the human genome. Genome Res. 11**:** 803-816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang, M.Q. 2002. Computational prediction of eukaryotic protein-coding genes. Nat. Rev. Genet. 3**:** 698-709. [DOI] [PubMed] [Google Scholar]